Introduction

Reconstructing complex network from time series has been widely applied to characterize nonlinear dynamic behavior in a time-dependent system from the observed time series. Typically, scholars detect the dynamic features from single time series or the relationships between two different time series1,2,3,4. However, in a real complicated system, there are usually more than one or two time series which intertwine and interact with each other. The evolution of the interaction behavior between multivariate time series can help us to uncover the hidden dynamic interaction information. For coping with the increased complexity, new complex network methods are required to transfer the evolution of the time-varying relationships of multivariate time series to a complex network and to explore the underlying evolution mechanism affected by the multi-information fusion5.

Previous studies, in the last decade, have witnessed the success and effectiveness of complex network in analyzing nonlinear characteristics of time series in many fields, such as engineering, management, economic and biology6,7,8,9,10,11,12,13. Zhang and Small first proposed that univariate time series can be transformed to networks14. Lacasa et al. proposed the visibility graph algorithm to abstract the time point in time series to simple patterns and relationship15. It provided a new perspective for research on the complexity of time series by turning time series into graphs. Moreover, Gao et al. developed a novel multiscale limited penetrable horizontal visibility graph (MLPHVG) to analyze nonlinear time series16. Meanwhile, the concept of coarse graining in the phase space is widely used to describe the fluctuation of time series. After the coarse graining process, the volatility patterns of time series are expressed as modes. An et al. studied the complexity of the autocorrelation modes of univariate time series17. Based on the concept of the modes, Gao et al. built models and analyzed the volatility modes of the comovement and the cross-correlation between bivariate time series1, 3. Recently, some studies gradually focus on analyzing multivariate time series by taking the correlations or distances between time series as the relationship sets18,19,20,21.

Based on existing contributions above, there is still a big challenge to uncover the richer dynamic information in the fluctuation of inner relationships of multivariate time series. The correlation and distance between time series only reflect limited information. It is necessary to find a more appropriate and rigorous method to define the relationship between time series. In certain fields, like economics and neuroscience, Granger causality test has been widely used to measure the relationships between time series22,23,24,25. One of the advantages of Granger causality test is that it can statistically measure the extent to which one time series explains the change of another time series in the future26,27,28, and detect the directed links between time series. The most existing works focus on the long-term causality between time series, ignoring the dynamic adjustment mechanism of short-term fluctuation toward to the long-term equilibrium28,29,30,31. Recently, some studies developed various time-varying causality methods to investigate the dynamical linkages between some economic variables, such as stock market and exchange rate, spot and futures crude oil prices, and crude oil and stock markets32,33,34,35,36. However, these researches still essentially analyzed the causalities between bivariate time series, lacking the systematic perspective to uncover the hidden dynamic interaction information between multivariate time series, and to understand the evolution mechanism of the complicated system.

In this paper, we define the two-dimensional matrix which contains all causalities between any two time series as the causality patterns. If a time series is divided into several fragments (sub-periods), the causality pattern of time series in the long term can be described by the union by all the short-term causality patterns in sub-periods. The evolution of the causality patterns forms a time-varying process of transition, which can help us learn the fluctuation of the relationships between time series. In the process of transition, there are different types of causality patterns that convert to each other and form a multivariate time-varying causality transition network, which will reveal the structure characteristics of the evolutionary behavior of the relationships between multivariate time series.

The main purpose of this paper is to propose a novel network model to detect the nonlinear dynamic features from the evolution behavior of the time-varying causalities between multivariate time series. First, we test the short-term causalities between any two time series and map the transition behavior of the causality patterns into the network. Then, we study the transition characteristics of the causality patterns using the complex network analytical approach, including the distribution of the causality patterns, the transition patterns and the clustering effect in the transition process.

Network Model

The Granger causality test

The Granger causality test was proposed by Clive W. J. Granger37. For given stationary time series x(t), the autoregressive model is given by:

$$x(t)=\sum _{i=1}^{m}{\alpha }_{i}x(t-i)+{\varepsilon }_{x}(t)$$
(1)

ε x (t) denotes the residual error and m denotes the lag intervals for x(t). Now we suppose we have another stationary time series y(t). If x(t) is influenced by both the past value from y(t) and itself, the model can be given by:

$$x(t)=\sum _{i=1}^{p}{\alpha }_{i}x(t-i)+\sum _{j=1}^{q}{\beta }_{i}y(t-j)+{\varepsilon }_{x|y}(t)$$
(2)

It forms a vector autoregression model around x(t). p is the lag length of x(t) and q is the lag length of y(t). In this paper, we use the Bayesian Information Criterion (BIC) to automatically select p and q. If x(t) is influenced by both the past value from y(t) and itself, we can set a null hypothesis: H 0 = β 1 = β 2 = …… = β m  = 0, which means y(t) does not Granger cause x(t). To test this hypothesis, we can use the homogeneity test of variances as follows:

$$F=\frac{(RS{S}_{r}-RS{S}_{u})/q}{RS{S}_{u}/(T-p-q-1)} \sim F(q,T-p-q-1)$$
(3)

RSS t is the residual sum of squares without the lagged variable y(t). RSS u is the residual sum of squares with the lagged variable y(t). T denotes the sample size.

If \(F\ge {F}_{\alpha }(q,\,T-p-q-1)\), we reject the null hypothesis, which means y(t) Granger causes x(t). In this paper, we choose the significance level α = 0.05 as the causality threshold to determine the causality among time series. It means if p value, which can be calculated according to F-statistic, ≤ 0.05, y(t) Granger causes x(t).

The construction of the multivariate time-varying causality transition network

To obtain the time-varying Granger causality between time series, we use the sliding window to divide time series into several sub-periods. Compared with dividing time series into different individual time periods, the advantage of sliding window is that they contain the features of memory and transitivity1, 17, 38. In this paper, the length of a sliding window should satisfy three conditions: (1) Data in each sub-period should be stationary, which is one of the precondition of Granger causality test. (2) The length of sliding windows should serve the needs of the analysis1, 3, 4. If the goal is to study the transition characteristics of the causality patterns in the short term, the length can be set to a smaller value. If the goal is to understand the transition characteristics in the long term, the length can be set to a larger value. (3) The diversity of the causality patterns and transitions among them should be guaranteed. As we know, with the increase in the length of sliding windows, data in the sub-period will be more similar to the original time series.

Let w represents the length of a sliding window. First, we choose day t as start point and get sub-period t , which is from day t to day t + (w − 1). Then, we choose day t + 1 as start point and get sub-period t+1 which is from day t + 1 to day t + (w - 1 + 1). By that analogy, we can obtain a series of sub-periods. Next, we construct the multivariate time-varying causality transition network following three steps.

Step 1: Defining the Granger causality between any two time series. In a sub-period, we test the Granger causality between any two time series. If time series j Granger causes time series i, GC ij  = 1. If time series j does not Granger cause time series i, GC ij  = 0.

$$G{C}_{ij}=\{\begin{array}{l}1,\,j\,Grangers\,Cause\,i\,\\ 0,\,j\,doesn\mbox{'}t\,Granger\,Cause\,i\end{array}$$
(4)

Step 2: Defining the causality patterns. After determining the Granger causality between any two time series, the Granger causalities of all pairs of time series form a n × n matrix.

$$GC{M}_{t}=[\begin{array}{ccc}G{C}_{11}(t) & \cdots & G{C}_{1n}(t)\\ \vdots & \ddots & \vdots \\ G{C}_{n1}(t) & \ldots & G{C}_{nn}(t)\end{array}]$$
(5)

In this paper, we choose four time series, so n = 4. Although previous studies found that time series can be predicted by its own past (self-entropy)39, 40, however, our method is mainly to analyze the evolution process of the interactions between different time series, so we don’t include the causality between a time series and itself in this paper. Thus, the Granger Causality matrix can be shown in Table 1.

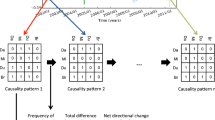
Table 1 The 4 × 4 Granger Causality Matrix.
Full size table

To better represent the Granger causality among time series as the causality patterns, we can turn the matrix into an expression. For example, if GC ij  = 1, it means time series j Granger causes time series i and can be signified as i(j). Then if the existing Granger causalities in a sub-period are S2(S1,S4) and S3(S1,S4), the causality pattern would be represented as P(S2(S1,S4), S3(S1,S4)) (Fig. 1).

Figure 1
figure 1

The definition of the causality patterns.

Full size image

Step 3: Constructing the multivariate time-varying causality transition network. As the sliding windows move, we obtain a series of causality patterns. One causality pattern is converted to another as time goes by: pattern 1 → pattern 2 → pattern 3 → …… → pattern n (n = T − w + 1). Because the conversion between two types of causality patterns would repeat in the transition process, the trajectory of the conversion among causality patterns forms a network. To map the transition network, we take the causality patterns as nodes and the succeeding sequence relations between the causality patterns as edges. The weight of an edge is the frequency of the transition between two types of causality patterns. The process of building the multivariate time-varying causality transition network is shown in Fig. 2.

Figure 2
figure 2

Schematic illustration of constructing the multivariate time-varying causality transition network.

Full size image

Sample data

In this paper, we focus on the relationships between multivariate time series. As the precondition of our work, there should be the theoretical and realistic relationships between time series. Based on this, we choose four real time series to study the transition behavior of the causality patterns from the international oil market. They are the West Texas Intermediate spot price (W), the Brent spot price (B), the Dubai spot price (D) and the Minas spot price (M). These four international crude oil benchmark prices are authoritative in the international oil market and represent four oil market in different regions41. The cointegration or causal relationships between them have been studied from different perspectives by other scholars32, 42. We use the daily price because the shock transmission among oil prices is very fast. The data cover the period from January 2, 2003 to December 31, 2015.

P t denotes the daily closing price of crude oil on day t. The daily price return of crude oil is calculated as follows:

$${r}_{t}=\,\mathrm{ln}({P}_{t})-\,\mathrm{ln}({P}_{t-1})$$
(6)

The results of the stationarity tests of the returns of four oil prices are shown in Table 2.

Table 2 Results of the stationarity tests.
Full size table

Results

Statistical features of the transition process

Before constructing the multivariate time-varying causality transition network, we do the sensitivity analysis to select the appropriate length of sliding window. With the increasing of the length of the sliding window, it can be seen in Fig. 3(a) that the number of nodes and edges both decrease, while the densities of networks increase and the average path length of networks decrease (Fig. 3(b)). Combining the results of the sensitivity analysis with the three conditions we have discussed above, in this paper, we set the size of a sliding window for 50 days. We also choose other 3 kinds of length of sliding window, i.e., 100 days, 500 days and 1000 days, to analyze the dynamic features of the multivariate time-varying causality transition process, please see the detail in the Supplementary Information.

Figure 3
figure 3

Sensitivity analysis. (a) Number of nodes and edges for different lengths of sliding window. (b) The density of networks and the average path length for different lengths of sliding window.

Full size image

In the full period, the Granger causalities existing in four time series (Brent spot price, Dubai spot price, Minas spot price, WTI spot price) are B(W), D(B,M,W) and M(B,W), which means that W Ganger causes B; B, M and W Granger cause D; and B and W Granger cause M (Table 3). The results make us understand the Granger causality among the international benchmark oil prices in the long term. Time series change over time, however, so the relationships between time series also change over time.

Table 3 The Granger Causality Matrix in the full period.
Full size table

After constructing the multivariate time-varying causality transition network, we obtain 230 nodes and 1021 edges. Each node represents a causality pattern. Therefore, there are 230 types of causality patterns in the selected period of data. With the help of the sliding windows, we divide the time series into 3032 fragments, meaning that there should be 3032 causality patterns. However, there are only 230 types of causality patterns in the network. The number of the edges (1021) in actuality is also much fewer than the number (3031) in theory. Thus, the evolution of the time-varying causalities between different time series has some characteristics of complexity including concentricity, repetitiveness and regression.

The key causality patterns in the transition process

To recognize the key causality patterns in the transition process, we use the weighted degree to measure the importance of causality patterns. The weighted degree is a comprehensive index to measure the importance of the nodes which considers not only the number of its adjacent nodes but also the weight connecting to its adjacent nodes. Weighted degree is calculated as follows:

$${w}_{i}={w}_{i}^{in}+{w}_{i}^{out}=\sum _{j\in {N}_{i}}{w}_{ji}+\sum _{j\in {N}_{i}}{w}_{ij}$$
(7)

N i denotes the set of the nodes connecting to node i. w ij denotes the weight of the edge from node j to node i. w ij denotes the weight of the edge from node i to node j. As we defined, we take the frequency of the transition between two types of causality patterns as the weight of an edge.

Weighted degree of the nodes obeys power law distribution \(p(w) \sim {w}^{-\lambda }\) (Fig. 4(a)). This means there are a few key causality patterns in the network. The cumulative distribution of the nodes’ weighted degree shows that 20% of the nodes shoulder 85% of the weight (Fig. 4(b)). This implies that a few types of causality patterns play a major role in the process of the transition and that international crude oil market is statistically significantly not random. The oscillations of the market are driven by a few types of causality patterns. After ranking the nodes by weighted degree, we can recognize the key causality patterns (Table 4). Comparing to the long-term causality pattern P(B(W), D(B,M,W), M(B,W)), some long-term causalities don’t appear statistically frequently in some periods, like D(M). Meanwhile, there are some short-term causalities which aren’t the significant causalities in the long term, like B(W). Due to the competition among different oil producing regions, the production and supply in different regions would have influence on each other. The massive and varying market information affect the market all the time. Thus, the state of the market would not keep exactly same with that in the long term. Recognizing the special short term causalities can provide the useful information to keep the decisions more dynamical and well-adapted.

Figure 4
figure 4

The distribution of the weighted degree.

Full size image
Table 4 Top 10 causality patterns and their weighted degree in the dynamic Granger causality network.
Full size table

The transition patterns in the transition process

After recognizing the key causality patterns in the transition process, we find that a complete transition unit consists of not only nodes but also edges between nodes. A basic transition unit, which can be called the transition pattern, should contain two nodes and their edge: \({T}_{ij}=\{patter{n}_{i},patter{n}_{j}\}\). T ij represents the transition process by which pattern i converts to pattern j . Different transition patterns superimpose together and form the complete transition process. In this paper, we divided time series into 3032 fragments, so there are 3021 transition patterns theoretically. However, there are only 1021 weighted and directed edges in actuality. According to Fig. 5, the distribution of the weight of the transition patterns follows power law. Thus, a few certain key transition patterns exit in the transition process. These phenomena show that the transition among causality patterns is not a random process while it follows the rules in which the transition process is controlled by some key causality patterns. More specifically, these key causality patterns tend to convert to themselves. For example, P(B(W),D(B,W),M(B,W)) → P(B(W),D(B,W),M(B,W)).

Figure 5
figure 5

The distribution of weight of edges.

Full size image

As shown in Fig. 6, the key causality patterns have many transition objects. It means that the key causality patterns convert to several causality patterns including themselves. However, only a few transition objects have high transition probability. The transition object of a key causality pattern which has the highest transition probability is the key causality pattern itself. Other causality patterns tend to convert to these key causality patterns and these key causality patterns tend to convert to themselves. Thus, a few key causality patterns have important regulating effect in the transition process and induce the transition process to show the characteristics of the regression. In other words, the key causality patterns can control the randomness of the transition process.

Figure 6
figure 6

The transition probabilities of the key causality patterns. We choose the edges with weight > 1.

Full size image

The clustering effect in the transition process

Based on the study of the key causality patterns, we found that some causality patterns convert to each other more frequently rather than converting to other causality patterns. This phenomenon makes some causality patterns and their relations form some clusters. The causality patterns in a cluster connect relatively closely to each other, so each cluster represents a special transition type. The analysis of clusters can provide some reference information for predicting the development of the relationship among time series. Blondel provided an algorithm to divide the network into clusters accurately and efficiently43. The algorithm is based on modularity in the networks44 (For details on the algorithm of dividing clusters, please see ref. 38). Applying the algorithm, we divide the network into 14 clusters. The amount of the nodes among the three clusters accounts for 68.69%. Therefore, the three clusters are the main clusters that can represent the entire network (Fig. 7).

Figure 7
figure 7

The clustering effect in the multivariate time-varying causality transition network. Note: red-cluster 1(31.3%), yellow-cluster 2(20%), blue-cluster 3(17.39%).

Full size image

One cluster has different transition ability to different clusters. The transition ability from cluster m to cluster n can be calculated as1: \(T{A}_{mn}=\sum _{i\in m,\,j\in n}{w}_{ij}\), where w ij is the weight from node i to node j. The distribution of the transition abilities between any two clusters is shown in Fig. 8. According to the distribution of the transition abilities, the transition abilities in one cluster are larger than the transition abilities between two different clusters, which proves that the cluster partition is effective. The clusters are independent and represent different transition types of the causality patterns.

Figure 8
figure 8

The distribution of transition abilities among the clusters.

Full size image

Extracting the three major clusters from the multivariate time-varying causality transition network, each cluster forms one sub network (Fig. 9). Analyzing the structure of three sub networks can help us understand the characteristics of three major clusters. According to Table 5, cluster 1 has the most nodes and edges. Cluster 2 has fewer nodes and edges than cluster 1. Cluster 3 has the least nodes and edges. It means there are many causality patterns and they frequently convert to each other in cluster 1. In cluster 3, there are both fewer causality patterns and conversion among the causality patterns. The average path length of cluster 2 is the shortest but the average clustering coefficient is the largest. It means the network structure of cluster 2 is the tightest. On the contrary, the average path length of cluster 3 is the longest while the average clustering coefficient is the smallest. It means the network structure of cluster 3 is loosest. Thus, the transition of the causality patterns is multidirectional and unpredictable in cluster 2 whereas the transition of the causality patterns in cluster 3 is the chain transition that has a certain direction.

Figure 9
figure 9

The three sub networks formed by three major clusters.

Full size image
Table 5 The structure characteristics of three major clusters.
Full size table

The distribution of the transition process among the causality patterns in the three major clusters over time is shown in Fig. 10. According to Fig. 10, the causality patterns cluster at time 1600, time 2500 and time 3000 in cluster 1. The distribution of the causality patterns in cluster 2 is denser than that in cluster 1. Considering that nodes in cluster 2 are less than that in cluster 1, the causality patterns convert to others more frequently in cluster 2. The distribution of the causality patterns in cluster 3 is relatively sparse and clusters at time 300, time 2100, time 2400 and time 2700.

Figure 10
figure 10

The distribution of the causality patterns in three major clusters over time.

Full size image

Discussion and Conclusion

In this paper, our major aim is to explore the evolution characteristics of the time-varying relationships between multivariate time series by transferring the dynamic relationship transition behavior to complex network. We firstly tested the short-term causalities between any two time series and defined the causality pattern which can describe the causalities between multivariate time series. Then, we transformed the transitions between causality patterns to complex network. We analyzed the structure characteristics of the multivariate time-varying causality transition network to understand the dynamic behavior of the fluctuation of the relationships between multivariate time series, including the distribution of the causality patterns, the transition patterns and the clustering effect in the transition process.

In this paper, we chose four crude oil prices as the sample data. The results showed that the method is helpful to find the evolution features of the structure of the international crude oil market. First, the method can recognize a few key causality patterns in the transition process. These statistically frequent causality patterns reflected the main states of market. Some short-term relationships between different time series, which were caused by complicated information from outside environment, should be equally concerned, although they may not appear in the long term. Second, the method can recognize the key causality patterns which had important regulating effect in the transition process. When other causality patterns converted to these key causality patterns, they tended to convert to themselves rather than other causality patterns. It means that the key causality patterns can control the randomness of the transition process. This feature has important value for investors and decision makers to predict the next state of the international oil market. For example, if the present causality pattern is the key causality patterns, such as P(B(W),D(B,W),M(B,W)) and P(D(B,W),M(B,W)), the next causality pattern would likely be itself. Third, the method can recognize the clustering effect in the transition process. Different clusters showed the inside special structures which had important reference value for predicting the development of the causality among time series. For example, the transition of the causality patterns in cluster 3 was the chain transition but exhibited strong uncertainty in cluster 2. It means if the present causality pattern is in cluster 3, investors and decision makers can refer to the historical path of the fluctuation of short-term causality; if the present causality pattern is in cluster 2, we must prepare several coping strategies (Fig. 9).

To judge the applicability of the proposed method, we have added some simulated experiments and done the additional analysis. By contrast with realistic system, random time series with the lengths as the oil prices were generated following the random walk process. We also generated white noise series with the lengths as the oil prices. To make the time series more general, we respectively generated three groups of four dimensional random time series and three groups of four dimensional white noise series. Both random time series and white noise series represent the simulated system. The analysis of the realistic system and the simulated system were both made based on typological structure indexes of time-varying causality transition network (Table 6). The results showed that there are significant differences between the realistic network and the simulated networks. Realistic network had more nodes and edges. This means the evolution of the relationships between real time series has more diversities, which are caused by the complicated factors in the real world. The modularity class of the realistic network was much higher than the simulated networks. This means the clustering effect is more significant in the evolution of the relationships between real time series. The density, the average clustering coefficient and the average path length showed that nodes connect to each other more tightly in the stochastic networks, which also means the evolution of the relationships between simulated time series has less diversities. These results indicated that the proposed method can reliably uncover the hidden information in the evolution process of the relationship between the real time series, which doesn’t exist in the simulated system.

Table 6 The network structure characteristics of the realistic network and the stochastic network.
Full size table

Moreover, we have done the additional analysis to examine the effect of causality thresholds and the length of data. Except the significance level 0.05 in our paper, we chose the significance level 0.01 and 0.1 to determine the causality among time series. Also, we chose different length of data, which respectively covered 3 years (2013–2015), 6 years (2010–2015) and 9 years (2007–2015), to build the multivariate time-varying causality transition networks. All results indicated that the transitions of the causality patterns exhibit similar characteristics. See the details in the Supplementary Information.

The main research purpose of this study is to break the limit of the existing research on univariate time series and bivariate time series and examine the transition behavior of the causality among multivariable time series. The running of a system can be influenced by other systems, however, and the reality is more complex. We will focus on the interaction on different systems in the future research so that we can investigate the inner rules in the entire system. Meanwhile, our method mainly aims to analyze the evolution of the relationships between certain important time series. With the increase of the number of time series, the relationship structures between time series will become more and more complicated. As a result of lacking the same relation patterns at different time, it will be difficult to transfer the evolution of the relation patterns to a network. The results of this paper show that the present method is effective if we study the evolution of the relationships between a few time series. In our future work, we will improve the method and make it more effective when considering more time series into the models.