Introduction

Since the discovery of the graphene, two-dimensional (2D) materials have generated significant interests in recent year1,2,3. Their amazing physics has inspired extensive research on van der Waals (VDW) bonded heterostructures and application-oriented configurations. VDW bonded magnetic materials are of great interest as building blocks for heterostructures in spin-based information technologies4, 5. For example, it has been indicated that the application of VDW magnetic materials in data storage technology could result in several-order of magnitude increase in the recording densities6.

For the practical application, the ideal VDW bonded magnetic material should maintain its ferromagnetism upon exfoliating down to single layer and must have a high Curie temperature (T C ). Within this context, Fe3GeTe2, a VDW metallic ferromagnet, has recently attracted significant attention due to its high Curie temperature and the prediction of the important coexistence of ferromagnetic (FM) and metallic properties upon exfoliating down to nanosheets7, 8.

Fe3GeTe2 is a layered material which belongs to the P63/mmc space group7. It contains Fe3Ge slabs separated by VDW bonded Te layers. The Fe atoms occupy two inequivalent Wyckoff positions, one situated in a hexagonal net in a layer with only Fe atoms and the other covalently bounded in an adjacent layer9. Fe3GeTe2 undergoes a paramagnetic (PM)-FM transition with the Curie temperature as high as 220 K7. Electronic correlations and quantum fluctuations have been found to be crucial in determining the magnetism in this compound10. In order to understand the nature of the magnetic phase transition in detail, we have investigated its critical behavior, expecting the universality class to which the material belongs to give important clues. It is found that the obtained set of exponents does not belong to any single universality class but lies between 3D Heisenberg model and mean field model. The magnetic exchange distance is found to decay as J(r) ≈ r −4.6, which is close to that of mean-field model (r −4.5) with long-range interaction.

Results and Discussion

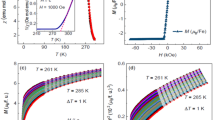
Figure 1(a) shows the temperature dependence of magnetization M(T) for Fe3GeTe2 under zero-field-cooling and field-cooling with an applied field of 1000 Oe. An abrupt PM-FM transition can be observed to occur near 220 K. The inset of Fig. 1(a) gives the isothermal magnetization M(H) at 2 K, which exhibits a typical FM ordering behavior. These results are in good agreement with previous reports11. Figure 1(b) and (c) show the isothermal magnetization data around T C and its Arrott plot, respectively12. A positive slope is clearly observed in the Arrott plot, indicating the second-order nature of the PM-FM transition13. However, all lines are not parallel to each other, suggesting that Landau mean-field model is not valid for Fe3GeTe2 and a modified Arrott plot should be used.

Figure 1
figure 1

(a) Temperature dependence of magnetization M(T) for Fe3GeTe2 under H = 1000 Oe, the inset shows the isothermal magnetization M(H) at 2 K. (b) Initial magnetization M-H and (c) Arrott plots M 2 vs H/M around T C for Fe3GeTe2.

Full size image

The modified Arrott plot (MAP) was then employed to figure out the proper values of critical exponents. For a set of appropriate exponents, the modified Arrott plot should be a series of parallel lines in the high field region with the same slope of S(T) = dM 1/β /d(H/M)1/γ. To obtain an appropriate starting point, we first use four three-dimensional (3D) models, the 3D-Heisenberg model (β = 0.365, γ = 1.336), 3D-XY model (β = 0.345, γ = 1.316), 3D-Ising model (β = 0.325, γ = 1.24), and tricritical mean-field model (β = 0.25, γ = 1.0) to make MAP14, 15. As shown in Fig. 2(a–d), quasi-straight lines are observed in the high field region for all these plots. It can be seen that the lines in Fig. 2(d) are not parallel to each other, suggesting that the tricritical mean-field model is not appropriate to describe the critical behavior of Fe3GeTe2. However, all lines in Fig. 2(a–c) are almost parallel to each other.

Figure 2
figure 2

The isotherms of M 1/β vs.(H/M)1/γ with (a) 3D-Heisenberg model, (b) 3D-XY model, (c) 3D-Ising model and (d) tricritical mean-field model.

Full size image

According to the scaling hypothesis16, the spontaneous magnetization M S (T) below T C , the inverse initial susceptibility χ 0 −1(T) above T C and magnetization M at T C can be described with the following mathematical definitions:

$${M}_{S}(T)={M}_{0}{(-\varepsilon )}^{\beta },\varepsilon < 0,T < {T}_{C}$$
(1)
$${{\chi }_{0}}^{-1}(T)=({h}_{0}/{m}_{0}){\varepsilon }^{\gamma },\varepsilon > 0,T > {T}_{C}$$
(2)
$$M=D{H}^{1/\sigma },\varepsilon =0,T={T}_{C}$$
(3)

where ε = (T − T C )/T C is the reduced temperature; M 0 , h 0 /m 0 and D are the critical amplitudes, respectively.

In order to obtain the proper values of β and γ for Fe3GeTe2, a rigorous iterative method was further adopted17. The starting values of M S (T) and χ 0 −1(T) are determined from the high field data in 3D-Ising model following Eqs (1) and (2). The obtained new values of β and γ are then used to figure out new MAP. It should be mentioned that while fitting the straight lines, the free parameter critical temperature T C is varied to get the best fitting results. This process is repeated until the iterations converge. After doing this exercise, the stable values of exponents, β = 0.324 ± 0.002 and γ = 1.071 ± 0.005, have been obtained (shown in Fig. 3(a)). It is noted that at low field region, the replotted isotherms are slightly curved as they represent averaging over domains magnetized in different directions16. Nevertheless, in high field region, there is a set of good reasonably good parallel straight lines. Moreover, the isotherm is found to pass through the origin at 215.0 K, which is the critical temperature T C of Fe3GeTe2. To check which model is the most suitable one, we have calculated the normalized slope NS = S(T)/S(T C ) and compared them with the ideal value NS = 118, which is shown in Fig. 3(b). For the description of the critical behavior of Fe3GeTe2, the MAP generated by the set of exponents obtained in the iterative method is supreme over other theoretical models. For T > T C NS of 3D-XY model is close to unity, while for T < T C the 3D-Ising model is the best. This indicates that the critical behavior of Fe3GeTe2 may not belong to a single universality class.

Figure 3
figure 3

(a) Modified Arrott plot of isotherms with β = 0.324 and γ = 1.071 for Fe3GeTe2. (b) Normalized slopes (NS = S(T)/S(T C )) as a function of temperature with five sets of critical exponents for Fe3GeTe2.

Full size image

The finally obtained M S (T) and χ 0 −1(T) are plotted as a function of temperature in Fig. 4(a). Using the values of M S (T) and χ 0 −1(T), Eq. (1) gives β = 0.327 ± 0.003, T C  = 215.10 ± 0.02 K and Eq. (2) gives γ = 1.079 ± 0.005, T C  = 215.15 ± 0.08 K, respectively. This estimated critical exponents and T C are reasonably close to the values obtained from the MAP in Fig. 3(a). We use the Kouvel-Fisher (KF) technique to get a further check of the critical exponents and T C 19. According to KF method, M S (dM S /dT)−1 and χ 0 −1(dχ 0 −1 /dT)−1 plotted against temperature should be straight lines with slope 1/β and 1/γ, respectively. As shown in Fig. 4(b), the linear fits to the data yield β = 0.322 ± 0.004, T C  = 215.06 ± 0.10 K and γ = 1.063 ± 0.008, T C  = 215.23 ± 0.14 K. The values of critical exponents and T C calculated using both MAP and KF plot match reasonably well (see Table 1), suggesting that the obtained values are unambiguous. The difference between these values give an estimate of the uncertainties on these values.

Figure 4
figure 4

(a) Temperature dependence of M S and χ 0 −1 for Fe3GeTe2 with the fitting solid curves. (b) Kouvel-Fisher plot of M S (dM S /dT)−1 and χ 0 −1(dχ 0 −1 /dT)−1 for Fe3GeTe2 with the fitting solid curves.

Full size image
Table 1 Comparison of critical exponents of Fe3GeTe2, CrSiTe3 and CrGeTe3 with different theoretical models.
Full size table

Figure 5 shows the isothermal magnetization M(H) at T C  = 215.0 K, with the inset plotted on a log-log scale. According to Eq. (3), the M(H) at the critical temperature should be a straight line on the log-log scale with the slope 1/δ. Such a fitting yield δ = 4.261 ± 0.009. Using the Widom scaling relation δ = 1 + γ/β with the values of β and γ determined from the MAP and KF plot16, we obtain δ = 4.300 ± 0.045 and δ = 4.301 ± 0.065, respectively, which agree well with the critical isothermal analysis. These results prove that the obtained critical exponents are reliable and accurate within experimental precision.

Figure 5
figure 5

Isothermal M(H) at T C with the inset plane on log-log scale for Fe3GeTe2 (the solid line is fitted).

Full size image

It is important to check whether the obtained critical exponents and T C can generate a scaling equation of state for this system. According to the scaling hypothesis, in the asymptotic critical region, the magnetic equation is written as22:

$$M(H,\varepsilon )={\varepsilon }^{\beta }{f}_{\pm }(H/{\varepsilon }^{\beta +\gamma })$$
(4)

where f + for T > T C and f − for T < T C , respectively, are the regular functions. Therefore, the renormalized magnetization m = ε −β M(H, ε) versus h = ε −(β+γ) H should follow two universal rules: one for T < T C and the other for T > T C . As shown in Fig. 6(a,b), all data collapse into two different curves: one below T C and another above T C , indicating that the interactions get properly renormalized in critical regime following scaling equation of state.

Figure 6
figure 6

Scaling plots of renormalized magnetization m vs renormalized field h (a) below and (b) above the critical temperature for Fe3GeTe2.

Full size image

The critical exponents of Fe3GeTe2 obtained in this study, along with those of theoretical models are summarized in Table 1. It is seen that the obtained exponents cannot be categorized into any conventional universality classes. The exponent β is close to that of 3D-Ising model, which might be the origin of large magnetocrystalline anisotropy in Fe3GeTe2. While γ approaches to that of mean field or tricritical mean field model. It is then important to understand the nature as well as the range of interaction in this material. For a homogeneous magnet, the universality class of the magnetic phase transition depends on the exchange interaction J(r). A renormalization group theory analysis predicts J(r) decays with distance r as23:

$$J(r)\approx {r}^{-(3+\sigma )}$$
(5)

where σ is a positive constant. Moreover, the susceptibility exponent γ is predicted as:

$$\gamma =1+\frac{4}{d}\frac{n+2}{n+8}{\rm{\Delta }}\sigma +\frac{8(n+2)(n-4)}{{d}^{2}{(n+8)}^{2}}\times [1+\frac{2G(\frac{d}{2})(7n+20)}{(n-4)(n+8)}]{\rm{\Delta }}{\sigma }^{2}$$
(6)

where \({\rm{\Delta }}\sigma =(\sigma -\frac{d}{2})\) and \(G(\frac{d}{2})=3-\frac{1}{4}{(\frac{d}{2})}^{2}\), n is the spin dimensionality. In the present case, it is found that the magnetic exchange distance decays as J(r) ≈ r −4.6, which should lie between that of the 3D Heisenberg model and the mean-field mode17, 24, 25. It is known that short range magnetic exchange interaction contributes to the 3D Heisenberg model, while the mean field model works with a long range magnetic exchange interaction12. The magnetic exchange distance is found to decay as J(r) ≈ r −4.6, which is close to mean-field model (r −4.5) with long-range interaction.

The critical exponents of Fe3GeTe2 may be compared with those expected for different Hamiltonians and universality classes. Taroni et al. have accomplished a comprehensive study of critical exponents values for 2D magnets. They found that the critical exponent β for a 2D magnet should lie in 0.1 ≤ β ≤ 0.25 26, which means Fe3GeTe2 showing 3D critical phenomenon clearly.

At the first sight, it is remarkable and intriguing that a 3D magnetic behavior is observed in a VDW bonded magnet. The 3D magnetic characteristics suggest that the interlayer coupling should not be as weak as the VDW bonding interaction between two adjacent Te layers only. One possibility is that some Fe atoms might occupy the position in the VDW gap, like the case in the isostructural compound Ni3GeTe2 7, 27. However, experiment results of X-ray diffraction, Mossbauer spectroscopy and scanning transmission electron microscopy clearly indicate that such an intercalation of Fe is absent in Fe3GeTe2 27, 28, suggesting that an alternative mechanism may take effect.

CrXTe3 (X = Si, Ge and Sn) and MPS3 (M = Mn, Fe, and Ni) are recognized as two major VDW bonded magnetic materials. Chromium Tellurides CrXTe3 (X = Si, Ge and Sn) belong to a rare category of ferromagnetic semiconductors possessing a 2D layered structure29. Detailed critical analysis and neutron scattering experiments prove that the critical behavior for CrSiTe3 falls into the universality class of 2D Ising model30, 31. Compared with CrSiTe3, CrGeTe3 exhibits a smaller VDW gap and a larger cleavage energy, which lead to a transition of critical behavior from 2D Ising to 3D tricritical mean-field model20. It is noted that the mean distances (d) between two adjacent Te layers that across the VDW gap is 0.374 nm in Fe3GeTe2 7, which is much smaller than that of CrSiTe3 d CrSiTe3  = 0.423  nm and very close to that of CrGeTe3 d CrGeTe3  = 0.377  nm 21, 32. The 3D magnetic characteristics might be associated with the smaller VDW gap and higher cleavage energy in Fe3GeTe2 system.

Transition metal phosphorus trisuflide (or thiophosphate), MPS3 (M = Mn, Fe, and Ni), are VDW antiferromagnets. All three principal spin Hamiltonians are reported in these compounds, i.e. 2D Heisenberg critical behavior in MnPS3, 2D XY magnetic behavior in NiPS3 and 2D Ising magnetism in FePS3 33. Further neutron measurements indicate that NiPS3 undergoes a critical phase transition between 3D and 2D at T ∼ 0.9T N 34. A similar crossover is also found in MnPS3, which is confirmed to 2D anisotropic Heisenberg model for whole range except 3D magnetism just below T N 35. For Fe3GeTe2, our critical analysis is restricted in a narrow region around T C (|(T − T C )/T C | ≤ 0.1), which suggests the 3D critical behavior observed in Fe3GeTe2 might be operating similar to that in MPX3. Quite recently, it has been reported that the ferromagnetic layers of Fe3GeTe2 actually order antiferromagnetically along the c-axis below 152 K9, suggesting a 2D antiferromagnetic (AFM) ground state. Considering the similar 2D AFM ground state at low temperature and 3D critical behavior near phase transition temperature in Fe3GeTe2 and MPX3, it is thus of great interest to investigate whether a critical phase transition from 3D to 2D will occur with decreasing temperature in Fe3GeTe2 like that in MPX3.

Conclusion

In summary, we have reported a comprehensive study on the critical behavior of the PM-FM phase transition in the high T C VDW bonded ferromagnet Fe3GeTe2. We obtain a set of reliable critical exponents by using various techniques including modified Arrott plot, Kouvel-Fisher method, and critical isotherm analysis. The critical exponents obtained from different methods are consistent with each other and show well-obeyed scaling behavior. The set of obtained critical exponents does not belong to any single universality class but lies between 3D Heisenberg model and mean field model. The magnetic exchange distance is found to decay as J(r) ≈ r −4.6, which is close to that of mean-field model (r −4.5) with long-range interaction. The 3D critical characteristics of Fe3GeTe2 might be associated with its smaller VDW gap and higher cleavage energy. Further studies are needed to investigate whether a critical phase transition from 3D to 2D will occur with decreasing temperature in Fe3GeTe2.

Methods

Single-crystalline sample of Fe3GeTe2 was prepared by the chemical vapor transport technique11. The structure and phase purity were confirmed by single-crystal and powder X-ray diffraction measurements at room temperature. The magnetization was measured using a Quantum Design SQUID-VSM magnetometer with the magnetic field applied parallel to c axis of the sample. Isotherms were collected at an interval of 0.5 K around T C . Each curve should be initially magnetized. The applied magnetic field H a has been corrected by the considering of the demagnetization factor36, and the calculated H was used for the analysis of critical behavior.