Introduction

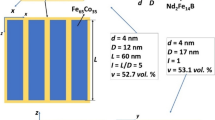
There are two issues in rare-earth (RE) permanent magnets (PM) for full applications. One is RE mineral security, and the other is a low Curie temperature of Nd-Fe-B magnet. The figure of merit of PM is its maximum energy product, (BH)max. The (BH)max can be estimated as (BH)max = (B r)2/4 for H ci > B r/2 or (BH)max = (B r − H ci)H ci for H ci < B r/2 1. B r is the remanent magnetic flux density, and H ci is the intrinsic coercivity, which is mainly controlled by the magnetocrystalline anisotropy constant (K). Therefore, high B r and H ci are needed for a large (BH)max. In addition, the PM must also have a corresponding high Curie temperature (T c) to retain the figure of merit at typical operating temperatures. In an effort to increase the (BH)max of RE-free permanent magnets, concepts of exchange coupling between hard and soft magnetic phases have been proposed2, 3. Exchange coupling makes full use of high H ci from the hard phase and B r from the soft phase of a hard/soft composite magnet. Therefore, a large (BH)max of a composite magnet can be achieved. In the magnetic exchange coupled composite, the magnetization direction of the soft phase is pinned to the magnetization direction of the hard phase4. This implies that the exchange coupled two-phase magnet behaves like a single-phase magnet. However, the soft magnetic phase needs to be thinner than twice the domain wall thickness (2δ w) of hard magnetic phase for full exchange coupling2. Thus, the increasing rate of (BH)max with the amount of soft phase is limited. Although the previously proposed models2, 3 predict the magnetization in the unit of emu/cm3 (M) and K of an exchange coupled thin film magnet reasonably well, a model directly applicable to a powdered (bulk) hard/soft nanocomposite magnets is not yet reported. In this paper, we developed a model for the magnetization in the unit of emu/g (σ s) and H ci of powdered hard/soft composite based on, experimentally accessible, the mass fraction of hard and soft magnetic phases instead the volume fraction. The prediction of the developed model was compared with the experimental σ s and H ci of Sm2Co7/Fe-Co, MnAl/Fe-Co, MnBi/Fe-Co, and BaFe12O19(BaM)/Fe-Co, where Sm2Co7, MnAl, MnBi, and BaM are hard magnetic phases, and Fe-Co is a soft magnetic phase.

Derivation of Equations

We now derive the equations for σ s and H ci in terms of mass fraction of composite. According to theoretical studies on a two-phase composite magnet, the saturation magnetization2 and anisotropy constant3 of a composite can be expressed as:

$$M={f}_{s}{M}_{s}+{f}_{h}{M}_{h}$$
(1)

and

$$K={f}_{s}{K}_{s}+{f}_{h}{K}_{h},$$
(2)

where M is the saturation magnetization, K is the magnetocrystalline anisotropy constant, and f is the volume fraction. h and s in the subscript denote hard and soft phases, respectively. Because of the experimental difficulty of obtaining M and K (per unit volume) of powdered composite, we seek to develop expressions for σ s and H ci (per unit mass) of a two-phase magnetic composite using experimentally accessible σ s and H ci for both hard and soft phases. Noting that M in Eq. (1) is magnetic moment per unit volume (typically in the unit of emu/cm3), they can be expressed as:

$$M=\frac{{\rm{magneticmoment}}}{{\rm{volume}}}=\frac{{\rm{magneticmoment}}}{{\rm{mass}}}\cdot \frac{{\rm{mass}}}{{\rm{volume}}}=\sigma \cdot \rho $$

where \(\sigma \) is the saturation magnetization (per unit mass in the unit of emu/g) and ρ is the mass density (in the unit of g/cm3). Therefore, the σ (the subscript s will be omitted for now to avoid the confusion with quantities for soft phase) of two-phase magnetic composites can be written as:

$$\sigma =\frac{{\sigma }_{h}{\rho }_{h}\,{f}_{h}+{\sigma }_{s}{\rho }_{s}\,{f}_{s}}{{\rho }_{h}\,{f}_{h}+{\rho }_{s}\,{f}_{s}}.$$
(3)

H ci due to magnetocrystalline anisotropy5 is

$${H}_{ci}=\frac{\alpha K}{\sigma \rho },$$
(4)

where α is a constant dependent on the crystal structure and degree of alignment. α is 2 in the case of aligned particles6 while for unaligned (random) particles, α can have different values for different crystals (for instance, 0.64 for cubic crystals7 and 0.96 for uniaxial crystals). Then, H ci of the two-phase magnetic composite can be modified to equation (5) by combining Eqs (2) and (4):

$${H}_{ci}=\alpha \frac{(1-{f}_{h}){K}_{s}+{f}_{h}{K}_{h}}{(1-{f}_{h}){\sigma }_{s}{\rho }_{s}+{f}_{h}{\sigma }_{h}{\rho }_{h}}.$$
(5)

By replacing K in Eq. (5) using Eq. (4), Eq. (5) becomes

$${H}_{ci}=\frac{{\sigma }_{h}{\rho }_{h}{H}_{h}\,{f}_{h}+{\sigma }_{s}{\rho }_{s}{H}_{s}\,{f}_{s}}{{\sigma }_{h}{\rho }_{h}\,{f}_{h}+{\sigma }_{s}{\rho }_{s}\,{f}_{s}},$$
(6)

where H h and H s are the intrinsic coercivities of hard and soft phases, respectively. Therefore, the H ci of a composite can now be estimated by experimental H h and H s instead of the K h and K s . Furthermore, since it is difficult to measure the volume fraction of a powdered sample, we further develop equations for σ s and H ci of a two-phase composite in terms of the mass fraction. Since f h is the volume fraction of hard magnetic phase, i.e.,

$${f}_{h}=\frac{{V}_{h}}{{V}_{h}+{V}_{s}},$$
(7)

where V is the volume. Therefore, Eqs (3) and (6) become

$$\sigma =\frac{{\sigma }_{h}{V}_{h}{\rho }_{h}+{\sigma }_{s}{V}_{s}{\rho }_{s}}{{V}_{h}{\rho }_{h}+{V}_{s}{\rho }_{s}}$$
(8)

and

$${H}_{ci}=\frac{{\sigma }_{h}{H}_{h}{V}_{h}{\rho }_{h}+{\sigma }_{s}{H}_{s}{V}_{s}{\rho }_{s}}{{\sigma }_{h}{V}_{h}{\rho }_{h}+{\sigma }_{s}{V}_{s}{\rho }_{s}},$$
(9)

respectively. Dividing both the numerator and denominator in Eqs (8) and (9) by the total mass, i.e. (V h ρ h + V s ρ s), we get:

$$\sigma =\frac{{\sigma }_{h}\frac{{V}_{h}{\rho }_{h}}{{V}_{h}{\rho }_{h}+{V}_{s}{\rho }_{s}}+{\sigma }_{s}\frac{{V}_{s}{\rho }_{s}}{{V}_{h}{\rho }_{h}+{V}_{s}{\rho }_{s}}}{\frac{{V}_{h}{\rho }_{h}}{{V}_{h}{\rho }_{h}+{V}_{s}{\rho }_{s}}+\frac{{V}_{s}{\rho }_{s}}{{V}_{h}{\rho }_{h}+{V}_{s}{\rho }_{s}}}$$
(10)

and

$${H}_{ci}=\frac{{\sigma }_{h}{H}_{h}\frac{{V}_{h}{\rho }_{h}}{{V}_{h}{\rho }_{h}+{V}_{s}{\rho }_{s}}+{\sigma }_{s}{H}_{s}\frac{{V}_{s}{\rho }_{s}}{{V}_{h}{\rho }_{h}+{V}_{s}{\rho }_{s}}}{{\sigma }_{h}\frac{{V}_{h}{\rho }_{h}}{{V}_{h}{\rho }_{h}+{V}_{s}{\rho }_{s}}+{\sigma }_{s}\frac{{V}_{s}{\rho }_{s}}{{V}_{h}{\rho }_{h}+{V}_{s}{\rho }_{s}}}.$$
(11)

The mass fraction of hard (f h m) and soft (f s m) magnetic phases are

$${f}_{h}^{m}=\frac{{V}_{h}{\rho }_{h}}{{V}_{h}{\rho }_{h}+{V}_{s}{\rho }_{s}}\,{\rm{and}}\,{f}_{s}^{m}=\frac{{V}_{s}{\rho }_{s}}{{V}_{h}{\rho }_{h}+{V}_{s}{\rho }_{s}},$$
(12)

respectively, where V h ρ h is the mass of hard phase and V s ρ s is the mass of soft phase. Accordingly, Eqs (10) and (11) become

$$\sigma ={\sigma }_{h}\,{f}_{h}^{m}+{\sigma }_{s}(1-{f}_{h}^{m})$$
(13)

and

$${H}_{ci}=\frac{{\sigma }_{h}{H}_{h}\,{f}_{h}^{m}+{\sigma }_{s}{H}_{s}(1-{f}_{h}^{m})}{{\sigma }_{h}\,{f}_{h}^{m}+{\sigma }_{s}(1-{f}_{h}^{m})},$$
(14)

respectively.

Eqs (13) and (14) can now be used to estimate the σ s and H ci of a two-phase magnet by only considering the mass fraction (f h m or f s m) of hard and soft phases if their saturation magnetization and intrinsic coercivity are known.

Experimental Validation

In order to validate the efficacy of Eqs (13) and (14), we synthesized four different composites, Sm2Co7/Fe-Co, MnAl/Fe-Co, MnBi/Fe-Co, and BaM/Fe-Co, by mixing hard and soft magnetic particles in an appropriate weight ratio and characterized them for magnetization and coercivity. It is noted that three different Fe-Co compositions, i.e., Fe50Co50, Fe65Co35, and Fe80Co20, were used for Sm2Co7/Fe-Co composites. The σ s and H ci of Fe50Co50, Fe65Co35, and Fe80Co20 are 236 emu/g and 75 Oe, 240 emu/g and 80 Oe, and 232 emu/g and 65 Oe, respectively.

Figure 1(a) and (b) show the f h m dependence of σ s and H ci for Sm2Co7/Fe-Co composite with various compositions of Fe-Co. The σ s decreases linearly as the amount of hard phase (Sm2Co7) increases in Fig. 1(a). The experimental results (open symbol) are well fitted to our developed equation (13) (solid line). It is noted that at lower concentration of hard phase, deviation of experimental σ s from the solid (theoretical) line is getting larger. In Fig. 1(b), experimental H ci is excellently fitted to the developed equation (14), especially, for the composite with Fe65Co35.

Figure 1
figure 1

The mass fraction (f h m) of Sm2Co7 dependence of (a) saturation magnetization (σ s) and (b) intrinsic coercivity (H ci) of Sm2Co7/Fe-Co. The open and closed squares indicate experimental and calculated σ s and H ci, respectively, for Sm2Co7/Fe50Co50 composites, circles indicate experimental and calculated σ s and H ci for Sm2Co7/Fe65Co35 composites, and triangles indicate experimental and calculated σ s and H ci for Sm2Co7/Fe80Co20 composites.

Full size image

As shown in Fig. 2(a) and (b), the σ s of MnAl/Fe-Co composite linearly decreases by increasing the content of hard phase, and the H ci increases by following the developed equation (14). Both experimental σ s and H ci are in good agreement with the present model.

Figure 2
figure 2

The mass fraction (f h m) of MnAl dependence of (a) saturation magnetization (σ s) and (b) intrinsic coercivity (H ci) of MnAl/Fe-Co. The black solid line and red closed circle indicate calculated and experimental data, respectively8.

Full size image

It was also found that the σ s and H ci of MnBi/Fe-Co composite magnet in Fig. 3 (a) and (b) are well fitted to Eqs (13) and (14). Lastly, Eqs (13) and (14) are also validated by the experimental σ s and H ci of BaM/Fe-Co composite shown in Fig. 4(a) and (b).

Figure 3
figure 3

The mass fraction ( f h m) of MnBi dependence of saturation magnetization (σ s) and (b) intrinsic coercivity (H ci) of MnBi/Fe-Co. The black solid line and red closed circle indicate calculated and experimental data, respectively.

Full size image
Figure 4
figure 4

The mass fraction ( f h m) of BaM dependence of saturation magnetization (σ s) and (b) intrinsic coercivity (H ci) of BaM/Fe-Co. The black solid line and red closed circle indicate calculated and experimental data, respectively.

Full size image

It is noted that a kink in the hysteresis loop becomes more obvious as the f h m decreases, indicating weak or no exchange coupling (not shown in this paper). Therefore, regardless of exchange coupling, the present model can be used to estimate σ s and H ci of any powdered hard/soft magnet composite.

Summary

In summary, we have modified the previously proposed models1, 3 for magnetization (M) and anisotropy constant (K) of a hard/soft composite magnet to use mass fraction instead of the volume fraction of hard or soft phase for magnetization (σ s) and intrinsic coercivity (H ci) of powdered hard/soft composite. Our modified equations have been validated by experimental σ s and H ci of Sm2Co7/Fe-Co, MnAl/Fe-Co, MnBi/Fe-Co, and BaM/Fe-Co composites. Regardless of exchange coupling, the developed equations can be used to predict the σ s and H ci of a powdered hard/soft composite magnet. The present model can provide guidance for the design of exchange coupled hard/soft composite magnets.