Main

Integrated quantum photonics—because of the availability of mature fabrication technologies, sophisticated information-processing tools at room temperature, and robustness to decoherence—is considered one of the most compelling approaches for the development of future nonclassical technologies1,2,3. The current semiconductor industry is able to fabricate highly compact and robust, mass-producible, on-chip photonic devices4, and major advances have demonstrated the capability of generating and controlling entangled quantum optical states on-chip5,6, which is of paramount importance for quantum key distribution (QKD)7,8 and quantum information processing (QIP)9,10,11,12,13,14,15,16,17,18,19,20,21. In particular, existing on-chip realizations include two-photon interference9,10, teleportation11, quantum walks12, boson sampling13, QIP involving multiple entangled photons14,15,16, error-protected qubits17, noise-resilient qudits18,19,20, cluster states21 and even the development of quantum photonic processors16,20 are just a few examples considered to be the watershed of integrated quantum photonic technologies.

Notably, all previous on-chip entangled quantum photonic sources8,22 and the pioneering on-chip demonstrations of nonclassical functionalities have until now been dependent on external excitation lasers, making these systems non-reproducible, bulky, impractical, and thus unsuitable for out-of-laboratory use or production at large scale12,13,14,15,16,17,18,19,20,21. To address this drawback, it is critical to realize a fully integrated quantum light source of entangled photons, as this will allow all stages of QIP to be on a single chip, ultimately leading to the required stability and scalability3,4. Until now, the major technical challenge preventing a turnkey quantum light system has been the integration of a stable and tunable laser with a filter (which is crucial to eliminate the noise that suppresses quantum phenomena18) and a nonlinear parametric source of entangled photons (that is, creating signal and idler photons through spontaneous parametric effects)4,23,24.

The absence of a unique material platform that suitably provides all quantum photonic functionalities (low-loss guiding, filtering, efficient parametric generation of entangled photon pairs, and their active manipulation) while at the same time providing lasing gain is the main factor impeding monolithic integration. A broad range of photonic platforms—for example, silica (SiO2)14, silicon-on-insulator (SOI)9, silicon nitride (Si3N4)8,10, lithium niobate6, AlGaAs25, AlGaAs-OI26,27, gallium arsenide (GaAs), indium arsenide (InAs), indium phosphide (InP)22 and a potpourri of exotic compounds28 and two-dimensional (2D) materials29—have been investigated in the context of quantum processing and parametric photon-pair generation. Low-loss indirect or high-bandgap materials with a high refractive index (for example, Si, SiO2 and Si3N4) are most commonly preferred for light guiding, signal processing and for efficient spontaneous parametric effects and thus entangled photon-pair generation, whereas direct-bandgap III–V semiconductors (such as InAs, GaAs and InP) are suitable for optical gain and lasing. Unfortunately, the fabrication techniques/process flows for each group of materials differ and are often not compatible with one another24. Thus, the hybrid integration of an excitation laser with a parametric photon source into a combined photonic circuit, drawing the best advantages of the different materials while avoiding their deficiencies, is considered the key step towards achieving a fully integrated on-chip quantum device23,24.

In addition to parametric spontaneous sources, semiconductor quantum dots (QDs), excited either optically or electrically, can emit single24 and entangled photons30 in compact forms. However, it is difficult to integrate QDs with a fully operational quantum photonic circuit due to the random growth of QDs on wafers, the presence of charge noise, the lack of a precise emission wavelength and the need for cryogenic cooling to ensure an indistinguishable, narrowband (approximately megahertz) and deterministic single-photon output. The QDs are thus generally connected with the rest of the circuit by optical fibres, which makes the device bulky, or by wafer-bonding, where loss of the single-photon signal due to misalignment and refractive-index mismatch at the circuit interface is unavoidable24.

The emission from InP quantum wells covers the entire C band, making InP a perfect candidate for a semiconductor optical amplifier (gain medium) and to realize lasers that will drive on-chip quantum light sources. However, the intrinsic waveguide losses in such amplifiers and in InP passive waveguides are high. This imposes a short photon lifetime on the laser cavity, causing a high spectral linewidth. A solution to this is to extend the photon lifetime with hybrid integration of waveguide feedback circuits based on Si3N4 waveguides31; this offers a broad transparency window covering the entire C band, with remarkably low loss. Moreover, Si3N4 has a high nonlinear refractive index (n2 ≈ 2.4 × 10−19 m2 W−1), moderately high mode confinement, low material dispersion, near-to-zero Raman scattering32,33 and, due to the large bandgap, an absence of two-photon absorption (TPA) in the telecom wavelength range. This absence of TPA in Si3N4 permits operation in a high-power regime, effectively reducing the intrinsic laser linewidth to the sub-kilohertz range. These characteristics make Si3N4 particularly suitable for nonlinear and quantum photonic applications8,32,33,34. Over the past few years, compact, high-Q Si3N4 microresonators35,36 with ultranarrow resonant linewidth and extremely small mode volumes have been employed in the classical domain for the generation of low-threshold Kerr frequency combs8,32,33,34, as well as in the quantum domain for the realization of a squeezed state of light37 and entangled photon pairs via spontaneous four-wave mixing8. Very recently, mode-locked microcombs have been reported using laser-integrated photonic chips38,39,40.

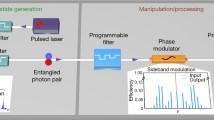
In this article we address the aforementioned challenges related to full integration and demonstrate a hybrid, integrated turnkey quantum light source emitting frequency-bin entangled qubit and qudit states. The system is illustrated in Fig. 1a and consists of an electrically pumped III–V reflective semiconductor optical amplifier (RSOA) based on InP, providing optical gain, which is butt-coupled to a low-loss Si3N4 waveguide feedback circuit (Supplementary Section 1). The reflective coating at the amplifier side and a Sagnac mirror at the opposite end together form a laser cavity. After the gain stage, three microring resonators (MRRs) with different radii (R1 > R2 > R3) and thus different free spectral ranges (FSRs) are arranged in a cascaded fashion, creating a Vernier filter (Fig. 1a) that is tunable through the incorporated microring phase shifters. All three rings are over-coupled to the adjacent bus in an all-pass configuration for high transmission of the central (lasing) Vernier mode and to achieve lasing actions (overall gain ≈ total losses). The combination of low propagation loss and tight guiding via the high index contrast in the Si3N4 waveguides enables the realization of MRRs with small radii, which is vital to realize Vernier filters with large FSRs. This is followed by a Mach–Zehnder interferometer and the Sagnac mirror. To mitigate the effect of back-reflection arising from the refractive-index mismatch between the InP and the Si3N4 circuit interface31, waveguide tapering and tilting at the Si3N4 input as well as antireflection coating at the interfaces have been considered (Methods). Finally, our material choice (InP–Si3N4) in combination with Vernier filtering (Fig. 1a, stage 1) leads to single-frequency laser emission from the gain medium (Fig. 1c), which is ideal for exciting only a particular longitudinal mode of the MRRs. The intracavity laser field (set at 193.4 THz (1,550 nm), tunable over the C band) back-reflected from the Sagnac mirror acts as an excitation field for a nonlinear spontaneous four-wave mixing (SFWM) process within the third MRR (R3). This in turn produces correlated signal/idler photon pairs in the frequencies symmetric to the excitation field, forming a bi-photon quantum frequency comb (QFC). The QFC excited by a continuous-wave source generally dwells in high-dimensional Hilbert space, because the idler and signal photons are in a superposition of multiple frequency modes owing to the energy conservation of SFWM18. The advantages of this configuration are twofold: (1) the parametric quantum source is directly incorporated in the laser cavity, such that the excitation field is locked to the Vernier resonance for stable operation, and (2) the Vernier filter (Fig. 1a, stage 1) directly suppresses the amplified spontaneous emission (ASE) from the InP gain at the relevant frequencies.

Fig. 1: A laser-integrated photonic quantum light source of frequency-bin entangled photon pairs.
figure 1

a, An electrically pumped InP RSOA providing optical gain is coupled to a Si3N4 chip containing a three-microring (R1, R2 and R3) Vernier filter and a Mach–Zehnder interferometer (MZI) with a Sagnac (loop) mirror. The FSRs of R1, R2 and R3 are ~107 GHz, ~167 GHz and ~199 GHz, respectively. The spectral positions of the ring resonances can be adjusted using electrically driven integrated microheaters to provide a single frequency filter in the gain bandwidth via the Vernier effect. Together with the gain section and the cavity built by the end mirror and loop mirror, the system allows laser operation on this filter line. The backward-propagating laser field acts as the excitation signal for a SFWM process within the third ring, R3, producing a QFC. The working principle of the device is illustrated in insets (i) to (iii). b, Measured transmission spectra of microrings R1, R2 and R3. Here, rescaling of the data leads to a varying background. c, Classical output spectrum showing the laser line at a frequency of 193.4 THz with a side-mode suppression ratio (SMSR) of >55 dB. The measured SMSR is limited by the dynamic range of the optical spectrum analyser (OSA). d, Measurements utilizing single-photon detectors (Methods) allowed determination of an SMSR of ~112 dB, and an ASE suppression of ~56 dB.

Full size image

To analyse the quantum properties of the source, we performed photon correlation measurements on several resonance pairs (Fig. 2a) at generation stage 2 (Fig. 1a) by using the set-up configuration and measurement procedure described in Supplementary Section 4. Our measurements revealed coincidence counts (Fig. 2b) demonstrating the generation of signal/idler photon pairs over several resonance pairs (Fig. 2c,d) and thus the creation of a bi-photon QFC. From the full-width at half-maximum (FWHM) of the measured coincidence histogram, as shown for one resonance pair in Fig. 2b, the resonance linewidth was calculated to be 1.63 GHz, which is in good agreement (Methods and Supplementary Section 2) with the measured resonance linewidth of ring R3 (~2 GHz; Supplementary Sections 3 and 4). A photon coherence time of ~188 ps was deduced. We obtained four resonant pairs with major coincidence counts, as shown in Fig. 2c, revealing an ~1-THz photon-pair generation bandwidth as a consequence of the normal dispersion regime, that is, a positive group delay dispersion (GDD) at the excitation wavelength. For photon-pair generation we explicitly chose the third MRR (R3), excited by the backward-propagating field, for one major advantage: the noise, emerging from the ASE present in the system, is intrinsically suppressed due to the chip configuration. Specifically, the peripheral lasing cavity, composed of the reflecting facet of the RSOA and the Sagnac mirror, has wide resonant modes with much smaller FSR (<1 GHz) than that of the third ring (199 GHz), leading to a continuous ASE spectrum emanating from the gain medium. This situation is sketched in Fig. 1a. The noise originating from the gain medium decreased at the Vernier filtering stage, in forward propagation (Fig. 1a, stage 1), as also manifested by the measured MRR transmission in Fig. 1b. Characterization by performing single-photon count measurements at off-resonant frequency components before and after the Vernier filtering stage revealed that the ASE was suppressed by ~56 dB (Fig. 1d), enabling the realization of high-quality photon pairs from our device (Methods). Additionally, in contrast to the use of a single ring for pair generation, our device structure facilitated filtering of the excitation field, whereas the photons generated in ring R3 passed directly to the device output (Methods). The backward-propagating excitation field was partially coupled into ring R2 and was thus partly filtered from the generated photon pairs at the output port. We measured a maximum coincidence-to-accidental ratio (CAR) of 80 per signal/idler resonance pair (Fig. 2c). A system with such a performance can be readily implemented in many quantum scenarios18. Furthermore, for a detected excitation field power of ~3.9 mW, we determined a detection rate of ~620 Hz, as well as a calculated generation rate of ~8,200 Hz at the device output, that is, considering the insertion losses of the filter as well as the quantum efficiencies of the detectors. In comparison with previously demonstrated material platforms utilized for entangled photon-pair generation, performance parameters including generation rate and CAR are generally of the same order of magnitude or higher compared to amorphous silicon, crystalline silicon and AlGaAs-OI27 waveguide structures, and lower than the AlGaAs-OI ring structure26. A detailed comparison with the first electrically pumped AlGaAs laser diode combined with intracavity parametric photon-pair generation25 revealed that the device presented in this study provides much higher performance parameters and compactness and is thus relevant for real-world applications.

An optimal photon-pair generation rate (brightness) is generally achieved in the over (critical) coupling regime of the resonators41. Most importantly, to guarantee lasing operation, a high transmission of the centre Vernier filter mode is necessary, which also requires over-coupled resonators. Our device design thus provides optimal conditions for photon-pair generation and lasing operation. The photon generation rate and generation bandwidth can be increased by suitably tailoring and flattening the GDD of the Si3N4 waveguide. Further reductions in surface roughness and waveguide loss can improve the intrinsic Q factors36 and ASE suppression, which will lead to increased generation rates and CAR.

Fig. 2: Performance characteristics of the quantum light source.
figure 2

a, Photon pairs created through the SFWM process reside on spectrally symmetric signal and idler resonances. fp denotes the pump frequency. Regions outlined by dotted boxes indicate the filter regions for the Bell test and the QST measurements. b, Histogram of time difference between coincidence counts collected for 300 s showing photon-pair correlations. The FWHM of the peak, that is, the second-order cross-correlation time, is 139 ps, matching the 1.63-GHz resonance linewidth. The coherence time was calculated as ~188 ps. c, CAR for particular frequency pairs for a detected excitation power of 3.9 mW. d, Detection rate, that is, the number of coincidence counts per second, for the respective frequency pairs. Error bars in c and d represent the 87% confidence bounds of the coefficient retrieved from the standard deviation of the coincidence counts. The spectral response of the 200-GHz-wide notch filter (NF), for rejection of the excitation field used, is illustrated with grey shading in all plots.

Full size image

The photon source directly emits frequency-bin-entangled high-dimensional states, as verified by the Bell test and quantum state tomography measurements. A frequency shift via an electro-optic modulator (EOM) was used to superimpose individual frequency modes to implement quantum interference and projection measurements (Methods). We defined the two-qubit (2D) and two-qutrit (3D) states by selecting the second, third and fourth frequency modes for both the signal and idler photons (Fig. 2a). As these frequency pairs have similar state amplitudes (Fig. 2c,d), we expect maximally entangled Bell states to be generated18. The quantum interference patterns for the qubit and qutrit states are shown in Fig. 3, top row, yielding raw visibilities of \({V}_{2-3}^{\,(2)} = {0.975\pm 0.002}\) and \({V}_{3-4}^{\,(2)} = {0.976\pm 0.002}\) for qubits and \({V}_{2-3-4}^{\,(3)} = {0.968\pm 0.004}\) for qutrits (without background subtraction). These values violate the respective Bell inequalities for qubits and qutrits by greatly exceeding the threshold values of ~0.7071 and ~0.7746, respectively (Methods)18. We also reconstructed the density matrices corresponding to the generated quantum states by quantum state tomography (QST; Methods). The absolute and argument values of the respective density matrices are shown in Fig. 3, bottom row. The source generates Bell states with excellent fidelities of \({F}_{2-3}^{\,(2)} = {0.988\pm 0.01}\) and \({F}_{3-4}^{\,(2)} = {0.981\pm 0.01}\) for qubits and \({F}_{2-3-4}^{\,(3)} = {0.806\pm 0.02}\) for qutrits. The latter shows an improved fidelity of \({F}_{2-3-4}^{\,(3),\,{{\rm{noise}}}} = {0.857\pm 0.02}\) by taking 6% linear noise into account, whereas the qubit case does not show a substantial improvement with this approach (Methods). Furthermore, the 2D density matrices show a violation of the CHSH inequality with Bell parameters up to S = 2.793, which is in good agreement with the values derived from the Bell tests of up to S = 2.760 (Methods and Supplementary Sections 5 and 6). These measurements prove the excellent quality of the qubit/qudit pairs and in turn their large potential for applications in quantum technologies.

Fig. 3: Bell inequality violation and QST of frequency-bin entangled qubit and qutrit states.
figure 3

Top row: Bell test characterization of qubit and qutrit states. The error bars show the square root of the absolute count numbers. The error of the noise background is too small to be displayed. Bottom row: quantum state tomography for qubit and qutrit QFC states. a, Two-qubit state (composed of second and third resonances). b, Two-qubit state (composed of third and fourth resonances). c, Two-qutrit state (composed of second, third and fourth resonances). Fidelity F was calculated with respect to the 3D Bell state mixed with 6% linear noise. The superscripts in parentheses denote the dimension of the quantum state and the subscripts represent the numbers of the frequency bins on which the tomography was performed.

Full size image

Our measurements on qutrits42 do not yet exhaust the maximum number of ring resonances. The maximum number of signal/idler pairs with efficient pair generation rates is limited by the SFWM bandwidth, which depends on the dispersion of the Si3N4 waveguide. Bell-test and QST measurements are limited by the maximum number of frequency modes that can be mixed, which is determined by the ratio of the FSR and the EOM driving frequency (Methods). In this sense, the designed FSR of the ring resonator during photon-pair generation could be decreased, which enables increasing the number of frequency modes for mixing, and in turn our access to the effective dimensions. However, a decrease in the resonator FSR could decrease the total Vernier FSR to an extent that leads to violation of single pump frequency oscillation in the cavity by creating more lasing modes within the spectral gain bandwidth used in our experiments. Therefore, according to the Vernier principle, this procedure is also limited and needs careful handling to prevent extra possible challenges such as the need for filtering out more excitation modes.

In conclusion, building on the latest advances in hybrid integration technologies, we have presented an electrically pumped laser-integrated versatile photonic quantum light source entirely on-chip. The sub-millimetre-sized chip accommodates a laser cavity and a Vernier filtering stage capable of generating high-quality, low-noise entangled photon pairs residing in high-dimensional Hilbert space. We have attained a remarkably high pair generation rate of 8,200 counts s−1, a maximum CAR of >80 and a CAR of at least (~40) for all four resonance pairs, spanning ~1 THz around 1,550 nm. The state fidelity close to unity (0.99) and the quantum interference visibility of 96% are superior to previous demonstrations with external lasers18, yet here within a much smaller footprint.

The proposed design enables intrinsic long-term subwavelength stability and high complexity with a large number of sources, as well as seamless integration with subsequent, upscaled quantum processing circuits. Therefore, our approach can be exploited in nearly every demonstrated on-chip QIP scheme, for example, for boson sampling, teleportation and certified quantum random number generation. Future steps will focus on including this source in fully integrated programmable quantum processors where piezo or electro-optic phase shifters can be used to realize desired state generation, for example, a hyper-entangled or cluster state21, and state processing. In this context, in addition to frequency-bin encoding, multiplexing of the presented source, which is easily achievable, can realize the widely used path-encoded quantum states. We thus envisage our end-to-end integrated, tiny quantum light source will be an elementary constituent of densely packed programmable photonic quantum processors2,16,20 in the near future. Moreover, this portable high-performing multi-level (M-ary) entangled photon source is of great importance for quantum communications. It can readily serve as a practical, mass-producible building block to drive quantum networks, with the possibility to use frequency-encoding, and is perfectly suited for state-of-the-art telecommunications components3. By significantly reducing the payload, and being robust and stable, it could be perfect for applications in quantum satellite communications. Finally, this work could be considered as a step towards achieving quantum advantage on-chip using photons43.

Methods

Design and fabrication of the hybrid quantum photonic source

The design of the laser-integrated hybrid photonic source is shown schematically in Fig. 1a. It includes a III–V RSOA, hybrid-integrated with a Si3N4-based feedback circuit. The RSOA and feedback chip are end-butt-coupled using adhesive bonding such that the III–V waveguide and the Si3N4 waveguide are in the same plane. A standard RSOA fabricated by Fraunhofer HHI44 containing a 700-μm-long InP-based quantum-well amplifier provides optical gain around the central wavelength of 1,550 nm. According to the gain chip specifications, the mode field diameter at the end facet is 3.5 μm in both directions. One end facet is curved upwards at 9° (Fig. 1a), and coated with anti-reflective against the polymer (index n ≈ 1.5), which matches the refractive index of the Si3N4 waveguide. The antireflection coating reduces the back-reflection of light within a broad spectral range from the amplifier towards the amplifier. The 9° curvature further minimizes the back-reflection. One mirror of the laser cavity is formed by a highly reflective coating (R = 0.90) on the end facet of this amplifier.

For the realization of the feedback circuit, we chose Si3N4-based TriPleX waveguides with an asymmetric double-stripe cross-section, as described in ref. 45. This cross-section comprises (from bottom to top) a 70-nm Si3N4 layer, a 100-nm SiO2 layer and a 175-nm Si3N4 layer, all embedded in SiO2 cladding. The on-chip waveguides are 1.1 μm wide. This waveguide cross-section supports single TE00 transversal mode propagation with low propagation losses (<0.1 dB cm−1) and low bend loss (~0.01 dB cm−1) at tight bend radii (down to 100 μm), which enables the design of a sharp spectral filter with high finesse and large FSR. The spectral filter on this feedback circuit is formed by three consecutive MRRs31,38,46,47. These rings have circumferences of 1,579 μm, 1,005 μm and 850 μm, corresponding to FSRs of 107 GHz, 169 GHz and 199 GHz, respectively. These ring circumferences were chosen carefully, based on the ratios of co-prime numbers 13, 11 and 7, to utilize the Vernier principle. The ring bending radius needed to be larger than 100 μm for maintaining negligible bending losses (<0.01 dB cm−1). The bending radius of the smallest ring (~135 μm) is sufficiently small that the Vernier FSR is greater than the gain bandwidth, ensuring single-mode oscillation of the laser field. The designed bus-to-ring power coupling coefficient is 0.03. The Vernier filter selects a single frequency and suppresses the ASE background from the RSOA over a bandwidth of 15.3 THz, which covers the entire gain bandwidth. The second mirror of the laser cavity is formed by a Sagnac loop after a balanced and tunable Mach–Zehnder interferometer (MZI), to reflect and extract an adjustable fraction of the intracavity light. Light can be coupled out from the cavity at any of the ports depicted in Fig. 1a. All ports are coupled to an array of single-mode polarization-maintaining fibres. To maximize the coupling efficiency, and to prevent undesired feedback from the interfaces between the gain chip, feedback chip and fibres, several measures were taken, including waveguide tapering and tilting31. Specifically, for interfacing with the gain chip and with the output fibres, both lateral and vertical tapering are applied for low-loss coupling. The thickness of the top silicon nitride layer is adiabatically reduced to zero towards the edge of the chip. For optimal coupling with the HHI gain chip, the waveguide width is adiabatically increased to 2.2 μm. The calculated mode-field diameter (MFD) is then 3.9 μm (horizontal) × 3.3 μm (vertical), which matches well with the gain chip specification. The waveguide is curved downwards at 19.8° to match the InP curved waveguide, taking Snell’s law into account. For optimal coupling with a polarization-maintaining single-mode fibre, the thickness of the Si3N4 top layer is also adiabatically reduced to zero towards the chip edge. The waveguide width is reduced to 0.8 μm. The calculated MFD is then 10 μm × 10 μm to match the fibre MFD of 10.1 μm (Nufern PM1550-XP). One of the many advantages of the designed chip is that it does not rely on free space and grating couplers at the input and output stage. Therefore, the extraction efficiency of the designed chip is expected to be very high. The calculated maximum mode overlap between gain chip and feedback chip is −0.26 dB (94%), and the losses between the feedback chip and fibres are negligible. Measured values for transmission between fibre and feedback chip typically vary between 0.5 dB (89%) and 0.8 dB (83%). These values are optimized by proper mode matching at the chip interfaces.

It is also worth mentioning the uniqueness of the designed chip in providing different extraction efficiencies for pump photons and signal–idler photon pairs at the output port. Signal and idler photon pairs are generated in ring R3 via SFWM. The entangled photons cannot couple to ring R2 when the resonances of R1, R2 and R3 are aligned at 193.4 THz (central mode). However, only the pump photons can couple to ring R2 and thereby pass through all three rings, oscillating back and forth at 193.4 THz and instigating lasing action. Therefore, once in the access waveguide, the circuit ideally provides close-to-100% extraction efficiency for the nonclassical photon pairs at the output channel, while at the same time partially inhibiting the pump photons and blocking the associated noise from appearing at the output port. In practice, there are slightly different extraction efficiencies for the signal and idler photons due to waveguide dispersion. To summarize, the architecture offers very high extraction efficiencies for signal–idler pairs while acting as an intrinsic band-rejection filter for the pump photons at the output port.

For thermal tuning of the MRRs, the MZI and an extra phase shifter for the cavity length, resistive heaters are placed on top of these elements. Fabrication of the feedback chips was carried out with a process flow as described in ref. 45. After wafer-processing, the gain chip, feedback chip and fibres were aligned and permanently fixed together with adhesive bonding. The heaters and amplifier were wire-bonded to a printed circuit board for convenient electronic control. Finally, the optical chips and fibres, as well as the corresponding electronics, were mechanically fixed on a common mount to form a single and stable assembly for the hybrid photonic quantum source.

MRR design parameters

The free spectral ranges, Q factors and coupling conditions of R1, R2 and R3 are vital parameters with direct impacts on lasing action, Vernier filtering and the coherence time of the generated signal–idler pairs, so they must be designed carefully. The propagation loss for the waveguide was measured to be 0.158 dB cm−1 using the cut-back method with a set of long spirals on the same wafer. It is computationally demanding to numerically simulate the entire laser—the InP-gain section, the Si3N4 feedback section including the MRR Vernier filter, the MZI and the Sagnac loop—with any conventional method, such as finite-difference time-domain simulations or the finite-element method to determine the bus-to-ring coupling factor for efficient laser operation. In this case, the designed bus-to-ring power coupling coefficient (κ2) was optimized experimentally to be 0.03. Using these values, and the ring circumferences, the theoretical values of the Q factors and corresponding theoretical values of the resonance FWHMs were calculated. The general formula for the loaded Q factors of a microring of radius R, which is asymmetrically coupled to an input and an output bus (add-drop configuration) with amplitude transmission coefficients of r1 and r2, respectively, is given by48

$${Q}\approx {\frac{\uppi {n}_{\rm{g}}L\sqrt{\left({r}_{1}{r}_{2}a\right)}}{{\lambda }_{{{{\rm{res}}}}}\left(1-{r}_{1}{r}_{2}a\right)}},$$
(1)

where ng, L(= 2πR), λres and a are the group index, perimeter of the ring, resonating wavelength and the round-trip loss, respectively. The intrinsic Q factor can be calculated by setting transmissions r1 and r2 to 1.

The experimental values of the Q factors were determined from the measured transmission spectra of the three rings, R1, R2 and R3, by fitting Lorentzian curves. An example is given in the Supplementary Information (Supplementary Fig. 2) at the pumping wavelength (193.4 THz). All obtained values are listed in Supplementary Table 1. Theoretically calculated Q factors for R1, R2 and R3 match the experimental values closely.

The round-trip amplitude loss factors a1, a2 and a3 for R1, R2 and R3 are 0.9971, 0.9982 and 0.9985, respectively, and greater than the amplitude transmission coefficients (r1 = r2 = r = 0.9848). Accordingly, all three rings are over-coupled to the adjacent bus in the all-pass configuration48. The coupling coefficients are much larger than the single round-trip losses. The gap between the bus waveguides and the ring waveguides is 1,675 nm for all rings. The ring resonators are racetrack resonators, where the coupling section is a (short) straight section. The rings in the Vernier filter are designed to operate in the over-coupled regime to guarantee lasing action; that is, the overall loss of the system is compensated by the gain. The total losses in the Vernier filter should be kept much lower than the level of undesired back-reflections in the laser circuit. Other than this, although the under-coupling condition secures a higher loaded Q factor compared to over/critical coupling, the preferred choice for microrings implemented in nonclassical photon-pair generation is usually over/critical coupling for the following reasons: (1) for a given intrinsic Q factor of an MRR, the photon-pair generation rate (brightness) is maximized in the over (critical) coupling condition41; (2) for the compensation of thermal effects on coupling49 and (3) for minimization of the detrimental effects of undesired fabrication inaccuracies on the loaded Q factor49. Therefore, in this work, the over-coupling condition is propitious both for lasing and for photon-pair generation.

Finally, it is important to note that intrinsic Q factors are mainly limited by scattering losses due to the roughness of the waveguide sidewalls. A high intrinsic Q factor of a microring in principle always facilitates a higher and brighter photon-pair generation rate. However, the higher the Q factors, the harder it is to align the resonant notches of rings R1, R2 and R3 for the Vernier operation. In addition, for quantum interference measurements of frequency-bin encoded states it is harder to match the narrow resonances, and even a slight drift in frequency over time would have a drastic effect and diminish the overlap, and thus the interference signal.

Calculation of coherence time from the cross-correlation measurement

The coherence time of a photon in our system—a bi-photon QFC—is directly related to its interference capability with another photon in the time domain. A longer coherence time is desirable for many applications, for example, in developing quantum memories. On the other hand, a longer coherence time corresponds to a narrower resonance linewidth, which for quantum interference measurements of frequency-bin encoded states introduces difficulties related to the spectral superposition of the frequency bins as well as frequency drifts, and thus can diminish the interference signal.

The photon coherence time (τcoh) is, to a first approximation, related to the loaded Q factor (QL) or the resonance linewidth (Δν). The QL of a microring is affected by the coupling coefficient and limited by the scattering losses due to the roughness of the waveguide sidewalls, placing a fundamental restriction on the resonator linewidth and the photon coherence time. The loaded Q factor describes the overall photon decay rate of the entire ring cavity. The loaded Q factor is directly related to the resonator linewidth and can be given by \({Q}_{{{{\rm{L}}}}}^{-1}\,\)\(={Q}_{{{{\rm{i}}}}}^{-1}+{Q}_{{{{\rm{c}}}}}^{-1}\), where Qc in turn depends upon ring-to-bus coupling coefficients and the intrinsic Q factor Qi on the intrinsic losses of the waveguide. Considering a single-mode source50, the coherence time depends on the cavity resonant linewidth, which takes a Lorentzian shape according to τcoh = 1/(πΔν). Besides the loaded Q factor, the width and the shape of the cavity resonances are also influenced by the dispersion of the Si3N4 microring resonator.

In this article we found the coherence time from the obtained histogram of the coincidence count measurement, that is, the cross-correlation time. The signal–idler temporal correlation can be given by the Glauber second-order cross-correlation function \({g}_{{{{\rm{si}}}}}^{(2)}\):

$${g}_{{{{\rm{si}}}}}^{(2)}={1+\frac{2\uppi \Delta \nu }{2R}\exp \left(-2\uppi \Delta \nu \left\vert \tau \right\vert \right)},$$
(2)

where Δν is the cavity linewidth, R is the photon-pair generation rate and τ is the signal–idler cross-correlation or the delay. The function given by equation (2) was fitted to the experimental datapoints to determine the second-order cross-correlation time as 139 ps and the resonance linewidth as 1.629 GHz, yielding a coherence time of 188 ps. However, determination of the coherence time via the cross-correlation measurement considers an equal resonance linewidth for the signal and idler field and a perfect energy matching, that is, a constant ring FSR. The FSR changes due to dispersion, which shifts the resonances with respect to the energy matching (in our case <100 MHz being negligible). Therefore, the coherence time of a heralded single photon can deviate slightly from the values that are obtained from the measured pure resonance linewidth. Accordingly, the estimated resonator linewidth is consistent with the measured linewidth from the resonator transmission, within experimental tolerance. Finally, because the photons are created though the SFWM effect in the resonator, the coherence time of the photons is independent of the gain medium decay rate.

The limiting factors of our system associated with achieving a high coherence time are explained in the following. As mentioned earlier, a high Q factor is associated with a narrower resonance linewidth. It is thus extremely difficult to align the resonant modes of the high-Q microrings constituting the Vernier filter to a single frequency over a long period of time, which would be detrimental for stable operation of the system. Another limiting factor for the Q factor and thus the photon coherence time in our Vernier laser configuration is that the ring coupling coefficient needs to be larger than the round-trip loss coefficient so as to have a good transmission of the Vernier filter such that lasing starts for the external cavity defined by the reflecting end of the RSOA and the Sagnac mirror. A decrease in the ring coupling coefficient via geometry optimization of the coupler could match the ring coupling to the round-trip loss coefficient, leading to higher Q factors, as would be possible in a pure single-ring configuration under external excitation. However, in this case, the Vernier filter transmission will be lower, such that the laser, as a result of large losses, would not start based on feedback from the external cavity.

Noise suppression capability of the Vernier filter

Performance parameters such as CAR, interference visibilities and the fidelities of the generated entangled quantum states strongly rely on the efficiency (extinction ratio) of the noise suppression filter18. One essential performance parameter of the device is a high side-mode suppression ratio (SMSR) to ensure that the laser oscillates at a single frequency and that there are no unwanted side modes appearing in the spectral domain.

ASE suppression by the Vernier filter is achieved with the experimental set-up illustrated in Supplementary Fig. 3a and Supplementary Section 3. The experiment was based on the detection of single counts for the idler and signal frequency modes symmetric to an excitation frequency of 193.4 THz by gradually detuning the programmable filter (bandwidth of 25 GHz) along the entire C band. We first performed the experiment at the through port of ring R1 (Fig. 1a), which enabled us to directly measure the ASE emitted by the RSOA gain medium, that is, at the stage before the Vernier filtering occurs. We then performed the same experiment at the device output port, that is, the photon output of ring R3.

To define the noise suppression, we calculated the average detected single counts over the frequency range as 76.67 GHz and 0.18 MHz, before and after Vernier filtering, respectively. Hence, an average noise suppression of at least ~56 dB was obtained. We also performed the following calculation to retrieve the SMSR, by first defining the number of photons per second at a laser frequency of 193.4 THz for the given laser power of 3.9 mW:

$${N}_{{{{\rm{photon}}}}}={\frac{{P}_{{{{\rm{laser}}}}}}{{E}_{{{{\rm{photon}}}}}}=\frac{{P}_{{{{\rm{laser}}}}}}{\left(h\times \nu \right)}\approx 3.04\times {10}^{16}\,{{{\rm{Hz}}}}},$$
(3)

where Nphoton represents the number of photons per second or the single count rate, Plaser is the laser power, Ephoton is the photon energy, h is Planck’s constant and ν is the frequency of the photons emitted by the laser. Relating the photon rate of the laser field and the measured average count rate after the filter allows us to determine an SMSR of ~112 dB.

Quantum interference measurement

We performed a dedicated Bell-test measurement for both the 2D and 3D states. This kind of measurement can give an indication of a violation of the classical Bell inequality and is used extensively to prove the presence of entanglement18.

We used resonance modes 2, 3 and 4, which had approximately the same count rates. By mixing two or three of these resonant modes, we thus expected to measure a Bell state of the form

$${\left\vert \psi \right\rangle } = {\mathop{\sum }\limits_{k=2}^{4}{c}_{k}{\left\vert k\right\rangle }_{\rm{s}}{\left\vert k\right\rangle }_{{\rm{i}}}\approx \frac{1}{\sqrt{3}}\mathop{\sum }\limits_{k=2}^{4}{\left\vert k\right\rangle }_{\rm{s}}{\left\vert k\right\rangle }_{\rm{i}}}.$$
(4)

Starting from this, we created the following projections for signal and idler by mixing all present signal and idler modes, respectively, and applying phases as follows:

$${\left\vert {\psi }_{{{{\rm{proj}}}},\,2}\right\rangle } = {\frac{1}{\sqrt{2}}\left(\left\vert \overline{k}\right\rangle +{\rm{e}}^{i\theta }\left\vert \overline{k}+1\right\rangle \right)}$$
(5)
$${\left\vert {\psi }_{{{{\rm{proj}}}},\,3}\right\rangle } = {\frac{1}{\sqrt{3}}\left({\rm{e}}^{i\theta }\left\vert \overline{k}\right\rangle +\left\vert \overline{k}+1\right\rangle +{\rm{e}}^{i2\theta }\left\vert \overline{k}+2\right\rangle \right)}$$
(6)

with \({\bar{k}} = {2}\) (2D and 3D) and \({\bar{k}} = {3}\) (only 2D). We tuned the phase θ from 0 to π for the signal and idler in steps of π/10 rad and measured the coincidence counts. The analytical expression for the intensities of the interfered signal as a function of phase θ is given by

$${C}_{2}{\left(\theta \right)} = {1+{\epsilon }_{2}\cos (2\theta )}$$
(7)
$${C}_{3}{\left(\theta \right)} = {3+2{\epsilon }_{3}\left[2\cos (2\theta )+\cos (4\theta )\right]}.$$
(8)

To fit these curves, we used the maximum of the noise background from the set of measurements as a lower bound of the curve. We were able to reach this limit because of the meticulous synchronization of the EOM frequency to the FSR, enabling perfect destructive interference. We did not subtract the background. From the parameter ϵD, which measures the deviation from the maximally entangled state, the visibility VD can be derived as

$${V}^{\,(2)}={\epsilon }_{2}$$
(9)
$${V}^{\,(3)} = {\frac{3{\epsilon }_{3}}{2+{\epsilon }_{3}}}.$$
(10)

Violation of the Bell inequality is achieved for \({\frac{1}{\sqrt{2}}\approx 0.7071 < {V}^{\,(2)}}\) and \({\frac{3\left(6\sqrt{3}-9\right)}{6\sqrt{3}-5}\approx 0.7746 < {V}^{\,(3)}}\), which is proof of the presence of entanglement18. We obtained values of \({V}_{2-3}^{\,(2)} = {0.975\pm 0.002}\) and \({V}_{3-4}^{\,(2)} = {0.976\pm 0.002}\) for qubits and \({V}_{2-3-4}^{\,(3)} = {0.968\pm 0.004}\) for qutrits, violating the Bell inequality. Note that the superscripts in parentheses denote the dimension of the quantum state and the subscripts represent the numbers of frequency bins on which the Bell test was performed.

Density matrix reconstruction

We used QST to reconstruct the density matrix from a tomographically complete set of projection measurements (quorum), described by projection wavevectors \({\left\vert {\psi }_{\nu }\right\rangle}\) (ref. 51). We thus expect the coincidence counts to be

$${n}_{v} = {C\left\langle {\psi }_{v}\right\vert \hat{\rho }\left\vert {\psi }_{v}\right\rangle}$$
(11)

for a constant C, depending on the measurement time, pair generation rate, losses and so on. Using our experimental data as nν, we reconstruct \({\hat{\rho }}\) using the relations18,51

$${\hat{\rho }} = {{C}^{-1}\mathop{\sum}\limits_{v}{M}_{v}{n}_{v}}$$
(12)
$${M}_{v} = {\mathop{\sum}\limits_{x}{\varGamma }_{x}{\left({B}^{-1}\right)}_{x,\,v}}$$
(13)
$${B}_{x,\,y} = {\left\langle {\psi }_{x}\right\vert {\varGamma }_{y}\left\vert {\psi }_{x}\right\rangle}$$
(14)
$${C} = {\mathop{\sum}\limits_{k}{n}_{k}\,\,{{\rm{for}}}\,\,{\rm{tr}}\left\{{M}_{k}\right\}} = {1}$$
(15)

For 2D we applied the \({\left\vert \overline{k}\right\rangle}\), \({\left\vert \overline{k}+1\right\rangle}\), \({\frac{1}{\sqrt{2}}\left(\left\vert \overline{k}\right\rangle +\left\vert \overline{k}+1\right\rangle \right)}\) and \({\frac{1}{\sqrt{2}}\left(\left\vert \overline{k}\right\rangle +i\left\vert \overline{k}+1\right\rangle \right)}\) projections for signal and idler, resulting in a total of 16 projection measurements.

For the 3D QST42, the method given in the last paragraph was extended and we applied the projections

$${\frac{1}{\sqrt{2}}\left(\left\vert \bar{k}\right\rangle +\left\vert \bar{k}+1\right\rangle \right)}$$
(16)
$${\frac{1}{\sqrt{2}}\left({\rm{e}}^{\frac{2\uppi }{3}i}\left\vert \bar{k}\right\rangle +{\rm{e}}^{-\frac{2\uppi }{3}i}\left\vert \bar{k}+1\right\rangle \right)}$$
(17)
$${\frac{1}{\sqrt{2}}\left({\rm{e}}^{-\frac{2\uppi }{3}i}\left\vert \bar{k}\right\rangle +{\rm{e}}^{\frac{2\uppi }{3}i}\left\vert \bar{k}+1\right\rangle \right)}$$
(18)
$${\frac{1}{\sqrt{2}}\left(\left\vert \bar{k}\right\rangle +\left\vert \bar{k}+2\right\rangle \right)}$$
(19)
$${\frac{1}{\sqrt{2}}\left({\rm{e}}^{\frac{2\uppi }{3}i}\left\vert \bar{k}\right\rangle +{\rm{e}}^{-\frac{2\uppi }{3}i}\left\vert \bar{k}+2\right\rangle \right)}$$
(20)
$${\frac{1}{\sqrt{2}}\left({\rm{e}}^{-\frac{2\uppi }{3}i}\left\vert \bar{k}\right\rangle +{\rm{e}}^{\frac{2\uppi }{3}i}\left\vert \bar{k}+2\right\rangle \right)}$$
(21)
$${\frac{1}{\sqrt{2}}\left(\left\vert \bar{k}+1\right\rangle +\left\vert \bar{k}+2\right\rangle \right)}$$
(22)
$${\frac{1}{\sqrt{2}}\left({\rm{e}}^{\frac{2\uppi }{3}i}\left\vert \bar{k}+1\right\rangle +{\rm{e}}^{-\frac{2\uppi }{3}i}\left\vert \bar{k}+2\right\rangle \right)}$$
(23)
$${\frac{1}{\sqrt{2}}\left({\rm{e}}^{-\frac{2\uppi }{3}i}\left\vert \bar{k}+1\right\rangle +{\rm{e}}^{\frac{2\uppi }{3}i}\left\vert \bar{k}+2\right\rangle \right)}.$$
(24)

Again, the surplus modes for signal and idler, which were not required for the specific projection, were blocked by a programmable filter. No count adjustment/correction was needed, as every projection we used consists of exactly two modes for signal and idler, respectively.

In reality, a density matrix corresponding to a physical quantum state has to be Hermitian and positive semi-definite. Due to experimental imperfections, this is usually not the case for a reconstructed matrix. This is treated by applying a maximum likelihood estimation, which is a numerical optimization finding the closest physical density matrix relative to the measurement data51.