Introduction

Almost 30 years after the discovery of superconductivity in Sr2RuO4 (SRO)1, the symmetry of its superconducting order parameter (SCOP) remains an open question. Initially, its similarities with 3Helium made it a prime candidate for spin-triplet pairing2, corroborated by various measurements3,4,5,6,7,8,9,10,11. Along with observations of time-reversal symmetry breaking (TRSB) supporting a two-component order parameter12,13, the superconducting (SC) state was believed for a long time to be a chiral p-wave spin-triplet. However, conflicting evidence presented in various studies remained to be explained14,15. First, the presence of nodal excitations is unexpected in a chiral p-wave SC16,17,18,19. Second, the low critical field Hc2 exhibited by SRO is typical for Pauli-limited spin-singlet SC20 and the transition into the normal state upon applying a magnetic field appears to be first-order21,22, with indications of a Fulde-Ferrell-Larkin-Ovchinnikov state for a certain parameter range, strongly pointing to a singlet SCOP23. Third, none of the topologically protected edge states predicted in chiral p-wave states were observed in experiments24,25,26,27, although this could be explained by a high Chern number28.

In recent years, the chiral p-wave picture has basically been dismissed. First, the careful replications of key nuclear magnetic resonance experiments previously interpreted as supporting spin-triplet pairing have highlighted a heating effect and instead concluded that the SCOP corresponds to spin-singlet pairs29,30,31. Second, applying uniaxial strain along the x principal crystallographic axis was found to enhance the critical temperature (Tc)32,33 and to lower the Fermi-liquid coherence scale34. This enhancement was shown to be maximal where the FS undergoes a Lifshitz transition, corresponding to a van-Hove singularity (vHs) in the density of states (DOS), at a time-reversal invariant momentum point, inconsistent with odd-parity SCOPs like p-wave35. Nowadays, a consensus appears to be crystallizing around the spin-singlet and even-parity natures of the SCOP, yet the debate is still ongoing. While ultrasound experiments support the conclusion of a two-component order parameter36,37 inferred by the observation of TRSB and the splitting between Tc and the TRSB transition temperature38,39, there are no two-temperature signatures in bulk thermodynamical experiments such as specific heat and elastocalorimetry as well as scanning SQUID microscopy40,41,42,43. As a result of this plethora of experimental evidence, SRO can be seen both as a critical playground for testing theories with the goal of potentially unifying some of these contradicting observations and as a testbed to verify whether our interpretations of specific experiments are valid. Either way, it constitutes an ideal system to considerably advance our understanding of the mechanisms for unconventional superconductivity44.

Many theoretical proposals have been put forward as potential SCOPs. Initially classified as a chiral p-wave45,46,47,48,49,50,51,52, the recent experimental evidence motivated further proposals, including two-dimensional states such as s + idxy53,54,55,56, \({d}_{{{{{\rm{x}}}}}^{2}-{{{{\rm{y}}}}}^{2}}+i{g}_{{{{\rm{xy}}}}({{{{\rm{x}}}}}^{2}-{{{{\rm{y}}}}}^{2})}\)56,57,58,59,60,61, a combination of even and odd-parity irreducible representations (irreps)62, inter-orbital pairing63,64, d + d65, and \({d}_{{{{{\rm{x}}}}}^{2}-{{{{\rm{y}}}}}^{2}}\) (plus odd-frequency)66,67,68,69. Some three-dimensional states were also proposed, for example, Eg dyz + idzx70,71 and helical px + py72.

A general overview of possible ordering states in terms of their irreducible representations is given in refs. 63,73.

In this paper, we investigate the leading superconducting instabilities of SRO using functional renormalization group (FRG) calculations74, applied to a realistic model of the electronic structure derived from density functional theory (DFT)75 that includes spin-orbit coupling (SOC). Note that previous studies of SRO using FRG were performed on tight-binding models, fitted to photoemission spectroscopy measurements46,48,59,76,77,78. In order to compare to experiments, we study the effect of uniaxial strain, tracking the evolution of Tc as well as the type of ordering. We find a phase diagram with two different magnetic orders that compete with a single SCOP transforming like the B1g irrep (often labeled as \({d}_{{{{{\rm{x}}}}}^{2}-{{{{\rm{y}}}}}^{2}}\)-wave). This competition is found to depend sensitively on the choice of interaction parameters. We show that a proper range of parameters leads to an increase of the superconducting Tc in good agreement with experiments.

Methods

Density functional theory

We use DFT75,79,80 and the Quantum ESPRESSO DFT package81,82 with the PBE exchange-correlation functional83 to calculate the electronic structure. Cell parameters and internal coordinates of the crystal structure in the I4/mmm space group are relaxed in the conventional cell until all force components are smaller than 1 mRy/a0 (a0: Bohr radius) and all components of the stress tensor are smaller than 0.5 kbar, yielding a relaxed in-plane (out-of-plane) lattice constant of a0 = 3.878 Å (c = 12.900 Å). To calculate the strained structures, we fix one in-plane lattice constant of the conventional cell to the strained value, anew = (1 − s)a0, and relax the two orthogonal cell parameters as well as the internal coordinates as described above. After relaxation, we use the corresponding primitive unit cells containing one ruthenium atom each, i.e., three t2g orbitals. We use scalar-relativistic ultrasoft pseudopotentials from the GBRV library84, with the 4s and 4p (2s) semicore states for both strontium and ruthenium (for oxygen) atoms included in the valence. In the scalar-relativistic approximation, the spin-orbit coupling term is dropped85. The energy cutoffs for the wave functions and charge density are set to 60 Ry and 720 Ry, respectively. We use a 12 × 12 × 12 Monkhorst-Pack k-point grid to sample the Brillouin-zone and a smearing of 0.01 Ry utilizing the Methfessel-Paxton scheme. To describe the low-energy physics we construct three ruthenium-centered t2g-like maximally localized Wannier functions for each strained structure using Wannier9086,87,88. Spin-orbit coupling is included by first performing the DFT calculation without it and then adding a local SOC λSOC = 200 meV to account for the correlation-induced enhancement over the DFT value.

Functional renormalization group

In order to account for strong local electronic correlations in this multi-orbital system, we consider the Hubbard-Kanamori interaction Hamiltonian89

$$\begin{array}{ll}{\hat{H}}_{{{{\rm{int}}}}}\,=\,\sum\limits_{{{{\rm{il}}}}}U{\hat{n}}_{{{{\rm{il}}}}}^{\uparrow }{\hat{n}}_{{{{\rm{il}}}}}^{\downarrow }+\sum\limits_{{{{{\rm{il}}}}}_{1}\ne {{{{\rm{l}}}}}_{2}}(U-2{J}_{{{{\rm{dd}}}}}){\hat{n}}_{{{{{\rm{il}}}}}_{1}}^{\uparrow }{\hat{n}}_{{{{{\rm{il}}}}}_{2}}^{\downarrow }\\\qquad\,\,\, \quad+\sum\limits_{{{{\rm{i}}}}\sigma {{{{\rm{l}}}}}_{1}\ne {{{{\rm{l}}}}}_{2}}(U-3{J}_{{{{\rm{dd}}}}}){\hat{n}}_{{{{{\rm{il}}}}}_{1}}^{\sigma }{\hat{n}}_{{{{{\rm{il}}}}}_{2}}^{\sigma }\\ \,\,\,\quad\qquad-\sum\limits_{{{{{\rm{il}}}}}_{1}\ne {{{{\rm{l}}}}}_{2}}{J}_{{{{\rm{ss}}}}}{\hat{c}}_{{{{{\rm{il}}}}}_{1}}^{\uparrow ,{\dagger} }{\hat{c}}_{{{{{\rm{il}}}}}_{1}}^{\downarrow }{\hat{c}}_{{{{{\rm{il}}}}}_{2}}^{\downarrow ,{\dagger} }{\hat{c}}_{{{{{\rm{il}}}}}_{2}}^{\uparrow }+\sum\limits_{{{{{\rm{il}}}}}_{1}\ne {{{{\rm{l}}}}}_{2}}{J}_{{{{\rm{ss}}}}}{\hat{c}}_{{{{{\rm{il}}}}}_{1}}^{\uparrow ,{\dagger} }{\hat{c}}_{{{{{\rm{il}}}}}_{1}}^{\downarrow ,{\dagger} }{\hat{c}}_{{{{{\rm{il}}}}}_{2}}^{\downarrow }{\hat{c}}_{{{{{\rm{il}}}}}_{2}}^{\uparrow }\end{array}$$
(1)

where U is the intra-orbital on-site Coulomb repulsion, while Jdd (Jss) is the density-density (spin-flip and pair hoping) part of the Hund’s coupling. In the rotationally invariant formulation where O(3) symmetry is satisfied, Jdd = Jss = J. Although usually equal, the distinct effect of Jdd and Jss when they are treated independently is discussed in Supplementary Note 2. Our calculations are performed in the regime of U/W = 0.3 − 0.5, with W being the total bandwidth and U being the Hubbard interaction. We restrict ourselves to a situation with an on-site Hubbard-Kanamori interaction, as with this type of interaction, we reproduce the dominant spin-spin susceptibilities peak position in comparison to the interacting spin-spin susceptibility measured in neutron scattering experiments90, see Supplementary Note 2. Any interaction resulting in an analog peak structure should give the same physical results, as we argue in Supplementary Note 5.

The strong electronic correlations emerging from the Hubbard-Kanamori interactions are incorporated to the non-interacting downfolded systems using the FRG74,91. FRG is technically an exact method to calculate the effective action function of a given quantum action. It does so by introducing a scale-dependent cutoff (here we use a sharp energy cutoff) in the non-interacting propagator of the system. By taking derivatives with respect to this cutoff, one generates an infinite hierarchy of flow equations. In practice, this hierarchy must be truncated to become numerically tractable, making the method perturbatively motivated.

In this work, we employ the standard level-2 truncation, neglecting all three and more particle vertices. The validity of this approximation in the weak-to-intermediate coupling regime can be motivated by a power-counting argument to prove the RG-irrelevance of higher-order terms74. Furthermore, we neglect the frequency dependence of the interaction, again motivated by the power-counting argument and the self-energy. This approach was applied to various systems including SRO46,48,76,77,78,92,93,94,95,96,97,98,99,100,101,102,103 and can be viewed as a diagrammatically unbiased extension of the random phase approximation.

In practice, we solve the flow equations from an energy scale much larger than the bandwidth and then integrate towards lower energies until we hit a divergence in one of the three diagrammatic channels labeled the particle-particle (PP), particle-hole (PH), and crossed particle-hole (\(\overline{\,{{\mbox{PH}}}\,}\)) channels. A divergence is associated with a phase transition as the corresponding susceptibility also diverges. Information on the ordering type can be extracted from the susceptibilities as well as linearized gap equations104.

We employ the truncated unity approximation which allows us to reduce the memory required computationally105,106,107.

For the FRG simulations, we use the TU2FRG code107. For convergence, we include all form-factors up to a distance of 8.2 Å, which amounts to a total number of 75 basis functions per orbital in the unit cell, i.e., all lattice harmonics up to the fifth (sixth) are included (depending on whether the constant is counted as harmonic or not). We checked for convergence by increasing the number of form-factors included near the phase transition between the magnetic and the superconducting phase for a few data points in the phase diagram. The simulations are performed on a 36 × 36 momentum-mesh in the x − y plane for the vertex function. The loop integration is performed using a FFT approach and an additional refinement of 45 × 45 is employed to achieve higher energy resolution. The results of the integration do not differ upon changing the resolution of the loop integration.

By using an enhanced value of the SOC, the effects of local interactions on SOC are already included on the single-particle level of the calculations. We do not suffer from double counting at that level since we neglect the flow of the self-energy. As a consequence, however, our calculation does not take into account the renormalized effective mass of quasi-particles.

Results

Electronic structure

To describe the low-energy electronic structure of SRO for the different strain values, we perform ab initio DFT calculations downfolded onto the t2g orbitals of the ruthenium atoms using maximally localized Wannier functions as detailed in the methods section. There is extensive literature using tight-binding Hamiltonians from ab initio electronic structure calculations based on DFT for SRO, presenting overall very consistent results at the DFT level. Beyond DFT, it was shown that replacing the local SOC parameter of 100 meV obtained within DFT with a value twice as large λSOC ≃ 200 meV yielded a considerably better agreement with the experimentally observed Fermi surface108, in consistent with the correlation-induced enhancement predicted theoretically109,110. Indeed, this parameter adjustment leads to improved agreement with the FS both in the unstrained case and with the experimentally observed critical strain108,109,110,111,112,113,114,115. A comparison to a selection of previously published tight-binding models is shown in Supplementary Note 1. Note that the addition of SOC breaks the SU(2) spin symmetry, but preserves an orbitally dependent SU(2) (so-called pseudospin) symmetry68. We keep the SOC fixed for all strain values.

In order to account for strong electronic correlations in this multi-orbital system, we use for most parts of this paper the O(3) symmetric Hubbard-Kanamori parametrization of the interaction Hamiltonian89, which involves two key energy scales: the on-site Hubbard repulsion U and the Hund coupling J - see methods. As done routinely in FRG calculations46,48,76,77,78,92,93,94,95,96,97,98,99,100,101,102,103, we neglect the flow of the self-energy in our calculations. Hence, the interaction parameters (U, J) should be considered as effective interactions with significance within our FRG framework rather than having a first-principle meaning. In this perspective, it is important to explore how the various instabilities are tuned by varying the interaction parameters. The guiding principles for constructing the model utilized follow two rules

  • We start from state-of-the-art DFT with added spin-orbit coupling λSOC such that we do have the right Fermi surface.

  • The choice of our interaction parameters is restricted in such a manner that, from the Wannier model defined above, we recover the correct peak positions of the interacting spin-spin susceptibility as measured in experiments.

The FS and the density of states (DOS) obtained from this downfolded t2g model are displayed in Fig. 1. The left column corresponds to the unstrained system (ϵxx = 0) and the right columns to the optimally uniaxially strained system for which the Fermi level is at the vHs (\({\epsilon }_{{{{\rm{xx}}}}}={\epsilon }_{{{{\rm{xx}}}}}^{{{{\rm{vHs}}}}}\)). Note that \({\epsilon }_{{{{\rm{xx}}}}}^{{{{\rm{vHs}}}}}\) does not include quasi-particle renormalization and therefore is not the same value as in experiments. The D4h space group symmetry of the unstrained system is lowered down to D2h by uniaxial strain and the B1g irreducible representation of D4h, of greatest relevance to our study, turns into the Ag irreducible representation of D2h.

Fig. 1: Partial density of states and Fermi surface for the three t2g orbitals.
figure 1

Unstrained (a, c) and the optimally strained (b, d) systems. The optimal stain of 0.8% corresponds to the system being closest to the Lifschitz transition. Here, a (b) is the lattice parameter in the x (y) direction, with a = b in the ϵxx = 0 case. The black dots indicate the position of the vHs of the dxy orbital. The three dominant spin-density wave ordering vectors q1, q2, and q3 are highlighted in black, gray, and pink, respectively. The first Brillouin-zone is marked by a black square. We mark the Γ and Z points by red crosses. Furthermore, we labeled the α, β, and γ sheets on the FS for ϵxx = 0. In the unstrained case, the partial DOS for the dxz and dyz orbitals is identical, which is emphasized by the color mixing.

Full size image

Note the slightly unusual presentation of the FS in Fig. 1: this is due to the transformation from a tetragonal basis into a x–y plane which has to be done in this fashion to ensure the periodicity of the downfolded model in the two-dimensional primitive cell. Due to this, we have not a single but two kz values in the first primitive cell, i.e., the Z-point is located at the corner of the black square. All the results that follow are obtained for the quasi-2D model restricted to kz = 0 and kz = 2π/c, shown in Fig. 1. We verify that they agree with the results from full 3D calculations in Supplementary Note 6.

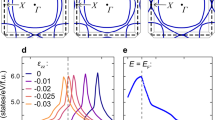
The lowering of the symmetry under uniaxial strain lifts the degeneracy between the dxz and the dyz orbitals of the ruthenium atom, as seen in the DOS in Fig. 2. It also splits the dxy van-Hove singularity into two parts: one drifting away from the FS (x-direction) and one drifting towards the FS and crosses it at the Lifschitz transition (\({\epsilon }_{{{{\rm{xx}}}}}^{{{{\rm{vHs}}}}} \sim 0.8 \%\) strain). On the FS shown in Fig. 2, we also highlight the dominant nesting vectors of the bare particle-hole susceptibility (\({\chi }_{{{{\rm{PH}}}}}^{0}\)), see Supplementary Note 2. First, q1 = (2π(3a)−1, π(3b)−1) (and all those related by symmetry) connects the α and β sheets of the FS. Second, q2 = (π(2a)−1, π(2b)−1) is connecting two van-Hove singularities and should become relevant at large interactions. Third, q3 = (π(3a)−1, π(3a)−1) also connects the α and β sheet of the FS. These vectors are consistent with the dominant spin-fluctuations observed in neutron scattering experiments90,116. Note that there is a family of nesting vectors connecting α and β sheets, all close to q1.

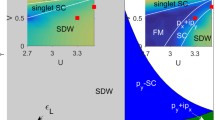
Fig. 2: Phase diagrams in the U-J parameter space.
figure 2

In (a), we visualize the unstrained and in (b) the strained systems. The background color indicates the critical scale Λc, proportional to the ordering energy scale, with the corresponding colorbar on the right. The phases are either a B1g superconductor (Ag under uniaxial strain), two different spin-density waves (SDWs), or a Fermi-liquid (FL). The q-vectors associated with the SDWs are shown in Fig. 1.

Full size image

With these insights from the non-interacting FS and DOS in mind, we proceed with the phase diagrams as a function of U and J for the unstrained and the \({\epsilon }_{{{{\rm{xx}}}}}={\epsilon }_{{{{\rm{xx}}}}}^{{{{\rm{vHs}}}}}\) cases. The results are presented in Fig. 2. The background color corresponds to the energy scale Λc (expressed in meV) at which a divergence of the corresponding coupling is observed. The fastest divergent coupling corresponds to the dominant instability, which can either be superconductivity (in which case Λc is expected to be proportional to the Berezinskii-Kosterlitz-Thouless117,118,119 critical temperature TBKT) or a spin-density wave (SDW) (in which case Λc can be interpreted as the characteristic scale associated with the growth of the correlation length) (Because of Mermin-Wagner theorem (which is not obeyed by FRG), a finite Tc is expected for the BKT transition into the SC phase, while Tc = 0 for an SDW breaking SU(2)).

At the lowest U and J values, we find no divergence down to the lowest energy scale resolvable with our momentum resolution and thus conclude that the system remains in the Fermi-liquid (FL) state down to that scale. Apart from this unique point, we find three types of instabilities. Up to moderate U and low but finite J, we find a \({{{{\rm{d}}}}}_{{x}^{2}-{y}^{2}}\) superconducting instability (corresponding to B1g symmetry for the unstrained system, turning into Ag for the strained one). Upon increasing U or J, we find that the dominant instability becomes an SDW with ordering vector q1. At even larger U and J, the system undergoes a high-temperature transition to another SDW phase characterized by the ordering vector q2. These ordering vectors are visible in both non-interacting and interacting susceptibilities. Since we do not incorporate the effect of the self-energy, we cannot observe the shift of the q3 peak observed in ref. 55.

Phase diagram and magnetic orderings

The q1-SDW is driven by strong nesting between the α and β sheets. A corresponding peak in the spin-spin susceptibility has been well discussed both in the context of experimental observations6,120 and theoretical discussions54,67. It should be noted that this vector connects two different values of kz when backfolded in the three-dimensional Brillouin-zone. Its in-plane analog, q3 = (π(3a)−1, π(3a)−1), was found to be subleading in earlier three-dimensional studies using the random phase approximation (RPA)54. The q3 peak is also found in DMFT calculations including vertex corrections55,121. Here, we find the q1 ordering to be the leading one, with the q3 ordering also diverging but with a smaller absolute magnitude. The increase of Λc can be understood in terms of the Stoner criterion being fulfilled at a larger scale for larger U or J. At higher energy scales, the vHs are strongly smeared. This effect increases the importance of the q2 ordering vector connecting two vHs points, leading to the emergence of the q2-SDW phase.

When applying uniaxial strain, the parameter range where we find an SDW is increased. This can be understood from the increase of the DOS at the Fermi level, which leads to a larger \({\chi }_{{{{\rm{PH}}}}}^{0}\) and thereby a smaller interaction is required to fulfill the Stoner criterion. Beyond this effect, straining does not affect the structures of the phases and the q2-phase is still observable in the same parameter region, as the changes of the FS due to strain have counteracting effects: while in the y-direction the FS touches the vHs, drifts further away from it in the x-direction.

Note that as we increase the strain beyond the Lifschitz transition, we do not find the SDW that is observed in experiments38,41. The emergence of this phase has been understood as the removal of all curvature of the γ sheet between the upper/lower vHs and the \(X/{X}^{{\prime} }\) points, which leads to strong nesting along this direction122. We do not observe this phase at any investigated strain value. As was pointed out in ref. 123, strain suppresses quantum fluctuations preventing the ordered magnetic state, such that at high strain the phase transition emerges. Therefore, observing this transition in a diagrammatically unbiased approach is currently out of reach numerically, as it would require a full inclusion of the frequency dependence as well as multi-loop contributions124. We hope to overcome this shortcoming in the future.

Superconductivity

In the following, the superconducting phase is analyzed using a linearized gap equation on the FS. As shown in Fig. 3, we find a gap that transforms according to a B1g for ϵxx = 0 (Ag for \({\epsilon }_{{{{\rm{xx}}}}}={\epsilon }_{{{{\rm{xx}}}}}^{{{{\rm{vHs}}}}}\)) representation of the D4h (D2h) point groups. In the band basis, this state has a dominant overlap with the \({d}_{{{{{\rm{x}}}}}^{2}-{{{{\rm{y}}}}}^{2}}\) harmonic and its main weight stems from the dxy orbital. Such a type of superconductor has been observed in several other studies53,54,58,59,66,67,68,122,125. Although spin-orbit mixing distributes pairing over the different FS sheets, the dominant dxy orbital character that we find does lead to a larger pairing on the γ sheet. It should be noted however that experiments indicate that the gap function is sizeable on all three Fermi surface sheets. This potential difficulty could be resolved by employing an analysis based on the combination of FRG and mean-field theory126.

Fig. 3: Example of superconducting order parameters found in Fig. 2, calculated from a linearized gap equation in orbital space.
figure 3

They correspond to U = 1.1 eV and J = 0.22 U. The 3 × 3 matrices represent the spin-orbital states of the paired electrons in the inter-pseudospin channel since the intra-pseudospin terms are vanishing. Each panel shows the momentum structure. We present in a, b the unstrained case with ϵxx = 0 and the optimally strained case with \({\epsilon }_{{{{\rm{xx}}}}}^{{{{\rm{vHs}}}}}\) respectively. The SCOP transforms like the one-component B1g (Ag) irreducible representation of the D4h (D2h) group which requires some components to be purely imaginary due to the transformation behavior of the spin-orbitals under rotational symmetries68. Since the gap function is only known up to a prefactor, we rescale it from −1 to 1, and the sign and value are encoded in the colorbar. The first Brillouin-zone is marked by the gray square.

Full size image

The spectrum of the pair-pair susceptibility at Λc contains the information of all possible subleading SCOPs. By analyzing this spectral distribution, we find a clear separation of the eigenvalue of the \({d}_{{{{{\rm{x}}}}}^{2}-{{{{\rm{y}}}}}^{2}}\) superconducting state by at least one order of magnitude from all eigenvalues of other SCOPs, for all parameters investigated. While this excludes any immediate degenerate state, no statement about the proximity of different symmetry states or individual critical temperatures can be drawn from FRG, because within this method the dominant instability is signaled by a divergent coupling and susceptibility (Again we stress that Λc is not to be confused with the leading eigenvalue from an Eliashberg calculation λ. Most importantly, we have Λc ∝ Tc instead of the exponential suppression from the gap equation). However, from the hierarchy standpoint, we still can extract tendencies toward different orderings as discussed in Supplementary Note 3. This hierarchy reveals that the p-wave pairing state46,48,78 is always clearly subleading by a large margin and both extended s-wave and g-wave are consistently closer to the d-wave. We simulate the full 3D model at a selected point to check for the consistency of our 2D simulations. The results of these 3D simulations are shown in Supplementary Note 6 and agree with the 2D results.

The superconducting phase is generated by a spin-fluctuation mechanism. The couplings U and J are crucial tuning knobs determining the onset of the phase and also control the transition to the neighboring magnetic phase. When increasing U, the transition to an SDW is understood from the underlying ladder-type diagrams diverging as soon as U becomes larger than the critical value. Below that critical U, the still strong spin-fluctuations can drive a superconducting instability. However, increasing J has a more complex effect since it affects two different physical processes, which we discuss in terms of two distinct couplings, Jss and Jdd in Eq. (1). Jss promotes spin-flip and pair-hopping processes, thus reducing the tendency to order magnetically while also increasing pair-correlations. Jdd decreases inter-orbital density-density interactions, which reduces the inter-orbital repulsion between electrons on the same site. We unravel which of the two effects is most relevant for a) superconductivity and b) the magnetic transition. This is achieved by varying the two quantities independently, first in a simple RPA calculation and then in a full FRG calculation.

For the simple RPA calculation, we calculate \({\chi }_{{{{\rm{PH}}}}}^{0}\) at Λ = 11.6 meV. We chose U = 0.3 eV to circumvent the Stoner instability and vary Jss and Jdd between 0.0U and 0.3U independently. The dominant components of the bare susceptibility are presented in Supplementary Fig. 5 of Supplementary Note 4. In general, we observe that varying Jss has barely any effect on \({\chi }_{{{{\rm{PH}}}}}^{{{{\rm{RPA}}}}}\). Jdd, on the other hand, increases the inter-orbital components by a significant amount. Therefore we expect Jss to have a weaker impact on the superconducting transition. Physically this is expected since Jss hampers the spin-fluctuations that are required to obtain an effective attraction required by the superconducting state. To support this claim and understand better the underlying interference mechanism, we developed a simple 2-band toy model in Supplementary Note 4.

In the full FRG simulation, we verify these conclusions, i.e., increasing Jss leads to a transition only at much larger values than the one for Jdd. See Supplementary Fig. 5. Interestingly, Jss will generate a stronger admixture of higher-order angular momentum superconductivity hosted by the dyz and dxz orbitals. These are however still subleading to the \({d}_{{{{{\rm{x}}}}}^{2}-{{{{\rm{y}}}}}^{2}}\) superconducting state.

Influence of strain

Finally, we compare our results with experiments. We do so by examining the effect of strain from ϵxx = 0.0% to ϵxx = 1.3% on the leading instability of different (U, J) combinations. The general behavior of Tc is consistent with earlier studies76,122,127, while the predicted phases partially differ. The different critical scales Λc can be interpreted as an estimate for Tc of the instability. The results for all superconducting data points are summarized in Fig. 4.

Fig. 4: Effect of strain ϵxx on the critical scale Λc, the density of states and comparision to experiments.
figure 4

Effect of strain ϵxx on the critical scale Λc for different values of U and J (a) and values of U and J for each line given in the upper right. DOS in the dxy orbital depends on ϵ (b) and theoretically predicted enhancement of Λc due to uniaxial strain as a function of its value for ϵxx = 0 (c). Each dotted line in the upper left plot corresponds to one U − J combination given in the upper right. There is a clear correlation between Λc(ϵxx = 0) and the ratio of increase in Tc which can be seen in both a, c. The experimental data points in c are extracted from ref. 33. A proposed mechanism that explains this enhancement is detailed in the text.

Full size image

For systems that start with a large initial critical scale at zero strain (Λc(ϵxx = 0)), no significant enhancement with respect to strain is found. The enhancement of Tc is much larger when Λ(ϵxx = 0) is smaller. This effect can be understood by looking at the DOS: large energy scales, or large temperatures, correspond to smeared-out features in the DOS. Thus, the shift of the vHs due to strain is irrelevant since the vHs are not resolved, i.e., the DOS at the Fermi level does not change under strain. The lower Λc, the sharper the vHs will become. Therefore, its shift enhances the DOS at the FS more strongly which in turn leads to a larger increase of Tc. Thus, a lower Λc(ϵxx = 0) yields an enhancement of Tc with ϵxx which is both larger and takes place over a narrower range of strain. Once the vHs have crossed the Fermi level, Tc is expected to go down again since we rapidly reduce the DOS at the Fermi level when straining further. Note that the nesting which generates the attractive interaction is not strongly asymmetric under strain, as can be seen in Fig. 1. Therefore, it cannot explain the asymmetry of ΛC observed in Fig. 4. However, the density of states is asymmetric, see Fig. 4, giving rise to the observed asymmetry in ΛC.

To compare our results to experiments, we evaluate \({\Lambda }_{c}({\epsilon }_{{{{\rm{xx}}}}}^{{{{\rm{vHs}}}}})/{\Lambda }_{c}({\epsilon }_{{{{\rm{xx}}}}}=0)\) and plot it versus Λc(ϵxx = 0), hence measuring the increase of the critical scale depending on the initial one. We extract the corresponding experimental values from ref. 33 by calculating the ratio of the maximal Tc and the Tc at ϵxx = 0. These results are summarized in Fig. 4. We observe that the experiments indeed fit the data predicted by FRG and we can extract a line of U and J combinations along which the experiment is reproduced. We find that the values on the line are around U = 1.1, 1.4 eV, and J = 0.143 U, 0.1 U. Again, we emphasize that these should be considered as effective values valid within our FRG formalism.

Discussion

In summary, we studied SRO starting from a first-principles description of its electronic structure and using a diagrammatically unbiased FRG approach. Using this framework, we investigated the influence of uniaxial strain as well as the different contributions of Hund’s coupling. We identified that the inter-orbital interaction reduction due to the density-density term Jdd is the main driving force favoring superconducting order, which we found to be a pseudospin-singlet \({d}_{{{{{\rm{x}}}}}^{2}-{{{{\rm{y}}}}}^{2}}\). Lastly, we showed that the experimental increase of Tc as a function of strain can be recovered on a quantitative level from FRG simulations and from a comparison to these experiments we extracted effective values of the interaction parameters.

Our results highlight the dominance of a single \({d}_{{{{{\rm{x}}}}}^{2}-{{{{\rm{y}}}}}^{2}}\) SCOP that transforms like the B1g representation (Ag under uniaxial strain). We note that, while this SCOP agrees with many experimental measurements, it cannot explain the evidence for two-components and time-reversal symmetry breaking. From the experimentally observed behavior of the time-reversal symmetry condition, we can infer that a partner of our found SCOP is required to remain invariant under moving the vHs through the Fermi level. This condition would be for example fulfilled by states with nodal lines along the x direction60,61 or odd-frequency superconductors68,69.

An interesting direction for future studies would be to investigate the effect of interaction terms consistent with D4h symmetry but breaking full cubic symmetry. This could potentially influence the competition between different low-energy orders109. There are also many potential routes toward a more accurate investigation of the superconducting state. First, even though SRO is nearly perfectly layered, including the third spatial dimension increases the number of allowed ordering types73. Secondly, taking into account the frequency dependence of the gap function and self-energy would allow us to gauge the relevance of the proposed odd-frequency state. Finally, an important advance would be to start the FRG flow from a correlated starting point, i.e., from dressed quasi-particles and their effective interactions. This could for example be achieved by starting the FRG from a DMFT128 description of the normal state.