A hybrid framework for estimating nonlinear functions of quantum states

Abstract

Estimating nonlinear functions of quantum states, such as the moment ${{{\rm{tr}}}}({\rho }^{m})$, is of fundamental and practical interest in quantum science and technology. Here we show a quantum-classical hybrid framework to measure them, where the quantum part is constituted by the generalized swap test, and the classical part is realized by postprocessing the result from randomized measurements. This hybrid framework utilizes the partial coherent power of the intermediate-scale quantum processor and, at the same time, dramatically reduces the number of quantum measurements and the cost of classical postprocessing. We demonstrate the advantage of our framework in the tasks of state-moment estimation and quantum error mitigation.

Introduction

Quantum measurement is one of the fundamental building blocks of quantum physics, connecting the quantum world to its classical counterpart. The linear expectation value of the quantum state ρ in the form ${{{\rm{tr}}}}(O\rho )$ can be measured directly in the basis of the observable O by Born’s rule. However, the measurement of nonlinear functions, such as the Rényi entropy and the moment ${P}_{m}={{{\rm{tr}}}}({\rho }^{m})$, generally involves quantum circuits interfering among m copies of the state ρ by the generalized swap test^1,2,3,4, which transform nonlinear functions to linear ones on all that copies. Although there are significant experimental advances for the m = 2 case^5,6,7,8, it is still challenging to extend to a larger degree m with a moderate system size on current quantum platforms⁹.

Recently, alternative approaches based on the randomized measurement (RM)¹⁰, such as the shadow estimation^11,12, are proposed. By postprocessing the results from random basis measurements of sequentially prepared states, the shadow estimation is efficient for measuring local observables and the fidelity to some entangled states. However, when measuring nonlinear functions, such as the purity P₂, RM protocol inevitably needs an exponential number of measurements and postprocessings^12,13,14, which hinders its further applications for large systems.

By trading off the swap test and the RM protocol, here we propose a hybrid framework for estimating nonlinear functions of quantum states to fill the gap between them, which inherits their advantages and reduces weaknesses. Specifically, one can conduct RM on a few jointly prepared copies of the state by utilizing the partial coherent power of the quantum processor, and then estimate many nonlinear functions in a more efficient way, i.e., less demanding on both the quantum hardware and classical post-processing.

The nonlinear function of quantum states ${\{{\rho }_{i}\}}_{i = 1}^{m}$ with some observables ${\{{O}_{i}\}}_{i = 1}^{m}$ of interest reads

$${{{\rm{tr}}}}({O}_{1}{\rho }_{1}{O}_{2}{\rho }_{2}\cdots {O}_{m}{\rho }_{m}),$$

(1)

which is general and includes, such as the state overlap and fidelity^15,16,17, the purity and higher-order moments^18,19, quantum Fisher information²⁰, out-of-time-ordered correlators^21,22, and topological invariants^23,24. For simplicity, hereafter we mainly adopt the moment function P_m to illustrate the framework, where ${O}_{i}={{\mathbb{I}}}_{d}$ and ρ_i = ρ in Eq. (1), and assume ρ is an n-qubit state, i.e., $\rho \in {{{{\mathcal{H}}}}}_{d}={{{{\mathcal{H}}}}}_{2}^{\otimes n}$ with d = 2ⁿ.

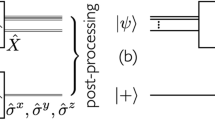
Before moving to the following Results, let us first take a quick review of the swap test and the RM protocol for measuring P_m, respectively. The moment can be written as ${P}_{m}={{{\rm{tr}}}}({S}_{m}{\rho }^{\otimes m})$, with S_m the shift operation on ${{{{\mathcal{H}}}}}_{d}^{\otimes m}$ satisfying ${S}_{m}\left\vert {{{{\bf{b}}}}}_{1},{{{{\bf{b}}}}}_{2}\cdots \,,{{{{\bf{b}}}}}_{m}\right\rangle =\left\vert {{{{\bf{b}}}}}_{2},\cdots {{{{\bf{b}}}}}_{m},{{{{\bf{b}}}}}_{1}\right\rangle$, with each $\{\left\vert {{{\bf{b}}}}\right\rangle \}$ the basis of each copy. Using the swap test, one can measure P_m efficiently with complete coherent control over multiple copies of the state, as illustrated in Fig. 1a. In particular, one initializes a control qubit and prepares the m-copy state ρ^⊗m, and then conducts the Controlled-shift operation

$${{{{\rm{CS}}}}}_{m}={\left\vert 0\right\rangle }_{c}\left\langle 0\right\vert \otimes {{\mathbb{I}}}_{{d}^{m}}+{\left\vert 1\right\rangle }_{c}\left\langle 1\right\vert \otimes {S}_{m}.$$

(2)

Finally one measures the control qubit to get the value of P_m^1,2. The corresponding quantum circuit requires a quantum processor with a total of N = nm + 1 qubits. Although the shift operation on m-copy can be expressed as a product of 2-copy swap operations, this approach would significantly increase the quantum circuit depth. Furthermore, preparing m copies of the state in parallel imposes stringent demands on quantum memories. Therefore, the generalized swap test presents significant challenges for cases where m ≥ 3.

Fig. 1: Illustrations of generalized swap test, shadow protocol¹², and hybrid shadow protocol.

All these three protocols in (a) (b) and (c) can be divided into two phases, the quantum experiment and the classical postprocessing labeled by green arrows. In (c) of hybrid shadow protocol, one measures not only the control qubit but also the last copy of ρ after the random evolution U. The information of U and measurement results ${\hat{b}}_{c}$ and $\widehat{{{{\bf{b}}}}}$ are used to construct the unbiased estimator $\widehat{{\rho }^{t}}$ according to Eq. (6), and thus estimate t-degree function ${o}_{t}={{{\rm{tr}}}}(O{\rho }^{t})$ directly. One can also patch them together to estimate higher-degree functions like ${P}_{m}={{{\rm{tr}}}}({\rho }^{m})$ by Eq. (8). Note that the collected RM results can also be processed with other postprocessing protocols¹⁰, as shown in Proposition 2 for P₃.

The RM toolbox¹⁰ was recently developed to ease the experimental challenge mentioned above^25,26,27. Compared with swap test, one only needs to control a single-copy state to realize the estimation. For shadow estimation¹², independent snapshots of the state $\{{\widehat{\rho }}_{(i)}\}$ can be constructed using data conllected in RMs, as shown in Fig. 1b. This is referred to as the shadow set and has the property that the expectation ${\mathbb{E}}({\widehat{\rho }}_{(i)})=\rho$. Denote the random unitary evolution sampled from some ensemble as $U\in {{{\mathcal{E}}}}$, and the Z-basis measurement result as b = {b₁b₂ ⋯ b_n} ∈ {0, 1}ⁿ,

$$\widehat{\rho }={{{{\mathcal{M}}}}}^{-1}\left({U}^{{\dagger} }\left\vert \widehat{{{{\bf{b}}}}}\right\rangle \left\langle \widehat{{{{\bf{b}}}}}\right\vert \widehat{{{{\bf{b}}}}}U\right),$$

(3)

where $\widehat{{{{\bf{b}}}}}$ is a random variable with probability $\left\langle {{{\bf{b}}}}\right\vert U\rho {U}^{{\dagger} }\left\vert {{{\bf{b}}}}\right\rangle$, and the inverse (classical) postprocessing channel ${{{{\mathcal{M}}}}}^{-1}$ is determined by the chosen ${{{\mathcal{E}}}}$^{12,28,29,30,31}. For instance, ${{{\mathcal{E}}}}$ can be the global or local Clifford ensemble, denoted as Clifford and Pauli measurements hereafter, respectively. After constructing the shadow set, the unbiased estimator of P_m can be constructed as

$${{{\rm{tr}}}}\left({S}_{m}{\widehat{\rho }}_{(1)}\otimes {\widehat{\rho }}_{(2)}\otimes \cdots {\widehat{\rho }}_{(m)}\right).$$

(4)

In principle, any nonlinear function can be obtained with only an n-qubit quantum processor using sequential RMs. However, the number of measurements needed generally scales exponentially with the qubit number, and the scaling becomes worse for larger m values, such as m≥3^12,13.

Results

Hybrid framework for nonlinear functions

By trading off the quantum and classical resources, here we develop a hybrid framework for nonlinear functions. All proofs and more detailed discussions are left in Supplementary Notes 1-4.

For a nonlinear function of degree m such as P_m, where $m=\sum\nolimits_{i = 1}^{L}{m}_{i}$, we demonstrate that it can be estimated using a quantum processor with only $N=n(\mathop{\max }_{i}{m}_{i})+1$ qubits. The core idea is to conduct RM on ρ^t, where t = m_i, by leveraging the coherent operation on t copies of ρ. Note that as t = 2 one needs the 3-qubit Controlled-swap operation also known as quantum Fredkin gate^32,33, by observing that the swap operation can be decomposed to qubit-wise ones. Quantum Fredkin gate has been realized, say, in the photonic system³⁴.

Instead of directly reading the control qubit outcome to obtain P_t, as in the swap test, we perform RM on one of the prepared t copies of ρ. As the permutation symmetry holds, the RM can be performed on any copy, like the final one shown in Fig. 1c. By measuring the expectation value of the Pauli-X operator on the control qubit and performing the projective measurement on the final copy, we obtain

$$\begin{array}{ll}{{{\rm{tr}}}}[{X}_{c}\otimes {{\mathbb{I}}}_{d}^{\otimes (t-1)}\otimes \left\vert {{{\bf{b}}}}\right\rangle \left\langle {{{\bf{b}}}}\right\vert \,U\,{{{{\rm{CS}}}}}_{t}\,\left({\left\vert +\right\rangle }_{c}\left\langle +\right\vert \otimes {\rho }^{\otimes t}\right)\,{{{{\rm{CS}}}}}_{t}^{{\dagger} }\,{U}^{{\dagger} }]\\ =\frac{1}{2}\left\{{{{\rm{tr}}}}[{X}_{c}{\left\vert 1\right\rangle }_{c}\left\langle 0\right\vert ]{{{\rm{tr}}}}\left[\left\langle {{{\bf{b}}}}\right\vert U{S}_{t}{\rho }^{\otimes t}\,{U}^{{\dagger} }\left\vert {{{\bf{b}}}}\right\rangle \right]\right.\\ \quad+{{{\rm{tr}}}}[{X}_{c}{\left\vert 0\right\rangle }_{c}\left\langle 1\right\vert ]{{{\rm{tr}}}}[\left\langle {{{\bf{b}}}}\right\vert U{\rho }^{\otimes t}{S}_{t}^{{\dagger} }\,{U}^{{\dagger} }\left\vert {{{\bf{b}}}}\right\rangle]\left.\right\}\\ =\left\langle {{{\bf{b}}}}\right\vert U{\rho }^{t}{U}^{{\dagger} }\left\vert {{{\bf{b}}}}\right\rangle .\end{array}$$

(5)

Here the identity operators ${{\mathbb{I}}}_{d}^{\otimes (t-1)}$ are on the first t − 1 copies, and the projective measurement $\left\vert {{{\bf{b}}}}\right\rangle \left\langle {{{\bf{b}}}}\right\vert$ and random unitary U is on the final t-th copy, as shown in Fig. 2. The result in the last line indicates that one can effectively conduct RM on ρ^t.

Fig. 2: The demonstration of Eq. (5) by the tensor diagram.

The vertical dotted lines denote the periodic boundary condition, i.e., the trace operation. The shift operation S_t and its conjugate ${S}_{t}^{{\dagger} }$ are represented by the cyclic permutations of the indices (legs) of the t copies of ρ.

The full measurement procedure is listed in Algorithm 1, which aims to construct the shadow set ${\{{\widehat{{\rho }^{t}}}_{(i)}\}}_{i = 1}^{M}$ of ρ^t from the RM results collected in Fig. 1c, and these shadow snapshots can be used to estimate more complex nonlinear functions. We show the general form of the hybrid framework in Supplementary Note 2 for the m-degree function in Eq. (1). We also remark that other postprocessing strategies on these RM data could also be adopted for some specific functions of the state^18,19,35, like state overlap.

Algorithm 1

Hybrid shadow estimation

Input: M × K sequentially prepared ρ^⊗t and control qubit initially set as ${\left\vert 0\right\rangle }_{c}$.

Output: The shadow set ${\{{\widehat{{\rho }^{t}}}_{(i)}\}}_{i = 1}^{M}$.

1: for i = 1 to M do

2: Randomly choose $U\in {{{\mathcal{E}}}}$ and record it.

3: for j = 1 to K do

4: Conduct the quantum circuit shown in Fig. 1c.

5: Measure the control qubit and the final copy of ρ^⊗t in the computational basis $\{\left\vert {b}_{c}\right\rangle \}$ and $\{\left\vert {{{\bf{b}}}}\right\rangle \}$.

6: Construct the unbiased estimator ${\widehat{{\rho }^{t}}}_{(i)}^{(j)}$ using the results ${b}_{c}^{(i,j)}$ and b^(i, j) by Eq. (6), where i and j denoting the jth measurement under the i-th unitary.

7: end for

8: Average K results under the same unitary to get ${\widehat{{\rho }^{t}}}_{(i)}=\frac{1}{K}{\sum }_{j}{\widehat{{\rho }^{t}}}_{(i)}^{(j)}$.

9: end for

10: Get the shadow set $\left\{{\widehat{{\rho }^{t}}}_{(1)},{\widehat{{\rho }^{t}}}_{(2)},\cdots {\widehat{{\rho }^{t}}}_{(M)}\right\}$, which contains M independent estimators of ρ^t.

Theorem 1

Suppose one conducts the circuit shown in Fig. 1c for once (M = K = 1), the unbiased estimator of ρ^t shows

$$\widehat{{\rho }^{t}}:= {(-1)}^{{\widehat{b}}_{c}}\cdot {{{{\mathcal{M}}}}}^{-1}\left({U}^{{\dagger} }\left\vert \widehat{{{{\bf{b}}}}}\right\rangle \left\langle \widehat{{{{\bf{b}}}}}\right\vert U\right),$$

(6)

such that ${{\mathbb{E}}}_{\{U,{b}_{c},{{{\bf{b}}}}\}}\left(\widehat{{\rho }^{t}}\right)={\rho }^{t}$. Here b_c and b are the measurement results of the control qubit and the final copy from ρ^⊗t, respectively; the inverse classical postprocessing ${{{{\mathcal{M}}}}}^{-1}$ depends on the random unitary ensemble applied.

Furthermore, to evaluate ${o}_{t}={{{\rm{tr}}}}(O{\rho }^{t})$ with O being some observable, the variance shows

$$\begin{array}{ll}{{{\rm{Var}}}}(\widehat{{o}_{t}})\,=\,{{{\rm{Var}}}}\left[{{{\rm{tr}}}}(O\widehat{\rho })\right]+\left[{{{\rm{tr}}}}{(O\rho )}^{2}-{{{\rm{tr}}}}{(O{\rho }^{t})}^{2}\right]\\ \qquad\qquad\le \,\parallel {O}_{0}{\parallel }_{{{{\rm{shadow}}}}}^{2}+{{{\rm{tr}}}}{(O\rho )}^{2}\end{array}$$

(7)

where ${{{\rm{Var}}}}\left[{{{\rm{tr}}}}(O\widehat{\rho })\right]$ is the variance of measuring O on the original single-copy shadow snapshot $\widehat{\rho }$, which can be upper bounded by the square of shadow norm ∥O₀∥_shadow¹² for the traceless operator ${O}_{0}=O-{{{\rm{tr}}}}(O){{\mathbb{I}}}_{d}/d$.

Theorem 1 is the central result of this work, which gives the unbiased estimator of ρ^t and also relates the statistical variance to the previous single-copy one, i.e., t = 1¹². The proof and related discussions are left in Supplementary Note I. Note that the shadow norm is also related to the chosen random unitary ensemble¹². According to Eq. (7), the hybrid shadow can dramatically reduce the variance of estimating nonlinear functions compared with the original shadow protocol. Take the Pauli measurement as an example, for a k-local observable O, the shadow norm $\parallel {O}_{0}{\parallel }_{{{{\rm{shadow}}}}}^{2}\le {4}^{k}\parallel O{\parallel }_{\infty }^{2}$¹² and thus the variance of evaluating ${{{\rm{tr}}}}(O{\rho }^{t})$ is independent of the total qubit number n by Eq. ((7)). However, the variance of the original shadow protocol shows an exponential scaling with n^12,13. This point is also clarified by the numerical result in Fig. 3a. We will discuss this advantage in detail in the application of quantum error mitigation later.

Fig. 3: Scaling of errors and the measurement times using OS, HS, and HR protocols.

Here the state is the noisy n-qubit GHZ state $\rho =0.8\left\vert {{{\rm{GHZ}}}}\right\rangle \left\langle {{{\rm{GHZ}}}}\right\vert {{{\rm{GHZ}}}}+0.2{{\mathbb{I}}}_{d}/d$. The random Pauli measurements are used for (a), (c), and (d), and the random Clifford measurements are used for (b). In (a), (b), and (c), we set M = 10 and K = 1 for OS and HS, and M = 2 and K = 5 for HR. In (a), we estimate local observable $O={\sigma }_{Z}^{1}\otimes {\sigma }_{Z}^{2}$. In (b), we estimate ${F}_{2}=\left\langle GHZ\right\vert {\rho }^{2}\left\vert GHZ\right\rangle$ with $O=\left\vert GHZ\right\rangle \left\langle GHZ\right\vert$. In (d), we set M = 400 and find the total measurement is about MK = 200d^0.75 to keep the error less than 0.1 using HR.

Furthermore, one can repeat the above procedure for all $\widehat{{\rho }^{{m}_{i}}}$ and patch them together to evaluate more complex functions. For P_m the unbiased estimator now shows

$${{{\rm{tr}}}}\left({S}_{L}\widehat{{\rho }^{{m}_{1}}}\otimes \widehat{{\rho }^{{m}_{2}}}\otimes \cdots \widehat{{\rho }^{{m}_{L}}}\right).$$

(8)

With the hybrid framework, one can equivalently transform an m-degree function in the original shadow protocol in Eq. (4) to a lower L-degree one here. This not only reduces the sampling and postprocessing cost, but also makes other postprocessing strategies^19,35 available for higher-degree functions. In particular, the postprocessing cost is reduced from ${{{\mathcal{O}}}}({M}^{m})$ to ${{{\mathcal{O}}}}({M}^{L})$. We take the moment estimation of P₃ as an example to show these advantages.

Besides the functions like o_m and P_m here, we give the hybrid shadow estimation for more general functions of Eq. (1) in Supplementary Note II, by directly extending Theorem 1.

Application for the moment estimation

In this section, we explicitly show how to construct the unbiased estimator for the moments, by taking the third moment P₃ as an example. We also analyse the statistical variance under finite measurement times here.

We divide m = 3 to 2 + 1 to estimate ${P}_{3}={{{\rm{tr}}}}({S}_{2}{\rho }^{2}\otimes \rho )$. For $\widehat{{\rho }^{2}}$, by following Algorithm 1 (K = 1, t = 2) one collects the shadow set

$$\left\{{\widehat{{\rho }^{2}}}_{(1)},{\widehat{{\rho }^{2}}}_{(2)},\cdots {\widehat{{\rho }^{2}}}_{(M)}\right\};$$

(9)

one also collects the shadow set of ρ using the original shadow estimation,

$$\left\{{\widehat{\rho }}_{(1)},{\widehat{\rho }}_{(2)},\cdots {\widehat{\rho }}_{({M}^{{\prime} })}\right\},$$

(10)

and then combines two sets to get the estimator of P₃.

Proposition 1

By combing the shadow sets $\{{\widehat{{\rho }^{2}}}_{(i)}\}$ and $\{{\widehat{\rho }}_{({i}^{{\prime} })}\}$, one gets the unbiased estimator of P₃ as

$$\widehat{{P}_{3}}=\frac{1}{M{M}^{{\prime} }}\sum\limits_{i\in [M],{i}^{{\prime} }\in [{M}^{{\prime} }]}{{{\rm{tr}}}}\left({S}_{2}{\widehat{{\rho }^{2}}}_{(i)}\otimes {\widehat{\rho }}_{({i}^{{\prime} })}\right).$$

(11)

Suppose one applies the random Pauli measurements, the variance of $\widehat{{P}_{3}}$ can be upper bounded by

$${{{\rm{Var}}}}\left(\widehat{{P}_{3}}\right)\le {{{\rm{tr}}}}\left({\rho }^{2}\right)\left[\frac{d+1}{M}+{{{\rm{tr}}}}\left({\rho }^{2}\right)\frac{{d}^{3}}{{M}^{2}}\right],$$

(12)

with $M={M}^{{\prime} }$ for simplicity.

The result of Eq. (12) is almost the same as that of P₂ using the original shadow estimation (Eq. (D16) in Ref. ¹³). This indicates that the hybrid framework reduces the statistical error from a 3-degree problem to a 2-degree one, with coherent access to a limited (t = 2) quantum hardware. We leave the analysis of the estimator and the statistical variance for random Clifford measurements and higher-order moments in Supplementary Note III.

Moreover, one can adopt another postprocessing protocol³⁵ with the same measurement data collected in Algorithm 1, and the estimator ${\widehat{{P}_{3}}}^{{\prime} }$ is given in Proposition 2. This protocol with Pauli measurements mainly works for 2-degree functions and is proved infeasible for higher-degree ones¹⁴. With the hybrid framework here, one can make it feasible for the 3-degree function P₃ and also reproduce the same variance scaling of P₂ in the original protocol^16,35, indicating the advantage again.

Proposition 2

Using the RM results, $\{{\widehat{{b}_{c}}}^{(i,j)},{\widehat{{{{\bf{b}}}}}}^{(i,j)}\}$, collected in Algorithm 1 for t = 2, one can construct an alternative unbiased estimator of P₃ as

$${\widehat{{P}_{3}}}^{{\prime} }=\frac{1}{MK(K-1)}\sum\limits_{i\in [M]}\sum\limits_{j\ne {j}^{{\prime} }\in [K]}{(-1)}^{{\widehat{b}}_{c}^{(i,j)}}{X}_{c\backslash p}\left({\widehat{{{{\bf{b}}}}}}^{(i,j)},{\widehat{{{{\bf{b}}}}}}^{(i,{j}^{{\prime} })}\right).$$

(13)

Here the choice of the postprocessing function, ${X}_{c}({{{\bf{b}}}},{{{{\bf{b}}}}}^{{\prime} })=-{(-d)}^{{\delta }_{{{{\bf{b}}}},{{{{\bf{b}}}}}^{{\prime} }}}$ or ${X}_{p}({{{\bf{b}}}},{{{{\bf{b}}}}}^{{\prime} })=\mathop{\prod }\nolimits_{k = 1}^{n}-{(-2)}^{{\delta }_{{b}_{k},{{b}_{k}}^{{\prime} }}}$, depends on the RM primitives, random Clifford or Pauli measurements.

For Pauli measurements, the variance is about

$${{{\rm{Var}}}}\left({\widehat{{P}_{3}}}^{{\prime} }\right)={{{\mathcal{O}}}}\left(\frac{{d}^{{\log }_{2}3}}{M{K}^{2}}\right).$$

(14)

To complement the above analytical results, in Fig. 3c, we numerically study the scaling of the statistical errors for estimating P₃, using the estimators $\widehat{{P}_{3}}$ in Eq. (11) and ${\widehat{{P}_{3}}}^{{\prime} }$ in Eq. (13), and also the one from the original shadow protocol¹³, in the regime d ≫ M(K). They are denoted for short as Hybrid Shadow (HS), Hybrid Random (HR) and Original Shadow (OS), respectively. The numerical results, which correspond to the standard variance, are consistent with the analytical ones, and we summarize them together in Table 1.

Table 1 The statistical errors for estimating P₃ with different protocols

The numerical errors correspond to the standard variance, and are consistent with the theoretical predictions. As shown in Fig. 3a for the noisy GHZ state, α = 1.05 < 1.5 for HS as predicted by Eq. (12); α = 0.75 is quite close $({\log }_{2}3)/2=0.80$ in Eq. (14) for HR; α = 1.91 < 3 for OS¹³.

Consequently, in practise one needs $M={{{\mathcal{O}}}}({d}^{1.27})$ for OS, $M={{{\mathcal{O}}}}({d}^{1.05})$ for HS, and $K={{{\mathcal{O}}}}({d}^{0.73})$ for HR to make the error less than some constant. It is clear that HS and HR from the hybrid framework both show an advantage compared to OS, and HR is the most efficient one for P₃. In Fig. 3d, we further find the total number of measurements is about MK = 200d^0.75 to make Error(P₃)≤0.1, showing great enhancement than OS protocol^13,20. And the advantage of the hybrid framework is more significant for measuring higher-order moments like P₄, and we leave more discussions in Supplementary Note III and IV.

Application in quantum error mitigation

Recently purified-based methods are proposed^36,37 for quantum error mitigation^38,39,40,41 by virtually purifying multiple copies of the prepared states. Suppose the perfect target state is Ψ and the noisy prepared state is ρ. The central task there is to estimate ${o}_{m}:= {{{\rm{tr}}}}(O{\rho }^{m})$, and use the normalized value ${o}_{m}/{P}_{m}\to {{{\rm{tr}}}}(O\Psi )$ to approach the target value ${{{\rm{tr}}}}(O\Psi )$ with Ψ the noiseless state, which can suppress the error exponentially with the copy-number m. The original protocol is based on the swap test to measure o_m, and very recently there have been ones by shadow estimation^42,43. There is also an experimental advance for that of m = 2⁴⁴, however, similarly it is still challenging to extend both approaches to m≥3. Here we show that the hybrid framework gives various advantages on estimating o_m.

Suppose one has access to the coherent operation on m-copy quantum states. By only adopting the classical postprocessing, the shadow set collected in Algorithm 1 for t = m can be reused for many different observables {O_i}, say totally T ones, and the estimation error scales like ${{{\mathcal{O}}}}(\log (T))$ using the median-of-mean technique¹². However, in principle the swap test approach should adopt different quantum circuits for different observables³⁷, and also the error would scale linearly ${{{\mathcal{O}}}}(T)$. This advantage is significant for quantum chemistry simulation with the polynomial number of terms in Hamiltonian^44,45,46.On the other hand, compared to OS protocol⁴², HS significantly reduces the statistical variance and thus the sampling cost. For instance, suppose one applies Pauli measurements with OS protocol to estimate o_m for a local observable O. Since ${o}_{m}={{{\rm{tr}}}}({O}_{m}{\rho }^{\otimes m})$ and ${O}_{m}:= \frac{1}{2}(O{S}_{m}+{S}_{m}^{{\dagger} }O)$ the symmetrized observable is actually a global one with locality about mn^12,13, and thus the shadow norm scales exponentially with n. While in HS protocol, the variance is independent of the qubit number n by Eq. (7). See Fig. 3a for this exponential advantage as t = 2, and similar advantage also appears in the fidelity estimation using the Clifford measurements as shown in Fig. 3b, with more discussions left in Supplementary Note IV.

In reality, one generally can not implement Algorithm 1 directly for t = m when m ≥ 3 due to the hardware limitation. Like the moment estimation, one can alternatively patch low-degree snapshots to measure higher-degree o_m. For instance, when m = 3 and t = 2, similar as Eq. (11), one can construct the estimator $\widehat{{o}_{3}}={(M{M}^{{\prime} })}^{-1}{\sum }_{i,{i}^{{\prime} }}{{{\rm{tr}}}}({O}_{2}{\widehat{{\rho }^{2}}}_{(i)}\otimes {\widehat{\rho }}_{({i}^{{\prime} })})$, and the error also scales logarithmically with the total number of observebles. In addition, one can construct an alternative estimator ${\widehat{{o}_{3}}}^{{\prime} }$ by the following Eq. (13). Similar as in the moment-estimation of P₃, both estimators show statistical error advantages compared to the original shadow. The details of the unbiased estimator for general observable O and numerical results are left in Supplementary Note IV.

Discussion

The hybrid framework proposed here utilizes the partial coherent power of quantum devices and can act as a subroutine for many quantum information tasks, for instance, measuring entanglement^47,48,49,50, characterizing quantum chaos^51,52, and constructing quantum algorithms^53,54,55. Note that the framework reduces to previous RM protocols as t = 1 in Algorithm 1, and the advantage essentially comes from the coherent processing the few-copy state. So it is intriguing to build the ultimate result of this replica advantage^8,56 considering the limited quantum memory. Moreover, it is also appealing to extend the current framework to quantum channel^57,58,59,60 and boson or fermion systems^61,62.