Introduction

Spin systems have emerged as a promising platform for quantum sensing1,2,3,4 with applications ranging from tests of fundamental physics5,6 to mapping fields and temperature profiles in condensed matter systems and life sciences3. Improving the sensitivity of these qubit sensors has so far largely relied on increasing the number of sensing spins and extending spin coherence through material engineering and coherent control. However, with increasing spin density, dipolar interactions between individual sensor spins cause single-qubit dephasing7,8 and, in the absence of advanced dynamical decoupling9,10,11, set a limit to the sensitivity.

Although dipolar interactions in dense spin ensembles lead to complex evolution, they can provide a resource for the creation of metrological states that enable sensing beyond the SQL. Current approaches to create such states (i.e., GHZ states and SSS, see Supplementary Fig.1) either require all-to-all interactions12,13,14,15 or single-qubit addressability16,17,18, which are challenging to implement experimentally. An alternative approach that relies on adiabatic state preparation requires less control but results in preparation times that increase exponentially with system size19,20, leaving this method susceptible to dephasing.

Variational methods provide a powerful tool for controlling many-body quantum systems21,22,23. Such methods have been proposed for Rydberg-interacting atomic systems24,25 and demonstrated in trapped ions26. However, these techniques rely either on all-to-all interactions (i.e., trapped ions26) or strong coupling within a finite radius (i.e., Rydberg atoms24,27,28) which are generally absent in solid-state spin ensembles. In this work, we develop a variational algorithm that drives dipolar-interacting spin systems [Fig. 1(a)] into highly entangled states. The resulting states can be subsequently used for Ramsey-interferometry-based single parameter estimation1. The required system control relies solely on uniform single-qubit rotations and free evolution under dipolar interactions. Different spatial distributions of the spins (later referred as ‘spin configuration’) including 2D regular arrays and 3D random spin configurations are investigated. The generated states resemble GHZ states or SSS depending on the spin-pattern geometry and the depth of the variational circuit. Experimental imperfections such as finite initialization/readout fidelity and dephasing noise are discussed for the example of a 2D regular array. The requirements on those imperfections for beating the SQL are given. Potential experimental platforms include dipolar-interacting ensembles of nitrogen-vacancy (NV) centers, nitrogen defects in diamond (P1), rare-earth-doped crystals, and ultra-cold molecules.

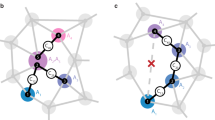
Fig. 1: Preparation of metrological states by variational ansatz.
figure 1

a Schematic of a dipolar-interacting spin ensemble in a 3D-random configuration. b The quantum circuit consists of three parts: a sequence for generating entanglement (entangler), phase accumulation (Ramsey) and single-qubit readout in the Pz basis. Dipolar interactions during Ramsey interference are eliminated by dynamical decoupling7,9,32. The measurement outcome is processed on a classical computer and used to determine the next generation for θ. c Gate sequence of each variational layer and the Wigner distributions for a 5-spin state after each gate. d Illustration of an optimization process on a 3-spin system with m = 1. The contour plots show the 2D projection of the multidimensional θ space for fixed ϑ1. The orange points mark the sampling positions in the parameter space. Convergence to the global maximum is reached in the 63rd generation.

Full size image

Results

Variational ansatz

As shown in Fig. 1(b), the variational circuit \({{{\mathcal{S}}}}({{{\boldsymbol{\theta }}}})={{{{\mathcal{U}}}}}_{m}...{{{{\mathcal{U}}}}}_{2}{{{{\mathcal{U}}}}}_{1}\) is constructed by m layers of unitary operations. Each \({{{{\mathcal{U}}}}}_{i}\) consists of the parameterized control gates

$${{{{\mathcal{U}}}}}_{i}={R}_{y}\left(\frac{\pi }{2}\right)D\left({\tau }_{i}^{{\prime} }\right){R}_{y}\left(-\frac{\pi }{2}\right){R}_{x}\left({\vartheta }_{i}\right)D\left({\tau }_{i}\right),$$
(1)

where \({R}_{\mu }(\vartheta )=\exp (-i\vartheta \mathop{\sum }\nolimits_{j = 1}^{N}{S}_{j}^{\mu })\) are single-qubit rotations and \({S}_{j}^{\mu }\)(μ ∈ {x, y, z}) is the μ component of the j-th spin operator. \(D(\tau )=\exp (-i\tau {H}_{{{{\rm{dd}}}}}/\hslash )\) is the time evolution operator of the spin ensemble under dipolar-interaction Hamiltonian \({H}_{{{{\rm{dd}}}}}={\sum }_{i < j}{V}_{ij}(2{S}_{i}^{z}{S}_{j}^{z}-{S}_{i}^{x}{S}_{j}^{x}-{S}_{i}^{y}{S}_{j}^{y})\). The coupling strength between two spins at positions ri and rj is

$${V}_{ij}=\frac{{\mu }_{0}}{4\pi }\frac{{\gamma }_{i}{\gamma }_{j}{\hslash }^{2}}{{\left\vert {{{{\bf{r}}}}}_{i}-{{{{\bf{r}}}}}_{j}\right\vert }^{3}}\frac{(1-3\cos {\beta }_{ij})}{2},$$
(2)

with μ0 the vacuum permeability, ℏ the reduced Planck constant, γ the spin’s gyromagnetic ratio, and βij the angle between the line segment connecting (ri, rj) and the direction of bias magnetic field. An evolutionary algorithm29 (Method) is applied on the m-layer circuit which contains 3m free parameters constituting the vector \({{{\boldsymbol{\theta }}}}=({\tau }_{1},{\vartheta }_{1},{\tau }_{1}^{{\prime} },...\,,{\tau }_{i},{\vartheta }_{i},{\tau }_{i}^{{\prime} },...\,,{\tau }_{m},{\vartheta }_{m},{\tau }_{m}^{{\prime} })\). Each τi is restricted to \({\tau }_{i}\in [0,1/{\bar{f}}_{{{{\rm{dd}}}}}]\) where \({\bar{f}}_{{{{\rm{dd}}}}}\) is the average nearest-neighbor interaction strength for the considered spin configuration. After the metrological relevant states are generated by the variational ansatz, a Ramsey sequence1,30,31 is applied to detect the external magnet field signal. During the Ramsey propagation1 the spins accumulate a field dependent phase for a time τ. Prior to the readout, a Rx(π/2) rotation converts this phase into a signal-dependent Pz expectation value. For the spin systems in which the dipolar interaction cannot be turned on and off at will, a Waugh-Huber-Haeberlen (WAHUHA) type dynamical decoupling sequence7,9,32 is applied to cancel the dipolar interactions during the signal accumulation. The Ansatz in Eq. (1) is the most general set of global single-qubit gates that preserves the initial collective spin direction 〈∑iSi〉/∣〈∑iSi〉∣, here chosen to be the x-direction24, Supplementary Note 1. Although this Ansatz does not enable universal system control33,34,35, Supplementary Discussion, we show that with increasing circuit depth, sensing near the HL can be achieved. A gradient-free black-box optimization algorithm is used for searching the parameter space {θ} for an entangler that generates a desired metrological state. As shown in Fig. 1(d), the algorithm samples the parameter space θ following a Gaussian distribution. In each generation, the algorithm iteratively updates the mean and variance of the Gaussian distribution according to the resulting cost function. This semi-random searching process is able to effectively jump out of local maxima.

Metrological cost function

The Ramsey protocol shown in Fig. 1(b) encodes the quantity of interest in the accumulated phase ϕ = ωtR, with ω the detuning frequency and tR the Ramsey sensing time. The Classical Fisher Information (CFI)1 quantifies how precisely one can estimate an unknown parameter ϕ under a measurement basis. Our variational approach treats the spin systems as a black-box for which the algorithm finds a control sequence that maximizes the CFI associated with the parameter estimation problem

$${{{{\rm{CFI}}}}}_{\phi }=\mathop{\sum}\limits_{z}{{{\rm{Tr}}}}[{P}_{z}{\rho }_{\phi }]{\left(\frac{\partial \log {{{\rm{Tr}}}}[{P}_{z}{\rho }_{\phi }]}{\partial \phi }\right)}^{2}.$$
(3)

The sum runs over the 2N basis states \(\left\vert z\right\rangle ={\otimes }_{i = 1}^{N}\left\vert {s}_{i}^{z}\right\rangle\), where \({s}_{i}^{z}\) are the eigenvalues of \({S}_{i}^{z}\). \({P}_{z}\equiv \left\vert z\right\rangle \left\langle z\right\vert\) denotes the corresponding measurement operator and ρϕ the density matrix. The CFI is chosen as cost function because it quantifies the sensitivity of a measurement outcome to an external signal and measures the maximal achievable sensitivity for a given measurement basis1,36. Measurement operators such as parity (\({P}_{z}^{\pi }\)) or total spin polarization (\({P}_{z}^{tot}\)) result in a smaller outcome space and are therefore more efficient in experimental implementations25,37,38,39, but contain less information than Pz. While we optimize the measurement for Pz in the main text, the obtained results also hold for measurements of \({P}_{z}^{tot}\) and \({P}_{z}^{\pi }\). We found that when measuring \({P}_{z}^{tot}\) or \({P}_{z}^{\pi }\) the results improve when compared to Pz. Please check Supplementary Fig. 3 for detailed discussion.

Numerical results for regular and disordered spin configurations

We start by testing our approach for three distinct regular spin configurations. Figure 2(a) shows the CFI after optimization for spins arranged on a linear chain (blue), a two-dimensional (2D) square lattice (orange), and a circle (green). All three configurations result in states with CFI above the SQL. When multiple circuit layers are added, the CFI further improves. Next, we simulate the case of disordered three-dimensional (3D) spin configurations (later referred as 3D-random). In our simulations the spins are randomly located in a box of length L ∝ N1/3 (constant spin density). Compared to the regular spin array, the disordered case shows a noticeable saturation of the CFI as a function of N [Fig. 2(b)]. The N at which this saturation occurs can be increased by increasing the circuit depth [Fig. 2(c)]. This result for small N is different from the infinite sized systems where time evolution under dipolar interactions D(τ) alone is not sufficient to generate metrologically useful entangled state (note, dipolar interactions in a 3D-random configuration average to zero, i.e., \(\langle (1-3{\cos }^{2}\theta )\rangle =0\)). We attribute the observed metrological gain in Fig. 2(b) to a finite-size effects for small spin ensembles. This is in stark contrast to the 2D case where dipolar interaction does not average out40 or regular 3D patterns41.

Fig. 2: Optimization results of different spin configurations.
figure 2

a Top: CFI for m = 1 (circles) and m = 7 (triangles) circuits. The colors correspond to the configurations shown below. Bottom: schematics of different spin configurations. The numbers in the 2D square lattice pattern label the order in which spins are added to form a lattice of size N. b Average CFI for 50 configurations of 3D-randomly distributed spins. Error bars stand for the standard deviations of the optimized CFI from different spin configurations. (Error bars for m = 2, 3, 5 are omitted for clear presentation). c Average number of layers required to achieve a CFI within a given percentage of the HL in the case of 3D-random configuration. The fit m = aNb + c with b = 2.45 (goodness of fit R2 = 0.996) serve as a guide to the eye. The same data also fits to an exponential model with slightly lower R2 = 0.995. The investigation of deeper circuits becomes increasingly challenging as the efficiency of the employed optimization algorithm steeply decreases for m > 9. See Supplementary Figs. 2,5,6 and Supplementary Methods for more details.

Full size image

Entanglement characterization

We investigate the N-qubit entangled states created by our variational method. The resulting states are visualized by plotting out the phase space quasiprobability distribution of the spin wavefunction in terms of the Wigner function (for more details on how the density matrix of a spin system is connected to the Wigner function, we refer to refs. 42,43,44; examples of Wigner distributions for specific states can be found in Supplementary Fig. 1). Figure 3(a) shows the corresponding Wigner distributions for a regular 2D spin array (top) and the average Wigner distributions for 50 different 3D-random spin configurations (bottom). In both cases, the optimized states resemble GHZ states when N is small and m is large. For large N and small m, the states are close to SSS. Non-Gaussian states that provide sensitivity beyond the SSS but lower than GHZ states are also generated. Our algorithm tends to drive the system into a GHZ state that lives in J = N/2 total angular momentum subspace, as it has the unique property of attaining the HL in Ramsey spectroscopy45.

Fig. 3: Entanglement build-up in metrological states.
figure 3

a Wigner distributions versus spin number for m = 2 and m = 7 in the case of 2D square lattice and 3D-random configurations. The projected states into the J = N/2 total angular momentum subspace are shown here. b von-Neumann entanglement entropy for one specific 3D-random configuration of 9 spins for m = 2 and m = 7. Individual spins are labeled with an integer 1 through 9 to facilitate the discussion in the main text. The color of each data point corresponds to the von-Neumann entropy noted in the color bar to the right. Entangled clusters are marked by solid black lines. c Histograms depicting the maximal size of entangled clusters for 50 3D-random configurations. The number of spins per entangled clusters increases with circuit depth. d Average CFI (blue) and state preparation time (orange) versus m. Error bars indicate the standard deviations of CFI/state preparation time from different 3D random spin configurations. The state preparation time is given as a unitless quantity \({\bar{f}}_{{{{\rm{dd}}}}}T\) with \(T=\mathop{\sum }\nolimits_{i = 1}^{m}({\tau }_{i}+{\tau }_{i}^{{\prime} })\).

Full size image

For quantitatively analysing the build-up of entanglement, the von-Neumann entanglement entropy (\({E}_{{{{\rm{vN}}}}}=-{{{\rm{Tr}}}}({\rho }_{{{{\rm{s}}}}}{\log }_{2}{\rho }_{{{{\rm{s}}}}})\))46 is used as a measure for the degree of entanglement between a spin subsystem (\({\rho }_{{{{\rm{s}}}}}={{{{\rm{Tr}}}}}_{{{{\rm{s}}}}}{\rho }_{{{{\rm{tot}}}}}\)) and the remaining system. As an example, we explore one case of a 3D-random configuration of 9 spins. Figure 3(b) shows the von-Neumann entropy of each spin after employing a 2-layer circuit (left) and a 7-layer circuit (right). In the case of m = 2, the achieved degree of entanglement is modest with spin No.6 for example showing no substantial entanglement with the surrounding spins. When the circuit depth is increased to 7, all spins display substantial entanglement. While the single-particle entropy detects spins unentangled with the remaining system, it does not determine whether all spins are entangled with each other or entanglement is local. We distinguish these two scenarios by identifying the smallest clusters with EvN ≤ 0.4. For m = 2, the spin ensemble segments into 5 clusters [Fig. 3(b)], while for m = 7 only 2 clusters are found. The results verify that multiple layers are required to overcome the anisotropy of the dipolar interaction [Eq. (2)] when building up entanglement over the entire system. Finally, in Fig. 3(c) we analyze the size of the largest cluster for each of the 50 spin configurations and observe an overall increase of the largest cluster size and a decrease of the variance.

State preparation time

Minimizing the preparation time is central in practical applications, as it increases bandwidth, reduces decoherence, and enables more measurement repetitions1. Figure 3(d) shows the average state preparation time for 8 spins in 50 different 3D-random configurations as a function of layer number. The preparation time increases with the layer number and is inversely proportional to the average dipole coupling strength of the nearest-neighbor spins \({\bar{f}}_{{{{\rm{dd}}}}}\). Compared to adiabatic methods19, our approach results in an 11 × reduction of the preparation time to reach the same CFI for identical spin number and density (see Supplementary Note 8 for detailed derivation). This is of particular importance when imperfections, such as dephasing, are taken into consideration.

State preparation under decoherence, initialization, readout and erasure errors

Until now our analysis assumed full coherence and perfect spin initialization and readout. We also assumed the spin configuration is fixed during each run of the optimization. However, dephasing, initialization, readout and erasure errors will be limiting factors in experimental implementations. We next examine the impact of such imperfections on state preparation and sensing. Figure 4(a) and (b) show the optimized CFI in the presence of imperfect initialization and finite readout fidelity for spins on a 2D square lattice. The algorithm is limited by computational resources and able to perform optimization for imperfect initialization for up to 8 spins. Beyond-SQL sensitivity is reached for 75% initialization fidelity (for N ≤ 8) and 92% readout fidelity (for N ≤ 10), respectively.

Fig. 4: Performance under imperfections.
figure 4

a CFIϕ under finite initialization fidelity (IF). \({{{\rm{IF}}}}=\frac{{N}_{\uparrow }-{N}_{\downarrow }}{N}\), where N↑ (N↓) denotes the number of spins in the \(\left\vert \uparrow \right\rangle\) (\(\left\vert \downarrow \right\rangle\)) state at the beginning of the sensing protocol in Fig. 1(b). b CFIϕ under finite readout fidelity (RF). RF = 1 − p(↓∣↑) = 1 − p(↑∣↓). c Optimized Wigner functions and CFIϕ of a 10-spin state versus different readout fidelities (RF). For comparison, the row `CSS' represents the CFIϕ for a coherent spin state given the same RF. See Supplementary Fig. 9 for more information. d Average CFIϕ under finite loading efficiency. Effective spin number N* is the averagely loaded spin number for a given configuration and loading efficiency. e CFIϕ in the presence of decoherence in the entangler. f Ramsey protocol’s results of the generated states when considering non-Markovian noise during signal accumulation (see Supplementary Fig. 8 for more details). All data correspond to the optimized states from 2D square lattice configuration using a 5-layer circuit.

Full size image

For further understanding the impact of readout fidelity on the optimized metrological states, we plot out the resulting states optimized under different readout fidelities. Figure 4(c) indicates that without readout errors, the Wigner distribution of the resulting state is close to a GHZ state. However, with a finite readout error rate, our algorithm drives the system into a state resembling a SSS. When the readout noise is further increased, the SSS transforms into a coherent spin state (CSS). The results agree with the fact that GHZ states are sensitive to single-spin readout errors while SSS are more robust47.

In addition to the discussed spin readout and initialization errors many experimental platforms also suffer from changing spin configurations between consecutive runs. This so-called erasure error is caused by a finite ionization/deionization rate in the case of NV centers48,49 and a finite loading possibility in the case of cold molecules50. Figure 4(d) shows the optimized average CFI versus the average number of loaded spins N* per cycle. The obtained results indicate that our approach is comparable robust to erasure errors, with beyond-SQL sensitivity for loading efficiencies as low as 50%.

During the state preparation, decoherence (T2) reduces entanglement. We assume independent, Markovian dephasing of each spin as described by a Lindblad master equation46. Figure 4(e) shows the CFI for various T2 times using the previously optimized gate parameters for 2D square lattice. While a finite T2 decreases the CFI, coherence times exceeding 0.5/fdd result in states with beyond-SQL sensitivity for N ≤ 8. Here, fdd denotes the nearest-neighbor interaction strength for 2D square lattice. For small T2 the resulting state will converge toward a CSS, which results in a sensitivity set by the SQL.

Sensitivity in a non-Markovian environment

In addition to impacts on state preparation, dephasing affects performance in Ramsey interferometry. In the presence of spatially uncorrelated Markovian noise, entanglement does not lead to a beyond-SQL scaling51,52. In a non-Markovian environment, this limitation does not hold53,54,55. Such as in a solid-state spin system, slow evolution of nuclear spins leads to correlated noise8,56 on the sensing qubit. We examine the performance of our optimized states in a non-Markovian noise environment. We adopt a noise model53 in which the amplitude of single-spin coherence reduces according to

$${\rho }_{01}(t)={\rho }_{01}(0){e}^{-{\left(\frac{t}{{T}_{2}}\right)}^{\nu }}$$
(4)

where ν is the stretch factor set by the noise properties. The time evolution under Ramsey propagation is simulated with a generalized Lindblad master equation54. The sensing performance of optimized states is characterized by the square of the signal-noise-ratio SNR2 ∝ CFIω/tR (see Supplementary Notes 2–7). Figure 4(f) shows their performance compared to the CSS and the GHZ states for a ν = 2 and ν = 4 noise exponent8. The created entangled states provide an advantage over uncorrelated states. For small spin numbers, the SNR follows the HL scaling53.

Proposed experimental platforms

Candidate systems for realizing the proposed variational approach need to possess long T2 coherence time, strong dipolar-interacting strength, and high initialization and readout fidelity. Recent developments in solid-state spin systems and ultracold molecules have demonstrated coherence times that exceed dipolar coupling times (\(1/{\bar{f}}_{{{{\rm{dd}}}}}\)) as well as high-fidelity spin initialization and readout. Table 1 lists the experimentally observed parameters for different candidate systems, including NV ensembles, P1 centers in diamond, rare-earth doped crystals, and ultracold molecule tweezer systems.

Table 1 Parameters of different experimental platforms
Full size table

The listed \({T}_{2}^{({{{\rm{DD}}}})}\) in Table 1 are lower bounds for the actual T2. Specifically, \({T}_{2}^{({{{\rm{DD}}}})}\) represent the experimental coherence measured under WAHUHA-type dynamical decoupling, which contains remaining dephasing terms caused by dipolar interaction11. On the other hand, our protocol relies on the presence of dipolar interaction for the generation of the desired entangled states. Therefore dipolar interaction between spins is part of the system Hamiltonian that does not contribute to dephasing during the state preparation. Thus, the relevant coherence is the single particle T2 in the absence of dipolar spin-spin interacting (see Supplementary Table 1).

Discussion

This work introduces a variational circuit that efficiently generates entangled metrological states in a dipolar-interacting spin system. The required system parameters are within the reach of several experimental platforms. When directly running this variational method on an experimental platform, metrological states can be generated without the prior knowledge of the actual spin locations. While this study remains limited to small system sizes (N ≤ 10, limited by computational resource), our results are of immediate interest to nanoscale quantum sensing where spatial resolution is paramount and the finite sensor size limits the number of spins that can be utilized. Specific examples include the investigation of 2D materials57,58,59,60, structures and dynamics of magnetic domains61,62, vortex structures in superconductivity63,64, and magnetic resonance spectroscopy on individual proteins and DNA molecules65,66,67,68.

Extending our investigation to N > 10 can either be achieved by utilizing symmetries in regular arrays or directly testing our optimization algorithms on an actual experimental platform. The developed method is also potentially applicable to preparing other highly entangled states relevant to quantum computing and quantum communication.

Method

Gradient-free optimization: CMA-ES

The optimization in the 3m dimensional parameter space is highly non-convex [Fig. 1(d)] due to the large inhomogeneity of the interaction strength. In our setting, the previously used Dividing Rectangles algorithm22,24 cannot converge to a beyond-SQL result despite large number of iterations. We address this challenge by using the Covariance Matrix Adaptation Evolution Strategy (CMA-ES) as our optimization algorithm29. CMA-ES balances the exploration and exploitation process when searching in the parameter space so that convergence is reached after <~2000 generations for N, m ≤ 10. This corresponds to about 108 repetitions of the Ramsey experiment, which can be further reduced if collective measurement observables are measured (Supplementary Fig. 3).

We reduce the complexity of the optimization by restricting τi within \([0,1/{\bar{f}}_{{{{\rm{dd}}}}}]\) where \({\bar{f}}_{{{{\rm{dd}}}}}\) is the average nearest-neighbor interaction strength for the considered spin configuration. Setting a large parameter searching range for the interaction gates’ time τi would potentially ensure the global maximum CFI location is included in the parameter space. However, when the upper bound of τi is much bigger than \(1/{\bar{f}}_{{{{\rm{dd}}}}}\), the evolution of neighboring spin pairs is fast when sweeping τi. This would introduce a huge amount of local maximum points in the parameter search so that it is impractical for the black-box optimization algorithm to converge to that global maximum point. A good value for \({\bar{f}}_{{{{\rm{dd}}}}}\) can be estimated from the doping level of the spin defects (NV, P1, rare-earth ions) or the distance between the cold molecule tweezers. Measuring the fast oscillation frequency in Ramsey experiments will also provide an estimate of the \({\bar{f}}_{{{{\rm{dd}}}}}\).