The cluster decomposition of the configurational energy of multicomponent alloys

Abstract

The cluster expansion method (CEM) is a widely used lattice-based technique in the study of multicomponent alloys. Despite its prevalent use, a clear understanding of expansion terms is lacking. We present a modern mathematical formalism of the CEM and introduce the cluster decomposition—a unique and basis-independent decomposition for functions of the atomic configuration in a crystal. We identify the cluster decomposition as an invariant ANOVA decomposition; and demonstrate how functional analysis of variance and sensitivity analysis can be used to interpret interactions among species. Furthermore, we show how the mathematical structure of the cluster decomposition enables numerical evaluation that scales with the number of clusters and is independent of the number of species. Overall, our work enables rigorous interpretations of interactions among species, provides opportunities to explore parameter estimation beyond linear regression, introduces a numerical efficient implementation, and enables analysis of cluster expansions based on established mathematical and statistical principles.

Introduction

Computational methods based on lattice models are used extensively in the applied physical sciences. The cluster expansion (CE) method provides a mathematical framework for representing and parameterizing generalized lattice models with discrete configurations^1,2,3. The CE method coupled with Monte Carlo (MC) sampling has become an established technique to compute thermodynamic properties of multicomponent crystals^4,5. The CE method plays an active role in materials science research, particularly in the study of metallic alloys^6,7,8, semiconductors^9,10, superionic conductors^11,12, battery electrodes¹³, and surface catalysis¹⁴. Moreover, researchers are continuously developing methodologies that are based on or utilize the CE method. Recent advances have introduced generative models as alternative ways to compute free energies^15,16. Additionally, the mathematical formalism of the CE has been used to develop methodological extensions to parameterize functions of continuous degrees of freedom^17,18,19,20, which can be used to represent vector and tensor material properties^21,22, and capture full potential energy landscapes through the recently proposed atomic CE²³.

The core of the CE method is the expansion of a function of configurational variables distributed over a crystallographic lattice. The mathematical formalism of the CE comprises a harmonic expansion of functions over a tensor-product domain²⁴. Intuitively, such a formalism leads to expansions that are generalizations of the Ising model^25,26, which can be expressed as follows,

$$\begin{array}{l}H({{{\boldsymbol{\sigma }}}})\,=\,\sum\limits_{\beta }{J}_{\beta }\sum\limits_{\alpha \in \beta }\prod\limits_{i\in [N]}{\phi }_{{\alpha }_{i}}({{{{\boldsymbol{\sigma }}}}}_{i})\\\qquad\quad=\,\sum\limits_{\beta }{J}_{\beta }\sum\limits_{\alpha \in \beta }{\Phi }_{\alpha }({{{\boldsymbol{\sigma }}}}),\end{array}$$

(1)

where σ is a string of occupation variables that represent the chemical species residing on each of N crystallographic sites. α are multi-indices of length equal to N, that are used to label the univariate site functions ${\phi }_{{\alpha }_{i}}$. β are sets of symmetrically equivalent multi-indices. And J_β are the expansion coefficients which are referred to in the literature as effective cluster interactions^3,5. The product of site functions over all sites is referred to as a product function or a cluster basis function⁵, which we compactly write as Φ_α.

The resemblance to the Ising model is evident when considering binary configuration variables σ_i = ± 1, for which ϕ₀ = 1 and ϕ₁(σ_i) = σ_i can be used as a basis. With such a choice, the cluster basis functions Φ_α are constructed from products of spin variables, and Equation (1) is a direct generalization of the Ising model to higher-degree interactions. Similarly, a binary CE using site indicator functions: ${\phi }_{1}({{{{\boldsymbol{\sigma }}}}}_{i})={{{{\boldsymbol{1}}}}}_{{\sigma }_{1}}({{{{\boldsymbol{\sigma }}}}}_{i})$, is a generalization of the lattice gas model²⁷, or a generalization of the q-state Potts model when an overcomplete representation is used^28,29.

The connections between classical lattice models and the CE method have been used by practitioners to directly interpret CEs. For example, it is common practice to evaluate the spatial decay of interactions^30,31 and interpret the effects of chemical interactions between species^3,12,29 by directly examining expansion coefficients. However, for complex systems with three or more components, coefficient values depend non-trivially on the choice of basis(The number of distinct basis in lattice gas CE sets grows with the number of components. In a Fourier CE, there are infinitely many basis set choices for 3 or more components. In an overcomplete representation²⁸ there are infinitely many expansion coefficient choices that represent a given function.), and so relying solely on intuition from classical lattice models to directly interpret coefficients can be ambiguous and even misleading. As a simple analogy, consider the case of elasticity theory. Although any choice of basis for the representation of stress and strain tensors is suitable for calculations of elastic deformation, much of our understanding of the mechanics of elasticity would be out of reach if we attempted to interpret tensor elements in an arbitrary basis instead of turning to the concept of stress and strain invariants. The CE method has so far been missing the latter.

In this work, we address these ambiguities by demonstrating that any CE that employs an orthonormal basis can be expressed as a unique and basis-independent decomposition, which call the cluster decomposition (CD). From the analysis of uniqueness and basis independence, we are able to extract invariants—which are properties of a physical system or our approximation thereof, but not of the particular choice of basis. We demonstrate a direct relationship between the CD and well-established expansions of random variables, known as ANOVA or Sobol decompositions³² among other names^33,34. We subsequently show that the CD has analytic properties that allow a much deeper understanding of the structure and enable formal interpretations of expansion terms. We then illustrate a practical use case of the CD and use relevant concepts from functional analysis of variance (fANOVA) and sensitivity analysis (SA) to gain mathematically rigorous insight from CD and MC simulations of a ternary alloy. Our presentation establishes the CD as a mathematically formal framework that enables one to analyze the contribution of the interactions among clusters of chemical species to the configurational energy of alloys in a rigorous and unambiguous way.

In Section 2.1, we provide a concise overview of the CE formalism and present the construction of CEs using orthonormal basis functions. In Section 2.1.3, we use the mathematical framework of the CE to motivate the development of a unique and basis-free representation. To do so, we analyze the geometry of orthonormal cluster basis sets and demonstrate that the norms of expansion coefficients associated with the same orbit of crystallographic sites are invariant to the choice of basis. In Section 2.2, we introduce the cluster decomposition (CD), which is a unique decomposition of the configurational energy into multi-body terms. In the CD each orbit of symmetrically equivalent site clusters is represented by a single term, independent of the number of allowed species, in contrast to a CE in which the number of correlation functions per orbit scales with the number of allowed species. In Section 2.2.1, we provide a formal interpretation of the multi-body terms by establishing the CD as a symmetrically invariant functional ANOVA decomposition. In Section 2.2.2, we leverage the nature of the CD to obtain a decomposition of the variance of the configurational energy and use the terms of this decomposition to define sensitivity indices that enable formal ranking and comparisons of the energy contributions of the terms included in a CD. Finally, in Section 2.3, we present illustrative applications of the concepts discussed by means of a brief example involving the CrCoNi medium entropy alloy.

Results

Fourier CEs

We begin by presenting the CE mathematical formalism^1,35 used to create expansions of the form presented in Equation (2). We present a perspective on the CE formalism which highlights the underlying tensor-product nature of the formalism. Our perspective leads to a more concise, intuitive, and computationally efficient formulation. We will then use the CE formalism presented to derive the cluster decomposition and prove its invariance and uniqueness in Section 2.2. A summary of the symbols and notation used throughout the paper can be found in Supplementary Note 1.

The CE formalism is concerned with the representation of symmetrically invariant functions of atomic configuration. The CE of a configuration Hamiltonian H is commonly written as follows,

$$\begin{array}{l}H({{{\boldsymbol{\sigma }}}})\,=\,N\sum\limits_{\beta }{m}_{\beta }{J}_{\beta }\sum\limits_{\alpha \in \beta }\frac{1}{{m}_{\beta }N}{\Phi }_{\alpha }({{{\boldsymbol{\sigma }}}})\\\qquad\quad=\,N\sum\limits_{\beta }{m}_{\beta }{J}_{\beta }{\Theta }_{\beta }({{{\boldsymbol{\sigma }}}}),\end{array}$$

(2)

where Θ_β are called correlation functions and m_β are the crystallographic multiplicities per normalizing unit, usually the number of sites in a primitive or unit cell of the disordered structure. N is the number of such units being considered. J_β are the effective cluster interaction parameters.

The correlation functions Θ_β ensure that the expansion in Equation (2) is symmetrically invariant. Furthermore, to enable tractable parameterizations and evaluations, a CE is truncated to include only a small number of relevant terms, including only correlation functions over clusters with a small number of sites and which are physically compact. Finally, expressing the expansion as a density by dividing by N results in the widely used CE of the configurational energy of bulk crystals^1,5.

Configuration space and cluster basis functions

The domain of a CE is the space of all possible atomic configurations over a given disordered crystal structure. The space of atomic configurations σ is formally a product space, i.e., the Cartesian product of sets Ω_i of allowed species—which we refer to as site spaces—associated with each of N crystallographic sites. Each configuration variable σ_i ∈ Ω_i represents the species occupying the i-th site. The function space over configurations σ is then a tensor-product space of the function spaces over each configuration variable σ_i²⁴.

A set of basis functions Φ_α that span the tensor-product space over atomic configurations can be obtained by first constructing a basis for the function spaces over single configuration variables σ_i. Doing so requires finding a total of n = ∣Ω_i∣ linearly independent functions ${\phi }_{{\alpha }_{i}}$, α_i = 0, …, n − 1. An obvious choice is the set of all n indicator functions ${{{{\boldsymbol{1}}}}}_{{{{{\boldsymbol{\sigma }}}}}_{i}}$ for each of the allowed species σ_i ∈ Ω_i. However, such a choice does not result in a basis in which the configurational energy can be represented effectively using only a small subset of basis functions, i.e., a basis that allows a sparse or compressible representation.

Following the original CE formulation¹, we can obtain a suitable representation by requiring that (1) one of the basis functions is constant ϕ₀ = 1, and (2) that the basis be orthonormal under the following inner product^30,35,

$$\langle {\phi }_{j},{\phi }_{k}\rangle =\sum\limits_{{{{{\boldsymbol{\sigma }}}}}_{i}\in {\Omega }_{i}}{\rho }_{i}({{{{\boldsymbol{\sigma }}}}}_{i}){\phi }_{j}({{{{\boldsymbol{\sigma }}}}}_{i}){\phi }_{k}({{{{\boldsymbol{\sigma }}}}}_{i})$$

(3)

where ρ_i(σ_i) is an a-priori probability mass function of finding each of the allowed σ_i ∈ Ω_i on the i-th site. A uniform probability is most often used, but formally it should be equal to the concentration of chemical species in the non-interacting limit³⁰. We call a site basis that satisfies the above two requirements a standard site basis.

The basis set over the configuration product space is then given by the tensor product of the single site basis sets^36,37. Equivalently, a basis function Φ_α is the tensor product of a site basis function from each of the N sites,

$${\Phi }_{\alpha }=\bigotimes\limits_{i=1}^{N}{\phi }_{{\alpha }_{i}},$$

(4)

where the specific basis function taken for each site is indexed by the corresponding element α_i of the multi-index α.

In practice, the product basis functions can be evaluated as N-fold products involving a specified sequence of site basis functions evaluated at the corresponding configuration variable as follows^1,37,

$${\Phi }_{\alpha }({{{\boldsymbol{\sigma }}}})=\prod\limits_{i=1}^{N}{\phi }_{{\alpha }_{i}}({{{{\boldsymbol{\sigma }}}}}_{i})$$

(5)

If all site basis sets are orthonormal with respect to the inner product given in Equation (3), then it follows that the resulting set of product basis functions Φ_α are orthonormal with respect to the following inner product (a proof is given in Supplementary Note 2)^24,35,

$$\langle {\Phi }_{\alpha },{\Phi }_{\gamma }\rangle =\sum\limits_{{{{\boldsymbol{\sigma }}}}}{{{\boldsymbol{\rho }}}}({{{\boldsymbol{\sigma }}}}){\Phi }_{\alpha }({{{\boldsymbol{\sigma }}}}){\Phi }_{\gamma }({{{\boldsymbol{\sigma }}}}),$$

(6)

where the sum is over all possible configurations σ; and ${{{\boldsymbol{\rho }}}}({{{\boldsymbol{\sigma }}}})={\prod }_{i = 1}^{N}{\rho }_{i}{({{{\boldsymbol{\sigma }}}})}_{i}$ is the a-priori product probability distribution. The inner product in Equation (6) can be interpreted as an expectation value in the non-interacting limit.

Including ϕ₀ = 1 in all site bases is necessary so that Equation (2) is a hierarchical expansion, and therefore allows sparse or compressible representations. In the resulting expansion, the effective domain of each function Φ_α is the space of occupation variables of a cluster of sites S given by the indices of non-zero elements of the multi-index α, which we refer to as the support, supp(α), of the multi-index. As a result, the product functions Φ_α are cluster functions if and only if ϕ₀ = 1 in all site basis sets. With this requirement, a cluster function can be written solely in terms of clusters of sites S = supp(α) and the corresponding non-zero entries of the multi-index α, which we call a contracted multi-index ${\widehat{\alpha}}$,

$${\Phi }_{\alpha }({{{\boldsymbol{\sigma }}}})={\widehat{\Phi }}_{\widehat{\alpha }}({{{{\boldsymbol{\sigma }}}}}_{S})=\prod\limits_{i=1}^{| S| }{\phi }_{{\widehat{\alpha }}_{i}}({{{{\boldsymbol{\sigma }}}}}_{{S}_{i}})$$

(7)

Expression (7) makes the effective domain of cluster functions explicit and separates the functional form of a cluster function from the particular cluster of sites it acts on, i.e., cluster functions that operate on symmetrically equivalent clusters have the same functional form (indicated by $\widehat{\alpha }$), but differ in their effective domain (indicated by S). We will refer to cluster functions that are constructed using a standard site basis as Fourier cluster functions, and a resulting expansion as a Fourier CE, in order to distinguish from CEs that use ϕ₀ = 1 but do not use orthogonal site basis functions.

Since we are working with a discrete and countable domain, site basis functions are nothing more than vectors ${\phi }_{{\alpha }_{i}}\in {{\mathbb{R}}}^{{n}_{i}}$ (where n_i = ∣Ω_i∣) if we simply treat Ω_i as a sequence by specifying an order for the allowed species. We can therefore represent cluster functions over a cluster S as a Cartesian tensor by computing them using a real vector tensor product (instead of using an N-fold product as in Equations (5) and (7)),

$${\widehat{\Phi }}_{\widehat{\alpha }}=\bigotimes\limits_{i=1}^{| S| }{\phi }_{{\alpha }_{i}}$$

(8)

$${\widehat{\Phi }}_{\widehat{\alpha }}\in {{\mathbb{R}}}^{{n}_{1}\times \ldots \times {n}_{| S| }}$$

(9)

In doing so, we obtain a practical and numerically efficient implementation, that serves as a complimentary and arguably more intuitive depiction of the mathematical formalism presented thus far. Based on Equation (9) cluster functions can be represented as multi-dimensional arrays, where each dimension is associated with a site in a cluster S; and the entries along a given dimension correspond to the allowed species at that site. Then, the value of a cluster function Φ_α evaluated at a configuration σ_S is given directly by the value of the corresponding array element.

Symmetry invariance and correlation functions

The final component necessary to construct Fourier CEs of crystalline materials is the construction of expansion functions of configurations that are invariant to the crystallographic symmetry of the underlying structure. Constructing such symmetry invariant basis functions is achieved by averaging over the action of all symmetry operations in the space group of the underlying disordered crystal structure³⁷.

Symmetry operations transform configurations σ by permuting its elements. Similarly, the application of a symmetry operation on a cluster basis function Φ_α results in a permutation of site basis functions. The permutation of site basis functions in Φ_α can be suitably specified by the corresponding permutation of the elements of its multi-index α. The sets of symmetrically equivalent cluster basis functions can then be identified by the orbits β constructed from permutations of the multi-indices α. The correlation functions Θ_β used in the CE in Equation (2) are precisely the average of cluster basis functions Φ_α over orbits β.

However, we present an equivalent but simpler way to construct invariant basis functions by leveraging our approach of treating cluster basis functions ${\widehat{\Phi }}_{\widehat{\alpha }}$ explicitly as real space tensors. We introduce the concept of reduced correlation functions, which are obtained by averaging cluster basis functions over orbits of symmetrically equivalent contracted multi-indices $\widehat{\alpha }$, i.e., only over permutations of site functions over a fixed cluster of sites S. Reduced correlation functions are given as follows,

$${\widehat{\Theta }}_{\beta }({{{{\boldsymbol{\sigma }}}}}_{S})=\frac{1}{{\widehat{m}}_{\beta }}\sum\limits_{\widehat{\alpha }\in \widehat{\beta }}{\widehat{\Phi }}_{\widehat{\alpha }}({{{{\boldsymbol{\sigma }}}}}_{S}),$$

(10)

where $\widehat{\beta }$ is an orbit of symmetrically equivalent contracted multi-indices $\widehat{\alpha }$ (permutations of site functions over a fixed cluster of sites S); or equivalently, the set $\widehat{\beta }$ can also be obtained by converting all indices α ∈ β to contracted multi-indices $\widehat{\alpha }$. ${\widehat{m}}_{\beta }=| \widehat{\beta }|$ is the total number of contracted multi-indices in $\widehat{\beta }$.

Reduced correlation functions are also Cartesian tensors (since they are the sum of tensors), and for practical purposes can be precomputed and stored as multi-dimensional arrays for efficient evaluation. In doing so, correlation functions can be efficiently computed by taking averages of the array elements corresponding to the occupancy σ_S of each of the symmetrically equivalent site clusters S ∈ B. Evaluating correlation functions for subsequent prediction using array access is much more time efficient (time complexity ${{{\mathcal{O}}}}(1)$) than computing the ∣S∣-fold products given in Equation (7) (time complexity ${{{\mathcal{O}}}}(| S| )$).

The correlation functions used in Equation (2) can then be expressed in terms of reduced correlation functions by averaging over symmetrically equivalent clusters of sites S,

$${\Theta }_{\beta }({{{\boldsymbol{\sigma }}}})=\frac{1}{{m}_{B}N}\sum\limits_{S\in B}{\widehat{\Theta }}_{\beta }({{{{\boldsymbol{\sigma }}}}}_{S})$$

(11)

where B is an orbit of symmetrically equivalent clusters of sites S ⊆ [N], m_B = ∣B∣/N is the site cluster orbit multiplicity per normalizing unit N.

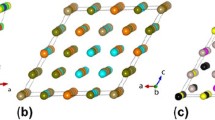
Figure 1 shows a graphical illustration of the relationship amongst the various multi-indices and basis functions we have introduced using a representative triplet cluster of sites in a cubic rocksalt unit cell as an example. Figure 1 depicts the relationship between multi-indices α, contracted multi-indices $\widehat{\alpha }$, and cluster basis functions ${\widehat{\Phi }}_{\widehat{\alpha }}$. Figure 1 also shows a graphical representation of orbits β of multi-indices α, the corresponding orbits $\widehat{\beta }$ of contracted multi-indices $\widehat{\alpha }$, and the resulting permutation invariant reduced correlation function ${\widehat{\Theta }}_{\beta }$.

Fig. 1: Graphical representation of a multi-index α, a corresponding contracted multi-index $\widehat{\alpha }$, and the resulting triplet cluster basis function ${\widehat{\Phi }}_{\widehat{\alpha }}$ over a three-point cluster of sites in a rocksalt unit cell.

Graphical representation of an orbit of multi-indices β, a corresponding orbit of contracted multi-indices $\widehat{\beta }$, and the resulting triplet reduced correlation function ${\widehat{\Theta }}_{\beta }$. The different colored spheres represent multi-index values. Gray spheres correspond to zero values, i.e., constant site functions ϕ₀ = 1. Translucent color wedges on the remaining sites (those not included in the highlighted cluster) illustrate the partial occupancy, or equivalently, the site basis function choices at each site.

Invariants in Fourier CEs

We motivate the search for a basis-independent representation of a CE by making a geometric observation. By their orthogonality, standard site basis sets are related by rotations about the hyperplane normal to the function ϕ₀. This observation is illustrated graphically for a ternary site space in Fig. 2a. Any ternary standard site basis must include two orthogonal basis functions that lie on the plane orthogonal to ϕ₀.

Fig. 2: Geometry and transformations between Fourier basis sets.

a Geometry of standard site basis sets for a ternary site space. Two standard site basis sets related by a rotation of 2π/3 are shown. Both basis sets include the constant ϕ₀. Any arbitrary rotation about ϕ₀ results in a distinct standard site basis. b Block-diagonal change of basis matrix relating the two different sets of Fourier cluster basis functions up to quadruplets constructed using the site basis sets in a.

By considering the geometry of standard site bases, we can show that the change of basis matrix (CBM) between two Fourier cluster basis sets is block-diagonal, and any term connecting cluster functions over symmetrically distinct clusters is zero. A derivation is given in Supplementary Note 3. A visualization of the CBM between two Fourier cluster bases of a ternary system is shown in Fig. 2b. Since each of the diagonal blocks in the CBM is unitary, it follows that the norm of expansion coefficients within each block is invariant to any change of orthogonal basis. In other words, a change of orthogonal basis does not mix cluster basis functions over symmetrically distinct clusters.(In contrast, basis transformations involving a non-orthogonal basis set, such as those using site indicator functions, will mix across symmetrically distinct clusters.)

Formally, these invariance relations can be expressed as a sum of the squares of expansion coefficients associated with a single symmetrically distinct cluster of sites S as follows,

$$\sum\limits_{\gamma\,:\,{{{\rm{supp}}}}(\gamma )=S}{J}_{\gamma }^{{\prime} 2}=\sum\limits_{\alpha\,:\,{{{\rm{supp}}}}(\alpha )=S}{J}_{\alpha }^{2}$$

(12)

where ${J}_{\gamma }^{{\prime} 2}$ and ${J}_{\alpha }^{2}$ are coefficients in the Fourier expansion of a function H using two distinct Fourier cluster basis sets.

Equation (12) applies to any function of configuration regardless of symmetry. When dealing with a symmetrically invariant function, we can group the sums by orbits of symmetrically equivalent site clusters B and obtain the following invariance relation,

$$\sum\limits_{\eta \in L(B)}{\widehat{m}}_{\eta }{J}_{\eta }^{{\prime} 2}=\sum\limits_{\beta \in L(B)}{\widehat{m}}_{\beta }{J}_{\beta }^{2}$$

(13)

where L(B) = {β: supp(α) ∈ B ∀ α ∈ β} are sets of orbits β of multi-indices α with symmetrically equivalent supports, i.e., corresponding to the group of correlation basis functions that operate over the same orbit B.

The cluster decomposition

Based on the invariance of expansion coefficients given in Equation (13), we rewrite the CE in Equation (1) in terms of reduced correlation functions grouped by orbits B of site clusters as follows,

$$H({{{\boldsymbol{\sigma }}}})=\sum\limits_{B}\sum\limits_{\widehat{\beta }\in \widehat{L}(B)}{\widehat{m}}_{\beta }{J}_{\beta }\sum\limits_{S\in B}{\widehat{\Theta }}_{\beta }({{{{\boldsymbol{\sigma }}}}}_{S}),$$

(14)

where $\widehat{L}(B)$ are sets of orbits $\widehat{\beta }$ of contracted multi-indices representing all symmetrically distinct permutations of site basis functions over the sites in the clusters S—we use the symbol “L” to stand for labeling, i.e., $\widehat{L}(B)$ is the set of symmetrically distinct labelings of a cluster of sites S ∈ B with site basis functions.

The two inner sums in Equation (14) are independent and can be re-arranged to obtain a far more physically intuitive many-body expansion that includes only a single term per relevant cluster S irrespective of the number of allowed species,

$$H({{{\boldsymbol{\sigma }}}})=\sum\limits_{B}\sum\limits_{S\in B}\sum\limits_{\widehat{\beta }\in \widehat{L}(B)}{\widehat{m}}_{\beta }{J}_{\beta }{\widehat{\Theta }}_{\beta }({{{{\boldsymbol{\sigma }}}}}_{S})$$

(15)

$$=\sum\limits_{B}\sum\limits_{S\in B}{\widehat{H}}_{B}({{{{\boldsymbol{\sigma }}}}}_{S})$$

(16)

where the n-body terms ${\widehat{H}}_{B}({{{{\boldsymbol{\sigma }}}}}_{S})$ account for the energy originating from the interactions between the species that reside on a cluster S ∈ B. For clusters S with more than one site, ∣S∣ > 1, we will therefore call these terms cluster interactions.(Not to be confused with the expansion coefficients J_β which were named effective cluster interactions based on a binary Fourier CE.).

Following the original CE formalism, Equation (16) can also be written as a density by averaging cluster interactions ${\widehat{H}}_{B}$ over symmetrically equivalent clusters S ∈ B,

$$\begin{array}{l}H({{{\boldsymbol{\sigma }}}})\,=\,N\sum\limits_{B}{m}_{B}\left(\frac{1}{{m}_{B}N}\sum\limits_{S\in B}{\widehat{H}}_{B}({{{{\boldsymbol{\sigma }}}}}_{S})\right)\\\qquad\quad=\,N\sum\limits_{B}{m}_{B}{H}_{B}({{{\boldsymbol{\sigma }}}})\end{array}$$

(17)

We will refer to the terms H_B with ∣S∣ > 1 for all S ∈ B as mean cluster interactions, and as composition effects for point clusters (∣S∣ = 1). We use P to represent an orbit of single sites (∣S∣ = 1, ∀ S ∈ P) when an explicit distinction between point terms and cluster interactions is needed.

We call Equations (16) and (17) the cluster decomposition (CD) of the configuration energy H(σ). Note that we have purposefully written the CD in terms of reduced correlation functions ${\widehat{\Theta }}_{\beta }$ such that the cluster interactions${\widehat{H}}_{B}$ are in fact also Cartesian tensors and can be suitably represented as arrays with the same dimensions as the underlying cluster basis functions given in Equation (9).

This tensor representation also facilitates efficient computations and manipulations of the CD. By representing cluster interactions as multi-dimensional arrays, the computational complexity of evaluating the energy of a structure is substantially reduced since there is no longer need to compute the values of correlation functions individually. This practical benefit is significant, as Equations (16) and (17) have the same number of terms for a given crystal structure regardless of the number of species or components. When using a CD for inference, such as MC sampling, the computational time complexity is only a function of the cluster orbits ${{{\mathcal{O}}}}(| B| )$, and is independent of the number of allowed species (see Equation (16)). In contrast, evaluating a CE scales with the number of species ${{{\mathcal{O}}}}(\beta )={{{\mathcal{O}}}}(\widehat{L}(B)\times B)$ (see Equation (2)), where the number of site basis permutations $| \widehat{L}(B)|$ scales as with the number of species n as n^∣S∣ excluding symmetry.

While it is possible to obtain an expression similar to Equation (16) that retains the practical benefits for any choice of site basis, whether orthogonal or not, a true CD can only be obtained from a Fourier CE. This distinction is fundamental because decompositions obtained with CEs that use non-orthogonal basis lack the analytical properties that we discuss in the rest of this work.

It follows directly from Equation (13) that the norm of the cluster interactions ${\widehat{H}}_{B}$ are invariant to a change of standard basis, i.e., they are invariant to arbitrary basis rotations orthogonal to ϕ₀,

$$| | {\widehat{H}}_{B}| {| }_{2}^{2}=\sum\limits_{\widehat{\beta }\in \widehat{L}(B)}{\widehat{m}}_{\beta }{J}_{\beta }^{2},$$

(18)

We call the squared norm of a cluster interaction $| | {\widehat{H}}_{B}| {| }_{2}^{2}$ the effective cluster weight of a cluster S ∈ B. In addition, we define the total cluster weight as the effective cluster weight multiplied by the multiplicity of its orbit, ${m}_{B}| | {\widehat{H}}_{B}| {| }_{2}^{2}$.

Figure 3a shows CE coefficients grouped by site cluster orbits for two Fourier CEs of the same fit of the configuration energy of a CrCoNi alloy. Figure 3a also shows the square root of the resulting effective cluster weights for both expansions. Unsurprisingly, these values are exactly the same for both expansions since they are precisely the invariants given in Equations (13). Figure 3b also shows a visualization of a point term, nearest neighbor pair, and triplet cluster interactions as multi-dimensional arrays for a CD of the same CrCoNi fit. This compact representation of cluster interactions as multi-dimensional arrays, allows one to read off the interaction energy for a particular cluster occupancy directly from the corresponding array element. For example, we can readily determine which interactions are favorable (negative) and which are unfavorable (positive). Most importantly, since it is basis-independent such interpretations are unambiguous, in contrast to attempting to do so using the expansion coefficients of particular basis sets shown in Fig. 3a.

Fig. 3: Invariance and visualization of cluster interactions.

a Expansion coefficients (effective cluster interactions) grouped by orbits B of site clusters for two Fourier cluster expansions of the same function of the configurational energy of a CrCoNi alloy using two different basis sets (stems), and the square root of the corresponding effective cluster weights (translucent bars) as defined in Equation (18). b Visualization of the main effect (point), nearest neighbor pair, and triplet cluster interactions as multi-dimensional arrays for the resulting cluster decomposition of the same CrCoNi alloy function used in a. Each array entry represents the energy contribution of a single cluster occupied accordingly, i.e., blue (yellow) represents favorable (unfavorable) interactions.

In addition to their cluster weight invariance, cluster interactions have the following mathematical properties (derivations and proofs are given in Supplementary Note 4):

• 1. $\langle {\widehat{H}}_{B}\rangle =0$ (zero mean)

• 2. $\langle {\widehat{H}}_{B},{\widehat{H}}_{D}\rangle =0$ for B ≠ D (orthogonal)

• 3. $\langle {\widehat{H}}_{B},{F}_{{{{\mathcal{D}}}}}\rangle =0$ for any set of orbits ${{{\mathcal{D}}}}$ such that $B\,\notin\,{{{\mathcal{D}}}}$ and any function ${F}_{{{{\mathcal{D}}}}}$ that can be expanded using Fourier basis functions Φ_α with supp(α) ∈ D for $D\in {{{\mathcal{D}}}}$. (irreducible)

From properties (1) and (2) it follows that the CD of a given function H is unique³⁸; meaning there exists one and only one set of cluster interactions ${\widehat{H}}_{B}$ for any given H (a proof is given in Supplementary Note 5). As a result, the cluster weights and cluster interaction values plotted in Fig. 4 are intrinsic properties of the function H and can therefore be considered properties of the physical system (to within the validity of the regression approximation), irrespective of the choice of basis. Furthermore, uniqueness and the properties listed above imply that Equations (16) and (17) are ANOVA representations of H(σ)^32,38. In fact, re-written in such a form, a Fourier CE is nothing more than a fANOVA representation, in which by symmetry, interactions among equivalent clusters S ∈ B are given by the same function ${\widehat{H}}_{B}$. By extension, using a CD as an effective Hamiltonian to define a Boltzmann distribution is equivalent to log-density ANOVA estimation of a probabilistic graphical model^39,40,41.

Fig. 4: Estimated sensitivity indices and cluster interactions of cluster decompositions truncated at pairs and triplets.

a Cluster sensitivity indices of two fitted CrCoNi CDs (one including only pairs, and another including pairs and triplets) sorted by cluster diameter. Effective (total) cluster sensitivity indices are shown with solid (translucent) colors. b Nearest-neighbor cluster interactions as two-dimensional arrays. Each entry of the array represents the interaction energy between the corresponding nearest neighbor species.

Statistical interpretation of cluster interactions

Using the properties of ANOVA representations, we can obtain a much deeper understanding of the terms in a CD. ANOVA terms are constructed from hierarchical inclusion-exclusion of expectation values conditioned on the occupancy of clusters. For example, as already known from the original CE formalism¹, the constant term is equal to the mean energy in the non-interacting limit, ${J}_{{{\emptyset}}}={H}_{{{\emptyset}}}=\langle H({{{\boldsymbol{\sigma }}}})\rangle$. In the statistics literature, ${J}_{{{\emptyset}}}$ is usually referred to as the grand mean⁴². The point terms, ${\widehat{H}}_{P}({{{{\boldsymbol{\sigma }}}}}_{i})$ are the difference between the mean conditioned on the i-th site and the grand mean, ${\widehat{H}}_{P}({{{{\boldsymbol{\sigma }}}}}_{i})=\langle H({{{\boldsymbol{\sigma }}}})| {{{{\boldsymbol{\sigma }}}}}_{i}\rangle -\langle H({{{\boldsymbol{\sigma }}}})\rangle$. The point terms of an ANOVA representation are called main effects⁴². The main effects are the mean contribution that a specific species σ_i residing on the i-th site has on the total energy, and the average of main effects in the CD represents the portion of the energy that depends on composition only.

The remaining terms involving clusters S with more than one site are referred to in the statistics literature as interactions⁴², which further motivates our terminology. The cluster interaction ${\widehat{H}}_{B}({{{{\boldsymbol{\sigma }}}}}_{S})$ of a cluster S is the mean conditioned on the sites in cluster S minus the cluster interactions of all its sub-clusters T ⊂ S,

$${\widehat{H}}_{B}({{{{\boldsymbol{\sigma }}}}}_{{{{\boldsymbol{S}}}}})=\langle H({{{\boldsymbol{\sigma }}}})\,|\,{{{{\boldsymbol{\sigma }}}}}_{S}\rangle -\sum\limits_{T\subset S}{\widehat{H}}_{C}({{{{\boldsymbol{\sigma }}}}}_{{{{\boldsymbol{T}}}}})$$

(19)

Equation (19) clarifies the nature of a cluster interaction as the mean contribution (under the a-priori product distribution) to the total energy that originates solely from a single cluster S ∈ B and none of its sub-clusters. Hence, the terms in the CD represent energetic interactions among species occupying the sites of a cluster that cannot be captured by any lower-order interactions. Moreover, we have an exact interpretation of the elements in the cluster interactions tensor shown in Fig. 3; they are the mean energy conditioned on the specific occupation σ_S of that cluster, with all interactions of sub-clusters T ⊂ S conditioned on the corresponding occupation σ_T removed.

In our exposition, we started with a representation of a CD using a Fourier CE. However, since the CD is basis-independent, we can discard the concept of a basis altogether. In fact, in fANOVA and related literature, a function is decomposed into its ANOVA representation by directly appealing to Equation (19)^32,38. This approach has been used in concurrent work⁴³ that provides an axiomatic exposition of the CE and the CD. This exposition is equivalent to the formalism of tensor-product fANOVA decompositions⁴⁰ that we have presented here.

Variance decomposition & cluster sensitivity indices

As the name analysis of variance suggests, a CD also comprises a decomposition of the variance of the configuration energy under the a-priori non-interacting product measure P(σ) = ∏_iρ_i(σ_i)³⁸. The total variance of a Fourier CE can be conveniently computed from the expansion coefficients as follows,

$${{{\rm{Var}}}}[H({{{\boldsymbol{\sigma }}}})]=\langle {H}^{2}\rangle -{\langle H\rangle }^{2}$$

(20)

$$=\sum\limits_{\alpha }{J}_{\alpha }^{2}-{J}_{{{{\mathbf{0}}}}}^{2}=\sum\limits_{\alpha \ne {{{\mathbf{0}}}}}{J}_{\alpha }^{2}$$

(21)

where 0 is the multi-index of all zeros, and where we have used the orthonormality of Fourier cluster functions.

By grouping terms by multi-indices with the same support and subsequently by symmetrically equivalent multi-indices, Equation (21) can be re-written as,

$${{{\rm{Var}}}}[H({{{\boldsymbol{\sigma }}}})]=\sum\limits_{B\ne {{\emptyset}}}\sum\limits_{S\in B}\sum\limits_{\widehat{\beta }\in \widehat{L}(B)}{\widehat{m}}_{\beta }{J}_{\beta }^{2}$$

(22)

$$=N\sum\limits_{B\ne {{\emptyset}}}{m}_{B}| | {\widehat{H}}_{B}| {| }_{2}^{2}$$

(23)

Where we identify the innermost sum in Equation (22) as the effective cluster weights.

From on Equation (21), we see that the variance of a single cluster interaction is equal to its effective cluster weight, ${{{\rm{Var}}}}[{\widehat{H}}_{B}]=| | {\widehat{H}}_{B}| {| }_{2}^{2}$. Equation (22) can be explicitly expressed as a variance decomposition in terms of individual cluster variances as follows,

$${{{\rm{Var}}}}[H({{{\boldsymbol{\sigma }}}})]=N\sum\limits_{B\ne {{\emptyset}}}{m}_{B}\,{{{\rm{Var}}}}[{\widehat{H}}_{B}({{{{\boldsymbol{\sigma }}}}}_{S})]$$

(24)

By computing the variance of Equation (19), we can show that the effective cluster weights correspond to the conditional variance associated with a cluster with all lower-order variances subtracted,

$${{{\rm{Var}}}}[{\widehat{H}}_{B}({{{{\boldsymbol{\sigma }}}}}_{{{{\boldsymbol{S}}}}})]={{{\rm{Var}}}}[H({{{\boldsymbol{\sigma }}}})| {{{{\boldsymbol{\sigma }}}}}_{S}]-\sum\limits_{T\subset S}{{{\rm{Var}}}}[H({{{\boldsymbol{\sigma }}}})| {{{{\boldsymbol{\sigma }}}}}_{T}]$$

(25)

In other words, an effective cluster weight is the variance in the non-interacting limit that can be attributed to a single cluster only and to none of its sub-clusters.

The variance decomposition resulting from the CD provides motivation and interpretation for the choice of regularization used when fitting. For example, Ridge regularization can be interpreted as setting an upper cutoff to the total variance. The use of Tikhonov regularization can be used to more finely set variance cutoffs for specific correlation functions. Group-wise regularization² can be directly motivated as a judicious form to regularize cluster interactions H_B directly and tune the resulting relative variance contributions. Finally, estimation algorithms with hierarchical inclusion/exclusion of clusters^2,4,44,45,46, can be motivated by appealing to statistical concepts of hierarchically well-formulated models⁴⁷ that satisfy marginality constraints⁴⁸, or that abide by heredity principles under so-called weak or strong hierarchy constraints^49,50.

The variance decomposition inherent in the CD also allows one to formally rank the importance of each cluster interaction by following the prescription of Sobol’s sensitivity indices³², which are used extensively in variance-based sensitivity analysis. Accordingly, we define the effective cluster sensitivity index ${\widehat{\tau }}_{B}$ as the fraction of the total variance of H carried by the interactions of a cluster S ∈ B,

$${\widehat{\tau }}_{B}=\frac{{{{\rm{Var}}}}[{\widehat{H}}_{B}({{{{\boldsymbol{\sigma }}}}}_{S})]}{{{{\rm{Var}}}}[H({{{\boldsymbol{\sigma }}}})]}$$

(26)

We define the cluster sensitivity index τ_B as the normalized fraction of the total variance of H(σ) contributed by the cluster interaction ${\widehat{H}}_{B}$ per normalizing unit, ${\tau }_{B}={m}_{B}{\widehat{\tau }}_{B}$. Cluster sensitivity indices provide a mathematically formal and basis-independent route for evaluating trends in the strength of interactions, such as their decay with respect to the number of sites and increasing spatial diameter. Cluster sensitivity indices can be directly computed from a CE by using Equation (18). Furthermore, global sensitivity indices of a cluster S, can be computed by summing effective cluster indices over all sub-clusters or over all clusters with non-zero intersections with S^32,51.

Example—CrCoNi medium entropy alloy

As a brief example demonstrating a practical use case of the CD, we fit two expansions of a CrCoNi medium entropy alloy: (1) a less accurate expansion (in terms of cross-validation error) that includes pairs terms only (pair fit), and (2) a more accurate expansion including pairs and triplets (triplet fit). Details of the DFT calculations used to generate training data and the regression procedure to obtain the final fits are given in Section 4. Our approach follows a recent study of the CrCoNi alloy³¹ which uses the CE method and Wang–Landau sampling to explore the role of pair and triplet interactions in tuning short-range order (SRO) and the resulting experimentally observed peak in the heat capacity around 940 K⁵². We will use the cluster decomposition formalism to carry out the corresponding calculations and analysis in order to illustrate how a richer and deeper insight is obtained directly from comparing the thermodynamic results obtained from each CD without the need for ad-hoc models to analyze interactions between species. We aim only to demonstrate the possibility of more in-depth analysis via the CD as an illustration, but we do not attempt to make any novel scientific claims about this particular alloy.

The cluster sensitivity indices for the resulting cluster decompositions are shown in Fig. 4a in order of increasing number of sites and cluster diameter. The selected pair clusters between the two fits are not exactly the same because they result from statistical fits using different feature matrices and a regression algorithm with inherent feature selection. Accordingly, obtaining different selected pair cluster interactions and values for the two different fits is expected. We also note that our rigorous claims of uniqueness, invariance, and interpretability deal with a given function and not the process of statistical approximation used to obtain it—our work opens worthwhile ways to develop basis-independent estimation, but that is beyond the scope of this work.

Although the same starting pool of pair terms is used in both fits, five pair interactions are selected in the pair-only fit, and six pair interactions are selected in the fit that includes triplets. Both fits include the first, second, and fourth nearest neighbor pair interactions, as well as a pair interaction with a 7.48 Å diameter. The pair-only fit includes an additional pair interaction with a diameter of 6.6 Å, while the triplet fit includes the third nearest neighbor (though with a noticeably lower sensitivity index) and an additional pair interaction with an 8.98 Å diameter. These differences in the selection of pairs for the two fits are attributed to the statistical-based feature selection of the regularized regression we have used.

The cluster sensitivity indices for the nearest neighbor pair interaction and three of the four included triplet interactions in Fig. 4 are labeled with figures of their representative clusters S. We observe that the nearest neighbor pair is a sub-cluster of all three labeled triplet clusters. This is not unexpected given that we obtain the fits using hierarchical constraints, i.e., for any triplet cluster interaction included, the interactions of all its sub-clusters must also be included. However, there is a clear selection of triplet clusters that include the nearest neighbor pair over other selected pair interactions for which triplets that include these were also present and fully sampled (full rank) in the initial pool of clusters. Furthermore, we observe that the cluster sensitivity index for the nearest neighbor pair interaction (first red bar in both fits) is lower in the triplet fit than in the pair-only fit. This behavior can be rationalized as an effect of the possible renormalization of interactions⁵³ from the different levels of truncation used in the two fits.

By inspecting Fig. 4a, b, we see that the interactions shown in Fig. 3 are of different orders of magnitude. The cluster sensitivity index of the main effect is about 2 orders of magnitude larger than that of higher-degree interactions. In Fig. 4b, we see that nearest neighbor interactions are of the order of 10 meV, and therefore main effects are of eV magnitude. We can identify the most important cluster interactions, rank their importance, and compare different fits on rigorous grounds by using cluster sensitivity indices. The point terms account for the overwhelming majority of the variance, however their contributions, are only relevant when the composition is not fixed (i.e., in the grand canonical ensemble). In both fits, the nearest neighbor and second nearest neighbor interactions are the most important (largest sensitivity), with significant contributions coming from triplet interactions in the triplet fit.

Figure 4b shows the nearest neighbor pair interactions for both fits. The energy contributions arising from the interaction between specific species can be obtained by directly inspecting the values of the cluster interaction elements. For example, a Cr-Cr nearest neighbor interaction in the pair fit contributes ~20 meV to the total energy, and a Cr-Co contributes ~−20 meV. Thus, we can expect SRO to favor Cr-Co nearest neighbor pairs over Cr-Cr; though this behavior will be adjusted by the triplet interactions that includes nearest neighbor pairs. Comparing the nearest neighbor pair interactions between the two fits, we see that the attraction/repulsion and of relative magnitude trends are the same. For example, in both fits Cr-Co nearest neighbor pairs have the strongest attractive interaction, and Cr-Ni have the second strongest attractive interaction. However, we observe that the overall magnitude of nearest neighbor pair interaction values in the triplet fit is lower than those of the pair-only fit, in accordance with their cluster sensitivity indices. These observations suggest that the inclusion of triplet interactions modifies the strength but not the trends among nearest neighbor pair interactions, and as a result, triplet interactions will indeed tune the resulting SRO and heat capacity without changing the overall trend.

Finally, the relative trends of the nearest-neighbor interactions obtained directly from the CD (Fig. 4b) agree with previous results that had to be obtained via an ad-hoc and less accurate nearest-neighbor pair model³¹. Using the cluster decomposition we are able to directly obtain the interaction energy from both fits and compare the overall importance of interactions arising from different clusters by using their cluster sensitivity indices. Hence the CD enables mathematically rigorous analysis and interpretation of the interactions among chemical species without the need to resort to auxiliary models—an essential component so far absent in the CE formalism.

SRO and the K-state phenomenon

Configuration entropy has been found to be the main driver of the K-state phenomenon characterized by a peak in the heat capacity of the CrCoNi alloy, specifically by way of an ordering transition that favors CrNi and CrCo nearest neighbor pairs. The ordering transition is observed to be driven predominantly by nearest neighbor pair interactions but substantially tuned by many-body interactions³¹. This behavior is foreshadowed by our previous analysis of nearest-nearest neighbor cluster interactions and cluster sensitivity indices. Nonetheless, to further illustrate the use of the CD, we corroborate the origin of the peak in the heat capacity, explicitly compute SRO behavior, and further substantiate the predicted roles of higher-order interactions using a Wang–Landau estimation of the density of states.

We computed nearest-neighbor pair SRO, internal energy, and the resulting heat capacity via equiatomic canonical Wang–Landau sampling. Figure 5 shows the nearest-neighbor pair SRO, the internal energy, and the heat capacity computed for the pair fit, the triplet fit, as well as a truncated CD that includes only the pair interactions from the triplet fit (the six pair interactions in the rightmost plot in Fig. 4a). The middle column in Fig. 5, also shows the contribution to the internal energy coming from nearest-neighbor interactions, second nearest neighbor interactions, the 7.48 Å interaction, and triplet interactions. All other interactions are plotted in gray curves. Since the sum of all interactions in each simulation gives the total internal energy, the CD allows us to obtain a breakdown of the finite temperature interactions arising from different clusters.

Fig. 5: Nearest-neighbor pair probabilities (SRO), internal energy, nearest neighbor pair energy, and normalized heat capacity.

The nearest neighbor pair energy is plotted with a solid blue curve, and the internal energy with a solid red curve. Pair fit results (top), triplet fit results (bottom, solid), truncated triplet fit to pairs (bottom, translucent/dot-dash).

For all cases, we observe that the start of the ordering transition and the inflection of internal energy are congruent with the location of the peak in the heat capacity; suggesting that, as previously reported³¹, the ordering transition is the main cause for the peak in heat capacity associated with the K-state phenomenon. Specifically, the peak in the heat capacity predicted with the pair fit occurs at 620 K and the peak predicted with the triplet fit happens at 1300 K. We observe favorable ordering tendencies between CrCr and CrNi nearest neighbor pairs and a decrease in the probability of observing CoNi pairs as foreshadowed by directly inspecting their cluster interactions shown in Fig. 4b.

We obtain a much richer picture by observing the contributions to the internal energy arising from the included cluster interactions. Above the transition temperature, the magnitude of contributions of each cluster follows the order set by the cluster sensitivity indices shown in Fig. 4a, which we rationalize by interpreting the expectation operation used in their ANOVA statistical interpretation—such as in Equation (19)—as the ensemble average in the random (high temperature) limit. However, we observe that the order of contributions to the internal energy changes at the phase transition, which we attribute to the covariance that emerges between cluster interactions at finite temperatures. Notably, the contribution from 7.48 Å pair interaction in the pair and triplet fit begins to overcome all other contributions as temperature decreases. In contrast, the contribution of the second nearest neighbor interaction decays to zero for the pair fit, but remains the most important in the triplet fit. These observations point to the importance of considering both cluster sensitivity indices and effects at finite temperatures when studying the role of different interactions in determining thermodynamic properties.

The agreement between the nearest-neighbor pair energies and SRO of the two CDs that include only pair interactions shown in Fig. 5, suggests that the overall SRO and total internal energy trends are set predominantly by the first and second nearest-neighbor pair interactions (those with the highest cluster sensitivity from Fig. 4b). Furthermore, the qualitatively similar trend of the internal energy and nearest-neighbor pair energy in all CDs further corroborates this conclusion.

However, the role of the second nearest neighbor pair below the transition temperature is markedly different when triplets are included in the fit. As we noted, the contributions of the second nearest neighbor pair decay to zero for the pair-only fit, but remain the most important for the triplet fit as well as the truncated triplet fit. This observation may be indicative of a renormalization⁵³ of excluded interactions in the pair fit, since the second nearest neighbor contribution does not decay when triplets are removed after fitting in the truncated triplet fit. In contrast, the internal energy contributions of the 7.48 Å pair do not decay and are qualitatively similar in both pair and triplet fit. This is indicative that this cluster interaction is not affected by renormalization, which we can further motivate by positing that all higher-order interactions that include the long-range 7.48 Å that are excluded from the fit have negligible contributions.

Considering the similarity of the resulting heat capacity from the CDs with pairs only suggests that the transition is indeed driven predominantly by nearest-neighbour pair interactions. It is interesting to note that the transition temperature for the CD obtained from truncating the triplet fit is lower than that of the pair fit. This behaviour can also be attributed to the removal of higher-order contributions from triplets that were not renormalized into pair interactions during fitting.

By comparing the results from the CD that includes triplet interactions with the pair-only CDs, we can observe that triplet terms tune the SRO values, reduce the fraction of internal energy attributed to pair terms, and raise the transition temperature. Additionally, the triplet interactions qualitatively change the nature of the transition, as observed by the more abrupt changes in SRO values and internal energy and the narrower heat capacity peak compared to the corresponding values obtained from CDs with pairs only. To delve deeper, one could inspect the triplet interaction values from their array representations (as shown in Fig. 3) to better understand the specific roles in tuning the ordering transition.

The computed internal energy and heat capacity, which are total system values, could have been suitably obtained from the CE formalism only. However, the formal breakdown of contributions from the different cluster interactions that result from the CD formalism permits a richer analysis of the role of these interactions. For this particular example, we have leveraged the CD formalism, in particular, the breakdown of energy into statistically independent cluster contributions and their cluster sensitivity indices, to faithfully explain the primary origin of the K-state phenomenon in the CrCoNi medium entropy alloy. We also characterized the primary role of nearest-neighbour interactions in setting ordering trends and the transition temperature and clarified the role of longer-range pairs and triplet interactions in tuning both of these quantities. All of the presented conclusions based on our results agree with those reported previously³¹; however, by using the CD, we have shown how results leading to these conclusions can be more effectively calculated and further substantiated with the mathematically formal analysis resulting from the CD.

Discussion

In this work, we introduce the CD as a versatile framework for representing the configurational energy of multicomponent materials. Unlike CEs that rely on an arbitrary choice of basis, the CD offers a basis-independent representation in terms of cluster interactions. In contrast to correlation functions, cluster interactions are physically intuitive, numerically more efficient, and mathematically meaningful. To achieve this, we revisited the mathematical formalism of the CE method and provided a modern exposition that emphasizes its tensor-product structure. This enables us to obtain a more intuitive, compact, and numerically efficient representation of cluster interactions.

We further established a direct connection between the CD and functional analysis of variance (ANOVA). Specifically, we showed that the cluster interaction terms in the CD can be interpreted as conditional expectation values in the non-interacting limit, with lower-order effects removed. We also discussed the nature of the CD as a variance decomposition and introduced cluster sensitivity indices as a formal measure to rank and compare the importance of the contributions of different cluster interactions. This provides a mathematically rigorous interpretation of the CD and the nature of the cluster interactions.

As an illustrative example, we used the CD formalism to explain the role of SRO in the K-state phenomenon of the CrCoNi medium entropy alloy. We demonstrated how the CD can be used to analyze the contributions arising from the interactions among species in different clusters and explain their effects in setting and tuning ordering tendencies and transition temperatures.

We believe that substantially more insight, use cases, and parameter estimation methods beyond what we have presented can be developed using the CD and its formal statistical properties. The statistical literature is ripe with analysis techniques and methodology—such as aforesaid log-density ANOVA models^40,41 and sensitivity analysis^32,51—that can be directly leveraged in applications using parameterized lattice models. Methods that can be used for direct estimation of cluster interactions and cluster indices in fully basis-independent manners already exist in the statistics literature^32,39,41,51. Moreover, the formalism of the CD is not limited to scalar functions of discrete degrees of freedom as presented here. In fact, a CD can be obtained for any representation of scalar, vector, or tensor-valued function over a tensor-product space by following the same approach we have presented. Related expansions and generalizations such as spin CEs, expansions of elastic properties, and the atomic CE^{17,18,19,21,22} can be recast as a CD and thus open the door to continued and significant developments based on rigorously established mathematical and statistical grounds.

Methods

Density functional theory calculations

The pair and triplet expansions were fit using a set of 500 training structures with up to 12 atoms per super-cell. The energy of the training structures was computed with density functional theory (DFT) using the Vienna ab initio simulation package (VASP) with the projector-augmented wave method^54,55. The DFT calculations were performed using a plane-wave basis set with an energy cutoff of 520 eV, and a reciprocal space discretization of 200 k-points per Å. Electronic exchange-correlation effects are described using used the Perdew-Burke-Ernzerhof (PBE) generalized gradient approximation exchange-correlation functional⁵⁶. All calculations were converged to 10⁻⁵ eV in total energy for electronic loops and 0.01 eV/Åfor forces. All DFT calculations are performed following the Materials Project⁵⁷MetalRelaxSet settings defined in the pymatgen Python package⁵⁸.

Mixed-integer quadratic programming hierarchically constrained structured sparsity fits

The two fits were done using a mixed-integer quadratic problem formulation of a grouped ℓ₀ pseudo-norm and ℓ₂ norm regularization to obtain hierarchically constrained structured sparsity between cluster interactions. The regression method used is a simple generalization of a recently proposed method used to obtain fits with hierarchical constraints between correlation functions^2,46. Our choice of regularization results in efficient cluster selection and ensures that strong hierarchy constraints are respected in the resulting CDs^47,49,50. The regression optimization problem used is given as follows,

$$\begin{array}{l}\mathop{\mathrm{min}}\limits_{{{{\boldsymbol{J}}}}}\,\,{{{{\boldsymbol{J}}}}}^{\mathrm{T}}\left({{{{\mathbf{\Pi }}}}}^{\mathrm{T}}{{{\mathbf{\Pi }}}}+{\lambda }_{1}{{{\boldsymbol{I}}}}\right){{{\boldsymbol{J}}}}-2{{{{\boldsymbol{E}}}}}^{\mathrm{T}}{{{\mathbf{\Pi }}}}{{{\boldsymbol{J}}}}+{\lambda }_{0}\mathop{\sum}\limits_{B}{z}_{B}\\\qquad\begin{array}{l}\,{{\mbox{subject to}}}\,\quad -M{z}_{B}{{{\mathbf{1}}}}\,\le \,{{{{\boldsymbol{J}}}}}_{B}\le M{z}_{B}{{{\mathbf{1}}}}\\\qquad\qquad\qquad\qquad\;{z}_{B}\,\in \,\{0,1\}\\\qquad\qquad\qquad\qquad\;{z}_{B}\,\le \,{z}_{D}\quad \forall D\,\,{{\mbox{s.t.}}}\,\,D \,{\sqsubset}\, B\end{array}\end{array}$$

(27)

where J is a vector of all expansion coefficients, J_B are the coefficients corresponding to a single orbit B; Π is a matrix of the correlation vectors of all training structures; E is a vector of DFT computed energies; I is the identity matrix; 1 are vectors of all ones, ${\lambda }_{0},{\lambda }_{1}\in {{\mathbb{R}}}_{+}$ are hyper-parameters; $M\in {{\mathbb{R}}}_{+}$ is a fixed parameter; and z_B are slack variables that determine whether a group of coefficients J_B associated with a single cluster interaction is zero or non-zero, i.e., active (z_B ≠ 0) or inactive (z_B = 0). The notation D ⊏ B means that any cluster T ∈ D is a sub-cluster T ⊂ S of some cluster S ∈ B. We refer the reader to the aforementioned references^2,46 for further details on this regression methodology.

The final expansion fits are converged to a fivefold root mean squared cross-validation of 12.8 meV/atom (triplet fit) and 14.9 meV/atom (pair fit). The final fits include non-zero pair and triplet interactions with diameters up to 9 Å and 4.3 Å, and non-zero pair interactions with diameters up to 7.5 Å, respectively, both based on a 2.49 Å primitive lattice constant.

Wang–Landau density of states calculations

The canonical equiatomic Wang–Landau sampling used to directly approximate the density of states was done using supercells with 216 sites (6 × 6 × 6 supercells of a primitive face-centered cubic structure.). Wang–Landau simulations are converged to a fill factor value < 10^−6 52 as shown in Fig. 6.

Fig. 6: Convergence of Wang–Landau density of states calculations.

Convergence curves of histogram modification (fill) factors with respect to the number of simulation steps taken.