Electronic structure prediction of multi-million atom systems through uncertainty quantification enabled transfer learning

Abstract

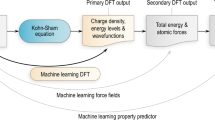
The ground state electron density — obtainable using Kohn-Sham Density Functional Theory (KS-DFT) simulations — contains a wealth of material information, making its prediction via machine learning (ML) models attractive. However, the computational expense of KS-DFT scales cubically with system size which tends to stymie training data generation, making it difficult to develop quantifiably accurate ML models that are applicable across many scales and system configurations. Here, we address this fundamental challenge by employing transfer learning to leverage the multi-scale nature of the training data, while comprehensively sampling system configurations using thermalization. Our ML models are less reliant on heuristics, and being based on Bayesian neural networks, enable uncertainty quantification. We show that our models incur significantly lower data generation costs while allowing confident — and when verifiable, accurate — predictions for a wide variety of bulk systems well beyond training, including systems with defects, different alloy compositions, and at multi-million-atom scales. Moreover, such predictions can be carried out using only modest computational resources.

Introduction

Over the past several decades, Density Functional Theory (DFT) calculations based on the Kohn-Sham formulation^1,2 have emerged as a fundamental tool in the prediction of electronic structure. Today, they stand as the de facto workhorse of computational materials simulations^3,4,5,6, offering broad applicability and versatility. Although formulated in terms of orbitals, the fundamental unknown in Kohn Sham Density Functional Theory (KS-DFT) is the electron density, from which many ground state material properties — including structural parameters, elastic constants, magnetic properties, phonons/vibrational spectra, etc., may be inferred. The ground state electron density is also the starting point for calculations of excited state phenomena, including those related to optical and transport properties^7,8.

In spite of their popularity, conventional KS-DFT calculations scale in a cubic manner with respect to the number of atoms within the simulation cell, making calculations of large and complex systems computationally burdensome. To address this challenge, a number of different approaches, which vary in their computational expense and their range of applicability, have been proposed over the years. Such techniques generally avoid explicit diagonalization of the Kohn-Sham Hamiltonian in favor of computing the single particle density matrix⁹. Many of these methods are able to scale linearly with respect to the system size when bulk insulators or metals at high temperatures are considered^{9,10,11,12,13}, while others exhibit sub-quadratic scaling when used for calculations of low-dimensional materials (i.e., nanostructures)^14,15. Contrary to these specialized approaches, there are only a handful of first-principles electronic structure calculation techniques that operate universally across bulk metallic, insulating, and semiconducting systems, while performing more favorably than traditional cubic scaling methods (especially, close to room temperature). However, existing techniques in this category, e.g.^16,17, tend to face convergence issues due to aggressive use of density matrix truncation, and in any case, have only been demonstrated for systems containing at most a few thousand atoms, due to their overall computational cost. Keeping these developments in mind, a separate thread of research has also explored reducing computational wall times by lowering the prefactor associated with the cubic cost of Hamiltonian diagonalization, while ensuring good parallel scalability of the methods on large scale high-performance computing platforms^18,19,20,21. In spite of demonstrations of these and related methods to study a few large example problems (e.g.^22,23,24), their routine application to complex condensed matter systems, using modest, everyday computing resources appears infeasible.

The importance of being able to routinely predict the electronic structure of generic bulk materials, especially, metallic and semiconducting systems with a large number of representative atoms within the simulation cell, cannot be overemphasized. Computational techniques that can perform such calculations accurately and efficiently have the potential to unlock insights into a variety of material phenomena and can lead to the guided design of new materials with optimized properties. Examples of materials problems where such computational techniques can push the state-of-the-art include elucidating the core structure of defects at realistic concentrations, the electronic and magnetic properties of disordered alloys and quasicrystals^25,26,27,28, and the mechanical strength and failure characteristics of modern, compositionally complex refractory materials^29,30. Moreover, such techniques are also likely to carry over to the study of low dimensional matter and help unlock the complex electronic features of emergent materials such as van-der-Waals heterostructures³¹ and moiré superlattices³². Notably, a separate direction of work has also explored improving Density Functional Theory predictions themselves, by trying to learn the Hohenberg-Kohn functional or exchange correlation potentials^33,34,35. This direction of work will not have much bearing on the discussion that follows below.

An attractive alternative path to overcoming the cubic scaling bottleneck of KS-DFT — one that has found much attention in recent years — is the use of Machine Learning (ML) models as surrogates^36,37. Indeed, a significant amount of research has already been devoted to the development of ML models that predict the energies and forces of atomic configurations matching with KS-DFT calculations, thus spawning ML-based interatomic potentials that can be used for molecular dynamics calculations with ab initio accuracy^{38,39,40,41,42,43}. Parallelly, researchers have also explored direct prediction of the ground state electron density via ML models trained on the self-consistent electron density obtained from KS-DFT simulations^{34,44,45,46,47,48}. This latter approach is particularly appealing, since, in principle, the ground state density is rich in information that goes well beyond energies and atomic forces, and such details can often be extracted through simple post-processing steps. Development of ML models of the electron density can also lead to electronic-structure-aware potentials, which are likely to overcome limitations of existing Machine Learning Interatomic Potentials, particularly in the context of reactive systems^49,50. Having access to the electron density as an intermediate verifiable quantity is generally found to also increase the quality of ML predictions of various material properties^44,51, and can allow training of additional ML models. Such models can use the density as a descriptor to predict specific quantities, such as defect properties of complex alloys^52,53 and bonding information⁵⁴. Two distinct approaches have been explored in prior studies to predict electron density via Machine Learning, differing in how they represent the density – the output of the machine learning model. One strategy involves representing the density by expanding it as a sum of atom-centered basis functions^55,56. The other involves predicting the electron density at each grid point in a simulation cell. Both strategies aim to predict the electron density using only the atomic coordinates as inputs. While the former strategy allows for a compact representation of the electron density, it requires the determination of an optimized basis set that is tuned to specific chemical species. It has been shown in⁵⁵ that the error in the density decomposition through this strategy can be reduced to as low as 1%. In contrast, the latter strategy does not require such optimization but poses a challenge in terms of inference - where the prediction for a single simulation cell requires inference on thousands of grid points (even at the grid points in a vacuum region). The former strategy has shown good results for molecules⁵⁵ while the latter has shown great promise in density models for bulk materials especially metals^46,48,57. In this work, we use the latter approach.

For physical reasons, the predicted electron density is expected to obey transformations consistent with overall rotation and translation of the material system. Moreover, it should remain invariant under permutation of atomic indices. To ensure such properties, several authors have employed equivariant-neural networks^{45,58,59,60,61}. An alternative to such approaches, which is sufficient for scalar valued quantities such as electron density, is to employ invariant descriptors^46,47,58,59. We adopt this latter approach in this work and show through numerical examples that using invariant features and predicting electron density as a scalar valued variable indeed preserves the desired transformation properties.

A key challenge in building surrogate models of the ground state electron density from KS-DFT calculations is the process of data generation itself, which can incur significant offline cost⁶². In recent work⁵¹, we have demonstrated how this issue can be addressed for chiral nanomaterials⁶³. For such forms of matter, the presence of underlying structural symmetries allows for significant dimensionality reduction of the predicted fields, and the use of specialized algorithms for ground state KS-DFT calculations^64,65,66. However, such strategies cannot be adopted for bulk materials with complex unit cells, as considered here. For generic bulk systems, due to the confining effects of periodic boundary conditions, small unit-cell simulations alone cannot represent a wide variety of configurations. To obtain ML models that can work equally well across scales and for a variety of configurations (e.g. defects^67,68), data from large systems is also essential. However, due to the aforementioned cubic scaling of KS-DFT calculations, it is relatively inexpensive to generate a lot of training data using small sized systems (say, a few tens of atoms), while larger systems (a few hundred atoms) are far more burdensome, stymieing the data generation process. Previous work on electron density prediction^47,48 has been made possible by using data from large systems exclusively. However, this strategy is likely to fail when complex systems such as multi-principal element alloys are dealt with, due to the large computational cells required for such systems. This is especially true while studying compositional variations in such systems since such calculations are expected to increase the overall computational expense of the process significantly.

In this work, we propose a machine-learning model that accurately predicts the ground state electron density of bulk materials at any scale, while quantifying the associated uncertainties. Once trained, our model significantly outperforms conventional KS-DFT-based computations in terms of speed. To address the high cost of training data generation associated with KS-DFT simulations of larger systems — a key challenge in developing effective ML surrogates of KS-DFT — we adopt a transfer learning (TL) approach⁶⁹. Thus, our model is first trained using a large quantity of cheaply generated data from simulations of small systems, following which, a part of the model is retrained using a small amount of data from simulations of a few large systems. This strategy significantly lowers the training cost of the ML model, without compromising its accuracy. Along with the predicted electron density fields, our model also produces a detailed spatial map of the uncertainty, that enables us to assess the confidence in our predictions for very large scale systems (thousands of atoms and beyond), for which direct validation via comparison against KS-DFT simulations data is not possible. The uncertainty quantification (UQ) properties of our models are achieved through the use of Bayesian Neural Networks (BNNs), which systematically obtain the variance in prediction through their stochastic parameters, and tend to regularize better than alternative approaches^70,71,72. They allow us to systematically judge the generalizability of our ML model, and open the door to Active Learning approaches⁷³ that can be used to further reduce the work of data generation in the future.

To predict the electron density at a given point, the ML model encodes the local atomic neighborhood information in the form of descriptors, that are then fed as inputs to the BNN. Our neighborhood descriptors are rather simple: they include distance and angle information from nearby atoms in the form of scalar products and avoid choosing the basis set and “handcrafted” descriptors adopted by other workers^{39,74,75,76,77}. Additionally, we have carried out a systematic algorithmic procedure to select the optimal set of descriptors, thus effectively addressing the challenge associated with the high dimensionality of the descriptor-space. We explain this feature selection process in section “Selection of optimal set of descriptors”. To sample this descriptor space effectively, we have employed thermalization, i.e., ab initio molecular dynamics (AIMD) simulations at various temperatures, which has allowed us to carry out accurate predictions for systems far from training. Overall, our ML model reduces the use of heuristics adopted by previous workers in notable ways, making the process of ML based prediction of electronic structure much more systematic. Notably, the point-wise prediction of the electronic fields via the trained ML model, make this calculation scale linearly with respect to the system size, enabling a wide variety of calculations across scales.

In the following sections, we demonstrate the effectiveness of our model by predicting the ground state electron density for bulk metallic and semiconducting alloy systems. In particular, we present: (i) Predictions and error estimates for systems well beyond the training data, including systems with defects and varying alloy compositions; (ii) Demonstration of the effectiveness of the transfer learning approach; (iii) Uncertainty quantification capabilities of the model, and the decomposition of the uncertainty into epistemic and aleatoric parts; and (iv) Computational advantage of the model over conventional KS-DFT calculations, and the use of the model to predict the electron density of systems containing millions of atoms.

Results

In this section, we present electron density predictions by the proposed machine learning (ML) model for two types of bulk materials — pure aluminum and alloys of silicon-germanium. These serve as prototypical examples of metallic and covalently bonded semiconducting systems, respectively. These materials were chosen for their technological importance and because the nature of their electronic fields is quite distinct (see Supplementary Fig. 4), thus presenting distinct challenges to the ML model. Additionally, being metallic, the aluminum systems do not show simple localized electronic features often observed in insulators^78,79, further complicating electron density prediction.

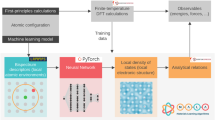
The overview of the present ML model is given in Fig. 1. The models are trained using a transfer learning approach, with thermalization used to sample a variety of system configurations. In the case of aluminum (Al), the model is trained initially on a 32-atom and subsequently on a 108-atom system. Corresponding system sizes for silicon germanium (SiGe) are 64 and 216 atoms respectively. Details of the ML model are provided in “Methods”.

Fig. 1: Overview of the present Machine Learning (ML) model.

The first step is the training data generation via ab initio simulations shown by the arrow at the top. The second step is to generate atomic neighborhood descriptors x(i) for each grid point, i, in the training configurations. The third step is to create a probabilistic map (Bayesian Neural Network with DenseNet like blocks consisting of skip connections) from atomic neighborhood descriptors x(i) to the charge density at the corresponding grid point ρ(i). The trained model is then used for inference which includes (i) descriptor generation for all grid points in the query configuration, (ii) forward propagation through the Bayesian Neural Network, and (iii) aggregation of the point-wise charge density ρ(i) to obtain the charge density field ρ.

We evaluate the performance of the ML models for a wide variety of test systems, which are by choice, well beyond the training data. This is ensured by choosing system sizes far beyond training, strained systems, systems containing defects, or alloy compositions not included in the training. We assess the accuracy of the ML models by comparing predicted electron density fields and ground state energies against DFT simulations. In addition, we quantify the uncertainty in the model’s predictions. We decompose the total uncertainty into two parts: “aleatoric” and “epistemic”. The first is a result of inherent variability in the data, while the second is a result of insufficient knowledge about the model parameters due to limited training data. The inherent variability in the data might arise due to approximations and round-off errors incurred in the DFT simulations and calculation of the ML model descriptors. On the other hand, the modeling uncertainty arises due to the lack of or incompleteness in the data. This lack of data is inevitable since it is impossible to exhaustively sample all possible atomic configurations during the data generation process. Decomposing the total uncertainty into these two parts helps distinguish the contributions of inherent randomness and incompleteness in the data to the total uncertainty. In the present work, a “heteroscedastic” noise model is used to compute the aleatoric uncertainty, which captures the spatial variation of the noise/variance in the data.

Error estimation

To evaluate the accuracy of the model, we calculated the Root Mean Squared Error (RMSE) for the entire test dataset, including systems of the same size as the training data as well as sizes bigger than training data. For aluminum, the RMSE was determined to be 4.1 × 10⁻⁴, while for SiGe, it was 7.1 × 10⁻⁴, which shows an improvement over RMSE values for Al available in ref. ⁴⁷. The L¹ norm per electron for Aluminuum is 2.63 × 10⁻² and for SiGe it is 1.94 × 10⁻² for the test dataset. Additionally, the normalized RMSE is obtained by dividing the RMSE value by the range of respective ρ values for aluminum and SiGe. The normalized RMSE for aluminum and SiGe test dataset was found to be 7.9 × 10⁻³ for both materials. Details of training and test dataset are presented in Supplementary Section VI. To assess the generalizability of the model, we evaluate the accuracy of the ML model using systems much larger than those used in training, but accessible to DFT. We consider two prototypical systems, an Aluminium system having 1372 atoms (Fig. 2) and a Silicon Germanium (Si_0.5 Ge_0.5) system having 512 atoms (Fig. 3). The model shows remarkable accuracy for both of these large systems. The RMSE is 3.8 × 10⁻⁴ and 7.1 × 10⁻⁴ for aluminum and SiGe respectively, which confirms the high accuracy of the model for system sizes beyond those used in training.

Fig. 2: 1372 atom aluminum simulation cell at 631 K.

Electron densities a calculated by DFT and b predicted by ML. The two-dimensional slice of (b) that has the highest mean squared error, as calculated by c DFT and predicted by d ML. e Corresponding absolute error in ML with respect to DFT. f–h Magnified view of the rectangular areas in (c–e) respectively. The unit for electron density is e Bohr⁻³, where e denotes the electronic charge.

Fig. 3: 512 atoms Si_0.5Ge_0.5 simulation cell at 2300 K.

Electron densities a calculated by DFT and b predicted by ML. The two-dimensional slice of (b) that has the highest mean squared error, as calculated by c DFT and predicted by d ML. e Corresponding absolute error in ML with respect to DFT. The unit for electron density is e Bohr⁻³, where e denotes the electronic charge.

We now evaluate the performance of the ML model for systems containing extended and localized defects, although such systems were not used in training. We consider the following defects: mono-vacancies, di-vacancies, grain boundaries, edge, and screw dislocations for Al, and mono-vacancies and di-vacancies for SiGe. The electron density fields predicted by the ML models match with the DFT calculations extremely well, as shown in Figs. 4 and 5. The error magnitudes (measured as the L¹ norm of the difference in electron density fields, per electron) are about 2 × 10⁻² (see Fig. 6). The corresponding NRMSE is 7.14 × 10⁻³. We show in Uncertainty quantification, that the model errors and uncertainty can be both brought down significantly, by including a single snapshot with defects, during training.

Fig. 4: Electron density contours for aluminum systems with localized and extended defects — Left: calculated by DFT, Right: predicted by ML.

a (Top) Mono-vacancy in 256 atom aluminum system, (Bottom) Di-Vacancy in 108 atom aluminum system, b (1 1 0) plane of a perfect screw dislocation in aluminum with Burgers vector $\frac{{a}_{0}}{2}[110]$, and line direction along [110]. The coordinate system was aligned along $[1\bar{1}2]$–$[\bar{1}11]$–[110], c (Top) (0 1 0) plane, (bottom) (0 0 1) plane of a [001] symmetric tilt grain boundary (0^∘ inclination angle) in aluminum, d Edge dislocation in aluminum with Burgers vector $\frac{{a}_{0}}{2}[110]$. The coordinate system was aligned along [110]–$[\bar{1}11]$–$[1\bar{1}2]$ and the dislocation was created by removing a half-plane of atoms below the glide plane. The unit for electron density is e Bohr⁻³, where e denotes the electronic charge.

Fig. 5: Electron Density Prediction for SiGe system with vacancy defects.

Electron density contours and absolute error in ML for SiGe systems with a–c Si double vacancy defect in 512 atom system d–f Ge single vacancy defect in 216 atom system densities a, d calculated by DFT, b, e predicted by ML, and c, f error in ML predictions. Note that the training data for the above systems did not include any defects. The unit for electron density is e Bohr⁻³, where e denotes the electronic charge.

Fig. 6: A comparison of the accuracy in the prediction of the charge density (in terms of the L¹ norm per electron between ρ^DFT and ρ^scaled), and the error (in Ha/atom) in the ground state total energy computed using ρ^DFT and ρ^scaled, for Al (left), and SiGe (right) systems.

ρ^scaled is the scaled ML predicted electron density as given in Eq. (6). We observe that the errors are far better than chemical accuracy, i.e., errors below 1 kcal mol⁻¹ or 1.6 milli-Hartree atom⁻¹, for both systems, even while considering various types of defects and compositional variations. Note that for Si_xGe_1−x, we chose x = 0.4, 0.45, 0.55, 0.6.

Another stringent test of the generalizability of the ML models is performed by investigating Si_x Ge_1−x alloys, for x ≠ 0.5. Although only equi-atomic alloy compositions (i.e., x = 0.5) were used for training, the error in prediction (measured as the L¹ norm of the difference in electron density fields, per electron) is lower than 3 × 10⁻² (see Fig. 6). The corresponding RMSE is 8.04 × 10⁻⁴ and NRMSE is 7.32 × 10⁻³. We would like to make a note that we observed good accuracy in the immediate neighborhood (x = 0.4 to 0.6) of the training data (x = 0.5). Prediction for x = 0.4 is shown in Fig. 10. The prediction accuracy however decreases as we move far away from the training data composition. This generalization performance far away from the training data is expected. We have also carried out tests with aluminum systems subjected to volumetric strains, for which the results were similarly good.

Our electron density errors are somewhat lower than compared to the earlier works^46,47, At the same time, thanks to the sampling and transfer learning techniques adopted by us, the amount of time spent on DFT calculations used for producing the training data is also smaller. To further put into context the errors in the electron density, we evaluate the ground state energies from the charge densities predicted by the ML model through a postprocessing step and compare these with the true ground state energies computed via DFT. Details on the methodology for postprocessing can be found in the ‘Methods’ section, and a summary of our postprocessing results can be seen in Fig. 6, and in Supplementary Table 4 and Supplementary Table 5. On average, the errors are well within chemical accuracy for all test systems considered and are generally ${{{\mathcal{O}}}}(1{0}^{-4})$ Ha atom⁻¹, as seen in Fig. 6. Furthermore, not only are the energies accurate, but the derivatives of the energies, e.g., with respect to the supercell lattice parameter, are found to be quite accurate as well (see Fig. 7). This enables us to utilize the ML model to predict the optimum lattice parameter — which is related to the first derivative of the energy curve, and the bulk modulus — which is related to the second derivative of the energy curve, accurately. We observe that the lattice parameter is predicted accurately to a fraction of a percent, and the bulk modulus is predicted to within 1% of the DFT value (which itself is close to experimental values⁸⁰). Further details can be found in the Supplementary Material. This demonstrates the utility of the ML models to predict not only the electron density but also other relevant physical properties.

Fig. 7: The energy curve with respect to different lattice parameters for a 2 × 2 × 2 (left) and 3 × 3 × 3 (right) supercell of aluminum atoms.

Overall, we see excellent agreement in the energies (well within chemical accuracy). The lattice parameter (related to the first derivative of the energy plot) calculated in each case agrees with the DFT-calculated lattice parameter to ${\mathcal{O}}(1{0}^{-2})$ Bohr or better (i.e., it is accurate to a fraction of a percent). The bulk modulus calculated (related to the second derivative of the energy plot) from DFT data and ML predictions agree to within 1%. For the 3 × 3 × 3 supercell, the bulk modulus calculated via DFT calculations is 76.39 GPa, close to the experimental value of about 76 GPa⁸⁰. The value calculated from ML predictions is 75.80 GPa.

Overall, the generalizability of our models is strongly suggestive that our use of thermalization to sample the space of atomic configurations, and the use of transfer-learning to limit training data generation of large systems are both very effective. We discuss uncertainties arising from the use of these strategies and due to the neural network model, in addition to the noise in the data, in the following sections.

Uncertainty quantification

The present work uses a Bayesian Neural Network (BNN) which provides a systematic route to uncertainty quantification (UQ) through its stochastic parameters as opposed to other methods for UQ, for instance ensemble averaging⁸¹. Estimates of epistemic and aleatoric uncertainties for the following systems are shown: a defect-free Al system with 1372 atoms (Fig. 8), a 256-atom Al system with a mono-vacancy (Fig. 9a–d), and a Si_0.4Ge_0.6 alloy (Fig. 10). Note, for the results in Fig. 9a–d the training data does not contain any systems having defects, and for the results in Fig. 10 the training data contains only 50 − 50 composition.

Fig. 8: Uncertainty quantification for 1372 atom aluminum system.

a ML prediction of the electron density, b Epistemic Uncertainty c Aleatoric Uncertainty d Total Uncertainty shown along the dotted line from the ML prediction slice. The uncertainty represents the bound ± 3σ_total, where, σ_total is the total uncertainty. The unit for electron density is e Bohr⁻³, where e denotes the electronic charge.

Fig. 9: Uncertainty quantification for a 256 atom aluminum system with a mono vacancy defect.

a ML prediction of the electron density shown on the defect plane, b Epistemic uncertainty c Aleatoric uncertainty d Uncertainty shown along the black dotted line from the ML prediction slice. The uncertainty, represents the bound ± 3σ_total, where, σ_total is the total uncertainty. Note that the model used to make the predictions in (a–d) is not trained on the defect data, as opposed to the model used for (e), where defect data from the 108 atom aluminum system was used to train the model. The uncertainty and error at the location of the defect reduce with the addition of defect data in the training, as evident from (d, e). The unit for electron density is e Bohr⁻³, where e denotes the electronic charge.

Fig. 10: Uncertainty quantification for Si_0.4Ge_0.6 system.

a ML prediction of the electron density, b Epistemic Uncertainty c Aleatoric Uncertainty d Total Uncertainty shown along the dotted line from the ML prediction slice. The uncertainty represents the bound ± 3σ_total, where, σ_total is the total uncertainty. The unit for electron density is e Bohr⁻³, where e denotes the electronic charge.

In these systems, the aleatoric uncertainty has the same order of magnitude as the epistemic uncertainty. This implies that the uncertainty due to the inherent randomness in the data is of a similar order as the modeling uncertainty. The aleatoric uncertainty is significantly higher near the nuclei (Figs. 8, 10) and also higher near the vacancy (Fig. 9). This indicates that the training data has high variability at those locations. The epistemic uncertainty is high near the nucleus (Figs. 8, 10 since only a small fraction of grid points are adjacent to nuclei, resulting in the scarcity of training data for such points. The paucity of data near a nucleus is shown through the distribution of electron density in Supplementary Fig. 4. For the system with vacancy, the aleatoric uncertainty is higher in most regions, as shown in Fig. 9c. However, the epistemic uncertainty is significantly higher only at the vacancy (Fig. 9b), which might be attributed to the complete absence of data from systems with defects in the training.

To investigate the effect of adding data from systems with defects in the training, we added a single snapshot of 108 atom aluminum simulation with mono vacancy defect to the training data. This reduces the error at the defect site significantly and also reduces the uncertainty (Fig. 9e). However, the uncertainty is still quite higher at the defect site because the data is biased against the defect site. That is, the amount of training data available at the defect site is much less than the data away from it. Thus, this analysis distinguishes uncertainty from inaccuracy.

To investigate the effect of adding data from larger systems in training, we compare two models. The first model is trained with data from the 32-atom system. The second model uses a transfer learning approach where it is initially trained using the data from the 32-atom system and then a part of the model is retrained using data from the 108-atom system. We observe a significant reduction in the error and in the epistemic uncertainty for the transfer learned model as compared to the one without transfer learning. The RMSE on the test system (256 atom) decreases by 50% when the model is transfer learned using 108 atom data. The addition of the 108-atom system’s data to the training data decreases epistemic uncertainty as well since the 108-atom system is less restricted by periodic boundary conditions than the 32-atom system. Further, it is also statistically more similar to the larger systems used for testing as shown in Supplementary Fig. 5. These findings demonstrate the effectiveness of the Bayesian Neural Network in pinpointing atomic arrangements or physical sites where more data is essential for enhancing the ML model’s performance. Additionally, they highlight its ability to measure biases in the training dataset. The total uncertainty in the predictions provides a confidence interval for the ML prediction. This analysis provides an upper bound of uncertainty arising out of two key heuristic strategies adopted in our ML model: data generation through thermalization of the systems and transfer learning.

Computational efficiency gains and confident prediction for very large system sizes

Conventional KS-DFT calculations scale as ${\mathcal{O}}({{N}_{\rm{a}}}^{3})$ with respect to the number of atoms N_a, whereas, our ML model scales linearly (i.e., ${{{\mathcal{O}}}}({N}_{{{{\rm{a}}}}})$), as shown in Fig. 11. This provides computational advantage for ML model over KS-DFT with increasing number of atoms. For example, even with 500 atoms, the calculation wall times for ML model is 2 orders of magnitude lower than KS-DFT. The linear scaling behavior of the ML model with respect to the number of atoms can be understood as follows. As the number of atoms within the simulation domain increases, so does the total simulation domain size, leading to a linear increase in the total number of grid points (keeping the mesh size constant, to maintain calculation accuracy). Since the machine learning inference is performed for each grid point, while using information from a fixed number of atoms in the local neighborhood of the grid point, the inference time is constant for each grid point. Thus the total ML prediction time scales linearly with the total number of grid points, and hence the number of atoms in the system.

Fig. 11: Computational time comparison between DFT calculations and prediction via trained ML model. (Top) Aluminum, (Bottom) SiGe.

The DFT calculations scale ${{{\mathcal{O}}}}({{N}_{{{{\rm{a}}}}}}^{3})$ with respect to the system size (number of atoms N_a), whereas, the present ML model scales linearly (i.e., ${{{\mathcal{O}}}}({N}_{{{{\rm{a}}}}})$). The time calculations were performed using the same number of CPU cores and on the same system (Perlmutter CPU).

Taking advantage of this trend, the ML model can be used to predict the electronic structure for system sizes far beyond the reach of conventional calculation techniques, including systems containing millions of atoms, as demonstrated next. We anticipate that with suitable parallel programming strategies (the ML prediction process is embarrassingly parallel) and computational infrastructure, the present strategy can be used to predict the electronic structure of systems with hundreds of millions or even billions of atoms. Recently, there have been attempts at electronic structure predictions at million atom scales. In⁸², a machine learning based potential is developed for germanium-antimony-tellurium alloys, effectively working for device scale systems containing over half a million atoms. Another contribution comes from Fiedler et al.⁴⁸, where they present a model predicting electronic structure for systems containing over 100,000 atoms.

We show the electron densities, as calculated by our ML model, for a four million atom system of Al and a one million atom system of SiGe, in Figs. 12 and 13 respectively. In addition to predicting electron densities, we also quantify uncertainties for these systems. We found that the ML model predicts larger systems with equally high certainty as smaller systems (see Supplementary Fig. 3). The confidence interval obtained by the total uncertainty provides a route to assessing the reliability of predictions for these million atom systems for which KS-DFT calculations are simply not feasible. A direct comparison of ML obtained electron density with DFT for large systems is not done till date, mainly because simulating such systems with DFT is impractical. However, recent advancements in DFT techniques hold promise for simulating large-scale systems^21,83,84. In future, it will be worthwhile to compare ML predicted electron density for large systems and the electron density obtained through DFT, utilizing these recently introduced DFT techniques.

Fig. 12: Prediction of electronic structure for aluminum system containing ≈ 4.1 million atoms.

The unit for electron density is e Bohr⁻³, where e denotes the electronic charge.

Fig. 13: Prediction of electronic structure for Si_0.5Ge_0.5 system containing ≈ 1.4 million atoms.

The unit for electron density is e Bohr⁻³, where e denotes the electronic charge.

Reduction of training data generation cost via transfer learning

One of the key challenges in developing an accurate ML model for electronic structure prediction is the high computational cost associated with the generation of the training data through KS-DFT, especially for predicting the electron density for systems across length-scales. A straightforward approach would involve data generation using sufficiently large systems wherein the electron density obtained from DFT is unaffected by the boundary constraints. However, simulations of larger bulk systems are significantly more expensive than smaller systems. To address the computational burden of simulating large systems, strategies such as “fragmentation" have been used in electronic structure calculations^85,86. Further, certain recent studies on Machine Learning Interatomic Potentials suggest utilizing portions of a larger system for training the models^87,88. To the best of our knowledge, there is no corresponding work that utilizes fragmentation in ML modeling of the electron density. In this work, to address the issue, we employed a transfer learning (TL) approach. We first trained the ML model on smaller systems and subsequently trained a part of the neural network using data from larger systems. This strategy allows us to obtain an efficient ML model that requires fewer simulations of expensive large-scale systems compared to what would have been otherwise required without the TL approach. The effectiveness of the TL approach stems from its ability to retain information from a large quantity of cheaper, smaller scale simulation data. We would like to note however, that the transfer learning approach is inherently bound by the practical constraints associated with simulating the largest feasible system size.

As an illustration of the above principles, we show in Fig. 14, the RMSE obtained on 256 atom data (system larger than what was used in the training data) using the TL model and the non-TL model. We also show the time required to generate the training data for both models. For the Al systems, we trained the TL model with 32-atom data first and then 108-atom data. In contrast, the non-TL model was trained only on the 108-atom data.

Fig. 14: Models with Transfer Learning (TL) and without Transfer Learning (Non-TL).

a, c Root mean square error (RMSE) on the test dataset and b, d Computational time to generate the training data. In the case of aluminum (a, b), the TL model is trained using 32 and 108 atom data. For SiGe (c, d), the TL model was trained using 64 and 216 atom data. In the case of aluminum, the non-TL model is trained using 108 atom data. Whereas, in the case of SiGe, the non-TL model is trained using 216 atom data.

The non-TL model requires significantly more 108-atom data than the TL model to achieve a comparable RMSE on the 256-atom dataset. Moreover, the TL model’s training data generation time is approximately 55% less than that of the non-TL model. This represents a substantial computational saving in developing the ML model for electronic structure prediction, making the transfer learning approach a valuable tool to expedite such model development. Similar savings in training data generation time were observed for SiGe as shown in Fig. 14. In the case of SiGe, the TL model was first trained using 64 atom data and then transfer learned using 216 atom data.

Discussions

We have developed an uncertainty quantification (UQ) enabled machine learning (ML) model that creates a map from the descriptors of atomic configurations to the electron densities. We use simple scalar product-based descriptors to represent the atomic neighborhood of a point in space. These descriptors, while being easy to compute, satisfy translational, rotational, and permutational invariances. In addition, they avoid any handcrafting. We systematically identify the optimal set of descriptors for a given dataset. Once trained, our model enables predictions across multiple length scales and supports embarrassingly parallel implementation. As far as we can tell, our work is the first attempt to systematically quantify uncertainties in ML predicted electron densities across different scales relevant to materials physics. To alleviate the high cost of training data generation via KS-DFT, we propose a two-pronged strategy: i) we use thermalization to comprehensively sample system configurations, leading to a highly transferable ML model; and ii) we employ transfer learning to train the model using a large amount of inexpensively generated data from small systems while retraining a part of the model using a small amount of data from more expensive calculations of larger systems. The transfer learning procedure is systematically guided by the probability distributions of the data. This approach enables us to determine the maximum size of the training system, reducing dependence on heuristic selection. As a result of these strategies, the cost of training data generation is reduced by more than 50%, while the models continue to be highly transferable across a large variety of material configurations. Our use of Bayesian Neural Networks (BNNs) allows the uncertainty associated with these aforementioned strategies to be accurately assessed, thus enabling confident predictions in scenarios involving millions of atoms, for which ground-truth data from conventional KS-DFT calculations is infeasible to obtain. Overall, our ML model significantly decreases the reliance on heuristics used by prior researchers, streamlining the process of ML-based electronic structure prediction and making it more systematic.

We demonstrate the versatility of the proposed machine learning models by accurately predicting electron densities for multiple materials and configurations. We focus on bulk aluminum and Silicon-Germanium alloy systems. The ML model shows remarkable accuracy when compared with DFT calculations, even for systems containing thousands of atoms. In the future, a similar model can be developed to test the applicability of the present descriptors and ML framework for molecules across structural and chemical space^89,90,91,92. As mentioned above, the ML model also has excellent generalization capabilities, as it can predict electron densities for systems with localized and extended defects, and varying alloy compositions, even when the data from such systems were not included in the training. It is likely that the ensemble averaging over model parameters in the BNNs, along with comprehensive sampling of the descriptor space via system thermalization together contribute to the model generalization capabilities. Our findings also show a strong agreement between physical parameters calculated from the DFT and ML electron densities (e.g. lattice constants and bulk moduli).

To rigorously quantify uncertainties in the predicted electron density, we adopt a Bayesian approach. Uncertainty quantification by a Bayesian neural network (BNN) is mathematically well-founded and offers a more reliable measure of uncertainty in comparison to non-Bayesian approaches such as the method of ensemble averaging. Further, we can decompose the total uncertainty into aleatoric and epistemic parts. This decomposition allows us to distinguish and analyze the contributions to the uncertainty arising from (i) inherent noise in the training data (i.e. aleatoric uncertainty) and (ii) insufficient knowledge about the model parameters due to the lack of information in the training data (i.e. epistemic uncertainty). The aleatoric uncertainty or the noise in the data is considered irreducible, whereas the epistemic uncertainty can be reduced by collecting more training data. As mentioned earlier, the UQ capability of the model allows us to establish an upper bound on the uncertainty caused by two key heuristic strategies present in our ML model, namely, data generation via the thermalization of systems and transfer learning.

The reliability of the ML models is apparent from the low uncertainty of its prediction for systems across various length-scales and configurations. Furthermore, the magnitude of uncertainty for the million-atom systems is similar to that of smaller systems for which the accuracy of the ML model has been established. This allows us to have confidence in the ML predictions of systems involving multi-million atoms, which are far beyond the reach of conventional DFT calculations.

The ML model can achieve a remarkable speed-up of more than two orders of magnitude over DFT calculations, even for systems involving a few hundred atoms. As shown here, these computational efficiency gains by the ML model can be further pushed to regimes involving multi-million atoms, not accessible via conventional KS-DFT calculations.

In the future, we intend to leverage the uncertainty quantification aspects of this model to implement an active learning framework. This framework will enable us to selectively generate training data, reducing the necessity of extensive datasets and significantly lowering the computational cost associated with data generation. Moreover, we anticipate that the computational efficiencies offered via the transfer learning approach, are likely to be even more dramatic while considering more complex materials systems, e.g. compositionally complex alloys^93,94.

Methods

Ab initio molecular dynamics

To generate training data for the model, Ab Initio Molecular Dynamics (AIMD) simulations were performed using the finite-difference based SPARC code^95,96,97. We used the GGA PBE exchange-correlation functional⁹⁸ and ONCV pseudopotentials⁹⁹. For aluminum, a mesh spacing of 0.25 Bohrs was used while for SiGe, a mesh spacing of 0.4 Bohrs was used. These parameters are more than sufficient to produce accurate energies and forces for the pseudopotentials chosen, as was determined through convergence tests. A tolerance of 10⁻⁶ was used for self-consistent field (SCF) convergence and the Periodic-Pulay¹⁰⁰ scheme was deployed for convergence acceleration. These parameters and pseudopotential choices were seen to produce the correct lattice parameters and bulk modulus values for the systems considered here, giving us confidence that the DFT data being produced is well rooted in the materials physics.

For AIMD runs, a standard NVT-Nosé Hoover thermostat¹⁰¹ was used, and Fermi-Dirac smearing at an electronic temperature of 631.554 K was applied. The time step between successive AIMD steps was 1 femtosecond. The atomic configuration and the electron density of the system were captured at regular intervals, with sufficient temporal spacing between snapshots to avoid the collection of data from correlated atomic arrangements. To sample a larger subspace of realistic atomic configurations, we performed AIMD simulations at temperatures ranging from 315 K to about twice the melting point of the system, i.e. 1866 K for Al and 2600 K for SiGe. Bulk disordered SiGe alloy systems were generated by assigning atoms randomly to each species, consistent with the composition.

We also generate DFT data for systems with defects and systems under strain, in order to demonstrate the ability of our ML model to predict unseen configurations. To this end, we tested the ML model on monovacancies and divacancies, edge and screw dislocations, and grain boundaries. For vacancy defects, we generated monovacancies by removing an atom from a random location, and divacancies by removing two random neighboring atoms before running AIMD simulations. Edge and screw dislocations for aluminum systems were generated using Atomsk¹⁰². Further details can be found in Fig. 4. Grain boundary configurations were obtained based on geometric considerations of the tilt angle — so that an overall periodic supercell could be obtained, and by removing extra atoms at the interface. For aluminum, we also tested an isotropic lattice compression and expansion of up to 5%; these systems were generated by scaling the lattice vectors accordingly (while holding the fractional atomic coordinates fixed).

Machine learning map for charge density prediction

Our ML model maps the coordinates ${\{{{{{\bf{R}}}}}_{I}\}}_{I = 1}^{{N}_{{{{\rm{a}}}}}}$ and species (with atomic numbers ${\{{Z}_{I}\}}_{I = 1}^{{N}_{{{{\rm{a}}}}}}$) of the atoms, and a set of grid points ${\{{{{{\bf{r}}}}}_{i}\}}_{i = 1}^{{N}_{{{{\rm{grid}}}}}}$ in a computational domain, to the electron density values at those grid points. Here, N_a and N_grid refer to the number of atoms and the number of grid points, within the computational domain, respectively. We compute the aforementioned map in two steps. First, given the atomic coordinates and species information, we calculate atomic neighborhood descriptors for each grid point. Second, a neural network is used to map the descriptors to the electron density at each grid point. These two steps are discussed in more detail subsequently.

Atomic neighborhood descriptors

In this work, we use a set of scalar product-based descriptors to encode the local atomic environment. The scalar product-based descriptors for the grid point at r_i consist of distance between the grid point and the atoms at R_I; and the cosine of angle at the grid point r_i made by the pair of atoms at R_I and R_J. Here i = 1, …, N_grid and I, J = 1, …, N_a. We refer to the collections of distances i.e., ∣∣r_i − R_I∣∣ as set I descriptors, and the collections of the cosines of the angles i.e., $\frac{({{{{\bf{r}}}}}_{i}-{{{{\bf{R}}}}}_{I})\cdot ({{{\bf{r}}}}i-{{{{\bf{R}}}}}_{J})}{| | {{{{\bf{r}}}}}_{i}-{{{{\bf{R}}}}}_{I}| | \,| | {{{\bf{r}}}}i-{{{{\bf{R}}}}}_{J}| | }$ are referred to as set II descriptors.

Higher order scalar products such as the scalar triple product, and the scalar quadruple product which involve more than two atoms at a time can also be considered. However, these additional scalar products are not included in the descriptor set in this work since they do not appear to increase the accuracy of predictions.

Since the predicted electron density is a scalar valued variable, invariance of the input features is sufficient to ensure equivariance of the predicted electron density under rotation, translation, and permutation of atomic indices (as mentioned in refs. ^58,59). Since the features of our ML model are scalar products and are sorted, they are invariant with respect to rotation, translation, and permutation of atomic indices. In Supplementary Section I we show through a numerical example that our model is indeed equivariant. Further details of the descriptor calculation are also presented in that section.

Selection of optimal set of descriptors

As has been pointed out by previous work on ML prediction of electronic structure^46,47, the nearsightedness principle^79,103 and screening effects¹⁰⁴ indicate that the electron density at a grid point has little influence from atoms sufficiently far away. This suggests that only descriptors arising from atoms close enough to a grid point need to be considered in the ML model, a fact which is commensurate with our findings in Fig. 15.

Fig. 15: Convergence of error with respect to the number of descriptors, shown for aluminum.

The blue line shows the convergence with respect to N_set I, while the other three lines show convergence with respect to N_set II. The optimal N_set I and N_set II are obtained where their test RMSE values converge.

Using an excessive number of descriptors can increase the time required for descriptor-calculation, training, and inference, is susceptible to curse of dimensionality, and affect prediction performance^105,106. On the other hand, utilizing an insufficient number of descriptors can result in an inadequate representation of the atomic environments and lead to an inaccurate ML model.

Based on this rationale, we propose a procedure to select an optimal set of descriptors for a given atomic system. We select a set of M (M≤N_a) nearest atoms from the grid point to compute the descriptors and perform a convergence analysis to strike a balance between the aforementioned conditions to determine the optimal value of M. It is noteworthy that the selection of optimal descriptors has been explored in previous works, in connection with Behler-Parinello symmetry functions such as¹⁰⁷ and¹⁰⁸. These systematic procedures for descriptor selection eliminate trial-and-error operations typically involved in finalizing a descriptor set. In ref. ¹⁰⁸, the authors have demonstrated for Behler-Parinello symmetry functions that using an optimal set of descriptors enhances the efficiency of machine learning models.

For M nearest atoms, we will have N_set I distance descriptors, and N_set II angle descriptors, with N_set I = M and N_set II ≤ ^MC₂.

The total number of descriptors is N_desc = N_set I + N_set II. To optimize N_desc, we first optimize N_set I, till the error converges as shown in Fig. 15. Subsequently, we optimize N_set II. To do this, we consider a nearer subset of atoms of size M_a ≤ M, and for each of these M_a atoms, we consider the angle subtended at the grid point, by the atoms and their k nearest neighbors. This results in N_set II = M_a × k, angle based descriptors, with M_a and k varied to yield the best results, as shown in Fig. 15. The pseudo-code for this process can be found in Supplementary Algorithm 2 and Supplementary Algorithm 3. Further details on feature convergence analysis are provided in the Supplementary Material.

Bayesian neural network

Bayesian Neural Networks (BNNs) have stochastic parameters in contrast to deterministic parameters used in conventional neural networks. BNNs provide a mathematically rigorous and efficient way to quantify uncertainties in their prediction.

We use a Bayesian neural network to estimate the probability $P(\rho | {{{\bf{x}}}},{{{\mathcal{D}}}})$ of the output electron density ρ for a given input descriptor ${{{\bf{x}}}}\in {{\mathbb{R}}}^{{N}_{{{{\rm{desc}}}}}}$ and training data set ${{{\mathcal{D}}}}={\{{{{{\bf{x}}}}}_{i},{\rho }_{i}\}}_{i = 1}^{{N}_{d}}$. The probability is evaluated as:

$$P(\rho | {{{\bf{x}}}},{{{\mathcal{D}}}})={\int}_{{{{\Omega }}}_{w}}P(\rho | {{{\bf{x}}}},{{{\bf{w}}}})P({{{\bf{w}}}}| {{{\mathcal{D}}}})d{{{\bf{w}}}}\,.$$

(1)

Here w ∈ Ω_w is the set of parameters of the network and N_d is the size of the training data set. Through this marginalization over parameters, a BNN provides a route to overcome modeling biases via averaging over an ensemble of networks. Given a prior distribution P(w) on the parameters, the posterior distribution of the parameters $P({{{\bf{w}}}}| {{{\mathcal{D}}}})$ are learned via the Bayes’ rule as $P({{{\bf{w}}}}| {{{\mathcal{D}}}})=P({{{\mathcal{D}}}}| {{{\bf{w}}}})P({{{\bf{w}}}})/P({{{\mathcal{D}}}})$, where $P({{{\mathcal{D}}}}| {{{\bf{w}}}})$ is the likelihood of the data.

This posterior distribution of parameters $P({{{\bf{w}}}}| {{{\mathcal{D}}}})$ is intractable since it involves the normalizing factor $P({{{\mathcal{D}}}})$, which in turn is obtained via marginalization of the likelihood through a high dimensional integral. Therefore, it is approximated through techniques such as variational inference^70,109,110 or Markov Chain Monte Carlo methods¹¹¹. In variational inference, as adopted here, a tractable distribution q(w∣θ) called the “variational posterior” is considered, which has parameters θ. For instance, if the variational posterior is a Gaussian distribution the corresponding parameters are its mean and standard deviation, θ = (μ_θ, σ_θ). The optimal value of parameters θ is obtained by minimizing the statistical dissimilarity between the true and variational posterior distributions. The dissimilarity is measured through the KL divergence ${{{\rm{KL}}}}\left[q({{{\bf{w}}}}| {{{\boldsymbol{\theta }}}})\,| | \,P({{{\bf{w}}}}| {{{\mathcal{D}}}})\right]$. This yields the following optimization problem:

$$\begin{array}{ll}{{{{\boldsymbol{\theta }}}}}^{* }\;=\,\arg \mathop{\min }\limits_{{{{\boldsymbol{\theta }}}}}{{{\rm{KL}}}}\left[q({{{\bf{w}}}}| {{{\boldsymbol{\theta }}}})\,| | \,P({{{\bf{w}}}}| {{{\mathcal{D}}}})\right]\\\quad\;\; =\,\arg \mathop{\min }\limits_{{{{\boldsymbol{\theta }}}}}\displaystyle\int\,q({{{\bf{w}}}}| {{{\boldsymbol{\theta }}}})\log \left[\frac{q({{{\bf{w}}}}| {{{\boldsymbol{\theta }}}})}{P({{{\bf{w}}}})P({{{\mathcal{D}}}}| {{{\bf{w}}}})}P({{{\mathcal{D}}}})\right]d{{{\bf{w}}}}\,.\end{array}$$

(2)

This leads to the following loss function for BNN that has to be minimized:

$${{{{\mathcal{F}}}}}_{{{{\rm{KL}}}}}({{{\mathcal{D}}}},{{{\boldsymbol{\theta }}}})={{{\rm{KL}}}}\left[q({{{\bf{w}}}}| {{{\boldsymbol{\theta }}}})\,| | \,P({{{\bf{w}}}})\right]-{{\mathbb{E}}}_{q({{{\bf{w}}}}| {{{\boldsymbol{\theta }}}})}[\log P({{{\mathcal{D}}}}| {{{\bf{w}}}})]\,.$$

(3)

This loss function balances the simplicity of the prior and the complexity of the data through its first and second terms respectively, yielding regularization^70,71.

Once the parameters θ are learned, the BNNs can predict the charge density at any new input descriptor x. In this work, the mean of the parameters (μ_θ) are used to make point estimate predictions of the BNN.

Uncertainty quantification

The variance in the output distribution $P(\rho | {{{\bf{x}}}},{{{\mathcal{D}}}})$ in Eq. (1) is the measure of uncertainty in the BNN’s prediction. Samples from this output distribution can be drawn in three steps: In the first step, a j^th sample of the set of parameters, ${\widehat{{{{\bf{w}}}}}}_{j = 1,...,{N}_{s}}$, is drawn from the variational posterior q(w∣θ) which approximates the posterior distribution of parameters $P({{{\bf{w}}}}| {{{\mathcal{D}}}})$. Here, N_s is the number of samples drawn from the variational posterior of parameters. In the second step, the sampled parameters are used to perform inference of the BNN (f_N) to obtain the j^th prediction ${\widehat{\rho }}_{j}={f}_{N}^{{\widehat{{{{\bf{w}}}}}}_{j}}({{{\bf{x}}}})$. In the third step, the likelihood is assumed to be a Gaussian distribution: $P(\rho | {{{\bf{x}}}},{\widehat{{{{\bf{w}}}}}}_{j})={{{\mathcal{N}}}}({\widehat{\rho }}_{j},\sigma ({{{\bf{x}}}}))$, whose mean is given by the BNN’s prediction, ${\widehat{\rho }}_{j}$, and standard deviation by a heterogenous observation noise, σ(x). A sample is drawn from this Gaussian distribution ${{{\mathcal{N}}}}({\widehat{\rho }}_{j},\sigma ({{{\bf{x}}}}))$ that approximates a sample from the distribution $P(\rho | {{{\bf{x}}}},{{{\mathcal{D}}}})$. The total variance of such samples can be expressed as:

$${{{\rm{var}}}}(\rho )={\sigma }^{2}({{{\bf{x}}}})+\left[\frac{1}{{N}_{s}}\sum\limits_{j=1}^{{N}_{s}}{\left({\widehat{\rho }}_{j}\right)}^{2}-{\left({\mathbb{E}}({\widehat{\rho }}_{j})\right)}^{2}\right]\,.$$

(4)

Here, ${\mathbb{E}}({\widehat{\rho}}_j) = \frac{1}{N_s} \sum_{j=1}^{N_{s}}f_{N}^{{\widehat{\mathbf{w}}}_{j}}({\mathbf{x}})$. The first term, σ²(x), in Eq. (4) is the aleatoric uncertainty that represents the inherent noise in the data and is considered irreducible. The second term (in the square brackets) in Eq. (4) is the epistemic uncertainty, that quantifies the modeling uncertainty.

In this work, the aleatoric uncertainty is learned via the BNN model along with the charge densities ρ. Therefore, for each input x, the BNN learns two outputs: ${f}_{N}^{{{{\bf{w}}}}}({{{\bf{x}}}})$ and σ(x). For a Gaussian likelihood, the noise σ is learned through the likelihood term of the loss function Eq. (3) following¹¹² as:

$$\log P({{{\mathcal{D}}}}| {{{\bf{w}}}})=\sum\limits_{i=1}^{{N}_{d}}-\frac{1}{2}\log {\sigma }_{i}^{2}-\frac{1}{2{\sigma }_{i}^{2}}{({f}_{N}^{{{{\bf{w}}}}}({{{{\bf{x}}}}}_{i})-{\rho }_{i})}^{2}\,.$$

(5)

Here, N_d is the size of the training data set. The aleatoric uncertainty, σ, enables the loss to adapt to the data. The network learns to reduce the effect of erroneous labels by learning a higher value for σ², which makes the network more robust or less susceptible to noise. On the other hand, the model is penalized for predicting high uncertainties for all points through the $\log {\sigma }^{2}$ term.

The epistemic uncertainty is computed by evaluating the second term of Eq.(4), via sampling ${\widehat{{{{\bf{w}}}}}}_{j}$ from the variational posterior.

Transfer learning using multi-scale data

Conventional DFT simulations for smaller systems are considerably cheaper than those for larger systems, as the computational cost scales cubically with the number of atoms present in the simulation cell. However, the ML models cannot be trained using simulation data from small systems alone. This is because, smaller systems are far more constrained in the number of atomic configurations they can adopt, thus limiting their utility in simulating a wide variety of materials phenomena. Additionally, the electron density from simulations of smaller systems differs from that of larger systems, due to the effects of periodic boundary conditions.

To predict accurately across all length scales while reducing the cost of training data generation via DFT simulations, we use a transfer learning approach here. Transfer learning is a machine learning technique where a network, initially trained on a substantial amount of data, is later fine-tuned on a smaller dataset for a different task, with only the last few layers being updated while the earlier layers remain unaltered⁶⁹. The initial layers (called “frozen layers”) capture salient features of the inputs from the large dataset, while the re-trained layers act as decision-makers and adapt to the new problem.

Transfer learning has been used in training neural network potentials, first on Density Functional Theory (DFT) data, and subsequently using datasets generated using more accurate, but expensive quantum chemistry models¹¹³. In contrast, in this work, transfer learning is employed to leverage the multi-scale aspects of the problem. Specifically, the present transfer learning approach leverages the statistical dissimilarity in data distributions between various systems and the largest system. This process is employed to systematically select the training data, ultimately reducing reliance on heuristics, as detailed in the Supplementary Material (see Supplementary Fig. 5). This approach allows us to make electron density predictions across scales and system configurations, while significantly reducing the cost of training data generation.

In the case of aluminum, at first, we train the model using a large amount of data from DFT simulations of (smaller) 32-atom systems. Subsequently, we freeze the initial one-third layers of the model and re-train the remaining layers of the model using a smaller amount (40%) of data from simulations of (larger) 108-atom systems. Further training using data from larger bulk systems was not performed, since the procedure described above already provides good accuracy (Figs. 6, 14), which we attribute to the statistical similarity of the electron density of 108 atom systems and those with more atoms (Supplementary Fig. 5). A similar transfer learning procedure is used for the SiGe model, where we initially train with data from 64-atom systems and subsequently retrain using data from 216-atom systems. Overall, due to the non-linear data generation cost using DFT simulations, the transfer learning approach reduces training data generation time by over 50%.

Postprocessing of ML predicted electron density

One way to test the accuracy of the ML models is to compute quantities of interest (such as the total ground state energy, exchange-correlation energy, and Fermi level) using the predicted electron density, ρ^ML. Although information about the total charge in the system is included in the prediction, it is generally good practice to first re-scale the electron density before postprocessing^51,54, as follows:

$${\rho }^{{{{\rm{scaled}}}}}\left({{{\bf{r}}}}\right)={\rho }^{{{{\rm{ML}}}}}({{{\bf{r}}}})\frac{{N}_{{{{\rm{e}}}}}}{\displaystyle{{\int}_{{{\Omega }}}{\rho }^{{{{\rm{ML}}}}}({{{\bf{r}}}})d{{{\bf{r}}}}}}\,.$$

(6)

Here, Ω is the periodic supercell used in the calculations, and N_e is the number of electrons in the system. Using this scaled density, the Kohn-Sham Hamiltonian is set up within the SPARC code framework, which was also used for data generation via AIMD simulations^95,96,97. A single step of diagonalization is then performed, and the energy of the system is computed using the Harris-Foulkes formula^114,115. The errors in predicting ρ^ML(r), and the ground state energy thus calculated, can be seen in Fig. 6. More detailed error values can be found in Supplementary Table 4 and Supplementary Table 5.