INTRODUCTION

Ever since the discovery of cuprate superconductivity in 1986 by Bednorz and Müller1, the anomalous behavior of the pristine, as well as the doped cuprate, has eluded theoretical explanation and still remains an unsolved problem in condensed matter physics. La2CuO4 (LCO), in particular, has been a significant challenge to describe within a coherent theoretical framework. The Hohenberg–Kohn–Sham density functional theory (DFT)2,3 with some classes of popular exchange-correlation (XC) approximations fails spectacularly to capture the insulating antiferromagnetic ground state of LCO, let alone the metal insulator transition (MIT) under doping4. Specifically, the local spin-density approximation (LSDA) XC functional incorrectly predicts the parent compound to be a metal, yielding a vastly underestimated value for the copper magnetic moment of 0.1μB5,6 compared to the experimental value of 0.60 ± 0.05μB7. The Perdew-Burke-Ernzerhof (PBE) generalized gradient approximation (GGA)8 still predicts LCO to be a metal with a slightly improved magnetic moment of 0.2μB9. The Becke-3–Lee–Yang–Parr (B3LYP)10,11,12,13 hybrid functional correctly explains the AFM ground state in LCO but fails to capture the MIT upon doping14. These failures have led to the (incorrect) belief that DFT is fundamentally incapable of capturing the physics of the cuprates and other correlated materials. Therefore, “beyond DFT” methodologies, such as the quantum Monte Carlo methods15, DFT+U16,17, and dynamical mean-field theory (DMFT)18,19,20 have been introduced to handle strong electron correlation effects. These approaches have been useful for understanding the physics of the cuprates, although they typically introduce ad hoc parameters, such as the Hubbard U, to tune the correlation strength, which limits their predictive power.

Recent progress in constructing advanced density functional approximations (DFA) provides a viable new pathway for addressing the electronic structures of correlated materials. In particular, the strongly-constrained and appropriately-normed (SCAN) meta-GGA21, which obeys all 17 known constraints applicable to a meta-GGA functional, has been shown to accurately predict many key properties of the pristine and doped La2CuO4 and YBa2Cu3O622,23,24. In LCO, SCAN correctly captures the size of the optical bandgap, the magnitude and the orientation of the copper magnetic moment, and the magnetic form factor in comparison with the corresponding experimental results23. In near-optimally doped YBa2Cu3O7, 26 competing uniform and stripe phases are identified24. In this case, the treatment of charge, spin, and lattice degrees of freedom on the same footing is crucial in stabilizing the stripe phases without invoking any free parameters. Furthermore, SCAN has been applied to the Sr2IrO4 parent compound yielding the subtle balance between electron correlations and strong spin-orbit coupling in excellent agreement with experiment25.

SCAN’s success in the copper and iridium oxides is a significant achievement for the DFT and suggests capability for treating a wider class of correlated materials. SCAN, however, is well-known to yield overly large saturation magnetization in elemental metals (e.g., Fe and Ni)26,27,28 and has the problem of numerical instabilities29,30,31,32, which may limit its applicability. A number of natural questions, therefore, arise: Is SCAN a unique XC density function that is able to correctly capture a variety of properties of the cuprates or do other meta-GGAs perform similarly well? How do hybrid XC functionals perform in comparison? Answers to these questions are important for benchmarking the performance of SCAN and related DFAs and for opening a pathway to their more extensive use.

With this motivation, this paper compares the accuracy of 13 DFAs. In particular, we assess the efficacy of LSDA33,34, PBE8, SCAN21, SCAN-L35, rSCAN31, r2SCAN32, r2SCAN-L36, TPSS37, revTPSS38, MS039, MS240, M06L41, and HSE0642,43,44,45 with respect to their predictions for crystal, electronic, and magnetic structures of the pristine and doped prototypical high-temperature superconductors La2−xSrxCuO4. Various XC density functionals were employed to span the levels of the Perdew–Schmidt hierarchy46, allowing us to evaluate the performance of each functional class for the description of correlated condensed matter systems.

Results and discussion

Methodology

The theoretical foundation of DFT was laid by Hohenberg and Kohn2 when they considered the electron density rather than the wave function as the fundamental object for addressing the many-body problem. This concept was later extended by Kohn and Sham (KS) by replacing the complicated many-electron problem with an auxiliary non-interacting system that leads to the one-electron Schrödinger like equations3, providing a practical approach to solve for the ground-state electron density and ground-state energy of the many-body system. The beauty of the KS approach is that it explicitly separates the non-interacting kinetic energy and the long-range Hartree energy, which describes the classical electrostatic repulsion between electrons, from the remaining exchange-correlation energy. An exact solution for the ground-state total energy and electron density is then obtained, in principle, although in practice, the XC energy must be approximated.

The total energy of the many-body electron system, within the Kohn–Sham DFT framework can be written as:

$${{{{E}}}}={{{{{T}}}}}_{{{{\rm{s}}}}}+{{{{{E}}}}}_{{{{\rm{ext}}}}}+{{{{{E}}}}}_{{{{\rm{H}}}}}+{{{{{E}}}}}_{{{{\rm{xc}}}}},$$
(1)

where Ts is the non-interacting kinetic energy, Eext is the external potential energy, EH is the Hartree energy, and Exc contains the remaining energy contributed by the many-body XC effects. The first three terms in Eq. (1) can be obtained exactly while the last term has to be approximated. Various approximations for Exc can be arranged on the rungs of the Perdew–Schmidt hierarchy46. The lowest rung of the hierarchy is LSDA that is based on local electron densities nσ. On the next rung, the GGA class adds density gradients ∇nσ to LSDA. This is followed by meta-GGAs that come in two flavors, adding either the non-interacting kinetic energy density τσ or a Laplacian dependence ∇2nσ or both in comparison with GGAs. Here σ denotes the two spin channels. The XC energy for meta-GGAs is defined as

$$\begin{array}{ll}{{{{{E}}}}}_{{{{\rm{xc}}}}}^{{{{\rm{MGGA}}}}}[{{{{{n}}}}}_{\uparrow },{{{{{n}}}}}_{\downarrow }]=\\ \qquad\qquad\qquad\quad\int {{{\rm{{d}}}^{3}}}{{{\bf{r}}}}{{{{n}}}}({{{\bf{r}}}}){{{{\rm{\varepsilon }}}}}_{{{{\rm{x}}}}}^{{{{\rm{unif}}}}}({{{{n}}}}){{{{{F}}}}}_{{{{\rm{xc}}}}}({{{{{n}}}}}_{\uparrow },{{{{{n}}}}}_{\downarrow },\nabla {{{{{n}}}}}_{\uparrow },\nabla {{{{{n}}}}}_{\downarrow },{\nabla }^{2}{{{{{n}}}}}_{\uparrow },{\nabla }^{2}{{{{{n}}}}}_{\downarrow },{\tau }_{\uparrow },{\tau }_{\downarrow }).\end{array}$$
(2)

where \({\varepsilon }_{{{{\rm{x}}}}}^{{{{\rm{unif}}}}}({{{{n}}}})\) is the exchange energy per electron for the uniform electron gas and Fxc is an enhancement factor.

By including τ, the meta-GGA functional becomes more flexible and allows for satisfying a greater number of exact constraints compared to GGAs. Furthermore, by defining a dimensionless variable \({{{\rm{\alpha }}}}=\frac{{{{{\tau }}}}-{{{{{\tau }}}}}^{{{{\rm{w}}}}}}{{{{{{\tau }}}}}^{{{{\rm{unif}}}}}}\), where \({{{{{\tau }}}}}^{{{{\rm{unif}}}}}=(3/10){(3{\pi }^{2})}^{2/3}{{{{{n}}}}}^{5/3}\) is the kinetic energy density of the uniform electron gas and τw = ∣∇n∣2/8n is the von Weizsäcker kinetic energy density, a meta-GGA can recognize slowly varying densities, single-orbital systems, and non-covalent bonds between two closed shells21,47,48. Moreover, since τ is determined from the set of KS orbitals, meta-GGAs with explicit τ dependence are intrinsically non-local in nature. DFAs in this class include SCAN, Regularized SCAN (rSCAN)31, regularized-restored SCAN (r2SCAN)32,49, Tao–Perdew–Staroverov–Scuseria (TPSS)37, revised-TPSS (revTPSS)38, meta-GGA made simple 0 (MS0)39, meta-GGA made simple 2 (MS2)40, and the Minnesota functional (M06L)41.

Trickey et al. recently substituted functions of ∇2n(r) for τ(r) in meta-GGA XC functionals, leading to SCAN-L35,50 and r2SCAN-L36 XC density functionals, among others, which yield similar (but not identical) performance to the original orbital dependent versions. The last class considered in this article are the hybrid functionals, which were originally designed to combine a semi-local DFA with the exact exchange of the Hartree–Fock single determinant to improve predictions of molecular thermochemical properties. The idea is that since the semi-local DFAs typically overbind while Hartree–Fock underbinds, their combination would presumably capture the correct balance between the two limits. The XC energy for the screened hybrid functional of Heyd, Scuseria, and Ernzerhof (HSE) is given by

$$\begin{array}{ll}{{{{{E}}}}}_{{{{\rm{xc}}}}}^{{{{\rm{HSE}}}}}=a{{{{{E}}}}}_{{{{\rm{x}}}}}^{{{{\rm{HF}}}},{{{\rm{SR}}}}}(\omega )+(1-a)\,{{{{{E}}}}}_{{{{\rm{x}}}}}^{{{{\rm{PBE}}}},{{{\rm{SR}}}}}(\omega )\\ \qquad\qquad +\,{{{{{E}}}}}_{{{{\rm{x}}}}}^{{{{\rm{PBE}}}},{{{\rm{LR}}}}}(\omega )+{{{{{E}}}}}_{{{{\rm{c}}}}}^{{{{\rm{PBE}}}}},\end{array}$$
(3)

where a is the exact exchange admixing parameter whose typical value is 1/451. Here, the screening parameter ω defines the separation range, \({{{{{E}}}}}_{{{{\rm{x}}}}}^{{{{\rm{HF}}}},{{{\rm{SR}}}}}(\omega )\) the short-range HF exact exchange, and \({{{{{E}}}}}_{{{{\rm{x}}}}}^{{{{\rm{PBE}}}},{{{\rm{SR}}}}}(\omega )\) and \({{{{{E}}}}}_{{{{\rm{x}}}}}^{{{{\rm{PBE}}}},{{{\rm{LR}}}}}(\omega )\) the short and long-range components, respectively, of the PBE exchange functional. The admixing parameter value of a = 1/4 has been justified through a consideration of molecular thermochemical properties52.

Ground-state crystal structure

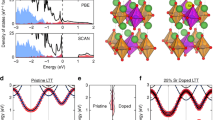
The phase diagram of the cuprates displays a complex intertwining of magnetic and charge-ordered states that evolve with doping to reveal a superconducting dome. Interestingly, structural phase transitions associated with various octahedral tilt modes53,54 mainly follow the electronic phase boundaries.55 At high temperatures LCO is found to be tetragonal (HTT) with all CuO6 octahedra aligned axially. A phase transition occurs upon lowering the temperature resulting in a low-temperature orthorhombic (LTO) phase where the octahedra are tilted along the (110) zone diagonal. An additional low-temperature tetragonal (LTT) phase arises upon substituting La with Ba or Nd, where the octahedral tilts are aligned along the (100) and (010) directions in alternating CuO2 layers. Therefore, in order to properly disentangle the connection between the electronic and the physical properties of the cuprates, it is imperative to capture the correct ground-state crystal structure. To calculate the total energies of various crystalline phases, we consider the \(\sqrt{2}\,\) × \(\sqrt{2}\) supercell of the body-centered-tetragonal I4/mmm primitive unit cell to accommodate both the octahedral tilts and the (π, π) AFM order within the CuO2 planes. We treat the doping within a relatively simple “δ- doping” scheme in which one La atom in the supercell is replaced by a Sr atom to yield an average hole doping of 25%22. This approach has been recently used for doping LSCO via molecular beam epitaxy techniques56. Figure 1a shows the crystal structures of LCO and LSCO in the LTO phase where the CuO6 octahedra have been shaded blue and orange to represent the AFM order. The Sr doping site is also indicated.

Fig. 1: LTO crystal structure and brillouine zone considered for the calculation.
figure 1

a Theoretically predicted crystal structure of La2−xSrxCuO4 in the LTO phase for x = 0.0 and 0.25. Copper, oxygen, lanthanum, and strontium atoms are represented by blue, red, green, and yellow spheres, respectively. Octahedral faces are shaded in blue (orange) to denote spin-up (down). Black dotted lines mark the unit cell. b A schematic of the non-magnetic (NM) and anti-ferromagnetic (AFM) Brillouin zone, where the path followed in the electronic dispersions in Fig. 6 is marked.

Full size image

Figure 2a and d present energy differences between the AFM and NM phases for the pristine and doped La2−xSrxCuO4 in each crystal structure for the DFAs considered. Firstly, we note that LSDA does not stabilize an AFM order over the Cu sites, whereas in PBE the AFM phase is marginally more stable, consistent with the previous studies22. All meta-GGAs find the AFM phase to be the ground state, with an energy separation of −0.2 to −0.9 eV between the AFM and NM states in the pristine structure, whereas in the doped case the energy difference is smaller by a factor of two. These trends are consistent across the various crystal structures.

Fig. 2: Various energy calculations obtained for all three phases using different DFAs.
figure 2

a Energy differences between the G-AFM and NM phases for the HTT (green upside-down triangle), LTO (white diamond), and LTT (blue triangle) structures for various XC density functionals. b, c Relative energies per formula unit for AFM in pristine LCO between LTO and HTT (b) and LTO and LTT (c). d–f Same as a–c except that these panels refer to LSCO instead of LCO.

Full size image

Figure 2b, c, e, f presents energy differences between the HTT, LTT, and LTO crystal structures for pristine and doped La2−xSrxCuO4 for various density functional approximations. In all cases, the HTT phase lies at much higher energy compared to the LTO and LTT phases. Difference between the LTO and LTT appears more delicate. For the undoped case, only SCAN correctly predicts LTO to be the ground state, while LSDA, rSCAN, r2SCAN, and r2SCAN-L find LTO and LTT to be nearly degenerate with an energy difference of less than 1 meV. In the doped case, all XC functionals correctly predict the ground state to be LTT57, while SCAN and rSCAN yield a marginal energy difference between LTT and LTO. Note that near 12% doping, the LTO and LTT phases are found experimentally to be virtually degenerate22.

Figure 3 shows the equilibrium lattice constants for LCO in the HTT, LTT, and LTO phases. The LSDA and PBE values were taken from ref. 22 and experimental values from refs. 58,59,60. The LSDA is seen to underestimate the lattice constant for all crystal structures. PBE, on the other hand, underbinds the atoms and yields an exaggerated orthorhombicity in the LTO phase, similar to the super-tetragonality spuriously predicted by PBE for ferroelectric materials61. TPSS, revTPSS, MS0, MS2, SCAN, SCAN-L, rSCAN, r2SCAN and r2SCAN-L correct PBE by reducing the b lattice constant in line with the experimental values in LTO and LTT.

Fig. 3: Comparison of the theoretically obtained and experimental lattice constants a, b, c for the HTT, LTT, and LTO crystal structures using various density functional approximations for La2CuO4.
figure 3

The lattice constant values are divided by corresponding experimental values.

Full size image

Curiously, all XC density functionals underestimate the lattice parameters in the HTT phase, except for PBE and M06L. The empirical M06L XC functional predicts lattice constants with greater accuracy than other XC functionals in all cases. Note that HTT is a high-temperature phase and therefore the experimental lattice constant should, in principle, be corrected for finite-temperature effects for comparison with DFT results. Figure 4 considers the octahedral tilt angles. Here, M06L underestimates the tilt angle, while all other XC functionals overestimate it within a few degrees. We note, however, that the experimental tilt angles should be regarded as average values because the CuO6 octahedra are not rigid objects: these octahedra couple to various phonon modes and deform dynamically. Molecular dynamics or phonon calculations will be needed to capture the octahedral tilts more accurately.

Fig. 4: Theoretically predicted values of octahedra tilt angle using various density functional approximations for LCO.
figure 4

The LSDA and PBE values are taken from ref. 22 The octahedra tilt values for LTO, LTT, and HTT are divided by corresponding experimental values.

Full size image

Lattice constants and octahedral tilts are not included for r2SCAN-L in Figs. 3 and 4 because we found a non-zero stress tensor at the energy-minimized equilibrium volume in this case. This suggests an error in the stress tensor implementation of r2SCAN-L, see Supplementary Discussion 1 in the Supplementary Materials for more details. The experimental structures were therefore used for the electronic and magnetic properties calculations using r2SCAN-L. The experimental structures were also used for HSE06-based calculations as the computational cost for hybrid XC functionals is much greater than the meta-GGAs.

Notably, within the “SCAN family” of XC density functionals (SCAN, SCAN-L, rSCAN, and r2SCAN) all members show similar performance for lattice constants and tilt angles (Figs. 3 and 4). The potential speedup of running r2SCAN-L in a density-only KS scheme and the improved numerical performance inherited from r2SCAN suggest that r2SCAN-L could be used to optimize geometry followed by a single point SCAN or r2SCAN calculation for obtaining electronic properties. This approach may also present an advantage of minimizing the numerical challenges associated with SCAN. A similar scheme was suggested in ref. 62 in the context of spin-crossover prediction.

Electronic and magnetic structures

Figure 5 compares the theoretically predicted electronic bandgaps and copper magnetic moments obtained from various XC functionals for the three crystalline phases of LCO. The range of experimentally observed bandgaps63,64,65, and median copper magnetic moments7 are marked by the gray and blue shaded regions, respectively. LSDA and PBE greatly underestimate the bandgaps and magnetic moments because they fail to stabilize the AFM order. A large variation is seen in the results of the meta-GGAs. TPSS and revTPSS both underestimate the bandgaps and magnetic moments. MS0, MS2, and SCAN yield values that lie within the experimental ranges. Other meta-GGAs predict reduced bandgaps and magnetic moments that are below experimental values. M06L underestimates both the moment and the bandgap value, possibly due to the bias towards molecular systems which is encoded in its empirical construction. M06L yields ferrimagnetic order and, therefore, the average of the magnetic moment is given in Fig. 5. Finally, the hybrid functional (HSE06) overestimates bandgaps, predicting a value of around 3 eV, and it also overestimates magnetic moments.

Fig. 5: Band gap and magnetic moment values from various DFAs.
figure 5

Theoretical predicted values of a electronic bandgap and b copper magnetic moment for all three phases of pristine LCO obtained within various density functional approximations. The gray shaded region in a gives the spread in the reported experimental values for the leading edge gap63,64,65. In b, the blue shaded region represents the experimental value of magnetic moment7. The LSDA and PBE values are taken from ref. 22.

Full size image

Ando66 has stressed that one should estimate the bandgap not from the lowest energy absorption peak, but from the leading edge gap in the optical spectra63. The leading edge gives the minimum energy needed by an electron to be elevated from the valence to the conduction band, in good agreement with the transport gap in the cuprates. In contrast, the energy of the absorption peak in the optical spectrum depends on finer details of the electronic structure such as the presence of flat bands or Van Hove singularities. The theoretically predicted bandgaps here should be compared to the fundamental bandgaps67,68,69,70, which are typically larger than the corresponding optical bandgaps due to excitonic effects. Notably, a recent measurement on LCO reports an optical bandgap of about ≈1.3 eV64.

Regarding magnetic moments, the values obtained by neutron scattering involve uncertainties since the copper form factor is not a priori known. Appendix E of ref. 23 compares copper magnetic moments from various experiments, including the values given in the recent review of Tranquada7. Note that, when estimating the copper magnetic moment, we have increased the Wigner–Seitz radius of the integration sphere beyond the default 1.16–1.91 Å (the Cu–O bond length) in order to fully capture the magnetic density centered on the copper atomic site and the part originating from strong hybridization between the copper and oxygen atoms (see Supplementary Discussion 2 in the Supplementary materials for more details).

While these predicted magnetic moments are in approximate agreement with the experimentally measured value, it has been suggested that this is not the correct comparison. This is because (1) given a static magnetic moment, fluctuation can cause a 30% reduction71. (2) DFT works with spin symmetry breaking72, and the DFT magnetic moments should be compared to the static value. We believe this issue is unresolved and that self-consistency can capture some average effects of fluctuation due to the DFT correlation potential. We hope to discuss this further in a future publication.

Figure 6 presents the electronic band dispersions in pristine and doped La2CuO4 in the LTO crystal structure for the AFM phase using SCAN, r2SCAN, r2SCAN-L, M06L, and HSE06. The copper (red circles) and planar oxygen (blue dots) orbital contributions are overlayed. For all XC functionals, LCO is seen to be an insulator. At the valence band edge, SCAN, r2SCAN and r2SCAN-L produce a significant avoided crossing between the \({{{{{d}}}}}_{{x}^{2}-{y}^{2}}\) and in-plane oxygen dominated bands along Γ − M and \({{{\rm{M}}}}-\bar{{{\Gamma }}}\), but this feature is essentially absent in M06L. In SCAN and r2SCAN, the gap is direct, with its smallest value occurring at M symmetry point or very close to it. In contrast, r2SCAN-L and M06L predict indirect bandgaps. Finally, the conduction bands in M06L display significant spin splittings indicative of ferrimagnetic ordering consistent with the observed ferrimagnetic moments.

Fig. 6: Band structure and density of states (DOS) from various DFAs.
figure 6

Electronic band structure and density of states of LCO and LSCO in the LTO phase using a SCAN, b r2SCAN, c r2SCAN-L, d M06L, e HSE06. The contribution of Cu-\({{{{{d}}}}}_{{{{{{x}}}}}^{2}-{{{{{y}}}}}^{2}}\) and O-px + py are marked by the red and blues shadings, respectively. The path followed by the dispersion in the Brillouin zone is shown in Fig. 1b.

Full size image

Turning to the doped system in Fig. 6, all meta-GGAs are seen to capture the metal-insulator transition, with various XC functionals producing small differences in band splittings around the Fermi level. In contrast, HSE06 maintains a small gap and predicts a nearly flat impurity-like band just above the Fermi level, consistent with the B3LYP results14. See Supplementary Figs. 2, 3 and 4 in the Supplementary Materials for further details of the electronic band dispersions in LTO, LTT, and HTT phases. The SCAN-based magnetic moments and bandgaps given in this study differ by ~0.02μB and 0.11 eV, respectively, from those given in ref. 22. These small differences, which do not affect the overall conclusions of ref. 22, are due to an error in the VASP implementation that was used in ref. 22.

Effective U and exchange coupling

The bandgap that develops in the half-filled Cu \({{{{{d}}}}}_{{x}^{2}-{y}^{2}}\) dominated band by splitting the up- and down-spin bands is due to strong multi-orbital intrasite electron–electron interactions. The strength of these interactions is a key quantity that can be used to characterize various regions of the phase diagram and classify the phenomenology of the cuprate family as a whole73. In order to estimate the correlation strengths implicit in the underlying XC density functionals, we map our site-resolved partial densities of states to a multi-orbital Hubbard model74 along the lines of ref. 23. For this purpose, we consider a d orbital μ of spin σ in a ligand field with on-site correlations in the mean field, and express its energy as

$$\begin{array}{ll}{{{{{E}}}}}_{\pm }^{{{{\rm{\mu }}}}{{{\rm{\sigma }}}}}={{{{{E}}}}}_{{{{\rm{atomic}}}}}^{{{{\rm{\mu }}}}}+{{{{U}}}}\left\langle {n}_{{{{\rm{\mu }}}}\bar{\sigma }}^{\pm }\right\rangle +{{{{U}}}}^{\prime} \mathop{\sum}\limits_{\nu \ne \mu }\left\langle {n}_{\nu \bar{\sigma }}^{\pm }\right\rangle \\ \qquad\quad +\,({{{{U}}}}^{\prime} -{{{{{J}}}}}_{{{{\rm{H}}}}})\mathop{\sum}\limits_{\nu \ne \mu }\left\langle {n}_{\nu \sigma }^{\pm }\right\rangle \pm {{{{h}}}},\end{array}$$
(4)

where ± indexes the bonding (−) and anti-bonding (+) states, and h is the hybridization strength. μ(ν) and spin \(\sigma (\bar{\sigma }=-\sigma )\) are orbital and spin indices, respectively, and \(\langle {n}_{\mu \sigma }^{\pm }\rangle\) is the average electron occupation for a given state in the mean field. By taking the difference between the up- and down-spin channels and summing over bonding and anti-boding levels, U and JH can be shown to connect the spin splitting of a given orbital to the differences in various spin-dependent orbital occupations,

$${{{{{E}}}}}^{{{{\rm{\mu }}}}\uparrow }-{{{{{E}}}}}^{{{{\rm{\mu }}}}\downarrow }={{{{U}}}}({{{{{N}}}}}_{{{{\rm{\mu }}}}\downarrow }-{{{{{N}}}}}_{{{{\rm{\mu }}}}\uparrow })-{{{{{J}}}}}_{{{{\rm{H}}}}}\mathop{\sum}\limits_{{{{\rm{\nu }}}}\ne {{{\rm{\mu }}}}}({{{{{N}}}}}_{{{{\rm{\nu }}}}\uparrow }-{{{{{N}}}}}_{{{{\rm{\nu }}}}\downarrow }),$$
(5)

where \({{{{{N}}}}}_{{{{\rm{\mu }}}}{{{\rm{\sigma }}}}}=\mathop{\sum }\nolimits_{\pm }\langle {n}_{\mu \sigma }^{\pm }\rangle\). Furthermore, Eμσ may be obtained from the density of states:

$${{{{{E}}}}}^{{{{\rm{\mu }}}}{{{\rm{\sigma }}}}}=\mathop{\int}\nolimits_{W}{{{{{g}}}}}_{{{{\rm{\mu }}}}{{{\rm{\sigma }}}}}({{{\rm{\varepsilon }}}}){{{\rm{\varepsilon }}}}{{{\rm{d}}}}{{{\rm{\varepsilon }}}}$$
(6)

where W represents the bandwidth. The average spin splitting of a given orbital can then be expressed as:

$${{{{{E}}}}}^{{{{\rm{\mu }}}}\uparrow }-{{{{{E}}}}}^{{{{\rm{\mu }}}}\downarrow }=\mathop{\int}\nolimits_{W}[{{{{{g}}}}}_{{{{\rm{\mu }}}}\uparrow }({{{\rm{\varepsilon }}}})-{{{{{g}}}}}_{{{{\rm{\mu }}}}\downarrow }({{{\rm{\varepsilon }}}})]{{{\rm{\varepsilon }}}}{{{\rm{d}}}}{{{\rm{\varepsilon }}}}.$$
(7)

We thus arrive at the following coupled set of equations for the interaction parameters,

$$\begin{array}{ll}\mathop{\int}\nolimits_{W}\,[{{{{{g}}}}}_{{{{\rm{\mu }}}}\uparrow }({{{\rm{\varepsilon }}}})-{{{{{g}}}}}_{{{{\rm{\mu }}}}\downarrow }({{{\rm{\varepsilon }}}})]{{{\rm{\varepsilon }}}}{{{\rm{d}}}}{{{\rm{\varepsilon }}}}={{{{U}}}}({{{{{N}}}}}_{\mu \downarrow }-{{{{{N}}}}}_{\mu \uparrow })-{{{{{J}}}}}_{{{{\rm{H}}}}}\mathop{\sum}\limits_{{{{\rm{\nu }}}}\ne {{{\rm{\mu }}}}}({{{{{N}}}}}_{{{{\rm{\nu }}}}\uparrow }-{{{{{N}}}}}_{{{{\rm{\nu }}}}\downarrow }).\end{array}$$
(8)

By using the copper-atom-projected partial density-of-states in the AFM phase of LTO La2CuO4 where the \({{{{{d}}}}}_{{x}^{2}-{y}^{2}}\) orbital is half-filled and all other orbitals are completely filled, we can simplify the preceding set of coupled equations into the form:

$$\mathop{\int}\nolimits_{W}[{{{{{g}}}}}_{{{{{{d}}}}}_{{x}^{2}-{y}^{2}}\uparrow }({{{\rm{\varepsilon }}}})-{{{{{g}}}}}_{{{{{{d}}}}}_{{x}^{2}-{y}^{2}}\downarrow }({{{\rm{\varepsilon }}}})]{{{\rm{\varepsilon }}}}{{{\rm{d}}}}{{{\rm{\varepsilon }}}}={{{{U/2}}}}$$
(9)
$$\mathop{\int}\nolimits_{W}[{{{{{g}}}}}_{({{{\rm{\mu }}}}\ne {{{{{d}}}}}_{{x}^{2}-{y}^{2}})\uparrow }({{{\rm{\varepsilon }}}})-{{{{{g}}}}}_{({{{\rm{\mu }}}}\ne {{{{{d}}}}}_{{x}^{2}-{y}^{2}})\downarrow }({{{\rm{\varepsilon }}}})]{{{\rm{\varepsilon }}}}{{{\rm{d}}}}{{{\rm{\varepsilon }}}}={{{{{J}}}}}_{{{{\rm{H}}}}}/2$$
(10)

Finally, we evaluate ∫W[gμ↑(ε) − gμ↓(ε)]εdε over the full band width W for each orbital to solve for U and JH. The estimated values of U and JH so obtained are presented in Table 1. The average spin splittings are strongly orbital dependent23, and we have taken the largest value as the upper bound on JH.

Table 1 Theoretically predicted values of U and JH using various DFAs for three different phases of pristine LCO.
Full size table

Results of Table 1 show that TPSS and revTPSS yield a smaller value for U compared to the recent cRPA calculations (~3.2 eV)75, since they fail to adequately capture the bandgaps and magnetic moments, while M06L, SCAN-L, and r2SCAN-L yield comparable values. MS0, MS2, rSCAN, and r2SCAN, find larger values than the cRPA values. The hybrid HSE06 XC functional predicts exaggerated values for U.

In order to determine the exchange coupling strength, we use a mean-field approach, where we map the total energies of the AFM and ferromagnetic (FM) phases onto those of a nearest-neighbor spin \(-\frac{1}{2}\) Heisenberg Hamiltonian76,77,78. The difference in the energies of the AFM and FM phases in the mean-field limit is given by

$${{\Delta }}{{{{E}}}}={{{{{E}}}}}_{{{{\rm{AFM}}}}}-{{{{{E}}}}}_{{{{\rm{FM}}}}}={{{\rm{JNZ}}}}{{\, \langle \,}{{{{S}}}} {\, \rangle \,}}^{2}$$
(11)

where N is the total number of magnetic sites in the unit cell, S =1/2 is the spin on each site, and Z is the coordination number. Since the in-plane interactions within the Cu–O planes in La2CuO4 are much stronger than the interplanar interactions, we take Z = 4. For our AFM \(\sqrt{2}\times \sqrt{2}\) unit cell, N = 4. In this way, we obtain the J values for various XC functionals listed in Table 2.

Table 2 Theoretically predicted values of exchange coupling using various XC functionals for three different phases of pristine LCO.
Full size table

Table 2 shows that SCAN is most accurate in predicting the experimental value of −133 ± 3 meV79,80,81 for the exchange coupling in LCO. MS0 and MS2 slightly overestimate J compared to SCAN. TPSS, revTPSS, SCAN-L, rSCAN, r2SCAN and r2SCAN-L underestimate and HSE06 significantly overestimates J. M06L failed to converge for the FM case. Notably, here and in ref. 23, our modeling involves only the nearest-neighbor J in keeping with the related experimental analysis. We would expect some renormalization of the J values if we were to include next and higher nearest neighbors in our modeling.

In order to gain further insight into the multi-orbital nature of the electronic structure, two additional descriptors were estimated: (1) Charge-transfer energies between the Cu 3d and O 2p orbitals (Δdp); and (2) the tetragonal splitting of the eg states (\({{{\Delta }}}_{{{{{{e}}}}}_{{{{{g}}}}}}\)), which are defined as

$${{{\Delta }}}_{{{{{dp}}}}}={\varepsilon }_{{{{{d}}}}}-{\varepsilon }_{{{{{p}}}}}$$
(12)

and

$${{{\Delta }}}_{{{{{{e}}}}}_{{{{{g}}}}}}={\varepsilon }_{{x}^{2}-{y}^{2}}-{\varepsilon }_{{z}^{2}}.$$
(13)

The various band centers εμ are defined using the corresponding partial density-of-states as

$${{{{\rm{\varepsilon }}}}}_{{{{\rm{\mu }}}}}=\frac{\int {{{{\rm{g}}}}}_{{{{\rm{\mu }}}}}({{{\rm{\varepsilon }}}}){{{\rm{\varepsilon }}}}{{{\rm{d}}}}{{{\rm{\varepsilon }}}}}{\int {{{{\rm{g}}}}}_{{{{\rm{\mu }}}}}{{{\rm{(\varepsilon )d\varepsilon }}}}},$$
(14)

along the lines of refs. 82 and 83. We used an integration window of −8 eV to the top of the band in Eq. (14). This window covers only the anti-bonding bands for \({{{\Delta }}}_{{{{{{e}}}}}_{{{{{g}}}}}}\). Results of Table 3 show that compared to PBE, the meta-GGAs generally tend to enhance Δdp and \({{{\Delta }}}_{{{{{{e}}}}}_{{{{{g}}}}}}\) due to the stabilization of the AFM order. TPSS and revTPSS performances are comparable to PBE while other meta-GGAs predict larger Δdp and \({{{\Delta }}}_{{{{{{e}}}}}_{{{{{g}}}}}}\) values. For the doped case, Δdp increases, whereas \({{{\Delta }}}_{{{{{{e}}}}}_{{{{{g}}}}}}\) reduces compared to the pristine results. HSE06 predicts significantly large Δdp and \({{{\Delta }}}_{{{{{{e}}}}}_{{{{{g}}}}}}\) for both pristine and doped cases.

Table 3 Theoretically predicted values of the charge-transfer energies between Cu 3d and O 2p orbitals and two Cu energy splitting using various XC functionals for three different phases of pristine LCO and doped LSCO systems.
Full size table

Meta-GGA performance

The present results for the crystal, electronic, and magnetic properties clearly demonstrate that meta-GGAs provide an improvement over LSDA and PBE. Among the various meta-GGAs considered (TPSS, revTPSS, MS0, MS2, SCAN, rSCAN, r2SCAN, M06L), M06L is less satisfactory for predicting the LCO properties, which is heavily parameterized for molecular systems. The earlier generalized-KS (gKS) meta-GGAs such as TPSS and revTPSS are less accurate than the more recently developed approximations (e.g., SCAN). The success of SCAN is a consequence of its enforcing all the known 17 rigorous constraints that a semi-local functional can satisfy21. In addition, SCAN localizes d electrons better by reducing self-interaction errors that tend to over-delocalize d electrons in the presence of ligands involving s and p electrons70. SCAN thus stabilizes the magnetic moment of Cu and opens a sizable bandgap in LCO22, its shortcomings in exaggerating magnetic moments in 3d elemental solids notwithstanding26.

rSCAN solves the numerical grid issues encountered in SCAN by regularizing the problematic interpolation function of SCAN with a smooth polynomial, which unfortunately violates exact constraints31,32, and some of rSCAN’s transferability is lost84,85. r2SCAN retains the smoothness of rSCAN and maximally restores the exact constraints violated by the regularization of rSCAN and it has been shown to improve the accuracy over rSCAN while maintaining the numerical efficiency32. In the present study of cuprates, r2SCAN and rSCAN both perform similarly, with only slight underestimations of the bandgaps and magnetic moments.

By replacing the kinetic energy density with the Laplacian of the electron density and thus de-orbitalizing the underlying meta-GGAs, SCAN-L35 and r2SCAN-L36 are constructed from SCAN and r2SCAN, respectively. The XC potentials in SCAN-L and r2SCAN-L are locally multiplicative while in their orbital dependent parent functionals, the potentials are non-multiplicative. Perdew et al.69 have shown that for a given DFA, the gKS orbital bandgap is equal to the corresponding fundamental bandgap in solids, which is defined as the second-order ground-state energy difference with respect to electron number. This indicates that within the gKS formalism a DFA with better total energy also improves the band gap70. The preceding statement also applies to DFAs with multiplicative potentials as they have the same potentials in the KS and gKS schemes. The bandgaps and copper magnetic moments from SCAN-L and r2SCAN-L are consistently underestimated compared to the corresponding values from the parent SCAN and r2SCAN XC functionals.

M06L being an empirical functional is heavily parametrized. It is constructed by fitting to molecular data sets, and therefore, it tends to be less reliable for systems outside its fitting set with limited transferability.

Why does HSE06 open a gap in the doped LSCO?

HSE06 with the admixing parameter value of 1/4 works well for bandgap predictions in semiconductors. This improvement is due to the reduction of the self-interaction error present in PBE through the introduction of exact exchange68,70. However, Hartree–Fock is not applicable to metallic systems where there is no bandgap to separate the occupied and unoccupied bands. Therefore, hybrid functionals are not suited for metallic systems.

With the preceding consideration in mind, it is reasonable that the HSE06 XC functional produces an insulator in LCO but fails to capture the metal-insulator transition under doping. Figure 7 shows HSE06-based band structures of LSCO for various mixing parameters “a”. For a = 0, HSE06 is reduced to PBE, and thus predicts LSCO to be metallic. At a = 0.05, a slight change in the band structure can be seen: the conduction bands are slightly pushed up and split due to the stabilization of the magnetic moments on Cu, and the bands around the Fermi level at X start to separate from one another. Increasing a to 0.15 results in a separation of the valence bands at the Fermi level and the splitting of the conduction bands, and the two valence bands near the Fermi level split off from the remaining valence bands. Finally, at the standard value of a = 0.25, the highest valence band completely splits off, leaving a 0.2 eV gap at the Fermi level. The resulting conduction band displays significant spin splitting, indicative of a strong uncompensated ferrimagnetic order. Our spin-density calculations show that the spin-down band now lies just above the Fermi level where the doped hole is localized in the copper d\({}_{{z}^{2}}\) and apical oxygen pz hybridized band, see in Supplementary Fig. 5a of the Supplementary Material. Moreover, the band-projected charge density for the spin-down band (Supplementary Fig. 5b) clearly displays a d\({}_{{z}^{2}}\) orbital shape for copper sites and a pz orbital shape on the apical oxygen sites, similar to the results from B3LYP14.

Fig. 7: Band structures for HSE06 functional with different mixing parameter values.
figure 7

Band structure comparison by varying mixing parameter in the HSE06 hybrid functional for a a = 0, b a = 0.05, c a = 0.15, and d a = 0.25 in doped LTO phase. The blue-filled and red empty circles correspond to copper d\({}_{{{{{{z}}}}}^{2}}\) and copper d\({}_{{{{{{x}}}}}^{2}-{{{{{y}}}}}^{2}}\) orbitals, respectively. The projection strength is denoted by marker size.

Full size image

The band structures presented in Fig. 7 show that for small values of the mixing parameter (a), the conduction band and valence bands around the M point near the Fermi level are more dominated by copper d\({}_{{x}^{2}-{y}^{2}}\) states. As the value of the mixing parameter increases, the copper d\({}_{{z}^{2}}\) orbitals gain more weight. This implies that, as the fraction of exact exchange increases, electrons are more localized on in-plane copper atoms. This is expected since the LSDA gives the extreme covalent regime while the Hartree–Fock leads to the extreme ionicity.

Our study demonstrates that the meta-GGA class of XC functionals within the generalized Kohn–Sham scheme correctly predict many experimental results for pristine LCO, and also capture the insulator-to-metal transition with Sr doping. Among the different meta-GGAs considered, SCAN’s performance for structural, electronic, and magnetic properties of LCO/LSCO is closest to the corresponding experimental results. In contrast, the hybrid XC functional (HSE06) fails to capture the metal-insulator transition and overestimates the magnetic moments and band gaps in pristine LCO, and it needs adjustment of the standard 25% value of the mixing parameter to produce the metallic states. Our study thus indicates that the meta-GGAs provide a robust new pathway for the first-principles treatment of strongly correlated materials.

Methods

Computational methods

The calculations were performed using the pseudopotential projector-augmented wave method86 implemented in the Vienna ab initio simulation package (VASP)87,88. The energy cutoff for the plane-wave basis set was taken to be 550 eV for all meta-GGA calculations and 520 eV for HSE06-based computations. In order to sample the Brillouin zone, for meta-GGAs, an 8 × 8 × 4 Γ-centered k-point mesh was used while a smaller mesh of 6 × 6 × 2 was used for the HSE06 hybrid functional. The structures were initially relaxed for meta-GGAs using a conjugate gradient algorithm with an atomic force tolerance of 0.008 eV/Å and total energy tolerance of 10−5 eV. HSE06 calculations on the doped systems were carried out using a damped algorithm. The computational cost for HSE06-based computations is much larger than for the meta-GGAs, and for this reason, a smaller number of k-points and less strict energy tolerance were used in conjunction with using the unrelaxed (experimental) structures.