Introduction

Degeneracies in the bulk energy bands of crystals were intensively studied in the early days of band theory1. Recent breakthroughs have shed new light into this old topic by associating topological invariants with these degenerate points or lines2,3,4, and by extending the discussion from electrons to phonons5,6,7, photons8, magnons9 and excitons10. Among the degenerate points, twofold degenerate Weyl points always appear in pairs that can be topologically characterised with opposite Chern numbers11,12,13,14, and fourfold degenerate Dirac points have a linear dispersion in both electronic15,16,17,18,19,20 and phononic systems21,22. When the band crossings are one-dimensional in momentum space, they can form nodal lines, nodal rings or nodal chains, depending on their shape23,24,25,26,27,28,29,30,31, and these line crossings are protected by symmetries such as mirror or \({{{\mathcal{PT}}}}\) (where \({{{\mathcal{P}}}}\) is the spatial inversion symmetry and \({{{\mathcal{T}}}}\) is the time-reversal symmetry)32,33. Recent advances, using both group-theoretical analysis and high-throughput calculations, have enabled a comprehensive understanding of bulk band degeneracies in both electrons34,35,36 and phonons22. These topological degeneracies exhibit unique physical properties such as a ‘quantum anomaly’37,38, enabling various applications from spintronics39 to topological quantum computation40.

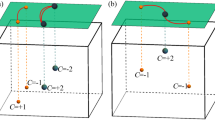
As a result of the bulk-boundary correspondence, the degenerate bulk points and lines are associated with topologically protected surface states, including surface arcs associated with Weyl and Dirac points41,42,43,44 and drumhead-like flat bands associated with nodal lines24,45. Similar to bulk band degeneracies, surface states can also exhibit band crossings in both semi-infinite slabs and finite slabs (with top and bottom surfaces)46. Here we focus on semi-infinite systems with only one surface. For Weyl points with Chern numbers of ±1, the associated helicoid surface states, whose isoenergy contours are Fermi arcs, form a continuous 2D surface in the energy-momentum space E-k and have no degeneracy47, as schematically shown in Fig. 1a. In topological insulators and topological crystalline insulators, the surface states become degenerate at a single point48,49,50,51,52, forming a surface Dirac cone, as shown schematically in Fig. 1b. In principle, two surface states can also cross along a line in the surface Brillouin zone, as shown schematically in Fig. 1c. However, like the bulk case, these surface line crossings need to be protected by additional symmetries47,53,54,55,56. While nodal line degeneracies in the bulk states have been thoroughly explored in a variety of quasiparticle band structures, the degenerate lines in the surface states have received less attention. The few examples of surface nodal lines all correspond to electronic band structures47,53,54,55,56,57 or artificial systems58,59. It is therefore desirable to identify more candidates in other quasiparticle spectra to fully understand the role of surface degeneracies.

Fig. 1: Different types of surface states in topological materials.
figure 1

a Nondegenerate helicoid surface states, b zero-dimensional degenerate Dirac surface states and c one-dimensional degenerate nodal-line surface states.

Full size image

Among all the quasiparticles, phonons are of particular interest as they describe intrinsic ionic vibrations. Moreover, the bosonic nature of phonons facilitates the exploration of topological phenomena in their entire spectrum. This is in contrast to fermionic systems (e.g. electronic systems) in which there is an additional constraint that degeneracies need to occur near the Fermi level to have an impact on the behaviour of the material. Furthermore, time-reversal symmetry is hard to break in phononic systems, and consequently, this extra symmetry requirement is automatically satisfied in phonons. These advantages have led to a recent surge of interest in characterising topological properties of phonons5,6,7,21,22,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76, but degenerate lines in surface phonon states have not yet been reported.

In this work, we propose that SnIP, an inorganic semiconductor with nodal-ring phonons in the bulk states, exhibits nodal-line surface states in the phonon spectrum using a combination of first-principles calculations, group theory analysis and Zak phase analysis. These surface states are doubly degenerate in a nodal line on the (100) surface. The surface nodal line is protected by the anti-unitary symmetry \(\vartheta ={{{\mathcal{T}}}}{\bar{M}}_{y}\), which is a combination of time-reversal symmetry \({{{\mathcal{T}}}}\) and glide mirror symmetry \({\bar{M}}_{y}\). With different surface terminations, we can alternatively get two surface nodal lines on different parts of the (100) surface Brillouin zone, which can be understood by different Zak phases in the presence of \({{{\mathcal{T}}}}{\bar{M}}_{y}\) symmetry. Our results suggest that similar surface degenerate lines/points will be found in other materials when there are extra symmetries to protect these surface degeneracies, and we believe that phonons can be a primary platform to study these degeneracies because of the presence of time-reversal symmetry and the flexibility to study the degeneracies in the entire phonon spectrum.

Results

Crystal structure and phonon dispersion

SnIP is an inorganic semiconductor with a double helix crystal structure, first synthesised in 2016, and can be formed without any templates77,78,79. The strong covalent bonds along the helices and the weak van der Waals interactions across the helices combine the electronic properties of inorganic semiconductors, such as high electron mobility80, and the mechanical properties of polymers, such as high flexibility81. In addition, by atomic substitution, a large material family with double helix structures has been predicted using first-principles calculations, providing a wide range of band gaps between 1 and 2.5 eV82. With a tunable bandgap and high mechanical flexibility, these quasi-one-dimensional semiconductors are extremely promising for next-generation devices ranging from mechanical sensors to optoelectronics81,82. Moreover, they can serve as a material platform to realise one-dimensional physical models such as the Su–Schrieffer–Heeger model83 and Majorana quantum wires84,85.

Bulk SnIP crystallises in the monoclinic space group P2/c (No. 13) with two double helices (SnIP)7 in the unit cell with stoichiometry (SnIP)14. The two double helices, alternatively left- and right-hand twisted, are stacked along the a direction. Each double helix is formed by an inner helical P chain and an outer helical SnI chain, as shown in Fig. 2a. The (SnIP)7 unit in each SnIP chain winding results in a 7/2 helix. From one phosphorus (yellow) atom to the next, the turning angle is about ±360∘/7 followed by a translation of c/7, and the same holds true for the tin (cyan) and iodine (navy) atoms in the SnI helix86. The calculated lattice parameters of a = 7.889 Å, b = 9.768 Å, c = 18.422 Å, and monoclinic distortion β = 110.21∘ match well with the measured ones77,79.

Fig. 2: Structural and vibrational properties of SnIP.
figure 2

a Crystal structure, b phonon dispersion and c Brillouin zone of SnIP. The orange region in the phonon dispersion highlighted in (b) corresponds to the topological features that we focus on. The phonon DOS is also shown in (b).

Full size image

The calculated phonon dispersion of SnIP is presented in Fig. 2b. It exhibits wide bandwidths along the helical direction, corresponding to the Γ-Y, C-Z, B-A and E-D high-symmetry lines in Fig. 2c, but, by contrast, phonon bands along other high-symmetry lines, especially those perpendicular to the helices, have a relatively flat dispersion, a result of the quasi-one-dimensional nature of this material. This is consistent with the fact that SnIP has strong covalent bonds along the one-dimensional helices but only weak van der Waals-like interactions between the double helices. As a result, SnIP fibres can be macroscopically bent by up to 90∘ without any significant Raman mode shifts, indicating that SnIP is an ultrasoft inorganic material and bending the helices has negligible influence on the phononic properties81.

There are 42 atoms in the unit cell of SnIP, corresponding to 126 phonon branches. The calculated atom-projected phonon density of states (DOS) in Fig. 2b indicates that the low-frequency modes below 4 THz are mainly vibrations involving the heavier Sn and I atoms, while those between 4–14 THz are dominated by the motion of the lighter P atoms. There are 14 phosphorus atoms in the unit cell, leading to 42 P-dominated bands in the phonon spectra, spanning branches 85 to 126. The phonon modes from 4 to 10 THz (branches 85–108) are more dispersive compared to the almost flat bands between 10 and 14 THz. The two double helices are related to each other by inversion/glide mirror symmetry, so there always exist two bands with similar eigenvalues and similar eigenvectors, corresponding to the P atoms from the two separate P chains, respectively (see the phonon dispersion between 4–8.5 THz in Supplementary Note 1 of the Supplementary Information).

Hereafter we focus on the frequency range 4–10 THz because the corresponding phonon bands are relatively ‘clean’ due to the large mass difference (between phosphorus and the other two elements) that separates them from the lower energy bands, and due to the strong intrachain vibrations that make them highly dispersive. This makes them an ideal playground for exploring topological features. In addition, these modes in the range 4–10 THz contribute to nearly half the thermal conductivity along the helix direction (see the phonon transport properties in Supplementary Note 2 of the Supplementary Information).

Nodal-ring phonons in SnIP

For the phonon modes between 4 and 10 THz, dominated by the vibrations of the relatively light P atoms, the phonon bands have a large dispersion along the helical direction but are almost flat along with the perpendicular directions, as shown in Fig. 2b. The band folding of the seven P atoms in a single helical P chain86 leads to several band crossings near the Brillouin zone boundary, especially in the flat band regions. After a comprehensive search for band crossing points between bands 85–108 (i.e. 4–10 THz), we find that the most promising band crossings are formed by phonon branches 92 and 93 with clean topological features in both bulk and surface states. Marked with # 92 and # 93 in Fig. 3b, these two bands cross along the Γ-Z high-symmetry line.

Fig. 3: Topological properties of SnIP.
figure 3

a Diagnosis process for the single nodal ring around the Z point using symmetry-based indicator theory for the lowest 92 bands. b Phonon band crossings between branches 92 and 93 and c the nodal rings in the bulk Brillouin zone, as well as their projections on the (100) surface.

Full size image

To understand the topological information of the band crossings between branches 92 and 93, we use symmetry-based indicator theories to analyze the degeneracies63,87,88,89,90,91. Because of the existence of a band crossing along the Γ-Z high-symmetry line, the compatibility condition is broken for the lowest 92 bands, as the compatibility relations can only be satisfied when the band structures have no (non-accidental) band crossings along any high-symmetry lines or at any high-symmetry points88. So we cannot use the symmetry-based indicator for space group No. 13. Instead, we need to find a maximal subgroup of SnIP that simultaneously satisfies the compatibility condition and has a nontrivial symmetry-based indicator. Among all the subgroups of space group No. 13 (space groups No. 2, No. 3 and No. 7), No. 2 is the only subgroup, which both satisfies the compatibility condition and has a symmetry-based indicator group: (i) the compatibility condition is satisfied because the twofold rotation symmetry in No. 13 that protects the band crossing along Γ-Z is absent in No. 2; (ii) space group No. 2 has a nontrivial symmetry-based indicator of \({{\mathbb{Z}}}_{2224}\equiv {{\mathbb{Z}}}_{2}\times {{\mathbb{Z}}}_{2}\times {{\mathbb{Z}}}_{2}\times {{\mathbb{Z}}}_{4}\), as discussed in detail in ref. 88. Therefore we can use \({{\mathbb{Z}}}_{2224}\) as indicators to diagnose topological degeneracy. For space group No. 2, there are eight high-symmetry points, i.e. high-symmetry points (qa, qb, qc) with qa,b,c = 0, 0.5. We obtain the irreducible representations (irreps.) at the eight corresponding high-symmetry points Γ (0,0,0), Z (0,0.5,0), B (0,0,0.5), Y (0.5,0,0), C (0.5,0.5,0), D (0,0.5,0.5), A (0.5,0,0.5) and E (0.5,0.5,0.5), as shown in Fig. 3a. We then compute the indicator accordingly. The resulting indicator (0101) implies that there is a single nodal ring around the Z point in SnIP formed by branches 92 and 93, which is verified by the numerical calculations in Fig. 3c.

We next examine in detail the nodal rings formed by bands 92 and 93. We zoom in the phonon dispersion on the Γ-B-D-Z plane in Fig. 3b. The band crossing formed by bands 92 and 93 along the Γ-Z high-symmetry line belongs to the single nodal ring around the Z point, carrying a quantised π Berry phase. The nodal ring crosses through the Brillouin zone boundary around the B-D high-symmetry line, and consequently, there are two nodal rings from two neighbouring Brillouin zones formed around the D point. We also plot the phonon dispersion around N (−0.01, 0.35, 0.51), another band crossing point on the neighbouring nodal ring, as shown in Fig. 3b. Most interestingly, we find that the two neighbouring nodal rings projected on the (100) surface have a large overlap, and the two drumhead-like surface states of the two bulk nodal rings form a doubly degenerate line along \(\bar{{{{\rm{B}}}}}\)-\(\bar{{{{\rm{D}}}}}\) (as discussed below).

Topological surface states of SnIP

We demonstrate the nodal-line surface states by calculating the surface local density of states (LDOS) from the imaginary part of the surface Green’s function92. We first study the surface along the (100) direction with the termination denoted as surface 1 in Fig. 4a–e. As shown in Fig. 4a, along the \(\bar{{{{\rm{D}}}}}\)-\(\bar{{{{\rm{Z}}}}}\) and \(\bar{{{{\rm{Z}}}}}\)-\(\bar{\Gamma }\) high-symmetry lines, two separate projections of the bulk band crossings (marked by navy and cyan arrows) belong to two single nodal rings from two neighbouring Brillouin zones respectively. The surface states are within the projections of the two bulk nodal rings, forming two nondegenerate drumhead-like surface states marked by navy and cyan triangles in Fig. 4a respectively. The surface states from the two crossing points along \(\bar{{{{\rm{D}}}}}\)-\(\bar{{{{\rm{Z}}}}}\) and \(\bar{{{{\rm{Z}}}}}\)-\(\bar{\Gamma }\) merge with each other at \(\bar{{{{\rm{D}}}}}\), and result in a doubly degenerate surface nodal line along \(\bar{{{{\rm{B}}}}}\)-\(\bar{{{{\rm{D}}}}}\) (green triangle). The surface nodal line ends at the crossing point of the two projected nodal rings marked by a green arrow in Fig. 4a.

Fig. 4: Topological surface states of SnIP.
figure 4

a Topological surface states of surface 1 along the (100) direction, as well as the surface arcs for phonon frequencies of b 6.410 THz, c 6.414 THz, d 6.415 THz and e 6.416 THz. f Topological surface states of surface 2 along the (100) direction, as well as the surface arcs for phonon frequencies of g 6.400 THz, h 6.410 THz, i 6.415 THz and j 6.420 THz.

Full size image

To have a better view of the doubly degenerate surface states along the \(\bar{{{{\rm{B}}}}}\)-\(\bar{{{{\rm{D}}}}}\) high-symmetry line, we plot the isofrequency surface arcs for different phonon frequencies in Fig. 4b–e. As shown in Fig. 4b, at the exact frequency of the doubly degenerate projected bulk band crossings (green arrow) along \(\bar{{{{\rm{B}}}}}\)-\(\bar{{{{\rm{D}}}}}\) at 6.410 THz, the two surface arcs (cyan triangle) merge at the projected bulk band crossings. For a phonon frequency of 6.414 THz, the two surface arcs (cyan triangle) move towards each other, forming two arc crossing points (green triangle) along \(\bar{{{{\rm{B}}}}}\)-\(\bar{{{{\rm{D}}}}}\) in Fig. 4c. At 6.415 THz, the two arc crossing points move to the \(\bar{{{{\rm{D}}}}}\) point until they merge into a single arc crossing point [green triangle in Fig. 4d]. Further increasing the phonon frequency eventually leads to two separate surface arcs as the two arcs no longer touch [navy triangle in Fig. 4f]. The arc crossing points on the isofrequency plane belong to the doubly degenerate surface nodal line in the frequency-momentum space [green triangle in Fig. 4a].

The surface nodal line in SnIP is protected by the combination of time-reversal symmetry and glide mirror symmetry \(\vartheta ={{{\mathcal{T}}}}{\bar{M}}_{y}\). For systems with time-reversal symmetry \({{{\mathcal{T}}}}\) and any nonsymmorphic spatial symmetry G, the ‘Kramers-like’ degenerate nodal line appears when \({({{{\mathcal{T}}}}G)}^{2}=-1\), either along the \({{{\mathcal{T}}}}G\) invariant lines or on the \({{{\mathcal{T}}}}G\) invariant planes, and a degenerate line can thus be protected by the \({{{\mathcal{T}}}}G\) symmetry. This applies to line degeneracies in both the bulk states93 and the surface states53,54,55. SnIP has glide mirror symmetry \({\bar{M}}_{y}=\{{M}_{y}\,| \,00\frac{1}{2}\}\), and \({({{{\mathcal{T}}}}{\bar{M}}_{y})}^{2}={{{{\rm{e}}}}}^{{{{\rm{i}}}}2\pi {q}_{z}}\) (qz in units of the reciprocal lattice vector 2π/c). On the (100) surface, both qz = 0 and qz = 0.5 are \({{{\mathcal{T}}}}{\bar{M}}_{y}\) invariant lines, and \({({{{\mathcal{T}}}}{\bar{M}}_{y})}^{2}=-1\) only occurs when qz = 0.5, corresponding to the \(\bar{{{{\rm{B}}}}}\)-\(\bar{{{{\rm{D}}}}}\) high-symmetry line. As a result, the doubly degenerate surface nodal line along \(\bar{{{{\rm{B}}}}}\)-\(\bar{{{{\rm{D}}}}}\) is protected by the \({{{\mathcal{T}}}}{\bar{M}}_{y}\) symmetry.

If we change the surface termination (denoted as surface 2) along the (100) direction, the doubly degenerate surface states along the \(\bar{{{{\rm{B}}}}}\)-\(\bar{{{{\rm{D}}}}}\) high-symmetry line in Fig. 4f no longer exist in the frequency range 6.410–6.415 THz but move to the lower frequency range 6.384–6.410 THz. The distribution of the surface nodal line changes to the other side of \(\bar{{{{\rm{B}}}}}\)-\(\bar{{{{\rm{D}}}}}\), from the purple shaded area in Fig. 5a to that in Fig. 5b.

Fig. 5: Zak phase analysis.
figure 5

Zak phase of a surface 1 and b surface 2 along the (100) direction. The purple and green shaded areas correspond to the total Zak phase γ = 2π and γ = 0, respectively.

Full size image

To explain the alternation between the distributions of the surface nodal line, we need to understand how \({{{\mathcal{T}}}}{\bar{M}}_{y}\) influences the Zak phase on the (100) surface Brillouin zone. The Zak phase provides information on the distribution of the doubly degenerate surface states on the (100) surface, and can be integrated along the (100) direction,

$$\gamma ({q}_{b},{q}_{c})={{{\rm{i}}}}\int\nolimits_{-\pi }^{\pi }\mathop{\sum}\limits_{\nu ={{{\rm{occu}}}}.}\left\langle \psi ({{{\bf{q}}}}\nu )\right|\frac{\partial }{\partial {q}_{a}}\left|\psi ({{{\bf{q}}}}\nu )\right\rangle d{q}_{a},$$
(1)

where ψ(qν) is the phonon eigenvector with wave vector q and band index ν. Note that on the (100) surface Brillouin zone, qb∥qy and qc∥qz, therefore we use (qx,qy,qz) instead of (qa,qb,qc) to be consistent with \({{{\mathcal{T}}}}{\bar{M}}_{y}\). When qz = 0.5, \({({{{\mathcal{T}}}}{\bar{M}}_{y})}^{2}=-1\) and \({\psi }_{1}(-{q}_{x},{q}_{y},0.5)=({{{\mathcal{T}}}}{\bar{M}}_{y})\cdot {\psi }_{2}({q}_{x},{q}_{y},0.5)\). Therefore, we can classify the phonon states at constant qy and qz = 0.5 into two subgroups {ψ1(q)} and {ψ2(q)}, i.e. {ψ1(q)} and {ψ2(q)} are \({{{\mathcal{T}}}}{\bar{M}}_{y}\) related. Therefore, for the \(\bar{{{{\rm{B}}}}}\)-\(\bar{{{{\rm{D}}}}}\) high-symmetry line (qz = 0.5) on the (100) surface Brillouin zone, the Zak phases for the two subgroups {ψ1(q)} and {ψ2(q)} are equal to each other, i.e. γ1(qy, 0.5) = γ2(qy, 0.5). Due to \({{{\mathcal{PT}}}}\), γ1(qy, 0.5) = γ2(qy, 0.5) is either 0 or π, which depends on the surface termination (i.e. choice of the inversion centre). When γ1(qy, 0.5) = γ2(qy, 0.5) = 0, there are no surface states as the total Zak phase γ = γ1 + γ2 = 0. When γ1(qy, 0.5) = γ2(qy, 0.5) = π, the total Zak phase γ = 2π, leading to doubly degenerate surface states. For surface 1, the purple shaded line in Fig. 5a has a total Zak phase of 2π with two surface states distributed in this area, while the green shaded area corresponds to γ = 0 and there are no surface states in this area. For surface 2, the Zak phase of the purple shaded area and the colourless area swap, as shown in Fig. 5b, and the distribution of the surface nodal line switches to the new purple shaded area. It should be noticed that the standard definition of Zak phase is in terms of modulo 2π, and a Zak phase of 2π is therefore equal to zero under this definition. However, in our case, a total Zak phase of 2π corresponds to γ1 = γ2 = π, i.e. two π Zak phase within each subgroup, indicating two surface states emerging from each subgroup. On the other hand, a total Zak phase of zero corresponds to two zero Zak phase within each group, leading to vanishing surface states.

It is worth mentioning that bending SnIP rods does not break the time-reversal and glide mirror symmetries on the (100) surface of SnIP. Therefore, the degenerate topological surface states remain unchanged under bending.

Discussion

In terms of fundamental physics and applications, topological bulk phonons in double-helical SnIP may lead to non-dissipative surface phonons, which offer a promising platform for designing thermal devices. The existence of surface nodal lines also provides opportunities to study surface transport properties for thermoelectric devices. As another example, the bulk and surface nodal lines/rings in the phonon spectra result in large phonon DOS, which may also enhance surface superconductivity. Additionally, because of its quasi-one-dimensional crystal structure, SnIP could also be a promising material platform to investigate one-dimensional physical models such as the Su–Schrieffer–Heeger (SSH) model83 and Majorana quantum wires84,85. With its high mechanical flexibility, it is also interesting to investigate the interplay between flexoelectricity and topology. Our work provides a starting point to explore all these phenomena and applications.

In summary, we find that double-helical SnIP exhibits nodal-ring phonons in the bulk and nodal-line phonons on the surface based on first-principles calculations and group theory analysis. Benefiting from a quasi-one-dimensional crystal structure, the lattice vibrational modes of the intrachain phosphorus atoms along the helices are highly dispersive. Due to the winding of the helix P chain, these phonon bands are folded at the Brillouin zone boundary, forming single nodal rings across the whole Brillouin zone. The overlap between the two neighbouring nodal rings on the (100) surface leads to a surface nodal line that is protected by the combination of time-reversal and glide mirror symmetries \({{{\mathcal{T}}}}{\bar{M}}_{y}\). We also propose that different surface terminations result in different distributions of the surface nodal line, which can be understood by different Zak phases in the presence of \({{{\mathcal{T}}}}{\bar{M}}_{y}\). We demonstrate that, similar to the bulk nodal lines, the surface nodal lines can widely exist when protected by extra symmetries. Our discoveries may offer opportunities to study the degeneracy of the topological surface states and their transport properties.

Methods

Density functional theory calculations

All density functional theory (DFT) calculations are performed using the Vienna ab initio simulation package (vasp)94,95. The generalised gradient approximation (GGA) is used in the Perdew–Burke–Ernzerhof (PBE) parametrization for the exchange-correlation functional with 14 valence electrons (4d105s25p2) for Sn, 7 valence electrons (5s25p5) for I and 5 valence electrons (3s23p3) for P. We use a plane-wave basis with a kinetic energy cutoff of 600 eV and a 7 × 5 × 3 k-mesh for structural relaxation until the energy difference is lower than 10−6 eV and the Hellman–Feynman force difference is lower than 10−4 eV Å−1. The D2 method of Grimme is used to describe the van der Waals interactions between the double helices96.

Lattice dynamics properties

The Hessian matrix and phonon frequencies are calculated based on the finite difference method using a 2 × 2 × 1 supercell with a 3 × 3 × 3 k-mesh. The phonon dispersion is obtained with the phonopy code97,98. The convergence of the supercell is checked by comparing the 2 × 2 × 1 and 1 × 1 × 2 supercells in Supplementary Note 1 of the Supplementary Information. The Born effective charges are also computed using a perturbative approach to account for the splitting between the longitudinal and transverse optical phonon modes (LO-TO splitting) near the Brillouin zone centre99, and we find that the LO-TO splitting has a minor influence on the topological properties of phonons because the topological features are far away from the zone centre.

Topological properties

To obtain the topological properties of the lattice vibrational modes, we use WannierTools to calculate the distribution of the band crossing points/lines in the whole Brillouin zone92. The phonon surface states on the (100) surface are computed using the surface Green’s function.