Introduction

The field of materials science has evolved from empirical paradigm to theoretical, computational, and data-driven science.1 Traditional material design always follows a route from a certain material with specific structure to the final properties, i.e., forward material design, but such a trial-and-error process takes great pains for time and effort to obtain a material with desired properties. With the rapid development of theoretical, computational, and data-driven paradigms recently, the inverse material design, starting from a specific function to the corresponding structure, opens up new avenues for accelerated materials discovery and application. Compared with natural materials, metamaterials constructed by artificial meta-atoms have much higher designability to facilitate an inverse design approach, so that the unavailable properties by traditional approach can be well achieved.

The emergence of metamaterials breaks the natural materials’ constraint and brings an unprecedented opportunity to fully control the electromagnetic waves (EMWs) from microwave to optical frequencies, including polarization, phase, and amplitude.2,3,4,5 Polarization, a basic characteristic of EMW, conveys valuable information and serves as a cornerstone in many optical phenomena. Manipulating the polarization of EMWs is vital to numerous applications from signal communication, spectroscopy to microscopy. However, traditional components suffer from bulky size and limited material resources. Chiral metamaterials are an important subset of metamaterials and have an additional mirror symmetry breaking in the propagation direction or two-dimensional plane. They can arbitrarily modulate the polarization of EMWs at sub-wavelength scales due to the strong chiral response from the handedness-selective EM resonance in the structures, demonstrating many intriguing phenomena and applications, such as negative refractive index,6,7 circular dichroism,8,9,10 asymmetric transmission,11,12,13,14,15 polarization rotation and conversion,16,17,18,19,20,21 chiral-selective absorber,22,23 and so forth. Recently, multifunctional metamaterials are highly desired to meet the increasing demand for miniaturization and complex application scenarios. Some researchers design anisotropic or active metamaterials to achieve the functionality integration by changing the helicity,24,25,26,27 polarization,28,29,30 propagation direction of incident waves,31 and external stimulation.32,33,34 All these studies aim at reshaping wavefronts, but more important and fundamental manipulation of polarization, such as basic functionalities of linear polarization rotation, linear-to-circular (or vice versa) polarization conversion, are rarely involved.

Most chiral metamaterials for polarization control are designed with a specified function. Typically, bilayer chiral metamaterials, consisting of two-layer closely stacked and mutually twisted resonators, are investigated for polarization rotation with sub-wavelength thicknesses;16 multilayer gratings17 and gold helix structures18 are proposed for broadband linear-to-circular and circular polarization conversion. Previous tunable or reconfigurable multifunctional chiral metamaterials35,36,37,38,39 usually need additional control systems, resulting in the difficulties in fabrication, reliability, and signal repeatability. Although the integration of circular asymmetric transmission with wavefront manipulation can make chiral metamaterials more versatile, the involved polarization control only relates to the circular polarization conversion.14,40 Recently, Yang et al. design a direction-controlled bifunctional metasurface polarizer, but it suffers from a low transmission and narrow bandwidth due to the strong coupling.41 Despite of the high importance in applications, it remains elusive to achieve a passive metamaterial for multifunctional polarization control with a high efficiency and broad bandwidth.

Aiming at such difficulty in multifunctional metamaterials, we utilize the inverse design method of model-based theoretical paradigm, which not only facilitates to discover metamaterials with desired functional characteristics but also endows people with clear physical understanding. Based on the scattering matrix, we obtain the restrictive conditions for specified polarization control and propose two multifunctional metamaterials with simple cascade configurations as examples. One exhibits linear-to-circular polarization conversion (meta-quarter-wave plate, m-QWP) and 45° polarization rotation (polarization rotator) for the forward and backward propagating linearly polarized (LP) waves, respectively, as illustrated in Fig. 1; while the other converts the forward and backward propagating LP waves into a circularly polarized (CP) wave with different handedness (an abnormal m-QWP). Theoretical calculation, numerical simulation, and experimental results all demonstrated that the chiral metamaterials both have an excellent waveform output and an ultrahigh transmission within a broad bandwidth. The obtained multifunction and excellent properties will greatly enrich the device design and be highly desired by the practical applications.

Fig. 1
figure 1

Schematic of a high-performance bifunctional chiral metamaterial which behaves as an m-QWP to convert the forward propagating LP wave into CP wave; while it acts as a 45° polarization rotator for the backward propagating LP wave

Full size image

Results

Theoretical analysis

In order to understand the mechanism of polarization control, we used the scattering matrix S to describe the scattering properties of metamaterials where only the zero-order Bloch mode exists. Because of the involved polarization rotation, it is convenient to use an equivalent four-port (two-port with x, y-polarization) network in the circuit theory to tackle this situation. Especially, when the media at the both sides of a metamaterial are same, S-parameters are equivalent to transmission and reflection coefficients. The scattering matrix S relates to the outgoing (\(\overleftarrow {E_x^o}\), \(\overleftarrow {E_y^o}\), \(\overrightarrow {E_x^o}\) and \(\overrightarrow {E_y^o}\)) and incoming electric fields (\(\overrightarrow {E_x^i}\), \(\overrightarrow {E_y^i}\), \(\overleftarrow {E_x^i}\) and \(\overleftarrow {E_y^i}\)), and can be written as

$$\left( \begin{array}{l}\overleftarrow {E_x^o} \\ \overleftarrow {E_{y}^{o}} \\ \overrightarrow {E_x^o} \\ \overrightarrow {E_y^o} \end{array} \right) = \left( {\begin{array}{*{20}{c}} {\overrightarrow {r_{xx}} } & {\overrightarrow {r_{xy}} } & {\overleftarrow {t_{xx}} } & {\overleftarrow {t_{xy}} } \\ {\overrightarrow {r_{yx}} } & {\overrightarrow {r_{yy}} } & {\overleftarrow {t_{yx}} } & {\overleftarrow {t_{yy}} } \\ {\overrightarrow {t_{xx}} } & {\overrightarrow {t_{xy}} } & {\overleftarrow {r_{xx}} } & {\overleftarrow {r_{xy}} } \\ {\overrightarrow {t_{yx}} } & {\overrightarrow {t_{yy}} } & {\overleftarrow {r_{yx}} } & {\overleftarrow {r_{yy}} } \end{array}} \right)\left( \begin{array}{l}\overrightarrow {E_x^i} \\ \overrightarrow {E_y^i} \\ \overleftarrow {E_x^i} \\ \overleftarrow {E_y^i} \end{array} \right) = {\boldsymbol{S}}\left( \begin{array}{l}\overrightarrow {E_x^i} \\ \overrightarrow {E_y^i} \\ \overleftarrow {E_x^i} \\ \overleftarrow {E_y^i} \end{array} \right),$$
(1)

where the symbols → and ← represent the forward and backward propagations, respectively, the elements rij and tij are the reflection and transmission coefficients of the i-polarization for a j-polarized incident wave (i, j = x, y). If the metamaterial is lossless, the real part of a complex power flow equals zero, leading to a unitary scattering matrix S which satisfies the following relation

$${\boldsymbol{S}}^\dagger {\boldsymbol{S}} = {\boldsymbol{I}},$$
(2)

where S† denotes the conjugate transpose, I is the identity matrix. For an ideal unreflective metamaterial, the S matrix can be expressed as

$${\boldsymbol{S}} = \left( {\begin{array}{*{20}{c}} 0 & 0 & {\overleftarrow {t_{xx}} } & {\overleftarrow {t_{xy}} } \\ 0 & 0 & {\overleftarrow {t_{yx}} } & {\overleftarrow {t_{yy}} } \\ {\overrightarrow {t_{xx}} } & {\overrightarrow {t_{xy}} } & 0 & 0 \\ {\overrightarrow {t_{yx}} } & {\overrightarrow {t_{yy}} } & 0 & 0 \end{array}} \right).$$
(3)

In the absence of Faraday media, the reciprocity theorem is applied, where S-parameters equal to their transposes Smn = Snm (m, n = 1, 2, 3, 4). By inserting Eq. (3) into Eq. (2), we can get the restrictive conditions for the forward propagating transmission matrix

$${\boldsymbol{T}}^f = \left( {\begin{array}{*{20}{c}} {\overrightarrow {t_{xx}} } & {\overrightarrow {t_{xy}} } \\ {\overrightarrow {t_{yx}} } & {\overrightarrow {t_{yy}} } \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{\mathrm{sin}}\phi e^{i\xi _{xx}}} & {{\mathrm{cos}}\phi e^{i\xi _{xy}}} \\ {{\mathrm{cos}}\phi e^{i\xi _{yx}}} & {{\mathrm{sin}}\phi e^{i\xi _{yy}}} \end{array}} \right),$$
(4)

where sinϕ and cosϕ \(\left( {0^\circ \le \phi \le 90^\circ } \right)\) are the transmission amplitudes; \(\xi _{xx}\), \(\xi _{yx}\), \(\xi _{xy}\), and \(\xi _{yy}\) are transmission phases of four components. Especially when \(0^\circ < \phi < 90^\circ\),\(\xi = \xi _{yy} + \xi _{xx} - \xi _{yx} - \xi _{xy} = (2n + 1)\pi\), where n = 0, ±1, ±2… is an integer. Let us consider an ideal unreflective and lossless m-QWP which converts the forward propagating x-polarized wave into LCP wave, the T matrix can be written as

$${\boldsymbol{T}}^f = \left( {\begin{array}{*{20}{c}} {\frac{1}{{\sqrt 2 }}} & {\overrightarrow {t_{xy}} } \\ { - \frac{i}{{\sqrt 2 }}} & {\overrightarrow {t_{yy}} } \end{array}} \right).$$
(5)

Comparing Eq. (5) with Eq. (4), we can get

$${\boldsymbol{T}}^f = \frac{1}{{\sqrt 2 }}\left( {\begin{array}{*{20}{c}} 1 & {e^{i\theta }} \\ { - i} & {e^{i(\theta + \pi /2)}} \end{array}} \right).$$
(6)

Obviously, structures with such T matrix (Eq. (6)) can convert the forward propagating x- or y-polarized wave into LCP or RCP wave, regardless of the value of θ (an arbitrary real number). However, the choice of variable θ will significantly affects the transmission performance for the backward propagating LP waves. Due to the absence of Faraday media, the Tb matrix for the backward propagating wave is obtained by simply interchanging the off-diagonal elements in the forward Tf matrix and written as

$${\boldsymbol{T}}^b = \frac{1}{{\sqrt 2 }}\left( {\begin{array}{*{20}{c}} 1 & { - i} \\ {e^{i\theta }} & {e^{i(\theta + \pi /2)}} \end{array}} \right).$$
(7)

It is noted that the relationship between Tf and Tb is only valid for a particular base where the Cartesian coordinate system is kept unchanged. From Eq. (7), the proper selection of θ can realize linear-to-circular polarization conversion or linear polarization rotation for the backward propagating LP waves. In the following section, we first choose several typical values of θ to explore abundant functionalities of polarization control. Then, we demonstrate how to construct these structures with peculiar T matrices.

For example, when the variable \(\theta = - \pi /2\), the forward and backward propagating matrices are expressed as

$${\boldsymbol{T}}_{\theta = - \pi /2}^f = {\boldsymbol{T}}_{\theta = - \pi /2}^b = \frac{1}{{\sqrt 2 }}\left( {\begin{array}{*{20}{c}} 1 & { - i} \\ { - i} & 1 \end{array}} \right).$$
(8)

Equation (8) indicates that this kind of structure behaves as a traditional m-QWP of converting x- or y-polarized wave into LCP or RCP waves, regardless of propagation directions. Meanwhile, the characteristic of Eq. (8) implies the elements are not independent but connected by trigonometric functions, a rotation by an angle φ = 45° leads to a diagonal form

$${\boldsymbol{T}}_{new}^f = {\boldsymbol{D}}_\varphi {\boldsymbol{T}}_{\theta = - \pi /2}^f{\boldsymbol{D}}_\varphi ^{ - 1} = \frac{1}{{\sqrt 2 }}\left( {\begin{array}{*{20}{c}} {1 + i} & 0 \\ 0 & {1 - i} \end{array}} \right),$$
(9)

where \({\boldsymbol{D}}_\varphi = \left( {\begin{array}{*{20}{c}} {\mathrm{cos}}\varphi & {\mathrm{-sin}}\varphi \\ {\mathrm{sin}}\varphi & {\mathrm{cos}}\varphi \end{array}} \right)\) is the rotation matrix. Hence, this structure can be regarded as an m-QWP with its slow axis at 45° with respect to both the x and y axes.

For θ = 0, the forward and backward propagating matrices become

$${\boldsymbol{T}}_{\theta = 0}^f = \frac{1}{{\sqrt 2 }}\left( {\begin{array}{*{20}{c}} 1 & 1 \\ { - i} & i \end{array}} \right),$$
(10)
$${\boldsymbol{T}}_{\theta = 0}^b = \frac{1}{{\sqrt 2 }}\left( {\begin{array}{*{20}{c}} 1 & { - i} \\ 1 & i \end{array}} \right).$$
(11)

From Eqs. (10) and (11), we conclude that this kind of structure has two different functions. For the forward LP waves, this structure behaves as an m-QWP to realize linear-to-circular polarization conversion; while it acts as a 45° polarization rotator for the backward propagating LP waves. To construct this bifunctional structure, we decompose the Eq. (10) into two matrices

$${\boldsymbol{T}}_{\theta = 0}^f = \frac{1}{{\sqrt 2 }}\left( {\begin{array}{*{20}{c}} 1 & { - i} \\ { - i} & 1 \end{array}} \right)\left( {\begin{array}{*{20}{c}} 1 & 0 \\ 0 & i \end{array}} \right).$$
(12)

According to the transfer matrix method, an LP wave passes through two structures (1 and 2) successively, the overall Tt matrix can be written as

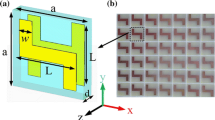
$${\boldsymbol{T}}_t = {\boldsymbol{T}}_2 \cdot {\boldsymbol{P}} \cdot {\boldsymbol{T}}_1,$$
(13)

where \({\boldsymbol{P}} = diag(e^{ - ink_0d},e^{ - ink_0d})\) is a phase delay term caused by the EMW’s propagation in homogenous medium (refractive index n, thickness d, and vacuum wave number k0) between two structures. For convenience, we neglect the phase delay term here which has no influence on the polarization control. Hence, this kind of bifunctional structure can be regarded as a cascading of two m-QWPs with a twist angle of 45°, where the slow axis of the front m-QWP is along with x axis, as shown in Fig. 1.

For \(\theta = \pi /2\), we can get the forward and backward propagating matrices

$${\boldsymbol{T}}_{\theta = \pi /2}^f = \frac{1}{{\sqrt 2 }}\left( {\begin{array}{*{20}{c}} 1 & i \\ { - i} & { - 1} \end{array}} \right),$$
(14)
$${\boldsymbol{T}}_{\theta = \pi /2}^b = \frac{1}{{\sqrt 2 }}\left( {\begin{array}{*{20}{c}} 1 & { - i} \\ i & { - 1} \end{array}} \right).$$
(15)

The Eqs. (14) and (15) indicate structures having such properties can convert the forward x-polarized or y-polarized wave into LCP or RCP wave; while it realizes an inverse function of converting the backward x-polarized or y-polarized wave into RCP or LCP wave. Similarly, we decompose the Eq. (14) into two matrices

$${\boldsymbol{T}}_{\theta = \pi /2}^f = \frac{1}{{\sqrt 2 }}\left( {\begin{array}{*{20}{c}} 1 & { - i} \\ { - i} & 1 \end{array}} \right)\left( {\begin{array}{*{20}{c}} 1 & 0 \\ 0 & { - 1} \end{array}} \right).$$
(16)

According to Eq. (16), this abnormal m-QWP can be obtained by cascading a meta-half-wave plate (m-HWP) and an m-QWP with a twist angle of 45°, where the slow axis of the front m-HWP is along with x axis. Besides, the m-HWP can also be decomposed by a cascaded m-QWP pair with a twist angle of 0° or 180°. Therefore, this abnormal m-QWP is entirely made up of the traditional m-QWPs.

It’s noted that the construction of bifunctional chiral metamaterial or abnormal m-QWP by cascading the traditional m-QWPs can be also guided and optimized by tensor sheet admittances (see Supplementary Information, Section I).19,20 Furthermore, if loss and reflection are taken into consideration in scattering matrices, the reciprocity is kept while the unitary property is broken, so that the components of transmission matrix (Eq. (4)) can be tuned independently, complicating the theoretical analysis. In the following section, we first design a high-performance m-QWP with a high transmission in broadband, and then combine m-QWPs with a twist angle to realize the diverse polarization control.

Meta-quarter-wave plate (θ = −π/2)

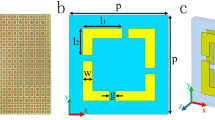
To construct high-performance multifunctional chiral metamaterials, we design an m-QWP to convert the LP wave into CP wave with a high transmission in a broad bandwidth. Single-layer metasurface can be served as an m-QWP, but the large dispersion limits its operation bandwidth due to the isolated electric response. An alternative way is using multilayer structure, where the formation of Fabry-Perot-like (F-P-like) interference between adjacent metasurfaces facilitates to achieve broadband and non-dispersive polarization manipulation with high transmission. Figure 2a depicts the optimized unit cell structure, composed of two metallic split ring resonators (SRRs) on both sides of an F4B board. We study the transmission properties of the two-layer metamaterial (TLM, structure 1) by using the commercial software CST Microwave Studio. Figure 2b shows the simulated results for the normal incidence of LP waves. Because the TLM is mirror-symmetric with respect to the xz plane, the cross-polarization transmission coefficients are equal to zero. The amplitudes of co-polarization are greater than 0.8 and the phase difference of \(\angle t_{yy} - \angle t_{xx}\) is about 90° ± 10° (Fig. 2c) in the off-resonance frequency range of 10.5–12.5 GHz (brown region).36 To quantitatively evaluate the performance of TLM as an m-QWP, we introduce Stokes parameters as

$$\begin{array}{l}S_0 = \left| {t_x} \right|^2 + \left| {t_y} \right|^2\\ S_1 = \left| {t_x} \right|^2 - \left| {t_y} \right|^2\\ S_2 = 2\left| {t_x} \right|\left| {t_y} \right|\cos \Delta \varphi \\ S_3 = 2\left| {t_x} \right|\left| {t_y} \right|\sin \Delta \varphi ,\end{array}$$
(17)

where \(\left| {t_x} \right|\) and \(\left| {t_y} \right|\) are the amplitude of transmitted electric fields along x and y directions, and \(\Delta \varphi {\mathrm{ = }}\angle t_y - \angle t_x\) is the transmission phase difference. The ellipticity angle χ is defined as

$$\chi = \frac{1}{2}{\mathrm{arcsin}}(S_3/S_0).$$
(18)
Fig. 2
figure 2

TLM as an m-QWP. a Schematic and geometric dimensions of the unit cell: p = 7.0 mm, D = 3.5 mm, r = 1.75 mm, R = 3.0 mm, and g = 0.75 mm. b Simulated transmission spectra and c phase difference for x- and y- polarized incident waves. d Calculated ellipticity angle χ

Full size image

When the ellipticity angle \(\chi = \pm 45^\circ\) or 0°, the transmitted waves are perfect RCP, LCP or LP waves, respectively. According to the simulated data, we obtain the ellipticity angle of \(\chi \ge 40^\circ\) (Fig. 2d) in the frequency range of 10.5–12.5 GHz, i.e. a nearly perfect RCP wave output with high transmission efficiencies in broadband for an LP incident wave at 45° with respect to the x and y axes.

Bifunctional chiral metamaterial (θ = 0)

Next, we combine two TLMs (structure 1 and 2, Eq. (12)) together which are oriented at a twist angle of 45° to each other and separated by an identical dielectric broad, resulting in a four-layer chiral metamaterial (FLCM), as shown in Fig. 3. Considering the coupling of two TLMs, we slightly adjust the periodicity of FLCM to p = 7.25 mm and keep other geometric parameters fixed. Numerical simulations and experiments are both carried out to study the electromagnetic properties of FLCM.

Fig. 3
figure 3

Top and bottom views of FLCM as a bifunctional polarization controller. The inset shows the scheme of the unit cell

Full size image

Figure 4a shows the simulated transmission results for the forward propagating LP waves. For the incident wave polarized in the x direction, the amplitudes of co-polarization transmission \(\left| {\overrightarrow {t_{xx}} } \right|\) and cross-polarization transmission \(\left| {\overrightarrow {t_{yx}} } \right|\) are closed to 0.7 in the off-resonance frequency range of 10.3–12.2 GHz (brown region), indicating a high transmission efficiency where the total transmission defined as \(\overrightarrow {T_x} = \left| {\overrightarrow {t_{yx}} } \right|^2 + \left| {\overrightarrow {t_{xx}} } \right|^2\) is greater 0.85, as shown in Fig. 4a1. Besides, the transmission phase difference of \(\Delta \overrightarrow {\varphi _x} {\mathrm{ = }}\angle \overrightarrow {t_{yx}} - \angle \overrightarrow {t_{xx}}\) is about −90° ± 10° in the off-resonance region (Fig. 4a2, a5). Based on Eqs. (17) and (18), we calculate the ellipticity angle as shown in Fig. 4a6, where a nearly perfect LCP wave \(\left( {\chi \le - 40^\circ } \right)\) with a high transmission is outputted in the frequency of 10.3–12.2 GHz. Similarly, the co-polarization transmission \(\left| {\overrightarrow {t_{yy}} } \right|\) and the cross-polarization transmission \(\left| {\overrightarrow {t_{xy}} } \right|\) are around 0.7 (Fig. 4a3), while the transmission phase difference of \(\Delta \varphi _y{\mathrm{ = }}\angle \overrightarrow {t_{yy}} - \angle \overrightarrow {t_{xy}}\) is about 90° ± 10° (Fig. 4a4, a5) for a normally incident y-polarized wave in the off-resonance frequency range of 10.0–12.5 GHz (brown region). The total transmission of \(\overrightarrow {T_y} = \left| {\overrightarrow {t_{xy}} } \right|^2 + \left| {\overrightarrow {t_{yy}} } \right|^2\) is greater than 0.71 and reaches a maximum of 0.97 at 11.5 GHz. Figure 4a6 shows the calculated ellipticity angle χ which is greater than 40° in the off-resonance region, indicating a high transmission for the nearly perfect RCP wave output. Figure 4b is the experimental results for the forward propagating LP waves, which agree with the simulated results well (Fig. 4a).

Fig. 4
figure 4

a Simulated and b measured results of the FLCM for the forward propagating x- and y-polarized waves. (a1, a3, b1 and b3) Transmission spectra, (a2, a4, b2 and b4) transmission phases, (a5 and b5) transmission phase differences, and (a6 and b6) calculated ellipticity angles χ of the transmitted waves

Full size image

According to the reciprocity theorem, the transmission coefficients of cross-polarization interchange when the propagation direction is reversed; however, the transmission coefficients of co-polarization keep unchanged. Hence, we can get the transmission phase difference for x- and y-polarized incident waves in the backward direction

$$\Delta \overleftarrow {\varphi _x} = \angle \overleftarrow {t_{yx}} - \angle \overleftarrow {t_{xx}} = \angle \overrightarrow {t_{xy}} - \angle \overrightarrow {t_{xx}} ,$$
(19)
$$\Delta \overleftarrow {\varphi _y} = \angle \overleftarrow {t_{yy}} - \angle \overleftarrow {t_{xy}} = \angle \overrightarrow {t_{yy}} - \angle \overrightarrow {t_{yx}} .$$
(20)

From Fig. 4a1–a4, the amplitudes of four components are almost equal to each other and the phase difference between \(\overrightarrow {t_{xx}}\) and \(\overrightarrow {t_{xy}}\) \(\left( {\overrightarrow {t_{yx}} ,\overrightarrow {t_{yy}} } \right)\) is closed to 0° (−90°, +90°) in the off-resonance frequency range, corresponding to the forward propagating matrix of Eq. (10) and indicating a 45° polarization rotation for x- and y-polarized incident waves in the backward direction. For the backward propagating x- and y-polarized waves, the total transmissions (\(\overleftarrow {T_x} = \left| {\overrightarrow {t_{xx}} } \right|^2 + \left| {\overrightarrow {t_{yx}} } \right|^2\) and \(\overleftarrow {T_y} = \left| {\overrightarrow {t_{xy}} } \right|^2 + \left| {\overrightarrow {t_{yy}} } \right|^2\)) are greater than 0.6 and 0.4 in the off-resonance frequency of 9.5–12.5 GHz, respectively, as shown in Fig. 5a1. Furthermore, the total transmissions can be abruptly improved by decreasing the off-resonance bandwidth. The transmission phase differences of \(\Delta \overleftarrow {\varphi _x}\) and \(\Delta \overleftarrow {\varphi _y}\) calculated by Eqs. (19) and (20) tend to be 0° and −180° in the off-resonance frequency region (Fig. 5a2). To evaluate the optical activity of our proposed structure, the polarization azimuth rotation angle η is defined as

$$\eta = \frac{1}{2}{\mathrm{arctan}}(S_2/S_1),$$
(21)

where S1 and S2 are taken from Stokes parameters. The polarization azimuth rotation angle η ranges from −90° to +90°. Figure 5a3 demonstrates the polarization azimuth rotation angle η closed to +45° or −45° for x- or y-polarized incident wave in the range of 9.5–12.5 GHz, respectively. Meanwhile, the ellipticity angle for x- and y-polarized incident waves are greater than −6.3° and lower than 8.3° (Fig. 5a4), respectively, indicating a nearly linear polarization. Therefore, our proposed FLCM can realize a near 45° polarization rotation with high transmission in broad bandwidth when the LP waves propagate backward. The experimental results shown in Fig. 5b are consistent with the simulated ones very well.

Fig. 5
figure 5

a Simulated and b measured results of the FLCM for the backward propagating x- and y-polarized waves. (a1 and b1) Transmission spectra, (a2 and b2) transmission phase differences, (a3 and b3) polarization azimuth rotation angles η, and (a4 and b4) calculated ellipticity angles χ of the transmitted waves

Full size image

The proposed FLCM not only has bifunctionality but also exhibits excellent properties of high transmission and broadband, which benefits from the formation of F-P-like interference (see Supplementary Information, Section II). Conventional method for tracking the F-P-like scattering processes is very complex due to the four layer interfaces, so we adopt a more convenient method of 4 × 4 transfer matrix in this case,42 where each layer of metasurfaces is treated as a zero-thickness impedance surface with the modified transmission and reflection coefficients acquired from numerical simulations. As shown in Fig. S1c, d, the calculated results of co- and cross-polarization transmission coefficients for x- and y-polarized incident waves coincide with simulated results (Fig. 4a1, a3) very well.

Abnormal meta-quarter-wave plate (θ = π/2)

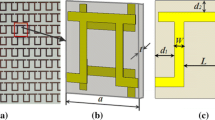
To better demonstrate the flexibility of design strategy, we cascade three m-QWPs to construct an abnormal m-QWP (Eq. (16)), as shown in Fig. 6a. The top two m-QWPs form an m-HWP and the back m-QWP is oriented at 45° with respect to the x axis, leading to a mirror symmetry breaking in the propagation direction. To balance the relationship between transmission amplitude and phase, we slightly increase the separation distance between two adjacent metasurfaces by 4.0 mm and keep other geometric parameters fixed. Figure 6b, c shows the simulated and experimental transmission results for the forward and backward propagating LP waves. Just as the theoretical analysis, the composite structure can convert the x- or y-polarized incident wave into LCP or RCP waves with high transmission efficiencies in broadband for the forward propagation direction; while it reverses its polarization conversion function for the backward propagation, i.e., convert x- or y-polarized incident wave into RCP or LCP waves, respectively.

Fig. 6
figure 6

Multilayer chiral metamaterial as an abnormal m-QWP. a Schematic of the unit cell. b Simulated and c measured results of transmission spectra (upper panels) and ellipticity angles (lower panels)

Full size image

Discussion

In summary, utilizing the inverse design method based on the scattering matrix, we demonstrate two multifunctional chiral metamaterials with different polarization controls for oppositely propagating directions, theoretically and experimentally. The FLCM composed of two m-QWPs with a twist angle of 45° is experimentally demonstrated to generate a nearly perfect LCP or RCP wave with a high transmission in a broad bandwidth, when the x- or y-polarized incident wave propagates forward. On the contrary, the FLCM works as a near 45° polarization rotation for the backward LP waves. We also verify that the high transmission at the off-resonance frequencies results from the F-P-like interference effect by the transfer matrix method. Furthermore, by employing such m-QWP, we design a high-performance bifunctional m-QWP that converts the forward (backward) propagating x- or y-polarized wave into the LCP (RCP) or RCP (LCP) wave. The proposed chiral metamaterials show many merits, such as high transmission, broad bandwidth, and bifunctionality, and may find potential applications in polarization-controlled devices. Moreover, the design strategy can be extended to terahertz and optical frequencies, enabling extensive applications.

Methods

Simulation

Numerical simulations are calculated by using the commercial software CST Microwave Studio. Due to the periodic structure, a single unit cell is simulated with periodic boundary conditions and wave ports in x, y and z directions, respectively. The dielectric constant of F4B material is 2.1 with a loss tangent of 0.003. The copper film is simulated with a thickness of 0.035 mm and a default conductivity of 5.99 × 107 S/m.

Fabrication and measurement

All the chiral metamaterial specimens are consisted of 30 × 30 unit cells and fabricated using the standard printed circuit board technology. The transmission measurements are carried out by a vector network analyzer (Agilent N5230) with two LP lens horn antennas in an anechoic chamber. The polarization state of the incidence can be adjusted by rotating the emitter with an angle of 0° or 90° to obtain either x- or y-polarized EM wave, and the receiver can be reconfigurable to co-polarization or cross-polarization states by rotating with an angle of 0° or 90° with respect to the emitting antenna, so that four components of the LP waves are all measured.