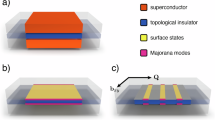
Abstract
We present a new scheme for Majorana modes in systems with nonsymmorphic-symmetry-protected band degeneracy. We reveal that when the gapless fermionic excitations are encoded with conventional superconductivity and magnetism, which can be intrinsic or induced by proximity effect, topological superconductivity and Majorana modes can be obtained. We illustrate this outcome in a system which respects the space group P4/nmm and features a fourfold-degenerate fermionic mode at (π, π) in the Brillouin zone. We show that in the presence of conventional superconductivity, different types of topological superconductivity, i.e., first-order and second-order topological superconductivity, with coexisting fragile Wannier obstruction in the latter case, can be generated in accordance with the different types of magnetic orders; Majorana modes are shown to exist on the boundary, at the corner and in the vortices. To further demonstrate the effectiveness of our approach, another example related to the space group P4/ncc based on this scheme is also provided. Our study offers insights into constructing topological superconductors based on bulk energy bands and conventional superconductivity and helps to find new material candidates and design new platforms for realizing Majorana modes.
Similar content being viewed by others
Introduction
Topological superconductors1,2,3,4,5 (TSCs) are renowned for hosting a special kind of quasiparticles, the Majorana modes, whose antiparticles are themselves. Owing to their potential application in fault-tolerant quantum computation4,6,7, a substantial effort has been made to search for the Majorana modes, and great advances have been achieved both in theory5,8,9,10,11,12,13,14,15,16,17,18 and in experiment19,20,21,22,23,24,25,26,27,28 over the past few decades. The p-wave superconductors have been suggested as promising candidates for the TSCs, and experimental signatures of p-wave superconductivity have been detected29,30,31. Various artificial devices have been proposed to support topological superconductivity, such as the heterostructure between a conventional superconductor and a topological insulator8 or the Rashba electron gas10,11, and experimental evidence for the Majorana modes have been observed21,27. Despite the progress, an efficient way towards platforms realizing the numerous exotic topological superconducting phases15,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48, especially the high-order topological superconducting states, is still elusive.
In recent years, remarkable strides have been made in understanding the topological states of matter. It is realized that the topological property of a system can be indicated by the symmetry information of its occupied bands at high-symmetry points, and the system must be topologically nontrivial if its symmetry information at these points differs from that of an atomic insulator49,50,51. A parallel formalism has also been developed for the TSCs52,53,54. Motivated by these achievements, we suggest a new scheme to realize TSCs, built on the heterostructure sketched in Fig. 1, based on symmetry-protected band degeneracies near the fermi energy and conventional superconductivity. Such fermionic modes, i.e., the band degeneracies, always carry different quantum numbers, such as rotation eigenvalues, mirror eigenvalues, etc. To make the core of our proposal clearer, let us start with the time-reversal symmetric BdG Hamiltonian with conventional superconductivity, i.e., the uniform s-wave pairing. In such a system, the chiral symmetry, which is the combined operation of the time-reversal symmetry and the particle-hole symmetry, maps a negative-energy state to a positive-energy state. Moreover, the unitary chiral symmetry commutes with the crystalline symmetries3,33,42, leading to that the two states related by the chiral symmetry carry the same quantum numbers. This property implies that in the system, the information of the symmetry eigenvalues corresponding to all the negative-energy states at the high-symmetry point in the Brillouin zone is always the same as the condition where the normal-state electronic states are fully occupied or fully unoccupied, which must be topologically trivial52. Notice that the above conclusion is always true, regardless of the location of the Fermi energy. Therefore, in the sense of the symmetry indicator, any time-reversal symmetric superconductor with uniform s-wave pairing is topologically trivial52,53,54. However, if the time-reversal symmetry is broken, such as by the magnetic orders, the above symmetry constraint fails. Moreover, as long as the eigenvalues of the crystalline symmetries carried by the negative-energy states are different from that in the time-reversal symmetric case, some nontrivial topology is indicated in the superconductor, and such a condition is most likely to occur when there is band degeneracy near the Fermi energy. More specifically, when the band degeneracy is encoded with magnetism, it will split; If the chemical potential resides within the split band gap, in the superconducting state, the symmetry eigenvalues carried by the positive-energy states will no longer match those of the negative-energy states, indicating the presence of nontrivial topology (more details in Supplementary Note 1). We illustrate this scheme in a system respecting the space group P4/nmm and show various topological superconducting states can be achieved in accordance with the different magnetic orders. To further show the effectiveness of our approach, we provide another example related to the space group P4/ncc in Supplementary Note 10. Compared with earlier proposals4,10,11,55, the key advantage here is that by leveraging the nonsymmorphic crystalline symmetries, the resulting phases of topological superconductivity are much richer. In recent years, the distinct irreducible representations (IRs) of the little group of the crystalline symmetries can assist in identifying different types of free fermionic excitations, such as the unconventional quasiparticles beyond Dirac and Weyl fermions56. Based on those abundant fermionic excitations, our method can be applied to a wide range of systems, and opens up a new direction of searching for novel topological superconducting phases in these materials.
It is based on systems with gapless fermionic excitations (the intermediate layer) protected by nonsymmorphic crystal symmetries. In the system, the magnetism (top) and the conventional superconductivity (bottom) can be induced through either the proximity effect or the intrinsic properties of the intermediate layer. The colored balls, black arrows and colored cones represent the different lattice sites, the magnetic moments and energy dispersion, respectively.
In the following, we focus on the space group P4/nmm, which has a four-dimensional irreducible projective representation at the Brillouin zone corner. We show that the antiferromagnetic (AFM) order and ferromagnetic (FM) order can both split the fourfold degeneracy into two twofold ones. In the presence of conventional superconductivity, the AFM order drives the system into a second-order TSC state coexisting with fragile Wannier obstruction, while the FM order results in a first-order TSC, as long as the chemical potential lies in the magnetic gap. These results may be relevant to iron-based superconductors and heterostructures thereof, which host intrinsic AFM order and high-Tc superconductivity.
Results
Fourfold degenerate fermion with SG 129
We begin with an introduction of the space group \({{\mathcal{G}}}=P4/nmm\) (#. 129), i.e., the symmetry group governing the iron-based superconductors. We focus on the quasi-two-dimensional (2D) case and consider the lattice in Fig. 2a, which is similar to the monolayer FeSe. The space group P4/nmm is nonsymmorphic, and it has a special group structure as follows57
where T is the translation group, D2d is the point group at the lattice sites, and Z2 is a two-element group, including the inversion symmetry, which switches the two sublattices in the lattice in Fig. 2a. As D2d and Z2 are defined on different points, Eq. (1) holds in a sense that symmetry operations are equivalent if they differ by a lattice translation, hence the quotient group on the left-hand side. According to Eq. (1), \({{\mathcal{G}}}/T\) can be generated by the generators of D2d and Z2, including the inversion symmetry {I∣τ0}, the mirror symmetry {My∣0} and the rotoinversion symmetry {S4z∣0}. Here, we express the symmetry operations in the form of the Seitz operators. In the generators, the point group parts act on the Cartesian coordinates as I : (x, y, z) ↦ (−x, −y, −z), My : (x, y, z) ↦ (x, −y, z), and S4z : (x, y, z) ↦ (y, −x, −z), and τ0 = a1/2 + a2/2 with a1 (a2) the primitive lattice translation along the x (y) direction in Fig. 2a.
a shows a quasi-2D lattice respecting group P4/nmm. The green and red balls label the two sublattices. The orange and brown dashed lines indicate the different edges considered in the text. The black dashed arrows represent a bending process from the (10) edge to the [11] and \([1\overline{1}]\) edges. b presents the bands obtained from Eq. (4), with G, X, M representing (0, 0), (π, 0), (π, π) in the Brillouin zone, respectively, with the other parameters set to be \(\{t,\, {t}^{{\prime} },\, \lambda \}=\{-1.0,0.8,0.5\}\). The blue dashed line in (b) represents the chemical potential considered in the text.
For electronic systems in the presence of spin-orbit coupling, group P4/nmm has only one single 4D IR at (π, π), i.e., the M point in the Brillouin zone, where all the symmetry operations in \({{\mathcal{G}}}/T\) are respected. It describes the fourfold degeneracy composed of two Kramers’ doublets, Jz = ±1/2 and Jz = ±3/2, with opposite parities, where Jz is the angular momentum defined according to {S4z∣0}. The degeneracy can be understood from the group structure in Eq. (1). The point group \({D}_{2d}^{D}\) (double group version of the point group D2d) supports two different 2D IRs corresponding to Kramers’ doublet Jz = ±1/2 and Jz = ±3/2 separately. At the M point, {S4z∣0} in \({D}_{2d}^{D}\) and {I∣τ0} in Z2 satisfy the following anticommutation relation
which enforces the degeneracy between the two 2D IRs labeled by Jz = ±1/2 and Jz = ±3/2 at M (more detailed analysis in Supplementary Note 2). In the paramagnetic state, besides crystalline symmetries, the time-reversal symmetry \({{\mathcal{T}}}\) also exists. Correspondingly, the system actually respects the type-II magnetic space group \(P4/nmm{1}^{{\prime} }\) (#. 129.412), which reads
Notice that the time-reversal symmetry does not affect the 4D fermionic IR at M.
Assuming trivial band structure at other high-symmetry points, we describe the fourfold degenerate fermion at M by the following tight-binding model58,59
where a single s orbital is assumed at each site in the lattice in Fig. 2a. In Eq. (4), the Pauli matrices si and σi (i = 1, 2, 3) stand for the spin and sublattice degrees, respectively. t (\({t}^{{\prime} }\)) is the nearest-neighbor intrasublattice (intersublattice) hopping. λ is the inversion-symmetric Rashba spin-orbit coupling, which arises due to the mismatch between the lattice sites and the inversion center60,61. The band structure based on \({{{\mathcal{H}}}}_{0}({{\bf{k}}})\) is plotted in Fig. 2b. We set the Fermi energy near the fourfold band degeneracy, as indicated in Fig. 2b, and consider conventional superconductivity in the system. The corresponding BdG Hamiltonian takes the form
in the basis ψ†(k) = (c†(k), is2σ0c(−k)). In Eq. (5), the Pauli matrix κi describes the Nambu spinor, μ is the chemical potential, and Δsc is the superconducting order parameter. In the superconducting state, the matrix form for the symmetry generators are \({{\mathcal{I}}}={s}_{0}{\sigma }_{1}{\kappa }_{0},\,{{{\mathcal{M}}}}_{y}=i{s}_{2}{\sigma }_{3}{\kappa }_{0}\) and \({{{\mathcal{S}}}}_{4z}={e}^{i{s}_{3}\pi /4}{\sigma }_{3}{\kappa }_{0}\)58, where \({{\mathcal{I}}},\,{{{\mathcal{M}}}}_{y}\) and \({{{\mathcal{S}}}}_{4z}\) correspond to {I∣τ0}, {My∣0}, {S4z∣0} respectively. The time-reversal symmetry takes the form \({{\mathcal{T}}}=i{s}_{2}{\sigma }_{0}{\kappa }_{0}K\) and the particle-hole symmetry \({{\mathcal{P}}}={s}_{2}{\sigma }_{0}{\kappa }_{2}K\), with K the complex conjugation operation. It is easy to check that the system described by \({{{\mathcal{H}}}}_{{{\rm{BdG}}}}\) in Eq. (5) is topologically trivial.
AFM order induced second-order TSCs
We study possible topological superconductivity in the structure sketched in Fig. 1, based on the above fourfold degenerate fermion. First, we consider the checkboard AFM order preserving the translational symmetries in the system as illustrated in Fig. 3a, and we assume the magnetic polarization along the z direction. Correspondingly, the system is described by the following Hamiltonian
with ΔAFM the strength of the AFM order. It is easy to check that, the system respects the type-III magnetic space group \(P{4}^{{\prime} }/{n}^{{\prime} }{m}^{{\prime} }m\) (#. 129.416)
We consider the effect of the AFM order on the fourfold degeneracy at M. Obviously, all the symmetry operations in \({{{\mathcal{G}}}}_{{{\rm{AFM}}}}/T\) preserve at the M point. A direct analysis shows that the fourfold degeneracy is broken into two twofold degenerate ones. It is the Jz = 1/2 (Jz = −1/2) state that is degenerate with the Jz = 3/2 (Jz = −3/2) state. A detailed group analysis is presented in the Supplementary Note 3. Such twofold band degeneracies arise from the relation \(\{{S}_{4z}| {{\bf{0}}}\}\{{M}_{xy}| {{{\tau }}}_{0}\}=\{{M}_{xy}| {{{\tau }}}_{0}\}\{{\overline{S}}_{4z}^{3}| {{{\bf{a}}}}_{{{\bf{1}}}}\}\), which at M leads to
Recalling that \({\overline{S}}_{4z}={S}_{4z}^{5}\), one immediately comes to the above conclusion. We simulate the bands in the presence of the AFM order numerically, and show the results at ΔAFM = 0.5 in Fig. 3a. Here, it is worth mentioning that the bands in Fig. 3a are always twofold degenerate due to the symmetry \(\{I| {{{\tau }}}_{{{\bf{0}}}}\}{{\mathcal{T}}}\) which exists at every k point in the Brillouin zone and satisfies \({(\{I| {{{\tau }}}_{{{\bf{0}}}}\}{{\mathcal{T}}})}^{2}=-1\).
a shows the normal bands for the system in Eq. (6) at ΔAFM = 0.5, with the AFM order illustrated in the inset. The blue dashed line represents the chemical potential at μ = 4.0. b shows the superconducting edge modes corresponding to the bands in (a) on the (10) edge. The edge modes on the right and left edges are degenerate. c shows an atomic insulator constructed by placing two Wannier orbits (WOs) with Jz = ±1/2 at 2c Wyckoff positions (the center of the square formed by the red and green balls), one WO with Jz = +1/2 at one of 2a Wyckoff positions (red balls) and one WO with Jz = −1/2 at the other 2a Wyckoff position (green balls). d shows an atomic insulator constructed by placing one WO with Jz = +3/2 at one of 2a Wyckoff positions and one WO with Jz = −3/2 at the other 2a Wyckoff position. e shows the low-energy superconducting spectrum (inset) and the real-space wavefunction profiles of the zero-energy modes, corresponding to the bands in (a). Open boundary conditions are set in both the [11] and \([1\overline{1}]\) directions. f shows the low-energy superconducting spectrum in the presence of a single vortex in (e). In the shadow region, among the three zero-energy modes, there are two vortex-bound Majorana modes (V.M.) and one corner-bound Majorana mode (C.M.). g and h show the real-space wavefunction profiles of the two V.M. in the shadow region in (f), and the C.M. in (f) has a similar wavefunction to that in (e). The color bars in (e), (g), and (h) are in the unit of 10−3. In the calculations, the superconducting order is set to be Δsc = 0.2.
As the magnetism breaks the time-reversal symmetry but preserves the particle-hole symmetry, the system belongs to class D which in the 2D case is characterized by a \({\mathbb{Z}}\) topological index, i.e., the Chern number, according to the Altland-Zirnbauer classification5. The Chern number can be calculated efficiently based on the symmetry eigenvalues carried by the occupied bands at the high-symmetry points. In systems respecting the fourfold rotational symmetry C4, in the weak-pairing condition, the Chern number Ch satisfies42
where m is the angular momentum carried by the Cooper pair, ξ(Γ) and ξ(M) are the products of the C4 eigenvalues of the occupied bands at Γ and M, respectively, and Nocc(Γ), Nocc(M) and Nocc(X) are the number of the occupied bands at Γ, M and X, respectively. Since C4 is equivalent to S4 in 2D systems, the formula in Eq. (9) applies to our consideration (In fact, in the nonsymmorphic group P4/nmm besides the S4z symmetry, there is also the C4z symmetry which is defined at the center of the square formed by the four nearest neighboring lattice sites in Fig. 2a, and we have specified this point in the Supplementary material. As group P4/nmm merely has one 4D IR at M, all the analyses related to S4z also work for C4z.). The conventional superconductivity carries zero angular momentum, i.e., m = 0. Therefore, the Chern number is completely determined by the S4z eigenvalues of the occupied bands at Γ and M, and for the condition in Fig. 3a, we find that Ch = 0, which is also confirmed by the gapped modes on the (11) and \([1\overline{1}]\) edges (see Supplementary Note 5). Nonetheless, the system is topologically nontrivial, as evidenced by the helical edge mode on the (10) edge in Fig. 3b. In fact, the system is a TSC protected by the antiunitary symmetry \({{{\mathcal{M}}}}_{y}{{\mathcal{T}}}\). We focus on high-symmetry line ky = π, where \({{{\mathcal{M}}}}_{y}{{\mathcal{T}}}\) and the particle-hole symmetry \({{\mathcal{P}}}\) preserve. Moreover, \({{{\mathcal{M}}}}_{y}{{\mathcal{T}}}\) serves as a pseudo time-reversal symmetry on line ky = π satisfying \({({{{\mathcal{M}}}}_{y}{{\mathcal{T}}})}^{2}=1\). Therefore, the ky = π line can be viewed as a 1D subsystem of the whole system, which belongs to symmetry class BDI5. The topological property of such a system is featured by the winding number,
with \(\widetilde{{{\mathcal{C}}}}={{{\mathcal{M}}}}_{y}{{\mathcal{T}}}{{\mathcal{P}}}\) being the pseudo-chiral symmetry on ky = π. We calculate the winding number straightforwardly, and it turns out w = 2 (details in Supplementary Note 4), which is consistent with the two zero-energy modes at ky = π on the (10) edge presented in Fig. 3e.
More interestingly, the above even winding number state is actually a second-order TSC state35,36,37,38 protected by \({{{\mathcal{M}}}}_{y}{{\mathcal{T}}}\). We demonstrate it numerically. As presented in Fig. 3e, a single Majorana mode exists at the corner between the neighboring (11) and \((1\overline{1})\) edges. To understand the phenomenon, we start with the helical mode in Fig. 3b. On the (10) edge, the symmetry \(\{{M}_{y}| {{\bf{0}}}\}{{\mathcal{T}}}\) and the particle-hole symmetry preserve. Considering the two symmetries, we can get the effective theory on the (10) edge as \({{{\mathcal{H}}}}_{(10)}=v{k}_{y}{\eta }_{1}\), with v the Fermi velocity and ηi the Pauli matrices in the space spanned by the helical edge mode. Then, we bend edge (10) into a right angle, with the two sides along the [11] and \([1\overline{1}]\) directions, as illustrated in Fig. 2a. The helical mode on each edge gains a mass, since \(\{{M}_{y}| {{\bf{0}}}\}{{\mathcal{T}}}\) breaks on the (11)/\((1\overline{1})\) edge. The gapped edge modes are depicted by the following effective theory
where \({m}_{(11)/(1\overline{1})}\) is the mass term on the (11)/\((1\overline{1})\) edge. Moreover, \(\{{M}_{y}| {{\bf{0}}}\}{{\mathcal{T}}}\) requires \({m}_{(11)}=-{m}_{(1\overline{1})}\). Therefore, Eq. (11) describes a massive Dirac theory, with the mass changing sign at the corner between the (11) and \((1\overline{1})\) edges. The mass domain results in a single Majorana mode at the corner62,63,64. Due to the pseudo-chiral symmetry \(\widetilde{{{\mathcal{C}}}}\), the corner Majorana modes carry chirality, and the modes with the same chirality cannot hybridize with each other. Thus, the classification for the second-order TSC here is \({\mathbb{Z}}\). Moreover, it is worth pointing out the above second-order TSC state exists in the condition \({(4t+\mu )}^{2}+{\Delta }_{{{\rm{sc}}}}^{2} \, < \, {\Delta }_{{{\rm{AFM}}}}^{2}\), i.e., the chemical potential in the AFM gap in the weak-pairing condition, and it belongs to a \({\mathbb{Z}}\) classification corresponding to the winding number along ky = π protected by \(\{{M}_{y}| {{\bf{0}}}\}{{\mathcal{T}}}\). We present more detailed analyses of the above effective edge theory and the topological phase transitions in Supplementary Note 5.
Interestingly, the negative energy states of the BdG Hamiltonian in Eq. (6) display both fragile Wannier obstruction and second-order topology. To this end, we treat the BdG band structure as an insulator, i.e., ignoring the particle-hole symmetry. Noting that particle-hole partners in the BdG bands carry opposite angular momenta, the angular momenta of the four “occupied" (negative energy) BdG bands are Jz = ±1/2, ±1/2 at G, Jz = −1/2, −1/2, −3/2, −3/2 at M, and Jz = ±1/2, ±1/2 at X. By exhaustion, one can show that no Wannier representation exist. However, if one includes two additional trivial bands (e.g., from core electrons) that are equivalent to two Wannier orbitals with Jz = ±3/2 each at one of the 2a Wyckoff positions shown in Fig. 3d, the combined six bands, nevertheless, become Wannier representable. The six Wannier orbitals are centered at Wyckoff position 2c with angular momenta Jz = ±1/2, ±1/2 and Wyckoff position 2a with Jz = −1/2, 1/2, as shown in Fig. 3c. Therefore, the occupied bands, despite not being Wannier representable, can be viewed as the difference between two Wannier representable systems, with six and two occupied bands, respectively, as shown in Fig. 3c, d. By definition, the four occupied bands display the fragile Wannier obstruction65. Formally, using the modern language of magnetic elementary band representation66, we express the fragile Wannier obstruction protected by the magnetic space group symmetries in Supplementary Note 6.
The elucidation of the fragile Wannier obstruction enables an alternative understanding of the second-order topology invoking only S4z. Ignoring the particle-hole symmetry, the stable second-order topology degenerates into the fragile Wannier obstruction. More specifically, from Fig. 3c, the six-orbital Wannier representation displays a filling anomaly. Indeed, viewed as an insulator, if we neglect the difference between two 2a sites in Fig. 3c, and combine both the ionic charge and electronic charge at 2a, the configuration is exactly the same as the Benalcazar-Bernevig-Hughes model35 for higher-order topology protected by fourfold rotation symmetry (equivalent with our S4z), only rotated by 45 degrees. It can be verified from ref. 67 that our model hosts a corner charge e/2 because of the mismatch of charge neutrality and rotation symmetry, which ensures a degeneracy of four corner states. In our system, corner states are pinned at zero energy by the particle-hole symmetry and they are Majorana zero modes. Since the filling anomaly requires only S4z, the corner zero modes are stable even when the corner is asymmetric under {My∣0}. In fact, to reveal the corner charge in an S4z symmetric sample, one only needs to avoid the edge terminations (10) and (01) where gapless edge modes are present due to additional mirror symmetries {My∣0}. Considering the various topology in the system, for clarity we summarize the relation between the symmetry and the topology in Table 1.
Vortex-bound Majorana modes
In the the second-order TSC state in the above, each vortex can bind two Majorana modes which are stable due to the S4z symmetry. The phenomenon is closely related to the fact that for group P4/nmm, the effective theory near M in the normal state can be viewed as a direct sum of two Rashba electron gas systems with angular momenta Jz = ±1/2 and Jz = ±3/2 separately. To make it clearer, we consider the low-energy theory near M in the second-order TSC state, for instance,
where q is defined with respect to the M point and the identity matrices are omitted for simplicity. Ignoring the high-order \({t}^{{\prime} }{q}_{x}{q}_{y}\) term, it is obvious to notice that \({{{\mathcal{H}}}}_{{{\rm{eff}}}}\) can be decoupled in the σ space, i.e., the sublattice space. In the σ = ±1 subspace, it describes a superconducting Rashba electron gas in the presence of a Zeeman field ±ΔAFM; and in each subspace, the vortex can bind a single Majorana mode10 carrying \({{{\mathcal{S}}}}_{4z}\) eigenvalue 1. Notice that in the presence of a vortex, the S4z symmetry takes eigenvalues ±1 and ±i. However, the σ = +1 subspace is spanned by the Kramers’ doublet Jz = ±1/2, while σ = −1 subspace is spanned by Jz = ∓3/2, which can be inferred from the basis of \({{{\mathcal{H}}}}_{{{\rm{eff}}}}\). When we consider the \({{{\mathcal{S}}}}_{4z}\) eigenvalue of the Majorana mode, in the σ = −1 subspace, the basis contributes an additional phase factor ei∓π = −1. Therefore, the vortex-bound Majorana mode in the σ = ±1 subspace has \({{{\mathcal{S}}}}_{4z}\) eigenvalue ±1. The two Majorana modes are immune to perturbations preserving the \({{{\mathcal{S}}}}_{4z}\) symmetry, such as the \({t}^{{\prime} }{q}_{x}{q}_{y}\) term in Eq. (12). Namely, the second-order TSC state in the above supports two Majorana modes in each vortex protected by the S4z symmetry, i.e., one with S4z eigenvalue +1 and the other −1. We carry out numerical simulations for the vortex-bound states and present the results in Fig. 3f–h. It is interesting to notice that in the second-order TSC state, the corner MZMs in Fig. 3e coexist with the two vortex-bound MZMs. This arises from the fact that, the vortex core is far away from the corners, making the corner MZMs can hardly feel the effect of the vortex.
FM order induced first-order TSCs
We also consider FM order in the system in Eq. (5), and we assume the magnetic polarization along the z direction. Correspondingly, the whole system can be depicted by the following Hamiltonian
where ΔFM is the strength of the FM order. We first study how the FM order affects the fourfold degenerate fermion at M in the normal state. According to the real-space configuration in Fig. 4a, the symmetry of the system is lowered to the type-III magnetic space group \(P4/n{m}^{{\prime} }{m}^{{\prime} }\) (#. 129.417)
with \({S}_{4}^{D}\) the double group generated by {S4z∣0}. All the symmetry operations in \({{{\mathcal{G}}}}_{{{\rm{FM}}}}/T\) maintain at the M point. A direct group theory analysis shows that the 4D IR in the paramagnetic state at M splits into two 2D IRs, similar to the AFM case. However, differently in the FM case, one corresponds to twofold band degeneracy between the Jz = 1/2 and Jz = −3/2 states and the other between the Jz = −1/2 and Jz = 3/2 states (more details in Supplementary Note 3). Such degeneracies can be understood from the anticommutation relation between {S4z∣0} and {I∣τ0} at M, proved in Eq. (2). We confirm the above analysis numerically in Fig. 4a.
a The bands in the presence of the FM order with ΔFM = 0.3. The inset in (a) illustrates the real-space configuration of the FM order. The blue dashed line in (a) represents the chemical potential at μ = 4.0. b shows the superconducting edge modes on the (10) edge corresponding to the bands in (a), with the edge modes on the right (left) edge marked by the red (green) color. In (a) and (b), the other parameters are the same as those in Fig. 2.
To study the topological property in systems depicted by \({{{\mathcal{H}}}}_{{{\rm{BdG,FM}}}}\) corresponding to the normal bands in Fig. 4a, we first calculate the Chern number. Based on the formula in Eq. (9) and the above analysis, the Chern number can be calculated to be ∣Ch∣ = 2, whose sign depends on the sign of ΔFM. To verify this, we simulate the superconducting edge modes numerically. As shown in Fig. 4b, two chiral modes appear on each edge corresponding to the normal state in Fig. 4a, which is consistent with the above analysis. In fact, the above chiral TSC state arises through a gap-close-reopen process at M as the FM order becomes stronger, and the phase transition occurs at \({(4t+\mu )}^{2}+{\Delta }_{{{\rm{sc}}}}^{2}={\Delta }_{{{\rm{FM}}}}^{2}\). Accordingly, in the weak-pairing condition, the system is a TSC with ∣Ch∣ = 2, as long as the chemical potential is in the FM gap (details in Supplementary Note 4). Moreover, the vortex in the chiral TSC state can also bind two Majorana modes, and the analysis is similar to that of the AFM case. We present a more detailed analysis and simulate the vortex-bound states numerically in Supplementary Note 8.
Discussion
We discuss the effects of the symmetry-breaking perturbations (For the TSC states, more essential are the symmetries in the magnetic states rather than the specific magnetic orders considered in Figs. 3a and 4a. Therefore, here we refer to the perturbations breaking the magnetic group symmetries.), which may arise from tilting the magnetization off the z direction in Figs. 3a and 4a, on the above TSC states. Obviously, the vortex-bound Majorana modes are sensitive to the {S4z∣0} breaking perturbations and will gap out immediately. However, the Majorana edge and corner modes can persist against the perturbations. The chiral TSC state is robust as long as the bulk energy gap is not closed. For the second-order TSC state, perturbations breaking \(\{{M}_{y}| {{\bf{0}}}\}{{\mathcal{T}}}\) gap out the helical Majorana mode on the (10) edge and break the \({\mathbb{Z}}\) classification of the corner Majorana modes to a \({{\mathbb{Z}}}_{2}\) one. Nevertheless, the corner Majorana modes can be more robust due to a S4z protected filling anomaly, or due to the boundary obstruction47,68.
In the proposal, the FM order can be replaced by an external magnetic field. More difficult is to construct the antiferromagnetic heterostructures, which require well-matched lattices between the magnetic layer and the layer offering the band degeneracy. A possible candidate is the heterostructure between the antiferromagnetism ACo2As2 (A = Ca, Ba, Sr) and the iron-based superconductors, whose lattice constants are similar69,70. A more feasible scheme lies in the magnetic materials. For example, in Eu1−xLaxFeAs271 and Sr2VO3−δFeAs72, magnetic layers exist next to the superconducting FeAs layer; and in Ba1−xNaxFe2As273 and Ba1−xKxFe2As274, a tetragonal AFM phase may coexist with the superconductivity. By methods of doping or gating, one may tune the chemical potential in the iron-based superconductors near the fourfold band degeneracy, and topological superconductivity can possibly be realized. We use the genuine bands of the iron-based superconductors to simulate the topological superconductivity in Supplementary Note 9.
In the above analysis, we have mainly focused on the TSC states in the space group P4/nmm and the possible material realization. However, as pointed out, our method can be applied to a wide range of systems with band degeneracy near the Fermi energy. To further demonstrate the effectiveness of our method, we analyze another case where the lattice respects the space group P4/ncc. The group protects an eightfold band degeneracy at (π, π, π) in the normal state. When conventional superconductivity is introduced, both the FM order and the C-type AFM order drive the system into the nodal TSC states, but the topological properties are different. More detailed analyses are presented in the Supplementary Note 10. Another interesting point worth mentioning is that the symmetry of the system in the presence of the magnetic order is determined by both the type of the magnetic order and the direction of the spin polarization, and it is possible that the higher-order TSC states can be realized by the simpler FM order, which deserves further study in the future.
In summary, we propose a general method that is based on the bulk energy bands and the conventional superconductivity to realize topological superconductivity. We show that by manipulating systems with crystal symmetry-protected fermionic excitations with magnetism, TSCs, including the high-order ones, can be generally obtained when conventional superconductivity is introduced, and the property of the TSCs is thoroughly determined by the property of the magnetism. Thus, our study provides a new method to realize the various types of topological superconductivity and can help to find new platforms to realize the Majorana modes.
Near the end of the paper, we became aware of a work75 in which the vortex-bound states in high-order TSCs are studied, and the conclusion of the work is consistent with our results in the second-order TSC state in the AFM case.
Methods
Symmetries in time-reversal invariant superconductors
Generally, a superconductor can be described by the following BdG Hamiltonian
in the basis \({\psi }^{{\dagger} }({{\bf{k}}})=({c}_{{{\bf{k}}},\uparrow }^{{\dagger} },\, {c}_{{{\bf{k}}},\downarrow }^{{\dagger} },\, {c}_{-{{\bf{k}}},\uparrow },\, {c}_{-{{\bf{k}}},\downarrow })\). Notice that we neglect other indices except for the spin index here. For a time-reversal symmetric superconductor, it respects the following three symmetries: the time-reversal symmetry \({{\mathcal{T}}}\), the particle-hole symmetry \({{\mathcal{P}}}\) and the combined chiral symmetry \({{\mathcal{C}}}={{\mathcal{P}}}{{\mathcal{T}}}\). These symmetries act on the Hamiltonian as follows
Moreover, in the basis for \({{{\mathcal{H}}}}_{{{\rm{BdG}}}}({{\bf{k}}})\) in Eq. (15), the above symmetries take the form \({{\mathcal{T}}}=i{s}_{2}{\kappa }_{0}K,\,{{\mathcal{P}}}={s}_{0}{\kappa }_{1}K\) and \({{\mathcal{C}}}=i{s}_{2}{\kappa }_{1}\). Besides the above local symmetries, the system also respects the crystalline symmetries. The crystalline symmetry \(\widetilde{g}\) transforms the BdG Hamiltonian as \(\widetilde{g}{{{\mathcal{H}}}}_{{{\rm{BdG}}}}({{\bf{k}}}){\widetilde{g}}^{-1}={{{\mathcal{H}}}}_{{{\rm{BdG}}}}({\widetilde{g}}^{-1}{{\bf{k}}})\), and has the form
In the above equation, η is determined by the pairing symmetry, i.e., gΔ(k)gT = ηΔ(k). In the present study, we focus on the conventional superconductivity, which belongs to the trivial irreducible representation of the crystalline symmetry group. Namely, η always equals 1 for \(\widetilde{g}\) in Eq. (17) in our consideration.
Then, we consider the commutation relation between the unitary chiral symmetry \({{\mathcal{C}}}\) and the crystalline symmetries. It can be directly shown
where we have taken use of the fact η = 1 in \(\widetilde{g}\). Recall that in a time-reversal symmetric system, the time-reversal symmetry commutes with all the crystalline symmetries, and in the normal state, it demands \(Tg{T}^{-1}=g=(i{s}_{2}K)g{(i{s}_{2}K)}^{-1}={s}_{2}{g}^{*}{s}_{2}\) where T stands for the time-reversal symmetry in the normal state. Therefore, we have \({{\mathcal{C}}}\widetilde{g}{{{\mathcal{C}}}}^{-1}=\widetilde{g}\) in Eq. (18), namely \([{{\mathcal{C}}},\, \widetilde{g}]=0\). The above commutation relation leads to that for any eigenstate \(\left\vert \phi ({{\bf{k}}})\right\rangle\) of \({{{\mathcal{H}}}}_{{{\rm{BdG}}}}({{\bf{k}}})\) carrying energy E(k), its chiral partner \({{\mathcal{C}}}\left\vert \phi ({{\bf{k}}})\right\rangle\) possesses energy −E(k) but the same symmetry eigenvalue with \(\left\vert \phi ({{\bf{k}}})\right\rangle\) for any crystalline symmetry. This means that in the level of the symmetry indicator, the system must be equal to the topological trivial superconductor. More detailed analyses are presented in Supplementary Note 1.
The calculation of winding number
To analytically calculate the winding number at ky = π in the AFM case, we rewrite \({{{\mathcal{H}}}}_{{{\rm{BdG,AFM}}}}\) in Eq. (6) in the basis diagonalizing the pseudo-chiral symmetry \(\widetilde{{{\mathcal{C}}}}\). After the basis transformation, \({{{\mathcal{H}}}}_{{{\rm{BdG,AFM}}}}\) takes an off-diagonal form in the Nambu space. In the specific AFM case, the off-diagonal block matrix Q(kx) in the upper right corner is
with \({q}_{\pm }({k}_{x})=-[2t(\cos {k}_{x}-1)-\mu ]{s}_{0}\pm 2\lambda \sin {k}_{x}{s}_{2}\pm {\Delta }_{{{\rm{AFM}}}}{s}_{3}\pm i{\Delta }_{{{\rm{sc}}}}{s}_{2}\). Accordingly, the winding number along ky = π can be calculated as
Here, ν(q±) characterizes the winding number of \(\det {q}_{\pm }({k}_{x})\) around the origin point in the complex plane. See more details in Supplementary Note 4.
A short review of MEBR
When we place the bases \(\{{\phi }_{i}^{\alpha }\}\) of the irreducible co-representations ui of these on-site magnetic point groups \({{{\mathcal{G}}}}_{{{\bf{x}}}}\) at their corresponding Wyckoff positions x, the induced co-representation \({({u}_{i})}_{{{\bf{x}}}}\uparrow {{\mathcal{G}}}\) of the space group \({{\mathcal{G}}}\) from the irreducible co-representations of the subgroup \({{{\mathcal{G}}}}_{{{\bf{x}}}}\) is referred to as magnetic elementary band representations (MEBR). In the AFM case, the four negative-energy bands host the co-representations
-
At G point: \({\bar{\Gamma }}_{7}\oplus {\bar{\Gamma }}_{7}\)
-
At M point: \({\bar{M}}_{7}\oplus {\bar{M}}_{7}\)
-
At X point: \({\bar{X}}_{3}{\bar{X}}_{5}\oplus {\bar{X}}_{2}{\bar{X}}_{4}\)
Therefore, our target band can only be expressed as a combination of MEBRs with the negative integer
which implies the fragile topology. See more details in Supplementary Note 7.
Model Hamiltonian used for SG 130
To illustrate the effectiveness and generality of our method, we introduce a more complex example for space group P4/ncc (#. 130). We start with the paramagnetic normal state, where the system actually respects the type-II magnetic space group \(P4/ncc{1}^{{\prime} }\). The group can be generated by the following symmetry operations
The magnetic space group \(P4/ncc{1}^{{\prime} }\) has one and only one eightfold irreducible representation at the A point, i.e., the (π, π, π) point, in the spinful condition. Namely, all the bands are eightfold degenerate and respect the same low-energy effective model in the spinful case. In the lattice model condition, the eightfold band degeneracy can be captured by the following tight-binding model76
Based on this model, we study the possible TSC states in the system when conventional superconductivity and different magnetic orders are introduced. More details are presented in Supplementary Note 10.
Data availability
All data needed to evaluate the conclusions in the study are present in the paper and/or the Supplementary Information. The data that support the findings of this study are available from the corresponding authors upon request.
Code availability
The computer code used for numerical calculation and theoretical understanding is available upon request from the corresponding authors.
References
Hasan, M. Z. & Kane, C. L. Colloquium: Topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Qi, X.-L. & Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).
Chiu, C.-K., Teo, J. C. Y., Schnyder, A. P. & Ryu, S. Classification of topological quantum matter with symmetries. Rev. Mod. Phys. 88, 035005 (2016).
Alicea, J. New directions in the pursuit of Majorana fermions in solid state systems. Rep. Prog. Phys. 75, 076501 (2012).
Schnyder, A. P., Ryu, S., Furusaki, A. & Ludwig, A. W. W. Classification of topological insulators and superconductors in three spatial dimensions. Phys. Rev. B 78, 195125 (2008).
Lian, B., Sun, X.-Q., Vaezi, A., Qi, X.-L. & Zhang, S.-C. Topological quantum computation based on chiral Majorana fermions. Proc. Natl Acad. Sci. USA 115, 10938–10942 (2018).
Kitaev, A. Y. Unpaired Majorana fermions in quantum wires. Phys.-Uspekhi 44, 131 (2001).
Fu, L. & Kane, C. L. Superconducting proximity effect and Majorana fermions at the surface of a topological insulator. Phys. Rev. Lett. 100, 096407 (2008).
Fu, L. & Berg, E. Odd-parity topological superconductors: theory and application to CuxBi2Se3. Phys. Rev. Lett. 105, 097001 (2010).
Sau, J. D., Lutchyn, R. M., Tewari, S. & Das Sarma, S. Generic new platform for topological quantum computation using semiconductor heterostructures. Phys. Rev. Lett. 104, 040502 (2010).
Lutchyn, R. M., Sau, J. D. & Das Sarma, S. Majorana fermions and a topological phase transition in semiconductor-superconductor heterostructures. Phys. Rev. Lett. 105, 077001 (2010).
Zhang, F., Kane, C. L. & Mele, E. J. Time-reversal-invariant topological superconductivity and Majorana Kramers pairs. Phys. Rev. Lett. 111, 056402 (2013).
Sau, J. D. & Brydon, P. M. R. Bound states of a ferromagnetic wire in a superconductor. Phys. Rev. Lett. 115, 127003 (2015).
Jiang, K., Dai, X. & Wang, Z. Quantum anomalous vortex and Majorana zero mode in iron-based superconductor Fe(Te,Se). Phys. Rev. X 9, 011033 (2019).
Fang, C., Gilbert, M. J. & Bernevig, B. A. New class of topological superconductors protected by magnetic group symmetries. Phys. Rev. Lett. 112, 106401 (2014).
Qin, S. et al. Quasi-1D topological nodal vortex line phase in doped superconducting 3D Dirac semimetals. Phys. Rev. Lett. 123, 027003 (2019).
Tiwari, A., Jahin, A. & Wang, Y. Chiral Dirac superconductors: second-order and boundary-obstructed topology. Phys. Rev. Res. 2, 043300 (2020).
Wu, Z. & Wang, Y. Nodal higher-order topological superconductivity from a \({{{\mathcal{C}}}}_{4}\)-symmetric Dirac semimetal. Phys. Rev. B 106, 214510 (2022).
Sasaki, S. et al. Topological superconductivity in CuxBi2Se3. Phys. Rev. Lett. 107, 217001 (2011).
Nadj-Perge, S. et al. Observation of Majorana fermions in ferromagnetic atomic chains on a superconductor. Science 346, 602–607 (2014).
Xu, J.-P. et al. Experimental detection of a Majorana mode in the core of a magnetic vortex inside a topological insulator-superconductor Bi2Te3/NbSe2 heterostructure. Phys. Rev. Lett. 114, 017001 (2015).
Wang, D. et al. Evidence for Majorana bound states in an iron-based superconductor. Science 362, 333–335 (2018).
Liu, Q. et al. Robust and clean Majorana zero mode in the vortex core of high-temperature superconductor (Li0.84Fe0.16)OHFeSe. Phys. Rev. X 8, 041056 (2018).
Kong, L. et al. Half-integer level shift of vortex bound states in an iron-based superconductor. Nat. Phys. 15, 1181–1187 (2019).
Machida, T. et al. Zero-energy vortex bound state in the superconducting topological surface state of Fe (Se, Te). Nat. Mater. 18, 811–815 (2019).
Kong, L. et al. Majorana zero modes in impurity-assisted vortex of lifeas superconductor. Nat. Commun. 12, 4146 (2021).
Vaitiekėnas, S. et al. Flux-induced topological superconductivity in full-shell nanowires. Science 367, eaav3392 (2020).
Li, M. et al. Ordered and tunable Majorana-zero-mode lattice in naturally strained LiFeAs. Nature 606, 890–895 (2022).
Joynt, R. & Taillefer, L. The superconducting phases of UPt3. Rev. Mod. Phys. 74, 235–294 (2002).
Ran, S. et al. Nearly ferromagnetic spin-triplet superconductivity. Science 365, 684–687 (2019).
Yang, J. et al. Spin-triplet superconductivity in K2Cr3As3. Sci. Adv. 7, eabl4432 (2021).
Song, Z., Fang, C. & Qi, Y. Real-space recipes for general topological crystalline states. Nat. Commun. 11, 4197 (2020).
Zhang, Z., Ren, J., Qi, Y. & Fang, C. Topological classification of intrinsic three-dimensional superconductors using anomalous surface construction. Phys. Rev. B 106, L121108 (2022).
Ono, S., Shiozaki, K. & Watanabe, H. Classification of time-reversal symmetric topological superconducting phases for conventional pairing symmetries. Phys. Rev. B 109, 214502 (2024).
Benalcazar, W. A., Bernevig, B. A. & Hughes, T. L. Quantized electric multipole insulators. Science 357, 61–66 (2017).
Song, Z., Fang, Z. & Fang, C. (d − 2)-Dimensional edge states of rotation symmetry protected topological states. Phys. Rev. Lett. 119, 246402 (2017).
Schindler, F. et al. Higher-order topological insulators. Sci. Adv. 4, eaat0346 (2018).
Geier, M., Trifunovic, L., Hoskam, M. & Brouwer, P. W. Second-order topological insulators and superconductors with an order-two crystalline symmetry. Phys. Rev. B 97, 205135 (2018).
Zhang, Z. et al. Controlling Dzyaloshinskii-Moriya interaction in a centrosymmetric nonsymmorphic crystal. Sci. Bull. 68, 1113–1118 (2023).
Ono, S. & Shiozaki, K. Towards complete characterization of topological insulators and superconductors: a systematic construction of topological invariants based on Atiyah-Hirzebruch spectral sequence. Preprint at https://arxiv.org/abs/2311.15814 (2023).
Zhang, R.-X., Cole, W. S., Wu, X. & Das Sarma, S. Higher-order topology and nodal topological superconductivity in Fe(Se,Te) heterostructures. Phys. Rev. Lett. 123, 167001 (2019).
Fang, C., Bernevig, B. A. & Gilbert, M. J. Topological crystalline superconductors with linearly and projectively represented C_{n} symmetry. Preprint at https://arxiv.org/abs/1701.01944 (2017).
Liu, T., He, J. J. & Nori, F. Majorana corner states in a two-dimensional magnetic topological insulator on a high-temperature superconductor. Phys. Rev. B 98, 245413 (2018).
Peng, Y. & Xu, Y. Proximity-induced Majorana hinge modes in antiferromagnetic topological insulators. Phys. Rev. B 99, 195431 (2019).
Pan, X.-H. et al. Lattice-symmetry-assisted second-order topological superconductors and Majorana patterns. Phys. Rev. Lett. 123, 156801 (2019).
Ahn, J. & Yang, B.-J. Higher-order topological superconductivity of spin-polarized fermions. Phys. Rev. Res. 2, 012060 (2020).
Wong, K. H. et al. Higher order topological superconductivity in magnet-superconductor hybrid systems. NPJ Quantum Mater. 8, 31 (2023).
Zou, J., Xie, Q., Song, Z. & Xu, G. New types of topological superconductors under local magnetic symmetries. Natl Sci. Rev. 8, nwaa169 (2021).
Bradlyn, B. et al. Topological quantum chemistry. Nature 547, 298–305 (2017).
Po, H. C., Vishwanath, A. & Watanabe, H. Symmetry-based indicators of band topology in the 230 space groups. Nat. Commun. 8, 50 (2017).
Song, Z., Zhang, T., Fang, Z. & Fang, C. Quantitative mappings between symmetry and topology in solids. Nat. Commun. 9, 3530 (2018).
Ono, S., Po, H. C. & Watanabe, H. Refined symmetry indicators for topological superconductors in all space groups. Sci. Adv. 6, eaaz8367 (2020).
Geier, M., Brouwer, P. W. & Trifunovic, L. Symmetry-based indicators for topological Bogoliubov–de Gennes Hamiltonians. Phys. Rev. B 101, 245128 (2020).
Ono, S., Po, H. C. & Shiozaki, K. \({{\mathbb{Z}}}_{2}\)-enriched symmetry indicators for topological superconductors in the 1651 magnetic space groups. Phys. Rev. Res. 3, 023086 (2021).
Mourik, V. et al. Signatures of Majorana fermions in hybrid superconductor-semiconductor nanowire devices. Science 336, 1003–1007 (2012).
Bradlyn, B. et al. Beyond Dirac and Weyl fermions: unconventional quasiparticles in conventional crystals. Science 353, aaf5037 (2016).
Hu, J. Iron-based superconductors as odd-parity superconductors. Phys. Rev. X 3, 031004 (2013).
Qin, S., Fang, C., Zhang, F.-c. & Hu, J. Spin-triplet superconductivity in nonsymmorphic crystals. Preprint at https://arxiv.org/abs/2208.09409 (2022).
Agterberg, D. F., Shishidou, T., O’Halloran, J., Brydon, P. M. R. & Weinert, M. Resilient nodeless d-wave superconductivity in monolayer FeSe. Phys. Rev. Lett. 119, 267001 (2017).
Qin, S., Fang, C., Zhang, F.-C. & Hu, J. Topological superconductivity in an extended s-wave superconductor and its implication to iron-based superconductors. Phys. Rev. X 12, 011030 (2022).
Fischer, M. H., Sigrist, M., Agterberg, D. F. & Yanase, Y. Superconductivity and local inversion-symmetry breaking. Annu. Rev. Condens. Matter Phys. 14, 153–172 (2023).
Zhang, F., Kane, C. L. & Mele, E. J. Surface state magnetization and chiral edge states on topological insulators. Phys. Rev. Lett. 110, 046404 (2013).
Yan, Z., Song, F. & Wang, Z. Majorana corner modes in a high-temperature platform. Phys. Rev. Lett. 121, 096803 (2018).
Wang, Q., Liu, C.-C., Lu, Y.-M. & Zhang, F. High-temperature Majorana corner states. Phys. Rev. Lett. 121, 186801 (2018).
Po, H. C., Watanabe, H. & Vishwanath, A. Fragile topology and Wannier obstructions. Phys. Rev. Lett. 121, 126402 (2018).
Elcoro, L. et al. Magnetic topological quantum chemistry. Nat. Commun. 12, 5965 (2021).
Takahashi, R., Zhang, T. & Murakami, S. General corner charge formula in two-dimensional Cn-symmetric higher-order topological insulators. Phys. Rev. B 103, 205123 (2021).
Wu, X. et al. Boundary-obstructed topological high-Tc superconductivity in iron pnictides. Phys. Rev. X 10, 041014 (2020).
Dai, P. Antiferromagnetic order and spin dynamics in iron-based superconductors. Rev. Mod. Phys. 87, 855–896 (2015).
Mao, H. & Yin, Z. Electronic structure and spin dynamics of ACo2As2 (A = Ba, Sr, Ca). Phys. Rev. B 98, 115128 (2018).
Yu, J. et al. Coexistence of ferromagnetism, antiferromagnetism, and superconductivity in magnetically anisotropic (Eu, La) FeAs2. NPJ Quantum Mater. 6, 63 (2021).
Ok, J. M. et al. Strong antiferromagnetic proximity coupling in the heterostructure superconductor Sr2VO3−δFeAs. Phys. Rev. B 105, 214505 (2022).
Avci, S. et al. Magnetically driven suppression of nematic order in an iron-based superconductor. Nat. Commun. 5, 3845 (2014).
Böhmer, A. et al. Superconductivity-induced re-entrance of the orthorhombic distortion in Ba1−x Kx Fe2As2. Nat. Commun. 6, 7911 (2015).
Zhang, R.-X. Bulk-vortex correspondence of higher-order topological superconductors. Preprint at https://arxiv.org/abs/2208.01652 (2022).
Wieder, B. J., Kim, Y., Rappe, A. M. & Kane, C. L. Double Dirac semimetals in three dimensions. Phys. Rev. Lett. 116, 186402 (2016).
Acknowledgements
This work is supported by the Ministry of Science and Technology (Grant No. 2022YFA1403901 and No. 2022YFA1403902), National Natural Science Foundation of China (Grant No. NSFC-12304163, NSFC-12325404, and NSFC-11920101005), National Key R&D Program of China (Grant No. 2022YFA1403800 and No. 2023YFA1406700), Innovation program for Quantum Science and Technology (Grant No. 2021ZD0302500), Chinese Academy of Sciences (Grant No. XDB33020000 and No. JZHKYPT-2021-8), the New Cornerstone Investigator Program, and the Beijing Institute of Technology Research Fund Program for Young Scholars. Z.F.W. and Y.W. are supported by NSF under award number DMR-2045781.
Author information
Authors and Affiliations
Contributions
Z.Y.Z., Z.F.W., Y.W. and S.S.Q. did the theoretical derivation and numerical calculation; C.F., F.-C.Z., J.P.H., Y.W., S.S.Q. provided the theoretical understanding. All authors discussed and contributed to the manuscript. S.S.Q. and Y.W. conceived the work.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Zhang, Z., Wu, Z., Fang, C. et al. Topological superconductivity from unconventional band degeneracy with conventional pairing. Nat Commun 15, 7971 (2024). https://doi.org/10.1038/s41467-024-52156-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-024-52156-1
- Springer Nature Limited