Introduction

QSLs are highly-entangled states of matter, in which no long-range magnetic order is observed, even in the absence of thermal fluctuations at zero temperature. Ever since P. W. Anderson’s proposal of a resonating valence bond phase as the ground state for the triangular lattice Heisenberg antiferromagnet1, QSLs have captured the attention of physicists across fields beyond quantum magnetism2. The reason lies in the wide range of exotic properties and phenomena that these intriguing states of matter display, ranging from fractionalization of spin excitations observed as an extended continuum in the excitation spectrum, to pinch-point singularities observed in the static spin-spin correlations and associated with U(1) QSLs or fracton phases3,4,5,6,7.

The QSL behavior is driven by strong zero-point quantum fluctuations, which are enhanced in the presence of high magnetic frustration. This is realized either by competing isotropic interactions, as in the Heisenberg model on the kagome lattice8,9,10, or by anisotropic interactions, such as in the Kitaev model on the honeycomb lattice11,12,13. On the other hand, low dimensionality also amplifies quantum fluctuations, which are thus more noticeable in one- or two-dimensional systems. However, in recent years much attention has been put into three-dimensional (3D) models and compounds. Even though zero-point quantum fluctuations are greatly suppressed in 3D, highly frustrated systems like the network of corner-sharing tetrahedra realized by the pyrochlore lattice still provide a suitable environment for the existence of QSLs, both theoretically and experimentally14,15,16. Indeed, several compounds have been synthesized which realize pyrochlore, hyperkagome, or hyper-hyperkagome lattices and display QSL behavior in 3D15,17,18. Although often it is found that QSL candidate materials order at some finite-temperature TN, their dynamic response is strongly influenced by the proximity to a quantum critical point where the order completely disappears. The quantum critical regime, emanating from the quantum critical point, leaves its characteristic fingerprint in the dynamic response even at finite temperatures, as long as TN ≪ |θCW|, where θCW is a Curie–Weiss temperature that defines the characteristic energy scale of the system. This allows testing theoretical predictions for QSLs in real materials, such as the existence of fractional excitations19,20,21.

Recently, it has been shown that a new 3D magnetic network exhibits a highly dynamic ground state. K2Ni2(SO4)3, a member of the langbeinite family, develops spin correlations below 20 K between S = 1 moments, with a peculiar ordered state arising below  ~1.1 K, freezing only around 1% of the available magnetic entropy and showing a tripling of the magnetic unit cell22,23. Furthermore, the application of B = 4 T magnetic field leads to a fully dynamical state down to the lowest temperatures. Another member of the langbeinite family, the KSrFe2(PO4)3 compound with S = 5/2, was also claimed to exhibit spin-liquid behavior24.

In this work, we combine both experimental and numerical methods to study the magnetic properties of K2Ni2(SO4)3 and its proximity to a spin-liquid model on a simpler lattice. We first perform density functional theory (DFT)-based energy mappings to obtain the Hamiltonian of the compound, taking into account its low-temperature structure. Using classical Monte Carlo (cMC) to study the magnetic ordering, we obtain the same tripling of the magnetic unit cell as observed experimentally. We then compare inelastic neutron scattering (INS) measurements with pseudo-fermion functional renormalization (PFFRG) calculations on the quantum S = 1 model, obtaining a good agreement. We finally trace the features observed in the spin structure factors to a nearby point in space which corresponds to a trillium lattice in which each triangle is turned into a tetrahedron. We analyze the spin-liquid properties of this tetra-trillium lattice and its surrounding areas in parameter space.

Results

Magnetic structure and Hamiltonian

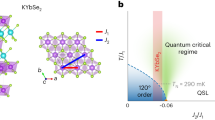
The underlying magnetic network in these compounds comprises two interconnected trillium lattices, based on two symmetry-inequivalent magnetic sites, shown in Fig. 1a. Each trillium lattice with four sites per unit cell consists of a network of corner-sharing triangles where each site participates in three triangles (see Fig. 1b). For K2Ni2(SO4)3, our DFT-based energy mapping calculations reveal three dominant exchange interactions: J3 and J5 constituting nearest-neighbor couplings within each trillium lattice, and J4 which couples the two trillium lattices (see the full list in Fig. 1a–c). In the limit J3, J5 → 0, the network transforms into a bipartite lattice, supporting a semi-classical antiferromagnetic state. The limit J4 → 0 describes two independent trillium lattices, which have been theoretically investigated in detail25,26 and shown to lead to a variant of the 120∘ order. Therefore, K2Ni2(SO4)3, with its magnetically highly correlated and dynamical state, represents a surprising revelation that indicates the proximity to an island of liquidity that has escaped the attention of the scientific community so far.

Fig. 1: Crystal and magnetic structure of K2Ni2(SO4)3.
figure 1

a Two trillium lattices of Ni2+ ions in K2Ni2(SO4)3 with the five nearest-neighbor couplings calculated by DFT energy mapping. b J3 and J5 form two independent trillium lattices. c J4 couples each ion from one trillium lattice to the nearest triangle of the second trillium lattice. For J4 = J5, magnetic ions form a network of corner-shared tetrahedra based on a trillium lattice, a tetra-trillium lattice. d Spin structure factor S(q) as a function of q = ∣q∣. Comparison between cMC calculations at T = 0 for the DFT model (bottom) and diffraction data at 100 mK taken from ref. 22 (top). A small Gaussian broadening is used for the cMC results. e The spin structure corresponding to the tripled magnetic unit cell determined by cMC is shown in a cut along the (111) plane for an L = 6 system. Black arrows represent the direction of the sum of moments within a single unit cell. The bond color indicates the angle between the unit cell moments. f Schematic of the proximity of the K2Ni2(SO4)3 Hamiltonian to a spin-liquid region and its effect at finite temperatures, where g is a function of the couplings Ji.

Full size image

While previous coupling values were reported for the room-temperature structure22, here we propose a new set of parameters calculated by DFT energy mapping based on a refined crystal structure at T = 100 K (see Supplementary Notes 1 and 2). The new values of exchange interactions (listed in Fig. 1a) are moderately renormalized compared to the room-temperature structure values but show the same hierarchy of interactions J4 > J5 > J3 > J1 > ∣J2∣, where J2 is the only ferromagnetic coupling. Specifically, room-temperature couplings relative to the dominant J4 = 5.545 K are J1 = 0.079 J4, J2 = − 0.030 J4, J3 = 0.203 J4, J5 = 0.472 J4, and for the T = 100 K structure they become J1 = 0.066 J4, J2 = −0.026 J4, J3 = 0.144 J4, J5 = 0.479 J4. The most significant difference occurs for J3, which changes by  ~30%. Even though K2Ni2(SO4)3 orders at about 1.1 K, the state seems to remain predominantly dynamic, with the persistence of the diffuse scattering and absence of magnon branches22,23. This makes it impossible to use the more standard approach for determining the exchange interactions, which relies on comparing the magnon dispersion with spin-wave theory (SWT). Furthermore, the magnetic unit cell consists of 216 spins, which represents a significant challenge for SWT. Alternatively, one could perform the comparison in the magnetic field-polarized state, where the magnetic order is trivial for SWT. However, the required polarizing magnetic field for K2Ni2(SO4)3 can be estimated to reach 25–30 T, and is therefore out of the reach of the current state-of-the-art facilities for INS measurements.

Even though the different sets of exchange parameters J1-J5 proposed for K2Ni2(SO4)3 are not very different, the magnetic order does change depending on the choice. To evaluate this, we perform cMC calculations on periodic systems consisting of L3 unit cells, where L is the linear size of the system. Because this method is best suited to detect classical magnetic orders in the absence of quantum fluctuations, it allows us to validate/invalidate the different Hamiltonians by comparing them to neutron scattering measurements below the critical temperature.

All our classical calculations indicate a transition to a magnetically ordered phase at finite temperatures. However, the lowest ground-state energy is only reached for L = 3n lattices (with critical temperature \({T}_{c}^{{{{\rm{cMC}}}}}/{J}_{4}=0.048(2)\)), while all other sizes (L ≠ 3n) give higher energies at T = 0, implying that the magnetic order is frustrated by periodic boundary conditions. The magnetic orders obtained for L = 12, 9, 6, and 3 are all identical, indicating a tripling of the magnetic unit cell and a perfect agreement with the Bragg points observed experimentally (Fig. 1d). Interestingly, if the DFT Hamiltonian corresponding to the room-temperature structure is used22, the L = 4n magnetic order has the lowest energy (only 0.09% below L = 3n), indicating a very sensitive landscape of complex magnetic configurations. Another recently suggested set of values with J3 = 023 leads to a quintupling of the magnetic unit cell, exhibiting the lowest ground-state energies for L = 5n lattices. These calculations evidence not only that it is not trivial to capture the experimentally observed Bragg structure22, but also give a certain level of confidence for the set of exchange interactions determined here based on the structure at 100 K.

The cMC magnetic structure for L = 3n, shown in Fig. 1e, comprises propagation vectors q1 = (1/3, 0, 0), q2 = (1/3, 1/3, 0) and q3 = (1/3, 1/3, 1/3). The resulting pattern is devoid of any particular spin textures like skyrmions and merons. In Fig. 1e, we show a view along the (111) plane for a L = 6 system, where black arrows on each node represent the direction of the net magnetic moment within each unit cell. The angles between neighboring cells are found to be close to 120∘. We do not expect a significant change in the calculated structure if the exchange parameters are slightly modified, as long as the tripling of the unit cell is preserved.

We should point out that the agreement between cMC and the weak magnetic Bragg scattering serves only to narrow down the appropriate set of Js. The ordered state in K2Ni2(SO4)3 remains highly dynamic down to the lowest temperatures22,23 and exactly how the weak static component emerges from a highly dynamic background remains to be investigated in future studies. A similarly strong dynamic ground state, with faint features of spin-glass order, has been observed in Tb2Hf2O727, with spin-liquid-like dynamics observed down to the lowest temperatures. In the rest of this work, we focus on temperatures above the ordering (T = 2 K) but significantly below the characteristic energy of the system (θCW = -18 K). In this case, the dynamic features above the ordering trace their origin to a region proximate in parameter space that exhibits purely spin-liquid characteristics and shows no magnetic order down to T = 0, as illustrated in Fig. 1f. Although the dynamics observed below the ordering temperature in K2Ni2(SO4)3 could potentially be also dominated by the spin-liquid-like features, as found for Tb2Hf2O7, it is also important to realize that entering the ordered state can significantly redistribute the scattering spectral weight, and often completely remove the spin-liquid features.

Dynamic and static spin structure factors

To characterize the dynamical features in K2Ni2(SO4)3, we have conducted INS experiments in three different directions within the (HLL) scattering plane. In Fig. 2, we present experimental results for the dynamical structure factor \({S}_{\exp }({{{\bf{q}}}},\ \omega )\) with the incident energy Ei = 2.8 meV obtained at 2 K, significantly above the appearance of order to avoid possible quasi-elastic scattering but well within the dynamical state. Energy-momentum plots along three principal directions show vertical streaks of intensity, four in each panel, indicating a non-dispersive type of excitations. The streaks are centered ~0.75 and 1.8 inverse units, and are very broad, excluding the possibility of a quasi-elastic scattering from ordering that would appear in a much denser grid at multiples of 1/3 of the unit cell22,23. The streaks are present both below and above the ordering, and their intensity fades very slowly towards high temperatures23. The upper energy bound of excitations is found to be ~2 meV, in agreement with the onset of correlations in specific heat below 20 K22. The energy dependence of the intensity of the scattering signal for various q-points found in the middle of broad peaks is featureless, with an approximately linear decreasing dependency on the energy (see Fig. 2d). Such q- and ω-dependence of the scattering intensity S(q, ω) allows us to estimate the equal-time magnetic structure factor

$${S}_{\exp }({{{\bf{q}}}}) \sim \int_{{\omega }_{1}}^{{\omega }_{2}}{S}_{\exp }({{{\bf{q}}}},\, \omega )\,d\omega$$
(1)

which can then be directly compared with theoretical predictions based on a given spin Hamiltonian. We note that a comparison on the level of S(q, ω) would be far from trivial, even within the ordered state due to multiple ordering vectors and 216 spins per magnetic unit cell. Additionally, SWT is by construction applicable for small deviations from a classical order; and in the case of K2Ni2(SO4)3, the deviations from the classical order cannot be taken as small perturbations, rendering it practically outside of the scope of a reliable application of a SWT. Finally, the ordered state of K2Ni2(SO4)3 proves to be rather peculiar, marked by only 1% of entropy release and weak magnetic Bragg scattering22. Other characteristic features of classical order, like oscillations in μSR and magnon dispersions, are completely absent22,23.

Fig. 2: Time-of-flight neutron scattering on single crystals of K2Ni2(SO4)3.
figure 2

Energy ω versus wave vector q for a q = (100), b q = (110) and c q = (111) directions. d Energy dependence of the dynamical structure factor \({S}_{\exp }({{{\bf{q}}}},\omega )\) obtained at several q-points (for which streaks of intensity are observed), revealing a monotonous decrease of intensity towards the high-energy background. q-points are: q1 = (0.50, 0.50, 0.00), q2 = (0.00, 1.70, 0.00), q3 = (0.65, 0.00, 0.00), q4 = (1.20, 1.35, 0.00), q5 = (0.50, 0.50, 0.50), q6 = (1.70, 0.00, 0.00), q7 = (0.00, 1.65, 1.65), q8 = (1.05, 1.40, 1.40).

Full size image

In Fig. 3a–c, we show the spin structure factor \({S}_{\exp }({{{\bf{q}}}})\) along three different planes in reciprocal space, obtained by integrating the intensity in the energy range from \({\omega }_{1} \sim {E}_{\min }=0.5\) meV to \({\omega }_{2} \sim {E}_{\max }=1\) meV. The extent of the incoherent scattering gives the lower limit, while the upper limit is found as an optimal value to maximize the signal-to-noise ratio. The patterns depicted carry fingerprints from the underlying magnetic lattice composed of two interconnected trillium lattices, with a hexagonal galaxy-like motif reflecting the chirality of the crystal structure (see Fig. 3c), arising from the non-centrosymmetric space group.

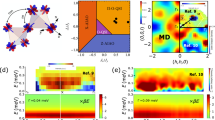
Fig. 3: Comparison of experimental and theoretical spin structure factors.
figure 3

Spin structure factor S(q) along different planes in reciprocal space (normalized by its maximum value within the plane, unless specified otherwise). a–c experimental data obtained by INS with the incident energy Ei = 5.0 meV, integrated in the range from 0.5 meV to 1.0 meV. In this case, the data is normalized by an arbitrary value of 11. d–f cMC calculations at T = 0.35 J4 (left half) and PFFRG calculations for Λ = 0.58 J4 (right half), using the form factor of Ni2+ ions. g–i line cuts along three principal directions indicated by white dashed lines in b.

Full size image

To reproduce these experimental patterns, we performed calculations using both quantum and classical approaches. In the quantum limit, we use PFFRG, which has been shown to produce accurate results in highly frustrated systems28,29,30,31,32. Within PFFRG, the renormalization-group flow is controlled by the cutoff frequency Λ, which is lowered from the interactions-free limit Λ = ∞ where the solution is known (see Supplementary Note 4). In this case, the flow breaks at Λ = 0.582 J4, indicating the presence of a magnetically ordered ground state. As is standard for the PFFRG calculations, the static spin correlations are measured slightly above the flow breakdown and, even though calculations are carried out at T = 0, the finite value of the renormalization-group parameter Λ produces an effect similar to finite temperature33. In an attempt to also simulate the experimental data using cMC, we perform calculations above the finite-temperature phase transition. We find an excellent agreement with the PFFRG calculations for a large range of temperatures and, particularly for T = 0.35 J4, we find the best quantitative agreement (see Fig. 3d–f). This quantum-to-classical correspondence at the level of static correlators has been previously reported in several frustrated 2D and 3D spin-1/2 Heisenberg models at finite temperatures34,35,36, some of which host a QSL ground state. However, it is important to note that this correspondence does not hold for the full dynamical spectrum of the models, which are different in quantum and classical systems. Very recently, it has been shown through perturbation theory that the quantum-to-classical correspondence breaks at fourth order in J/T, even though partial diagrammatic cancellations lead to good accuracy even at low temperatures37.

A more detailed comparison is obtained along the line cuts shown in Fig. 3g–i. As is evident from all three plots, there is very little difference between cMC and PFFRG results, upholding the quantum-to-classical correspondence. On the other hand, the agreement with the experiments is excellent in terms of the determination of peaks in the spin structure factor, which gives rise to pattern matching in the color plots. Deviations can be seen in terms of the predicted ratio of intensities of two principal peaks along [100] and [111], the width of peaks, as well as a qualitative difference at large q along [110]. At least partially, these deviations could be explained by the limitations of the finite energy range integration used in Eq. (1). A more thorough comparison would require a full theoretical description of S(q, ω). However, given the highly frustrated 3D network, the large unit cell, and the spin value S = 1, these calculations are beyond the reach of current theoretical methods. Despite this, we have shown that our theoretical description of K2Ni2(SO4)3 captures all the main aspects of its magnetism, covering both static and dynamic elements. That is to say, the DFT Hamiltonian we derived solely from the atomic positions enables us to reproduce the experimental Bragg structure and the magnetic unit cell below the phase transition (Fig. 1d) as well as the spin structure factor obtained by INS measurements above the ordering (Fig. 3a–c).

Proximity to a spin liquid

Due to the complexity of the underlying 3D magnetic network, with the classical limits for J3, J5 → 0 and J4 → 0, it is far from evident why it is so geometrically frustrated in the case of K2Ni2(SO4)3. Simpler networks with similar classically ordered ground states, like the square or triangular lattices, are very susceptible to the introduction of additional frustrating couplings which eventually drive them to spin-liquid states (J2/J1 ~ 0.5 and J2/J1 ~ 0.06 for the square38,39,40,41,42,43 and triangular lattice44,45,46,47,48,49, respectively, even though other non-magnetic states have been proposed for the square case50). In the context of a large variety of different compounds with the same structure, belonging to the langbeinite family, it represents an important task to pinpoint the source of the observed frustration. To this end, we have studied a wider range of the J3-J4-J5 parameter phase space with both PFFRG and cMC calculations. It turns out that the set of exchange parameters characterizing K2Ni2(SO4)3 lies very close to a so-far unexplored region where long-range magnetic order appears to be completely absent, centered around a particular point defined by J3 = 0, J4 = J5. In this limit, the lattice is composed of corner-sharing tetrahedra with every ion from one trillium lattice connected to the sites of the nearest equilateral triangle from the second trillium lattice (Fig. 1b), and therefore we call it a tetra-trillium lattice. In this lattice, half of all spins (i.e., those from one trillium lattice) are shared by three tetrahedra, while the remaining half (from the other trillium lattice) belongs to only one tetrahedron. Calculations performed in this limit do not show any signs of magnetic ordering in both classical S → ∞ (down to T = 0.001 J4) and extreme quantum S = 1/2, 1 limits (down to Λ = 0.01 J4) (see Supplementary Note 4), providing indications of spin-liquid behavior in both the classical and quantum limits.

The extent of the island of liquidity around the tetra-trillium lattice (indicated by the orange star in Fig. 4a), however, depends strongly on the spin value considered. For S = 1, PFFRG indicates a very narrow range around J3 = 0, with an extended set of values along the J5/J4 axis exhibiting a dynamical ground state, ranging from  ~0.8 up to  ~3.5. On the other hand, the S = 1/2 case exhibits the absence of magnetic order for J3 ≠ 0 for certain values of J5/J4 and extends up to larger J5/J4 below the pure trillium lattice limit J3 = J4 = 0. The wider area indicated by the line pattern in Fig. 4a indicates a region where it is numerically hard to determine the existence of a breakdown in the Λ-flow for the S = 1/2 case. Even beyond this region, the flow breakdowns are quite subtle, indicating weakly ordered phases. The set of parameters calculated with DFT for K2Ni2(SO4)3, indicated by a green circle in Fig. 4a, lies close to these putative spin-liquid regions. This becomes evident when the PFFRG spin structure factors from Fig. 3 are compared to the results obtained in the tetra-trillium lattice limit (at Λ = 0.01 J4) shown in Fig. 4c–e, as many of the features can be put in correspondence. Generally, the peaks become more smeared in the tetra-trillium limit, but there is no indication of a strong difference between the two phases. This provides evidence that the properties of K2Ni2(SO4)3 are governed by its proximity to the QSL phase in the tetra-trillium lattice19,20.

Fig. 4: The island of liquidity around the tetra-trillium lattice.
figure 4

a PFFRG correlated paramagnetic region, indicating no long-range order at T = 0, for S = 1/2 (red+blue) and S = 1 (red). The dashed part indicates the region where the existence of a flow breakdown is hard to determine for the S = 1/2 model. The green circle and orange star indicate the DFT model for K2Ni2(SO4)3 and the tetra-trillium lattice limit, respectively. b cMC calculations for the tetra-trillium lattice limit show no finite-size effects in the specific heat. Data for a single tetrahedron is also shown in a light-blue line. c–e Spin structure factor S(q) using cMC and PFFRG calculations for the tetra-trillium lattice on different planes at T = 0.001 J4 and Λ = 0.01 J4, respectively.

Full size image

In analogy to quantum spin ice, where a QSL arises out of a classical spin liquid (CSL) when adding quantum fluctuations, we address here the question of whether the classical tetra-trillium lattice also hosts a CSL which can potentially turn into a QSL when adding quantum fluctuations. The first indication is that cMC calculations show no ordering tendencies down to the lowest temperatures. However, a more conclusive proof of the CSL ground state in the classical limit can be constructed as follows. First, the Hamiltonian can be written as a disjoint sum of squared total spin in each tetrahedron (just as for the pyrochlore lattice). With this re-writing, the classical ground-state energy can be found exactly, given that a solution with zero net magnetic moment in each tetrahedron exists. This solution cannot exist for J5/J4 < 1/3, providing a theoretical limit (which we confirmed with cMC calculations). Second, for the tetra-trillium lattice, we confirmed that a collinear solution exists (which is also a solution of the Ising model) and clusters of 18 spins can be systematically found and flipped while conserving the property of vanishing total spin in each tetrahedron (see Supplementary Note 6). This allows the system to move through an extensive ground-state manifold and confirms the liquidity of this phase. Compared to the pyrochlore lattice, more spins are needed to construct a minimal flippable cluster because of the ramifications that occur at sites shared by three tetrahedra in the tetra-trillium lattice. When adding other couplings such as J1, J2, or J3, perfect squares cannot be completed anymore, and therefore the freedom to fluctuate is restricted. The cMC calculations show that even the smallest non-zero value of J3 results in a finite critical temperature (however small). On the other hand, for J5 > J4, no ordering is observed at least up to J5/J4 = 3.5. The spin structure factors corresponding to the CSL in the tetra-trillium lattice are shown in the left parts of Fig. 4c–e for T = 0.001 J4 in cMC.

The analogy between the tetra-trillium and the pyrochlore lattices can be advanced even further. As demonstrated in Fig. 4b, the specific heat per site reaches the value cv(T → 0) = 0.75 (without any phase transition) as in the CSL on the pyrochlore lattice, which indicates the absence of quartic modes associated with magnetic order51. Furthermore, the specific heat agrees quite well with that of a single tetrahedron, with small deviations occurring at intermediate temperatures 0.1 < T/J4 < 1.0, implying that the tetra-trillium lattice does not behave simply as a set of decoupled tetrahedra. In the case of the pyrochlore lattice, a U(1) (or Coulomb) CSL is realized, characterized by algebraically decaying correlations and an emergent gauge field that leads to pinch-point singularities in the spin structure factor3,52. As shown in Fig. 4, the spin structure factor of the tetra-trillium lattice does not present pinch-point singularities. This absence can be related to the non-bipartite character of the tetra-trillium lattice in terms of tetrahedra. In two dimensions it has been shown that this can lead to a so-called \({{\mathbb{Z}}}_{2}\) CSL, characterized by exponentially decaying correlations down to T = 0 and fractionalized magnetic moments53 (the properties derive actually from the eigenvalues of the adjacency matrix, which are gapped). Exponentially decaying correlations would also explain the negligible finite-size effects in Fig. 4b.

With these arguments, we have established that the classical version of the tetra-trillium model exhibits an extensive ground-state degeneracy and, hence, realizes a CSL. As in models on the pyrochlore lattice, these systems are particularly promising for realizing QSLs when adding quantum fluctuation. This is because quantum effects induce tunneling between the degenerate classical ground states (in our case via the aforementioned 18 spin-flip processes), which may lead to a liquid-like quantum superposition of extensively many classical states. This effect of quantum fluctuations is considerably different from the action of quantum fluctuations on top of a magnetically ordered state, where they merely induce a reduction of the ordered moment. Changing back the classical spins of the tetra-trillium model to S = 1 spins (as realized in K2Ni2(SO4)3) is expected to introduce substantial quantum fluctuations, particularly in the present case of isotropic Heisenberg interactions, which are devoid of any easy axis that can facilitate static spins. This fact, together with the observation that the PFFRG spin structure factors for the quantum S = 1 case at Λ = 0.01 J4 and the cMC results are considerably different (see Fig. 4c–e), evidences that the S = 1 tetra-trillium model is no longer a CSL. Nonetheless, quantum fluctuations are unable to select a unique magnetic ground-state out of the degenerate ground-state manifold of the CSL. Hence, the S = 1 tetra-trillium model remains magnetically disordered, as indicated by our PFFRG calculations. Taken together, these two observations make a QSL scenario for the S = 1 tetra-trillium model plausible. Changing the model parameters of the ideal tetra-trillium system back to the ones realized in K2Ni2(SO4)3 induces weak magnetic order, as seen in experiments and PFFRG. Nevertheless, key features of the spin structure factor of the ideal tetra-trillium system are still seen when simulating the system with the actual material parameters above the ordering transition, as is evident from a comparison between the PFFRG results in Figs. 3 and 4. Therefore, we conclude that the dynamics of K2Ni2(SO4)3 are still substantially governed by the quantum liquidity of the nearby ideal tetra-trillium point.

The evidence of strong dynamics seen in K2Ni2(SO4)3 opens a window of possibilities in search of exotic quantum phases born out of complex 3D lattice geometries beyond the iconic pyrochlore and hyperkagome lattices. Viewing the geometry as a tessellation of tetrahedra on a trillium lattice, we have unveiled a so-far unexplored frustration mechanism at play in the langbeinite family. The excellent agreement between experiment and theory demonstrated for K2Ni2(SO4)3 offers an opportunity to further test the applicability of theoretical concepts to a wider variety of compounds that belong to the langbeinite family. Our theoretical phase diagram identifying an island of liquidity centered around a highly frustrated tetra-trillium lattice provides a valuable guide in search of further promising QSL candidate materials. It is worth mentioning that despite the appearance of magnetic order outside of the identified regime, the ground states remain highly dynamic, thereby allowing for a wide temperature range where emergent phenomena arising out of an interplay between thermal and quantum fluctuations could be explored. An exciting task for future theoretical studies will be to identify possible structures of emergent gauge theories on the tetra-trillium lattice that could underlie the potential QSL behavior. Of particular interest in this context will be how the non-centrosymmetric character of the P213 (#198) crystallographic space group of K2Ni2(SO4)3 could give rise to a chiral QSL.

Methods

DFT-based energy mapping

We determine the Heisenberg Hamiltonian parameters for the T = 100 K structure of K2Ni2(SO4)3 by performing DFT-based energy mapping54,55 in the same way as was done for the room-temperature structure22. We use all electron DFT calculations with the full potential local orbital basis56 and a generalized gradient approximation (GGA) exchange-correlation functional57. We correct for strong electronic correlations on the Ni2+ 3d orbitals using a GGA+U functional58. We determine the parameters of the Heisenberg Hamiltonian written in the form

$$H={\sum}_{i < j}{J}_{ij}{{{{\bf{S}}}}}_{i}\cdot {{{{\bf{S}}}}}_{j}\,,$$
(2)

where Si and Sj are spin operators and every bond is counted once. We create a \(\sqrt{2}\times \sqrt{2}\times 1\) supercell with P21 space group that allows for eight symmetry-inequivalent spins. This provides 38 distinct energies of different spin configurations and allows us to resolve the eight nearest-neighbor exchange interactions, which we name J1 to J8. We choose the relevant value of the interaction U by demanding that the set of interactions match the experimental Curie-Weiss temperature.

Inelastic neutron scattering

Single crystal inelastic neutron scattering data was obtained on the time-of-flight (TOF) instrument LET59, ISIS (Didcot, UK) using four different crystals grown from the melt22. The crystals, amounting to a total mass of 0.45g, were co-aligned on aluminum posts, to access the (HHL) scattering plane. Cadmium shielding was used to reduce the background signal arising from brass and aluminum. The INS measurements were performed at T = 2 K, with three different incident energies of Ei = 2.8, 5, and 11.7 meV. The (HHL) reciprocal space maps were obtained by scanning over an angular range of 140° in 1° steps for 18 h, spending 7.5 min/° for a total of 140 runs. The Horace software was used for visualizing and analyzing the four-dimensional S(q, ω) data from the TOF experiment60. The single crystal TOF data was symmetrized with respect to symmetry operations in the P213 space group of K2Ni2(SO4)361,62. In our analysis, we normalized and added together data from different equivalent planes based on the space group symmetries. For the (100) and (110) families of planes we applied 8 symmetry operations to include reflection and inversion symmetries along the two perpendicular axes and about the origin respectively: (x, y, z), (−x, y, z), (x, −y, z), (x, y, −z), (−x, −y, z), (x, −y, −z), (−x, y, -z), (−x, −y, −z). For the (111) family of planes, we applied a 6-fold rotational symmetry.

Classical Monte Carlo

The cMC calculations were carried out using a logarithmic cooling protocol from T = 2 J4 down to T = 0.001 J4 with 150 temperature steps. Systems of up to 8 × 123 = 13824 unitary spins are considered. At each temperature, 105 cMC steps were performed. Each cMC step consists of N Metropolis trials and N overrelaxation steps intercalated, where N is the number of spins. The acceptance rate of the Metropolis trials is kept at 50% using the adapted Gaussian step63. Correlations are calculated over already thermalized states at selected temperatures by doing 4 × 105 cMC steps while measuring correlations once every 100 steps. All results are then averaged over 5 independent runs. The spin structure factors are calculated taking into account the positions of the Ni atoms corresponding to each model, as well as the form factor corresponding to Ni atoms.

Pseudo-fermion functional renormalization group

All results for S = 1/2 and S = 1 quantum spin models in this paper are obtained by standard PFFRG32 with the following specifications (general information on the method is provided in Supplementary Note 4). Vertex frequency dependencies are approximated by finite grids with exponentially distributed frequencies. The self-energy is evaluated for 1000 positive frequency arguments. Frequency grids for the two-particle vertex contain 32 positive values for each of the three transfer frequencies. Spin-correlations spanning over distances larger than three lattice constants of the underlying cubic lattice are neglected. After consideration of lattice translation symmetries, this implies the computation of spin-correlations along 1842 lattice vectors, or 622 vectors unrelated by lattice symmetries. For the computation of the phase diagram Fig. 4a, the maximum included correlation vector distance is reduced to two lattice constants, implying 186 vectors unrelated by symmetry. Flow equations are solved by the application of an explicit embedded Runge-Kutta (2, 3) method with adaptive step size64.