Introduction

Variance components and their functions are essential parameters of interest in selection experiments. In recent decades linear mixed model (LMM) analysis has become a popular tool for analyzing breeding data. The LMM analysis involves estimating variance components and predicting breeding values assuming the estimated variance components are correct. Several methods are available for the estimation of variance components (Searle et al. 2009), but Residual/Restricted Maximum Likelihood (REML) is the method of choice in pedigreed selection experiments (Lynch and Walsh 1998). The REML is a variation of the Maximum Likelihood (ML) method with an edge over the ML method in that the REML estimates of variance parameters are unbiased by the estimation of fixed effects (Patterson and Thompson 1971). The caveat is that the significant properties of the likelihood estimators are valid when the sample size approaches infinity, and the behavior of the same when working with small sample size is primarily unknown (Psutka and Psutka 2019). The likelihood theory suggests that the parameter estimates asymptotically have a multivariate normal distribution with covariance matrix given by the inverse of information matrix, i.e., the inverse of the matrix of second partial derivatives of the likelihood function (Meyer and Houle 2013). An estimate of sampling variance, a measure of the reliability of the parameter estimates (variance components and their functions), can be obtained from the inverse of the information matrix.

Though the estimation of sampling variance is straightforward, it is difficult to calculate reliable confidence intervals around functions (heritability) of these parameters (Waldmann and Ericsson 2006). Heritability, defined as the ratio of additive genetic variance to total phenotypic variance, is an important genetic parameter used to assess the potential for genetic improvement. The standard procedure to obtain the sampling variance of heritability is to linearly approximate the function with its first-order Taylor series expansion and then calculate the variance of this linear approximation (Meyer and Houle 2013) by the Delta method (Lynch and Walsh 1998). The REML analyses implemented in standard software packages such as WOMBAT (Meyer 2007), DMU (Madsen et al. 2014), ASREML (Gilmour et al. 2015), Echidna (Gilmour 2018), among others use the Delta method. However, the sampling variance might be biased under an incorrect asymptotic approximation, especially when sample size is small (Thai et al. 2013).

Moreover, while there are large-sample approximations for the sample variance of a REML variance estimator, it is unclear as to what amount of data constitutes a large enough sample size (Walsh and Lynch 2018). There are no direct approaches available to estimate the optimum sample size for a meaningful asymptotic approximation of likelihood estimates; hence, the large sample size is often a gray area. The multivariate normality of the likelihood estimates (the assumption under which the sampling variance of parameter estimates are quantified) is only valid when the sample size approaches infinity. Often, there is a lack of sufficient data to fulfill the conditions of optimal likelihood estimates. Therefore, the use of alternative approaches to evaluating uncertainties in variance components and their functions is desirable. Sampling-based methods are an option for estimating uncertainties associated with parameter estimates. Sampling approaches are usually aimed at generating a full distribution of parameter estimates instead of the point estimators. The full distribution of estimates can provide a complete picture of the uncertainties associated with estimating unknown parameters.

We aimed to compare the sampling variance in the estimates of variance components and heritability for three different traits (body weight with high heritability, body depth with medium heritability, and condition factor with low heritability) in Clarias magur (an Indian catfish species) obtained from the REML method with those obtained from sampling-based methods to assess whether the present moderate sample size was large enough to obtain a reliable asymptotic approximation. It was hypothesized that if the sample size contains sufficient information, the estimates obtained from various approaches should agree. Four well-known sampling-based methods were compared with the REML estimates viz., nonparametric bootstrapping, parametric bootstrapping, asymptotic sampling and Bayesian method to obtain a comprehensive picture of the uncertainty in the estimates of variance components and heritability.

Materials and methods

Dataset

The data used in the present study were from the base population of Clarias magur from an ongoing genetic selection program under ICAR-Central Institute of Fisheries Education, Mumbai, India. The Indian catfish, C. magur, is an economically important species with a high aquaculture potential. The fish used in the present study consisted of 78 fullsib families produced across 2 years (2014 and 2015) following a single pair mating design (each male mated with only one female—supplementary material attached as Annexure-1). The brooders were collected from three natural populations from three distinct geographical locations, viz., Andhra Pradesh, Assam, and West Bengal. Of the total 2328 fingerlings stocked, the measurements from 1413 survived fish were made after a year of communal rearing under mono and polyculture systems in different earthen ponds. The details of breeding, larval rearing, PIT tagging and communal rearing used in this study are described elsewhere (Jousy et al. 2018; Rameez et al. 2020). This study focused on the three important traits in aquaculture, body weight (BW), body depth (BD), and condition factor (K).

The animal model

An animal model in matrix notation takes the following form,

$${{{{y}}}} = {{{{X}}}}\beta + {{{{Zu}}}} + {{{{e}}}}$$

where y is a vector of observations on all individuals, β is a vector of fixed effects (stock, batch, pond, sex, and body-weight at stocking as linear covariate), X represents a design matrix (principally 0s and 1s) relating the fixed effects to each individual, u is a vector of random animal effects, Z is a design matrix relating the random effects to each individual and e is a vector of residual errors. It is assumed that random effects u and e are normally distributed with mean zero and variance-covariance matrix G and R respectively, u ~ N(0, G) and e ~ N(0, R).

G is a matrix that is made of additive genetic covariances between relatives i and j, which is given by twice the coefficient of coancestry (2Θij − the probability that an allele is drawn at random from individual i will be identical by descent to an allele drawn at random from individual j) times the additive genetic variance in the base population, i.e., \({{{{G}}}} = 2\Theta _{{{{{ij}}}}}{\it{\upsigma }}_{{A}}^2\) or \({{{{G}}}} = {{{{A}}}}_{{{{{ij}}}}}\sigma _{{A}}^2\), where A is known as the additive genetic (or numerator) relationship matrix and has elements Aij = 2Θij. e is assumed to be independently and identically distributed (iid). Hence the residual variance-covariance matrix is given by \({{{{R}}}} = \sigma _{{{{e}}}}^2{{{{I}}}}\), where \(\sigma _{{{{e}}}}^2\) is the residual variance and I is the identity matrix.

REML estimation of variance components

Mathematically REML is based on the linear transformation of the observation vector y to y* that removes the fixed effects from the model, with the help of a transformation matrix K such that KX = 0 (Lynch and Walsh 1998). Applying the transformation matrix then yields the model equation as y* = KZu + Ke and the REML estimates are essentially the ML estimates for these transformed variables (Kruuk 2004). The transformation matrix K is also called the matrix of error contrasts, and hence REML is sometimes known as Residual Maximum Likelihood (Littell et al. 2006). The variance components using the REML method were estimated in software Wombat (Meyer 2007) using an animal model. For an animal model with a single random effect, the REML analysis will provide estimates \(\sigma _{{A}}^2\) and \(\sigma _{{e}}^2\), from which the heritability was estimated as \({{{{h}}}}^2 = \sigma _{{A}}^2/\left( {\sigma _{{A}}^2 + \sigma _{{e}}^2} \right)\).

Prediction of random effects

In an animal model, the random effects of interest are known as the breeding values of individual animals. An individual’s breeding value for a given phenotypic trait is the total additive effect of its genes on that trait (Falconer and Mackay 1996). A general method for predicting random effects, known as the Best Linear Unbiased Predictor (BLUP), predicts individuals’ breeding values from field records of large and complex pedigrees (Lynch and Walsh 1998). Robinson (1991) lists four different derivations for BLUPs of which the one developed by Henderson (1973) can obtain BLUP for random effects simultaneously with the Best Linear Unbiased Estimators of the fixed effects and hence the method is popularly known as Henderson’s mixed model equation (MME). The MME for a general mixed model setting is:

$$\left[ {\begin{array}{*{20}{c}} {{{{{X}}}}^\prime {{{{R}}}}^{ - 1}{{{{X}}}}} & {{{{{X}}}}^\prime {{{{R}}}}^{ - 1}{{{{Z}}}}} \\ {{{{{Z}}}}^\prime {{{{R}}}}^{ - 1}{{{{X}}}}} & {{{{{Z}}}}^\prime {{{{R}}}}^{ - 1}{{{{Z}}}} + {{{{G}}}}^{ - 1}} \end{array}} \right]\,\left[ {\begin{array}{*{20}{c}} {\widehat \beta } \\ {\widehat {{{{u}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{{{X}}}}^\prime {{{{R}}}}^{ - 1}{{{{y}}}}} \\ {{{{{Z}}}}^\prime {{{{R}}}}^{ - 1}{{{{y}}}}} \end{array}} \right]$$

Suppose we assume that residual variance is iid, in that case, the R matrix can be factored out, and the MME for the animal model will reduce to (Isik et al. 2017):

$$\left[ {\begin{array}{*{20}{c}} {{{{{X}}}}^\prime {{{{X}}}}} & {{{{{X}}}}^\prime {{{{Z}}}}} \\ {{{{{Z}}}}^\prime {{{{X}}}}} & {{{{{Z}}}}^\prime {{{{Z}}}} + {{{{A}}}}^{ - 1}\alpha } \end{array}} \right]\,\left[ {\begin{array}{*{20}{c}} {\widehat \beta } \\ {\widehat {{{{u}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{{{X}}}}^\prime {{{{y}}}}} \\ {{{{{Z}}}}^\prime {{{{y}}}}} \end{array}} \right]$$

where, \(\alpha = \frac{{\sigma _{{e}}^2}}{{\sigma _{{A}}^2}}\,{{{{or}}}}\,\left( {1 - {{{{h}}}}^2} \right)/{{{{h}}}}^2\). The solutions to these equations are the best linear unbiased estimators of \(\widehat \beta\) and the best linear unbiased predictors of \(\widehat {{{{u}}}}\) for a given value of α. The BLUP breeding values were predicted by solving MMEs in Wombat (Meyer 2007) using estimated REML variances.

The standard error of heritability

Heritability is a nonlinear function (ratio) of variance components. The usual way to estimate the variance of a ratio is by the Delta method (Lynch and Walsh 1998). The Delta method uses the first-order Taylor series expansion of the function about the estimated \(\widehat \Theta\) parameter (Meyer and Houle 2013). For the nonlinear function heritability, \({{{{h}}}}^2 = {{{{f}}}}\left( \Theta \right) = \sigma _{{A}}^2/\left( {\sigma _{{A}}^2 + \sigma _{{e}}^2} \right)\), provided f(Θ) is differentiable and continuous around the estimated \(\widehat \Theta\), the variance of heritability is given as (Stefan 2017):

$${{{{Var}}}}\left( {{{{{h}}}}^2} \right) \approx \left( {\frac{{\partial {{{{h}}}}^2}}{{\partial \sigma _{{A}}^2}}} \right)^2\;\sigma _{\sigma _{{A}}^2}^2 + \left( {\frac{{\partial {{{{h}}}}^2}}{{\partial \sigma _{{e}}^2}}} \right)^2\,\sigma _{\sigma _{{e}}^2}^2 + 2\left( {\frac{{\partial {{{{h}}}}^2}}{{\partial \sigma _{{A}}^2}}} \right)\,\left( {\frac{{\partial {{{{h}}}}^2}}{{\partial \sigma _{{e}}^2}}} \right)\,\sigma _{\sigma _{{{A}}\prime }^2\sigma _{{e}}^2}$$

the square root of which gives the asymptotic standard error of heritability.

The functions, \(\left( {\frac{{\partial {{{{h}}}}^2}}{{\partial \sigma _{{A}}^2}}} \right) = \frac{{\sigma _{{e}}^2}}{{\left( {\sigma _{{A}}^2 + \sigma _{{e}}^2} \right)^2}}\) and \(\left( {\frac{{\partial {{{{h}}}}^2}}{{\partial \sigma _{{e}}^2}}} \right) = \frac{{ - \sigma _{{A}}^2}}{{\left( {\sigma _{{A}}^2 + \sigma _{{e}}^2} \right)^2}}\) are the partial derivatives of the function of heritability with respect to the estimated additive genetic variance and error variance, respectively. The notations, \(\sigma _{\sigma _{{A}}^2}^2\), \(\sigma _{\sigma _{{e}}^2}^2\) and \(\sigma _{\sigma _{{{A}}\prime }^2\sigma _{{e}}^2}\) are the variance of additive genetic variance, the variance of the error variance and covariance between additive genetic variance and error variance, respectively, all of which can be obtained from the asymptotic variance-covariance matrix. Based on the standard errors from the delta method, ~95% confidence intervals (CI) were computed as \({{{{h}}}}^2 \pm 1.96\widehat \sigma _{{{h}}^2}\).

Nonparametric bootstrap (NPBS)

A Nonparametric subject-wise bootstrap, wherein samples were drawn from the predicted random animal effects (BLUPs) and residuals, was performed. The resampling unit was a parent and its offspring, taking into account the family structure. The NPBS was performed under three different schemes. A total of 10,000 new datasets were generated, and for each data set, heritability was estimated using REML to obtain the sampling distribution of heritability estimates. The bootstrap samples were obtained as follows:

  1. 1.

    Fit the model, y = Xβ + Zu + e, to the data

  2. 2.

    Predict the random animal effects \(\widehat {{{{u}}}}\) and residuals \(\widehat {{{{e}}}}\)

  3. 3.

    Obtain vector of fixed effects as \(\widehat {{{{y}}}} = {{{{y}}}} - \left( {\widehat {{{{u}}}} + \widehat {{{{e}}}}} \right)\), where \(\widehat {{{{y}}}}\) is y vector corrected for effects of \(\widehat {{{{u}}}}\) and \(\widehat {{{{e}}}}\)

  4. 4.

    Draw random animal effects with replacement from predicted \(\widehat {{{{u}}}}\) (step 2) to obtain new \(\widehat {{{{u}}}}^ \ast\)

  5. 5.

    Draw residuals with replacement from predicted \(\widehat {{{{e}}}}\) (step 2) to obtain new \(\widehat {{{{e}}}}^ \ast\)

  6. 6.

    Create new y values \(\widehat {{{{y}}}}^ \ast\) as \(\widehat {{{{y}}}}^ \ast = \widehat {{{{y}}}} + \widehat {{{{u}}}}^ \ast + \widehat {{{{e}}}}^ \ast\)

  7. 7.

    Fit the model \(\widehat {{{{y}}}}^ \ast = {{{{X}}}}\beta + {{{{Zu}}}} + {{{{e}}}}\) to the new data set to estimate variance components and obtain heritability

  8. 8.

    Repeat the steps from 4 to 7 for 10,000 times

    The NPBS was performed in six ways viz., two methods of analysis (animal model and family model) by three sampling schemes:

    1. (1)

      u and e treated independently; bootstrap samples built separately from u and e without randomizing the families

    2. (2)

      Linkage between u and e maintained; bootstrap samples built from u + e without randomizing families and

    3. (3)

      Linkage between u and e maintained; bootstrap samples built from u + e randomizing the families.

The separation of the animal effect into genetic (u) and residual (e) components via the mixed model equations is in fact, just a computational strategy for fitting an animal effect that is correlated within families. In this data, where the genetic relationships are essentially defined as fullsib families (4 of the 78 are half-sib), the family model and animal model are (almost) equivalent, and the essential information required for bootstrapping is given by u + e nested in families.

Parametric bootstrap

Here, new data sets were generated by sampling values for the animal effects and residuals for the data and pedigree structure from a multivariate normal distribution with a mean zero and covariance matrix as estimated from the REML analysis, a form of model-based simulation. The parametric bootstrap sample was obtained as follows:

  1. 1.

    Fit the model y = Xβ + Zu + e to the data

  2. 2.

    Estimate the overall mean E(y) = Xβ

  3. 3.

    Generate random animal effect \(\widehat {{{{u}}}}\) and residuals \(\widehat {{e}}\) from the multivariate normal distribution

  4. 4.

    Create new \(\widehat {{y}}\) values as \(\widehat {{{{y}}}} = {{{{E}}}}\left( {{{{y}}}} \right) + \widehat {{u}} + \widehat {{e}}\)

  5. 5.

    Fit the model \(\widehat {{{{y}}}} = {{{{X}}}}{{\beta}} + {{{{Zu}}}} + {{{{e}}}}\) to the new data set to estimate variance components and obtain heritability

  6. 6.

    Repeat steps 3 to 5 for 10,000 times

Asymptotic sampling

A total of 10,000 sets of the variance components (both additive genetic variance and residual variances) were sampled from the multivariate normal distribution. The MVN was parameterized with the mean and covariance matrix obtained from the REML analysis. The heritabilities were estimated from the samples of variance components obtained in Wombat (Meyer 2007).

Bayesian estimation

The MCMCglmm package in R software, a combination of Gibbs sampling, slice sampling and Metropolis-Hastings updates, was used to generate the chain (Hadfield et al. 2019). The starting values generated by the default heuristic techniques within MCMCglmm were used to initialize the chain. A single chain was generated with a chain length of 10,00,000 iterations with a thinning interval of 100 iterations (which means only one iteration value is saved for every 100 iterations) to reduce the autocorrelation between successive values (de Villemereuil 2012). A burn-in period of 50,000 iterations was used to ensure the convergence of the chain before saving iteration values. A total of 9500 values of variance estimates were sampled from the chain for every trait, and heritability was estimated for each sampled variances.

An inverse-gamma distribution was used as the prior for variance components, and a diffuse normal prior centered around zero with a very large variance (108) was used for the mean (Hadfield et al. 2019). The inverse-gamma distribution was parameterized by two parameters nu (shape) and V (scale), where nu = 0.002 and V = 1. The inverse-gamma distribution allows for a weakly informative prior on variance components and U-shaped prior (with a very steep shape on the borders in 0 and 1) on the heritability (de Villemereuil 2012). For algebraic convenience, under the Bayesian method, the trait values of K was first multiplied with a constant (100 in this case) before estimation of the variance components.

Convergence was assessed visually by looking at trace plots of parameters. The convergence diagnostic as proposed by Geweke (1992) for Markov chains was used to statistically test the chain for convergence. It was based on a test for equality of the means of the first and last part of a Markov chain (by default, the first 10% and the last 50%). Geweke’s statistic was estimated as a statistical test for convergence using gewke.diag() function from the coda package in R. A thinning interval of 100 was used to reduce the autocorrelation and get a better effective sample size, wherein only one iteration value was picked from every 100 iterations. The thinning also reduces the memory required to hold results and lightens downstream analysis.

A 95% Highest Density Region (HDR) is interpreted as a 1 − α (0.95) probability that the interval contains the actual value of the unknown parameter as opposed to the 95% CI from the frequentist method where 1 − α (0.95) of the time the confidence intervals will enclose the parameter. HDRs are estimated by the HPDinterval() function from the coda package in R. The mode of the posterior distribution was estimated using the function posterior.mode() from the coda package in R. The kernel density plots were obtained using proc kde in SAS 9.3.

Results

REML estimates

The results from the REML analysis of variance components and heritability are presented in Table 1. The additive genetic variance (255.20) and the residual variance (325.20) for the body weight and other traits (Table 1) were obtained by REML using the average information algorithm, and the corresponding sampling variances were obtained from the inverse of the average information matrix. The heritability estimates of 0.44 for BW, 0.22 for BD, and 0.08 for K were obtained as the function of variance components (ratio of additive genetic variance and total phenotypic variance), and their sampling distributions were obtained by approximating the function with its first-order Taylor series expansion. The results and their corresponding approximate 95% CI are given in Table 1.

Table 1 Estimates of variance components, heritability with their sampling variance and confidence intervals for various traits.
Full size table

MCMC diagnostics

Convergence and autocorrelation

The additive genetic variances, residual variances and heritabilities for body weight are presented in Fig. 1, plotted against iteration number. This shows the fluctuation in sampled values over the iterations (50,000 to 1,000,000 after dropping the first 50,000 iterations, known as burn-in). The trace plot depicts a well-mixing chain, which moves through the entire subset of parameter space without settling to any particular region. The MCMC trace plots for BD and K also followed the same pattern (not presented). The Geweke’s test statistic was a standard Z-score; all the p values for the Z scores from Geweke diagnostics for convergence of variance components and heritabilities of BW, BD, and K were greater than 0.05. Since Geweke’s statistic did not reveal any significant difference between the mean of the values sampled from the first and the last parts of the Markov chains, it indicates convergence and proper mixing of the chains. Also, the thinning interval of 100 reduced the autocorrelation of samples within the range of −0.001 to 0.10 for different traits (Table 2). Autocorrelations for additive genetic variances and residual variances for BW, BD, and K at five different points of iterations are given in Table 2, where Lag 100 stands for autocorrelation of estimates 100 iterations apart. The autocorrelation between additive genetic variance within the traits ranged from −0.001 to 0.10 and 0.001 to 0.05 for the residual variance.

Fig. 1: Trace plots of the sampled values for additive variance, residual variance and heritability along the iterations from MCMC sampler for trait BW.
figure 1

(A) Additive genetic variance, (B) Residual variance, and (C) Heritability.

Full size image
Table 2 Autocorrelation values for different intervals for the MCMC chain.
Full size table

High-density regions (HDRs)

The posterior probability distribution of additive genetic variance, residual variance and heritabilities for trait BW are presented in Fig. 2 a, b. The additive genetic variance for BW ranged from 119.70 to 678.30 (See Fig. 2) with a 95% probability of the parameter values between 174.50 and 400.30, whereas the residual variance had 95% HDR ranging from 321.20 to 466.90 (Table 1). The posterior probability means of additive genetic variance and residual variance were 279.40, and 395.40 for BW, 0.0257 and 0.1070 for BD, 0.00124 and 0.00992 for K, and are presented in Table 1. The mean of the variance components and heritabilities for BW, BD and K are presented in Table 1. The heritabilities estimated by REML and the Bayesian method for BW, BD, and K were similar (Table 1).

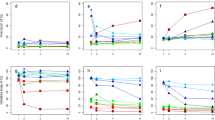
Fig. 2: Distribution of variance components and heritabilities estimated for BW from four methods.
figure 2

a A (Column 1: Additive variance; Column 2: Residual variance; Row 1: Bayesian MCMC, Row 2: NPBS AM scheme 1, Row 3: Parametric bootstrapping and Row 4: Asymptotic sampling. b Heritabilities Row1-Column1: Bayesian MCMC, Row1-Column2: NPBS AM scheme 1, Row2-Column1: Parametric bootstrapping and Row2-Column2: Asymptotic sampling.

Full size image

Heritability estimates of BW obtained from the posterior distribution of variance components ranged from 0.20 to 0.77 with the posterior mean and median heritability of 0.41 and the posterior mode of 0.43, with a standard error of 0.07 for the mean heritability (Table 1). HDR 95% regions of heritability for BW ranged from 0.27 to 0.54, indicating a 95% probability for the true value of heritability to lie between 0.27 and 0.54. The mean heritability for BD and K were 0.19 and 0.11, respectively, which were similar to their median heritabilities.

Bootstrap estimates

Nonparametric bootstrap sampling (NPBS)

The distribution of the variance components and heritabilities for BW obtained from nonparametric bootstrap is illustrated in Fig. 2 a, b. The distributions of variances and heritabilities of three traits are summarized in Table 1. A total of 10,000 bootstrap samples were obtained for each of the six scenarios, and the variance parameters were re-estimated by REML. Under the animal model, nonparametric bootstrap sampling was performed from the vector of animal effects (BLUPs) and residual effects sampling within fullsib (dam) families. The results are summarized in Table 1 with respect to the variance components and the heritability estimate. The 95% CI constructed for variance components and heritability by calculating the 2.5th and 97.5th percentile of bootstrap distribution is also given in Table 1.

The estimates of additive genetic variance (207.10–302.46), residual variance (Animal model: 230.00–358.52; Family model: 498.97–524.40) and heritabilities (0.34–0.51) for BW varied across the six NPBS schemes using animal model and family model, so as for BD and K (Table 1). For the NPBS models, resampling u and e independently without randomizing families (Scheme 1) gave rise to the lowest estimated residual variances for BW, BD, and K under the animal model; under the family model, scheme 2 had the lowest residual for K. Recognizing the dependence (correlation) between the estimates of and the randomization of families (Scheme 3) yielded the highest estimated residual variance for all traits under both animal model and family model. Assuming independent u and e in the animal model (Scheme 1) has inflated heritability (the quantum of inflation increased with decreasing REML heritability), and under dependent u and e assumption in the animal model, the non-randomization (Scheme 2) and randomization (Scheme 3) yielded heritability estimates with differences of the order 0.08 for BW (Scheme 2: 0.41; Scheme 3: 0.49), 0.03 for BD (Scheme 2: 0.32; Scheme 3: 0.29) and 0.01 for K (Scheme 2: 0.18; Scheme 3: 0.17). The family variance was the lowest under the independent u and e model even when the families were randomized (Scheme 1) for all three traits. Under the dependent u and e assumption in the family model, the family randomization (Scheme 3) gave higher family variance for BW. For BD and K, the non-randomization (Scheme 2) and the randomization (Scheme 3) yielded similar family variance. For both the animal and family model, the highest residual variance was observed under the dependent u and e model with family randomization for all three traits. Assuming independence of u and e, family model scheme 1 gave the lowest heritability for all three traits (Table 1). Additionally, the results from various NPBS schemes, applied on different data sets with varying family size and the total sample size randomly sampled from the original data, is attached as a supplementary file (Annexure-2).

Parametric bootstrap

The results obtained from the parametric bootstrap are presented in Table 1. The distribution of variance components and heritabilities for BW are illustrated in Fig. 2. The estimates of variance components were calculated as the mean of the parameter estimates from bootstrap samples and the confidence interval as the values lying between 2.5th and 97.5th percentile. The additive genetic variance and residual variance for different traits estimated from the parametric bootstrap, along with its standard errors, are provided in Table 1. The variance and heritability estimates for three traits obtained from the parametric bootstrap were similar to that of the REML estimates (Table 1).

Asymptotic sampling

The estimate of variance components and heritabilities for different traits were obtained as the mean of all the sampled values and is presented in Table 1. The distribution of the sampled values for additive genetic effects and residual effects and heritabilities for BW is given in Fig. 2 a, b. The values of variances and heritabilities estimated for the traits considered were similar to REML estimates.

Comparison of estimates

Variance components, heritabilities and their uncertainties were estimated from five different methods, of which the heritabilities ranged from 0.34 to 0.51 for BW, 0.11 to 0.38 for BD and 0.09 to 0.19 for K across the methods (Table 1). Estimates of heritabilities and standard errors obtained from REML, parametric bootstrap and asymptotic sampling were similar for different traits (BW: 0.44, BD: 0.22 and K: 0.10). MCMC sampling also gave similar heritability estimates as REML for different traits. Under the NPBS models, the average heritability of BW for Scheme 3 was 0.49 ± 0.07, less than 1 SD above the REML estimate. The other schemes disagreed more with the REML estimate, but the REML estimate was still well within the 95% coverage range. The 95% coverage probabilities of variance components and heritabilities from different methods for BW are given in Table 3. The coverage probabilities obtained for different methods ranged from 0.94 to 0.98 (Table 3). For the traits BD and K, the REML heritability was within the 95 % CL of the NPBS scheme 3 using both animal model and family model, and the largest bias was observed in scheme 1.

Table 3 Coverage probabilities for NPB: Nonparametric bootstrap, PB: Parametric bootstrap, BYS: Bayesian estimation, ASY: Asymptotic sampling.
Full size table

For subjective comparison, overlaid kernel density graphs for additive variance, residual variance and heritabilities of BW obtained from different sampling-based methods are illustrated in Fig. 3 a–c. These figures show that the distribution of additive genetic variance, residual variance and heritabilities are approximately normal. The location of the peak of distribution for the additive genetic variance does not vary significantly (well within 1 SD of REML estimate of additive variance) among the methods, with the smallest sampling variance for the additive genetic variance obtained from NPBS models (with a sharp peak and narrow confidence interval) giving higher confidence in the parameter estimated. Among different methods, the sampling variance for additive variance was high for the MCMC method with a wider confidence interval. The distribution for residual variance varied largely among methods (Fig. 3b), where both the lowest and the highest residual variance were obtained from NPBS models. Both the parametric bootstrap and asymptotic sampling gave rise to similar distribution for a residual variance. The sampling variance obtained from REML, parametric bootstrap, MCMC method and asymptotic sampling for a residual variance were similar. The parametric bootstrap, MCMC method and asymptotic sampling gave identical distribution for heritability estimates. The distribution for the NPBS model with independent u and e assumption largely varied from the empirical distribution of other methods (Fig. 3c).

Fig. 3: Overlaid kernel density graphs for BW obtained from different methods.
figure 3

a Additive genetic variances, b Residual variances, and c Heritabilities.

Full size image

Discussion

In REML estimation, the maximization of likelihood can be achieved differently depending upon the order of derivatives available (Thompson and Mäntysaari 1999). The precise class of algorithms are derivative-free (DF) methods, of which simplex/polytope (Nelder and Mead 1965) and Powell’s algorithms (Powell 1964) are more common. The most popular algorithm involving the first derivatives is Expectation-Maximization (EM REML) algorithm, while the Average-Information algorithm (AI REML) is the most popular involving second derivatives (Misztal 2008).

The DF approaches are fast for simple models, whereas they are expensive and unreliable for complicated models and have become obsolete (Gilmour et al. 1995). The EM algorithm was considered the most reliable but is slow in convergence and does not directly generate the standard error of the estimate. AI REML is popular because it is much easier to compute than other second derivative methods like Newton-Raphson and Fisher Scoring, it is not much more complicated than EM per iteration and it requires many fewer iterations (Gilmour et al. 1995). One advantage of using the Newton-Raphson or Average Information algorithm is that the matrix of the second derivatives of the log-likelihood evaluated at the optima, known as the Hessian matrix (H), is available upon completion. Serfling (1980) explained with the help of the asymptotic theory of maximum likelihood that matrix 2H−1 is an asymptotic variance-covariance matrix of the estimated parameters of G and R. In the breeding experiments, heritability is the primary genetic parameter used to assess the potential for genetic improvement. It is estimated as a non-linear function (ratio) of variance components (Meyer and Houle 2013; Stefan 2017). Under the REML method, the estimated heritability’s reliability/standard error (SE) is obtained from the first-order Taylor series approximation of the function of heritability. In all these methods, the estimation of reliabilities is based on the large sample (asymptotic) theory, where the test and confidence intervals are based on the asymptotic normality (Serfling 1980). These estimates of standard errors may be unreliable, especially under small sample sizes, since these methods are based on approximations (Littell et al. 2006). In the present study, we compared the variance components and their reliabilities and the precision of heritability estimates obtained from the REML method with the corresponding estimates obtained using various sampling methods.

The sampling-based methods are costly on time compared to the REML method. However, the time required for sampling-based methods depends upon the sample size, the number of iterations envisaged, and the software and the computational capacity. The recorded CPU time ranged from 45 to 90 min in the present study, depending upon the method (AMD A10-8700P Radeon R6, 10 Compute Cores 4 C+6 G 1.80 GHz with 8 GB installed RAM).

Bootstrap vs REML estimates

Bootstrap methods are an alternative approach for estimating the reliability/SE of parameters and constructing the confidence interval without assuming the symmetric distribution. Model-based bootstrapping was first developed under simple linear models, where bootstrap samples were based on residuals (Efron 1979; Efron and Tibshirani 1994). In the simple linear models, the residuals are resampled either from an estimated empirical distribution of the residuals (parametric bootstrap) or are resampled from the initial residuals without any distributional assumptions (nonparametric bootstrap). The resampled residuals are then added onto an estimate of the mean function obtained from the data (Morris 2002) to create a new set of observations to analyze. In the present study, the same idea was extended to the animal model by sampling with replacement from predictors of the random effects and residuals for nonparametric bootstrap and from an estimated multivariate normal distribution for parametric bootstrap. In the context of an animal model, the natural choice of predictors for random effects is BLUPs (BLUP bootstrap), as they are readily available in software packages and have optimality properties in predicting an individual’s random effect. However, the variance structure is defined by the sum of the random effect and the residual. A random effect is a shrunken form of a fixed effect. The balance of the fixed effect remains in the residual, so resampling needs to be done on the sum to reproduce the appropriate variance structure.

Different NPBS models were used in this study. The NPBS with an animal model assuming independence of u and e (Scheme 1) gave rise to a high heritability score for all the three traits (For BW REML: 0.44, Scheme 1: 0.51; BD REML: 0.22, Scheme 1: 0.38; and K REML: 0.10, Scheme 1: 0.19) wherein all three cases the residual variance was underestimated relative to REML. This suggests this bootstrapping process is not recreating the variance structure assumed for the model, and it is because the estimated random effect is correlated with the residual because of the shrinkage in its estimation. Combining an animal effect ((fi + eij)s) with the residual from another animal in the same family ((fi + eik)(1-s)) produces (fi + seij + (1-s)eik) in which the latter two terms tend to cancel producing a smaller residual than required. The math is different under the family model bootstrapping, where under scheme 1 the family variance is low, and the residual is high: the family effect (si fi) is combined with a residual (1-sk) fk + ekj typically from another family.

Under Schemes 2 and 3, adding the random and residual components at the individual level always yields a sum that is not disturbed by the shrinkage or whether it is fitted as an animal or family model. However, the average sampled genetic variance was inflated relative to the initial REML estimates in both cases for all traits, with a commensurate reduction in the residual variance. The REML solution has the same standard deviation and is well within 1 standard deviation (SD) of the mean under Scheme 3 for BW, within 2 SD for BD and K. However, the failure to randomize family effects under scheme 2 has resulted in a family variance 2 SD above the REML estimate. This indicates that Scheme 2 is not properly representing the variation in the data.

A simulation study by Morris (2002) demonstrated that the optimal properties of the BLUP do not transfer over to bootstrapping when the sample size is small, as a result of which the BLUP based bootstrap consistently underestimate the variability in the data. Further, he reported that the coverage probability of 90 % intervals for the variance components from BLUP bootstrap showed severe undercoverage problems. However, there were no undercoverage issues in the present study with the 95% confidence intervals for variance components and heritability, which add confidence to the optimality of the current sample size (Table 3). An increase in the coverage rate with an increase in sample size was reported by Thai et al. (2013). In our study, both nonparametric and parametric bootstrap gave similar coverage probabilities with slight differences in the values attributed to the total bootstrap sample size (10,000). Increasing the total bootstrap sample size might give exact coverage probability for nonparametric and parametric bootstrap. Searle et al. (2009) explained that the realizations of BLUP are shrinkage estimates and the overall effect of shrinkage estimation is the reduction in the variance surrounding realized BLUPs (Morris 2002). This reduction in variance is translated to every new data set generated by resampling from BLUP predictions. In a mixed model analysis with pedigree, the BLUP shrinkage is a function of the number of observations per family, the total number of observations, the observed vector of trait values and estimated variance components (Searle et al. 2009). So, one of the possible ways to reduce the effect of shrinkage would be to randomize the families while bootstrapping so that the overall shrinkage effect might cancel out.

The heritability estimated from the parametric bootstrap was similar to the REML estimate. In parametric bootstrap, the random variables were sampled from a multivariate normal distribution, resulting in an estimate identical to the REML method since the latter is based on the strong assumption of multivariate normality. A global nonparametric bootstrap was also performed (results not shown), in which the random animal effects and residuals were sampled from the respective vectors of BLUPs and residuals, wherein each vectors were respectively assumed to be one single sampling unit in contrast to assuming each fullsib family as the primary sampling unit. The global nonparametric bootstrap did not yield any meaningful result, where the estimated variance was near zero. The reason for this is, while performing bootstrapping, one of the concerns is that the resampling should appropriately mimic the actual data generating process that produced the data set (Flachaire 2005). It is evident that the classical bootstrap methods developed for simple linear models should be modified to take into account the characteristics of mixed-effects models (Das and Krishen 1999). In the setting of an animal model, the within-family correlation structure needs to be taken into account; thereby, one parent and its entire offspring will be the appropriate sampling unit for generating meaningful bootstrap samples, rather than a whole vector of animal effects (predicted breeding values).

Bayesian vs REML estimates

Bayesian methods are often touted for their ability to incorporate prior information when available, but the key utility of these methods is their ability to provide a complete description of the uncertainty of an estimate (Walsh and Lynch 2018). An MCMC chain of 10,00,000 iterations were run with a burn-in of 50,000 iterations (for better convergence and mixing of chain) and a thinning interval of 100 (to reduce autocorrelation), which yielded a total of 9500 sampled values of variance components and heritabilities. Convergence and autocorrelation are two critical issues to monitor when using the MCMC method. There is a possibility of a strong dependence of the values obtained in the first few iterations on the starting values. The chain is said to converge only after the dependence on the starting parameter has diminished. The visual examination of the trace suggested a well-mixing chain (Fig. 1). As a rule of thumb, if there is no trend in the trace, then the chain has achieved convergence (Hadfield et al. 2019). An autocorrelation of less than 0.10 in magnitude is considered reasonable (de Villemereuil 2012). Further, if the samples were drawn from the chain’s stationary distribution, the two means are equal, and Geweke’s statistic has an asymptotically standard normal distribution (Plummer et al. 2018).

One of the consequences of the large sample theory is the asymptotic normality of the posterior distribution, i.e., to say as n → ∞ (as more and more data arrive from the underlying process), the posterior distribution of θ approaches normality (Gelman et al. 2013). Examination of the distribution of the variance components (additive and residual; presented for BW in Fig. 2a) for different traits obtained from the MCMC sampler shows that the posterior distribution is approximately normal. The additive variance obtained from the REML analysis was in close agreement with the location parameters of the posterior distribution, whereas the REML residual variance was notably less in comparison with the Bayesian posterior estimate for BW and BD; however, for trait K in its original scale, the MCMC did not yield results similar to REML solutions which inflated the heritability. The probable reason could be that a weakly informative inverse gamma prior was used to obtain the posterior distribution. In the original scale, the likelihood estimates of variance components of K is of the order 10−7 and the parameterization of inverse gamma prior used in this study has its density function approaching infinity as the variance approaches zero. It means the information of the prior is maximum as the variance approached zero, or in other words, the only information available in the prior is that variance cannot be negative. The high information of prior near to zero will always overpower the information in the likelihood estimates as it approaches zero, which was the case with K (likelihood estimate of the order of 10−7). To remove this inconvenience, the observations of K were multiplied with an appropriate constant (100 in the present study), which yielded variance components of the order 10−7, the ratios of which estimated the heritability similar to REML. The scale corrected K values were used only in the Bayesian method. Gelman (2006) noted the popularity of the inverse gamma family of priors is due to its clean mathematical properties, wherein he discourages the use of inverse gamma prior due to the sensitivity of its parameterization towards the posterior inferences. However, in the present study, the MCMCglmm package was used, which does not offer the flexibility to use a different family of prior other than inverse gamma. Waldmann and Ericsson (2006) reported a high residual variance in the posterior distribution when comparing the REML and Gibbs sampling estimates of genetic parameters, which was the case with BW and BD in this study. However, according to Sorensen et al. (2002), the variance components from REML analysis should be identical to the Bayesian posterior distribution mode if the mixed models’ parameters are assigned non-informative uniform distributions. Another study by Guan et al. (2017) in turbot (a species of flatfish) showed that the Bayesian estimate of additive variance from the posterior mean was high compared to the REML estimate, whereas the Bayesian residual variance was low in comparison with the corresponding REML estimate. In the present study, a higher additive and residual variance were obtained from the posterior mean, median, and mode compared to the REML estimates for BW and BD, whereas for K, the MCMC variances agreed with REML solutions (Additive: 0.0011 and Residual: 0.0099). In a simulation study by Van Tassell and Van Vleck (1996), the variance components obtained from the posterior mean and REML estimates were similar, and the variance components obtained from the posterior mode was always low. Despite the difference in variances, the posterior distribution of heritability resulted in a similar value as that of the REML estimate, giving more confidence in our estimate. Several other studies also reported where both REML and Bayesian methods provide a similar estimate of heritability if the sample size is large and heritability is high (Waldmann and Ericsson 2006; Alijani et al. 2012; de Villemereuil et al. 2013; Guan et al. 2017). It should be noted that the standard error estimated from the posterior distribution was similar to the one obtained from the delta method. The approximate 95% CI of REML heritability agreed well with the 95% HDR of heritability of posterior distribution. An objective comparison between the estimates of the REML and Bayesian posterior distribution is difficult. However, heritabilities obtained from both the methods were in close agreement, which indicates that the likelihood function has an overpowering influence on the prior distribution. The influence of the prior distribution on the posterior diminishes under a large sample size (Walsh and Lynch 2018); nevertheless, only a prior sensitivity study can ascertain this claim, as noted by Blasco and Blasco (2017).

Asymptotic sampling vs REML estimates

Meyer and Houle (2013) described a simple alternative to estimate the sampling distributions of the functions of variance components by repeated sampling of parameter estimates from their asymptotic, multivariate normal (MVN) distribution and calculating the functions of interest for each sample inspecting their distribution across replicates. They further concluded that the sampling of REML estimates from asymptotic MVN distribution, specified by the inverse of the information matrix, offers a straightforward and computationally undemanding way to derive sampling distributions and confidence intervals for estimates of covariance components and their functions. Our study sampled 10,000 estimates of both additive genetic and residual variances for all three traits and estimated heritability for the combination of every sampled value. The mean of the variance components and heritabilities obtained from the asymptotic sampling were similar to the REML estimates for different traits. The standard error for variance components and heritabilities obtained from both methods were similar. In the present study, both the REML and asymptotic sampling performed equally well to estimate variance components’ uncertainties and functions. An admonition in sampling from asymptotic distribution is that, to yield a valid estimate of covariance, sampling distributions and confidence intervals, large sample properties should hold well, i.e., the inverse of the information matrix has to provide an adequate description of sampling covariance among the parameters estimated. The inverse of the information matrix could be obtained only with Newton–Raphson type algorithms or its variant, especially the average information algorithm (AIREML) (Gilmour et al. 1995), which utilizes second derivatives of log-likelihood.

The uncertainties surrounding the REML heritability could be inaccurate when the assumed asymptotic behavior is violated. Schweiger et al. (2016) describe different cases under which the asymptotic normality does not hold well, of which the most common cause is the sample size. They further demonstrated that the asymptotic CIs tend to be biased when the heritability estimated is relatively low or high, under which the Cls can spread beyond the natural boundaries of their parameters (e.g., negative heritabilities). In a breeding program, the number of families and the number of offspring per family that could be generated at a time is constrained by many factors. As we have noted previously, under large sample assumptions, it is not clear what constitutes a large sample (Walsh and Lynch 2018), making it hard to realize the goodness of asymptotic approximation. As an alternative, sampling-based approaches can be used to generate a full distribution of the estimates to construct CIs.

Of the alternate methods used in the present study, the parametric bootstrap and asymptotic sampling gave similar results for variance components and heritability as REML estimates for all the traits under study. Even though the methods were different, the underlying assumptions are the same and give rise to similar results. Nonparametric bootstrap is well-known for estimating the uncertainties in the data by generating a distribution of estimates. In our study, we have used the BLUP predictions for resampling to create new datasets. However, BLUP is a shrinkage estimator, and as a result, there can be a bias in the estimate of heritability; however, the bias can be reduced by sampling under appropriate assumptions. The NPBS scheme 3 has minimum assumptions, and also, the confidence interval constructed by this method encompassed the heritability estimated by the REML method. The Bayesian posterior mode for BW, BD, and K yielded heritability estimates similar to REML heritability; however, there were slight differences in the variance estimated from both methods.

We conclude that this study with 1413 observations representing 78 full-sib families has provided sufficient information to estimate the heritability of the traits analyzed with acceptable confidence using REML. Based on our study, we recommend to use the NPBS scheme 3 or Bayesian methods to estimate the heritability and its standard error when the information content of the data is in doubt.

Conclusion

Variance components and heritabilities are point estimates surrounded by statistical uncertainty. Confidence intervals derived from the standard error of the estimate describe the uncertainty of the estimate. The REML method assumes an underlying normal distribution leading to asymptotic normality of the estimators, but this may not hold for small sample sizes. When it is challenging to ascertain adequate sample sizes, it is possible to use sampling-based methods to generate a full distribution of estimates. In the present study, the REML estimates of variance components, heritability and the associated uncertainties for three traits were compared with different sampling-based approaches to understand if the data had sufficient information for the asymptotic assumptions to hold.

Even though the parametric bootstrap and asymptotic sampling yielded precisely the same variance components for all three traits as those estimated from the REML method, these two methods also assume multivariate normality under a large sample theory like REML, hence not the methods of the first choice. Moreover, the second moment of the assumed multivariate normality from which the parametric bootstrap and asymptotic sampling were performed was the REML estimate of variance components. The NPBS estimates vary based on the assumptions, where the stronger the assumption, the tighter was the distribution. Based on the NPBS results, obtaining the bootstrap sample by independently resampling the genetic and residual components is not valid because of the effect of shrinkage on the genetic effects meaning their estimates are correlated with the residual effects. However, it is necessary to randomize the family effects to sample the parameter space adequately. The REML solution for BW was within 1 SD, and BD and K within 2 SD of the bootstrap mean based on the randomization of family effects, indicating strong confidence in REML solutions. The heritability estimated from the mode of Bayesian posterior density did not deviate from the REML heritability for all traits. The randomized NPBS with linked genetic and residual effects is the sampling method with the least assumptions. To ascertain the adequacy of the sample size to estimate reliable genetic variation, we recommend NPBS scheme 3 as it provides high overlap with REML calculations and requires the least assumptions. The present study shows that the heritability estimated from different methods and schemes are similar to the REML estimates and the confidence intervals are of similar magnitude and largely overlapping. Hence, it is concluded that the present data set meets the assumptions made for likelihood analysis, and the heritability is well estimated by REML.