Introduction

Charge density waves (CDWs) are important phenomena, particularly for understanding strongly correlated electron systems. It is believed that these materials can be intimately connected to metal-insulator transitions (MITs)1,2,3,4,5 and superconductivity6,7,8,9. Depending on their underlying interactions, CDWs may be categorized into a few types, i.e., a Peierls instability10 induced by Fermi surface nesting, a Wigner crystal11 resulting from strong electron‒electron interactions, and a Kohn anomaly12 associated with simultaneous softening of coherent lattice vibrations, resulting in strong electron‒phonon interactions. The Peierls instability, on the one hand, has been extensively studied and is sometimes connected to conventional superconductors such as purple bronze13. The Wigner crystal, on the other hand, has been widely studied in organic conductors14,15,16,17,18,19 as well as inorganic systems6,7,20. There are indications that these materials are associated with unconventional superconductors, such as the stripe phase in cuprates21,22,23,24. Different types of CDWs have been observed in quasi-one-dimensional organic charge-transfer solids, for example, tetramethyltetrathiofulvalene (TMTTF)2X (X = AsF6, PF6)15,16. In organic systems, a higher-temperature Wigner crystal or charge localization is driven by electronic interactions, followed by a second low-temperature transition. For example, the low-temperature transition can involve the lattice, resulting in a spin-Peierls state. However, there are only a few inorganic systems with multiple types of CDWs6,7,25. Therefore, the coupling between a Wigner crystal and a Peierls instability in inorganic systems and how charge, orbital, and lattice degrees of freedom are involved are far from understood.

Well-known inorganic systems are transition metal oxides. Low-dimensional oxides often exhibit exotic properties and are frequently utilized as systems for hosting CDWs6,7,26,27,28,29. Of particular interest are quasi-one-dimensional metallic niobates, namely, the so-called Carpy-Galy phases AnBnO3n+2 = ABOx of the type SrNbOx, which have various structures and electronic properties depending on its oxygen content30,31,32,33,34,35,36,37,38. Generally, perovskite-related layered Carpy-Galy phases ABOx comprise the highest-Tc ferroelectrics, such as the n = 4 types of La4Ti4O14 = LaTiO3.5 and Sr4Nb4O14 = SrNbO3.5, and quasi-one-dimensional metals, such as the n = 5 types of La5Ti5O17 = LaTiO3.4 and Sr5Nb5O17 = SrNbO3.4, in which the delocalized electrons are embedded in a ferroelectric-like environment31,32,33,34,37. Recently, for the n = 4.5 type quasi-one-dimensional metal SrNbO3.45 and the Sr- and O-deficient n = 5 type quasi-one-dimensional metal Sr0.95NbO3.37, photoinduced dd-exciton-driven metal-insulator transitions were reported36,38. An example of a Carpy-Galy phase-type crystal structure is shown in Fig. 1a, b, namely, that of the n = 5 type quasi-one-dimensional metal SrNbO3.4. The formula SrNbO3.4 represents an ideal stoichiometric n = 5 type composition, and a slightly over-stoichiometric n = 5 type SrNbO3.41 was used to determine the crystal structure by single-crystal X-ray diffraction30. Along the a-axis, NbO6 octahedra networks form chain-like bonds, while zig-zag-like bonds are formed along the b-axis. Along the c-axis, there are five NbO6 octahedra with thick perovskite-type slabs or layers that are [110]perovskite oriented. Stoichiometric and nonstoichiometric Carpy-Galy phases of the type SrNbOx are highly anisotropic and display various interesting physical properties31,32,36,39,40. Transport measurements have shown a Nb-4d conductor and a ferroelectric insulator for SrNbO3 and SrNbO3.5, respectively, while for SrNbO3.41, transport, optical and angle-resolved photoemission spectroscopy measurements have interestingly shown two different energy gaps, and their sizes in units of K are ~125 K and ~325 K33,34,35. Intriguingly, CDWs may exist and can be responsible for the anisotropic transport and various gaps in these quasi-one-dimensional oxides. However, there is no direct evidence of CDWs, and the origin of these gaps and transport anisotropy remains unknown.

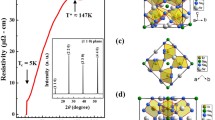
Fig. 1: Crystal Structural, Experimental Geometry, and off- and on-resonance Scattering at Soft X-ray.
figure 1

Crystal structure of the n = 5 type SrNbO3.4 projected on the orthorhombic (a) ac- and (b) bc-planes. The green, blue, and red balls denote Sr, Nb, and O atoms, respectively. c Schematic diagram of the resonant soft X-ray scattering measurement of the Sr0.95NbO3.37 single crystal. d L-scan of the Sr0.95NbO3.37 single crystal using a resonant O K-edge photon energy of 530.5 eV and an off-resonance of 1200 eV at approximately (001) and (002) 38 K and 350 K. e K-scan of the Sr0.95NbO3.37 single crystal using a resonant O K-edge photon energy of 530.5 eV with H = 0 and L = 1, 2 at 38 K. f H-scan of the Sr0.95NbO3.37 single crystal using a resonant O K-edge photon energy of 530.5 eV with K = 0 and L = 1, 2 at 38 K.

Full size image

In this article, we report two distinct and simultaneous commensurate CDWs in a single crystal of the quasi-one-dimensional metal Sr0.95NbO3.37 along one and the same nonmetallic axis, namely, the c-axis, using resonant soft X-ray scattering (RSXS) at the O K edge. One CDW is manifested in an electronic-(001) superlattice and emerges without lattice distortion below ~200 K. Therefore, one can associate it with a Wigner crystal. The other CDW peak manifests as an electronic-(002) Bragg peak and is accompanied by lattice distortion below ~150 K. Therefore, one can associate this peak with a Peierls-like instability. Interestingly, the electronic-(002) Bragg peak persists even up to 350 K but without observable lattice distortion. The emergence of both CDWs allows us, for the first time, to make a direct comparison between these CDWs and how these CDWs influence transport gaps, anisotropies, and anomalies within one system, namely, the quasi-one-dimensional metal Sr0.95NbO3.37. RSXS and X-ray absorption spectroscopy (XAS) measurements were performed at the soft X-ray-ultraviolet (SUV) beamline of the Singapore Synchrotron Light Source (SSLS)41.

Materials and methods

Sample preparation

The sample is one of the so-called Carpy-Galy phases, AnBnO3n+2 = ABOx, which adopts a perovskite-related layered structure, and many of them can also be prepared in a nonstoichiometric form32,37. The Sr- and O-deficient n = 5 type Sr0.95NbO3.37 sample is prepared by melting, reducing, and solidifying the corresponding fully oxidized Nb5+ composition Sr0.95NbO3.45 under a flow of 98% Ar + 2% H2 gas32. The process is performed in a GERO mirror furnace, where two polycrystalline sintered rods of Sr0.95NbO3.45 are processed by floating zone melting. The polycrystalline sintered rods are prepared by mixing an appropriate molar ratio of SrCO3 and Nb2O5, which was prereacted at an elevated temperature in air. After the prereaction, the mixture is ground into powder, once again mingled, pressed into the shape of two rectangular rods, and sintered at an elevated temperature in air. The experimental approaches, types and designs of the equipment, devices, and constructions used are similar to those presented comprehensively in ref. 42. The GERO mirror furnace is presented in Appendix 1 of ref. 42 Images of the melt-grown crystalline sample are shown in Supplementary Fig. 1a36. Pieces of the crystalline sample from the same batch are cleaved into flat plate shapes so that their surfaces were parallel to the c-axis (verified with X-ray diffraction).

Resonant soft X-ray scattering and X-ray absorption spectroscopy

Resonant soft X-ray scattering (RSXS) and X-ray absorption spectroscopy (XAS) measurements are carried out at the soft X-ray-ultraviolet (SUV) beamline of the Singapore Synchrotron Light Source (SSLS)41. A bulk Sr0.95NbO3.37 single crystal is kept inside the vacuum chamber of 10–9 mbar and illuminated with high-intensity photons from the synchrotron. For the RSXS measurements, X-ray photons with s-polarization and an E || ab-plane are used and impinge on the sample with the geometry shown in Fig. 1c. The scattered photons are measured using photodiodes to obtain the total fluorescence yield (TFY) of the sample. The XAS measurement is conducted using linearly polarized X-ray photons within the energy range of 520–570 eV; the sample is illuminated under grazing incidence. The X-ray photons are then absorbed by the sample, and an electric current is produced; this current is counted by a current meter to obtain the total electron yield (TEY) of the sample. All the spectra are normalized to the incident X-ray photon intensity. The temperature of the sample is increased from ~38 K to ~350 K via control of the sample holder temperature with a temperature sensor nearby the sample. For comparison, we also measured the temperature- and polarization-dependent XAS of a bulk SrNbO3.45 single crystal.

Density functional theory

Electronic structure calculations of n = 5 types of SrNbO3.4, as a representation of the Sr- and O-deficient n = 5 types of Sr0.95NbO3.37, are performed in the density functional theory framework as implemented in the Quantum ESPRESSO package43. The optimized norm-conserving Vanderbilt pseudopotential is employed for the exchange-correlation functional44. SrNbO3.4 is modeled using a unit cell consisting of 54 atoms in an orthorhombic structure with a space group of Pnnm. The lattice parameters a = 3.9896 Å, b = 5.6725 Å and c = 32.471 Å, which were experimentally determined via X-ray diffraction on Sr0.95NbO3.37, are used in the calculations, while the atomic positions are optimized until all the forces of the constituent atoms decreased than 10–3 Ry/Bohr. The self-consistent calculation is performed with a cutoff energy of 80 Ry and a Gaussian smearing of 0.01 Ry. A Monkhorst-Pack k-point mesh of 8 × 6 × 1 is used for atomic position optimization, whereas a denser mesh of 24 × 16 × 3 is utilized for the calculation of the density of states.

Results

Figure 1 shows the RSXS results for Sr0.95NbO3.37 at 38 K and 350 K using a selected resonant O K-edge photon energy of 530.5 eV, which is an electronic transition of O 1 s → O 2p hybridized with Nb 4d and an off-resonant at 1200 eV. To make a direct comparison as a function of photon energy and temperature, the RSXS result is normalized with a scattering correction factor:

$${C}_{f}\left(\omega ,T\right)=\frac{\lambda }{4\pi \,{\rm{Im}}\,{\rm{n}}(\omega ,T)}{\left(1-\frac{{\left(1-{\rm{Re}}\,{\rm{n}}\left(\omega ,T\right)\right)}^{2}+{\left({\rm{Im}}\,{\rm{n}}\left(\omega ,T\right)\right)}^{2}}{{\left(1+{\rm{Re}}\,{\rm{n}}\left(\omega ,T\right)\right)}^{2}+{\left({\rm{Im}}\,{\rm{n}}\left(\omega ,T\right)\right)}^{2}}\right)}^{2},$$
(1)

Here, \({\rm{Re}}\,{\rm{n}}\left(\omega ,T\right)\) and \({\text{Im}}\,{\rm{n}}\left(\omega ,T\right)\) are the real and imaginary parts of the complex index of refraction, respectively, as a function of the photon energy, \(\omega\), and temperature, \(T\), calculated from the XAS, and \(\lambda\) is the photon wavelength. We start our discussion at 38 K. The RSXS geometry is shown in Fig. 1c. Strikingly, we observe three different types of Bragg peaks, i.e., two different electronic orderings, namely, an electronic-(001) superlattice and an electronic-(002) Bragg peak, which are both commensurate and detected only at the on-resonant 530.5 eV, and a non-electronic-(002) Bragg peak due to lattice distortion, which is detected at the off-resonant 1200 eV (Fig. 1d–f). All the peaks are observed along the c-axis, which is one of two nonmetallic axes32,36. Based on the crystal symmetry and space group Pnnm, only the (002) reflection is allowed, but the (001) reflection is forbidden. Indeed, at an off-resonant voltage of 1200 eV, which is sensitive only to the crystal structure or any lattice distortion related to it, the electronic-(001) superlattice is absent, while the non-electronic-(002) Bragg peak is observed but is 30 times weaker in intensity than the electronic-(002) Bragg peak observed at the on-resonant 530.5 eV. We assign the non-electronic-(002) Bragg peak to lattice distortion because it occurs at off-resonance and low temperature and is very weak. As the temperature increases to 350 K, only the electronic-(002) Bragg peak persists, while the electronic-(001) superlattice and non-electronic-(002) Bragg peak completely vanish. At these two temperatures and photon energies, the electronic-(001) superlattice undergoes pure electronic ordering without observable lattice distortion at all measured temperatures, while the electronic-(002) Bragg peak is accompanied by a non-electronic-(002) Bragg peak at 38 K and electronic ordering only at 350 K. The electronic-(001) superlattice reflects pure electronic ordering and together with the relationship between its wavelength and charge density, as discussed later, is a fingerprint of the Wigner crystal. Such a Wigner crystal has been observed on the ladder of quasi-two-dimensional Sr14-xCaxCu24O416,20. However, the electronic-(002) Bragg peak is accompanied by the non-electronic-(002) Bragg peak at low temperature; therefore, it appears similar to a Peierls instability. The electronic (002) Bragg peak accompanied by lattice distortion is similar to the CDW observed in the chains of quasi-two-dimensional Sr14Cu24O417.

Figure 2 shows the temperature-dependent resonance profiles of the electronic-(001) superlattice and the electronic and nonelectronic (002) Bragg peaks. From the temperature contour plots (Fig. 2a–c), different transition temperatures and phases among these peaks are found. Taking the low temperature of 38 K as a reference, the electronic-(001) superlattice occurs up to ~200 K, which is assigned to the transition temperature of the superlattice (Fig. 2a). The electronic-(002) Bragg peak persists even up to ~350 K (Fig. 2b). However, the nonelectronic (002) Bragg peak is observed only below 150 K (Fig. 2c) and emerges from the lattice and/or is associated with lattice distortion. Above 150 K, the peak disappears, indicating the absence of lattice distortion. Taken together, the CDWs and lattice distortion data reveal that above 150 K, the CDWs are driven by long-range electron–electron interactions, while electron–lattice interactions are absent or negligible. As we gradually cooled the system below 150 K, we observed the emergence of the non-electronic-(002) Bragg peak alongside the electronic-(002) Bragg peak, revealing that both electron-electron and electron-lattice interactions played important roles. Hence, if we look at the system from high to low temperatures, electron‒electron interactions drive electron–lattice interactions, as electron–electron interactions exist prior to electron–lattice interactions. From the peak position and full width at half maximum (FWHM), we find that the intrinsic properties of the electronic-(001) and electronic (002) Bragg peaks differ from those of the non-electronic-(002) Bragg peak (Fig. S1). Interestingly, both the FWHM and peak position of the electronic-(001) superlattice and electronic-(002) Brag peak are, on the one hand, temperature independent. This structure is similar to that of the hole Wigner crystal in Sr14-xCaxCu24O416,20. This further supports the presence and importance of electron-electron interactions. The peak position and FWHM of the nonelectronic (002) Bragg peak, on the other hand, change as a function of temperature. This indicates a change in the lattice parameter, which reflects the expected expansion or contraction of the lattice, and a change in the coherence length of the crystal structure; i.e., it becomes shorter as the temperature increases.

Fig. 2: Temperature Dependent Resonant Profile and Correlation Length of Charge Density Waves and Lattice Distortion.
figure 2

Contour plot of the temperature-dependent (a) electronic-(001) superlattice, (b) electronic-(002) Bragg peak at 530.5 eV and (c) non-electronic-(002) Bragg peak at 1200 eV for the Sr0.95NbO3.37 single crystal. d Temperature-dependent resonance profile of the (001) superlattice and (002) Bragg peak using a resonant O K edge photon energy of 530.5 eV and an off-resonance of 1200 eV for the Sr0.95NbO3.37 single crystal. Temperature-dependent correlation length of the (001) superlattice and (002) Bragg peak along the (e) c-, (f) b- and (g) a-axis of the Sr0.95NbO3.37 single crystal.

Full size image

For qualitative analysis, the temperature-dependent resonance profile is normalized to the scattering correction factor for each temperature:

$${\rm{resonance\; profile}}=\left({\rm{area\; of\; the\; Bragg\; peak}}\right)/{C}_{f}\left(\omega ,T\right),$$
(2)

with \({C}_{f}(\omega ,T)\) from Eq. (1) and the corresponding polarization and temperature (Fig. 2d). Interestingly, at 530.5 eV, as the temperature increases, the resonance profile of the electronic-(001) superlattice decreases monotonically and eventually vanishes above 200 K. This monotonic decrease in intensity, observed at the O K edge and in the temperature range from 38 K to 200 K, is reminiscent of the hole Wigner crystal in the Cu-O ladder of Sr14Cu24O416,20. The electronic-(002) Bragg peak, on the other hand, persists even up to 350 K. At 1200 eV, only the non-electronic-(002) Bragg peak is observed, and its intensity decreases monotonically and is nearly invisible above 150 K. This indicates that below 150 K, charge-lattice coupling sets in, and an associated Peierls-like instability emerges; however, above 150 K, there is pure charge ordering and almost no charge-lattice coupling. A Peierls instability has been observed in the Cu-O chain of the spin-ladder material Sr14Cu24O417. This also indicates that the two CDWs in Sr0.95NbO3.37 have different origins.

The temperature-dependent correlation length along the c-axis, \({{\xi }}_{c}\left(T\right)\), is shown in Fig. 2e and is defined as follows:

$${{\rm{\xi }}}_{c}\left(T\right)=c/\Delta L\left(T\right),$$
(3)

where \(\Delta L(T)\) and c are the FWHM of the temperature-dependent L-scan and the lattice constant along the c-axis, respectively. At 38 K, surprisingly, the correlation length along the c-axis of the electronic-(001) superlattice, ξel-(001),c ~ 6000 Å, is significantly greater than that of the electronic-(002) Bragg peak at 530.5 eV, ξel-(002),c ~ 2300 Å, and the non-electronic-(002) Bragg peak at 1200 eV, ξnon-el-(002),c ~ 3600 Å. As the temperature increases, ξel-(001),c decreases, suggesting that disorder occurs and diminishes above ~200 K, whereas ξel-(002),c is almost constant even up to 350 K. Upon heating, ξnon-el-(002) first increases, below 100 K, it decreases, and eventually, it is no longer observable above ~200 K. The temperature-dependent correlation length in the ab-plane is shown in Fig. 2f, g. At 38 K, the ab-plane correlation length of the electronic-(001) superlattice is highly anisotropic (ξel-(001),a ~ 8100 Å and ξel-(001),b ~ 4000 Å). As the temperature increases, ξel-(001)a diminishes more rapidly than ξel-(001),b. Similarly, the ab-plane correlation length of the electronic-(002) Bragg peak is also highly anisotropic (ξel-(002),a ~ 2000 Å and ξel-(001),b ~ 1000 Å). As the temperature increases to 350 K, ξel-(002),a slightly increases up to ~2600 Å, and ξel-(002),b is nearly constant. Furthermore, the resonance profile and coherence length of the electronic-(001) superlattice and non-electronic-(002) Bragg peak phenomenologically fit the mean-field equation:

$${f}_{\text{mf}}\left(T\right)=A{\left(\frac{\tau -T}{\tau }\right)}^{\alpha },$$
(4)

Those of the electronic-(002) Bragg peak fit phenomenologically to the non-mean-field equation:

$${f}_{\text{nmf}}\left(T\right)=B{\left({e}^{\frac{T-\tau }{T}}+1\right)}^{-1}.$$
(5)

The temperature-dependent resonance profile is rather complex to fit within this simplified model only. We argue that this is due to the interplay of electron-electron and electron-lattice interactions. Details of the fitting of all Bragg peaks and the fitting parameters of the mean-field and non-mean-field equations are shown in Figs. S1–S4 and Tables S1-S2 in the Supplementary Information.

Figure 3 presents the temperature- and polarization-dependent complex dielectric susceptibility across the O K edge of Sr0.95NbO3.37. The complex dielectric susceptibility, \(\chi \left(\omega \right)={\rm{Re}}\,\chi \left(\omega \right)+{i}\,{\rm{Im}}\,\chi (\omega )\), is computed and analyzed in detail from the XAS data. The XAS data are normalized at off-resonance regimes (below and above the edge) using tabulated values45. It is proportional to \({\rm{Im}}\,\chi (\omega )\) and can be related to the absorption coefficient:

$$\mu \left(\omega \right)=\frac{4\pi }{\lambda }\text{Im}\,n(\omega ),$$
(6)

where \(n(\omega )\) is the index of refraction46, which is associated with \(\chi \left(\omega \right)\) via

$$n(\omega )=\sqrt{1+\chi (\omega )}.$$
(7)
Fig. 3: Complex Dielectric Susceptibility at O K Edge from X-ray Absorption Spectroscopy.
figure 3

Imaginary part of the complex dielectric susceptibility of the Sr0.95NbO3.37 single crystal at the O K edge along the a-, b- and c-axes at (a) 36 K and (b) 300 K. Real part of the complex dielectric susceptibility of the Sr0.95NbO3.37 single crystal at the O K edge along the a-, b- and c-axes at (c) 36 K and (d) 300 K.

Full size image

From \(\mu (\omega )\), we calculate \(\text{Im}{n}(\omega )\) and perform a Kramers–Kronig transformation to obtain \({\text{Re}}\,{\text{n}}(\omega )\); subsequently, we compute \(\chi \left(\omega \right)\)7,45,46,47. A well-observed \(\text{Im}\,\chi (\omega )\) peak at ~531 eV is attributed to the transition from O 1 s core-level states to unoccupied O 2p hybridized with Nb 4d states. At 36 K, the peak intensity of the O 2p – Nb 4d hybridization is the most significant for E || a, which is higher than that of E || b, while for E || c, it is significantly smaller. This shows that the charge distribution is present mostly along the a-axis, slightly reduced along the b-axis, and significantly smaller along the c-axis. Note that the average oxidation state/electronic configuration of the Nb ions in Sr0.95NbO3.37 is Nb4.84+/4d0.16, which simply results from Sr2+ and O2– and the charge neutrality in the formula Sr0.95NbO3.37; thus, the average density of the charges is 0.16 electrons/Nb ion. Strikingly, as the temperature increases to 300 K, spectral weight transfer occurs from the a-axis to the b- and c-axes (see Fig. 3a, b). This reveals that the charge is redistributed from the a-axis to the b- and c-axes. Such a charge redistribution significantly affects the electronic-(001) superlattice, resulting in a charge anisotropy in the ab-plane and approximatively a charge isotropy in the ac-plane at high temperature.

A similar trend is also found in \(\text{Re}\,\chi (\omega )\), as shown in Fig. 3c, d. Upon cooling, \({\text{Re}}\,\chi (\omega )\) for E || a significantly increases, which indicates the presence of unscreened charges yielding long-range electron‒electron interactions in Sr0.95NbO3.37 The unscreened charges introduce electronic correlation effects, which may transform the system into a Mott-like insulator36,40. Interestingly, the electronic correlations also enhance the long-range electron-electron interactions. Therefore, the interplay between the electronic correlation and the charge redistribution in O 2p – Nb 4d hybridization plays an important role in the observed Wigner crystal and Peierls instability. As a result, Sr0.95NbO3.37 is highly anisotropic.

Figure 4 shows contour plots of the temperature-dependent complex dielectric susceptibility across the O K edge along the a-, b-, and c-axes of Sr0.95NbO3.37. The contour plots at ~531 eV for \(\text{Im}\,\chi (\omega )\) (Fig. 4a–c) reveal that the charge redistribution attributed to O 2p – Nb 4d hybridization occurs gradually from the a-axis at low temperature to the b- and c-axes at high temperature. However, \(\text{Re}\,\chi (\omega )\) (Fig. 4d–f) increases with temperature, indicating that the long-range electron-electron interactions along the a-axis are weaker and become stronger along the b-axis and c-axis. The spectral weight transfer of both \(\text{Im}\,\chi (\omega )\) and \(\text{Re}\,\chi (\omega )\) occurs from ~531 eV to ~538 eV, revealing strong electronic correlations. This shows that the anisotropy in Sr0.95NbO3.37 is strongly influenced by a charge redistribution in the O 2p – Nb 4d hybridization and long-range electron–electron interactions.

Fig. 4: Contour Plots of Complex Dielectric Susceptibility Susceptibility as a Function of Temperature and Polarization.
figure 4

Contour plots of the temperature-dependent imaginary part of the complex dielectric susceptibility along the (a) a-, (b) b- and (c) c-axes and the temperature-dependent real part of the complex dielectric susceptibility along the (d) a-, (e) b- and (f) c-axis of the Sr0.95NbO3.37 single crystal at the O K edge.

Full size image

Figure 5 shows the spectral weight, the imaginary part of the index of refraction, \(\text{Im}{n}(\omega )\), and the resonance profile of the electronic-(001) superlattice and the electronic-(002) Bragg peak across the O K edge of Sr0.95NbO3.37. We conducted spectral weight analysis to quantify the electronic correlation and orbital occupancy in Sr0.95NbO3.37 using optical conductivity:

$${\sigma }_{1}\left(\omega \right)={\varepsilon }_{0}{\varepsilon }_{2}\left(\omega \right)\omega ,$$
(8)

where \({\varepsilon }_{0}\) is the vacuum permittivity and \({\varepsilon }_{2}(\omega )\) is the imaginary part of the complex dielectric function, which is proportional to \(\text{Im}\,\chi (\omega )\). This analysis is important because it obeys the f-sum (charge conservation) rule; therefore, we can determine the charge redistribution and its relationship to the observed charge orderings. The effective number of electrons participating in optical excitation within an energy range from \({E}_{1}\) to \({E}_{2}\) can be counted precisely through the spectral weight (Fig. 5a) as

$$W={\int }_{{E}_{1}}^{{E}_{2}}{\sigma }_{1}\left(\omega \right)d\omega .$$
(9)
Fig. 5: Spectral Weight, Resonance Profile of Charge Density Waves, and Index of Refraction at O K Edge.
figure 5

a Temperature-dependent spectral weight of the Sr0.95NbO3.37 single crystal at ~530–535 eV along the a-, b- and c-axes. b Resonance profile of the electronic-(001) superlattice and electronic-(002) Bragg peak of the Sr0.95NbO3.37 single crystal across the O K edge plotted together with the imaginary part of the complex index of refraction, \(\text{Im}{n}(\omega )\), of Sr0.95NbO3.37 and SrNbO3.45 along the a-axis. c Imaginary part of the complex index of refraction, \(\text{Im}{n}(\omega )\), of Sr0.95NbO3.37 and SrNbO3.45 along the b- and c-axes. Notably, Sr0.95NbO3.37 and SrNbO3.45 are related but different Carpy-Galy phases, AnBnO3n+2 = ABOx, namely, a nonstoichiometric (Sr- and O-deficient) n = 5 type and a stoichiometric n = 4.5 type, respectively32,34,36,37.

Full size image

For the O 2p – Nb 4d hybridization, we chose an energy range of ~530–535 eV. At the lowest temperature, the spectral weight along the a-axis is highest, followed by that along the b-axis and c-axis. Surprisingly, upon heating, spectral weight transfer occurs from the a-axis to the b- and c-axes. This means that at high temperatures, the charges are redistributed from O 2px – Nb 4dxy hybridized states to O 2py – Nb 4dxy and O 2pz – Nb 4dzy hybridized states, as further discussed later. By referring to the temperature-dependent electronic-(001) superlattice profile in Fig. 2, it is revealed that the superlattice is strong when the charges are mostly in the O 2px – Nb 4dxy hybridized states and in the ab-plane, while it becomes weak and not observable when the charges in the O 2pz – Nb 4dzy hybridized states are nearly equal to those in the O 2px – Nb 4dxy hybridized states.

The resonance profiles of the electronic-(001) superlattice and electronic-(002) Bragg peak across the O K edge at 38 K and 300 K are plotted together with \(\text{Im}{n}(\omega )\) of Sr0.95NbO3.37 (n = 5); for comparison, that of SrNbO3.45 (n = 4.5) is shown in Fig. 5b, c. The resonance profile is normalized in the same way as discussed above (see also Fig. S5 in the Supplementary Information for the prepeak regime). The n = 5 type Sr0.95NbO3.37 and n = 4.5 type SrNbO3.45 Carpy-Galy phases have different average oxidation states/electronic configurations of the Nb ions, namely, Nb4.84+/4d0.16 and Nb4.9+/4d0.1, respectively. This simply results from Sr2+ and O2– and from the charge neutrality in the formula Sr0.95NbO3.37 and SrNbO3.45; thus, the average density of the charges is δ = 0.16 and δ = 0.1 electrons per Nb ion, respectively. Indeed, a notable change in the \(\text{Im}{n}(\omega )\) intensity in the photon energy range from ~530 to ~535 eV for E || a is observed, while there is a less significant difference for E || b and E || c. This energy range corresponds to a charge distribution due to the hybridization between the Nb 4d and O 2p states (Fig. 6). This indicates that the charge is distributed mostly along the a-axis and induces anisotropy. Simultaneously, the resonance profiles of the electronic-(001) superlattice and electronic-(002) Bragg peak show strong resonance signals within this energy range, particularly at the edge of the absorption peak. This reveals that both the electronic-(001) superlattice and the electronic-(002) Bragg peak arise from the charge distribution and anisotropy near the Fermi level. Our theoretical calculations confirm that the charge distribution and anisotropy are more pronounced near the Fermi level and arise mainly from O 2px states hybridized with Nb 4dxy states (c.f. Figure 6). Notably, such a quasi-one-dimensional charge distribution accompanied by the emergence of a resonant signal strongly at the edge of the absorption peak is similar to the charge ordering in La2-xBaxCuO448 and Sr14Cu24O416,7. This indicates the similarity and importance of charge density waves in various correlated oxide systems. Both the electronic-(001) superlattice and the electronic-(002) Bragg peak truly arise from charge modulation, where the charges are mostly in the O 2p – Nb 4d hybridization region in the ab-plane and ordered along the c-direction.

Fig. 6: Density Functional Theory.
figure 6

Theoretically calculated projected density of states of the (a) Nb 4d and (b) O 2p states of the n = 5 type SrNbO3.4, which is used to represent the Sr- and O-deficient n = 5 type Sr0.95NbO3.37.

Full size image

Figure 6 shows the results of theoretical calculations based on density functional theory (DFT) on n = 5 type SrNbO3.4, which is used to represent the Sr- and O-deficient n = 5 type Sr0.95NbO3.37. The projected density of states (DOS) shows that the lowest energy states near the Fermi level emerge mainly from Nb 4dxy states and less from Nb 4dzy states, while at higher energies ( > 4 eV), the Nb 4dzy states dominate and are followed by Nb 4dx2-y2 states (Fig. 6a). By referring to \(\chi (\omega )\) (c.f. Figs. 3 and 4), the feature at ~530–535 eV along the a-axis arises from the hybridization between O 2px and Nb 4dxy states, while along the b- and c-axis, it emerges from O 2py – Nb 4dxy and O 2pz – Nb 4dzy hybridized states, respectively, which raises the anisotropy. At higher energies, i.e., at ~535–540 eV, Nb 4dx2-y2 is strongly hybridized with O 2px and 2py (Fig. 6b), resulting in an almost isotropic \(\chi \left(\omega \right)\) along the a-axis and b-axis. However, the O 2pz – Nb 4dzy hybridization results in a strong absorption peak along the c-axis. Furthermore, the symmetric spin-polarized DOS indicates that the spin contribution to the formation of CDWs in Sr0.95NbO3.37 is very negligible, if any. Notably, the CDWs may also be influenced by ferroelectric instability. Our experimental data, supported by theoretical calculations, show that the electronic structure and hybridization of Sr0.95NbO3.37 are anisotropic along the a-, b- and c-axes.

Discussion

It is worthwhile to discuss the strength of the electron‒electron interaction by means of the relationship between the observed wavelength λ = 1.0c of the Wigner crystal and the average charge density of δ = 0.16 electrons per Nb ion (the charge neutrality in Sr0.95NbO3.37 implies an average valence and electronic configuration of Nb4.84+/4d0.16 per Nb ion). In models of charge crystallization6, for n = 10 (i.e., overall 10 Nb atoms per unit cell in Sr0.95NbO3.37), λ = 1/(n×δ)c or 2/(n×δ)c in the strong or weak coupling limit, respectively, which requires δ = 0.1 or δ = 0.2. This suggests that the Wigner crystal is on the side of the strong coupling limit (δ = 0.1) because a fraction of the charges also contribute to the other electronic ordering. We next address the relationship between the temperature dependence of the RSXS and XAS data and the results of previous transport measurements32,33,34,35. Our results indicate that the interplay of the Wigner crystal, the Peierls-like instability, the high-temperature charge ordering, and the charge redistribution is responsible for the transport anisotropy and gaps in Sr0.95NbO3.37 and related niobates such as SrNbO3.41. The Wigner crystal and Peierls-like instability, which occur below room temperature, are responsible for the low-energy gap whose size in units of K is well below room temperature (refs. 33 and 34. report 125 K for SrNbO3.41 along the metallic a-axis). Alternatively, high-temperature charge ordering, which persists up to 350 K, is responsible for the high-energy gap whose size in units of K is above room temperature (ref. 35. reports 325 K for SrNbO3.41 along the nonmetallic c-axis). The charge redistribution and hybridization are also responsible for the transport anisotropy.

In conclusion, in the quasi-one-dimensional metal Sr0.95NbO3.37, by using RSXS supported by theoretical calculations, we observe two distinct and simultaneous commensurate CDWs, a Wigner crystal in the electronic-(001) superlattice due to strong electron‒electron interactions, and Peierls-like instability in the electronic-(002) Bragg peak due to the interplay of electron‒electron and electron–lattice interactions. The temperature-dependent RSXS data of these CDWs reveal that strong electron‒electron interactions drive electron–lattice interactions, which occur at low temperature, yielding different types of CDWs. The electronic-(001) superlattice occurs below ~200 K and appears without an observable lattice distortion. The electronic-(002) Bragg peak is accompanied by lattice distortion, which occurs below ~150 K. The correlation length, ξ, of the electronic-(001) superlattice is surprisingly larger than that of the electronic-(002) Bragg peak and highly anisotropic in all crystal axes, while ξ of the electronic-(002) Bragg peak is nearly isotropic along the a-axis and c-axis and smaller along the b-axis. Our results show that CDWs arise from charge anisotropy and redistribution in Nb 4d – O 2p hybridization and influence properties such as transport and optical gaps. Additionally, this study paves the way for utilizing RSXS to distinguish CDWs and calls for further investigation of electron‒electron and electron–lattice interactions in inorganic systems.