Introduction

Manipulating hot carrier cooling with harvesting of electron kinetics is an important avenue for developing promising technologies such as high-efficiency photovoltaics, photocatalysts, photodetectors, and spectral range analyzers1,2,3,4,5,6,7,8 which utilize carriers with energies greater than the bandgap. For example, a single-junction solar cell that reduces the losses associated with thermalization of hot carriers theoretically allows for efficiencies far beyond the Shockley−Queisser efficiency limit of conventional single-junction cells9,10,11. For these promising applications, however, evidence of hot carrier cooling suppression and suppression ability are fundamentally important for realizing high performance. Slowed hot carrier cooling phenomena have been reported for some materials and structures, such as perovskites, graphene, III-V quantum well structures, carbon nanotubes/nanowires, and silicon quantum dots comprising nanoparticles6,7,8,12,13,14,15,16,17. However, exploring and investigating such phenomena in new material structures is of great significance for developing promising technologies.

Important and exciting phenomena have been reported for phononic crystals with a variety of promising applications, such as sonic diodes, acoustic cloaking, optomechanics, and thermoelectrics18,19,20,21,22. However, hot carrier cooling suppression in a two-dimensional (2D) crystalline silicon phononic crystal has not yet been observed. Crystalline silicon is the most widely used material in the modern semiconductor and microelectronics industries. Manipulating hot carrier behavior in silicon phononic crystals would provide more opportunities for promising applications. For instance, we have theoretically investigated the potential of silicon phononic crystals for photovoltaic applications11, and the calculated limiting efficiency is 58%, which is almost twice the efficiency limit of 29.4% seen for a conventional crystalline silicon solar cell. However, these promising high-performance devices must be built with the premise that hot carrier cooling suppression exists in silicon phononic crystals. To date, however, such a phenomenon has not been experimentally observed and reported. It is very important and desirable to provide experimental proof as a fundamental basis for development of a variety of promising applications.

In the present work, we experimentally investigate hot carrier cooling behaviors in designed 2D structured crystalline silicon samples. Measurements and analyses were conducted with ultrafast transient absorption spectroscopy. Significantly enhanced suppression of hot carrier cooling was observed for the 2D silicon phononic crystal. Our findings show that 2D silicon phononic crystals may have potential for development of promising applications, such as ultrahigh-efficiency photovoltaics, beyond the S-Q limit.

Results and discussion

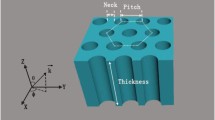
The reference sample used in this work was a commercially available silicon-on-sapphire (SoS) wafer, in which the silicon was an intrinsic monocrystalline thin film with a thickness of 550 nm and was epitaxially grown on a thick sapphire substrate. The 2D structured silicon samples were designed and fabricated based on the reference sample. The design is shown on the left side of Fig. 1a. The 2D silicon structure consists of an airy hole array with a square arrangement in a crystalline silicon matrix, where d denotes the diameter of the airy holes (naturally, radius r = d/2) and P defines the pitch of the periodic array. t is the thickness of the crystalline silicon thin film. A tilted-view scanning electron microscope (SEM) image of the fabricated 2D structured crystalline silicon sample is shown on the right of Fig. 1a. It can be clearly seen that the silicon in these holes was removed to form an airy hole array. In addition, a top-view SEM image of the present 2D structured silicon is presented in Fig. 1b. It is found from the two SEM images that a highly uniform 2D structured crystalline silicon was experimentally achieved, which showed excellent consistency with the designed parameters. Two 2D-structured silicon samples with two different geometric parameters were designed and fabricated: t = 550 nm, P = 1160 nm, and d = 1000 nm and t = 550 nm, P = 1160 nm, and d = 1060 nm. Photographs taken of the three samples are shown in Fig. S1 of the Supporting Information. Figure 1c shows measured static absorption (SA) spectra of the three samples as a function wavelength. The measured static absorption spectra will be subsequently compared with measured transient absorption (TA) spectra of the three samples for investigation and analysis of kinetics.

Fig. 1: SEM images of 2D structured silicon and the measured static absorption spectra.
figure 1

a Left: Schematic of the 2D structured silicon consisting of an airy hole array in a square arrangement in a crystalline silicon thin film matrix, where the diameter d of the airy hole and the pitch P of the periodic array are variables. Right: Tilted-view SEM image of the fabricated 2D structured silicon sample, where d = 1060 nm and P = 1160 nm; b Top-view SEM image of the fabricated 2D structured silicon with d = 1060 nm and P = 1160 nm; c Measured wavelength-dependent static absorption spectra of the three samples (the sapphire substrate is included), i.e., the reference sample and the two structured samples with d = 1000 nm and d = 1060 nm, respectively, where the vertical dashed line is used to guide the absorption comparison at 400 nm, i.e., the pump beam in the present TA measurements.

Full size image

Figure 2 shows the TA spectra for the three samples with the pump beam set at a wavelength of 400 nm (i.e., excitation energy of 3.1 eV). Figure 2a, b shows TA spectra over time and a corresponding 3D map for the reference sample, respectively. Similarly, Fig. 2b, c shows time-evolution TA spectra and 3D mapping of the 2D-structured silicon sample with d = 1000 nm. Figure 2e, f shows time-dependent TA spectra and 3D mapping for the structured silicon sample with d = 1060 nm, respectively. It is noted in Fig. 2 that the TA spectra (i.e., ΔA) present positive and negative signals. Normally, for direct bandgap semiconductors such as perovskites, the positive signals in the TA spectra correspond to photoinduced absorption, and the negative signals correspond to bleaching or stimulated emission. However, because crystalline silicon thin films are indirect bandgap semiconductors, there is nearly no bleaching phenomenon. The present observation of negative signatures and oscillations was experimentally reported and confirmed in a recent study23 in which a 2.5 μm-thick monocrystalline silicon plate was used. This feature is attributed to the large refractive index of Si (≈3.5), which leads to significant surface reflection of the probe radiation and thereby causes the thin sample to act as a Fabry–Pérot interferometer23. It is also found in Fig. 2 that there was no obvious evolution of the spectral shape with time, indicating that there were no additional dynamic processes. The TA signals in the present silicon samples should represent free carrier signals instead of exciton signals. Furthermore, by comparing the static absorption and TA spectra, it was found that more freedom was available for extracting peak dynamics for kinetics analyses.

Fig. 2: Measured TA spectra and 3D mappings.
figure 2

Measured TA spectra of the three samples versus time in the range 1 ps to 7 ns: a Reference sample; c Structured sample with d = 1000 nm; e Structured sample with d = 1060 nm. 3D maps of the three samples: b reference sample; d structured silicon sample with d = 1000 nm; f structured silicon sample with d = 1060 nm.

Full size image

To conduct the kinetics analysis, the measured TA dynamics of the three samples at different probe wavelengths were extracted, and the results are shown in Fig. S2 of the Supporting Information. Figure S2 shows that the kinetic processes in the reference sample were consistent for probe wavelengths of 897, 1100, and 1140 nm. Similarly, the kinetic processes were also consistent for the 2D silicon sample with d = 1000 nm at the three probe wavelengths 960, 980, and 1140 nm. The kinetic processes indicated consistency for the 2D silicon sample with d = 1060 nm at the five probe wavelengths 990, 1035, 1050, 1100, and 1160 nm. For analysis and comparison, the TA kinetics for probe wavelengths with high confidence were chosen for the three samples. Specifically, for the 2D silicon sample with d = 1000 nm, the TA kinetics at a probe wavelength of 1140 nm were chosen. For the 2D silicon sample with d = 1060 nm, the TA kinetics at a probe wavelength of 1100 nm were chosen. For the reference sample, the TA kinetics at the two probe wavelengths of 1100 and 1140 nm were chosen for comparison. The measured TA kinetics of the three samples at the chosen probe wavelengths were plotted using dots, as shown in Fig. 3a. When a pump beam of 400 nm was shone on these silicon samples, three processes were involved: (i) electrons/holes were excited to high energies above the bandgap (i.e., forming hot electrons); and (ii) these hot electrons decayed from high energies to band edges. This process usually includes carrier-carrier scattering (i.e., carrier thermalization via carrier-carrier collisions) and carrier-phonon scattering (i.e., hot carrier cooling via interactions between hot carriers and the lattice); the first carrier-carrier scattering process occurred very rapidly (<100 fs)24; and (iii) the electrons and holes recombine via radiative or nonradiative processes. Figure 3a shows that all three samples showed similar increases before 0.9 ps. However, these samples presented quite different behaviors after 0.9 ps. Specifically, for the reference, the TA increased from 0 to 0.9 ps and then dropped after 0.9 ps. This indicated that the above process (ii) occurred before 0.9 ps and that process (iii) occurred starting from 0.9 ps. For the 2D structured silicon with d = 1000 nm irradiated with a probe wavelength of 1140 nm, the ΔA decay was delayed compared with that of the reference. Surprisingly, for the structured silicon sample with d = 1060 nm, ΔA increased from 0 to 0.9 ps and, after that, continued to increase and reached a peak at ~35 ps. After 35 ps, it began to decay. It is inferred that process (ii) took place until ~35 ps. After 35 ps, process (iii) occurred. The results indicate that the structured silicon sample with d = 1060 nm has a remarkable ability to suppress hot carrier cooling. In principle, if proper energy selective contacts were designed to extract these hot carriers before they decay to band edges, high-performance devices such as ultrahigh-efficiency photovoltaic solar cells can be developed.

Fig. 3: Measured and fitted TA, calculated absorption in Si, and measured static absorption & TA spectra.
figure 3

a TA kinetics of the three samples: reference sample at probe wavelengths of 1100 nm and 1140 nm; structured silicon sample with d = 1060 nm at probe wavelength of 1100 nm; and structured silicon sample with d = 1000 nm at probe wavelength of 1140 nm. Dots represent the measurements, and lines represent the fits. b TA kinetics of the three samples: all samples were studied with probe wavelengths of 1080 nm. Dots represent the measurements, and lines represent the fits. c Calculated wavelength-dependent light absorption by silicon of the three samples, i.e., the reference sample (black curve), two structured samples with d = 1000 nm (blue curve) and d = 1060 nm (red curve), where the vertical dashed line is used to guide the absorption comparison at 400 nm, i.e., the pump beam. d Measured static absorption and TA spectra of the reference sample in the wavelength range 850–1200 nm. e Measured static absorption and TA spectra of the structured silicon with d = 1000 nm in the wavelength range 850–1200 nm. f Measured static absorption and TA spectra of the structured silicon with d = 1060 nm in the wavelength range 850–1200 nm.

Full size image

It is noted that the TA kinetics of the three samples were extracted and investigated at different probe wavelengths. For completeness, we also extracted and investigated the TA kinetics of the three samples with the same probe wavelength of 1080 nm, as shown in Fig. 3b. It was found that the behavior of the reference sample was similar to that shown for the reference sample in Fig. 3a. However, for the 2D silicon sample with d = 1000 nm, decay occurred faster than it did with a probe wavelength of 1140 nm. Remarkably, for the 2D silicon sample with d = 1060 nm, similar behaviors as a function of time were observed, i.e., the ΔA continued to increase and reached a peak after 0.9 ps.

The experimental results described above showed that energy transfer from hot electrons (or holes) to band edges can be inhibited by introducing airy hole arrays into the silicon thin film. However, the suppression abilities of the two structured silicon samples were quite different, which must be investigated from the standpoint of lifetimes. Using the measured TA kinetic processes and times, fitting can be conducted to obtain the lifetimes. Here, commercial Surface Xplorer analysis software was employed. The fitting results for the three samples are shown in Fig. 3a, b using lines. The fitting equation and its description are contained in the Supporting Information. Figure 3a, b shows that for the reference sample, an increasing curve and a two segment decreasing curve can be identified. Therefore, a single tau (τf) and two taus (τ1 and τ2) were used in our fitting model, where the single τf corresponds to hot carrier cooling and the two τ values correspond to carrier recombination. In contrast, for the structured silicon sample with d = 1060 nm, two segmented increasing curves and a decreasing curve were observed. This indicated that it is suitable to adopt two τ values (τf1 and τf2) to describe the hot carrier cooling process and a single τ value (τ1) to describe the carrier recombination process. Because a single cooling time is often used to describe hot carrier cooling behavior in the literature, we adopted an effective cooling time by weighting τf1 and τf2. The method for calculation of effective cooling time was also reported in the literature25. More details can be found in ref. 25 or Tables S1, S2 of the Supporting Information. It is necessary to point out that for samples illuminated by a laser pulse, the decay of hot electrons from high energies to band edges includes carrier-carrier scattering (i.e., carrier thermalization via carrier-carrier collisions) and carrier-phonon scattering (i.e., carrier cooling via interactions between hot carriers and the lattice). The first carrier-carrier scattering process occurs very rapidly, within <100 fs24. The response time of the measurement equipment used here is 120 fs. Therefore, the measured signals shown in Fig. 2 are for the hot carrier cooling process and carrier recombination process, i.e., after the carrier-carrier scattering process.

Based on the fitting results, the hot carrier cooling times were as follows: (i) for the reference sample, the cooling times were 0.45, 0.37 and 0.28 ps at probe wavelengths of 1080, 1100 and 1140 nm, respectively; (ii) for the 2D structured silicon sample with d = 1000 nm, the cooling times were 0.95 ps and 0.31 ps at probe wavelengths of 1080 and 1140 nm, respectively; (iii) for the 2D structured silicon sample with d = 1060 nm, the cooling times were 15.9 ps and 10.7 ps at probe wavelengths of 1080 and 1110 nm, respectively. By comparison, it was clear that the 2D structured silicon sample with d = 1060 nm demonstrated improvements over the other two cases corresponding to orders of magnitude.

To further solidify the analysis, we investigate the effects of light absorption differences for silicon in the three samples on the resulting cooling lifetime values. We calculated wavelength-dependent light absorption for the silicon in the three samples, as shown in Fig. 3c. Because the pump beam wavelength was 400 nm in the present measurements, we conducted the absorption comparison at 400 nm, as shown by the vertical dashed line in Fig. 3c. Absorption by the silicon thin film was obviously higher than that of the two-structured silicon at 400 nm, while absorption by the two-structured silicon was very close at a wavelength of 400 nm. In terms of relative comparison, this comparison result was consistent with the static absorption measurements (sapphire substrate is included); this is shown in Fig. 1c, where absorption by the reference sample is obviously higher than those of the two structured silicon samples, and absorption by the two structured silicon samples was almost the same. By comparison with the experimental results, the cooling times for the two structured silicon samples were remarkably different, which indicated that the light absorption difference in the samples did not have a critical effect on the lifetime. Figure 3d–f shows the measured static absorption and TA spectra of the three samples (i.e., reference sample, structured silicon with d = 1000 nm, and structured silicon with d = 1060 nm) over the wavelength range 850–1200 nm, where the three TA spectra obtained at times of −40, 160, and 800 fs were selected for demonstration. Figure 3d–f shows that the resonant peaks presented similarities between the static absorption and TA spectra for the three samples, which shows that there was a strong correlation between the static absorption and the TA spectra in terms of the resonant peaks. As a result, the amplitude of variations in the TA spectra mainly originated from variations in the baseline absorption. For the reference sample, the observed absorption oscillations with broadband features were typical and were attributed to the interference effects of planar ultrathin silicon. In contrast, for the other two structured silicon samples, oscillations were observed with more and narrower peaks, which was caused by the 2D structures of the samples. This opinion is supported by both the measured and simulated spectra, as shown in Figs. 1c and 3c.

Furthermore, the power density-dependent TA signals of the three samples were also measured and investigated to determine the underlying mechanism. The measured results are shown in Fig. 4, where the dots represent measurements and the red curves show fits to the data. Figure 4 indicates that a common phenomenon occurred for the three samples: the TA signals with increasing power density can be divided into three regions, i.e., a line region at low power densities, a transition region at middle power densities, and a saturation region at high power densities. Generally, the TA decay mechanism includes hot carrier relaxation and Auger recombination. Because the power density was as low as 20 μJ/cm2 in our experiments, excitation took place in a small signal region, and the excitation energy initiated a linear single-excitation process. Therefore, Auger recombination can be excluded.

Fig. 4: Measured power density-dependent normalized TA signals for the three samples.
figure 4

a Reference sample; b structured silicon sample with d = 1000 nm; c structured silicon sample with d = 1060 nm. The dots are measurements, and the red curves are the fit. The dashed lines are tangents in the low power density region.

Full size image

To perform a deeper analysis, we conducted calculations for phononic crystals by using Comsol Multiphysics software. More details can be found in the phononic crystal calculation section. As shown in Fig. 5c, a phononic bandgap was achieved for the 2D structured silicon with d = 1060 nm. Figure 5a shows that there was no phononic bandgap for the reference sample. This is understandable because for bulk or thin film crystalline silicon, there is no phononic bandgap in the frequency band structure due to phononic dispersion across the reduced wave vector. By comparison, the phononic band structures presented an evolution from the reference sample to the two structured silicon samples. Coincidently, the 2D structured silicon with d = 1000 nm presented a boundary in terms of phononic bandgap formation. A close look at the band structure indicates that there was no phononic bandgap formed for the 2D structured silicon with d = 1000 nm. In contrast, Fig. 5c shows that a clear phononic bandgap was achieved in the frequency range 2.5–2.8 × 109 Hz for the 2D structured silicon with d = 1060 nm. Compared with the structured sample with d = 1000 nm, we attribute the observed suppressed decay to the phononic bandgap. It is widely believed that hot carrier relaxation in silicon is primarily driven via decay from optical phonons to acoustic phonons26,27,28. It was also reported that a silicon phononic crystal with a sub-GHz bandgap could suppress up to 30% of the optical phonon relaxation, which is because 30% of all optical phonon relaxation processes involve acoustic phonons28,29. In addition, the 2D silicon phononic crystal with a low central frequency bandgap in the 3 × 108 Hz (or sub-GHz) range still demonstrated a strong capacity to affect high-frequency phonons in the THz regime via anomalous dispersion and reduced phonon group velocities29,30. This low bandgap affects high-frequency acoustic phonons in the THz regime as well as partial optical phonons29. As a result, the phononic crystal leads to a phonon bottleneck, which is most likely responsible for the observed suppression of hot carrier cooling in the present work.

Fig. 5: Calculated frequency band structures of the three samples.
figure 5

a Calculated frequency band structure for the reference sample; b calculated band structure for the structured sample with d = 1000 nm; c calculated band structure for the structured sample with d = 1060 nm, where the red band represents the phononic bandgap achieved.

Full size image

Conclusions

In summary, we reported direct experimental observations of significantly suppressed hot carrier cooling in a 2D silicon phononic crystal. In contrast to the reference sample, the 2D-structured silicon sample with d = 1060 nm demonstrated a strong capacity to suppress hot carrier cooling. This ability was investigated with the cooling lifetime. The results showed prolongation of cooling time by orders of magnitude. Frequency band structure simulations indicated that the 2D structured silicon sample with d = 1060 nm is a silicon phononic crystal. The present work presents direct experimental evidence and opens opportunities to develop promising technologies such as ultrahigh-efficiency silicon solar cells.

Experimental

Sample fabrication

Two-dimensional artificially structured crystalline silicon samples were prepared on a commercially available silicon-on-sapphire (SoS), where silicon is an intrinsic monocrystalline thin film with a thickness of 550 nm as the reference sample. The 2D patterns were designed and fabricated in a square arrangement with an electronic beam lithography (EBL, VB6 UHR-EWF) written polymethylmethacrylate (PMMA) mask and then etching in the vertical direction via a dry etching cluster (DRIE) consisting of the Oxford RIE Plasmalab System 100 with an ICP 380 source and the Oxford RIBE Ionfab 300. The PMMA film was prepared by hotplating at 180 °C for 2 min, spin coating at 2200 rpm and finally baking at 110 °C for 5 mins to achieve a thickness of 400 nm. The present etching parameters were as follows: a gas mixture of SF6 of 24 sccm and O2 of 6 sccm, a substrate temperature of 100 °C, a radio frequency power of 8 W, an ICP power of 800 W, a DC bias of 80 V, and an etching time of 70 s.

Measurement and characterization

Femtosecond transient absorption measurements

Femtosecond pump-probe transient absorption measurements were performed in which a regenerative amplified Ti:sapphire laser system (Coherent; 800 nm, 85 fs, 7 mJ/pulse, and 1 kHz repetition rate) was used as the laser source and a Helios spectrometer (Ultrafast Systems LLC) was included. The 800 nm output pulse from the regenerative amplifier was split into two parts with a 50% beam splitter. The transmitted part was used to pump a TOPAS optical parametric amplifier (OPA), which can generate laser pulses with wavelengths tunable from 250 nm to 2.5 μm. The 400 nm pump beam was made by frequency doubling one part of the 800 nm beam in the BBO crystal. The reflected 800 nm beam was split again into the two parts. One part constituting <10% was attenuated with a neutral density filter and focused onto a 2 mm thick sapphire window to generate a white light continuum (WLC) used for the probe beam. The probe beam was focused onto the sample using an Al parabolic reflector. After passing through the sample, the probe beam was collimated and then focused into a fiber-coupled spectrometer with CMOS sensors and detected at a frequency of 1 kHz. A series of neutral-density filters were used to adjust the power of the pump beam. The pump beam was focused on the sample with a beam waist of ~300 μm. The delay between the pump and the probe pulses was controlled with a motorized delay stage. The pump pulses were chopped by a synchronized chopper at 500 Hz, and the absorbance changes were calculated with two adjacent probe pulses (pump-blocked and pump-unblocked).

Characterization

SEM images were obtained by using scanning electron microscopy. The static absorption measurements were conducted by a UV–Vis–NIR Spectrophotometer (SolidSpec-3700, Shimadzu).

Phononic crystal calculations

For frequency band structure calculations, the time (t1)-dependent general elastic wave in Eq. 1 was used. The solution was expressed in the form of Eq. 2 based on the Bloch theorem. In addition, the Bloch-periodic boundary condition, expressed in Eq. 3, must be met at the boundaries of each unit cell due to the periodic nature of the phononic crystal:

$${\it{\nabla }}(C\left( R \right){\it{\nabla }}u\left( R \right)) - \rho \left( R \right)\partial 2\;u\left( R \right)/\partial t_1 = 0$$
(1)
$$u\left( R \right) = ei(k.R)uk\left( R \right)$$
(2)
$$uk(R + a) = ei(k.R)uk\left( R \right)$$
(3)

In the above three equations, u(R) is the displacement vector; C(R) and ρ(R) are the elastic constant and mass density of the materials, respectively; k is the wave vector in the first Brillouin zone; uk (R) is the displacement vector in the one-unit cell; and a is the base vector in the direct lattice vector. The frequency band structure and values of Eigen frequency as a function of wave vector can be obtained by solving Eq. 1–3. The calculations were conducted by using commercial software (Comsol Multiphysics 6.0). For the present calculations, three constants, namely, mass density ρ, Young’s modulus E, and Poisson’s ratio ν, are needed, and the parameter values adopted for crystalline silicon were ρ = 2330 kg/m3, E = 169 GPa, and ν = 0.28 for c-Si31,32,33.