1 Introduction

Long-distance power transmission lines of the HV/EHV classes are characterised by a chain structure that includes a number of substations that are connected to each other by overhead power lines. One of the core issues of the further expansion of transit capacities and the synchronization of connections between the power grids is above all the improvement of the capacity of long-distance power transmission lines.

It is known that with high voltages and high frequencies as well as with extremely long geometrical dimensions of the line, displacement and leakage currents cannot be taken into account. Therefore, the current value in the cross section of its conductors is not the same along the line. Current flows through the line conductors, creating a voltage drop and an alternating magnetic field. The resulting magnetic field in turn generates a self-induced electromotive force along the entire line. Because of this, the voltages between the conductors vary unevenly along the line [1]. Switching overvoltages occur during both planned and emergency switching. Planned line switchings, which have the highest intensity of implementation among all switchings, correspond to high values of overvoltages, which significantly interfere with these switchings. In distributed element circuits, such as high-voltage interconnection electric transmission line (ETL), changing the circuit mode results in the opening and closing of individual branches, as well as switching modes resulting from atmospheric phenomena. Switching one line causes a transient in the whole network. Therefore, the process in the switched section of the power transmission is largely determined by the features of the adjacent part of the circuit: the presence of outgoing lines, the parameters of the systems feeding them, etc. The resulting overvoltages or large currents can cause the insulation and individual parts of the electrical installation to collapse. The 300 km long unloaded line serves as a reactive power source. The passage of capacitive currents in this line through generators is one of the undesirable conditions of the network. Because the conversion of generators into reactive power operators has a negative effect on them and makes their operation unstable. From this perspective, especially in the switching modes, shunt compensation reactors (SR) are connected to the high-voltage busbars of the stations along with the ETL and receiving systems. Reactors play an important role in controlling reactive power in long-distance ETL and in limiting switching overvoltages. The role of shunt reactors (SR) at the beginning of a single-circuit line in limiting switching overvoltages and their switch-on and switch-off algorithms were examined in detail [2]. Studies have shown that SRs limit the switching overvoltages [3,4,5,6]. However, as previously mentioned, the role of shunt compensation reactors in high voltage and extra high voltage power grid (HV/EHV) alternating current (AC) multi-circuit lines over long distances has not been adequately studied despite the ever-evolving nature of the power sector, increasing energy demand and the need to meet that demand in a timely manner.

Another important factor that the occurrence of overvoltage in HV/EHV ETL is closely related to the compensation and redistribution of reactive powers. In addition to other measures for reactive power distribution and limitation of overvoltages, SRs are used [7, 8]. Such reactors influence switching overvoltages and the regulation of reactive powers. Studies have shown that it is not advisable to keep them on all the time in the circuit, as the parameters of such reactors do not change. Although it has recently been considered advisable to use reactors with variable parameters, reactors are switched off to provide maximum power in long-distance lines when the parameters of the reactors remain unchanged, and in low-load modes, they connect to the grid in order to compensate for the capacitive susceptance and to limit overvoltages. However, despite the complexity of variable parameter reactors, their high cost and a number of technical difficulties, they are widely used in areas where excessive overvoltages are generated. Nevertheless, these reactors do not radically solve the problem. It is therefore necessary to compensate for harmonics that result from their non-linear properties [9, 10].

In view of the above, it is proposed to increase the combined shunt compensation rate in double-circuit and multi-circuit long-distance ETL and, on the other hand, to eliminate the disadvantages inherent in shunt compensation. In order to overcome such shortcomings, it is proposed to install UR in parallel in addition to SR at the beginning and end of the ETL, which compensate for the interphase capacitance in overhead lines with HV/EHV and limit switching overvoltages [11].

First, the use of SRs and URs at the beginning and end of the line was considered by choosing different lengths and different operating modes in a single-circuit long-distance ETL, then switching overvoltages were analysed. It was found that without URs in the line no reliable protection against switching overvoltages is guaranteed and the protection of the ETL should be reconsidered. The use of URs with overvoltage limiters (OVL) for double-circuit high-voltage ETL was then checked [12, 13].

2 Calculation method

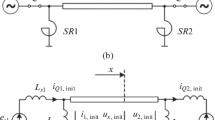
The problem of losses in double-circuit and multi-circuit lines is also relevant. Since double circuit lines have a great influence on electromagnetic compatibility, ferro resonance phenomena, transition and quasi-stable modes should be taken into account as influencing factors when selecting reactors [14] First, the following calculation scheme was chosen. (see Fig. 1). The calculation equations of multi-conductor ETL for the nodes of the circuit are expressed as follows [15]:

$$ \begin{gathered} - \frac{\partial u}{{\partial x}} = L_{0} \frac{\partial i}{{\partial t}} + f\left( {\frac{\partial i}{{\partial t}},i} \right), \hfill \\ - \frac{\partial i}{{\partial x}} = C_{0} \frac{\partial u}{{\partial t}} + \varphi \left( {\frac{\partial u}{{\partial t}},u} \right) \hfill \\ \end{gathered} $$
(1)
$$ \begin{gathered} u_{d} - u_{p} + Z\left( {i_{d} - i_{p} } \right) + h\left[ {Z\varphi_{e} \left( {\frac{{\partial u_{e} }}{\partial t},u_{e} } \right) + f_{e} \left( {\frac{{\partial i_{e} }}{\partial t},i_{e} } \right)} \right] + 0\,(h^{2} ) = \,0; \hfill \\ - u_{d} + u_{q} + Z\left( {i_{d} - i_{q} } \right) + h\left[ { - Z\varphi_{e} \left( {\frac{{\partial u_{e} }}{\partial t},u_{e} } \right) + f_{e} \left( {\frac{{\partial i_{e} }}{\partial t},i_{e} } \right)} \right] + 0(h^{2} ) = \,0; \hfill \\ \end{gathered} $$
(2)
Fig. 1
figure 1

In HV/EHV voltage double-circuit long-distance ETL, shunt compensation and high voltage OVL are combined at the beginning and end of the line

Full size image

Here, \(Z={\left({L}_{0}{C}_{0}^{-1}\right)}^{\text{0,5}}\) is the wave impedance of the lossless line, ud, up, uq, id, ip, iq – (1) and (2), are the voltages and currents at the coordinate points (x, t), (x—h, t- τ) in the solution area of the equation. t, τ are distance and time dependents variables. The ratio of these variables is the same as the electromagnetic wave velocity along the.

\({f}_{\phi }=(\frac{\partial u}{\partial t},u)\)—is a function that takes into account the corona effect, and \(\tau ={\left({L}_{0}{C}_{0}\right)}^{\text{0,5}}\cdot h\) is a calculation step [16, 17].

Considering the double-circuit ETL in Fig. 1 above, we can write the following expression for the wave processes at the time of connecting long-distance ETL at the start node (I) and the end node (III) point of the circuit:

Side I

$$ \begin{gathered} e\left( t \right) = L_{T} \frac{di}{{dt}} + u_{1} . \hfill \\ u_{1} = L_{1} \frac{{di_{r1} }}{dt};\,u_{1} = L_{2} \frac{{di_{r2} }}{dt}. \hfill \\ u_{1} = L_{wi} \frac{{di_{w1} }}{dt} + u_{w1} ;\,\,u_{1} = L_{w2} \frac{{di_{w2} }}{dt} + u_{w2} ; \hfill \\ \end{gathered} $$
(3)

Side III

$$ \begin{gathered} e^{/} \left( t \right) = L_{T} \frac{di}{{dt}} + u^{/}_{1} . \hfill \\ u^{/}_{1} = L^{/}_{1} \frac{{di_{r1} }}{dt};\,u^{/}_{1} = L^{/}_{2} \frac{{di_{r2} }}{dt}. \hfill \\ u^{/}_{1} = L^{/}_{wi} \frac{{di_{w1} }}{dt} + u^{/}_{w1} ;\,u^{/}_{1} = L^{/}_{w2} \frac{{di_{w2} }}{dt} + u^{/}_{w2} ; \hfill \\ \end{gathered} $$
(4)

Looking back on the chosen calculation scheme, we can express the calculation equations for the intermediate points at the beginning (I) and at the end (III) of the circuit as follows:

Side I

$$ \begin{gathered} - u_{1} + \left( {Z + Z_{n} } \right)i_{x1} = v_{q1} ; \hfill \\ - u_{1} + \left( {Z + Z_{n} } \right)i_{x2} = v_{q2} ; \hfill \\ \end{gathered} $$
(5)

Side III

$$ \begin{gathered} u^{/}_{1} + \left( {Z + Z_{n} } \right)i^{/}_{x1} = v^{/}_{p1} ; \hfill \\ u^{/}_{1} + \left( {Z + Z_{n} } \right)i^{/}_{x2} = v^{/}_{p2} . \hfill \\ \end{gathered} $$
(6)

If we consider the voltage across the neutral of the UR in the double-circuit ETL circuit shown in Fig. 1, the value of u0 can be expressed as follows:

$$ u_{0} = \frac{{u_{1a} + u_{1b} + u_{1c} }}{3};u_{1a} + u_{1b} + u_{1c} = 0;u_{0} = 0;u_{1a} + u_{1b} + u_{1c} \ne 0;u_{0} \ne 0. $$
(7)

The voltage difference of formulas (5) and (6) can be expressed as follows:

$$ \left( {Z + Z_{n} } \right)\left( {i_{x1} - i_{x2} } \right) = v_{q1} - v_{q2} . $$
(8)
$$ \left( {Z + Z_{n} } \right)\left( {i^{/}_{x1} - i^{/}_{x2} } \right) = v^{/}_{q1} - v^{/}_{q2} $$
(9)

where,

$${v}_{q}=-{u}_{q}+Z{i}_{q}+\delta \left(\pm {u}_{3}\right)+{\theta }_{1}-{\theta }_{2}$$
$${v}_{p}={u}_{p}+Z{i}_{p}-\delta \left(\pm {u}_{3}\right)+{\theta }_{1}+{\theta }_{2};$$

If we consider the expression (5) obtained from the voltage difference for the nodes at the beginning of the line (I), then this expression is as follows:

$$ \begin{gathered} i_{x1} = i - i_{r1} - i_{r2} - i_{w1} - i_{w2} - i_{x2} , \hfill \\ \left( {Z + Z_{n} } \right)\left( {i_{r} - i_{r1} - i_{r2} - i_{w1} - i_{w2} - i_{x2} } \right) = v_{q1} - v_{q2} , \hfill \\ \left( {Z + Z_{n} } \right)\left( {i_{r} - i_{r1} - i_{r2} - i_{w1} - i_{w2} } \right) - 2\left( {Z + Z_{n} } \right)ix_{2} = v_{q1} - v_{q2} , \hfill \\ ix_{2} = 0.5(Z + Z_{n} )^{ - 1} \left[ {v_{q1} - v_{q2} - \left( {Z + Z_{n} } \right)\left( {i_{r} - i_{r1} - i_{r2} - i_{w1} - i_{w2} } \right)} \right], \hfill \\ 2u_{1} + \left( {Z + Z_{n} } \right)\left( {i_{x1} + i_{x2} } \right) = v_{q1} + v_{q2} , \hfill \\ \end{gathered} $$
(10)

If in Fig. 1 we express the node (I) at the beginning of the circuit as follows, then:

$$ \begin{gathered} \frac{di}{{dt}} = L_{T}^{ - 1} \left[ {e\left( t \right) - u_{1} } \right], \hfill \\ \frac{{di_{r1} }}{dt} = L_{r1}^{ - 1} u_{1} , \hfill \\ \frac{{di_{r2} }}{dt} = L_{r2}^{ - 1} u_{1} , \hfill \\ \frac{{di_{w1} }}{dt} = L_{w1}^{ - 1} \left( {u_{1} - u_{01} } \right), \hfill \\ \frac{{di_{w2} }}{dt} = L_{w2}^{ - 1} \left( {u_{1} - u_{02} } \right) \hfill \\ \end{gathered} $$
(11)

3 Mathematical modelling of a double-circuit power transmission line.

In the calculation scheme shown in Fig. 1, we can express the source as follows:

$$ e\left( t \right) = \left| {\begin{array}{*{20}c} {e_{1} } \\ {e_{2} } \\ {e_{3} } \\ \end{array} } \right| = \left| {\begin{array}{*{20}c} {E_{m} \sin (\omega t + \phi )} \\ {E_{m} \sin (\omega t + \phi + {\raise0.7ex\hbox{${2\pi }$} \!\mathord{\left/ {\vphantom {{2\pi } 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}})} \\ {E_{m} \sin (\omega t + \phi - {\raise0.7ex\hbox{${2\pi }$} \!\mathord{\left/ {\vphantom {{2\pi } 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}})} \\ \end{array} } \right| $$
(12)
$$ u = \left| {\begin{array}{*{20}c} {u_{a1} } \\ {u_{b1} } \\ {u_{c1} } \\ \end{array} } \right|;\,i = \left| {\begin{array}{*{20}c} {i_{a1} } \\ {i_{b1} } \\ {i_{c1} } \\ \end{array} } \right|;\, i_{p} = \left| {\begin{array}{*{20}c} {u_{pa1} } \\ {u_{pb1} } \\ {u_{pc1} } \\ \end{array} } \right|;\,\,i_{q} = \left| {\begin{array}{*{20}c} {u_{a1} } \\ {u_{b1} } \\ {u_{c1} } \\ \end{array} } \right|; $$
(13)
$$ i_{{OVL_{I} }} = \left| {\begin{array}{*{20}c} {u_{{OVL_{Ia} }} } \\ {u_{{OVL_{Ib} }} } \\ {u_{{OVL_{Ic} }} } \\ \end{array} } \right|;\,i_{{OVL_{III} }} = \left| {\begin{array}{*{20}c} {u_{{OVL_{IIIa} }} } \\ {u_{{OVL_{IIIb} }} } \\ {u_{{OVL_{IIIc} }} } \\ \end{array} } \right|; $$
(14)

Having obtained the expressions, for phase 1 of the previous circuit, with parallel connection of the OVL and with no load on the transformers with insulated neutral, we can write the following:

$$\frac{d{\varphi }_{1}}{dt}={u}_{{T}_{I}}-{u}_{0}$$
(15)

Here, \({\phi }_{1}\) is the phase 1 flux linkage, \({u}_{{T}_{I}}\) is the phase 1 voltage of the transformer, and \({\text{U}}_{0}\) -is the neutral voltage.

If we switch on the transformer while it is live, we can express the total equality of current and current for the two phases as follows (flux linkage \({\phi }_{1}\) and current magnetization \({{i}_{\mu }}_{1}\)):

$${\phi }_{1}={\phi }_{2}+{\phi }_{3};{i}_{\mu 1}={i}_{\mu 2}+{i}_{\mu 3}$$

As can be seen in formula (15), the voltages and currents in the phases of a transformer can be expressed as follows 5:

$$(1+G){u}_{T}+(Z+{Z}_{n})i={v}_{p}$$
(16)

here \(i={i}_{OVL}+{i}_{r}+{i}_{UR},\) \({i}_{r}={i}_{\mu }\). \({i}_{OVL}\) is the matrix of the current flowing through the OVL, and \({u}_{T},{i}_{T}\) the matrix of the currents and voltages of the transformer, and \({i}_{UR}\)-is the UR.

Based on expressions (15) and (16) we can write the following expressions for each phase:

$$ \begin{gathered} u_{T1} = (1 + G)_{1}^{ - 1} v_{p1} - (1 + G)_{1}^{ - 1} + \left( {Z_{11} - Z_{12} } \right)i_{T1} \hfill \\ u_{T} 2 = u_{T} 3 = (1 + G?)_{2} ?^{( - 1)} v_{p} 2 + 0.5(1 + G)_{2} \hfill \\ \end{gathered} $$
(17)

where, \(G=\text{0,83}{\left(\frac{f}{50}\right)}^{\text{0,62}}\left[1-{e}^{-{\text{3,05}}^{\left(\frac{{U}_{M}}{{U}_{N}}\right)}}\right], \frac{1}{MOm\bullet km}\) is taken into account.

\(\left(\frac{{U}_{M}}{{U}_{N}}\right)\) is the overvoltage ratio. When the neutral voltage is zero:

$$ u_{0} = \frac{1}{3}\left( {u_{T1} + u_{T2} + u_{T3} } \right) = \frac{1}{3}(1 + G)_{1}^{ - 1} \left( {v_{p1} + v_{p2} + v_{p3} } \right); $$
(18)

When using OVLs for HV/EHV double-circuit power lines, Eq. (15) will be written as follows:

$$ \left( {{1}\, + \,G} \right)u_{{\text{T}}} \, + \,\left( {{\text{Z}}\, + \,{\text{Z}}_{{\text{n}}} } \right){\text{i}}\, = \,\upsilon_{{{\text{p2}}}} \,{\text{v}}_{{{\text{p}}2}} \,{\text{v}}_{{{\text{p}}2}} $$
(19)

where i = iOVL + ir, ir, = iµ. \(\text{i}={\text{i}}_{\text{OVL}}+{\text{i}}_{\text{r}},{\text{i}}_{\text{r}}={\text{i}}_{\upmu }\) \(\text{i}={\text{i}}_{\text{OVL}}+{\text{i}}_{\text{r}},{\text{i}}_{\text{r}}={\text{i}}_{\upmu }\) Where, iOVL -\({\text{i}}_{\text{OVL}}-\) \({\text{i}}_{\text{OVL}}-\) is the matrix of the current flowing through the OVL. For current and voltage of the transformer, we can write the following expression:

$$ \begin{gathered} \frac{d\phi }{{dt}} = u_{T} - u_{0} ; \hfill \\ u_{T} = \left[ {v_{p} - \left( {Z + Z_{n} } \right)i\mu } \right]\left( {Z + Z_{n} } \right)i_{YGM} - u_{0} ; \hfill \\ i_{OVL} = f\left( {u_{T} } \right) \hfill \\ \end{gathered} $$
(20)

The mathematical model based on the proposed calculation schemes consists of nodes and power transmission equations. Mathematical models of switching overvoltages, due to radial and non-radial switching of lines and atmospheric phenomena in high-voltage multi-circuit ETL are developed together with mathematical models of substation elements and a calculation algorithm is created from both models.

When developing the calculation algorithm, the purpose of the switching unit, the splitting the SS circuits, the complexity of the URs and their structure should be taken into account. It is known that the characteristics of the transition processes and the amount of overvoltage in the URs are determined by several criteria. With this in mind, the structure and parameters of high-voltage substations on long-distance lines with URs should first be considered. (because SS is viewed as a multi-frequency circuit). It should be noted that in long-distance ETLs with URs, the frequencies of the voltage fluctuations in the discharged part of the buses, electrical devices with low power, buses in the sockets of electrical switches, busbars, voltage transformer socket, disconnectors and arresters, contacts in UR disconnectors, etc. depend on the transition time of the wave in the bus system when switching. With regard to the optimal distribution of powers in the ETL, the equivalent schemes for connecting the ETL to the source should be based on the calculation scheme. Therefore, in long-distance ETLs with URs, the equipment parameters on the supply side must be taken into account in order to reflect the processes on the switching area side of the bus system and at the source of the power transmission. This method enables the research-based calculation scheme to be simplified significantly and the accuracy of the analysis to be increased. It should be noted that the choice of the calculation scheme is based on the data and research in order to determine the effectiveness of the developed numerical calculation method and the special algorithm for high-frequency switching overvoltages, as well as the effectiveness of high-frequency overvoltage limitation even if UR enter the switching circuit [18]. Based on the algorithm for the analysis of high-frequency arc overvoltages in complex networks with URs, the calculations are carried out by sequentially determining voltages and currents at the inner and node points of the line at equal intervals (first calculation step from the perspective of time).

The algorithms developed at the Institute of Physics are used to calculate the currents and voltages at the nodes of the calculation scheme. Using the expressions (1)-(19), a calculation grid shown in Fig. 2 is constructed and the information for the moment (t + 2τ)\(\left(\text{t}+2\uptau \right)\) \(\left(\text{t}+2\uptau \right)\) and (t + τ)\(\left(\text{t}+\uptau \right)\) \(\left(\text{t}+\uptau \right)\) in the basic and sub-requirements are placed sequentially according to the initial conditions.

Fig. 2
figure 2

Three-dimensional calculation grid

Full size image

It is proposed to use a third-degree spline interpolation method to calculate and determine the currents and voltages at the nodes of the calculation scheme (as well as for the beginning and the end of the line) and to increase the efficiency [19,20,21,22]. In previous dissertation papers, issues such as coronal events in ETL, ferro resonance events at high voltages, etc. were examined with ɡ(x,y)\(\text{g}\left(\text{x},\text{y}\right)\) \(\text{g}\left(\text{x},\text{y}\right)\), the single-variable interpolation function. The proposed cubic spline-interpolation method increases the calculation time without losing the continuity for calculating the values of voltages and currents at additional points inside the line and provides high accuracy of voltage and current in the starting area of the line. At the closest approximation in comparison, tertiary spline polynomials can be used.

Using the difference method shown in Fig. 3, the finite-difference approximation approach for each part of (x,t)- (x + 2 h,t)\(\left(\text{x},\text{t}\right)-\left(\text{x}+2\text{h},\text{t}\right)\) \(\left(\text{x},\text{t}\right)-\left(\text{x}+2\text{h},\text{t}\right)\), the two-variable third-degree polynomial in each ɡ(x,y)\(\text{g}\left(\text{x},\text{y}\right)\) \(\text{g}\left(\text{x},\text{y}\right)\),\(\text{g}\left(\text{x},\text{y}\right)\) \(\text{g}\left(\text{x},\text{y}\right)\) part of the grid can be shown as follows [4, 23,24,25,26]:

$$g\left(x,y\right)={g}_{k,l}\left(x,y\right)=\sum_{i,j=0}^{3}{a}_{i,j}^{k,l}{\left({x}_{k}-x\right)}^{i}{\left({y}_{l}-y\right)}^{j},$$
(21)

k = 1,2,3…, (0,t), (2 h,t), (4 h,t),…, (2nh,t)n \(\text{k}=\text{1,2},3,\dots ,\left(0,\text{t}\right),\left(2\text{h},\text{t}\right),\left(4\text{h},\text{t}\right),\dots ,\left(2\text{nh},\text{t}\right)\text{ n}\) \(\text{k}=\text{1,2},3,\dots ,\left(0,\text{t}\right),\left(2\text{h},\text{t}\right),\left(4\text{h},\text{t}\right),\dots ,\left(2\text{nh},\text{t}\right)\text{n}\)- is the number of.

Fig. 3
figure 3

The finite-difference scheme for approximation of ETL equations

Full size image

coordinate reference points. If we consider Eq. (21), where the voltages and currents at the additional points within the grid are equidistant from each other and are H1 = H2 = H3 = … = Hn at a timing step, the equations can be expressed as:

$$ \begin{aligned} g\left( {x_{i - 1} ,y} \right) = & H_{i - 1,j - 1} \frac{{\left( {y_{i} - y} \right)^{3} }}{{6\tau_{i} }} + H_{i - 1,j} \frac{{\left( {y - y_{j - 1} } \right)^{3} }}{{6\tau_{i} }} + \left( {f_{i - 1,j - 1} - \frac{{H_{i - 1,j - 1} \tau_{j}^{2} }}{6}} \right)\frac{{y_{i} - y}}{{\tau_{i} }} + \\ + & \left( {f_{i - 1,j} - \frac{{H_{i - 1,j} \tau_{j}^{2} }}{6}} \right)\frac{{y - y_{j - 1} }}{{\tau_{i} }} \\ \end{aligned} $$
(22)
$$g\left({x}_{i},y\right)={H}_{i,j-1}\frac{{\left({y}_{i}-y\right)}^{3}}{6{\tau }_{i}}+{H}_{i,j}\frac{{\left({y-y}_{j-1}\right)}^{3}}{6{\tau }_{i}}+\left({f}_{i,j-1}-\frac{{H}_{i,j-1}{\tau }_{j}^{2}}{6}\right)\frac{{y}_{i}-y}{{\tau }_{i}}+\left({f}_{i,j}-\frac{{H}_{i,j}{\tau }_{j}^{2}}{6}\right)\frac{{y-y}_{j-1}}{{\tau }_{i}}$$
(23)

where,\({H}_{ij}={g}_{yy}\left({x}_{i,}{y}_{i}\right), {h}_{i}={x}_{i}-{x}_{i-1},{M}_{ij}={g}_{xx}\left({x}_{i,}{y}_{i}\right),{\tau }_{i}={y}_{i}-{y}_{j-1}.\)

If we consider the functions \({g}_{xx}\left({x}_{i-1,}y\right)\) and \({g}_{xx}\left({x}_{i,}y\right)\) according to the formula (22), then we can express the values of \({g}_{x}\left({x}_{,}y\right)\) as follows:

$${g}_{xx}\left({x}_{i-1},y\right)={K}_{i-1,j-1}\frac{{\left({y}_{i}-y\right)}^{3}}{6{\tau }_{i}}+{K}_{i-1,j}\frac{{\left({y-y}_{j-1}\right)}^{3}}{6{\tau }_{i}}+\left({M}_{i-1,j-1}-\frac{{K}_{i-1,j-1}{\tau }_{j}^{2}}{6}\right)\frac{{y}_{i}-y}{{\tau }_{i}}+\left({M}_{i-1,j}-\frac{{K}_{i-1,j}{\tau }_{j}^{2}}{6}\right)\frac{{y-y}_{j-1}}{{\tau }_{i}}$$
(24)

where, \({K}_{ij}={g}_{xxyy}\left({x}_{i},{y}_{i}\right)\)

$${g}_{xx}\left({x}_{i},y\right)={K}_{i,j-1}\frac{{\left({y}_{i}-y\right)}^{3}}{6{\tau }_{i}}+{K}_{i,j}\frac{{\left(y-{y}_{j-1}\right)}^{3}}{6{\tau }_{i}}+\left({M}_{i,j-1}-\frac{{K}_{i,j-1}{\tau }_{j}^{2}}{6}\right) \frac{{y}_{i}-y}{{\tau }_{i}}+\left({M}_{i,j}-\frac{{K}_{i,j}{\tau }_{j}^{2}}{6}\right)\frac{{y-y}_{j-1}}{{\tau }_{i}}$$
(25)

In this way, if we revisit at formula (21), we can write that expression for the function \({g}_{xx}\left({{x}_{i}}_{,}y\right)\) as follows:

$$g\left(x,y\right)={g}_{xx}\left({x}_{i-1},y\right)\frac{{\left({x}_{i}-x\right)}^{3}}{6{\tau }_{i}}+{g}_{xx}\left({x}_{i},y\right)\frac{{\left(x-{x}_{j-1}\right)}^{3}}{6{\tau }_{i}}+\left(g\left({x}_{i-1},y\right)-\frac{{g}_{xx}\left({x}_{i-1},y\right){h}_{j}^{2}}{6}\right)\frac{{x}_{i}-x}{{h}_{i}}+\left(g\left({x}_{i},y\right)-\frac{{g}_{xx}\left({x}_{i},y\right){h}_{i}^{2}}{6}\right)\frac{x-{x}_{i-1}}{{h}_{i}}$$
(26)

Voltage and current at the coordinate points \(\left(x,t\right)\) from the multi-conductor ETL difference method in relation to the established system of equations are calculated using the following formula:

$$ \begin{gathered} u_{d} = 0,5\left( {1 + \sigma } \right)^{ - 1} \left[ {u_{p} + u_{q} + Z\left( {i_{p} - i_{q} } \right) - 2\sigma \left( { \pm u_{3} } \right)} \right] + 2\theta_{2} \hfill \\ i_{d} = 0,5\left( {Z + Z_{n} } \right)^{ - 1} \left[ {u_{p} - u_{q} + Z\left( {i_{p} - i_{q} } \right) + 2\sigma \left( { \pm u_{3} } \right)} \right] + 2\theta_{1} \hfill \\ \end{gathered} $$
(27)

Here, \({u}_{p},{u}_{q,}{i}_{p},{i}_{q} p\left(x-h,t-\tau \right),q\left(x+h,t-\tau \right)\) are the known values of the voltage and current column matrices at the points \(p\) and \(q\) points of the multi-conductor ETL with the given coordinates. Where, \(\theta =arctg\frac{{a}_{km}}{{h}_{k}+{h}_{m}}\), \(a-\) is the distance between the conductors, \({h}_{k},{h}_{m}-\) is the height of the suspension (\(k\ne m\)).

The numerical calculation of the electromagnetic wave processes in double-circuit ETL using the calculation Eqs. (27) obtained by the multi-conductor ETL difference method can be expressed as follows:

$$ \begin{gathered} u_{{d_{I} }} + \left( {Z + Z_{n} } \right)_{I} i_{{d_{I} }} + \left( {Z + Z_{n} } \right)_{I - II} i_{{d_{II} }} + \left( {Z + Z_{n} } \right)_{I - T} i_{T} = v_{{p_{I} }} + v_{{p_{I - II} }} + v_{{p_{I - T} }} , \hfill \\ u_{{d_{II} }} + \left( {Z + Z_{n} } \right)_{I - II} i_{{d_{I} }} + \left( {Z + Z_{n} } \right)_{II} i_{{d_{II} }} + \left( {Z + Z_{n} } \right)_{II - T} i_{T} = v_{{p_{II} }} + v_{{p_{I - II} }} + v_{{p_{II - T} }} , \hfill \\ - ud_{I} + \left( {Z + Z_{n} } \right)_{I} i_{{d_{I} }} + \left( {Z + Z_{n} } \right)_{I - II} i_{{d_{II} }} + \left( {Z + Z_{n} } \right)_{I - T} i_{T} = v_{{q_{I} }} - v_{{q_{I - II} }} - v_{{q_{I - T} }} , \hfill \\ - u_{{d_{II} }} + \left( {Z + Z_{n} } \right)_{I - II} i_{{d_{I} }} + \left( {Z + Z_{n} } \right)_{II} i_{{d_{II} }} + \left( {Z + Z_{n} } \right)_{II - T} i_{T} = v_{{q_{II} }} + v_{{q_{I - II} }} + v_{{q_{II - T} }} . \hfill \\ \end{gathered} $$
(28)

After calculating the currents and voltages at the beginning and end of the line, the currents, and voltages for the points \(2h, 4h, 6h\), etc. are also calculated from the calculation grid \(\left(t+\tau \right)\). These quantities are calculated using a system of Eqs. (21)-(27). Using the two-variable third-degree spline-interpolation method to determine the values in each part of \(\left(x,t\right)-\left(x+2h,t\right)\), formula (21) can be defined as follows:

$$ g_{p} = u\left( {x_{1} + y_{1} + 2h,t + \tau } \right) + Zi\left( {x_{1} + y_{1} + 2h,t + \tau } \right) - Z_{0} \left[ {i_{02} \left( {x_{1} + y_{1} + 4h,t - 2\tau } \right) - i_{01} \left( {x_{1} + y_{1} + 4h,t - 2\tau } \right)} \right] + Z_{3} \mathop \sum \limits_{{k = 1_{k} }}^{3} i\left( {x_{1} + y_{1} + 4h,t - 2\tau } \right) + \theta_{1\gamma } , $$
$$ \begin{aligned} g_{p} = & - u\left( {x_{2} + y_{21} + 2h,t + \tau } \right) + Zi\left( {x_{2} + y_{2} + 2h,t + \tau } \right) + Z_{0} [i_{02} \left( {x_{2} + y_{2} + 4h,t - 2\tau } \right) - i_{01} \left( {x_{2} + y_{2} + 4h,t - 2\tau } \right)] \\ + & Z_{3} \mathop \sum \limits_{{k = 1_{k} }}^{3} i\left( {x_{21} + y_{2} + 4h,t - 2\tau } \right) - \theta_{2\gamma } , \\ \end{aligned} $$

The currents and voltages at the points \(2h, 4h, 6h\dots \), etc. of the calculation grid \(\left(t+2\tau \right)\) can be determined as follows:

$${u}_{d}=\text{0,5}{\left(1+\sigma \right)}^{-1}\left[u\left({x}_{1}+{y}_{1}+2h,t+\tau \right)+u\left({x}_{2}+{y}_{2}+2h,t+\tau \right)+Zi\left({x}_{1}+{y}_{1}+2h,t+\tau \right)-i\left({x}_{2}+{y}_{2}++4h,t+\tau \right)-2\sigma \left(\pm {u}_{3}\right)\right]+{2\theta }_{2},$$
$${i}_{d}=\text{0,5}{\left(Z+{Z}_{n}\right)}^{-1}\left[u\left({x}_{1}+{y}_{1}+2h,t+\tau \right)-u\left({x}_{2}+{y}_{2}+2h,t+\tau \right)+Zi\left({x}_{1}+{y}_{1}+2h,t+\tau \right)-\left({x}_{2}+{y}_{2}+4h,t+\tau \right)-+2\sigma \left(\pm {u}_{3}\right)\right]+{2\theta }_{1}.$$

Here, \(\left({u}_{p}, {u}_{q}, {i}_{p,}\right)\) and \({i}_{q,}\) are known voltages and currents at the points \(p\) and \(k\) with coordinates \(p\left(x-h,t-\tau \right),q\left(x+h,t-\tau \right)\) on the ETL, \(t,\tau -\) are distance and time dependent variables, \(k\) -is the dimensional column matrix:

$${\theta }_{1}=\left|\begin{array}{c}{\theta }_{11}\\ {\theta }_{12}\\ {\theta }_{13}\end{array}\right|, {\theta }_{1}=Z=\sum_{k=1}^{3}{\chi }_{k{i}_{k}},$$

\({Z}_{1}\) and \({\chi }_{k}\) are matrix coefficients and currents. \(k\)- dimensional column matrix is:

$${\theta }_{2}=hZ\sum_{k=1}^{3}{G}_{k}{u}_{fck}$$

Here, \({u}_{fck}\) is the known voltage at the point\(f\), \(,h\) is the distance based calculation step, \(Z\) is the square matrix of the wave impedance of the lossless line, and \({G}_{k}\) are the coefficients from (17) [27,28,29,30,31,32,33].

These expressions are used to perform calculations related to the electromagnetic wave processes in multi-conductor ETL, as well as related to the switching overvoltages in inter-system power transmission.

4 Simulation results and discussion

A symmetrical double-circuit, three-phase transmission line with two overhead lines is used as a model for a computer simulation to study transient electromagnetic processes during overvoltages. The studies are conducted for the purpose of testing the 500 kV in 380 km ETL with the following special parameters:

$${U}_{nom}=500 kV,l=380 km, { X}_{1F}{=0.29\text{ Om}/\text{km }, { X}_{0F}=1.0760\text{ Om}/\text{km}, { r}_{0\text{F}}=1.4{\cdot 10}^{-8} \text{Om}/\text{km}, { r}_{0\text{T}}=3.88{\cdot 10}^{-7} \text{Om}/\text{km},{ r}_{0\text{Z}}=4\cdot 10}^{-8} \text{Om}/\text{km}, { L}_{0F}=1.357{\cdot 10}^{-9} H/km, { L}_{0T}=2.107{\cdot 10}^{-9} H/km, {\text{ g}}_{0\text{F}}=2.8{\cdot 10}^{-14}Sm/km,{\text{ g}}_{0\text{T}}\approx 0,{ { C}_{0\text{FT}}=0.0512{\cdot 10}^{-14} F/km, C}_{0\text{F}}=0.6817{\cdot 10}^{-14} F/km, { C}_{0\text{FF}}=0.902{\cdot 10}^{-14} F/km,$$

reactor parameters:\({X}_{r}=1520\text{ Om}, { x}_{N}=0,\) system parameters:\({X}_{1}=20\text{ Om}, { X}_{0}=6.456\text{ Om}.\)

Based on the mathematical model developed, the simulation was conducted at the beginning of the line. The curves of the voltages at the beginning of the line with SR and UR when switching on switches which is presented in Fig. 4. The curves of the voltages at the beginning of the line with SR without UR when switching on switches which is presented in Fig. 5.

Fig. 4
figure 4

Voltage variation curves in phases A, B and C at the beginning of the line with SR and UR

Full size image
Fig. 5
figure 5

Voltage variation curves in phases A, B and C at the beginning of the line SR without UR

Full size image

The proposed mathematical model was tested for smoothness by comparing SR with UR connected to the beginning of the line and without UR connected to the beginning of the line. Analysing the voltage curve at the beginning of the line, we can see that when SR is switched on with UR together, the voltage decreases (Fig. 4). The same processes were simulated. All the wave processes generated during switching were measured over 0.8 s and recorded. Voltage variation curves are provided for the beginning of the line in both circuits. It is found that the maximum instantaneous value of voltage at the beginning of the line without UR is greater than that with SR and UR. In comparison, reliable protection was found to be provided for the overvoltages generated during switching when there is a UR on the line.

Thus, switching control with UR not only reduces the maximum overvoltages but also significantly reduces the range of the maximum overvoltages on the line.

We aim to advance the mathematical modelling of electromagnetic processes for the analysis of transients in ETL during an atmospheric phenomenon in our next research.

5 Conclusion

In this article, the mathematical modelling of electromagnetic wave processes during switching overvoltages in a multi-circuit inter-system ETL was explored as follows:

A general approach was achieved using mathematical methods in a double-circuit intersystem power transmission line. The waves occurring in long-distance transmission lines were analysed and the results evaluated. A third order spline-interpolation method was used to calculate the currents and voltages at the nodes and to determine the exact values. The analyses have clearly shown that in long-distance transmission lines, the UR connected in parallel with the SR at the beginning and end of the line provide reliable protection against overvoltages generated and prevent the occurrence of electromagnetic wave processes in the power transmission line. It was found that no reliable protection against switching overvoltages is ensured in the long-distance ETL in the absence of UR. With average lengths of 380–560 km and minimum degrees of compensation \({k}_{\text{r}}=0.7\div 0.8\), the reduction in the fundamental harmonic voltage, depending on the location of the SR with UR, is 2–3%, which obviously can be considered overvoltage in practical calculations.

Therefore, the proposed calculation equations can be used in process modelling for electromagnetic waves, taking into account URs at the beginning and end of the line in HV/EHV double-circuit long-distance ETLs, in order to avoid overvoltages in complex distributed element circuits. In addition, according to the calculation scheme shown in Fig. 1, the results of a calculation experiment based on computer modelling of the electromagnetic wave processes of the OVL connected in parallel to the UR at the beginning and end of a HV/EHV double-circuit ETL allows the voltage and current values to be kept within normal limits to increase the efficiency.

The results of the curves obtained from the calculation are based on the case of a SR and an UR at the beginning of the 500 kV double-circuit long distance ETL.