1 Introduction

Water is related to various parts of the hydrologic cycle. It arrives the earth surface in the form of precipitation and snowmelts, and during runoff, it percolates the subsurface, employing gravitational forces to infiltrate permeable geo-layers [1]. Groundwater accumulates within the phreatic or saturated zone underlying the vadose zone, which is the zone of partial water saturation [2, 3]. The water table (top of the aquiferous zone) could either be high (implying shallowness to the near surface) or low (implying greater depth). High water tables are common during periods of heavy rainfall, snow or ice melts, while low water tables are typical during arid seasons [4]. Subterranean water flow via porous and permeable rocks trends from zones of high elevation and pressure to zones of low elevation and pressure, implying movement from regions of high hydraulic head to regions of low hydraulic head. The larger the hydraulic head difference, the faster the groundwater flow rate or discharge [5] as expressed by Darcy’s law

$$Q = K \cdot A\frac{\Delta h}{{\Delta l}}$$
(1)

where Q is the groundwater discharge, K is the hydraulic conductivity, A is the cross-sectional area, \(\frac{\Delta h}{\Delta l}\) is the hydraulic gradient (hydraulic head difference).

Groundwater is considered a viable source of potable water compared to surface water resources. This is because as groundwater passes through soil and rock formations, it undergoes filtering, leading to the elimination of contaminants like rock sediments and micro-organisms, although some dissolved solids and toxicants are difficult to purify naturally despite huge depths of subsurface travel [4, 5]. The filtering capacity of soil and rock is influenced by rock minerology and composition. For example, sewage is filtered at approximately 30-45 m during percolation when it travels through sandy loam and organic humus [5]. The filtering process is undertaken via decomposition and ion absorption by humus and argillitic minerals. On the other hand, highly fractured granitic/limestone rocks (which are highly permeable) are incapable of purifying sewage even at very great depths of travel owing to the rapidity of fluid/material flow through such rock materials [5]. Sources of groundwater pollution include pesticides, fertilizers, organic manure, and herbicides employed during agricultural activities. Other sources are sewage, oil spills, saltwater intrusion, industrial acid mine drainage, and leachate from landfills [2, 4,5,6,7,8] Groundwater pollution is especially insidious since its damaging impacts are not easily evident. Percolation of contaminants takes place within rocks, not land, hence it may take a long time for contamination to be detected. The slow rate of groundwater’s travel through subsurface rocks generates time lapses between the period when a contaminant product starts its journey within the vadose zone, to when it finally ends in the aquifer system. This makes pollutant detection more difficult [2, 4]. How susceptible groundwater is to contamination is influenced by regional geology, nature of contaminant material, and length of stay of groundwater within the aquifer before its extraction. The shorter the length of groundwater’s stay prior to extraction (e.g., in shallow aquifers), the less the opportunity for moderation and filtration of toxic contaminants, leading to greater concentrations of toxicity [2, 4, 5]. It is therefore important that groundwater pollution be prevented in the first place, as its cleanup procedures are more difficult and expensive compared to cleanup of surface water sources [2, 4]. Preventative and responsive methods are required to safeguard local water systems. However, from a financial viewpoint, preventative methods are superior to reactive methods, as reactiveness implies higher cost and more challenging cleanup, and in some cases, it may be impractical [2, 8].

One of such preventative approaches involves the generation of groundwater models and maps to indicate regions of vulnerability. Groundwater vulnerability models delineate indices within an aquifer system that determines to what extent groundwater quality will be degraded by an introduced pollutant [9]. Several factors affect groundwater vulnerability. These include the type of groundwater confinement, the lithology of the overburden strata, the depth to the water table, the attenuation capacity of the pollutants as it moves through the vadose zone, the thickness of the overburden, and the hydraulic conductivity within the water bearing formations [10,11,12,13]. With the burgeoning population in the study area located in Southern Nigeria, coupled with increasing rates of urbanization and industrialization, groundwater resources (which happens to be the sole potable water source in the region) is highly predisposed to contamination as a result of anthropogenic activities. Not only must new groundwater sources be found and exploited to supply the current water needs of a growing population, safeguards also have to be applied to protect dwindling water supplies from contamination. Availability of potable surface or groundwater resources is a basic requirement, impacting extent of economic development within nations, and facilitating the achievement of UN Sustainable Development Goals [14,15,16].

To ensure a continuous supply of safe potable water in the study area, geophysical methods [17,18,19,20,21,22,23,24] were undertaken to investigate the extent of aquifer susceptibility to contamination. These geophysical techniques have the ability to detect variation in properties like electromagnetic and resistivity distribution within the earth’s surface [25,26,27,28,29]. The reason these methods have been a preferred choice in groundwater investigation and other environmental research projects is because of their portability, non-invasiveness, ease/rapidity of data acquisition, and reduced ambiguity with regards to measurement interpretation [30,31,32,33,34,35]. Geo-electrical techniques, for example, inject direct current into the earth via current electrodes and measure the resulting potential difference via potential electrodes to generate measures of subsurface apparent resistivity which are later inverted to generate true earth resistivity values. The variation in soil resistivity is then employed to generate tomographic images delineating subsurface electro-stratigraphy [36,37,38,39]. The geo-resistivity values generated are influenced by soil permeability, porosity, pore fluid ionic content, and mineralization of clay particles within the subsurface [40, 41]. Contrasts in geo-electrical properties within a region can delineate the geoelectric layers, identify locations of aquiferous sequences, evaluate susceptibility of the aquifer to contamination, and generate vulnerability indices for the aquifer.

Characterization of aquifer vulnerability can be undertaken using statistical models, process-based computer models, or index-based models [42,43,44,45,46,47]. Statistical models measure the chance of a given pollutant surpassing a given concentration. Process-based computer models are used to estimate the travel times of percolating pollutants, their concentrations, and the length of time the pollutant stays within a given layer. Such methodologies are expensive and require huge datasets for the simulations to be undertaken. Index-based models, on the other hand, employ a range of parameters associated with a certain degree of vulnerability. These parameters are dissected into ranks or classes that are used to determine are used to determine the extent of contamination. This work employed index-based models: the aquifer vulnerability index (AVI) model and the groundwater confinement (G), overlaying strata (O) and depth to groundwater (D) model (abbreviated as GOD), in its assessment of aquifer vulnerability. These modelling techniques were chosen for their effectiveness in generating accurate models of aquifer vulnerability. The Aquifer Vulnerability Index (AVI) modelling technique assessed aquifer vulnerability via estimates of overburden thickness (T) and hydraulic conductivity (K) whereas the GOD technique assessed aquifer vulnerability using measures of groundwater confinement (G), lithology of overburden (O) and depth to water table (D). In addition, a Dar-Zarrouk parameter (longitudinal conductance) was used to complement the index-based modeling techniques by generating measures of aquifer protectivity rating.

The goal of this research therefore, was to employ geo-electrical technology in the evaluation of aquifer vulnerability and protectivity using AVI models, GOD models, and Dar-Zarrouk parameters. The study also aimed at appraising the corrosivity of the overburden layers. Corrosivity is an important measure since high topsoil corrosivity would cause damage to underground pipes/utilities, resulting in percolation of toxic pipeline materials into subterranean water resources. The results obtained from geo-electrical surveying will be applied in the identification of lithological and geologic formations. The increasing population in the region, coupled with high rates of industrialization and urbanization, has exerted intense pressure on available water resources, necessitating this study. Zones of groundwater susceptibility would be mapped to aid in monitoring pollution-related problems. Though groundwater is exposed to other risks such as over-abstraction, drought, etc., the focus here was contamination. Mapping and modelling of groundwater vulnerability to contamination is critical for its management and conservation.

2 Geology of study area

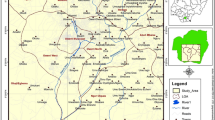
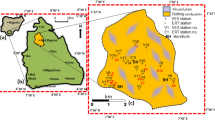
The study area is located in Mkpat Enin, Akwa Ibom, Nigeria between latitudes 4.614° and 4.628° N, and longitudes 7.500° and 7.783° E (Fig. 1). The region is bounded on the north by Oruk Anam Local Government Area, on the south by Eastern Obolo Local Government Area, on the East by Onna Local Government Area, and on the west by Ikot Abasi Local Government Area. The region has an average elevation of 186 m above sea level and an equatorial climate comprising two major seasons: the rainy season (April to October) and the dry season (November to February) with a short harmattan spell between December and January [48, 49]. The mean annual rainfall in the region is approximately 3549 mm and the mean annual temperature is between 25 and 30°, though temperatures during the dry season do rise to values as high as 35 °C [48]. The region is drained by the Cross-River, Kwa-Iboe River, Imo River and their tributaries. The geology of the region comprises Tertiary-Quaternary Coastal Plain Sands, otherwise termed the Benin Formation, which is the uppermost layer of the Niger Delta sedimentary formation [50, 51]. Benin Formation is the major hydrogeological unit in Nigeria’s Niger Delta Region [52] and constitutes more than 80% of the region. The Benin Formation comprises fine to coarse grained arenaceous materials (which are poorly sorted at some locations), sandstones and gravels of varying thicknesses intercalated with argillites [52]. There also exists deposits of fluvial loose sands, sandy clay, alluvium, beach sands, and lagoonal sands located primarily around the riverine areas [50, 51, 53]. The Benin Formation is underlain by the paralic Agbada Formation, which is the main hydro-carbon producing unit in the Niger Delta region [51, 54]. The Agbada Formation overlies the shaly Akata Formation [53].

Fig. 1
figure 1

Geologic map of the study area

Full size image

3 Materials and methods

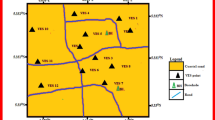
Geo-electrical methods were employed to acquire geo-electrostratigraphic data at twenty vertical electrical sounding (VES) stations with the ABEM SAS 1000 terrameter and its accessories. The VES stations were geo-referenced with a Global Positioning System (GPS). The Schlumberger array configuration was used. Current was injected between a pair of current electrodes A and B, and a second pair of potential electrodes M and N, was used to measure the potential difference between the current electrodes. The current electrode spacing (AB = a) was increased from 2 to 400 m, while the potential electrode spacing (MN = b) was increased from 0.5–20 m. The current electrodes were incrementally spaced out from a central point in an approximately logarithmic manner at equivalent intervals from the center, the aim being to increase the depth of current penetration. The potential electrodes were fixed while symmetrical expansions of the current electrodes were undertaken about a center. In order to generate recognizable and measurable potential readings, the potential electrode spacings were increased minutely for very large current electrode spacings. Expanding the distance between the current electrodes enabled an increment in value of the potential difference generated by the potential electrodes. In general, the MN/2 spacing had to be approximately one-fifth of the AB/2 spacing for optimal results. Schlumberger configuration was employed for its excellent depth of current penetration, its good sensitivity to vertical subsurface layers, its fast speed of data acquisition, and its mitigation of errors arising from near-surface lateral inhomogeneities [28].

Using measures of injected current and potential difference values, the terrameter employed Ohm’s law

$$R_{a} = \frac{V}{I}$$
(2)

to generate measures of the apparent resistance Ra. The geometric factor of the Schlumberger array G was given by:

$$G = \pi \left( {\frac{{a^{2} }}{b} - \frac{b}{4}} \right)$$
(3)

where a is the current electrode spacing, and b is the potential electrode spacing. Values of apparent resistivity \({\rho }_{a}\) (i.e., the mean resistivity of the geo-layer through which the injected current had travelled) were generated by multiplying apparent resistance Ra by the geometric G factor such that

$$\rho_{a} = \pi \left( {\frac{{a^{2} }}{b} - \frac{b}{4}} \right)\frac{\Delta V}{I}$$
(4)

Given a subsurface with homogenous and isotropic layers, the resistivity values generated from Eq. (4) would be considered as the true resistivity of the earth model. However, since the subsurface is typically heterogeneous, the true earth resistivity is dependent on the geometry of the electrode configuration employed, the spacing between the current and potential electrodes, the orientation of the electrode array with respect to subsurface heterogeneities, and the spatial variation of resistivity within the soil media. As the geo-layers do not always have horizontal stratification, what was generated from Eq. (4) was the apparent resistivity \({\rho }_{a}\) and not the true earth resistivity. To generate true earth resistivity models would require inversion using a reconstruction algorithm [55] or inversion software. Prior to the employment of computer-based inversion software, bi-logarithmic graphs were generated with apparent resistivity values plotted as ordinate versus half the current electrode spacing (AB/2) plotted as abscissa. Values generated from those plots were used as input within the WINRESIST inversion software which generated inverse models via an iterative procedure that aimed to reduce the difference between the acquired field data and the theoretical data [56,57,58]. The iterations were undertaken for each sounding station until a root mean square error of < 5% was generated. The true earth model curves indicated the mean resistivity, thickness and depth of each geo-layer, and the curve signature.

2D electrical resistivity tomography surveys were also undertaken at four stations to complement information obtained from the vertical electrical sounding surveys. Wenner array was employed, with a minimum and maximum electrode spacing of 5 m and 105 m respectively. The electrodes were moved at 5 m intervals. A 2D inversion software, RES2DINV, was used to reconstruct 2D resistivity tomograms that would delineate the resistivity, thickness, and depth variations within the geo-layers.

4 Results and discussion

Table 1 illustrates the results obtained from the VES inversion curves. Figure 2 shows representative VES curves delineating the subsurface resistivity distribution. Varying curve types that delineated the spatial distribution of resistivity within the lithological layers were obtained. The geological interpretation of the inverted earth models was corroborated by results obtained from borehole logs [48]. The first layer (motley topsoil) had resistivity values ranging from 12.7 to 664.2 Ωm with a mean of 168.2 m while its thickness ranged from 0.6 to 5.3 m with a mean of 2.3 m. The second layer (sandy clay) had resistivity values ranging from 2.3 to 1203.8 Ωm with a mean of 278.5 Ωm while its thickness ranged from 1.6 to 42.7 m with a mean of 14.3 m. The third layer (fine sand), interpreted as the aquiferous layer due to its large thickness compared to the other geo-layers, had resistivity values ranging from 54.3 to 2574.0 Ωm while the thickness ranged from 22.7 to 133.5 m with a mean of 79.1 m. The fourth layer (coarse sand) had resistivity values ranging from 26.1 m to 1405.6 Ωm with a mean of 357.1 m. Figures 3, 4 and 5 illustrates the iso-parametric maps indicating the spatial distribution of the resistivity values within the first, second and third lithological layers. To corroborate earth models generated from vertical electrical soundings, 2D resistivity tomograms obtained from electrical resistivity tomography surveys conducted at four stations were generated and the results displayed in Fig. 6a–d. The uppermost layer of the tomographic images indicated low resistivity zones, a possible result of arenite-argillitic intercalations. These low resistivity argillitic sequences reduced overburden permeability, decreasing the aquifer’s susceptibility to contamination.

Table 1 Summary of results obtained from VES inversion curves generated from WINRESIST inversion program
Full size table
Fig. 2
figure 2

a–d Representative inversion curves obtained from WINRESIST indicating measures of the first order geo-electrical indices: mean resistivity, mean thickness, and mean depth of each geo-layer

Full size image
Fig. 3
figure 3

Iso-parametric map indicating the spatial distribution of resistivity values within the first lithological layer (motley topsoil)

Full size image
Fig. 4
figure 4

Iso-parametric map indicating the spatial distribution of resistivity values within the second lithological layer (sandy clay)

Full size image
Fig. 5
figure 5

Iso-parametric map indicating the spatial distribution of resistivity values within the aquiferous lithological layer (fine sand)

Full size image
Fig. 6
figure 6

a–d Spatial distribution of electrical resistivity within the survey area as generated from 2D electrical resistivity tomography surveys

Full size image

The Dar-Zarrouk parameter (longitudinal conductance) was employed to appraise the aquifer’s protective capacity via employment of first-order geo-electrical indices. The protective capacity of an aquifer defined the overburden layer’s ability to impede percolation of toxicants into the aquiferous zones. Given that the region’s aquifer system is unconfined, the aquifer’s primary defense against pollutant percolation were the arenite-argillitic intercalations. The low permeability of the argillitic sequences would impede pollutant infiltration and consequently protect the aquifer from contamination. Longitudinal conductance \({S}_{L}\) was given as

$$S_{L} = \mathop \sum \limits_{n}^{i = 1} \frac{{h_{i} }}{{\rho_{i} }}$$
(5)

where \({\rho }_{i}\) is the resistivity of ith overburden layer, \({h}_{i}\) is the thickness of ith overburden layer, and \(n\) is the number of overburden layers.

High values of longitudinal conductance implied greater aquifer protectivity. It also meant that the overburden had a large thickness and reduced resistivity (increased conductivity). Figure 7 illustrates the iso-parametric map indicating spatial distribution of overburden thickness. The water table typically trends in the direction of terrain topography, hence an aquifer’s protective capacity would be dependent on thickness of the litho- stratigraphic layers above the water table. Formations comprising argillites or shale typically have high values of conductivity, implying greater aquifer protective rating. Pervious materials (e.g. sand and gravel) with high resistivity values have reduced ratings of aquifer protectivity. The formations in the study area comprised arenaceous materials intercalated with argillitic materials which reduced soil permeability making it difficult for contaminants to infiltrate the lithological layers [59]. The aquifer protectivity ratings based on values of longitudinal conductance values [47, 60] are shown in Table 2. Measures of longitudinal conductance within the study area are given in Table 3. The table showed that longitudinal conductance values varied from 0.0076 to 1.95 mhos with a mean of 0.32 mhos, implying moderate protectivity. Locations with good protectivity indicated zones of optimal groundwater abstraction, implying that such regions were less prone to contamination. Figure 8 shows the iso-parametric map illustrating the spatial distribution of longitudinal conductance within the study area. The figure indicates that the regions within the north-east had low protectivity, resulting either from shallowness of the aquifer, thin overburden thickness, highly permeable overburden materials, or the absence of clay sequences. Such zones had a high propensity to contaminant percolation.

Fig. 7
figure 7

Iso-parametric map indicating the spatial distribution of the overburden thickness within the study area

Full size image
Table 2 Aquifer protective ratings based on values of longitudinal conductance [60]
Full size table
Table 3 Measures of corrosivity, longitudinal conductance, and GOD model indices
Full size table
Fig. 8
figure 8

Iso-parametric map indicating the spatial distribution of longitudinal conductance within the study area

Full size image

Most civil engineering works entail laying of pipes within the topsoil. These pipes are susceptible to corrosion when the soil media is corrosive [61]. The corrosion of underground pipes, apart from causing rusting and consequent leakage within such pipes, will leach chemicals used in pipe manufacture into the aquifer. Corrosivity is typically evaluated with measures of topsoil resistivity [61,62,63] (see Table 4). Corrosivity within the study are ranged from 12.7 to 664.2 Ωm with a mean of 168 0.2 Ωm, implying a gamut from practically non-corrosive to moderately corrosive (see Table 3). Figure 9 illustrated the iso-parametric map indicating the spatial distribution of corrosivity within the area. within the study area. Approximately 50% of the region was moderately corrosive, implying unsuitability of those regions for laying underground water pipes.

Table 4 Classification of soil corrosivity based on resistivity of the topsoil [61,62,63]
Full size table
Fig. 9
figure 9

Iso-parametric map indicating the spatial distribution of corrosivity within the study area. Practically non-corrosive is classified as 1, slightly corrosive is classified as 2, moderately corrosive is classified as 3, and very corrosive is classified as 4

Full size image

Index-based modelling techniques were also used to assess aquifer vulnerability to contamination. These modelling techniques were the GOD and AVI methods. These techniques did not require a plethora of parameters to give measures of groundwater vulnerability, yet they generated results as accurate as those obtained from other qualitative and quantitative methods. The GOD model [13] used the Groundwater confinement (G), overlying strata (O) and depth to groundwater (D) parameters. Table 5 showed that a confined aquifer had a value of 0, while an unconfined one had a value of 1. The implication is that once an aquifer was confined, it had little or no susceptibility to contamination, and could rarely be contaminated. Confined aquifers are typically enclosed by aquitards, and have difficulty being recharged via percolation from overlying fluids. The study area, however, had an unconfined aquifer, implying that it was prone to contamination. The second parameter in the GOD model meant Overlying strata (O), i.e., the nature of overburden material overlying the aquifer. From Table 5, it was shown that the smaller the permeability of the overlying strata, the smaller the vulnerability index. The third parameter in the GOD model implied the depth to groundwater (D). Table 5 indicated that the greater the depth to groundwater, the less prone the aquifer system was to contamination, and vice versa. The overall GOD index was deduced by finding the product of the three parameters: groundwater occurrence (G), overlying strata (O) and depth to aquifer (D), such that:

$$GOD = \left( G \right) \times \left( O \right) \times \left( D \right)$$
(6)
Table 5 Classification of GOD model indices based on the parameters: Groundwater Occurrence (G), Overlying strata (O) and Depth to groundwater (D)
Full size table

The values of the GOD model indices were then used to determine the class of vulnerability based on Table 6. The GOD indices within the study area ranged from 0.35–0.63 with a mean of 0.49, implying moderate aquifer vulnerability (see Table 3). Approximately 70% of the sounding stations indicated average susceptibility ratings. The spatial distribution map of GOD values is shown in Fig. 10.

Table 6 Categorization of class of vulnerability based on measures of GOD indices
Full size table
Fig. 10
figure 10

Iso-parametric map indicating the spatial distribution of GOD indices within the study area

Full size image

The Aquifer Vulnerability Index (AV1) modeling technique [64] was also employed to generate measures of aquifer susceptibility via computation of hydraulic resistance \(C\) such that

$$C = \mathop \sum \limits_{i}^{n} \frac{{h_{i} }}{{K_{i} }}\quad {\text{where}}\;{\text{i}} = 1,2, \ldots {\text{n}}.$$
(7)

where \({h}_{i}\) is thickness of the ith overburden layers; \({K}_{i}\) is the hydraulic conductivity of ith overburden layers, and \(n\) is the number of overburden layers. Equation 7 implied that high fluid flow rate (hydraulic conductivity K), would decrease the measures of hydraulic resistance C, leading to increased aquifer vulnerability (Table 7). In addition, a small overburden thickness (h) would decrease the measures of hydraulic resistance C, increasing aquifer vulnerability. The aquifer vulnerability index (AVI) was computed by taking the logarithm of hydraulic resistance C, such that

$$AVI = \log C$$
(8)
Table 7 Categorization of class of vulnerability based on measures of hydraulic resistance and AVI
Full size table

The AVI values within the study area ranged from 1.73–4.10 with a mean of 3.03 (Table 8), implying moderate aquifer vulnerability. The iso-parametric map indicating the spatial distribution of the AVI values was indicated on Fig. 11. Table 8 showed that approximately 50% of the sounding stations showed moderate susceptibility to contamination. The results obtained are in consonance with those generated from the Dar-Zarrouk parameter and GOD model indices, and showed that in general, the aquifer has moderate susceptibility to contamination. These results have illustrated the efficacy of geo-electrical technology in the delineation of aquifer protectivity, vulnerability, and soil corrosivity.

Table 8 Measures of AVI obtained at the vertical electrical sounding stations
Full size table
Fig. 11
figure 11

Spatial distribution map of AVI model values

Full size image

5 Conclusion

Surficial geophysical surveys were undertaken within a coastal milieu to investigate aquifer vulnerability to contamination. Primary geo-electrical indices were obtained from VES data, and 2D ERT surveys were undertaken to complement information derived from the soundings. To appraise aquifer vulnerability, longitudinal conductance measures were obtained, and the values ranged from 0.0071–1.95 mhos, with a mean of 0.32 mhos, indicating moderate aquifer protectivity. Soil corrosivity was evaluated using topsoil resistivity measures and results indicated moderate corrosivity within the area. Indexed-based modeling methods GOD and AVI were used to complement information obtained about aquifer protectivity. Measures of GOD and AVI, alongside their iso-parametric maps, indicated how aquifer vulnerability varied spatially across the study area. The GOD and AVI indices indicated that the region had moderate aquifer susceptibility to contamination. This was a possible result of arenite-argillaceous intercalations, which served as a protective seal over the aquifer. These results corroborated those obtained from longitudinal conductance indices which had indicated that the aquifer system had average protectivity. Anthropogenic pollutants in the region include industrial and domestic wastes, and agricultural pollutants such as pesticides, herbicides, insecticides, hence this work will aid in development of strategies for pollutant mitigation. Further, it will aid policy makers in developing effective aquifer monitoring and conservation stratagems.