1 Introduction

Slope stability analysis is performed mainly to analyze the performance of man-made slopes such as embankments, dams, or natural slopes under various conditions [1, 2]. Slope failure or landslides are considered one of the most devastating natural disasters and the third most common cause of casualties and infrastructural damage [3]. A landslide is a sudden movement of a soil mass or rock down a slope due to unstable slope conditions and different external factors. Landslides mainly occur when the shear stress acting on soil exceeds the strength of the soil [4]. Although the primary reason for slope failure, which results in a landslide, is rainfall, other natural hazards that work as triggering mechanisms are volcanic eruptions and earthquakes [5, 6].

Slope failure triggered by earthquakes is not as common as slope failure due to rainfall; nevertheless, this topic requires special attention due to this type of disaster’s unpredictable and catastrophic nature. According to [7, 8], the number of fatalities due to earthquake-induced slope failure or landslides is estimated to be 71,000 between 1968 and 2008. Studies show earthquakes with Mw = 4.0 cannot trigger any slope failure or landslides, and those with Mw = 9.2 can trigger slope failure events affecting the 500,000 km2 land area [9]. Catastrophic earthquakes with Mw > 6 occurring in hilly areas can trigger fatal landslides, resulting in extensive casualties and economic losses [10].

Historically, the Peruvian earthquake of May 31, 1970, and the Sikkim earthquake in 2011 triggered landslides that caused extensive devastation and casualties in the affected area [11,12,13,14]. The great 1964 earthquake in Alaska with Mw = 9.2 triggered a landslide that caused high economic loss [9, 15]. In 2015, the Gorkha earthquake in Nepal triggered 19,332 landslides [16]. The 1995 Kobe earthquake, which hit Kobe city, Japan, with a magnitude of Mw = 6.9, triggered 674 landslides within an area of 700 km2 [17]. The damage caused by this earthquake makes it one of the most devastating earthquakes in the history of Japan. To date, the seismic acceleration of the Kobe earthquake has been widely used for seismic performance analysis of different structures. Earthquakes are unpredictable natural disasters that increase the difficulty of predicting landslides due to earthquakes where soil properties play a vital role [18]. Therefore, proper investigations of the seismic vulnerability of landslide-prone sites should be performed to prevent economic losses and casualties.

Bangladesh experiences heavy rainfall every year, which triggers flash floods in hilly areas, resulting in slope failure and landslides [19]. A landslide inventory developed by [20] revealed that most landslides or slope failures in Bangladesh occurred in Chittagong (208) and Rangamati (193). In Bangladesh, more than 350 casualty reports have been found due to landslide incidents in the last 30 years [21, 22]. The previous catastrophic landslide that hit Rangamati in 2017 resulted in 168 casualties and destroyed at least 40,000 houses [23]. Therefore, it is evident that the Chittagong Hill Tracts, especially the Rangamati area, are highly vulnerable to slope failure due to external factors and need proper investigation and remedial techniques.

Bangladesh is situated on three tectonic plates with blind and shallow faults [24] and is considered one of the most tectonically active locations in the world. Situated at the junction of three tectonic plates—Eurasia, India, and Burma-Bangladesh has faced several devastating and numerous minor earthquakes over the past two hundred (200) years [25]. The Great Indian Earthquake of 1897, which had a magnitude of Mw 8.7, was one of the most significant earthquakes in recorded history, with 1542 fatalities, which was felt throughout Bangladesh [26]. Recently, [27] noted that, based on the discrepancy between energy storage in this region and historical earthquake occurrence, there is an exceedingly high likelihood that a large earthquake will occur around the Himalayan region. Studies have shown that the hilly regions of Bangladesh are situated near the Chittagong-Myanmar fold and thrust belt (CMFB), which is amenable to a Mw 8.5 earthquake [28]. Similarly, [29] found that the Tripura fault, which is located near the hilly areas of Bangladesh, is the most active fault zone and poses a considerable risk of future seismic activities. Therefore, it is essential to validate the vulnerability of this area to not only rainfall-induced landslides but also earthquake-induced landslides, as Rangamati has active faults nearby.

Karl Von Terzaghi first introduced pseudostatic analysis to determine the seismic response of distinct kinds of structures, such as embankments, dams, retaining walls, and slopes [30]. In this process, a potential failure surface is analyzed with a seismic force that represents the earthquake loading instead of using the “acceleration time history” of a historical earthquake incident [30]. The pseudostatic method can be used in combination with the limit equilibrium method (LEM) or finite element method (FEM) for seismic slope stability analysis [31]. Two kinds of pseudostatic approaches are used depending on the type of structures being analyzed [32] as follows:

  • Force-based analysis.

  • Deformation-based analysis.

In the force-based analysis, horizontal and vertical seismic coefficients are used to determine seismically induced inertia force which is simpler than the deformation-based analysis. In the case of deformation-based analysis, the whole mesh is subjected to simple shear conditions [32]; on the other hand, in force-based analysis, the seismic coefficients, especially the horizontal coefficients, are significant. [30] Originally suggested Kh = 0.1 for severe earthquakes, Kh = 0.2 for destructive earthquakes and Kh = 0.5 for catastrophic earthquakes [33]. Therefore, it is important to choose coefficients properly for analysis and design purposes. Previously, several researchers [34,35,36,37,38] used the pseudostatic method for stability analysis of several types of slopes with different soil characteristics, slope angles, weather features, and earthquake zones. These studies showed that pseudostatic analysis is a simple and useful way of obtaining seismic-induced slope stability analysis results.

The main problem of the pseudostatic approach is that it does not provide the permanent displacement of the soil, which is also a crucial parameter. In the 1965 Rankine lecture, Nathan Newmark described a technique for determining a slope’s permanent displacement by employing actual seismic motion to evaluate a slope’s stability. This technique is referred to as Newmark’s permeant displacement analysis, rigid block analysis, or Newmark’s sliding block (NSB) analysis. He considered using a stiff sliding block in a basic analysis to determine the slope’s deformation. Compared to the stress-deformation method, the NSB method is easier to use as it only illustrates how much an earthquake affects geotechnical structures [39]. Previously, different researchers used this method to analyze different slopes, such as submarine [40] and unsaturated [41], under various dynamic and seismic conditions.

2 Study area

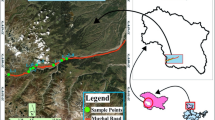
Rangamati is a district located in the Chittagong Hill Tracts of Bangladesh. This district lies between 22°37′60 N and 92°12′00 E [42] and 77 km from the Chittagong district, which is a famous tourist attraction location. It is the largest district of Bangladesh and borders with India and Myanmar to the east and Chittagong and Khagrachhari to the west [43]. This area has experienced a magnitude 6 earthquake in the past. Figure 1 shows Bangladesh’s seismicity and fault zones collected from the USGS [25]. Most of the faults in Bangladesh are in the Rangamati district, which makes Rangamati a potential hazard zone for future earthquakes and earthquake-induced slope failure.

Fig. 1
figure 1

Seismic incidents in and around Bangladesh in the last 50 years

Full size image

According to [44], Bangladesh has four seismic zones with different seismic zone coefficients ranging from 0.20 to 0.36. The Rangamati region falls in the second-highest zone based on the seismic coefficient (Z = 0.28), which indicates a high seismic risk in the Rangamati area. Most of the areas of this district are hilly areas with high slopes, as shown in Fig. 2, with numerous inhabitants. Although the drainage conditions of the soils in this district’s hilly regions are excellent, the soils of the valleys lack good drainage, resulting in flash flooding [45]. The average annual precipitation in this area is greater than 2500 mm [43]. Excessive rainfall is the root cause of surface runoff, which ultimately results in soil erosion in this area [46]. Three distinct locations were chosen for this study, which are as follows:

  1. i.

    Slope adjacent to Shahid Abdul Ali Academy (22°38′58.9ʺ N 92°11′47ʺ E),

  2. ii.

    Slope adjacent to the Police Line School (22°38′28ʺ N 92°11′42.7ʺ E) &

  3. iii.

    Slope near Prabin Park (22°38′21.4ʺ N 92°11′39.1ʺ E).

Fig. 2
figure 2

Slope map of Rangamati and study locations

Full size image

These sites were selected based on a comprehensive analysis of historical data related to rainfall-induced and earthquake-triggered slope failures. This involved field surveys that were used to gather information about previous incidents, including the timing and characteristics of slope failures. The locations are also crucial for the local community, as location 1 is near Rangamati Park and a school. Location 2 has two adjacent schools; one is at the top of the slope, and location 3 has a nearby road connecting some villages with the main road. These areas are populated with residences and local businesses, making any slope failure in these regions potentially hazardous and detrimental to the community.

3 Sample collection

This study included software-based slope stability analysis using the pseudostatic approach in the analysis software GEO5. First, soil samples were collected from three distinct locations at Rangamati Sadar. Disturbed and undisturbed soil samples were carefully collected from the hilly terrain’s top, middle, and bottom segments. The collected soil samples were promptly transported to the Geotechnical Engineering Lab at Ahsanullah University of Science and Technology in Dhaka, Bangladesh. Different soil parameters, such as grain size distribution, dry unit weight, saturated unit weight, angle of internal friction, and cohesion, were obtained by several laboratory tests. Laboratory tests were conducted at both the Geotechnical Engineering Laboratory of Ahsanullah University of Science and Technology and the Bangladesh University of Engineering and Technology. These soil parameters serve as crucial inputs for the subsequent slope stability analysis and are shown in Table 1,

Table 1 Soil parameters used for pseudostatic analysis
Full size table

4 Methodology

After obtaining the soil parameters, a pseudostatic analysis of the slope stability under seismic excitation was performed using GEO5 software by the pseudostatic approach. This method was chosen based on its widespread application, notably highlighted by [30] as the earliest and most straightforward technique for seismic stability analysis of both natural and stabilized slopes. The research utilized GEO5 version 2023, incorporating the latest updates available up to the analysis date. Different slope configurations were generated with varying angles of 30°, 45°, 60°, and 75° which were subsequently analyzed by GEO5 using variation in the different seismic coefficients given in Table 2.

Table 2 Values of the horizontal and vertical seismic coefficients used in the study
Full size table

Horizontal and vertical seismic coefficients have different effects on the FS values. In the pseudostatic approach, seismic excitation can be applied as horizontal and vertical seismic coefficients, as shown in Figs. 3 and 4.

Fig. 3
figure 3

Basic principle of pseudostatic analysis

Full size image
Fig. 4
figure 4

Slope Stability Analysis in GEO5

Full size image

4.1 Principles of GEO5 software

GEO5 is a geotechnical and geological analysis software package developed by Fine Software. In this software, the earthquake frame serves to input earthquake coefficients during slope stability analysis. This method applies seismic effects such as the horizontal seismic coefficient (Kh) and vertical seismic coefficient (Kv). The horizontal seismic coefficient is the ratio between the horizontal and gravitational accelerations. A coefficient of 0 represents a horizontal acceleration of 0.0 mm/s2, 0.15 represents 1500 mm/s2, and 0.3 represents 3000 mm/s2 [47]. The horizontal seismic coefficient works by introducing an additional horizontal force in a slice of the slope, which can be calculated by Eq. 1,

$$\text{Horizontal}\,\text{force}, F={K}_{h }\times {W}_{slice}$$
(1)

where Kh = horizontal seismic coefficient, and Wslice = weight of the soil slice in the slope.

The vertical seismic coefficient (Kv), on the other hand, works either downward (Kv < 0) or upward (Kv > 0) and increases or decreases the unit weight of soil and material surcharge, so these values are positive and negative, respectively [47].

4.2 Displacement analysis by Newmark’s method

The displaced or soil mass above the slip surface is regarded in the Newmark (1965) method as a rigid block on an inclined plane surface, as depicted in Fig. 5. Historical earthquake data is imported for the analysis, and the conventional PS LEM is applied using varying acceleration values derived from the seismic motion. The yield acceleration, or Ay, is the acceleration value that is chosen when the slope’s factor of safety is reduced to 1. The block starts to slide and acquires a velocity in relation to the underlying mass’s velocity whenever it experiences an acceleration greater than the yield acceleration. The block continues to move when the acceleration falls below the yield acceleration. Motion persists until the block’s velocity in relation to the underlying mass is zero. The block will slip if the acceleration surpasses the yield acceleration once more. This stick–slip motion pattern continues until the accelerations are smaller than the yield acceleration, and the relative velocity eventually drops to zero. The resisting force between the block and the underlying surface will then cause the block to stop sliding. The accelerations are regarded as rectangular pulses that exceed Ay when calculating the system’s velocity and permanent displacement [48,49,50].

Fig. 5
figure 5

Representation of the slope from Newmark’s analysis, the original slope (at left), and the considered slope (at right)

Full size image

Newmark’s displacement analysis requires acceleration time history data from an earthquake as an input, and for this study, the displacement of the slopes was determined by using the acceleration time history of the 1995 Kobe earthquake shown in Fig. 6.

Fig. 6
figure 6

Acceleration time-history of the 1995 Kobe earthquake

Full size image

The permanent displacement was determined by Newmark’s sliding block (rigid block method) analysis using Slide2 software. The Slide2 software uses a sliding block to determine the slope behavior under seismic excitation to analyze the permanent displacement of deformation of the slope. This software analyzes the behavior of the slope and returns the displacement value of each slip surface along with the critical surface having maximum permanent displacement [51].

5 Slope stability analysis results

This study analyzed different slopes of varying angles and materials, and FS and displacement values were obtained. The safety factors with increasing slope for the three locations with varying slope angles and different seismic conditions are shown in Figs. 7, 8, 9, 10, 11, 12, 13, 14, 15.

Fig. 7
figure 7

FS vs. Seismic Coefficient graph (Kv fixed, Kh variable)

Full size image
Fig. 8
figure 8

FS vs. Seismic Coefficient graph (Kh fixed, Kv variable)

Full size image
Fig. 9
figure 9

FS vs. Seismic Coefficient graph [Both variable, (Kv/Kh = 1)]

Full size image
Fig. 10
figure 10

FS vs. Seismic Coefficient graph (Kv fixed, Kh variable)

Full size image
Fig. 11
figure 11

FS vs. Seismic Coefficient graph (Kh fixed, Kv variable)

Full size image
Fig. 12
figure 12

FS vs. Seismic Coefficient graph [Both variable, (Kv/Kh = 1)]

Full size image
Fig. 13
figure 13

FS vs. Seismic Coefficient graph (Kv fixed, Kh variable)

Full size image
Fig. 14
figure 14

FS vs. Seismic Coefficient graph (Kh fixed, Kv variable)

Full size image
Fig. 15
figure 15

FS vs. Seismic Coefficient graph [Both variable, (Kv/Kh = 1)]

Full size image

5.1 Safety factors

The GEO5 software uses the bishop method of slices to determine the FS value of a slope, which is the ratio of the resisting moment to the driving moment [52]. In this method, it is assumed that the failure surface of the slope lies within a soil type that behaves in accordance with the Mohr‒Coulomb failure criterion. According to the seismic slope stability analysis, various seismic coefficients change the driving moment by changing the overall weight of the slope, which results in a variation in the FS.

5.1.1 Location 1

Figures 7, 8, 9 shows the FS values for the different slope angles at location 1. With an increase in the seismic coefficient, the FS tends to decrease. Again, with increasing slope angle, the FS drastically decreases, and at a 75° angle, it approaches the unsafe value at no seismic coefficient.

5.1.2 Location 2

Figures 10, 11, 12 describe the FS values for different slope angles for location 2. With increasing seismic coefficient, the FS tends to decrease. While increasing the slope angle drastically decreases the FS. However, the FS value at this location is relatively higher than that observed at the other study locations.

5.1.3 Location 3

Figures 13, 14, 15 shows the FS values for the different slope angles at location 3. With increasing seismic coefficient, the FS tends to decrease. Again, with increasing slope angle, the FS drastically decreases. The FS in this location was the lowest among the three studied areas. At a 60° slope angle and higher, the FS falls below the required safe value.

5.2 Permanent displacements

The permanent displacement of slopes under seismic excitations can be obtained by utilizing Newmark’s method of displacement. Generally, the permanent displacement of a single slope is closely related to the contribution of the cohesion of the soil to the critical acceleration and seismic acceleration waveforms [53]. This is why different displacements can be obtained for different waveforms and peak times of an earthquake.

This study included the permanent displacement of different slopes at distinct locations in the Rangamati district under the seismic acceleration of the Kobe earthquake. Figure 16(a–d) show the different maximum displacements of a failure plane or different slope angles at location 1.

Fig. 16
figure 16

Permanent Displacement of the slopes of location 1 with different angle a 30° b 45° c 60° and d 75°

Full size image

All the other permanent displacement records of the study locations for varying slope angles are shown in Fig. 17. Each bar in Fig. 17 represents the permanent displacement of the slope according to Newmark’s method. In locations 1 and 2, the initial bars are below 1 mm because, for a slope angle of 30° for location 1 and 30° and 45° for location 2, the displacement is lower than 1 mm. The permanent displacements of the slopes at location 1 and location 2 are pretty similar, in addition to which location 2 presents the lowest displacement values. On the other hand, the maximum permanent displacements were seen in location 3. This is due to the cohesion of the soil at these locations. As the cohesion at location 2 is slightly greater than that at other locations, the displacement is also lower. On the other hand, location 3 has the lowest cohesion, resulting in a greater slope displacement.

Fig. 17
figure 17

Location-wise permanent displacements of slopes with varying angle

Full size image

5.3 Comparison of numerical results with real scenario

Historically, Rangamati faced different slope failure incidents that caused damage to people’s lives and economies. Among these incidents, almost 22% are due to hill cutting, 21% are due to rainfall, and 12% are due to earthquakes [54]. Earthquakes are unpredictable and deadlier for locals, resulting in more deaths and economic losses. Landslide susceptibility maps developed by [55, 56] showed that the Rangamati municipality area is highly susceptible to landslides due to its geological, weather, and seismic characteristics. A geotechnical and geochemical study on the slope stability of Rangamati conducted by [43] showed that the natural slope of Rangamati is relatively stable due to soil characteristics, but with the influence of different external factors, such as rainfall and earthquakes, the FS value tends to decrease rapidly. Some of the most devastating landslides occurring in the Rangamati area are shown in Fig. 18.

Fig. 18
figure 18

Previously reported devastating landslide incidents in Rangamati

Full size image

The results obtained by the pseudostatic analysis show concerning situations for all the locations, especially location 3. The FS values also fall rapidly with increasing seismic coefficient and slope angle. These locations had previously experienced different slope failure incidents. Figures 19 and 20 show previous rainfall-induced slope failures at location 2 and location 3, respectively.

Fig. 19
figure 19

Slope failure in location 2

Full size image
Fig. 20
figure 20

Slope failure in location 3

Full size image

The assessed locations had 60° to 90° inclinations in some portions of the slopes, making them more susceptible to seismic-induced failure as they had a history of rainfall-induced failure. Again, in the case of a seismic event in the rainy season, when the soil on a slope is saturated, that will become even more vulnerable to catastrophic failure, leading to a landslide event.

6 Discussion

In this study, the FS decreased rapidly with the introduction and increase in the horizontal and vertical seismic coefficients, and the FS was the lowest for all the slopes when (Kh, Kv) = (0.3, 0.3). This value is equivalent to a horizontal acceleration of 3000 mm/s2. Among the three distinct locations, the most vulnerable is location three, as the FS decreases below 1.5 immediately after the slope exceeds 30°. By analyzing the slopes with no earthquake excitations and maximum earthquake excitations, the value of the FS decreased by 40–50% at all locations. This is a critical scenario as the FS becomes half of the normal FS, increasing the vulnerability of the slope to failure.

Figure 21 shows the overall FS values for three distinctive locations. The FS values are taken only for the most vulnerable conditions among the other seismic conditions, which are (Kh, Kv) = (0.3, 0.3). By assuming the most susceptible conditions for all three locations, it can be seen in Fig. 21 that location 3 is the most vulnerable. The slopes of location one and location two were identical. In these locations, the value of the FS drops below 1.5 after it reaches more than 50°.

Fig. 21
figure 21

Location-wise variation in the FS with respect to the slope angle

Full size image

On the other hand, the displacements at different slope angles in separate locations exhibited related results, as shown in Fig. 22. As the displacements due to seismic acceleration generally depend on the cohesion of the soil, the soil with the highest cohesion value exhibited the minimum displacement, which was location 2. The location with the minimum cohesion was location 3, which performed poorly in the displacement analysis and exhibited the largest displacement values among the studied locations.

Fig. 22
figure 22

Variation in the displacement with varying slope angle

Full size image

These locations require special slope stability measures, especially location 3, as the FS value is lowest even at a slope angle of 30°. Different structural measures, such as retaining walls, nailing, and anchoring of slopes, can be ideal for improving existing slopes’ FS values. Bioengineering techniques such as Geotextiles, Microbially Induced Calcite Precipitation (MICP), or Vetiver grass can also prove to be effective in this area because they increase the shear strength of the soil and thus increase the FS.

7 Conclusion

This study investigated the earthquake-induced slope deformation risk or landslide risk at three locations in the Rangamati district. A pseudostatic approach involving variations in seismic forces in horizontal and vertical directions was utilized to determine the critical scenario for seismic slope instability. Among the three locations, the most vulnerable location is location 3. This may be due to the geological features of location 3, as the soil in this location has a high saturated unit weight and low cohesion. As we know, in pseudostatic analysis, the chance of failure increases with increasing saturated unit weight and seismic coefficient; this is why the FS at this location is lower than at other locations. Again, due to the lower cohesion, location 3 exhibited maximum displacement, which indicates a potential hazard in the case of seismic activity at this location.

Additionally, during the rainy season, there is a high probability of increasing the saturated unit weight, and any earthquake event at that time may cause critical slope failure under specific slope conditions, damaging life, and property. The natural slopes of these three locations are in danger of a landslide incident due to catastrophic seismic activity in that area. Therefore, proper precautionary measures should be taken to reduce casualties and economic losses. The authors will further assess these locations and some others in the Rangamati area by deformation analysis and the seismic hazard potential in future studies.