SSCNet: learning-based subspace clustering

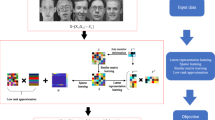
Abstract

Sparse subspace clustering (SSC), a seminal clustering method, has demonstrated remarkable performance by effectively solving the data sparsity problem. However, it is not without its limitations. Key among these is the difficulty of incremental learning with the original SSC, accompanied by a computationally demanding recalculation process that constrains its scalability to large datasets. Moreover, the conventional SSC framework considers dictionary construction, affinity matrix learning and clustering as separate stages, potentially leading to suboptimal dictionaries and affinity matrices for clustering. To address these challenges, we present a novel clustering approach, called SSCNet, which leverages differentiable programming. Specifically, we redefine and generalize the optimization procedure of the linearized alternating direction method of multipliers (ADMM), framing it as a multi-block deep neural network, where each block corresponds to a linearized ADMM iteration step. This reformulation is used to address the SSC problem. We then use a shallow spectral embedding network as an unambiguous and differentiable module to approximate the eigenvalue decomposition. Finally, we incorporate a self-supervised structure to mitigate the non-differentiability inherent in k-means to achieve the final clustering results. In essence, we assign unique objectives to different modules and jointly optimize all module parameters using stochastic gradient descent. Due to the high efficiency of the optimization process, SSCNet can be easily applied to large-scale datasets. Experimental evaluations on several benchmarks confirm that our method outperforms traditional state-of-the-art approaches.

1 Introduction

1.1 Background and limitation

Clustering constitutes a cornerstone task within the domain of machine learning. Particularly in the digital age, the ease of data acquisition from the Internet results in an abundant supply of unlabeled data. Given the prohibitive cost and time investment required for data labeling, clustering techniques have become instrumental in elucidating correlations within these datasets. Consequently, the development of efficient clustering algorithms for large datasets is highly important.

Sparse subspace clustering (SSC) [1] and low-rank representation (LRR) [2–4] have made significant strides over the past decade. By decomposing the data matrix into a self-representative sparse (or low-rank) term and a noise term, they are capable of capturing the global sparse (or low-rank) structure of the data. The robustness to noise of these methods has led to wide-scale application in diverse fields, including image clustering, segmentation and denoising. These methods have consistently outperformed traditional clustering methods, such as spectral clustering [5] and k-means.

However, there are limitations in SSC and LRR, especially when they are applied to large datasets. First, to assign clustering labels to new data, these methods necessitate recalculation, which consumes memory on the order of $\text{O}(n^{2})$, where n is the data size. This substantial memory requirement can render them ineffective for large-scale datasets. Second, both SSC and LRR rely on the “self-expression” property, presuming that the provided data matrix inherently serves as an effective dictionary for representation. Unfortunately, this property may not hold true in the absence of proper data pre-processing.

Finally, they execute subspace clustering through three isolated procedures: (1) dictionary construction, (2) affinity matrix learning, and (3) spectral clustering on the affinity matrix. Given the lack of integration between these steps, the derived dictionary and affinity matrix may be sub-optimal for subspace clustering.

In response to the aforementioned challenges, recent research has attempted to leverage the benefits of deep learning to address the first two limitations. By developing suitable network architectures and training strategies, various deep clustering methods [6–14] have shown encouraging results.

Existing deep clustering approaches can generally be categorized into two groups. The first encompasses auto-encoder-based methods, where different loss functions are embedded into the coder-layer of the auto-encoder [6, 8–10, 12]. The second group includes task transformation methods that reframe the clustering task as a set of pairwise classification problems. For instance, studies such as Refs. [7, 13] explored pairwise correlations between clusters or samples to guide the parameter learning of deep neural networks. However, these deep learning methods primarily concentrate on loss function design and network training, and they are not without their shortcomings, including a lack of robustness and high demand for data. Furthermore, these methods do not possess the strong generalization ability that traditional methods offer.

1.2 Solutions and contributions

To exploit the nonlinear representation capabilities of deep learning while preserving the geometric and theoretical properties of traditional methods, differential programming (DP) has emerged as a compelling alternative. Broadly speaking, DP first integrates learnable parameters into classical numerical solvers, followed by discriminative learning on the training data to derive task-specific optimization schemes. Given the widespread success of deep learning across many applications, many researchers treat deep neural networks as learnable units for integration with the optimization process. For example, Sprechmann et al. [15] employed a deep auto-encoder to address unstructured robust principal component analysis problems. Zhou et al. [16] uncovered the connection between sparse coding and long short-term memory (LSTM), while Peng et al. [17] reimagined the k-means algorithm as a network with a unique structure.

Through the lens of DP, most hyper-parameters associated with traditional methods can be jointly learned via deep learning optimizers [18–21], with additional learnable parameters supplementing the limited capacity of the original strategies. Generally, DP is considered a by-product of learning-based optimization, aiming to resolve traditional optimization problems in a differentiable and data-driven manner [22–24].

Although DP offers an efficient and differentiable solution to specific optimization problems, the constraint of differentiability precludes the direct application of DP modules to many operators, such as singular value decomposition (SVD) and matrix inversion. The differentiation of these operators remains an open problem within the machine-learning community. Indyk et al. [25] approximated low-rank decomposition via a differentiable power method, but it assumed large gaps between eigenvalues, which was rarely the case in clustering problems. In subspace clustering, SVD is pivotal. Most low-rank or sparse problems necessitate performing SVDs during the optimization procedure, implying that a differentiable SVD strategy could potentially illuminate the differentiation of most common low-rank or sparse optimization solvers, thereby generating a wealth of derived learning-based optimization methods. Notably, for SSC, the spectral clustering step involves an eigenvalue decomposition that cannot be bypassed.

Aligning with the principles of DP, we integrate all the steps of SSC with differential modules, including a universal differentiable eigenvalue decomposition module, and propose SSCNet to address the issues prevalent in subspace clustering and deep clustering. Specifically, first, we generalize the optimization procedure of the linearized alternating direction method of multipliers (L-ADMM) as a multi-block deep neural network, where each block corresponds to a step of the L-ADMM iteration. We then apply the DP framework to the SSC problem, jointly performing dictionary construction and affinity learning. This component acts as the first differentiable module in our unified network. Second, we reframe the spectral clustering process as two additional differentiable modules composed of an eigenvector mapping module and a k-means clustering module. To differentiate eigenvalue decomposition, we approximate manifold gradient descent on the Stiefel manifold and generate feasible points via a Cayley transform. Finally, by combining these differentiable modules, we obtain the proposed unified network, SSCNet, which can jointly learn the optimal dictionary, affinity matrix, and clustering parameters. We also introduce a novel re-weighting technique to handle the noise term in SSC. In terms of computational efficiency, SSCNet can be effectively optimized by stochastic gradient descent (SGD). Therefore, it is well-suited for large-scale datasets.

Our main contributions are summarized as follows:

• 1) By applying the DP framework to sparse representation and spectral clustering differentiation, we establish the novel SSCNet, which jointly learns the dictionary, affinity matrix, and clustering parameters. Unlike other deep clustering methods, SSCNet inherits the robustness of SSC and requires less training data.

• 2) We generalize manifold gradient descent as a differentiable multi-layer deep neural network capable of performing SVD or eigenvalue decomposition in a learning-based manner, which can be efficiently optimized by SGD. The proposed layer is highly versatile and may be of independent interest.

• 3) We provide several valuable techniques for effectively training SSCNet and conduct experiments on multiple datasets to evaluate the subspace clustering methods. Compared with state-of-the-art approaches, our SSCNet demonstrates superior performance.

2 Related work

2.1 Subspace clustering

For subspace clustering, most methods [1–4, 26–29] first need to learn the affinity matrix based on feature representations. Then, spectral clustering [5] is applied to group the samples based on the affinity matrix. Among the popular methods, LRR and SSC are two of the most classic methods. Based on self-representation, LRR imposes the nuclear norm, i.e., the sum of singular values, to constrain the affinity matrix under the low-rank assumption, while SSC utilizes the $\ell _{1}$-norm, i.e., the sum of absolute values of all entries, under the sparse assumption. As we mainly focus on SSC in this paper, we introduce the framework of SSC in detail. The objective function of SSC is

$$ \begin{aligned} & \min_{\boldsymbol{Z}, \boldsymbol{E}} \Vert \boldsymbol{Z} \Vert _{1} + \lambda \Vert \boldsymbol{E} \Vert _{1}, \\ & \text{s.t.} \ \boldsymbol{X}=\boldsymbol{X}\boldsymbol{Z}+ \boldsymbol{E}, \text{diag}(\boldsymbol{Z})=\boldsymbol{0}, \end{aligned} $$

(1)

where 0 is the all zero matrix, λ is the balance constant, Z is the desired sparse affinity matrix, X is the data matrix, and E is the error term. The $\ell _{1}$-norm $\Vert \cdot \Vert _{1}$ is defined by the sum of the absolute values of all the entries in the matrix. With the noise under a sparse pattern, SSC assumes that the data points obey an underlying linear structure and aim to sparsely represent each data instance by the linear combination of its neighbors from the same subspace. Based on SSC, Li and Vidal [26] proposed the structured SSC to jointly learn the original affinity matrix of SSC and the spectral clustering mapping function. Based on LRR, Xie et al. [4, 30] proposed an implicit block diagonal LRR. Feng et al. [27] and Lu et al. [28] investigated the block diagonal property of subspace clustering and provided a theoretical guarantee.

2.2 Deep clustering

With the label absent, defining a proper loss function for deep clustering is crucial. The existing deep clustering methods can be classified into two categories depending on whether the auto-encoder is adopted. For the first category, the total loss function is defined by summing the reconstruction loss of the auto-encoder and clustering loss of the latent representation layer. For the clustering loss, Xie et al. [6] and Guo et al. [10] proposed deep embedding clustering to adopt the Kullback–Leibler divergence loss, which used highly confident samples as supervision and then made samples in each cluster distributed more densely. Yang et al. [13] incorporated the k-means loss. Ji et al. [12] added a self-representation layer in the middle of the traditional auto-encoder. Peng et al. [9] used the subspace clustering loss to regularize the learning of latent representation. For the second category, specific loss functions are directly designed based on the last layer output without auto-encoder. Yang et al. [7] introduced a recurrent-agglomerative framework to merge clusters that were close to each other. Chang et al. [11] investigated the correlation between samples based on the normalized output and used such similarity as supervision. Bojanowski and Joulin [31] directly used fixed targets uniformly sampled from a unit sphere to constrain feature assignment. Shaham et al. [32] performed the spectral clustering using deep neural networks. Caron et al. [33] directly used the results of k-means as supervised labels to train neural networks.

2.3 Differentiable programming

Differentiable programming, called DP, can recast the existing optimization process as a differentiable module, and then the model can be optimized in a data-driven way. For example, Gregor and LeCun [34] unfolded the optimization of $\ell _{1}$-norm regularized sparse coding as a simple recurrent neural network (RNN). The number of RNN layers corresponds to the number of iterations, and the weights correspond to the dictionary. Zhou et al. [16] developed an LSTM formulation to solve the $\ell _{1}$-norm regularized sparse coding. Peng et al. [17] recast the updating rules of k-means as a fully connected network. Yang et al. [35] defined a deep architecture over the ADMM algorithm pipeline (ADMM-Net) for compressive sensing and magnetic resonance image reconstruction. Recently, Chen et al. [36] and Liu et al. [37] theoretically revealed that DP was not only a generalized optimization, but also benefited parameter learning and even brought the linear convergence when the original optimization was unconstrained, such as compressive sensing. Unlike previous works, Xie et al. [22] provided a unified differentiable framework for problems with linear constraints. This framework is generalized from the L-ADMM [38], named differentiable linearized ADMM (D-LADMM), which is more general and has fewer auxiliary variables than ADMM-Net. Moreover, its analysis shows that, with proper activation functions, the output of D-LADMM can solve the original optimization problem. In other words, D-LADMM can solve an optimization problem in a learning-based fashion under mild conditions. With such reformulation or transformation, the original problem can be solved by joint learning. The solution of the optimization can be efficiently computed with limited memory.

3 Preliminaries and general framework

In this section, we review the classic SSC and its solver—L-ADMM [38, 39] and introduce a general DP framework [22] to differentiate the solver.

3.1 Dictionary-based SSC

SSC contains two steps. The first step is to solve a convex or non-convex optimization problem to obtain the coefficient matrix Z and then construct a graph matrix W based on Z. The graph matrix W describes the pair-wise similarity between the training data. The second step is to perform spectral clustering on W. In particular, for spectral clustering, one needs an eigenvector decomposition of the Laplacian graph matrix and then utilizes k-means clustering on the eigenvectors to obtain the final clustering results.

In the first step, with a slight difference from the original SSC model, we consider a more general optimization problem—dictionary-based SSC with the given data sample matrix $\boldsymbol{X} \in \mathbb{R}^{d\times n}$:

$$ \min_{\boldsymbol{Z}, \boldsymbol{E}} \Vert \boldsymbol{Z} \Vert _{1} + \lambda \Vert \boldsymbol{E} \Vert _{2,1}, \quad \text{s.t.} \ \boldsymbol{X}=\boldsymbol{A}\boldsymbol{Z}+\boldsymbol{E}, $$

(2)

where $\Vert \boldsymbol{E} \Vert _{2,1} = \sum_{i} \|[\boldsymbol{E}]_{:,i} \|_{2}, [\boldsymbol{E}]_{:,i}$ is the i-th column of the error term $\boldsymbol{E} \in \mathbb{R}^{d\times n}$, $\boldsymbol{A} \in \mathbb{R}^{d\times m}$ is the desired basis matrix for the subspace, and $\boldsymbol{Z} \in \mathbb{R}^{m\times n}$ is the sparse affinity matrix. Since we want to maintain the robustness of the classic SSC, we model the sample-specific corruptions by $\ell _{2,1}$-norm to eliminate outliers. Note that one can learn the dictionary A and Z simultaneously in the DP framework, which we will show later. After obtaining the coefficient Z, we construct the graph matrix $\boldsymbol{W} \in \mathbb{R}^{n\times n}$. One can easily set $\boldsymbol{W} = |\boldsymbol{Z}|^{\mathrm{T}} + |\boldsymbol{Z}|$ when $\boldsymbol{A} = \boldsymbol{X}$. However, for a general dictionary A, it is more prevalent to set the $(i, j)$-th entry of W as follows:

$$ W_{ij} = \exp \biggl(-\frac{ \Vert \boldsymbol{z}_{i} - \boldsymbol{z}_{j} \Vert _{2}^{2}}{\sigma}\biggr), $$

(3)

where $\boldsymbol{z}_{i} = [\boldsymbol{Z}]_{:i}$ is the i-th column of the coefficient matrix and σ is a re-scaling constant. Note that the graph Laplacian matrix $\boldsymbol{L}\in \mathbb{R}^{n\times n}$ of W is $\boldsymbol{L} = \boldsymbol{D}-\boldsymbol{W}$, where D is a diagonal matrix with the i-th diagonal entry being $\sum_{j}W_{ij}$.

For the second step, we can perform spectral clustering. Given the cluster number k̃, we first find the k̃ eigenvectors $\boldsymbol{Y} \in \mathbb{R}^{n\times \tilde{k}}$ corresponding to the 2nd to the $(\tilde{k}+1)$-th smallest eigenvalues of the graph Laplacian matrix L. Then we treat each row of the $n\times \tilde{k}$ eigenvectors matrix Y as an instance and perform k-means clustering to obtain the final labels.

3.2 Linearized ADMM solver

The problem in Eq. (2) can be solved by the L-ADMM with the following updating rule:

$$ \textstyle\begin{cases} \boldsymbol{T}^{(k)} = \boldsymbol{A}\boldsymbol{Z}^{(k)} + \boldsymbol{E}^{(k)}-\boldsymbol{X}, \\ \boldsymbol{Z}^{(k+1)} = \mathcal{S}_{\alpha} (\boldsymbol{Z}^{(k)} - \alpha \boldsymbol{A}^{\mathrm{T}} (\boldsymbol{\lambda}^{(k)} + \beta \cdot \boldsymbol{T}^{(k)} ) ), \\ \boldsymbol{E}^{(k+1)} = \mathcal{\widetilde{S}}_{\frac{1}{\beta}} (\boldsymbol{X}-\boldsymbol{A}\boldsymbol{Z}^{(k+1)} - \frac{\boldsymbol{\lambda}^{(k)}}{\beta} ), \\ \boldsymbol{\lambda}^{(k+1)} = \boldsymbol{\lambda}^{(k)} + \beta ( \boldsymbol{A}\boldsymbol{Z}^{(k+1)} + \boldsymbol{E}^{(k+1)}- \boldsymbol{X} ), \end{cases} $$

(4)

where $\boldsymbol{\lambda}^{(k)}\in \mathbb{R}^{d\times n}$ is the Lagrange multiplier. α and β are parameters for the shrink operators. We need $\alpha > \|\boldsymbol{A}^{\mathrm{T}}\boldsymbol{A}\|$, i.e., α is greater than the spectral norm of the matrix $\boldsymbol{A}^{\mathrm{T}}\boldsymbol{A}$. The shrinkage operator [40] is defined as follows:

$$ \mathcal{S}_{\lambda} ( \boldsymbol{X} )_{ij}= \bigl( \vert x_{ij} \vert - \lambda \bigr)_{+} \operatorname{sign} (x_{ij}), $$

(5)

where $(x)_{+}:= \max \{0,x\}$, $x_{ij}$ is the $(i, j)$-th entry of X, and $\operatorname{sign}(\cdot )$ is the sign function. Similarly, the column-wise shrinkage operator is defined as follows:

$$ \bigl[\mathcal{\widetilde{S}}_{\lambda} ( \boldsymbol{X} ) \bigr]_{:i}= \bigl( \bigl\Vert [\boldsymbol{X} ]_{:,i} \bigr\Vert _{2} - \lambda \bigr)_{+} \frac{ [\boldsymbol{X} ]_{:,i}}{ \Vert [\boldsymbol{X} ]_{:,i} \Vert _{2}}. $$

(6)

Notably, we did not utilize the traditional ADMM to solve the problem in Eq. (2), since Liu et al. [41] showed that the linearized step did not make the optimization divergent. Fewer variables can reduce the computational complexity. As shown in the following subsection, we can reduce the number of learning parameters without introducing auxiliary variables, and hence accelerate the training speed. On the other hand, the traditional ADMM for the problem in Eq. (2) inverses the matrix $(\boldsymbol{I} + \boldsymbol{A}^{\mathrm{T}}\boldsymbol{A})$ in the iteration, where I is the identity matrix. However, when we generalize matrix A to a learnable and non-linear mapping, it is difficult to define the inverse of a neural network.

3.3 General D-LADMM

In this section, we introduce the general framework D-LADMM [22] to differentiate steps in Eq. (4). D-LADMM treats the iteration in Eq. (4) as one neural network block and converts some fixed parameters to learnable parameters, leading to a k-layer feed-forward neural network. By setting

$$ \boldsymbol{T}^{(k)} = \mathcal{A}_{\boldsymbol{\vartheta}_{1}^{k}}\bigl( \boldsymbol{Z}^{(k)}\bigr) + \boldsymbol{E}^{(k)}-\boldsymbol{X}, $$

(7)

we have the following updating rules:

$$ \textstyle\begin{cases} \boldsymbol{Z}^{(k+1)} = \eta _{\boldsymbol{\theta}_{1}^{k}} ({\boldsymbol{Z}}^{(k)} - {\mathcal{A}}_{\boldsymbol{\vartheta}_{2}^{k}}^{\mathrm{T}} (\boldsymbol{\lambda}^{(k)} + \boldsymbol{\beta}^{(k)} \circ {\boldsymbol{T}}^{(k)}) ), \\ \boldsymbol{E}^{(k+1)} = \zeta _{\boldsymbol{\theta}_{2}^{k}} ({\boldsymbol{X}} - {\mathcal{A}}_{\boldsymbol{\vartheta}_{1}^{k}} ({\boldsymbol{Z}}^{(k+1)}) - \frac{1}{\boldsymbol{\beta}^{(k)}}\circ \boldsymbol{\lambda}^{(k)} ), \\ \boldsymbol{\lambda}^{(k+1)} = \boldsymbol{\lambda}^{(k)} + \boldsymbol{\beta}^{(k)} \circ ({\mathcal{A}}_{\boldsymbol{\vartheta}_{1}^{k}}({\boldsymbol{Z}}^{(k + 1)}) + {\boldsymbol{E}}^{(k + 1)} - {\boldsymbol{X}}), \end{cases} $$

(8)

where $\Theta = \{\boldsymbol{\vartheta}_{1}^{k}, \boldsymbol{\vartheta}_{2}^{k}, \boldsymbol{\theta}_{1}^{k}, \boldsymbol{\theta}_{2}^{k}, \boldsymbol{\beta}^{k}\}_{k=0}^{K-1}$ are learnable matrices, ∘ is the Hadamard product, and parameterized functions $\eta (\cdot )$ and $\zeta (\cdot )$ are some non-linear activation functions with parameters $\boldsymbol{\theta}_{1}$ and $\boldsymbol{\theta}_{2}$, respectively. Here $\mathcal{A}_{\boldsymbol{\vartheta _{1}}}(\cdot ): \mathbb{R}^{d} \rightarrow \mathbb{R}^{m}$ and $\mathcal{A}_{\boldsymbol{\vartheta _{2}}}^{\mathrm{T}}(\cdot ): \mathbb{R}^{m} \rightarrow \mathbb{R}^{d}$, parameterized by $\boldsymbol{\vartheta _{1}}$ and $\boldsymbol{\vartheta _{2}}$, respectively, are non-linear parameterized mappings. The operator $\mathcal{A}_{\boldsymbol{\vartheta _{1}}}$ performs the mapping column-wisely if it is applied to the matrix. The two mappings are generalized from the dictionary A. $\mathcal{A}_{\boldsymbol{\vartheta _{2}}}^{\mathrm{T}}(\cdot ): \mathbb{R}^{m} \rightarrow \mathbb{R}^{d}$ is the generalized adjoint mapping of $\mathcal{A}_{\boldsymbol{\vartheta _{1}}}(\cdot )$. In general, we need only the parameterized functions $\mathcal{A}_{\boldsymbol{\vartheta _{1}}}$ and $\mathcal{A}_{\boldsymbol{\vartheta _{1}}}^{\mathrm{T}}$ to have a similar form, e.g., linear and adjoint mapping, convolution and deconvolution; their parameters $\boldsymbol{\vartheta _{1}}$ and $\boldsymbol{\vartheta _{2}}$ can be different. Note that $\boldsymbol{\beta}\in \mathbb{R}^{d\times n}$ in Eq. (4) is now a learnable matrix in contrast to a deterministic penalty parameter β. We expand the dimension of the penalty parameter such that the penalties in different directions are also learnable.

It is obvious that Eq. (8) is the same as Eq. (4) when $\eta (\cdot )$ and $\zeta (\cdot )$ are the original shrink operators and $\mathcal{A}_{\boldsymbol{\vartheta _{1}}}(\cdot )$ degenerates into the original dictionary A. Compared to L-ADMM, D-LADMM first converts the shrinkage operators in Eq. (4) into learnable activation functions, and then replaces the given matrix A with a non-linear parameterized mapping while expanding the dimension of the penalty parameter.

Unlike the original L-ADMM solver where no parameter is learnable, Eq. (8) can be treated as a block of a specially structured neural network and trained using SGD over the observation. Many empirical results, e.g., Refs. [17, 22, 34, 35, 42] showed that a trained k-layer DP model or its variants could obtain a good solution to the same quality within one or two orders of magnitude fewer iterations than the original optimization method. Especially, the results in Ref. [22] implied that, under mild conditions, Θ exists such that $\boldsymbol{Z}^{k}$ converges to the optimal solution set exponentially fast in terms of the layer number k. However, vanilla L-ADMM may struggle to have a linear convergence rate.

4 Differentiable SSC

In this section, we first specify each step of the differentiable solver in Eq. (8). Then, we introduce the objective to train this solver in an unsupervised way. Finally, we construct a sparse graph matrix based on the output of the differentiable SSC solver.

4.1 Differentiable solver for SSC

Our differentiable SSC consists of an affinity updating layer, a de-noising layer, and a multiplier updating layer. We discuss them in detail.

Affinity updating layer $\boldsymbol{Z}^{(k+1)}$. This layer corresponds to the first step in Eq. (8). We merge the dictionary construction step into the mapping $\mathcal{A}_{\boldsymbol{\vartheta}_{1}}$, so we assume that $d \ll m$.

Given the variables $\boldsymbol{Z}^{(k)}$, $\boldsymbol{E}^{(k)}$ and $\boldsymbol{\lambda}^{(k)}$, the first step in Eq. (4) is decomposed and generalized into two operations:

$$ \textstyle\begin{cases} \boldsymbol{T}^{(k)} = \mathcal{A}_{\boldsymbol{\vartheta}_{1}^{k}}( \boldsymbol{Z}^{(k)}) + \boldsymbol{E}^{(k)}-\boldsymbol{X}, \\ \boldsymbol{Z}^{(k + 1)} = \mathcal{R} ({\boldsymbol{Z}}^{(k)} - {\mathcal{A}}_{\boldsymbol{\vartheta}_{2}^{k}}^{\mathrm{T}}(\boldsymbol{\lambda}^{(k)} + \boldsymbol{\beta}^{(k)} \circ {\boldsymbol{T}}^{(k)} ); {\boldsymbol{B}}_{1}^{(k)}), \end{cases} $$

(9)

where weight $\boldsymbol{\beta}^{(k)} \in \mathbb{R}^{d\times n} \geq \boldsymbol{0}$, and the threshold matrix $\boldsymbol{B}^{(k)}_{1}\in \mathbb{R}^{m\times n}$ is learnable. Denote the rectified linear unit (ReLU) function as $r(\cdot )$, then $\mathcal{R}(\boldsymbol{X};\boldsymbol{B}) = {r}(\boldsymbol{X}- \boldsymbol{B}) - {r}(-\boldsymbol{X}-\boldsymbol{B})$. $\mathcal{R}(\cdot ;\boldsymbol{B})$ comes from the shrinkage operator $\mathcal{S}_{\lambda}(\cdot )$ and B is the threshold. We initialize the learnable weight $\boldsymbol{\beta}^{(k)}$ to all-one matrix 1 and the learnable threshold $\boldsymbol{B}^{(k)}_{1}$ to $\boldsymbol{1}\times 0.15$. When $k=0$, we set $\boldsymbol{Z}^{1} = \mathcal{A}_{\boldsymbol{\vartheta}_{2}}^{\mathrm{T}} (\mathcal{A}_{\boldsymbol{\vartheta}_{1}} (\boldsymbol{X} ) )$.

De-noising layer $\boldsymbol{E}^{(k+1)}$. This layer corresponds to the second step in Eq. (8). Given $\boldsymbol{Z}^{(k+1)}$ and $\boldsymbol{\lambda}^{k}$ as the input, the output of this layer is given by

$$ \boldsymbol{E}^{(k + 1)} = \mathcal{R} \bigl(\boldsymbol{X} - \mathcal{A}_{\boldsymbol{\vartheta}_{1}^{k}}\bigl(\boldsymbol{Z}^{(k + 1)}\bigr) - \boldsymbol{W}^{(k)}_{1} \circ \boldsymbol{ \lambda}^{(k)}; \boldsymbol{B}_{2}^{(k)} \bigr). $$

(10)

Similarly, $\boldsymbol{W}^{(k)}_{1}$ and $\boldsymbol{B}^{(k)}_{2} \in \mathbb{R}^{d\times n}$ are learnable parameters. $\mathcal{R}(\cdot )$ is the same as that in the affinity updating layer. We set $\boldsymbol{\lambda}^{(0)} = \boldsymbol{0}$ when $k=0$.

Note that we still adopt the non-linear function $\mathcal{R}(\cdot ;\boldsymbol{B})$ here. In practice, the dimension of data is usually large. The element-wise operation is more suitable for DNN training. For implementation convenience, we drop the constraint that $\boldsymbol{W}^{(k)}_{1} = 1/\boldsymbol{\beta}^{(k)}$.

Multiplier updating layer $\boldsymbol{\lambda}^{(k+1)}$. This layer corresponds to the final step in Eq. (8). Given $\boldsymbol{Z}^{(k+1)}$ and $\boldsymbol{E}^{(k+1)}$ as the inputs, the output of this layer is

$$ \boldsymbol{\lambda}^{(k + 1)} = \boldsymbol{ \lambda}^{(k)} + \boldsymbol{\beta}^{(k)} \circ \bigl( \mathcal{A}_{\boldsymbol{\vartheta}_{1}^{k}}\bigl( \boldsymbol{Z}^{(k+1)}\bigr) + \boldsymbol{E}^{(k+1)} - \boldsymbol{X}\bigr), $$

(11)

where the weight matrix $\boldsymbol{\beta}^{(k)} \in \mathbb{R}^{d \times n}$ is the same as that in the affinity updating layer.

4.2 Differentiable SSC objective

We now construct the optimization target for training our differentiable SSC module. Note that the optimization objective for the SSC problem is shown in Eq. (2). We choose a generalized objective instead of directly using Eq. (2) as a training objective. In Eq. (2), each column norm for E shares a common weight λ. Here, we assign different weights to different columns to ease the unbalanced data problem. Assuming that the outputs of our differentiable SSC are $\boldsymbol{Z}^{(K)}$ and $\boldsymbol{E}^{(K)}$, and we define the training loss for our differentiable SSC as follows:

$$ L_{\text{D-SSC}} = \sum_{i=1}^{n} w_{i} \bigl\Vert \bigl[\boldsymbol{E}^{(K)} \bigr]_{:,i} \bigr\Vert _{2} + \lambda \bigl\Vert \boldsymbol{Z}^{(K)} \bigr\Vert _{1}, $$

(12)

where n is the batch size for training and the adaptive weight $w_{i}$ can be calculated by

$$ w_{i} = 1- \frac{(1+\mathcal{T} ( \Vert [\boldsymbol{E}_{n} ]_{:,i} \Vert _{2}))^{-1}}{\sum_{i=1}^{n} (1+\mathcal{T} ( \Vert [{\boldsymbol{E}}_{n} ]_{:,i} \Vert _{2}))^{-1}}, $$

(13)

where $\mathcal{T}(\cdot )$ is a truncation function that clips the large value to a pre-defined maximum value. Here, $w_{i}$ is calculated by a variant of the student’s t-distribution [43] with a different power order. Inspired by adaptive boosting, the data sample that is difficult to reconstruct can obtain a larger weight $w_{i}$ than the others, and the truncation function can ensure that the loss is not too sensitive to the outliers contained in the data and prevent the outliers from obtaining too large weights. This re-weighting strategy can not only make the module focus on the hard examples but also alleviate the problem of unbalanced data distribution.

4.3 Graph matrix construction

We assume that the output of the differentiable SSC is $\boldsymbol{Z}^{(K)}$. Similar to the classic subspace clustering method, we construct the graph matrix W based on the coefficient matrix $\boldsymbol{Z}^{(K)}$. $W_{ij}$ represents the similarity between the coefficients $[\boldsymbol{Z}^{(K)}]_{:i}$ and $[\boldsymbol{Z}^{(K)}]_{:j}$. The $(i, j)$-th entry of the matrix W is defined by

$$ W_{ij} = \textstyle\begin{cases} \exp (-\frac{ \Vert \boldsymbol{z}_{i} - \boldsymbol{z}_{j} \Vert _{2}^{2}}{\sigma _{i}}), & \boldsymbol{z}_{j} \in \mathit{KNN}(\boldsymbol{z}_{i};N), \\ 0, & \text{otherwise,} \end{cases} $$

(14)

where $\boldsymbol{z}_{i} = [\boldsymbol{Z}^{(K)}]_{:i}$ corresponds to the i-th column of $\boldsymbol{Z}^{(K)}$ and $\mathit{KNN}(\boldsymbol{z}_{i};N)$ represents the N nearest neighbors of $\boldsymbol{z}_{i}$. We choose N from the range $[3,6]$ in the experiments. We set the scalar $\sigma _{i} >0$ by the median of all the positive $\|\boldsymbol{z}_{i} - \boldsymbol{z}_{j}\|_{2}^{2}$. We symmetrize W by setting $\boldsymbol{W} = (\boldsymbol{W} + \boldsymbol{W}^{\mathrm{T}})/2$.

Note that we can easily make this module differentiable by setting W as the Gaussian gram matrix of $\boldsymbol{Z}^{(K)}$, i.e., by Eq. (3), but we still choose the nearest neighbors here since it produces sparse neighbors, which can prevent our method from being affected by dense non-essential neighbors produced by its differentiable counterpart. More importantly, the non-differentiable KNN operator is equivalent to setting some values to zero in W. Clearing some channels to zero, such as dropout, is quite common in deep learning training, which essentially introduces explicit and implicit regularization effects. Instead of causing divergent learning, the regularization benefits generalization [44].

5 Differentiable spectral clustering

In this section, we provide a method to differentiate spectral clustering. The output of our differentiable SSC is the input of the differentiable spectral clustering module. Given the cluster number k̃, traditional spectral clustering contains two steps: (1) find the k̃ eigenvectors Y corresponding to the 2nd to the $(\tilde{k}+1)$-th smallest eigenvalues of the graph Laplacian matrix L; (2) take each row of the $n\times \tilde{k}$ eigenvectors matrix Y as a new feature of the input data and then perform k-means clustering on all the rows.

We first reformulate the eigenvector decomposition and provide a differentiable method to perform the decomposition approximately. Then, we differentiate the k-means clustering using a self-supervised strategy [33]. Finally, we introduce the training objective for the whole differentiable spectral clustering module.

5.1 Differentiable eigenvector approximation

Recall the definition of the graph Laplacian matrix $\boldsymbol{L} = \boldsymbol{D}-\boldsymbol{W}$, where D is a diagonal matrix with the i-th diagonal entry being $\sum_{j}W_{ij}$. The k̃ eigenvectors corresponding to the graph Laplacian matrix L are the solution of the following optimization problem:

$$ \min_{\boldsymbol{{Y}}\in \mathbb{R}^{n \times \tilde{k}}} \sum_{i,j} W_{ij} \bigl\Vert [\boldsymbol{{Y}} ]_{:,i} - [ \boldsymbol{{Y}} ]_{:,j} \bigr\Vert _{2}^{2} , \quad \text{s.t.} \ \boldsymbol{{Y}}^{\mathrm{T}}\boldsymbol{{Y}} = \boldsymbol{I}, $$

(15)

where k̃ is the cluster number. However, we do not directly perform the eigenvalue decomposition on the graph Laplacian matrix L here. The exact eigenvalue decomposition is non-differentiable, and how to differentiate it is still an open problem in the deep learning community. Indyk et al. [25] approximated the low-rank decomposition by a modified differentiable power method. However, this method might fail when the gaps among eigenvalues are small. Another problem with exact eigenvalue decomposition is that we cannot perform incremental learning for batch training, which is important for large-scale data. Therefore, an eigenvalue-gap independent and differentiable method is needed to solve the problem in Eq. (15). This method is provided below.

Optimization with orthogonality constraints. The usual method for solving the general orthogonality-constrained optimization problem is to perform the manifold gradient descent on the Stiefel manifold, which evolves along the manifold geodesic. Specifically, manifold gradient descent (GD) updates the variable in the manifold tangent space along the objective function gradient projected into the tangent plane. Then, the procedure is repeated in the tangent space of the updated variable [45]. As usual, manifold GD requires SVDs to generate feasible points on the geodesic, which is non-differentiable. Fortunately Refs. [46, 47] developed a technique to approximately solve an orthogonality-constrained optimization problem that only consists of matrix multiplication and addition and does not rely on SVDs.

Note that the variable is $\boldsymbol{Y} \in \mathbb{R}^{n\times \tilde{k}}$. Denote by $\boldsymbol{G}\in \mathbb{R}^{n\times \tilde{k}}$ the gradient of the objective function in Eq. (15) at Y. Then, the projection of G in the tangent plane of the Stiefel manifold at Y is PY, where $\boldsymbol{P} = \boldsymbol{G}\boldsymbol{Y}^{\mathrm{T}} - \boldsymbol{Y} \boldsymbol{G}^{\mathrm{T}}$ and $\boldsymbol{P} \in \mathbb{R}^{n\times n}$ [46]. We choose the canonical metric on the tangent space as the equipped Riemannian metric. Instead of parameterizing the geodesic of the Stiefel manifold along direction P using the exponential function, inspired by Refs. [46, 47], we generate feasible points by the following Cayley transform:

$$ \boldsymbol{Y}(t) = \boldsymbol{C}(t)\boldsymbol{Y}, $$

(16)

where

$$ \boldsymbol{C}(t) = \biggl(\boldsymbol{I} + \frac{t}{2}\boldsymbol{P} \biggr) \biggl(\boldsymbol{I} - \frac{t}{2}\boldsymbol{P} \biggr)^{-1}, $$

(17)

where I is the identity matrix and t is a parameter used for updating the current Y. One can easily verify that $\boldsymbol{Y}(t)$ has the following properties:

• 1) $\mathrm{d} \boldsymbol{Y}(0) / \mathrm{d}t = -\boldsymbol{P} \boldsymbol{Y}$;

• 2) $\boldsymbol{Y}(t)$ is smooth in t;

• 3) $\boldsymbol{Y}(0)= \boldsymbol{Y}$;

• 4) $(\boldsymbol{Y} (t ) )^{\mathrm{T}} \boldsymbol{Y} (t ) = \boldsymbol{I}$, $\forall t\in \mathbb{R}$, given $\boldsymbol{Y}^{\mathrm{T}}\boldsymbol{Y} = \boldsymbol{I}$.

It is obvious that $\boldsymbol{Y}(t)$ can result in a smaller objective function value than Y on the Stiefel manifold when t is in a proper range.

$\boldsymbol{Y}(t)$ is a reparameterization of the geodesic w.r.t. t on Stiefel manifold. When computing $\boldsymbol{Y}(t)$, no SVD is needed. A matrix inversion and several matrix multiplications are needed instead, which sheds light on solving the problem in Eq. (15) in a differentiable way. Note that matrix inversion may also be difficult to differentiate. Fortunately, when t is in a proper range, we can approximate the matrix inversion by a polynomial of P.

Eigenvector approximation. To solve the problem in Eq. (15), we compute the gradient G of the objective function

$$ \sum_{i,j} W_{ij} \bigl\Vert [ \boldsymbol{{Y}} ]_{:,i} - [\boldsymbol{{Y}} ]_{:,j} \bigr\Vert _{2}^{2}, $$

(18)

w.r.t. Y and search for a geodesic on the Stiefel manifold in the gradient direction to update the current Y.

Note that the matrix inversion $(\boldsymbol{I} - t\boldsymbol{P}/2 )^{-1}$ is time-consuming and hard to differentiate during back propagation. Observing that $\boldsymbol{C}(t)$ contains Neumann series, we consider approximating $\boldsymbol{C}(t)$ by a polynomial in P. Hence, given the current Y, we consider searching in the following curve:

$$ \boldsymbol{Y}(t) = \Biggl(\boldsymbol{I} + \sum _{i=1}^{r} 2^{- \frac{ (i-1 )i}{2}} (-t\boldsymbol{P} )^{i} \Biggr) \boldsymbol{Y}, $$

(19)

where r is the degree of the polynomial and $\boldsymbol{P} = \boldsymbol{G}\boldsymbol{Y}^{\mathrm{T}} - \boldsymbol{Y} \boldsymbol{G}^{\mathrm{T}}$. PY corresponds to the projection of G in the tangent plane at Y. In general, the approximation in Eq. (19) is the optimal r-th order polynomial for maintaining orthogonality.

Proposition 1

Assume that Y is from the Stiefel manifold, i.e., $\boldsymbol{Y}^{\mathrm{T}}\boldsymbol{Y} = \boldsymbol{I}$ and $\|\boldsymbol{P}\|$ is bounded, then we have

$$ \bigl\Vert \bigl(\boldsymbol{Y} (t ) \bigr)^{\mathrm{T}} \boldsymbol{Y} (t ) - \boldsymbol{I} \bigr\Vert = \mathrm{O} \bigl(t^{2r}2^{-r (r-1 )} \bigr), $$

(20)

where $\|\cdot \|$ is the matrix spectral norm. Furthermore, given the degree r, $\boldsymbol{Y}(t)$ in Eq. (19) is the optimal polynomial for maintaining the orthogonality.

Note that the boundness of P inherits from G, which is the gradient of the objective w.r.t. Y. By Proposition 1, we have $\boldsymbol{Y}(t) \approx \boldsymbol{C}(t)\boldsymbol{Y}$ when r is large. Moreover, we avoid the matrix inversion here and make the curve absolutely differentiable in Y.

Obviously, we have $\mathrm{d}\boldsymbol{Y}(0) / \mathrm{d}t = -\boldsymbol{P}\boldsymbol{Y}$ for the polynomial in Eq. (19). However, when $t>0$, the direction of the Cayley transform approximation $\boldsymbol{Y}(t)$ in Eq. (19) may deviate from the ideal direction $-\boldsymbol{P}\boldsymbol{Y}$. Fortunately, we can still ensure the descent of the objective when t satisfies some conditions.

Proposition 2

Assume that $\|\mathcal{P}^{\perp}_{\boldsymbol{Y}} \boldsymbol{P}\|_{F} := c_{p} < \infty$, where $\mathcal{P}^{\perp}_{\boldsymbol{Y}} = \boldsymbol{I} - \boldsymbol{Y}\boldsymbol{Y}^{\mathrm{T}}$ is the projector of the complementary space of $\operatorname{Span}\{\boldsymbol{Y}\}$. Given $t\in \mathbb{R}^{+}$, and let $\rho _{t} := tc_{p}$, if $\rho _{t}$ satisfies

$$ g(\rho _{t}) \cdot \biggl(1-\operatorname{erf} \biggl( \frac{2\ln 2-2\ln \rho _{t}}{2\sqrt{\ln 2}} \biggr)\biggr) + \frac{\rho _{t}}{\ln 2} < 1, $$

(21)

where

$$ g(\rho _{t}) := \frac {2\sqrt{{ \uppi }}\exp(\frac{(\ln \rho _{t})^{2}}{\ln 2})\ln \rho _{t}}{\rho _{t}(\ln 2)^{\frac{3}{2}}}, $$

(22)

then we have

$$ \bigl\langle \mathcal{P}_{\mathcal{T}_{\boldsymbol{Y}}} \bigl( \dot{ \boldsymbol{Y}} (t ) \bigr), \mathcal{P}_{ \mathcal{T}_{\boldsymbol{Y}}} (-\boldsymbol{G} ) \bigr\rangle _{\mathrm{c}}> 0, $$

(23)

where $\mathcal{P}_{\mathcal{T}_{\boldsymbol{Y}}} (\cdot )$ is the projector of the tangent space of Y, $\langle \boldsymbol{A}, \boldsymbol{B} \rangle _{ \mathrm{c}} := \operatorname{Tr} (\boldsymbol{A}^{ \mathrm{T}} \mathcal{P}^{\perp}_{\boldsymbol{Y}} \boldsymbol{B} )$ is the canonical inner product at the tangent space of Y, and G is the gradient of the objective.

Equation (23) indicates that $\boldsymbol{Y}(t)$ is a descent curve as long as t is in a wide range. Numerically, the condition in Eq. (21) can be satisfied when $\rho _{t}<0.8$. We may find the optimal $t^{*}$ such that

$$ t^{*} = \operatorname*{argmin}_{0 \leq t\leq \varepsilon} f(t) := \biggl( \sum _{i,j} W_{ij} \bigl\Vert \bigl[ \boldsymbol{Y} (t) \bigr]_{:,i} - \bigl[\boldsymbol{Y} (t) \bigr]_{:,j} \bigr\Vert _{2}^{2} \biggr) , $$

(24)

where ε is a pre-defined parameter to ensure the magnitude of $t^{*}$. Recall that we only concern that the optimal $t^{*}$ satisfies the condition in Eq. (21). We expand $f(t)$ at 0 via Taylor expansion:

$$ f(t) = f(0) + f'(0)\cdot t + f''(0)\cdot t^{2} + \mathrm{O} \bigl(t^{2}\bigr), $$

(25)

where $f'(0)$ and $f''(0)$ are the first and second order derivatives of $f(t)$ evaluated at 0, respectively. These two derivatives can be computed efficiently (see Appendixes A, B and C). We can obtain an approximated optimal solution $t^{*}$ via

$$ t^{*} = \min \{\varepsilon , \tilde{t} \},\quad \tilde{t} = - \frac{f'(0)}{f''(0)}. $$

(26)

Then we can update Y by $\boldsymbol{Y}(t^{*})$.

Differentiable eigenvector mapping layer $\boldsymbol{Y}^{(l)}$. Based on the above iterative steps for the eigenvector approximation, i.e., $\boldsymbol{Y} \to \boldsymbol{Y}(t^{*})$, we introduce the following eigenvector mapping layer, which is generalized from one step for approximation. We set $r =2$ for our layers.

Given the last layer output $\boldsymbol{Y}^{(l)}$, we have the following updating rules:

$$ \textstyle\begin{cases} \boldsymbol{P}^{(l+1)} = 2 (\boldsymbol{L}\boldsymbol{Y} \boldsymbol{Y}^{\mathrm{T}} - \boldsymbol{Y}\boldsymbol{Y}^{ \mathrm{T}}\boldsymbol{L} ) + \boldsymbol{Y}\boldsymbol{W}_{2}^{(l)} \boldsymbol{Y}^{\mathrm{T}}, \\ \tilde{t}^{(l+1)} = \frac{ \operatorname{Tr} (\boldsymbol{Y}^{\mathrm{T}} \boldsymbol{L} \boldsymbol{P} \boldsymbol{Y} )}{ \operatorname{Tr} (\boldsymbol{Y}^{\mathrm{T}}\boldsymbol{P} \boldsymbol{L} \boldsymbol{P}\boldsymbol{Y} - \boldsymbol{Y}^{\mathrm{T}}\boldsymbol{L}\boldsymbol{P}^{2}\boldsymbol{Y} )}, \\ t^{*} =\min \{\varepsilon , \tilde{t}^{(l+1)} \}, \\ \boldsymbol{Y}^{(l+1)} = (\boldsymbol{I} - t^{*} \boldsymbol{P} + \frac{(t^{*}{\boldsymbol{P}})^{2}}{2} \boldsymbol{P} )\boldsymbol{Y}, \end{cases} $$

(27)

where $\boldsymbol{W}_{2}^{(l)} \in \mathbb{R}^{\tilde{k}\times \tilde{k}}$ is the learnable matrix at each layer, $\operatorname{Tr}(\cdot )$ is the trace operator, ε is a parameter used to ensure Eq. (21) for $t^{*}$, and L is the graph Laplacian matrix of W. We randomly choose $\boldsymbol{Y}^{(0)}$ from the Stiefel manifold and fix it during training. We omit the superscript in the updating rules for convenience and clear writing. Note that when $\boldsymbol{W}_{2}^{(l)} = \boldsymbol{0}$, Eq. (27) is almost the same as one iteration of the manifold gradient descent, the introduced learnable parameters can help to find better updating direction when the gradient is inaccurate.

We bypass the matrix inversion and the exact SVD, and aim to solve the problem in Eq. (15) approximately. Consequently, we can solve the problem in Eq. (15) in a differentiable and learning-based manner by stacking the proposed eigenvector mapping layers in Eq. (27). Our eigenvector mapping layer can be easily modified to perform differentiable SVD, which is still difficult and is the main problem when connecting classic low rank-based structure methods and prevalent DNNs.

5.2 Differentiable k-means clustering

This section provides a method to differentiate k-means clustering by a self-supervised strategy. The input of this module is $\boldsymbol{Y}^{(\tilde{l})}$, which is the output of the eigenvector mapping layers.

In general, batch training makes the k-means clustering challenging to differentiate. The sampled data from different batches do not have the same eigenvector space. Thus, they cannot share cluster centers or parameters. We adopt a parametric function $\mathcal{G}_{\boldsymbol{\eta}}:\mathbb{R}^{\tilde{k}} \to \mathbb{R}^{ \tilde{k}}$ to further transform the input $\boldsymbol{Y}^{(\tilde{l})}$, where η is the learnable parameter of the parametric function. We want the function $\mathcal{G}_{\boldsymbol{\eta}}$ to embed the eigenvectors of different batches into a common feature space, where we can share the clusters and distance metric. In the experiments, we choose $\mathcal{G}_{\boldsymbol{\eta}}$ as a three-layer fully connected neural network.

On the other hand, k-means clustering assigns data to a cluster center, which is a discrete process. To overcome the non-differentiability, we utilize a self-supervised structure [33] to transform the clustering step into a classification step. Specifically, we alternate between clustering the input of this module to produce pseudo-labels using k-means and updating the parameters of this differentiable module by predicting these pseudo-labels. This self-supervised structure is illustrated in Fig. 1. In summary, we convert the non-differentiable assignment process into a differentiable classifier via the self-supervised structure.

Figure 1

Illustration of the self-supervised structure. We cluster the results of the eigenvector approximation and use the cluster assignments as pseudo-labels to learn the parameters of the differentiable modules. DSSCNet refers to differentiable sparse subspace clustering

5.3 Training objective

We provide the training objective for the two modules of the proposed differentiable spectral clustering. For the eigenvector mapping layers, we let

$$ L_{\mathrm{e}} = \operatorname{Tr} \bigl( \bigl({\boldsymbol{Y}}^{(\tilde{l})} \bigr)^{\mathrm{T}} {\boldsymbol{L}} \bigl({\boldsymbol{Y}}^{(\tilde{l})} \bigr) \bigr), $$

(28)

where $\boldsymbol{Y}^{(\tilde{l})}$ is the output of the final eigenvector mapping layer and L is the graph Laplacian matrix. Note that $L_{\mathrm{e}}$ is the same as the objective of the problem in Eq. (15). Due to the property 4) of $\boldsymbol{Y}(t)$, $\boldsymbol{Y}^{(\tilde{l})}$ approximately satisfies the constraint in Eq. (15).

We define $L_{\text{K}}$ as the loss of the k-means module. Denote by $\tilde{y}_{i} \in \mathbb{N}$ the pseudo-label of the data $\boldsymbol{x}_{i}\in \mathbb{R}^{d}$ and let $\boldsymbol{f}_{i}\in \mathbb{R}^{\tilde{k}}$ be the final output of the classifier in terms of $\boldsymbol{x}_{i}$ in the k-means module, where k̃ is the number of cluster. We utilize the softmax loss for the multi-classification problem for $L_{\text{K}}$

$$ L_{\text{K}} = - \sum_{i=1}^{n} \ln \biggl( \frac{\exp (\boldsymbol{f}_{i,\tilde{y}_{i}} - \max \{\boldsymbol{f}_{i} \} )}{\sum_{j=1}^{\tilde{k}} \exp (\boldsymbol{f}_{i,j} - \max \{\boldsymbol{f}_{i} \} )} \biggr), $$

(29)

where $\boldsymbol{f}_{i,j}$ is the j-th entry of the vector $\boldsymbol{f}_{i}$ and $\max \{\boldsymbol{f}_{i} \}$ is the maximal entry of this vector. $L_{\text{K}}$ is smooth and easy to differentiate. Notably, pseudo-label $\tilde{y}_{i}$ is obtained by performing k-means clustering on $\mathcal{G}_{\boldsymbol{\eta}} (\boldsymbol{Y}^{(\tilde{l})} )$ row-wisely, and $\boldsymbol{f}_{i}$ is the output of a two-layer classifier with $\mathcal{G}_{\boldsymbol{\eta}} (\boldsymbol{Y}^{(\tilde{l})} )$ being the input.

6 Training algorithm and complexity

6.1 Training algorithm

We recast all three steps of subspace clustering as differential modules and propose the SSCNet. One of the main differences between our proposed unified differentiable modules and traditional deep learning lies in the training algorithm. In most cases, other deep learning methods design a final loss function and use it to update all the network parameters in one iteration. In contrast, following the commonly used ideas of pre-training and fine-tuning, we assign each module an objective to retain the interpretability of the model. The training algorithm for the proposed SSCNet is outlined in Algorithm 1. We denote the learnable parameters of the differentiable modules of SSCNet as $\boldsymbol{\Theta}_{1}$, $\boldsymbol{\Theta}_{2}$ and $\boldsymbol{\Theta}_{3}$, respectively. We update the parameters of differentiable SSC more frequently because it is the first differentiable module with the main parameters. We solve all the optimization problems in this algorithm via SGD.

Algorithm 1

Training algorithm for the proposed SSCNet

Note that the non-differentiable KNN operator in graph construction does not harm the learning. Based on the proposed sparse graph matrix, SSCNet concerns only the local structure when learning the feature $\boldsymbol{Y}^{(\tilde{l})}$. The local distance is more significant than the global distance for the next module—k-means clustering. Usually, large spacing among clusters often leads to better results.

6.2 Complexity analysis

With the new data coming in, our SSCNet can provide their labels by forward propagation, while some traditional methods, such as LRR and SSC, need to perform the optimization again.

The computational complexity equals the consumption of a forward step. The data size is n, the clustering number is k̃, and $\boldsymbol{Z} \in \mathbb{R}^{m \times n}$. In our paper, $\mathcal{A}_{\boldsymbol{\vartheta _{1}}}(\cdot )$ and $\mathcal{A}_{\boldsymbol{\vartheta _{2}}}^{\mathrm{T}}(\cdot )$ are shallow convolutional networks with $3\times 3$ kernels. Considering element-wise operations, the computational complexity of one block of our differentiable SSC module is $\text{O}(ndm)$. For the eigenvector mapping module, it stacks the layers in Eq. (27), and each step of it consumes $\tilde{k}n^{2}$ FLOPs. Hence, the computational complexity of this module is $\text{O}(\tilde{k}n^{2})$. As shown in Fig. 1, the last k-means clustering module during the testing phase is a shallow classifier with $\mathcal{G}_{\boldsymbol{\eta}}({\boldsymbol{Y}}^{(\tilde{l})})$ being the input. Assuming that the shallow neural networks are in the width $\text{O}(h)$, the last module consumes $\text{O}(h^{2} + h\tilde{k})$ FLOPs. In summary, the total complexity is $\text{O}(ndm+\tilde{k}n^{2}+h^{2} + h\tilde{k})$.

The computational complexity of one block of D-SSC is the same as that of one iteration of L-ADMM, which is $\text{O}(ndm)$. The results of D-LADMM [22] indicate that the block number of D-LADMM is much smaller than the total iteration number of L-ADMM. Thus, the total complexity of one forward step of SSCNet is much lower than that of SSC.

7 Experiments

In this section, we verify the effectiveness of our SSCNet for clustering. Detailed comparisons with other methods and analyses are provided.

7.1 Experiment settings

7.1.1 Datasets

To evaluate the performance of our proposed methods, we conduct experiments on three commonly used datasets, namely the MNIST [48], the USPS, and the CIFAR-10 [49] datasets.

MNIST [48]. The MNIST dataset contains a total $70{,}000$ handwritten digits of 10 classes. Each image is in the size of $28 \times 28$. The digits are centered and size-normalized. In experiments, we adopt all images for clustering.

USPS. The USPS dataset consists of 9298 handwritten digits of 10 classes. Each image is $16 \times 16$ in size, and the pixel values are in the range of $[0,2]$.

CIFAR-10 [49]. The CIFAR-10 dataset has 10 classes of objects. It contains a total of $60{,}000$ color images of size $32\times 32$. We also adopt the entire dataset.

7.1.2 Method comparison

We compare our SSCNet with many state-of-the-art methods, including k-means, spectral embedded clustering (SEC) [50], autoencoder based k-means (AE + k-means) [51], deep embedded clustering (DEC) [6], improved DEC (IDEC) [10], joint unsupervised learning (JULE) [7], cascade subspace clustering (CSC) [9], deep subspace clustering (DSC) [12], and SpectralNet [32].

7.1.3 Evaluation metrics

We adopt two commonly used metrics, including the clustering accuracy (ACC) and the normalized mutual information (NMI) [52], to measure the performance. The $\text{NMI}(C, C')$ can be information-theoretically interpreted. It is defined by

$$ \begin{aligned} &\operatorname{NMI}\bigl(C, C'\bigr)\\ &\quad := \frac{\sum_{i=1}^{K} \sum_{j=1}^{S} \vert C_{i} \cap C'_{j} \vert \log \frac{N \vert C_{i}\cap C'_{j} \vert }{ \vert C_{i} \vert \vert C'_{j} \vert }}{\sqrt{(\sum_{i=1}^{K} \vert C_{i} \vert \log \frac{C_{i}}{N}) (\sum_{j=1}^{S} \vert C'_{j} \vert \log \frac{C'_{j}}{N})}}, \end{aligned} $$

(30)

where C and $C'$ represent the predicted partition and the ground truth partition, respectively.

For the ACC, we first need to map clusters to the corresponding ground truth labels by the best permutation mapping function ${map}(\cdot )$ obtained by the Hungarian algorithm [53]. The accuracy is defined as follows:

$$ \operatorname{ACC} = \frac{\sum_{i=1}^{N} \delta (c_{i}, {map} (r_{i} ) )}{N}, $$

(31)

where $c_{i}$ is the ground truth label, $r_{i}$ is the predicted label, and

$$ \begin{aligned} \delta (a, b) = \textstyle\begin{cases} 1, & \text{if } a = b, \\ 0, & \text{otherwise}. \end{cases}\displaystyle \end{aligned} $$

(32)

For these two metrics, the higher value represents better performance.

7.1.4 Network architecture

We use a convolutional neural network with three layers for each block’s nonlinear mapping function $\mathcal{A}_{\boldsymbol{\vartheta}_{1}}$. The kernel size is set to $3\times 3$, and the numbers of feature maps in each layer are 32, 64, and 128. The corresponding generalized adjoint mapping function $\mathcal{A}_{\boldsymbol{\vartheta}_{2}}$ is designed symmetrically. In addition, we set $\lambda =c_{1}=c_{2}=0.15$, and $\varepsilon =1.0\times 10^{-2}$. We use SGD with a learning rate ${lr}=3.0\times 10^{-4}$ to train the network, and we set the batch size to 256 for all datasets. Our implementation is based on Python and TensorFlow [54].

7.2 Performance comparison

In Table 1, we present the results of these related approaches on these three datasets. Some of the results are taken directly from their papers. Our method performs best on all these datasets under the ACC and NMI metrics. For example, on the USPS dataset, the NMI of our method is 0.9482, which is 1.6% higher than the second best result 0.9321 achieved by SpectralNet [32], while the third best result is 0.9130 of JULE [7]. Compared with traditional clustering methods, including k-means and SEC, these deep learning-based methods show much better results due to the powerful representation ability of deep neural networks. In addition, we can see that DEC achieves much better results than AE + k-means on all the datasets, which reflects the importance of joint learning. Our method can jointly learn the optimal parameters for dictionary construction, affinity matrix computing, and clustering, so it achieves outstanding performance.

Table 1 Experimental results on the MNIST, USPS, and CIFAR-10 datasets. The best results are in bold. NMI and ACC represent normalized mutual information and accuracy, respectively

All the clustering methods exhibit weaker performance on the CIFAR-10 dataset than on the other datasets. It is essential to emphasize that most unsupervised clustering methods employed in this study operate without the benefit of labeled data during training. The complex semantic information in CIFAR-10 images introduces additional complexity, which may challenge traditional clustering techniques. These methods tend to rely heavily on low-level features, such as color, which can lead to misclassifications, such as grouping images of grassy landscapes and animals in grassy environments.

The complexity of CIFAR-10 poses a significant challenge for unsupervised clustering and traditional methods. Our approach, which autonomously learns high-level semantic features, surpasses traditional clustering techniques when dealing with such complex datasets. However, while our method mitigates these challenges, it cannot completely overcome the inherent limitations of clustering methods and may not entirely eliminate feature-to-semantic mismatches.

7.2.1 Visualization

In Fig. 2, we visualize the clustering results with 1000 data points from the MNIST and the USPS datasets during training. We can observe that our proposed SSCNet converges quickly even though each module has its objective. The points of both datasets are well separated. SSCNet increases the separability of the results. Note the points with red and blue colors in epoch 50 of the USPS dataset; they are slightly mixed but separated in epoch 100.

Figure 2

Visualization of clustering results on subsets of 1000 MNIST and USPS data points during training. Different colors indicate different clusters. The first row shows the USPS result, and the second row corresponds to MNIST

7.3 Influence of blocks

In Fig. 3, we show the influence of the block number b on the results of the MNIST dataset. One block is generated from one iteration of the L-ADMM. The performance is improved with increased blocks initially. This phenomenon is consistent with the optimization process of traditional SSC, whose objective value decreases with increasing iteration number. The network tends to be stable when b is greater than 4. Therefore, we set the number of blocks for all the datasets to 4. Another observation is that when $b=0$, the differentiable SSC module of our network is a variant of the autoencoder since we let $\boldsymbol{Z}^{(1)} = \mathcal{A}_{\boldsymbol{\vartheta}_{2}}^{\mathrm{T}} (\mathcal{A}_{\boldsymbol{\vartheta}_{1}}(\boldsymbol{X}) )$. However, the performance is much better than AE + k-means. This phenomenon verifies that our other differentiable modules benefit the clustering, i.e., eigenvector approximation and self-supervised k-means. We can also conclude that the unified DP model can obtain better results than separated traditional deep learning models even without our D-LADMM structure. Specifically, the NMI of our method is 0.8421 when $b=0$, which is 0.0948 higher than that of AE + k-means. Our D-LADMM framework further improves the NMI to 0.9349 when $b=4$. These results demonstrate the superiority of the joint learning strategy and the proposed DP structure.

Figure 3

Influence of the number of blocks on the MNIST dataset. NMI and ACC represent normalized mutual information and accuracy, respectively

7.4 Discussion for exploring applications with larger datasets

A significant consideration is the practical applicability of our method to larger datasets. While our experiments use moderate-sized datasets, it is essential to consider their potential for dealing with larger and real-world datasets. As demonstrated in the algorithm complexity section, our method surpasses existing techniques in terms of efficiency and supports incremental learning for continued training on new data. However, one computational bottleneck that remains consistent with the original SSC algorithm is the step resembling eigenvalue decomposition, with a complexity of $\text{O}(kn^{2})$, where k signifies the number of clusters and n represents the dataset size. This computational aspect could be a limitation when applied to larger datasets. Our current study primarily focuses on differentiable programming. Hence, we maintain alignment with the original SSC algorithm w.r.t. the algorithm steps.

In addressing this scalability issue for larger datasets, a promising avenue for future research would involve the replacement of graph-based spectral clustering, which exhibits second-order complexity, with an efficient first-order clustering method. This strategic change could overcome the scalability limitations observed in our current implementation and open up new possibilities for applying our method to large-scale datasets in practice.

8 Conclusions

In this paper, we propose a novel SSCNet to address the existing limitations of SSC. We first recast the optimization step of the L-ADMM as a multi-block deep neural network. We then apply this approach to the SSC problem, learning dictionary, and affinity matrix. Second, a spectral embedding network is used to approximate the eigenvalue decomposition. A general and novel differentiable eigenvector mapping layer is proposed that can be applied to other problems. Finally, we adopt a self-supervised structure to overcome the non-differentiability of k-means. Experiments validate the effectiveness of our SSCNet.

Appendices

Appendix A: Derivatives of $f(t)$

Note that

$$ f(t) = \operatorname{Tr} \bigl(\boldsymbol{Y} (t )^{ \mathrm{T}} \boldsymbol{L} \boldsymbol{Y} (t ) \bigr). $$

Hence, we have

$$ \frac{\mathrm{d} }{\mathrm{d}\boldsymbol{Y}(t)}f(t) = \boldsymbol{Y}(t)^{ \mathrm{T}} \bigl(\boldsymbol{L} + \boldsymbol{L}^{\mathrm{T}} \bigr) = 2 \boldsymbol{Y}(t)^{\mathrm{T}} \boldsymbol{L}. $$

On the other hand, we have

$$ \frac{\mathrm{d}}{\mathrm{d}t} \boldsymbol{Y}(t) = \frac{\mathrm{d}}{\mathrm{d}t} \biggl({ \boldsymbol{I}} - t{\boldsymbol{P}} + \frac{t^{2}\boldsymbol{P}^{2}}{2}\biggr) \boldsymbol{Y} = - (\boldsymbol{I} - t\boldsymbol{P} ) \boldsymbol{P}\boldsymbol{Y}. $$

1.1 A.1 First-order derivative

By the chain rule, we can easily obtain the first-order derivative $f'(t)$:

$$ f'(t) = \operatorname{Tr} \biggl( \frac{\mathrm{d} f(t) }{\mathrm{d} \boldsymbol{Y}(t)} \frac{\mathrm{d}}{\mathrm{d}t} \boldsymbol{Y}(t) \biggr) = -2 \operatorname{Tr} \bigl( \boldsymbol{Y}(t)^{\mathrm{T}} \boldsymbol{L} (\boldsymbol{I} -t\boldsymbol{P} ) \boldsymbol{P} \boldsymbol{Y} \bigr). $$

Recall that

$$ \boldsymbol{P} = \boldsymbol{G}\boldsymbol{Y}^{\mathrm{T}} - \boldsymbol{Y} \boldsymbol{G}^{\mathrm{T}},\quad \boldsymbol{G} = 2 \boldsymbol{L} \boldsymbol{Y}. $$

Then, we can obtain

$$ f'(0) = -2 \operatorname{Tr} \bigl(\boldsymbol{Y}^{\mathrm{T}} \boldsymbol{L} \boldsymbol{P} \boldsymbol{Y} \bigr). $$

1.2 A.2 Second-order derivative

We have

$$\begin{aligned} f''(t) &= \frac{\mathrm{d} f'(t)}{\mathrm{d} t} \\ &=-2\operatorname{Tr} \biggl( \biggl(\frac{\mathrm{d}}{\mathrm{d}t} \boldsymbol{Y}(t) \biggr)^{\mathrm{T}} \boldsymbol{L} ( \boldsymbol{I} -t \boldsymbol{P} ) \boldsymbol{P}\boldsymbol{Y} \\ &\quad {}- \boldsymbol{Y}(t)^{\mathrm{T}}\boldsymbol{L}\boldsymbol{P}^{2} \boldsymbol{Y} \biggr) \\ &=2\operatorname{Tr} \bigl(({\boldsymbol{I}} -t{\boldsymbol{P}}) \boldsymbol{P} \boldsymbol{Y}\bigr)^{\mathrm{T}} \boldsymbol{L} ( \boldsymbol{I} -t \boldsymbol{P} )\boldsymbol{P}\boldsymbol{Y} \\ &\quad {}+\boldsymbol{Y}(t)^{\mathrm{T}}\boldsymbol{L}\boldsymbol{P}^{2} \boldsymbol{Y} ). \end{aligned}$$

Hence, we can further obtain

$$ f''(0) = 2\operatorname{Tr} \bigl(- \boldsymbol{Y}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{L} \boldsymbol{P} \boldsymbol{Y} + \boldsymbol{Y}^{\mathrm{T}}\boldsymbol{L}\boldsymbol{P}^{2} \boldsymbol{Y} \bigr). $$

We finish the calculation.

Appendix B: Proof of Proposition 1

Due to the skew-symmetry of P, we can obtain

$$ \boldsymbol{Y}(t)^{\mathrm{T}} = \Biggl(\boldsymbol{I} + \sum _{i=1}^{r} 2^{-\frac{ (i-1 )i}{2}}(-1)^{i+1} (t \boldsymbol{P} )^{i} \Biggr) \boldsymbol{Y}, $$

then, we can verify that

$$ \bigl(\boldsymbol{Y} (t ) \bigr)^{\mathrm{T}} \boldsymbol{Y} (t ) = \boldsymbol{Y}^{\mathrm{T}} \bigl({\boldsymbol{I}} + 2^{-r(r-1)} t^{2r} {\boldsymbol{P}}^{2r}\bigr) \boldsymbol{Y}. $$

We can see that all the terms with a degree less than $2^{r}$ have zero coefficients. The optimality is obvious. Moreover, when P is bounded, we can obtain

$$ \bigl\Vert \boldsymbol{Y}^{\mathrm{T}}\bigl( 2^{-r(r-1)} t^{2r} {\boldsymbol{P}}^{2r}\bigr)\boldsymbol{Y} \bigr\Vert = \mathrm{O}\bigl(2^{-r(r-1)}t^{2r}\bigr). $$

We now finish the proof.

Appendix C: Proof of Proposition 2

From Eq. (19), we have

$$ \frac{\mathrm{d}}{\mathrm{d}t} \boldsymbol{Y}(t) = \Biggl( - \boldsymbol{P}+ \sum _{i=2}^{r} 2^{-\frac{ (i-1 )i}{2}}i (-\boldsymbol{P} )^{i}t^{i-1} \Biggr) \boldsymbol{Y}. $$

We denote by

$$ \boldsymbol{R} = \Biggl(\sum_{i=2}^{r} 2^{-\frac{ (i-1 )i}{2}}i (-{\boldsymbol{P}} )^{i}t^{i-1}\Biggr). $$

Due to the skew symmetry of P, we have $\boldsymbol{R} = -\boldsymbol{R}^{\mathrm{T}}$. Then

$$ (-{\boldsymbol{P}} + {\boldsymbol{R}})^{\mathrm{T}} = {\boldsymbol{P}} - { \boldsymbol{R}}. $$

We now project $\frac{\mathrm{d}}{\mathrm{d}t} \boldsymbol{Y}(t)$ to the tangent space of Y

$$ \begin{aligned} \mathcal{P}_{\mathcal{T}_{\boldsymbol{Y}}} \bigl( \dot{ \boldsymbol{Y}} (t ) \bigr) &=\dot{\boldsymbol{Y}}(t) - \boldsymbol{Y}\bigl(\dot{ \boldsymbol{Y}}(t)\bigr)^{\mathrm{T}} \boldsymbol{Y} \\ &= (-{\boldsymbol{P}} {\boldsymbol{Y}} + {\boldsymbol{R}} {\boldsymbol{Y}}) - \boldsymbol{Y} \bigl({\boldsymbol{Y}}^{\mathrm{T}} {\boldsymbol{P}} - { \boldsymbol{Y}}^{\mathrm{T}}{\boldsymbol{R}}\bigr) \boldsymbol{Y} \\ &= \bigl({\boldsymbol{I}} + {\boldsymbol{Y}} {\boldsymbol{Y}}^{\mathrm{T}} \bigr) (-{\boldsymbol{P}} {\boldsymbol{Y}}) + \mathcal{P}_{\boldsymbol{Y}}^{ \perp }({ \boldsymbol{R}} {\boldsymbol{Y}}). \end{aligned} $$

Note that we already have

$$ \mathcal{P}_{\mathcal{T}_{\boldsymbol{Y}}} (-\boldsymbol{G} ) = -\boldsymbol{P}\boldsymbol{Y}. $$

Then we obtain

$$ \begin{aligned} & \bigl\langle \mathcal{P}_{\mathcal{T}_{\boldsymbol{Y}}} \bigl(\dot{ \boldsymbol{Y}} (t ) \bigr), \mathcal{P}_{\mathcal{T}_{\boldsymbol{Y}}} (-\boldsymbol{G} ) \bigr\rangle _{ \mathrm{c}} \\ &\quad = \operatorname{Tr}\bigl({\mathcal{P}}_{\mathcal{T}_{\boldsymbol{Y}}} (-{\boldsymbol{G}} ) {\mathcal{P}}_{\boldsymbol{Y}}^{\perp}{\mathcal{P}}_{\mathcal{T}_{\boldsymbol{Y}}} \bigl( \dot{\boldsymbol{Y}} (t ) \bigr)\bigr) \\ &\quad = \operatorname{Tr}\bigl(-{\boldsymbol{Y}}^{\mathrm{T}}{ \boldsymbol{P}}^{\mathrm{T}} {\mathcal{P}}_{\boldsymbol{Y}}^{\perp } (-{ \boldsymbol{P}} {\boldsymbol{Y}} + {\boldsymbol{R}} {\boldsymbol{Y}})\bigr) \\ &\quad = \Vert \boldsymbol{P}\boldsymbol{Y} \Vert _{\mathrm{c}} - \langle \boldsymbol{P}\boldsymbol{Y},\boldsymbol{R}\boldsymbol{Y} \rangle_{ \mathrm{c}}. \end{aligned} $$

Hence, it is obvious that when

$$ \|\mathcal{P}_{Y}^{\perp}({\boldsymbol{R}}) \|_{F} < \|\mathcal{P}_{Y}^{\perp}({\boldsymbol{P}}) \|_{F}:= c_{p}, $$

(C.1)

we have

$$ \bigl\langle \mathcal{P}_{\mathcal{T}_{\boldsymbol{Y}}} \bigl(\dot{\boldsymbol{Y}} (t ) \bigr), \mathcal{P}_{\mathcal{T}_{\boldsymbol{Y}}} (-\boldsymbol{G} ) \bigr\rangle _{ \mathrm{c}}>0. $$

Then, we obtain

$$ \begin{aligned}& \|\mathcal{P}_{Y}^{\perp}({ \boldsymbol{R}})\|_{F} \\ &\quad = \Biggl\Vert \sum _{i=2}^{r} 2^{-\frac{ (i-1 )i}{2}}i \bigl(- \mathcal{P}_{Y}^{\perp}({\boldsymbol{P}}) \bigr)^{i}t^{i-1} \Biggr\Vert \\ &\quad \leq \sum_{i=2}^{r} 2^{-\frac{ (i-1 )i}{2}}ic_{p}^{i}t^{i-1} \leq c_{p}\sum_{i=2}^{r} 2^{-\frac{i^{2}}{4}}i(c_{p}t)^{i-1} \\ &\quad \leq c_{p} \int _{2}^{\infty }2^{-\frac{x^{2}}{4}}x(c_{p}t)^{x-1} \mathrm{d} x \\ &\quad = c_{p} \cdot g(t)\cdot \biggl(1-\operatorname{erf} \biggl( \frac{2\ln 2-2\ln t}{2\sqrt{\ln 2}} \biggr)\biggr) + \frac{t}{\ln 2}, \end{aligned} $$

(C.2)

where the last step is given in the following section, $\rho _{t} = c_{p} t$ and

$$ g(t) := \frac {2\sqrt{{ \uppi }}\exp(\frac{\ln ^{2}t}{\ln 2})\ln t}{t\ln ^{\frac{3}{2}}2}. $$

A necessary condition for the inequality in Eq. (C.1) is

$$ g(t) \cdot \biggl(1-\operatorname{erf} \biggl(\frac{2\ln 2-2\ln t}{2\sqrt{\ln 2}} \biggr)\biggr) + \frac{t}{\ln 2} < 1, $$

which implies the condition in Proposition 2. We finish the proof.

3.1 C.3 Integral calculations for Eq. (C.2)

We have

$$ \int \frac {xt^{x-1}}{2^{\frac{x^{2}}{4}}} \mathrm{d} x = \frac{1}{t} \int \frac {xt^{x}}{2^{\frac{x^{2}}{4}}} \mathrm{d} x. $$

Note that

$$ \frac{\mathrm{d}t^{x}}{\mathrm{d}x} = \ln(t) t^{x},\quad \int \frac {x}{2^{\frac{x^{2}}{4}}} \mathrm{d} x = - \frac{2^{1-\frac{x^{2}}{4}}}{\ln 2}. $$

Integrating by parts, we obtain

$$ \int \frac {xt^{x}}{2^{\frac{x^{2}}{4}}} \mathrm{d} x =- \frac {t^{x}{\cdot}2^{1-\frac{x^{2}}{4}}}{\ln 2}+ { \frac {2\ln t}{\ln 2}} { \int}\frac {t^{x}}{2^{\frac{x^{2}}{4}}} \mathrm{d} x. $$

Now, we aim to solve the following

$$ \begin{aligned} { \int}\frac {t^{x}}{2^{\frac{x^{2}}{4}}} \mathrm{d} x &= { \int} \exp\biggl(\ln tx-\frac{\ln 2x^{2}}{4}\biggr) \mathrm{d} x \\ &= { \int} \exp\biggl(\frac{\ln ^{2} t}{\ln 2}- \biggl(\frac{\sqrt{\ln 2}x}{2}- \frac{\ln t}{\sqrt{\ln 2}} \biggr)^{2}\biggr) \mathrm{d} x. \end{aligned} $$

We substitute

$$ u=\frac {\ln 2x-2\ln t}{2\sqrt{\ln 2}}, $$

then we have

$$ \begin{aligned} \int\frac {t^{x}}{2^{\frac{x^{2}}{4}}} \mathrm{d} x &= { \int} \frac {2\exp(\frac{\ln ^{2} t}{\ln 2}-u^{2})}{\sqrt{\ln 2}} \mathrm{d} u \\ &={\frac {\sqrt{{ \uppi }}\exp(\frac{\ln ^{2} t}{\ln 2})}{\sqrt{\ln 2}}} { \int}\frac {2\exp(-u^{2})}{\sqrt{{ \uppi }}} \mathrm{d} u \\ &= \frac{\sqrt{{ \uppi }}\exp(\frac{\ln ^{2} t}{\ln 2})\operatorname{erf} (u)}{\sqrt{\ln 2}} \\ &= \frac{\sqrt{{ \uppi }}\exp(\frac{\ln ^{2} t}{\ln 2})\operatorname{erf} (\frac{\ln 2x-2\ln t}{2\sqrt{\ln 2}} )}{\sqrt{\ln 2}}. \end{aligned} $$

Then, we can conclude that

$$\begin{aligned} \int \frac {xt^{x-1}}{2^{\frac{x^{2}}{4}}} \mathrm{d} x &= - \frac {t^{x}{\cdot}2^{1-\frac{x^{2}}{4}}}{t\ln 2} \\ &\quad {}+ {\frac {2\ln t}{t\ln 2}} \frac{\sqrt{{ \uppi }}\exp(\frac{\ln ^{2} t}{\ln 2})\operatorname{erf} (\frac{\ln 2x-2\ln t}{2\sqrt{\ln 2}} )}{\sqrt{\ln 2}} \\ &= \frac {2\sqrt{{ \uppi }}\exp(\frac{\ln ^{2} t}{\ln 2})\ln t\operatorname{erf} (\frac{\ln 2x-2\ln t}{2\sqrt{\ln 2}} )}{t\ln ^{\frac{3}{2}} (2 )}\\ &\quad {}- \frac {t^{x-1}{\cdot}2^{1-\frac{x^{2}}{4}}}{\ln 2}. \end{aligned}$$

Due to

$$ \frac {t^{x-1}{\cdot}2^{1-\frac{x^{2}}{4}}}{\ln 2} \to 0,\quad \text{as } \vert {x} \vert \to \infty , $$

we have

$$ \begin{aligned} \int _{\infty}^{\infty } \frac {xt^{x-1}}{2^{\frac{x^{2}}{4}}} \mathrm{d} x &= g(t)\operatorname{erf} \biggl(\frac{\ln 2x-2\ln t}{2\sqrt{\ln 2}} \biggr)\bigg|_{2}^{ \infty} \\ &= g(t) \biggl(1-\operatorname{erf} \biggl(\frac{2\ln 2-2\ln t}{2\sqrt{\ln 2}} \biggr)\biggr) + \frac{t}{\ln 2}, \end{aligned} $$

where

$$ g(t) := \frac {2\sqrt{{ \uppi }}\exp(\frac{\ln ^{2} t}{\ln 2})\ln t}{t\ln ^{\frac{3}{2}} (2 )}. $$

We have now finished the calculation.