1 Introduction

Grinding is usually utilized as a final processing step to ensure the surface quality of the workpiece quality. Its competitiveness in processing high-quality surface quality workpiece and hard-brittle material is almost ahead of all other machining processes. Therefore, it is widely used variously in the industrial field. If the grinding process can be improved in terms of improving productivity, optimizing workpiece quality, and achieving high energy efficiency, it will undoubtedly promote technological progress [1].

At present, grinding technology is developing towards high-speed, efficient, high-precision, and green grinding. During the grinding process, the vast majority of the heat generated by the interaction between the grinding wheel and the workpiece is transferred into the workpiece, which can easily affect workpiece surface quality, causing thermal damage such as surface burns and cracks. If the grinding depth is large, secondary quenching may also occur. For processed workpiece, they only meet the design requirements in terms of geometric dimensions and accuracy, but the mechanical performance has not arrived at the criterion. Therefore, heat treatment is generally required to improve the hardness, strength, and other properties of the processed workpiece. During the heat treatment process, waste liquid and other pollutants generate, which is not helpful for environmental protection. Therefore, applying grinding genearated heat to the subsequent heat treatment process to reduce resource waste and environmental pollution is a good improvement method. Brinksmeier et al. proposed the grinding hardening and designed experiments to verify this machining process [2]. This method combines grinding strategy and heat treatment, utilizing heat in the workpiece machining process, and thus reducing the production cost of the workpiece [3]. Zarudi et al. conducted grinding hardening tests on tempered AISI4140 steel and found that the properties of the workpiece were significantly improved after grinding hardening [4].

The above researches indicate that the grinding hardening technology is with a good development prospects. The grinding force and the grinding temperature are two key factors affecting its surface strengthening effect and processing quality. Research should be carried out on grinding thermo-mechanical coupling processing. The prediction of grinding force during the machining process has always been a hot research topic for scholars, and has very important theoretical significance and application value, which is considered to be an important factor affecting grinding performance, wheel shape durability, workpiece surface quality, and process system deformation [5]. Currently, researchers have established mathematic models to predict grinding forces during the machining process. Werner et al. derived a grinding force equation with two structural coefficients, which can be adjusted to explain the chip formation force and sliding friction force [6]. It is generally believed that grinding force includes three parts: sliding force, plowing force, and cutting force. Therefore, Younis et al. proposed a model that includes sliding force, plowing force, and cutting force [7]. And Zhou et al. established a prediction model for ultrasonic vibration assisted grinding force, and derived an analytical expression for chip formation force based on Rayleigh probability density function, friction force, and griffith theory of abrasive fracture force [8].

The above research analyzed the changes in grinding force during the machining process by establishing a model. Moreover, the study of single abrasive grinding can better reveal the characteristics of grinding processing. Durgumahanti et al. proposed a mathematical model of the single abrasive grinding force with three stages and conducted experimental measurements [9]. Zhang et al. divided the grinding surface into three grinding zones: main grinding zone, plowing grinding zone, and sliding friction grinding zone. Then, a single abrasive grinding force model was established under different material removal methods, and the grinding force model of the entire grinding wheel was established considering the influence of size [10].

However, most of the abrasive particles are simplified to the same geometric shape to study grinding force and grinding heat. In actual machining, the shape, size, and position of the abrasive particles on the surface of the grinding wheel are irregularly distributed. Therefore, there is a significant error between the analysis results obtained by this simplified research method and the actual situation. Besides, the heat generated during the grinding process causes the workpiece surface temperature increase, and the distribution of grinding temperature is closely related to the performance of the workpiece. At present, in order to accurately calculate grinding heat and avoid thermal damage, various thermal models have been established to predict workpiece temperature [11].

DesRuisseaux et al. established a mathematical model for convective heat transfer and a temperature field distribution model based on the Jaeger moving heat source basic heat transfer model, taking into account the convective heat transfer effect during grinding [12]. Compared to rectangular heat sources, triangular heat sources are more in line with the actual situation in the machining process. Rowe et al. regarded the contact area between the grinding wheel and the workpiece as a moving heat source with oblique linear increase, showing that the grinding depth cannot be ignored as in small cutting depth grinding, so the contact area between the grinding wheel and the workpiece cannot be assumed to be horizontally distributed [13]. In addition to the above temperature field distribution research, Zerkle et al. described the heat transfer into the coolant by using a uniformly distributed convective heat transfer coefficient across the entire surface of the workpiece [12]. Hou et al. proposed a microscale thermal model considering the statistics of abrasive particle distribution on the wheel surface, and verified the accuracy and progressiveness of the model through experiments [14]. More in-depth research has been conducted on the grinding temperature field, but most of the consideration is to analyze the entire grinding contact zone as a heat source. However, in actual machining, a single abrasive contact zone corresponds to a point thermal source. These point thermal sources constitutes the temperature field. So the abrasive shape-position characteristic affects the grinding temperature accordingly.

This article models the grinding force based on the different shape and position characteristics of abrasive particles. The single abrasive grinding force analysis model is coupled to the temperature field model to study the temperature field distribution. Based on the obtained single abrasive grinding force and temperature fields, this paper proposes to study the influence of different abrasive shape and position feature ratios on the grinding thermal coupling process, providing valuable research basis for engineering practice.

2 Modeling of single abrasive grinding force with shape characteristic

In this section, analytical model of single abrasive grinding force is established based on different shape and position characteristics of abrasives. The grinding force of single abrasive grit and the total grinding force of contact zone are calculated by combining three grinding processes and the undeformed chip thickness.

2.1 Modeling of a single abrasive grinding force

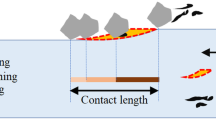
As shown in Fig. 1, it is widely accepted that the grinding process can be divided into rubbing, plowing and cutting stages [15]. When establishing an analytical model for single abrasive grit grinding force, the single abrasive grit grinding force is divided into three parts: sliding friction force, plowing force, and cutting force. The analytical model for a single shape abrasive grinding force is verified by our former research [1].

Fig. 1
figure 1

Grinding process between the workpiece and the abrasive

Full size image

The sliding force is caused by the elastic deformation between the abrasive particles and the workpiece, and it also changes with the wear of the abrasive particles [16]. This paper proposes an analytical method for estimating normal and tangential stresses in the wear plane region based on the Waldorf model for predicting cutting forces through tool wear [17]. The expression for the sliding force of a single abrasive particle is as follows:

$$\begin{gathered} {F_{{\text{rt}}}} = b\int_0^L {{\tau_{\text{W}}}(x){\text{d}}x} \hfill \\ {F_{{\text{rn}}}} = b\int_0^L {{\sigma_{\text{W}}}(x){\text{d}}x} \hfill \\ \end{gathered}$$
(1)

Where, \(b\) is contact width between abrasive particle and workpiece. \(L\) is width of abrasive wear zone. \({\tau_{\text{w}}}\) is tangential stress in abrasive wear zone. \({\sigma_{\text{w}}}\) is normal stress in abrasive wear zone.

$$\left\{ \begin{array}{lll} {\tau_{\text{w}}}(x) = {\tau_0} &0 < x < L(1 - \sqrt {{\tau_0}/{\sigma_0}} ) \hfill \\ {\tau_{\text{w}}}(x) = \mu {\sigma_{\text{w}}}(x) & L(1 - \sqrt {{\tau_0}/{\sigma_0}} ) < x < L \hfill \\ {\sigma_{\text{w}}}(x) = {\sigma_0}{[(L - x)/L]^2} & 0 < x < L \hfill \\ \end{array} \right.$$
(2)
$$\left\{ \begin{array}{lll} {\tau_0} = k\cos (2\gamma - 2\phi ) \hfill \\ {\sigma_0} = k[1 + \frac{{\uppi }}{2} - 2\rho - 2\phi + 2\gamma + \sin (2\gamma - 2\phi )] \hfill \\ \gamma = {\eta_{\text{p}}} + \varphi - {\sin^{ - 1}}(\sqrt 2 \sin (\rho )\sin ({\eta_{\text{p}}})) \hfill \\ {\eta_{\text{p}}} = 0.5{\cos^{ - 1}}(\mu ) \hfill \\ \phi = \frac{{\uppi }}{4} - \frac{\beta }{2} + \frac{\alpha }{2} \hfill \\ k = \frac{Y}{\sqrt 3 } \hfill \\ \end{array} \right.$$
(3)

Where, \(\rho\) is the angle between the unprocessed raised part and the horizontal plane caused by the radius of the abrasive head. \(\phi\) is the abrasive shear angle. \(\mu\) is the frictional coefficient. \(k\) is the shear flow stress of workpiece material. \(Y\) is the yield stress of workpiece material.

The plowing force generates when the abrasive particles interact with the workpiece and cause the elastic–plastic deformation. Before chips are formed, the force generates when the abrasive particles plow on the surface of the workpiece and can be calculated by considering the scratch hardness and the geometric relationship between the abrasive particles and the workpiece contact:

$$\left\{ \begin{gathered} {F_{{\text{pt}}}} = {H_s}S \hfill \\ {F_{{\text{pn}}}} = \frac{{{H_s}S}}{\mu } \hfill \\ \end{gathered} \right.$$
(4)

Where, \({H_s}\) is the scratch hardness of workpiece. \(S\) is contact area between abrasive particles and workpiece. \(\mu\) is frictional coefficient.

The critical undeformed chip thickness at which abrasive particles transition from plowing to cutting during the grinding process is called the minimum undeformed chip thickness [18]. In the process of single abrasive grinding, when the undeformed chip thickness is greater than the minimum undeformed chip thickness, it is in the cutting stage and comes to be cutting force. Therefore, considering the geometric relationship between the contact area of the abrasive and the workpiece, the cutting force in single abrasive grinding can be calculated by applying the Merchant model and the expression is as follows [19]:

$$\left\{ \begin{array}{ll} {\text{d}}{F_{{\text{ct}}}} = \frac{\tau \cos (\beta - \alpha )}{{\sin (\frac{{\uppi }}{4} - \frac{\beta - \alpha }{2})\cos (\frac{{\uppi }}{4} + \frac{\beta - \alpha }{2})}}{\text{d}}s \hfill \\ {\text{d}}{F_{{\text{cn}}}} = {\text{d}}{F_{{\text{ct}}}}\tan (\beta - \alpha ) \hfill \\ \end{array} \right.$$
(5)

Where, \(\tau\) is material flow stress. \(\beta\) is friction angle. \(\alpha\) is abrasive front angle. \(\mathrm{d}_s\) is contact area microelement.

2.2 Modeling of a single abrasive grinding force on different shapes

The grinding wheel is composed of abrasive particles, binders, and pores. Due to the unique production method of abrasive particles, the geometric shape of any two abrasive particles is generally different. With the help of the Olympus ultra depth of field digital microscope, it can be found that three major shape abrasive is observed in the microscopic field of view, namely the spherical shape, the conical shape and the pyramidal shape. The paper utilizes the validated single shape abrasive grinding force, and is extended to other shape abrasive grinding with the geometric shape variation. Therefore, simplified modeling of the geometric shape of abrasive particles should be carried out.

Based on the three stages of single abrasive grinding, the typical abrasive geometry is modeled by adding a wear zone at the bottom of the abrasive. In terms of the pyramid shaped abrasive, the machining process is correlated to the edge number of the paramid, such as triangular pyramid, the rectangular pyramid and etc. So the deduced formular is correlated to the edge number n. For pyramid shaped abrasive grains, the variation law of the grinding force with the number of edges n is derived. As shown in Fig. 2, the abrasive geometric modeling is established in this paper.

Fig. 2
figure 2

Modified geometry of abrasive grits

Full size image

Considering the geometric structure of the contact area and the geometric shape characteristics of spherical abrasive, a single abrasive grinding force analytical model is derived. The expression for the sliding force of a single spherical abrasive particle is as follows:

$$\left\{ \begin{gathered} {F_{{\text{rt}}}} = 2r\sqrt {1 - {{( - \frac{{h - {t_i}}}{r})}^2}} \int_0^L {{\tau_{\text{W}}}(x)} {\text{d}}x \hfill \\ {F_{\text{m}}} = 2r\sqrt {1 - {{( - \frac{{h - {t_i}}}{r})}^2}} \int_0^L {{\sigma_{\text{W}}}(x)} {\text{d}}x \hfill \\ \end{gathered} \right.$$
(6)

The expression for the plowing force of a single spherical abrasive particle is as follows:

$$\left\{ \begin{gathered} {F_{{\text{pt}}}} = {H_s}{t_i}\left[ {\frac{L}{2} + r\sqrt {1 - {{( - \frac{{h - {t_i}}}{r})}^2}} } \right] \hfill \\ {F_{{\text{pn}}}} = \frac{{{H_s}{t_i}}}{\mu }\left[ {\frac{L}{2} + r\sqrt {1 - {{( - \frac{{h - {t_i}}}{r})}^2}} } \right] \hfill \\ \end{gathered} \right.$$
(7)

The expression for the cutting force of a single spherical abrasive particle is as follows:

$$\begin{gathered} {F_{{\text{ct}}}} = \int_{{t_{{\text{cr}}}}}^{{t_{\text{m}}}} {\frac{{\tau \cos ({\beta_i} - {\alpha_i})}}{{\sin (\frac{{\uppi }}{4} - \frac{{{\beta_i} - {\alpha_i}}}{2})\cos (\frac{{\uppi }}{4} + \frac{{{\beta_i} - {\alpha_i}}}{2})}}2r\sqrt {1 - {{( - \frac{{h - {t_i}}}{r})}^2}{\text{d}}t} } \hfill \\ {F_{{\text{cn}}}} = \int_{{t_{{\text{cr}}}}}^{{t_{\text{m}}}} {\frac{{\tau \sin ({\beta_i} - {\alpha_i})}}{{\sin (\frac{{\uppi }}{4} - \frac{{{\beta_i} - {\alpha_i}}}{2})\cos (\frac{{\uppi }}{4} + \frac{{{\beta_i} - {\alpha_i}}}{2})}}2r\sqrt {1 - {{( - \frac{{h - {t_i}}}{r})}^2}{\text{d}}t} } \hfill \\ \end{gathered}$$
(8)
$$\left\{ \begin{array}{ll} {\alpha_i} = - {\sin^{ - 1}}(\frac{{h - {t_i}}}{r}) \hfill \\ \beta = {\tan^{ - 1}}\mu \hfill \\ h = \sqrt {{r^2} - {{(\frac{L}{2})}^2}} \hfill \\ \end{array} \right.$$
(9)

Where, \(r\) is radius of spherical abrasive. \({t_i}\) is the thickness of undeformed chips. \({t_{cr}}\) is the minimum undeformed chip thickness. \(L\) is the width of abrasive wear zone. \({\tau_w}\) is the tangential stress in abrasive wear zone. \({\sigma_w}\) is the normal stress in abrasive wear zone. \({H_S}\) is the scratch hardness of workpiece. \(\mu\) is the frictional coefficient. The workpiece material properties are considered in the above material parameters. Meanwhile, the force formation owes to the sliding, plowing and rubbing effect of the workpiece material removal process.

Considering the geometric structure and the geometric shape characteristic of conical abrasive particles, a single abrasive grinding force analytical model is derived. Due to the unique geometric shape of conical abrasive grains, the analytical model of cutting force is divided into two parts for calculation. The expression for the sliding force of a single conical abrasive particle is as follows:

$$\left\{ \begin{gathered} {F_{{\text{rt}}}} = b\int_0^L {{\tau_{\text{W}}}(x){\text{d}}x} \hfill \\ {F_{{\text{rn}}}} = b\int_0^L {{\sigma_{\text{W}}}(x){\text{d}}x} \hfill \\ \end{gathered} \right.$$
(10)
$$b = \left\{ \begin{array}{ll} 2r\sqrt {1 - {{( - \frac{{h - {t_i}}}{r})}^2}} &0 < {t_i} < {t_{{\text{nom}}}} \hfill \\ 2(r\cos {\alpha_{{\text{nom}}}} + ({t_i} - {t_{{\text{nom}}}})\tan ( - {\alpha_{{\text{nom}}}})) &{t_i} > {t_{{\text{nom}}}} \hfill \\ \end{array} \right.$$
(11)

The expression for the plowing force of a single conical abrasive particle is as follows:

$$\left\{ \begin{gathered} {F_{{\text{pt}}}} = {H_s}{t_i}[\frac{L}{2} + r\sqrt {1 - {{( - \frac{{h - {t_i}}}{r})}^2}} ] \hfill \\ {F_{{\text{pn}}}} = \frac{{{H_s}{t_i}}}{\mu }[\frac{L}{2} + r\sqrt {1 - {{( - \frac{{h - {t_i}}}{r})}^2}} ] \hfill \\ \end{gathered} \right.$$
(12)

The expression for the cutting force of a single conical abrasive particle is as follows:

$$\begin{array}{*{20}{c}} {\left\{ \begin{gathered} {F_{{\text{ct}}}} = \int_{{t_{{\text{cr}}}}}^{{t_{\text{m}}}} {\frac{{\tau \cos ({\beta_i} - {\alpha_i})}}{{\sin (\frac{{\uppi }}{4} - \frac{{{\beta_i} - {\alpha_i}}}{2})\cos (\frac{{\uppi }}{4} + \frac{{{\beta_i} - {\alpha_i}}}{2})}}} \hfill \\ {{\text{F}}_{{\text{cn}}}} = \int_{{t_{{\text{cr}}}}}^{t_m} {\frac{{\tau \sin ({\beta_i} - {\alpha_i})}}{{\sin (\frac{{\uppi }}{4} - \frac{{{\beta_i} - {\alpha_i}}}{2})\cos (\frac{{\uppi }}{4} + \frac{{{\beta_i} - {\alpha_i}}}{2})}}} \hfill \\ \end{gathered} \right.}&{{t_{{\text{cr}}}} < {t_i} < {t_{{\text{nom}}}}} \end{array}$$
(13)
$$\left\{\begin{array}{ll}F_{ct}=\begin{array}{ll}\int_{t_{cr}}^{t_{nom}}\frac{\tau\cos\left(\beta_{i}-\alpha_{i}\right)} {\sin\left(\frac{\uppi}{4}-\frac{\beta_{i}-\alpha_{i}}{2}\right)\cos\left(\frac{\uppi}{4}-\frac{\beta_{i}-\alpha_{i}}{2}\right)}2r\sqrt{1-\left(-\frac{h-t_{i}}{r}\right)^2\text{d}t+}\\\int^{t_m}_{t_{nom}}\frac{\tau\cos\left(\beta_i-\alpha_\mathrm{nom}\right)}{\sin\left(\frac{\uppi}{4}-\frac{\beta_{i}-\alpha_\mathrm{nom}}{2}\right)\cos\left(\frac{\uppi}{4}-\frac{\beta_{i}-\alpha_\mathrm{nom}}{2}\right)}2\left(r\cos\alpha_\mathrm{nom}+\left(t-t_\mathrm{nom}\right)\tan\left(-\alpha_\mathrm{nom}\right)\right)\text{d}t\end{array}\\F_{cn}=\begin{array}{ll}\int_{t_{cr}}^{t_{nom}}\frac{\tau\sin\left(\beta_{i}-\alpha_{i}\right)} {\sin\left(\frac{\uppi}{4}-\frac{\beta_{i}-\alpha_{i}}{2}\right)\cos\left(\frac{\uppi}{4}-\frac{\beta_{i}-\alpha_{i}}{2}\right)}2r\sqrt{1-\left(-\frac{h-t_{i}}{r}\right)^2\text{d}t+}\\\int^{t_m}_{t_{nom}}\frac{\tau\sin\left(\beta_i-\alpha_\mathrm{nom}\right)}{\sin\left(\frac{\uppi}{4}-\frac{\beta_{i}-\alpha_\mathrm{nom}}{2}\right)\cos\left(\frac{\uppi}{4}-\frac{\beta_{i}-\alpha_\mathrm{nom}}{2}\right)}2\left(r\cos\alpha_\mathrm{nom}+\left(t-t_\mathrm{nom}\right)\tan\left(-\alpha_\mathrm{nom}\right)\right)\text{d}t\end{array}\end{array}\right.t_{i}>t_\mathrm{nom}$$
(14)
$$\left\{ \begin{array}{llll} {\alpha_i} = - {\sin^{ - 1}}\frac{{h - {t_i}}}{r} \hfill \\ {\alpha_{{\text{nom}}}} = - {\sin^{ - 1}}\frac{{h - {t_{{\text{nom}}}}}}{r} \hfill \\ \beta = {\tan^{ - 1}}\mu \hfill \\ h = \sqrt {{r^2} - {{(\frac{L}{2})}^2}} \hfill \\ \end{array} \right.$$
(15)

When analyzing and modeling the grinding force of pyramidal abrasive particles in this paper, the pyramidal abrasives with wear zones are placed in a ball body for ease of modeling.

Considering the geometric shape characteristics of pyramidal abrasive particles and geometric analysis of the contact area, a single abrasive grinding force analytical model with the number of edges as the independent variable is derived. When the number of edges is greater than 4, the derived analytical model for single abrasive grinding force shows a significant difference. Therefore, the analytical model for pyramid grinding force is divided into two parts according to the number of edges. The expression for the sliding force of a single pyramidal abrasive particle is as follows:

$$\begin{gathered}{F_{{\text{rt}}}} = \left\{ {2{R_{\text{b}}}\sin (\frac{{\uppi }}{n}) + \frac{{{t_i}\left[ {2{R_{\text{a}}}\sin (\frac{{\uppi }}{n}) - 2{R_{\text{b}}}\sin (\frac{{\uppi }}{n})} \right]}}{h}} \right\}\int_0^L {{\tau_{\text{w}}}(x){\text{d}}x}\hfill n = 3,4\\\hfill \end{gathered}$$
(16)
$$\begin{gathered}{F_{{\text{rn}}}} = \left\{ {2{R_{\text{b}}}\sin (\frac{{\uppi }}{n}) + \frac{{{t_i}\left[ {2{R_{\text{a}}}\sin (\frac{{\uppi }}{n}) - 2{R_{\text{b}}}\sin (\frac{{\uppi }}{n})} \right]}}{h}} \right\}\int_0^L {{\sigma_{\text{w}}}(x){\text{d}}x}\hfill n = 3,4\hfill \\ \end{gathered}$$
(17)
$$\begin{array}{ll} {F_{{\text{rt}}}} = \left\{ \begin{array}{ll} 4{R_{\text{b}}}\sin (\frac{{\uppi }}{n})\left[ {\frac{1}{2} + \sum\limits_{i = 1}^{\text{m}} {{{( - 1)}^i}\cos (i\theta )} } \right] + \hfill \\ {t_i}\left[ {4{R_a}\sin (\frac{{\uppi }}{n})(\frac{1}{2} + \sum\limits_{i = 1}^{\text{m}} {{{( - 1)}^i}\cos (i\theta )} ) - 4{R_{\text{b}}}\sin (\frac{{\uppi }}{n})(\frac{1}{2} + \sum\limits_{i = 1}^{\text{m}} {{{( - 1)}^i}\cos (i\theta )} )} \right] \hfill \\ \end{array} \right\} \hfill \\ \mathop {}\nolimits \times \int_0^L {{\tau_{\text{w}}}(x){\text{d}}x} \mathop {}\limits n > 4 \hfill \\ \end{array}$$
(18)
$$\begin{array}{ll} {F_{{\text{rn}}}} = \left\{ \begin{array}{ll} 4{R_{\text{b}}}\sin (\frac{{\uppi }}{n})\left[ {\frac{1}{2} + \sum\limits_{i = 1}^{\text{m}} {{{( - 1)}^i}\cos (i\theta )} } \right] + \hfill \\ {t_i}\left[ {4{R_a}\sin (\frac{{\uppi }}{n})(\frac{1}{2} + \sum\limits_{i = 1}^{\text{m}} {{{( - 1)}^i}\cos (i\theta )} ) - 4{R_{\text{b}}}\sin (\frac{{\uppi }}{n})(\frac{1}{2} + \sum\limits_{i = 1}^{\text{m}} {{{( - 1)}^i}\cos (i\theta )} )} \right] \hfill \\ \end{array} \right\} \hfill \\ \mathop {}\nolimits \times \int_0^L {{\sigma_{\text{w}}}(x){\text{d}}x\mathop {}\limits } n > 4 \hfill \\ \end{array}$$
(19)

The expression for the plowing force of a single pyramidal abrasive particle is as follows:

$$\left\{ \begin{array}{ll} {F_{{\text{pt}}}} = {H_s}{t_i}\left\{ {\frac{{2{R_{\text{a}}}\sin (\frac{{\uppi }}{n}) - 2{R_{\text{b}}}\sin (\frac{{\uppi }}{n})}}{2h}} \right\} \hfill \\ {F_{{\text{pn}}}} = \frac{{{H_s}{t_i}}}{\mu }\left\{ {2{R_{\text{b}}}\sin (\frac{{\uppi }}{n}) + \frac{{2{R_{\text{a}}}\sin (\frac{{\uppi }}{n}) - 2{R_{\text{b}}}\sin (\frac{{\uppi }}{n})}}{2h}} \right\} \hfill \\ \end{array} \right.\mathop {}\nolimits \mathop {}\nolimits \mathop {}\nolimits n = 3,4$$
(20)
$$\begin{array}{ll} {F_{{\text{pt}}}} = {H_s}{t_i} \cdot \left\{ \begin{array}{ll} 4{R_{\text{b}}}\sin (\frac{{\uppi }}{n})[\frac{1}{2} + {\sum\limits_{i = 1}^{\text{m}} {( - 1)}^i}\cos (i\theta )] \hfill \\ + \frac{{{t_i}[4{R_{\text{a}}}\sin (\frac{{\uppi }}{n})(\frac{1}{2} + {{\sum\limits_{i = 1}^{\text{m}} {( - 1)} }^i}\cos (i\theta )) - 4{R_{\text{b}}}\sin (\frac{{\uppi }}{n})(\frac{1}{2} + {{\sum\limits_{i = 1}^{\text{m}} {( - 1)} }^i}\cos (i\theta ))]}}{2h} \hfill \\ \end{array} \right\}\mathop {}\nolimits n > 4 \hfill \\ {F_{{\text{pn}}}} = \frac{{{H_s}{t_i}}}{\mu } \cdot \left\{ \begin{array}{ll} 4{R_{\text{b}}}\sin (\frac{{\uppi }}{n})[\frac{1}{2} + {\sum\limits_{i = 1}^{\text{m}} {( - 1)}^i}\cos (i\theta )] \hfill \\ + \frac{{{t_i}[4{R_{\text{a}}}\sin (\frac{{\uppi }}{n})(\frac{1}{2} + {{\sum\limits_{i = 1}^{\text{m}} {( - 1)} }^i}\cos (i\theta )) - 4{R_{\text{b}}}\sin (\frac{{\uppi }}{n})(\frac{1}{2} + {{\sum\limits_{i = 1}^{\text{m}} {( - 1)} }^i}\cos (i\theta ))]}}{2h} \hfill \\ \end{array} \right\}\mathop {}\nolimits n > 4 \hfill \\ \end{array}$$
(21)

The expression for the cutting force of a single pyramidal abrasive particle is as follows:

$$\left\{ \begin{gathered} {F_{{\text{ct}}}} = \int_{{t_{{\text{cr}}}}}^{{t_{\text{m}}}} {\frac{{\tau \cos ({\beta_i} - \alpha )}}{{\sin (\frac{{\uppi }}{4} - \frac{{{\beta_i} - \alpha }}{2})\cos (\frac{{\uppi }}{4} + \frac{{{\beta_i} - \alpha }}{2})}}\left\{ {2{R_{\text{b}}}\sin (\frac{{\uppi }}{n}) + \frac{{{t_i}[2{R_{\text{a}}}\sin (\frac{{\uppi }}{n}) - 2{R_{\text{b}}}\sin (\frac{{\uppi }}{n})]}}{h}} \right\}} {\text{d}}t \hfill \\ {{\text{F}}_{{\text{cn}}}} = \int_{{t_{{\text{cr}}}}}^{t_m} {\frac{{\tau \sin ({\beta_i} - \alpha )}}{{\sin (\frac{{\uppi }}{4} - \frac{{{\beta_i} - \alpha }}{2})\cos (\frac{{\uppi }}{4} + \frac{{{\beta_i} - \alpha }}{2})}}\left\{ {2{R_{\text{b}}}\sin (\frac{{\uppi }}{n}) + \frac{{{t_i}[2{R_{\text{a}}}\sin (\frac{{\uppi }}{n}) - 2{R_{\text{b}}}\sin (\frac{{\uppi }}{n})]}}{h}} \right\}{\text{d}}t} \hfill \\ \end{gathered} \right.n = 3,4$$
(22)
$$\begin{array}{ll}F_\text{ct}=\int_{t_{cr}}^{t_m}\frac{\tau\cos{(\beta_{i}-\alpha})}{\sin\left(\frac{\uppi}{4}-\frac{\beta_{i}-\alpha}{2}\right)\cos\left(\frac{\uppi}{4}+\frac{\beta_{i}-\alpha}{2}\right)}\times\left\{ \begin{array}{ll}4R_b\sin\left(\frac{\uppi}{n}\right)\left[\frac{1}{2}+\sum\limits^m_{i=1}\left(-1\right)\cos\left(i\theta\right)\right]\\+\frac{t_i\left[4R_a\sin\left(\frac{\uppi}{n}\right)\left(\frac{1}{2}+\sum\limits^m_{i=1}\left(-1\right)^i\cos\left(i\theta\right) \right) - 4R_b\sin\left(\frac{\uppi}{n}\right)\left(\frac{1}{2}+\sum\limits^m_{i=1}\left(-1\right)^i\cos\left(i\theta\right) \right) \right]}{h}\end{array} \right\}\text{dt}&n>4\\F_\text{cn}=\int_{t_{cr}}^{t_m}\frac{\tau\sin{(\beta_{i}-\alpha})}{\sin\left(\frac{\uppi}{4}-\frac{\beta_{i}-\alpha}{2}\right)\cos\left(\frac{\uppi}{4}+\frac{\beta_{i}-\alpha}{2}\right)}\times\left\{ \begin{array}{ll}4R_b\sin\left(\frac{\uppi}{n}\right)\left[\frac{1}{2}+\sum\limits^m_{i=1}\left(-1\right)\cos\left(i\theta\right)\right]\\+\frac{t_i\left[4R_a\sin\left(\frac{\uppi}{n}\right)\left(\frac{1}{2}+\sum\limits^m_{i=1}\left(-1\right)^i\cos\left(i\theta\right) \right) - 4R_b\sin\left(\frac{\uppi}{n}\right)\left(\frac{1}{2}+\sum\limits^m_{i=1}\left(-1\right)^i\cos\left(i\theta\right) \right) \right]}{h}\end{array} \right\}\text{dt}&n>4\end{array}$$
(23)
$$\left\{ \begin{array}{llll} \begin{array}{*{20}{c}} {\alpha = - (\frac{{\uppi }}{2} - {\text{ta}}{{\text{n}}^{ - 1}}\frac{2h}{{{R_a} - {R_b}}}),\;L = \frac{3}{2}{R_{\text{b}}}}&{n = 3} \end{array} \hfill \\ \begin{array}{*{20}{c}} {\alpha = - (\frac{{\uppi }}{2} - {\text{ta}}{{\text{n}}^{ - 1}}\frac{\sqrt 2 h}{{{R_a} - {R_b}}}),\;L = \sqrt 2 {R_{\text{b}}}}&{n = 4} \end{array} \hfill \\ \theta = \frac{{(n - 2){\uppi }}}{n} \hfill \\ m = [\frac{n - 1}{4}] \hfill \\ \end{array} \right.$$
(24)

Where, \({R_{\text{a}}},{R_{\text{b}}}\) is circumscribed circle radius of upper and lower bottom surfaces of abrasive grains.

2.3 Abrasive grinding force on different shapes

The total grinding force during single abrasive grinding can be expressed as [20]:

$$\left\{ \begin{array}{ll} {F_{\text{t}}} = {F_{{\text{ct}}}} + {F_{{\text{pt}}}} + {F_{{\text{rt}}}} \hfill \\ {F_{\text{n}}} = {F_{{\text{cn}}}} + {F_{{\text{pn}}}} + {F_{{\text{rn}}}} \hfill \\ \end{array} \right.$$
(25)

After setting modeling parameters, uniform sizes of abrasive particles with different geometric shapes are set, and 6 pyramids are selected for pyramid shape abrasive. The 6 pyramid for pyramid shape abrasive represents the hexagonal pyramid, and the corresponding edge number of the barasive is 6. The modeling results of single abrasive grinding force obtained are shown in Fig. 3.

Fig. 3
figure 3

Single grit grinding force of different shapes

Full size image

From Fig. 3, for different shape of the abrasive with a same dimension size, the grinding force values are \(F_\mathrm{spherical} > F_\mathrm{conical} > F_\mathrm{pyramidal}\). It is because that the spherical shape shows a larger efficient size contact area during the material removal process, which gives a stonger force effect. When the undeformed chip thickness is less than the minimum undeformed chip thickness, there is only sliding force and plowing force, and the sliding force remains basically unchanged. The plowing force gradually increases with the increase of undeformed chip thickness. When the undeformed chip thickness is greater than the minimum undeformed chip thickness, the cutting force rapidly increases and becomes the main component of the grinding force. The total grinding force of a single abrasive grain increases with the increase of undeformed chip thickness.

3 Modeling of single abrasive grinding temperature with shape characteristic

Most of the grinding generated energy is converted into heat during the actual machining process. The heat transmitted to the workpiece can cause thermal damage such as grinding burns, phase transformation, residual stress, cracks, reduced fatigue strength and thermal deformation [21]. The grinding temperature field is of great significance in surface engineering. Due to the uneven distribution of abrasive particles on the surface of the grinding wheel, all effective abrasive particles undergo heat transfer with the workpiece. Therefore, based on different geometric features, a single abrasive grinding force analytical model is used to analyze and model the heat transfer process in the contact area of a single abrasive grinding, and the temperature field distribution in the contact area is obtained.

3.1 Heat source theory in grinding process

A triangular heat source is utilized to analyze the temperature field of single abrasive grinding. When calculating the triangular heat flux density, the contact arc length is evenly divided into n parts. The heat flux density at any point of a triangular heat source is expressed as follow:

$$\begin{gathered}q = \frac{{2n\Delta l{q_{\text{w}}}}}{{{l_{\text{c}}}}}\hfill 1 \leq n \leq \frac{{l_c}}{\Delta l}\hfill \\ \end{gathered}$$
(26)

Where, \({q_{\text{w}}}\) is heat flux density flowing into the workpiece. \({l_{\text{c}}}\) represents the abrasive contact size.

The grinding heat generated during surface grinding comes from the contact area between the grinding wheel and the workpiece. During the machining process, it is transmitted to the workpiece, grinding wheel, grinding debris, and grinding fluid respectively. The part of heat transmitted to the workpiece can cause the workpiece temperature variation. Dry grinding process is adopted, and the heat transmitted to the grinding fluid is ignored. Based on the analysis of grinding force in part 2, the total heat flux intensity in the grinding contact area can be expressed as [22]:

$${q_{\text{t}}} = \frac{{{F_{\text{t}}}{v_{\text{s}}}}}{{{l_{\text{c}}}b}}$$
(27)

Where, \({F_{\text{t}}}\) is grinding tangential force. \({v_{\text{s}}}\) is linear speed of grinding wheel. \(b\) is abrasive machining width.

The heat flux density of the incoming debris can be expressed as [21]:

$${q_{{\text{ch}}}} = \frac{{{\rho_{\text{w}}}{c_{\text{w}}}{v_{\text{w}}}{a_{\text{p}}}{T_{{\text{ch}}}}}}{{{l_{\text{c}}}}}$$
(28)

Where, \({\rho_{\text{w}}}\) is workpiece material density. \({c_{\text{w}}}\) is specific heat capacity of workpiece material. \({v_{\text{w}}}\) is workpiece feed speed. \({a_p}\) is grinding depth. \({T_{{\text{ch}}}}\) is melting temperature of workpiece material.

Assuming that the percentage of heat incoming to the workpiece is \(R\) and considering the wheel input heat \({q_{\text{s}}}\), the heat flux density of the incoming workpiece can be expressed as

$${q_{\text{w}}} = ({q_{\text{t}}} - {q_{\text{s}}} - {q_{{\text{ch}}}})R$$
(29)

Based on the study of the interaction between abrasive particles and workpieces in the grinding process, the heat distribution ratio model of workpieces and workpieces from a microscopic perspective is established as [23]:

$$R = {(1 + \frac{{0.97{k_{\text{g}}}}}{{\sqrt {{r_{\text{g}}}{v_{\text{s}}}{k_{\text{w}}}{\rho_{\text{w}}}{c_{\text{w}}}} }})^{ - 1}}$$
(30)

Where, \({k_{\text{g}}}\) is thermal conductivity of abrasive material. \({r_{\text{g}}}\) is contact radius between abrasive particle and workpiece. \({v_{\text{s}}}\) is the linear speed of grinding wheel. \({k_{\text{w}}}\) is thermal conductivity of workpiece material. \({\rho_{\text{w}}}\) is workpiece material density. \({c_{\text{w}}}\) is specific heat capacity of workpiece material.

The final heat flux into the workpiece can be expressed as:

$${q_{\text{w}}} = (\frac{{0.9{F_{\text{t}}}{v_{\text{s}}} - {\rho_{\text{w}}}{c_{\text{w}}}{v_{\text{w}}}{a_{\text{p}}}{T_{{\text{ch}}}}b}}{{{l_{\text{c}}}b}}){(1 + \frac{{0.97{k_{\text{g}}}}}{{\sqrt {{r_{\text{g}}}{v_{\text{s}}}{k_{\text{w}}}{\rho_{\text{w}}}{c_{\text{w}}}} }})^{ - 1}}$$
(31)

3.2 Method for temperature field of a single abrasive

The finite difference method is a commonly used method. The discretization finite elements of the target are solved, by replacing the partial differential with the deviation quotient of these discrete elements [24]. The grid division method is shown in Fig. 4.

Fig. 4
figure 4

Two-dimensional finite difference computational grid

Full size image

In the two-dimensional finite difference model, the grinding contact area can be approximated as a rectangle, and it is meshed using two sets of parallel and perpendicular straight lines. The side length of each grid is \(\Delta x\) or \(\Delta z\), and \(\Delta x = \Delta z\).

The straight line equation for grid division can be expressed as:

$$\left\{ \begin{array}{lll} z = {z_j} = j\Delta z &j = 0,1, \cdots n &n\Delta z = h \hfill \\ x = {x_j} = j\Delta x & j = 0,1, \cdots m& m\Delta x = l \hfill \\ \end{array} \right.$$
(32)

Where, \(l\) and \(h\) are the length and height of the grinding abrasive contact area, respectively. \(n\) or \(m\) is the number of shares divided.

The two-dimensional thermal conduction partial differential equation for the grinding contact area is expressed as [24]:

$$\frac{{{\partial^2}{T_{{\text{contact}}}}}}{{\partial {x^2}}} + \frac{{{\partial^2}{T_{{\text{contact}}}}}}{{\partial {z^2}}} = \frac{1}{\alpha }\frac{{\partial {T_{{\text{contact}}}}}}{\partial t}$$
(33)

Where, \({T_{{\text{contact}}}}\) is contact area temperature. \(t\) is time. \(\alpha\) is thermal diffusion coefficient of workpiece.

By using the finite difference dispersion method, the two-dimensional thermal conductivity partial differential equation is derived based on the second-order difference quotient:

$$\frac{{{T_{m + 1,n}}(t) + {T_{m - 1,n}}(t) - 2{T_{m,n}}(t)}}{{{{(\Delta x)}^2}}} + \frac{{{T_{m,n + 1}}(t) + {T_{m,n - 1}}(t) - 2{T_{m,n}}(t)}}{{{{(\Delta z)}^2}}} = \frac{1}{\alpha }\frac{{{T_{m,n}}(t + \Delta t) - {T_{m,n}}(t)}}{\Delta t}$$
(34)

Where, \({T_{m,n}}(t),{T_{m,n}}(t + \Delta t)\) are the temperature of a point \((m,n)\) in the contact area at \(t\) and \(t + 1\). And \(\Delta x = \Delta z\).

$${T_{m,n}}(t + \Delta t) = \frac{\alpha \Delta t}{{{{(\Delta x)}^2}}}[{T_{m - 1,n}}(t) + {T_{m + 1,n}}(t) + {T_{m,n - 1}}(t) + {T_{m,n + 1}}(t)] + [1 - 4\frac{\alpha \Delta t}{{{{(\Delta x)}^2}}}]{T_{m,n}}(t)$$
(35)

For the points on the surface boundary of the grinding contact area, the number of adjacent nodes becomes three, and heat is transmitted to the contact area through the action of single abrasive grinding. Due to the absence of coolant, convective heat transfer occurs when the workpiece comes into contact with air. The heat transfer model is shown in Fig. 5.

Fig. 5
figure 5

Heat transfer model of upper surface boundary in contact zone

Full size image

The heat transfer equation of the surface on the contact area is expressed as [25, 26]:

$${q_{(m - 1,1) \to (m,1)}} + {q_{(m + 1,1) \to (m,1)}} + {q_{(m,2) \to (m,1)}} + {q_{\text{w}}}A = {\rho_{\text{w}}}{c_{\text{w}}}V\frac{\partial T}{{\partial t}} + GA[{T_{m,1}}(t) - {T_{room}}]$$
(36)
$$\left\{ \begin{array}{lll} {q_{(m - 1,1) \to (m,1)}} = k\Delta z[\frac{{{T_{m - 1,1}}(t) - {T_{m,1}}(t)}}{\Delta x}] \hfill \\ {q_{(m + 1,1) \to (m,1)}} = k\Delta z[\frac{{{T_{m + 1,1}}(t) - {T_{m,1}}(t)}}{\Delta x}] \hfill \\ {q_{(m,2) \to (m,1)}} = k\Delta x[\frac{{{T_{m,2}}(t) - {T_{m,1}}(t)}}{\Delta z}] \hfill \\ \end{array} \right.$$
(37)

Where, \({q_{\text{w}}}\) is heat flux density flowing into the contact area surface. \({\rho_{\text{w}}}\) is workpiece material density. \({c_{\text{w}}}\) is specific heat capacity of workpiece material. \({T_{{\text{room}}}}\) is the temperature of environment. \(V = \Delta x\Delta z\). \(A = \Delta x\). \(G\) is comprehensive heat transfer coefficient.

$$G = {(\frac{1}{{{h_{{\text{contact}}}}}} + \frac{\Delta z}{{2k}})^{ - 1}}$$
(38)

Where, \({h_{{\text{contact}}}}\) is convective heat transfer coefficient in the contact area. \(k\) is thermal conductivity of workpiece material.

According to Eqs. (3) and (5), the heat transfer finite difference equation for the upper boundary of the grinding contact zone can be derived as:

$$\begin{gathered} {T_{m,1}}(t + \Delta t) = \frac{\alpha \Delta t}{{(\Delta x)}}[{T_{m - 1,1}}(t) + {T_{m + 1,1}}(t) + {T_{m,2}}(t) + \frac{G\Delta x}{k}{T_{{\text{room}}}}] \hfill \\ \mathop {}\nolimits \mathop {}\nolimits \mathop {}\nolimits \mathop {}\nolimits \mathop {}\nolimits + [1 - 3\frac{\alpha \Delta t}{{{{(\Delta x)}^2}}} - \frac{G\alpha \Delta t}{{k\Delta x}}]{T_{m,1}}(t) \hfill \\ \mathop {}\nolimits \mathop {}\nolimits \mathop {}\nolimits \mathop {}\nolimits \mathop {}\nolimits + \frac{\alpha \Delta t}{{k\Delta x}}{q_{\text{w}}} \hfill \\ \end{gathered}$$
(39)

Similarly, for areas on the surface of the grinding contact area that are not involved in machining or have not been completed, and there is no heat input, the boundary condition equation can be expressed as:

$$\begin{gathered} {T_{m,1}}(t + \Delta t) = \frac{\alpha \Delta t}{{(\Delta x)}}[{T_{m - 1,1}}(t) + {T_{m + 1,1}}(t) + {T_{m,2}}(t) + \frac{G\Delta x}{k}{T_{{\text{room}}}}] \hfill \\ \mathop {}\nolimits \mathop {}\nolimits \mathop {}\nolimits \mathop {}\nolimits \mathop {}\nolimits + [1 - 3\frac{\alpha \Delta t}{{{{(\Delta x)}^2}}} - \frac{G\alpha \Delta t}{{k\Delta x}}]{T_{m,1}}(t) \hfill \\ \end{gathered}$$
(40)

The analytical approach of the three-dimensional finite difference model is consistent with that of two-dimensional, but it is only extended to three-dimensional space.

3.3 Temperature field of a single abrasive

Due to the consideration of the temperature field in single abrasive grinding in this article, the size is set to \(6 \times 3 \times 3{\text{mm}}\). The selected workpiece material is 45 steel. The abrasive material is white corundum. The calculation parameters are shown in Table 1.

Table 1 Temperature field calculation parameters
Full size table

Taking spherical abrasive grains as an example, the time varying rule of two-dimensional temperature field in single abrasive grain grinding is obtained by finite difference method, as shown in Fig. 6. It can be seen that as the abrasive particles move forward on the surface of the contact area, the heat source also moves forward, resulting in a continuous forward movement of the temperature field generated by the abrasive heat source. The temperature decreases with the increase of the depth of the contact area, and the temperature at the bottom of the contact area between the abrasive particles is the highest. The temperature field shows an approximate elliptical distribution.

Fig. 6
figure 6

Two-dimensional dynamic temperature field of a single abrasive

Full size image

Taking spherical abrasive particles as an example, the variation law of three-dimensional temperature field is obtained through finite difference method solution, as shown in Figs. 7 and 8. It can be seen that the temperature field of single abrasive grinding advances in a banded distribution along the contact area with the movement of the abrasive particles, and is elliptical in the XZ plane, reaching its maximum value in the contact area between the bottom of the abrasive particles and the workpiece.

Fig. 7
figure 7

Three-dimensional dynamic temperature field in contact zone of the single grit grinding

Full size image
Fig. 8
figure 8

Three-dimensional dynamic temperature field of a single abrasive

Full size image

The temperature field in the grinding contact area of a single spherical abrasive, a conical abrasive, and a 6-pyramidal abrasive is solved respectively. When \(t = 0.3{\text{s}}\) is taken, the temperature distribution along the surface of the contact area with the same size and different shapes is compared and analyzed, as shown in Fig. 9.

Fig. 9
figure 9

Comparison of temperature distribution with different abrasive shapes

Full size image

It can be seen from Fig. 9 that different shapes of abrasive particles have a relatively obvious impact on the grinding temperature value, but the distribution trend of the surface temperature in the contact area is generally consistent, reaching the maximum value when the abrasive particles contact the surface, and then gradually decreasing. The maximum temperature order is listed as: \({T_{{\text{spherical}}}} > {T_{{\text{conical}}}} > {T_{{\text{pyramidal}}}}\).

4 Finite element validation with abrasive shape characteristic

The Deform-3D finite element software is applied to conduct the grinding process of 45 steel by a single white corundum abrasive grain, and validate the former regulation of the abrasive shape on the temperature distribution.

4.1 Material model building

The material of the abrasive grain in this study is white corundum, and its physical properties are shown in Table 2 [1].

Table 2 Physical properties of abrasive grit
Full size table

The workpiece used in this study is 45 steel, 45 steel is a high-quality carbon structural steel, which has a wide range of applications in mechanical processing. Its physical properties are shown in Table 3 [1].

Table 3 Physical property of 45 steel
Full size table

Simulation of single abrasive grinding with Deform-3D requires data that reflects the constitutive behavior of the workpiece material. Therefore, the establishment of a material constitutive model is a crucial part of the finite element simulation study of single abrasive grinding. The internal state variables of the material determine its constitutive relationship, and the internal variables of the material are usually composed of the dislocation density of the material, particle size [25]. The research shows that the J-C constitutive model is an ideal rigid-plastic strengthening model that can reflect the strain rate strengthening effect and the temperature rise softening effect, and is often used in the simulation study of cutting and grinding. The J-C constitutive model is in the following form:

$$\sigma = \left( {A + B{\varepsilon_e}^n} \right)\left[ {1 + C\ln \left( {\frac{\varepsilon }{{\varepsilon_0}}} \right)} \right]\left[ {1 - \left( {\frac{{T - {T_r}}}{{{T_m} - {T_r}}}} \right)} \right]$$
(41)

where, \(\sigma\) represents the equivalent forces; \(\varepsilon_e\) represents the equivalent plastic strain; \(\varepsilon\) represents the effective plastic strain; \(\varepsilon_0\) represents the reference plastic strain (general value is 1 \({s}^{-1}\)); \(T_r\) represents the room temperature; \(T_m\) represents the material melting temperature; A represents the initial yield stress; B represents the hardening modulus; n represents the hardening index; C represents the strain rate correlation coefficient; m represents the thermal softening coefficient.

In the simulation of this paper, the parameters of the 45-steel J-C constitutive model are selected as shown in Table 4 [1].

Table 4 J-C constitutive model parameters of 45 steel
Full size table

4.2 Finite element model (FEM) establishment

Abrasive grains are produced by crushing method, so the shape, size and position of abrasive grains distributed on the surface of the grinding wheel are irregular, that is, their shape and position characteristics are randomly distributed. It is impossible to fully reflect the real shape of shape abrasive grains in actual processing in simulation, and the research ideas for abrasive grain geometry in this chapter are consistent with the method used in Chapter 2, and several typical abrasive grain geometries are selected for finite element simulation analysis. Different abrasive grain geometries have no effect on the process setup of the finite element simulation, so this chapter uses ball abrasives as an example to perform finite element dynamic simulation of the single abrasive grinding process.

In this paper, F46 white corundum grinding wheel is selected, the particle size range is 425~355 μm, and the diameter of the sphere abrasive grain is set 360 μm in the simulation. This is shown in Fig. 10.

Fig. 10
figure 10

Geometric model of spherical grit

Full size image

In this chapter, a grinding wheel diameter of 350 mm and a grinding depth of 0.1 mm were selected. Therefore, in this chapter of finite element simulation, a 6 × 3 × 3 mm cuboid workpiece was established.

The parameter settings used in the finite element simulation are shown in Table 5. In the finite element simulation process, meshing is a very important step, and the meshing situation is closely related to the accuracy of the simulation results. The simulation in this paper adopts Lagrangian Incremental algorithm and adaptive mesh redivision technology, through the Lagrange method to simulate the deformation of the workpiece material, when the mesh distortion to a certain extent, it is repartitioned, which can realize the gradual separation of the simulated material from the workpiece to form chips [26].

Table 5 Setting of simulation parameters
Full size table

According to the above analysis, the abrasive grain and the workpiece are divided by tetrahedral mesh, the number of abrasive grain meshes is 8000, the number of parts is 70,000, and the grid refinement technology is adopted in the grinding contact area, and the mesh is further refined by applying window encryption.

4.3 Analysis of finite element simulation results

The 0.3 s grinding temperature field distribution cloud obtained by simulating the grinding temperature field of single spherical abrasive, conical abrasive grain and 6-pyramid abrasive grain by finite difference method and finite element method is respectively, as shown in Fig. 11. The above FEM results testify the validity of the FDM analysis.

Fig. 11
figure 11

Comparison of simulation results of temperature field between FDM and FEM

Full size image

5 Influence of abrasive shape-position characteristic on the grinding zone

The grinding temperature distribution is constituted of multiple thermal sources caused by a series of abrasives. Once the abrasives position and shape information are confirmed, the grinding temperature distribution can be obtained.

5.1 Grinding wheel topography model establishment

The abrasive grain vibration method is to give an initial position for the uniform distribution of all abrasive particles on the surface of the grinding wheel, and then let the abrasive particles vibrate randomly in three-dimensional space according to the set number of vibrations and vibration amplitude, so that the surface abrasive grain distribution of the grinding wheel after simulation is similar to the actual grinding wheel surface abrasive particle distribution [27]. The iterative equation for abrasive vibration is:

$$\left[ \begin{gathered} {x_{kn}} \hfill \\ {y_{kn}} \hfill \\ {z_{kn}} \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} {x_{k0}} \hfill \\ {y_{k0}} \hfill \\ {z_{k0}} \hfill \\ \end{gathered} \right] + \left[ \begin{gathered} \delta {x_{k1}} + \delta {x_{k2}} + ... + \delta {x_{kn}} \hfill \\ \delta {y_{k1}} + \delta {y_{k2}} + ... + \delta {y_{kn}} \hfill \\ \delta {z_{k1}} + \delta {z_{k2}} + ... + \delta {z_{kn}} \hfill \\ \end{gathered} \right]$$
(42)

Where, (\({x}_{k0}\),\({y}_{k0}{,z}_{k0}\)) represents the abrasive initial coordinates; (\({x}_{kn}\),\({y}_{kn}{,z}_{kn}\)) represents the abrasive final coordinates; \(\delta {y_{k1}}\), \(\delta {x_{k1}}\), \(\delta {z_{k1}}\) represents the a uniformly distributed random number within [\(-{L_r},{L_r}\)]; k represents the abrasive number; n represents the number of vibrations.

In the process of random vibration, there may be cases where the abrasive particles exceed the sampling range of the grinding wheel and the abrasive particles overlap. Two constraints are applied to the abrasive vibration conditions:

$$\left[ \begin{gathered} {x_{kn}} \hfill \\ {y_{kn}} \hfill \\ {z_{kn}} \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} {x_{k0}} \hfill \\ {y_{k0}} \hfill \\ {z_{k0}} \hfill \\ \end{gathered} \right] + \left[ \begin{gathered} \delta {x_{k1}} + \delta {x_{k2}} + ... + \delta {x_{kn}} \hfill \\ \delta {y_{k1}} + \delta {y_{k2}} + ... + \delta {y_{kn}} \hfill \\ \delta {z_{k1}} + \delta {z_{k2}} + ... + \delta {z_{kn}} \hfill \\ \end{gathered} \right]$$
(43)
$$\sqrt {{{({x_{ki}} - {x_{kj}})}^2} + {{({y_{ki}} - {y_{kj}})}^2}} \geq \frac{{{d_i} + {d_j}}}{2},{\text{i}} \ne {\text{j}}$$
(44)

5.2 Grinding wheel topography simulation

Based on the above analysis, mathematical programming was carried out to simulate the morphology of the grinding wheel. In this paper, F46 white corundum grinding wheel is selected, and its parameters are shown in Table 6.

Table 6 The grinding wheel parameters
Full size table

Through simulation calculation, the surface morphology of the grinding wheel as shown in Fig. 12 is obtained, figure (a) is the initial morphology of the grinding wheel surface, figure (b) is the surface morphology of the grinding wheel after adjusting the particle size, and figure (c) is the final surface morphology of the grinding wheel after the vibration of abrasive particles.

Fig. 12
figure 12

Simulation of grinding wheel surface topography

Full size image

5.3 Temperature distribution of the contact zone with shape-position characteristics

As shown in Fig. 13, the dynamic temperature field distribution of the grinding contact zone is randomly distributed in the case of random distribution of the abrasive grain shape characteristics in the grinding wheel contact zone:

Fig. 13
figure 13

Temperature field in grinding contact zone

Full size image

In Fig. 13, the temperature field during the grinding process is not evenly distributed along the width of the grinding wheel, and is not evenly distributed in the direction of the feed. This is because the temperature field of the grinding contact zone is generated by the discrete heating of a large number of abrasive particles on the surface of the grinding wheel and the grinding contact zone, and the single abrasive grain has little effect on the temperature increase during the grinding process, but under the action of all the effective abrasive particles involved in grinding in the grinding wheel contact zone, the temperature of the contact zone gradually rises.

These figure results show the FEM simulation with different specified shape abrasive proportion in terms of the average temperature and the temperature variance. This is not the repetitive results such as the simulative training or the experiments. So the error bars may not applied in the current curves. It Fig. 14a, with the increase of spherical abrasive grain ratio, the average temperature change of the contact zone surface shows an increasing trend. Moreover, it can be seen from the research content of Chapter 3 that the heat flux density of abrasive particles is proportional to its tangential force, so with the increase of spherical abrasive grain ratio, the temperature field temperature of the grinding contact zone generally shows an upward trend. It can be seen from Fig. 14b that with the increase of spherical abrasive grain ratio, the temperature variance of the surface of the contact zone increases, indicating that the discreteness of its temperature distribution increases, and the smaller spherical abrasive ratio grinding wheel can obtain a temperature field distribution with better uniformity.

Fig. 14
figure 14

Tendency of temperature in contact zone with spherical grit proportion

Full size image

As can be seen from Fig. 15, the average surface temperature of the contact zone gradually increases with the increase of the ratio of conical abrasive particles. This is because that the heat flux density is proportional to the grinding tangential force. As the ratio of conical abrasive grains increases, the tangential grinding force of the contact zone increases, so the temperature of the contact zone gradually increases. With the increase of the ratio of conical abrasive particles, the temperature field distribution in the contact zone is more discrete.

Fig. 15
figure 15

Tendency of temperature in contact zone with conical grit proportion

Full size image

It can be seen from Fig. 16 that with the increase of the ratio of 6-pyramid abrasive particles, the surface temperature and variance of the contact zone showed a downward trend, indicating that with the increase of the ratio of 6-pyramid abrasive particles, the temperature field distribution of the grinding contact zone was more uniform.

Fig. 16
figure 16

Tendency of temperature in contact zone with pyramid grit proportion

Full size image

6 Conclusion

The paper investigates influence of the abrasive shape-position characteristic on the grinding thermo-mechanical coupling by establishing the interaction force and discretized temperature model with abrasive information. The study can be utilized to provide valuable theoretical foundation for engineering practice by preparing stuructural wheel and its grinding property. The main conclusions are drawn as follows.

An interaction force model is established considering the abrasive position and shape information. It was found that the force value varies with the thickness of the undeformed chips. Moreover, the grinding force of a single abrasive grain is also influenced by the geometric shape of the abrasive grain, and the influence law is as follows: \(F_\mathrm{sphere} > F_\mathrm{circular cone} > F_\mathrm{6pyramids}\).

The mapped dynamic grinding temperature is actually discretized on the workpiece surface, which is on account of the diversity of the abrasive shape and its distribution. The different geometric shapes of abrasive grains have an impact on the temperature field of single abrasive grain grinding, and their influence law is the same as the situation of single abrasive grinding force.

Grinding wheel with higher spherical and conical abrasive particles, as well as lower pyramid shaped abrasive particle ratios, can produce greater specific grinding energy, but their temperature field distribution is relatively discretized. A grinding wheel with a higher proportion of pyramid shaped abrasive particles can produce a relatively uniform temperature field distribution in the contact area during machining.