1 Introduction

A wireless sensor network (WSN) is comprised of several sensors (nodes) that are interconnected and can process and exchange data with each other. These nodes are deployed to collect data for a variety of purposes, including exploration, monitoring, surveillance, and maintenance, to mention a few.

The necessity to know the position of the nodes must be handled since in many applications, the data must be linked to a location to be relevant such as with sensors used to monitor forest fires, military surveillance, etc. Placing GPS devices on each individual node and manually configuring their positions can be challenging, especially for large networks with thousands of sensors. This is mainly due to the high expenses associated with the sensors. To tackle this problem, a solution is to outfit a subset of sensors with GPS (referred to as anchors), and then estimate the locations of the other nodes by making use of these known anchor nodes and wireless communications. This approach helps overcome the impracticality caused by cost and scale.

Range-based methods in Wireless Sensor Networks (WSNs) are characterized by their reliance on establishing the distances between nodes within the network. Typically, these approaches involve the computation or measurement of the physical separation between sensor nodes. This aspect holds significance in various WSN applications, such as tracking, localization, and monitoring. Within range-based strategies, the task of establishing the location can be achieved by employing methods like analyzing Received Signal Strength (RSS), evaluating Time of Arrival (TOA), measuring the round trip duration, or even utilizing a fusion of these techniques [1]. These methodologies rely on estimating sensor distances to conclude the process of positioning [2].

Once the distances between sensor nodes are acquired, the localization procedure can be carried out through either a central processing unit or a distributed processing approach. The former proves to be less effective in extensive networks due to constraints in information transfer, insufficient processing capabilities, and unequal energy usage. On the contrary, the latter method is more adaptable and exhibits great scalability. Nonetheless, distributed processing comes with its own disadvantages, primarily its iterative nature. This characteristic can lead to heightened overall power consumption due to the need for a significant number of iterations for rapid convergence. Additionally, this approach can be susceptible to the propagation of errors, adding to its limitations [3].

It’s commonly understood that in range-based localization algorithms, the process of determining the positions of unknown sensors is closely tied to estimating the distances between them.This connection means that an unusual or non-typical distance estimation between sensors has the potential to lead to undesirable outcomes in the localization process [4,5,6,7,8,9]. This is why numerous studies have been conducted to address this scenario, with the goal of developing methods to filter, remove, or mitigate the impact of these undesired distances (outliers) on the localization procedure. For example, The study in [10] explores the use of the weighted three minimum distances method (WTM), which considers three minimal distances to enhance atypical RSSI measurements for localization. By utilizing an experimental channel model and a new location optimization formula, grounded in multilateration and distance estimation, this technique strives for more accurate positioning. Despite requiring more time for computation compared to other established algorithms like Semidefinite Programming (SDP), Levenberg-Marquardt (LM), and nonlinear least squares (NLS), it achieves more precise estimations. Also, in [4], the authors proposed an approach for removing atypical distance measurements. They achieve this by applying geometric constraints from the Cayley-Menger determinant and utilizing Euclidean norm, the 1-norm, minimization decoding algorithm. Large errors are initially identified with the assistance of neighboring anchor nodes connected to regular nodes. Subsequently, these significant errors are filtered out using a predefined threshold, resulting in the determination of the best-estimated positions for the unknown nodes. In the same way, in [7], initially, the Frobenius norm and the 1-norm (i.e., L1) are used to establish a framework for reconstructing an Euclidean Distance Matrix (EDM) that contains noise, outliers, and missing values. This process is referred to as Normalized Matrix Completion (NRMC). Subsequently, an efficient algorithm using an alternative address multiplier approach is developed to address the NRMC problem. Lastly, a multidimensional scaling method is utilized to determine the positions of unidentified nodes based on a complete EDM. Also, in [5], a novel approach utilizing the least squares (LS) method is introduced for Wireless Sensor Network (WSN) localization. This method involves determining the location by assessing a condition number derived from a coordinate matrix, which effectively prevents the presence of outliers. Also, the research introduces the concept of a condition number threshold to enhance location accuracy while mitigating the impact of outliers.

In the majority of the analyzed approaches, it’s crucial to keep the occurrence of outliers relative to the total number of measurements in the network as low as possible to ensure favorable outcomes [11]. For instance, the study development in [12] introduces a method named the greedy search-based random sample consensus (GS-RSC) algorithm for identifying non-line-of-sight (NLOS) measurements. This algorithm, through its dual components-the localization and identification modules-along with comprehensive time-difference-of-arrival (TDOA) data, effectively reduces errors from outliers and NLOS paths. By iteratively working in tandem, these modules accurately weed out irregular data, thus ensuring highly accurate localization solutions that are less affected by both outliers and NLOS-path errors. Furthermore, it’s important to take into account scenarios where outliers are caused by either a multiplying factor or a mitigating factor affecting the actual measurement value. For example, when estimating distances in wireless sensor networks using RSS readings, there are notable disadvantages. Ambient conditions such as obstructions and multipath propagation can affect signal strength, leading to inaccurate and atypical distance estimations. Variations in hardware can alter RSS signal strength, complicating the standardization of measurements across devices. Additionally, this method’s accuracy and reliability are constrained by its dependence on a predetermined model that correlates signal strength with distance, which might not accurately represent every deployment environment. To address this challenge, the proposed method, comprising two sequential phases, is an iterative process that progressively selects (or eliminates) anticipated outlier distances during each iteration. In the initial stage, an optimization method is employed to minimize the discrepancy between two EDMs, one serving as the reference and the other as the estimated EDM. In the second phase of the proposed approach, a heuristic method is utilized to eliminate the estimated distances between sensors that exhibit significant errors. It should be noted that at each iteration, the EDM is converted to positions using the MDS algorithm.

The remainder of this paper unfolds as follows: Sect. 2 describes the mathematical representation of the problem. Section 3 provides an overview of the proposed algorithm, covering both phases of the procedure: the minimization and selection of outliers. In Sect. 4, the experiment’s outcomes are presented, where the quantity of outlier measurements is systematically raised. Ultimately, Sect. 5 offers concluding remarks.

2 WSN Localization: Mathematical formulation problem

This research limits the discussion only to two dimensions (2D) for node localization in WSNs. Consider n randomly deployed sensor nodes over a certain area denoted as \(\textbf{S}=\left\{ s_1,s_2,s_3,\dots ,s_m,s_{m+1},\dots ,s_n \right\} \) with true locations

$$\begin{aligned}&\textbf{P} = [ \textbf{p}_1 = \left[ x_1, y_1 \right] ^T, \textbf{p}_2 = \left[ x_2, y_2 \right] ^T, \\&\textbf{p}_3 = \left[ x_3, y_3 \right] ^T, \dots , \textbf{p}_m = \left[ x_m, y_m \right] ^T, \\&\textbf{p}_{m+1} = \left[ x_{m+1}, y_{m+1} \right] ^T, \dots , \textbf{p}_n = \left[ x_n, y_n \right] ^T ] \end{aligned}$$

respectively; the first m sensor nodes have unknown positions whose position estimates are represented as

$$\begin{aligned}{} & {} \bar{\textbf{P}}=[ \bar{\textbf{p}}_1=\left[ x_1,y_1\right] ^T,\bar{\textbf{p}}_2=\left[ x_2,y_2\right] ^T,\\{} & {} \quad \bar{\textbf{p}}_3=\left[ x_3,y_3\right] ^T,\dots ,\bar{\textbf{p}}_m=\left[ x_m,y_m\right] ^T ] \end{aligned}$$

and the remainder \(n-m\) sensor nodes have known positions, obtained by GPS or a similar scheme (i.e., Anchors), with \(m n-m\). Let all sensor nodes have connectivity with any other sensor nodes in network, and the noisy distance \(r_{ij}\) between sensor nodes i and j can be estimated by methods like RSS, ToA, AoA or combination of them [13,14,15,16], where \(\left( i,j \right) \in \textbf{S}\times \textbf{S}\). The sets of undirected neighbors between sensors-sensors, sensors-anchors, and anchors-anchors can be described as

$$\begin{aligned}{} & {} \textbf{C}:=\left\{ \left( i,j \right) :1\le i \le m, \, 1 \le j \le m,\, i\ne j \right\} , \\{} & {} \textbf{K}:=\left\{ \left( k,l \right) :1\le l \le m,\, m+1 \le k \le n,\, l\ne k \right\} , \end{aligned}$$

and

$$\begin{aligned} \textbf{A}:=\left\{ \left( i,j \right) : m+1\le i \le n,\, m+1 \le j \le n,\, i\ne j \right\} , \end{aligned}$$

respectively. Here,

$$\begin{aligned} \left\| \textbf{p}_{i}-\textbf{p}_{j}\right\| =d_{ij},\, \forall \, (i,j)\in \textbf{C}, \end{aligned}$$

where \(d_{ij}\) represents the true distance between sensors i and j, and \(\left\| \cdot \right\| \) denotes the 2-norm. Similarly, \(\left\| \textbf{p}_{l}-\textbf{p}_{k}\right\| =d_{lk}, \,\forall \,(l,k)\in \textbf{K} \) where \(d_{lk}\) represents the true distance between the sensor l and the anchor k. Then, the position of unknown sensors (i.e., the first m nodes) can be estimated as the following non-convex optimization function [17,18,19,20,21].

$$\begin{aligned} \min _{\begin{array}{c} \bar{\textbf{p}}_1,\bar{\textbf{p}}_2,\dots ,\bar{\textbf{p}}_m \end{array}}\sum _{(i,j)\in \textbf{C} } \Bigl ( \left\| \bar{\textbf{p}}_{i}-\bar{\textbf{p}}_{j}\right\| -r_{ij}{\dot{{o}}}_{ij} \Bigl )^2+ \sum _{(k,l)\in \textbf{K} } \Bigl ( \left\| \bar{\textbf{p}}_{k}-\textbf{p}_{l}\right\| -r_{kl}{\dot{{o}}}_{kl} \Bigl )^2 \end{aligned}$$
(1)

where the noisy estimated distance between sensors i and j (or sensor l and anchor k) is composed as

$$\begin{aligned}{} & {} r_{ij}=d_{ij}+e_{ij}, \end{aligned}$$
(2)
$$\begin{aligned}{} & {} r_{kl}=d_{kl}+e_{kl}, \end{aligned}$$
(3)

respectively, and \(e_{ij}\) and \(e_{kl}\) have normal distribution \(\mathcal {N}(0,sd^2)\), which represent the noise introduced by the environment and the ranging measurement techniques, and sd is the standard deviation. Also, in many cases, a range measurement between sensor \(s_i\) and sensor \(s_j\) lies in an abnormal distance (i.e., an outliers) introduced as ȯ\(_{ij}\) that represents a random variable. The last problem can be established as a geometric undirected graph \(\textbf{G}=\left( \textbf{V},\textbf{L} \right) \) where \(\textbf{V}\) and \(\textbf{L}\) represent the set of vertices (i.e., sensor nodes \(\textbf{S}\)) and the set of edges (i.e., links among sensor nodes) \(\textbf{L}=\left\{ \left\{ i,j\right\} \,|\, (i,j) \in \textbf{V}\times \textbf{V}, i \ne j \right\} \), respectively. Then, the adjacency matrix (i.e., symmetric with zeros on its diagonal) of size \(N\times N\) can be represented as \(\textbf{MC}=(\textbf{MC}_{ij})\), where

$$\begin{aligned} \textbf{MC}_{ij}={\left\{ \begin{array}{ll}1 &{} \text{ if } \, \{i,j\} \in \textbf{L}\\ 0 &{} \text{ otherwise } \end{array}\right. } \end{aligned}$$
(4)

and the matrix distance, derived as weights of \(\textbf{MC}\), can be denoted as \(\textbf{D}=(\textbf{D}_{ij})\) with

$$\begin{aligned} \textbf{D}_{ij}={\left\{ \begin{array}{ll}r_{ij}{\dot{{o}}}_{ij} &{} \text{ if } \, \{i,j\}\in \textbf{L}\\ 0 &{} \text{ otherwise. } \end{array}\right. } \end{aligned}$$
(5)

Equation (1) can be redeveloped in a convex form using relaxation as follows:

$$\begin{aligned}&\underset{\textbf{Y}}{\min }\left\| \textbf{D}^2-K(\textbf{Y})\right\| ^{2}\nonumber \\&\text{ st }: \textbf{Y}\succeq 0 \end{aligned}$$
(6)

where the symmetric matrix \(\textbf{Y}=\bar{\textbf{P}}\bar{\textbf{P}}^T\) is constrained to be positive semidefinite, which is denoted by the expression \(\succeq 0\), and the operator \(K(\textbf{Y})=diag(\textbf{Y})\mathbbm {1}^T -2\textbf{Y} + \mathbbm {1}diag(\textbf{Y})^T\) [22]. Once obtained an estimation of \(\textbf{D}\) by a SDP or SOCP programming [23,24,25,26], a transformation from distances to positions using the MDS method must be employed [27, 28].

3 The Selection and Minimization Algorithm

As aforementioned in Sect. 2, range based localization algorithms are strongly dependent of accuracy on range estimates, so atypical range measurements can provide large errors on position estimates. In order to mitigate the effect of outliers, a centralized localization approach is proposed, and it is divided into two schemes: the minimization and outliers-selection processes. Here, the minimization stage is derived from Eq. (6) and can be rewritten as

$$\begin{aligned}&\textbf{Y}^{i+1}=\underset{\textbf{Y}^{i}}{\arg \,\min }\left\| \left( \textbf{D}^2-K(\textbf{Y}^{i}) \right) \odot \textbf{O}^{i}\right\| ^{2} \nonumber \\&\text{ st }: \textbf{Y}^{i} \succeq 0 \end{aligned}$$
(7)

where the symbol \(\odot \) denotes the Hadamard product between the matrices \(\textbf{D}^2-K(\textbf{Y}^{i})\) and \(\textbf{O}^{i}\).

In the optimization process (7), \(\textbf{O}^i=(o^i_{rs})\) represents a symmetric matrix of ones and zeros whose indexes of 1’s indicate those range measurements \(r_{rs}\) with \(\{r,s\} \in \textbf{L}\) with non potential outliers. Ideally, without outliers in range measurements \(\textbf{O}^i\equiv \textbf{MC}\) and with outliers in range measurements for instance \((s,t)\in \textbf{L}\) leads to \(o^i_{rs}=0\), then \(\#\{\{r,s\} \in \textbf{L}: o^i_{rs}=1\} < \#\textbf{L}\). Initially, at the iteration \(i=0,\, \textbf{O}^i\equiv \textbf{MC}\), and through iterations, the selection process (i.e., the second stage) modifies the matrix \(\textbf{O}^i\) with zeros in those indexes \(\{i,j\} \in \textbf{L}\) with potential outliers. In (7), the Hadamard product between the matrix \(\textbf{O}^i\) and the term \(\textbf{D}^2-K(\textbf{Y}^{i})\) allows the minimization process focuses only on those range measurements considered as non outliers. This kind of optimization problems with semidefinite constraints can be solved using a software like SEDUMI [29]. Once the optimization process (7) has finished, a new square distance matrix \(\textbf{Y}^{i+1}\) is generated, and it will be used in the selection process.

In the second stage (i.e., the selection process), the distance errors between \(\textbf{Y}^{i+1}\) and \(\textbf{D}^2\) are weighted by \(\textbf{O}^{i}\) as shown in the Eq. (8). Then, the distance errors between sensors obtained in (8) are normalized as indicated by Eq. (9)

$$\begin{aligned}&\textbf{W}_{ed}=\left( \left| \textbf{Y}^{i+1} - \textbf{D}^2 \right| ^{1/2} \right) \odot \textbf{O}^{i}, \end{aligned}$$
(8)
$$\begin{aligned}&\bar{\textbf{W}}_{ed}:=\dfrac{\textbf{W}_{ed}}{ \text {max}\left( \textbf{W}_{ed} \right) }= \begin{bmatrix} \frac{{\textbf{W}_{\text {ed}_1}}}{{m_1}} \\ \frac{{\textbf{W}_{\text {ed}_2}}}{{m_2}} \\ \vdots \\ \frac{{\textbf{W}_{\text {ed}_n}}}{{m_n}} \end{bmatrix}, \quad \nonumber \\&m_i = \max (\textbf{W}_{\text {ed}_i}), \quad i=1,\dots , n, \end{aligned}$$
(9)

where \(\textbf{W}_{\text {ed}_i},i=1,\dots ,n\) denotes the ith row of \(\textbf{W}_{\text {ed}}\) and the term \(\text {max}\left( \textbf{W}_{ed_i} \right) \) refers to its maximum component \(m_i\) which in turn corresponds to the maximum distance error of it. Each row of the \(\bar{\textbf{W}}_{ed}\) matrix is ultimately weighted with a maximum value of 1, which corresponds to the maximum distance error.

Utilizing the weight matrix \(\bar{\textbf{W}}_{ed}\) and the procedure denoted as \( \left[ \cdot \right] _x \) in (10), the x higher values that display notable distance errors, in each row of the matrix, are isolated. Here, \(x=round \left( \rho *n \right) \) where \(\rho \in \left[ 0,1 \right] \) represents a percentage of the total n sensors to be rule out. To elaborate, for each sensor, the process identifies its x neighboring sensors that possess the highest errors and convert them to 0s within a binary connectivity matrix \(\textbf{B}\). Meanwhile, the remaining sensors maintain a value of 1, indicating their role as non outlier measures within the localization process.

$$\begin{aligned} \textbf{B}=\left[ \bar{\textbf{W}}_{ed}\right] _x. \end{aligned}$$
(10)

Lastly, the outlier matrix \(\textbf{O}^i\) is modified for the subsequent iteration, as depicted in Equation (11). Thus, after finishing the selection process, a new refined binary matrix \(\textbf{O}^{i+1}\) is provided to the minimization process to start the iterative process again. It is important to note that within this approach, once the estimated distance with a neighboring sensor is recognized as an outlier, it ceases to contribute in the localization process. Also, for each sensor, having at least a minimum of \(\alpha \) measurements with nearby sensors is necessary; otherwise, this condition prevents the removal of additional neighboring sensors. Algorithm 1 summarizes this selection-minimization scheme in detail.

$$\begin{aligned} \textbf{O}^{i+1}=\textbf{O}^i \odot \textbf{B}. \end{aligned}$$
(11)
Algorithm 1
figure a

The SelMin algorithm that minimizes error distances among sensor nodes using an alternation process.

Full size image

It is worth mentioning that in row 9 of algorithm 1, the multi-dimensional scaling (MDS) procedure is used to convert the new estimated distance matrix into estimated sensor positions useful to compute the RMSE during the simulation process. Here, \(\textbf{A}\) represents the set of anchor positions in the network, and \(\rho \) is heuristically selected with a value of 0.15.

4 Analysis and Results

To evaluate the performance of the proposed algorithm, a test methodology has been created where 30 independent sensor networks are used. Each network contains 50 nodes, all interconnected in one hop, where only three nodes are non-collinear anchors. These sensor nodes are distributed randomly and independently in an area of [250 m x 250 m]. Taking into account the previous description, the process to generate the test networks is divided into three stages as shown in Fig 1.

Fig. 1
figure 1

Test methodology with 30 reference networks, each with 50 nodes and three reference anchors. The estimated distances between each sensor are affected by Gaussian noise and atypical errors (outliers)

Full size image

In a first stage, without loss of generality, all the true distances between each of the sensors in network 1 are affected by a Gaussian noise level (with zero mean) and two standard deviations (\(sd =1\) and \(sd = 3\)) determined by equations (2-3). This last process generates two independent test networks of network 1. This methodology is repeated for each of the remaining networks, generating two sets of 30 independent networks that will be used in stage two. In stage 2, outliers are randomly added to the estimated distances between sensors. These added outliers range from 0\(\%\) to 50\(\%\) in steps of 5. That is, each percentage level of outliers affects all 30 benchmark networks (a test set), so there will be 22 independent test sets for stage 3. It is important to mention that outliers between sensor-sensor and sensor-anchors are affected by the random variable ȯ\(_{ij}\), ȯ\(_{kl}\) respectively, described in equation (1), that takes only three possible values 0.1, 1 and 10. Obviously, when ȯ\(_{ij}\) or ȯ\(_{kl}\) is 1 there is not an outlier. For example, considering a connected network of 50 sensor nodes, so there are 2450 distance estimates between sensors. If only \(10\%\) of the distance measurements are affected by outliers, 2205 distance estimates will have ȯ\(_{ij}\) and ȯ\(_{kl}=1\), and the remaining 245 distance estimates will be randomly affected either by ȯ\(_{ij}\) and ȯ\(_{kl}=0.1\) or 10.

In the stage 3, every test set, composed by 30 networks, is used to evaluate the performance of the proposed algorithm (i.e., SelMin). Position estimates are evaluated using the RMSE metric as shown in Equation (12).

$$\begin{aligned} RMSE=\sqrt{\frac{1}{m}\overset{m}{\underset{i=1}{\sum }}\left\| \textbf{p}_{i}-\bar{\textbf{p}}_i\right\| ^2 } \end{aligned}$$
(12)

where \(\left\| \cdot \right\| \) represents the 2-Norm, \(\textbf{p}_{i}\) and \(\bar{\textbf{p}}_i\) are the true and estimated position of the sensor \(s_i\), respectively; and m is the number unknown sensors in the network. Also, the DSCL algorithm [30], which uses the Levenberg-Marquardt (LM) approach to obtain initial estimates [31], is used to compare the performance of the proposed method.

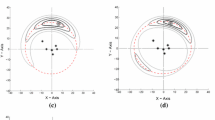
As described in Sect. 3, the proposed approach is composed of two processes: the minimization (7) and the selection (8-11) schemes working alternately. It is significant to notice that the selection procedure modifies \(\textbf{O}^i\) by attempting to omit outliers so that they are not taken into account in the minimization stage. If the term \(\textbf{O}^i\) remains constant, the proposed approach will only depend of the minimization stage. Thus, the outliers will significantly affect the minimization process. For example, figures 2 and 3 show the accuracy performance of the proposed scheme (with \(sd =1\) and \(sd =3\)) if only the minimization approach is used when \(\textbf{O}^i\equiv \textbf{MC}\) for \(i=\left\{ 1,2,3,...,10 \right\} \). It is clear that all iterations have the same pattern (or remains constant). As more outliers are added to the network, the RMSE rises as well. Clearly, the only findings that are helpful are those where the estimated distances between the sensors do not include any outliers.

Fig. 2
figure 2

Accuracy performance of the minimization scheme at different levels of outliers on range estimates and a standard deviation of one

Full size image
Fig. 3
figure 3

Accuracy performance of the minimization scheme at different levels of outliers on range estimates and a standard deviation of three

Full size image

Table 1 summarizes the performance of the optimization algorithm (7), which minimizes the error of distances between sensors when considering different levels of Gaussian noise and percentage of outliers in the measurements.

Table 1 Accuracy performance of the minimization approach at different percentage of outliers in the network when \(\textbf{O}^i\equiv \textbf{MC}\)
Full size table

Conversely, when the minimization scheme (7) is employed in conjunction with the outliers-selection approach (8-11), the estimation of distances between sensors shows notable improvement within a few iterations, as will be explained later. Fig. 4 shows the reduction in the number of outliers through iterations of the SelMin algorithm 1 with a noise level of \(sd = 1\). As can be observed, the algorithm completes the minimal outlier reduction for each contamination level in 8 iterations (averaged over the 30 networks), and the final RMSE for each contamination level is depicted in Fig. 5. As can be seen, while the removal of outliers is in process (8-11), the minimization approach (7) which indirectly affects the estimation of the sensor positions presents variations. However, once the outlier removal stabilizes (at iteration 8), so does the estimation of sensor positions. Table 2 displays the outcomes achieved of the SelMin and DSCL schemes after 10 iterations, considering various percentages of outliers and levels of noise.

Fig. 4
figure 4

The selection and the minimization process (SelMin approach) working alternatively to reduce outliers considering an \(sd = 1\)

Full size image
Fig. 5
figure 5

The selection and the minimization process (SelMin approach) working alternatively to reduce errors on position estimates considering an \(sd = 1\) with a zoom in the last five iterations

Full size image
Table 2 Accuracy performance and outliers reduction summary of the SelMin approach at different percentages of outliers and noise in the networks versus the DSCL approach
Full size table

Regarding to the SelMin approach, it is obvious that the precision of the estimated positions is reduced in direct proportion to how well outliers in the estimated distances between sensors are minimized. Regarding the last point, it can be considered that the RMSE position estimates, with \(sd=1\), between 0\(\%\) and 30\(\%\) of outliers present outstanding results as shown in Table 2. For instance, with 30\(\%\) of outliers (i.e., 734.8), these are reduced to 0.29\(\%\) (i.e., 7.2) giving a final RMSE of 9.22m of error in average.

On the other hand, Fig. 6 depicts the outliers reduction considering a Gaussian noise level of \(sd=3\) among distance measurements.

Fig. 6
figure 6

The selection and the minimization process (SelMin approach) working alternatively to reduce outliers considering an \(sd =3\)

Full size image
Fig. 7
figure 7

The selection and the minimization process (SelMin approach) working alternatively to reduce errors on position estimates considering an \(sd =3\) with a zoom in the last five iterations

Full size image

This procedure follows a similar behavior to that of the previous analysis. That is, all the levels of outliers suffer a considerable reduction, and these are minimized at 8 iterations. However, for this analysis, the best results are obtained in the range of \(0\%\) to \(25\%\) of outliers as shown Table 2. This means, assuming a \(25\%\) of outliers contamination in the measurements, the reduction is quite significant (from 613.1 to 3.4), producing an RMSE of 9.7m of inaccuracy on position estimates. As expected, the position estimations generally become less accurate with increasing errors from \(sd =1\) to \(sd = 3\) in the distance estimates between sensors in the 30 reference networks. Finally, after reducing the impact of outliers (after 8 iterations), the distance error is correspondingly minimized, as illustrated in Figure 7.

To evaluate the performance of the proposed algorithm, the same 30 reference networks and procedures, used previously, were tested in the DSCL algorithm and results are also summarized in the bottom of Table 2. Figures 8 and 9 show the error in the estimated positions after 10 iterations considering \(sd = 1\) and \(sd = 3\), respectively.

Fig. 8
figure 8

The Root Mean Square Error (RMSE) for position estimates provided by the DSCL algorithm is being assessed under a standard deviation (sd) of 1. This evaluation involves 10 iterations, and specific attention is given to the final five iterations

Full size image
Fig. 9
figure 9

The Root Mean Square Error (RMSE) for position estimates provided by the DSCL algorithm is being assessed under a standard deviation (sd) of 3. This evaluation involves 10 iterations, and specific attention is given to the final five iterations

Full size image

Contrasting the findings in Table 2, it is observed that when outliers are absent, the DSCL algorithm provides a slightly more accurate estimation of the sensor positions compared to the proposed algorithm. However, in the presence of outliers, the proposed scheme demonstrates remarkable performance, surpassing the DSCL algorithm.

5 Conclusions and Future Works

This paper introduces a method for enhancing centralized Wireless Sensor Network (WSN) localization based on range measurements. This method utilizes a two-step process: one step aims to reduce errors in distance measurements between sensor nodes, while the other step focuses on eliminating inconsistencies in distance measurements. This iterative dual-step approach enhances the system’s resilience to anomalies in distance estimates due to environmental factors and network configurations. Experimental results using simulated data sets confirm the effectiveness of this approach, particularly when a significant number of outliers distance estimates are present. For instance, results demonstrate that the proposed scheme achieves total or partial elimination of outliers in less than seven iterations, indicating not only its suitability for integration in hostile environments, particularly those relying on RSS measurements with hardware constraints, but also its potential for saving energy. On the other hand, when encountering outliers amounting to less than \(10\%\), the SelMin algorithm maintained a similar behavior regarding the minimization of the error in the position estimates, which indicates its robustness against a moderate presence of atypical measurements. Additionally, the algorithm maintains a satisfactory RMSE even at a 25\(\%\) outlier rate, exhibiting less than half the error compared to the DSCL algorithm in identical circumstances. In practical applications, the suggested method can be executed on constrained embedded systems, like Raspberry Pi and LattePanda, among others.

Shortly, there are plans to develop and test the proposed method in a distributed setting, taking advantage of matrix completion and multi-hop networks. An additional approach will be to employ real testbeds to evaluate the model under different constraints, such as noise ratio, anisotropic networks, and the number of anchor nodes. Additionally, future research will investigate the application of artificial intelligence techniques to identify“outliers”more thoroughly.