Using electron fluid models to analyze plasma thruster discharges

Abstract

Fluid models of the slow-dynamics of magnetized, weakly-collisional electrons lead to build computationally-affordable, long-time simulations of plasma discharges in Hall-effect and electrodeless plasma thrusters. This paper discusses the main assumptions and techniques used in 1D to 3D electron fluid models, and some examples illustrate their capabilities. Critical aspects of these fluid models are the expressions for the pressure tensor, the heat flux vector, the plasma-wall fluxes, and the high-frequency-averaged electron transport and heating caused by plasma waves, generated either by turbulence or external irradiation. The different orders of magnitude of the three scalar momentum equations characterize the electron anisotropic transport. Central points of the discussion are: the role of electron inertia, magnetically-aligned meshes versus Cartesian-type ones, the use of a thermalized potential and the infinite mobility limit, the existence of convective-type heat fluxes, and the modeling of the Debye sheath, and wall fluxes. Plasma plume models present their own peculiarities, related to anomalous parallel cooling and heat flux closures, the matching of finite plume domains with quiescent infinity, and solving fully collisionless expansions. Solutions of two 1D electron kinetic models are used to derive kinetically-consistent fluid models and compare them with more conventional ones.

Introduction

In the last decade, plasma propulsion has taken from chemical propulsion the leadership of primary in-space propulsion for many mission types: from large geostationary satellites to constellations of mid and mini satellites, space tugs, and plans for Lunar and Mars orbiting. The most mature technologies in plasma propulsion are the gridded ion thruster (GIT) and the Hall effect thruster (HET). GITs have better propulsive performances but are less throttable and more complex as a system (mainly electrically). Except for interplanetary missions, HETs tend to be cost-optimal, making them the dominant technology today [1].

With the boom of new space applications and more ambitious goals for classical ones, the requirements on new plasma thrusters are more demanding and varied. The design, testing, and certification of new HET prototypes is a very long and costly process, raising a serious concern on whether the expected large demand will be satisfied on time properly. The whole development cycle of a HET would benefit much if reliable, predictive simulations tools of all functional aspects of the thruster were available. A central bottleneck to achieve this is the reliable simulation of the plasma discharge, since this determines the propulsive performances of the thruster, the thermal loads on the thruster assembly, the requirements on the electric subsystem, and the degradation of thruster surfaces.

The physics of the plasma discharge in HETs is quite complex in phenomena and not fully understood yet, thus explaining the lack of fully predictive models. In particular, two characteristics of the discharge are at the core of the modeling issues. First, the plasma is rarefied, (i.e. weakly collisional) and the velocity distribution function (VDF) of each species can be non-Maxwellian. Plasma-wall interaction and collisional processes are specially affected by this. Thus, kinetic models are required, at least partially, for a fully-consistent description. Second, the plasma is meso-magnetized (i.e. electrons tend to be fully magnetized while ions are weakly magnetized in channel and plume), which gives rise to (i) anisotropic electron dynamics and (ii) high-frequency, wave-based turbulence. These two phenomena lead to the anomalous cross-field transport of electrons, which penalizes performances. However, after several decades of research, a minimally-reliable macroscopic model of that transport, to be implemented in codes describing HET long-time performances, is lacking.

In addition to mature plasma propulsion technologies, other ones are being researched, looking for potential advantages in terms of cost, simplicity, performances, application niche, etcetera. The electrodeless plasma thruster (EPT) family pertains to that category [2]. An EPT consists of two stages. First, there is the thruster channel, where plasma production and heating is achieved by absorption of the energy of electromagnetic (EM) waves generated by an external emitter. The second stage is a magnetic nozzle (MN) [3], i.e. a longitudinal convergent-divergent magnetic field, created by an external magnetic circuit and responsible of channeling and accelerating supersonically the plasma beam. The helicon plasma thruster (HPT) [4,5,6] and the electron cyclotron resonance thruster (ECRT) [7, 8] are two prominent designs of EPTs. While HETs and EPTs present obvious differences in their mechanisms to energize the plasma, the electron modeling framework for both of them is the same. Finally, the electron framework for HETs is also applicable to the high efficiency multistage plasma thruster [9] and the mid-power applied-field magnetoplasmadynamic thruster [10].

The weak collisionality of HET and EPT discharges makes particle-in-cell (PIC) formulations very efficient computationally (although noisy) for kinetic models of the plasma discharge. However, full-PIC 3D modeling of all plasma species, describing the long-time response (i.e. about 1-10 miliseconds) of the discharge is hardly affordable yet because of its huge computational cost. This is due to the smallness of the Debye length and the inverse of the plasma frequency. Furthermore, in a PIC formulation, the timesteps for advancing neutrals (subindex n), ions(i), and electrons(e) scale typically as $\Delta t_n \sim 10^2 \Delta t_i \sim 10^4 \Delta t_e.$ Consequently (and as it is customary in applied research), practical modeling must sacrifice some parts of the physics, and the selection depends on the goals of the study. For instance, for the analysis of fundamental phenomena in HETs, such as high-frequency instabilities and kinetic aspects of the plasma-wall interaction, the very slow dynamics of neutrals are highly simplified [11, 12]. On the contrary, to carry out parametric analyses of the long-time, full discharge in both thruster and plume, it is common to adopt: an axisymmetric (2D) configuration, the zero-Debye length limit, and a fluid modeling of electrons. This allows a numerical discretization with $\Delta t_e \sim \Delta t_i$ and larger spatial cells, that, together with the lower dimensionality, implies a reduction of about two orders of magnitude in computational cost (say from 3 months to 1 day).

This paper is devoted to discuss existing electron fluid models simulating the 1D to 3D slow dynamics of the plasma discharge in HETs and EPTs, highlighting capabilities, limitations, and aspects requiring further improvement. The paper attempts to compile the knowledge acquired by the author in developing and applying these fluid models. Naturally, to describe completely the plasma discharge, the electron model must be coupled with (kinetic or fluid) models of ions and neutrals. These are out of discussion in this paper but are treated in many works cited here and in recent reviews on HET discharge modeling [12,13,14].

3D Electron fluid models section describes the general 3D fluid model to be adopted for electrons, which corresponds to an 8-moment integral of the Boltzmann equation. High-frequency and slow dynamics of electrons are distinguished. The first ones would include both wave-based instabilities (in HETs and EPTs) and the plasma response to coherent EM waves (in EPTs). The interest here is on the slow-dynamics model, which includes time-averaged contributions from high-frequency oscillations and admits the drift-diffusive and zero-Debye length limits. Axisymmetric discharges in plasma thrusters section discusses the slow-dynamics model for axisymmetric discharges and the issues related to the magnetic anisotropy. The successful implementation of this model in simulation tools for HETs and EPTs is illustrated with examples. 1D axial fluid model section presents a reduced 1D axial model for HETs, highlighting recent advances. 1D models are quick to run and more flexible than 2D ones to analyze aspects such as electron inertia, empirical turbulence models, or even unstable longitudinal modes. Fluid models from 1D fully kinetic solutions section presents two different 1D kinetic models of electrons and the fluid models satisfied by their solutions. They are meant to illustrate the strengths and weaknesses of conventional fluid models. Electron fluid models for large plumes section focuses on the particularities of electron fluid models for large plasma plumes. Two cases are considered: a collisionless plasma channelled by an axisymmetric MN, and a general 3D scenario for weakly collisional plumes. The Appendix covers the modeling of the Debye sheath. In the zero-Debye length limit, these sheaths and their modeling are crucial to couple the quasineutral discharge to different types of thruster walls and to determine correctly fluxes of particles, momentum, and energy to the walls.

3D Electron fluid models

A general model

Electron macroscopic (i.e. fluid) models are obtained by taking velocity integral moments of the Boltzmann equation on the electron VDF. The main moments provide the equations for continuity, momentum, and energy [13, 15]:

$$\begin{aligned} \frac{\partial n_e}{\partial t}+\nabla \cdot n_e \varvec{u}_e = S_p, \end{aligned}$$

(1)

$$\begin{aligned} m_e\Big (\frac{\partial n_e \varvec{u}_e}{\partial t} + \nabla \cdot n_e \varvec{u}_e \varvec{u}_e\Big )= -e n_e \varvec{E} + \varvec{j}_e \times \varvec{B} -\nabla \cdot \bar{\bar{p}}_e+ \varvec{F}_{c}, \end{aligned}$$

(2)

$$\begin{aligned} \frac{\partial }{\partial t} \left( \frac{1}{2} m_eu_e^2n_e +\frac{3}{2} p_e \right) + \nabla \cdot \left[ \left( \frac{1}{2} m_eu_e^2n_e +\frac{3}{2} p_e \right) \varvec{u}_e +\bar{\bar{p}}_e\cdot \varvec{u}_e +\varvec{q}_e \right] = \varvec{j}_e \cdot \varvec{E} + Q_{c}. \end{aligned}$$

(3)

Here, $n_e$ is the number density, $\varvec{u}_e$ is the macroscopic velocity, $\bar{\bar{p}}_e$ is the pressure tensor, $p_e=n_eT_e=\text {trace}(\bar{\bar{p}}_e)/3$ is the scalar pressure, $\varvec{j}_e=-e n_e \varvec{u}_e$ is the current density, $\varvec{q}_e$ is the heat flux vector, $\varvec{E}$ and $\varvec{B}$ are the electromagnetic fields, $S_p$ is the electron production rate, and $\varvec{F}_c$ and $Q_c$ are collisional contributions. If $\bar{\bar{p}}_e$ reduces to $p_e \bar{\bar{I}}$, and $\varvec{q}_e$ is negligible, the above equations constitute a closed (isotropic and adiabatic) 5-moment model. The addition of a relation for the heat flux in terms of lower order moments –such as a Fourier’s conductive law for $\varvec{q}_e(n_e, T_e)$– constitutes the 8-moment isotropic model, typical of standard fluid dynamics [15]. This 8-moment model is the main one being used in the literature to describe electrons in HET and EPT discharges.

An alternative fluid model is the Chew-Goldberger-Low (CGL) one [16], which, for near-collisionless electrons immersed in a strong magnetic field $\varvec{B}= B\varvec{1}_\parallel$, shows the pressure tensor to be diagonal and anisotropic,

$$\begin{aligned} \bar{\bar{p}}_e=p_{\parallel e}\varvec{1}_\parallel \varvec{1}_\parallel +p_{\perp e}(\bar{\bar{I}}-\varvec{1}_\parallel \varvec{1}_\parallel ). \end{aligned}$$

(4)

The CGL model adds to Eq. (3) an equation for the parallel energy $3p_{\parallel e}/2$, and two closure laws for the components $q_{\parallel e}=\varvec{q}_e\cdot \varvec{1}_\parallel$ and $\varvec{q}_{\perp e}=\varvec{q}_e-q_{\parallel e}\varvec{1}_\parallel$ of the heat flux vector $\varvec{q}_e$. Particular cases of the CGL model will be found in Fluid models from 1D fully kinetic solutions section. Finally, higher-order models, such as the Grad 13-moment model [17], the maximum-entropy 14-moment [18], or Ramos’ 20-moment model [19], consider equations for all pressure tensor and heat flux vector components, and different closure laws. These high order models are currently too ambitious to simulate the electron fluid in the complex HET and EPT discharges.

The drift-diffusive, slow-dynamics model

The electron motion in these discharges includes both fast and slow dynamics, and is strongly affected by the magnetic field and the scarcity of collisions. Apart from transient phenomena, fast dynamics (with typical times below, say, 1 $\mu s$) are related to oscillations produced by several instabilities [12,13,14] and, in EPTs, by the external EM emission too. The comprehension of the electron dynamics benefits much from considering that fast and slow collective motions can be studied (almost) independently. The study of self-developed turbulence is particularly complex, due to the multiplicity of modes and their coupling. Kinetic models, generally particle-based, are needed for a complete picture of turbulence [20]. Slow-dynamics fluid models are suitable mainly to analyze the plasma transport problem (and thruster performances), but they include, in general, secular terms from time-averaged correlations among high-frequency variables. A consistent separation between fast and slow dynamics and the subsequent determination of these secular contributions, is still a formidable problem and the main weakness of slow-dynamics fluid models.

In plasma thrusters, the electron population is confined except for small flows (of high energy electrons) drifting with the ion flows to the thruster walls and the downstream plume. This justifies to claim the drift-diffusive limit for the electron fluid velocity,

$$\begin{aligned} u_e^2 \ll c_e^2 \equiv T_e/m_e. \end{aligned}$$

(5)

Next, if the electron distribution function is assumed near-Maxwellian, the electron pressure tensor is reduced to $\bar{\bar{p}}_e\simeq p_e \bar{\bar{I}}$. As a result the one-temperature, drift-diffusive, slow-dynamics expressions of the momentum and energy Eqs. (2) and (3) are

$$\begin{aligned} \varvec{0}= -e n_e \varvec{E} + \varvec{j}_e \times \varvec{B} -\nabla p_e+\varvec{F}_{c}+\varvec{F}_a, \end{aligned}$$

(6)

$$\begin{aligned} \nabla \cdot \varvec{P}^{\prime \prime }_e = \varvec{j}_e \cdot \varvec{E} + Q_{c}+Q_a- \frac{3}{2} \frac{\partial p_e}{\partial t}. \end{aligned}$$

(7)

with

$$\begin{aligned} \varvec{P}^{\prime \prime }_e = (5/2) n_eT_e \varvec{u}_e +\varvec{q}_e \end{aligned}$$

(8)

the flux of electron energy (in the drift-diffusive limit). For sake of simplicity in the nomenclature, the symbols for all plasma magnitudes here refer only to values averaged over the high-frequency range. The magnetic field induced by the (mild) electric currents in HETs and EPTs is marginal, so $\varvec{B}$ in Eq. (6) can be taken just as the static, applied magnetic field.

In the drift-diffusive limit and assuming that fourth-order moments are negligible, the diffusive equation for $\varvec{q}_e$ reduces to [15]

$$\begin{aligned} 0=-\frac{5p_e}{2e}\nabla T_e-\varvec{q}_e\times \varvec{B}+\varvec{Y}_{c}+\varvec{Y}_{a}, \end{aligned}$$

(9)

and closes the set of fluid equations. In Eqs. (6), (7), and (9), $\varvec{F}_c$, $Q_c$, and $\varvec{Y}_c$ account for the collisional contributions, while $\varvec{F}_a$, $Q_a$, and $\varvec{Y}_a$ are the ‘anomalous’ secular terms from the high-frequency dynamics (subscript e has been omitted in these two sets of variables). From Eq. (6), the electric field work appearing in Eq. (7) is

$$\begin{aligned} \varvec{j}_e \cdot \varvec{E}= \varvec{u}_e\cdot \nabla p_e -\varvec{u}_e\cdot (\varvec{F}_{c}+\varvec{F}_a). \end{aligned}$$

(10)

The term $(-\varvec{u}_e\cdot \varvec{F}_{c})$ is the standard Joule heating and $(-\varvec{u}_e\cdot \varvec{F}_a)$ plus Q_a constitutes the anomalous electron heating in Eq. (7).

The above equations constitute the main electron slow-dynamics model to be analyzed here. The discussion will cover, on one side, its application to different discharges and, on the other side, the validity of the drift-diffusion limit, the isotropic pressure assumption, and the conductive Fourier’s law (9).

In HETs, the anomalous terms would represent wave-based turbulence; in EPTs they would correspond to both turbulence and the plasma interaction with the EM mission. For instance, if the high-frequency contribution were due only to a high-frequency electric field $\varvec{E}^\prime$, one would have $\varvec{F}_a\approx \langle n_e^\prime \varvec{E}^\prime \rangle$ and $Q_a\approx \langle \varvec{j}_e^\prime \cdot \varvec{E}^\prime \rangle$, where $\langle \rangle$ means time-averaging over the high-frequency magnitudes (here identified with primes as superscripts). In general, high-frequency, short-length electron inertia is expected to contribute to the wave-based terms too [21, 22]. Consistent expressions for the three wave-based terms, $\varvec{F}_a$, $Q_a$, and $\varvec{Y}_a$, must be obtained from solving the high-frequency dynamics (where the drift-diffusive approximation is not expected to apply). In the case of EPTs, partially-consistent results have been obtained for the spatial map of absorbed power density $Q_a$ from the external irradiation, while terms $\varvec{F}_a$ and $\varvec{Y}_a$ have been ignored so far [23, 24]. The central importance of turbulent transport in HETs is acknowledged since their early development [25, 26] and a large effort is being made in determining $\varvec{F}_a$ (e.g. [20]), but this turbulent (macroscopic) force lacks a consistent characterization yet. Anyway, the discussion of the high-frequency dynamics is out of the scope of this paper. Here, simple empirical models, widely used in the HET's literature, will be used to complete and solve the slow-dynamics model.

The quasineutral plasma case

The electron drift-diffusive fluid model is matched with fluid or kinetic models for the different heavy species (neutrals, singly-charged ions,...). These provide, for each heavy species s, its density $n_s$, particle flux $\varvec{g}_s\equiv n_s\varvec{u}_s$, and higher-order magnitudes. For typical thruster conditions the plasma is quasineutral, thus satisfying

$$\begin{aligned} n_e=\sum _s Z_sn_s, \end{aligned}$$

(11)

with $Z_s$ the charge number of species s. Then, the electron continuity Eq. (1) can be substituted by the current conservation equation,

$$\begin{aligned} \nabla \cdot \varvec{j}_e=- \nabla \cdot \varvec{j}_i+S_c, \end{aligned}$$

(12)

where $\varvec{j}_i=\sum _s eZ_s\varvec{g}_s$ is the ion current density and $S_c$ represents any volumetric source of electric current (such as the cathode electron source in some HET models [27]).

The collisional force $\varvec{F}_{c}$ in Eq. (6) is expressed now as

$$\begin{aligned} \varvec{F}_{c}=-m_en_e\sum _s \nu _{es}(\varvec{u}_e-\varvec{u}_s) \equiv \mu _e^{-1}(\varvec{j}_e+\varvec{j}_c), \end{aligned}$$

(13)

with $\mu _e=e/(m_e\nu _e)$ the scalar mobility, $\nu _e=\sum _s \nu _{es}$ the total electron momentum transfer collision frequency, and $\varvec{j}_c=e n_e\sum _s (\nu _{es}/\nu _e)\varvec{u}_s$ the contribution of heavy species to $\varvec{F}_{c}$. Similarly, a Krook model on collisions yields, in Eq. (9),

$$\begin{aligned} \varvec{Y}_{c}=-\mu _e^{-1} \varvec{q}_e. \end{aligned}$$

(14)

Using Eq. (13), the momentum Eq. (6) can be re-expressed as a generalized Ohm’s law

$$\begin{aligned} \varvec{j}_e=\bar{\bar{\mu }}_e\cdot \left( -en_e\nabla \phi +\nabla p_e- \varvec{F}_a-\mu _e^{-1}\varvec{j}_c \right) , \end{aligned}$$

(15)

where $\phi$ is the electric potential (i.e. $\varvec{E}=-\nabla \phi$) and

$$\begin{aligned} \bar{\bar{\mu }}_e=\mu _e \left( \begin{array}{ccc} 1 &{} \chi b_z &{} -\chi b_y\\ - \chi b_z &{} 1 &{} \chi b_x\\ \chi b_y &{} -\chi b_x &{} 1 \end{array} \right) ^{-1} \end{aligned}$$

(16)

is the mobility tensor, with $\chi =\omega _{ce}/\nu _e \equiv B\mu _e$ the Hall parameter, and $(b_x,b_y,b_z)=\varvec{B}/B\equiv \varvec{1}_{\parallel }$. Next solving Eq. (9) for $\varvec{q}_e$ yields the Fourier’s law

$$\begin{aligned} \varvec{q}_e =- \bar{\bar{\mu }}_e \cdot \big [({5p_e}/{2e})\nabla T_e - \varvec{Y}_a\big ], \end{aligned}$$

(17)

which can be replaced in the definition of $\varvec{P}''_e$, Eq. (8). For the strongly-magnetized electron case of interest, it is $\chi \gg 1$ and the tensor $\bar{\bar{\mu }}_e$ is ill-conditioned [28, 29]. As later sections discuss this is the key difficulty to obtain accurate numerical solutions of Eqs. (15) and (17).

Equations (7) and (8) for the pair $(T_e, \varvec{P}^{\prime \prime }_e)$ have the same functional form than Eqs. (12) and (15) for the pair $(\phi , \varvec{j}_e)$. Hence the same numerical algorithms for the spatial derivatives can be implemented to the two pairs. Still, Eqs. (7)-(8) include nonlinear terms on $T_e$, which could require adding iterative schemes, and temporal derivatives.

Finally, the quasineutral plasma model must be completed with a model resolving the Debye sheaths around the thruster walls. Generally these are normal sheaths, with the wall potential lower than plasma potential, and the potential fall controlling the electron flux to the walls. An accurate sheath model for each type of surface is essential to determine correctly the plasma losses to the wall and the impact energies of heavy species. The Appendix discusses the sheath model and provides expressions for the perpendicular components of $\varvec{j}_e$ and $\varvec{P}^{\prime \prime }_e$ at the sheath edges, which are boundary conditions of the electron model in the quasineutral plasma.

An empirical turbulence model

Equation (15) includes $\varvec{F}_a$ as an extra force on the right side. A simple, widely-used, empirical model for the turbulent force is [30]

$$\begin{aligned} \varvec{F}_a=\alpha _a B \varvec{j}_{e},\quad \varvec{Y}_a=-\alpha _a B \varvec{q}_{e}, \quad Q_a=0, \end{aligned}$$

(18)

with $\alpha _a(\varvec{r})$ a dimensionless function, to be adjusted with experimental data. Equation (18) assumes that $\varvec{F}_a$ is parallel to $\varvec{u}_{e}$ and the turbulence level is ‘comparable’ in the three spatial directions, but there is no evidence supporting any of this; in Axisymmetric discharges in plasma thrusters section, a ‘scalar’ version of this model will be proposed. The appeal of Eq. (18) is that $\varvec{F}_a$ and $\varvec{Y}_a$ are easily combined with $\varvec{F}_c$ and $\varvec{Y}_c$ to constitute ‘effective’ collisional contributions. Thus, turbulence-modified collisional parameters are defined as

$$\begin{aligned} \nu _e^*=\nu _e+\alpha _a\omega _{ce}, \quad \mu _e^*=e/m_e\nu _e^*, \quad \chi ^*=B{\mu _{e}^*}, \end{aligned}$$

(19)

and they allow us to rewrite Eqs. (15) and (17) as

$$\begin{aligned} \varvec{j}_e=\bar{\bar{\mu }}_e^*\cdot \left( -en_e\nabla \phi +\nabla p_e-\mu _e^{-1}\varvec{j}_c\right) , \end{aligned}$$

(20)

$$\begin{aligned} \varvec{q}_e = -\frac{5p_e}{2e} \bar{\bar{\mu }}_e^* \cdot \nabla T_e. \end{aligned}$$

(21)

Clearly, the choice of $\alpha _a(\varvec{r})$ affects the electron response. For plasma discharges in conventional HETs, with quasi-radial magnetic field, expressions of $\alpha _a(z)$ with several free parameters are being used. The fitting of these parameters tries to replicate available experimental data, such as thrust and discharge current [31] or, better, the time-averaged $\phi (z)$ or $u_{zi}(z)$ in the mid-channel location [32]. A certain consensus on $\alpha _{a}(z)$ suggests it is smaller within the channel than in the near plume, and would present a minimum around the maximum of $E_z(z)$ [31,32,33,34]. In EPTs with a quasi-axial magnetic field, $\alpha _a=$const is being used [35], partly due to the limited experimental evidence on anomalous diffusion in these devices. In HETs with 2D magnetically-shielded (MS) topologies, the choice of $\alpha _a(\varvec{r})$ seems more delicate; however, axial functions $\alpha _a(z)$ are used too, supported on the idea that anomalous transport is larger in the near plume than inside the MS chamber.

Axisymmetric discharges in plasma thrusters

This axisymmetric configuration is the most interesting one for plasma thrusters, and it still allows the analysis of varied geometrical and magnetic details. A cylindrical reference frame {$\varvec{1}_z$, $\varvec{1}_r$, $\varvec{1}_{\theta }$} with coordinates (z, r, $\theta$) is adopted, and $\partial /\partial \theta =0$ is assumed for the slow-dynamics discharge. Additionally, a magnetic reference frame {$\varvec{1}_{\parallel }$, $\varvec{1}_{\top }$, $\varvec{1}_{\theta }$} is defined, with $\varvec{1}_{\parallel }=\cos \alpha _B \varvec{1}_z+\sin \alpha _B \varvec{1}_r$, $\alpha _B$ the local magnetic angle, and $\varvec{1}_{\top }=\varvec{1}_{\theta }\times \varvec{1}_{\parallel }$.

Let us use the notation $\nabla _k\equiv \partial /\partial \varvec{1}_k$ for partial derivatives. In the magnetic reference frame, the scalar electron momentum equations read

$$\begin{aligned} 0=en_e \nabla _\parallel \phi - \nabla _\parallel p_e +F_{\parallel c}+F_{\parallel a}, \end{aligned}$$

(22)

$$\begin{aligned} 0=j_{\theta e}B+en_e \nabla _\top \phi -\nabla _\top p_e +F_{\top c}+F_{\top a}, \end{aligned}$$

(23)

$$\begin{aligned} 0=-j_{\top e}B +F_{\theta c}+F_{\theta a}, \end{aligned}$$

(24)

where Eq. (24) does not contain electric and pressure forces. For $\chi \gg 1$, the dominant terms in each of these three scalar equations are of different order, indicating the large anisotropy of electron dynamics. Furthermore, the relative orders of the three equations differ between discharge regions, and differ between HETs and EPTs too. For instance, in the acceleration region of a HET, the dominant terms of Eqs. (22) to (24) are, respectively,

$$\begin{aligned} en_e \nabla _\parallel \phi , \quad en_e \nabla _\top \phi \sim j_{\theta e}B, \quad j_{\top e}B, \end{aligned}$$

and typical ratios among them are

$$\begin{aligned} \frac{en_e \nabla _\parallel \phi }{en_e \nabla _\top \phi } \sim \frac{1}{10}, \qquad \frac{j_{\top e}B}{j_{\theta e}B}\equiv \frac{u_{\top e}}{u_{\theta e}}\sim \frac{1}{100}, \end{aligned}$$

(25)

(except for the first ratio, tending to be O(1) in the anode region of a HET and in most of an EPT discharge). These relative values imply that contributions that are small in Eqs. (22) and (23), can be essential in the azimuthal momentum Eq. (24). Indeed, this is the case of collisional and turbulent azimuthal forces (and electron azimuthal inertia) in the absence of azimuthal electric and pressure forces.

In an axisymmetric configuration an alternative to the empirical turbulence model (18) is [36]

$$\begin{aligned} \varvec{F}_a=\alpha _a B j_{\theta e}\varvec{1}_\theta , \quad \varvec{Y}_a=-\alpha _a B q_{\theta e}\varvec{1}_\theta , \quad Q_a=0, \end{aligned}$$

(26)

which has the advantage of affecting only the azimuthal equations. This facilitates the assessment of $\alpha _a$ (comparing scalar magnitudes, instead of vector ones) and does not introduce a wave-based anomalous transport along the magnetic field. Then, solving for the components of the electron current yields

$$\begin{aligned} j_{\parallel e} = \mu _e\left( -en_e \nabla _\parallel \phi +\nabla _\parallel p_e \right) -j_{\parallel c}, \end{aligned}$$

(27)

$$\begin{aligned} j_{\top e} = \frac{ \mu _e (-en_e\nabla _\top \phi +\nabla _\top p_e)+\chi ^* j_{\theta c}-j_{\top c} }{1+\chi \chi ^{*}}, \end{aligned}$$

(28)

$$\begin{aligned} j_{\theta e}= \chi ^* (j_{\top e}-j_{\theta c}/\chi ). \end{aligned}$$

(29)

Similarly, the equations for the heat flux read

$$\begin{aligned} q_{\parallel e} = -\mu _e\frac{5p_e}{2e}\nabla _\parallel T_e, \end{aligned}$$

(30)

$$\begin{aligned} q_{\top e} =- \frac{\mu _e}{1+\chi \chi ^{*}}\frac{5p_e}{2e}\nabla _\top T_e, \end{aligned}$$

(31)

$$\begin{aligned} q_{\theta e}= \chi ^* q_{\top e}. \end{aligned}$$

(32)

The equations for $j_{\theta e}$ and $q_{\theta e}$ are uncoupled from the rest, and the contribution of $\varvec{j}_c$ to $\varvec{j}_e$ is small generally.

Wall conditions inside the thruster channel imply usually that $j_{\parallel e}\sim j_{\top e}$. Therefore, for $\chi ^*\gg 1$, the parallel and perpendicular derivatives on the right side of Eqs. (27) and (28) differ in $O(\chi \chi ^{*})$, say $O(10^5)$ in conventional HETs. As a result, in Eq. (27), we expect

$$\begin{aligned} en_e \nabla _\parallel \phi \approx T_e\nabla _\parallel n_e \gg |\mu _e^{-1}(j_{\parallel e}+j_{\parallel c})-n_e\nabla _\parallel T_e|. \end{aligned}$$

(33)

Then, to compute correctly $j_{\parallel e}$, it is convenient to define a ‘thermalized potential’ [26, 27, 37]

$$\begin{aligned} \Phi =\phi -\frac{T_e}{e}\ln \frac{n_e}{n_0}, \end{aligned}$$

(34)

which measures the deviation of the electron response from the Boltzmann relation; here, $n_0$ is a convenient reference value, generally chosen to operate with $n_e/n_0\sim 1$. Using $\Phi$, Eq. (27) becomes

$$\begin{aligned} j_{\parallel e}=-en_e \mu _e\nabla _\parallel \Phi + \Big (1-\ln \frac{n_e}{n_0}\Big ) n_e\mu _e\nabla _\parallel T_e -j_{\parallel c}. \end{aligned}$$

(35)

If the turbulence model (18) were used, $\mu _e$ and $\chi$ in Eqs. (27)-(32) would be substituted by $\mu _e^*$ and $\chi ^*$, respectively. For $\chi ^*\gg 1$, the only difference between the two turbulence models is in Eqs. (27) and (30). Incidentally and as the Appendix further comments, in a 2D inertialess model, Eq. (24) cannot include consistently ‘wall collisionality’, that is the loss of azimuthal momentum caused by exchanging magnetized electrons at the walls by unmagnetized ones.

Certain HET discharge models [13, 27, 34, 37] apply the so-called Morozov’s collisionless limit, $\mu _e\rightarrow \infty$, to Eqs. (30) and (35). This yields $\nabla _\parallel \Phi =0$ and $\nabla _\parallel T_e=0$, that is, magnetic lines are isothermal and the Boltzmann relation, $n_e \propto \exp (-e\phi /T_e)$, applies along them. The important drawback of this collisionless limit is that $j_{\parallel e}$ cannot be computed from the Ohm’s law (35). [An example of the computation of $\varvec{j}_e$ in a collisionless discharge, without Ohm’s law is given in 1D-axial kinetic model of a paraxial plume Section.]

Solving the 2D electron fluid equations in a cylindrical mesh yields $\nabla _z \Phi$ and $\nabla _r\Phi$, where from $\nabla _\parallel \Phi =\cos \alpha _B \nabla _z \Phi + \sin \alpha _B \nabla _r\Phi$. One expects

$$\begin{aligned} \nabla _z \Phi \sim \nabla _r\Phi \sim \nabla _\top \Phi \sim \chi ^{*2}\nabla _\parallel \Phi , \end{aligned}$$

(36)

but small numerical errors in the cylindrical derivatives of $\Phi (z,r)$ is likely to give, incorrectly, $\nabla _\parallel \Phi \gg \nabla _\top \Phi /\chi ^{*2}$. This error in the solution is known as numerical diffusion, and can be avoided by using a magnetic-field-aligned mesh (MFAM), where the derivatives of $\nabla _\parallel \Phi$ and $\nabla _\top \Phi$ are computed directly.

MFAMs are used for instance in the axisymmetric codes HALL2De [38] and HYPHEN [30, 36]. These meshes are very suitable for complex, oblique magnetic topologies, such as the example shown in Fig. 1(a) for the simulation of a MS-HET; notice the singular magnetic point inside the channel, separating regions with quasi-axial and quasi-radial magnetic lines. The big issue with MFAMs, well illustrated in Fig. 1(a), is they have very irregular cells and the mesh boundaries are not magnetically aligned [39]. This made delicate to derive accurate algorithms for spatial derivatives in MFAMs, mainly at boundary cells [40, 41]; for instance, algorithms based on weighted-least-squares methods lead to numerical diffusion and large errors in Eq. (35) at the channel boundaries.

Fig. 1

Simulation of an axisymmetric MS-HET with HYPHEN for a configuration similar to [31]. a MFAM: magnetic lines are in blue and the ortoghonal family is in red; the black box is the location of the central cathode which emits electrons and neutrals. b-f Time-averaged 2D maps of $n_e$, $T_e$, $\phi$, and the electron and ion currents in a meridian plane (i.e excluding the azimuthal components, $\varvec{\tilde{\jmath }}_e=\varvec{j}_e-j_{\theta e} \varvec{1}_\theta$, and same for ions)

The code HYPHEN complements the electron slow-dynamics fluid model with a PIC model for heavy species. Figure 1 shows a first example of the capabilities of the whole code for simulating a MS-HET. The plasma density and the map of $\varvec{j}_i$ are determined by the PIC model, and the other three variables by the electron model. The plot (e) of the longitudinal current $\varvec{\tilde{\jmath }}_e=\varvec{j}_e-j_{\theta e}\varvec{1}_\theta$ is particularly interesting: the cathode-emitted electron current splits into a beam travelling downstream and neutralizing the ion plume, and a beam entering the channel and ionizing neutrals; this second beam requires enough collisional events to be driven easily into the channel; and, inside the thruster, the lines around the null magnetic point guide the electron current, shielding it from the lateral walls. In plot (c) and as expected, $\nabla _\parallel T_e$ is small and magnetic lines are near-isothermal; $\nabla _\parallel \Phi$ (not shown here) is small too. On the contrary, isopotential lines on $\phi$ are not aligned with the magnetic field due to the term $\nabla _\parallel n_e$ in Eq. (34).

As a second example, Fig. 2 illustrates, for an ECRT, the coupled stationary response of (i) the electron slow-dynamics fluid model with (ii) the high-frequency (fluid) model for the electron-wave interaction [35]. This last one solves the Maxwell equations with a plasma cold dielectric tensor, dependent on $n_e$ and $T_e$ and computes $Q_a=\langle \varvec{j}'_e\cdot \varvec{E}'\rangle$. Figure 2 plots $Q_a$ and the different wave propagation regions in the Clemmow-Mullaly-Allis (CMA) diagram [42]. Most of the energy is deposited around the ECR surface and the central wave-emitting rod. Nonetheless, the large parallel thermal conductivity makes $T_e$ almost constant along each magnetic line. The plasma density map in Fig. 2 is determined by both the ionization rate and the density of neutrals. In contrast to an ECRT, the propagation and absorption of EM waves in an HPT has not a resonance character and the deposition map of $Q_a$ is more spread and gives rise to more complex maps of $T_e$ and $\phi$ [23, 24].

Fig. 2

Simulation of an axisymmetric ECRT with the hybrid code HYPHEN based on Ref. [35]. From left to right: absorbed power density map of external electromagnetic emission and stationary maps of $T_e$ and $n_e.$

1D axial fluid model

1D-axial (1Dz) fully-fluid models are widely used to understand, in a simplified scenario and at a low computational cost: central phenomena of the HET discharge, the sensitivity to design and operational conditions, and several longitudinal oscillations. Most 1Dz HET models [43,44,45,46,47,48] have considered the discharge only between the anode and a cathode surface, omitting the far plume. An extended model is presented here, which includes an internal volumetric cathode, the current-free far plume, and electron azimuthal inertia. Regarding this last one, the drift-diffusive approximation (5) plus the near closed-drift (25) in a HET implies

$$\begin{aligned} u_{\parallel e}^2 , u_{\top e}^2\ll u_{\theta e}^2 \ll c_e^2, \end{aligned}$$

(37)

so that azimuthal inertia can be considered relevant while still neglecting the other components. The model below will be able to analyze regions where $u_{\theta e} =O(c_e)$ and the drift-diffusive approximation fails. For instance, high $E\times B$ drifts are expected around the channel exit for high voltage operation, but it will shown that this is not the only case.

A 1Dz electron model describes the axisymmetric discharge by averaging electron properties along the radial direction. Admitting a variable beam cross-section area A(z) the divergence operator of a vector field $\varvec{v}$ in 1Dz becomes

$$\begin{aligned} \nabla \cdot \varvec{v} = \frac{1}{A} \frac{\partial }{\partial z}\left( Av_z\right) + v_{lat}, \end{aligned}$$

(38)

where $v_z$ is the r-averaged axial component and the source term $v_{lat}$ accounts for lateral fluxes across the boundary of A(z). Thus, the proposed 1Dz set of axial, time-dependent, quasineutral equations is

$$\begin{aligned} \frac{\partial n_e}{\partial t} +\frac{1}{A}\frac{\partial }{\partial z}(An_e u_{ze}) =S_p+S_c-S_w, \end{aligned}$$

(39)

$$\begin{aligned} 0=-j_{\theta e} B_r-\frac{\partial p_e}{\partial z} + en_e\frac{\partial \phi }{\partial z} -m_e u_{ze}n_e\nu _e^* , \end{aligned}$$

(40)

$$\begin{aligned} m_e\frac{\partial n_eu_{\theta e}}{\partial t} + \frac{m_e}{A}\frac{\partial }{\partial z } (An_eu_{ze}u_{\theta e}) =j_{ze} B_r - m_eu_{\theta e} \Big (n_e\nu _e^*+ \frac{S_w}{1-\delta _s}\Big ), \end{aligned}$$

(41)

$$\begin{aligned} \frac{\partial }{\partial t} \Big (\frac{m_e u_{\theta e}^2}{2}+\frac{3}{2}p_e\Big ) + \frac{1}{A} \frac{\partial }{\partial z} \left[ Au_{ze}\left( \frac{m_eu_{\theta e}^2}{2}+\frac{5}{2} p_e \right) +Aq_{ze} \right] = \\ -j_{ze}\frac{\partial \phi }{\partial z} -S_p\mathcal {E}_p-\frac{S_w\mathcal {E}_w}{1-\delta _s}, \end{aligned}$$

(42)

$$\begin{aligned} q_{ze}=-\frac{5p_e}{2m_e \nu _e^*}\frac{1}{1+\chi ^{*2}}\frac{\partial T_e}{\partial z}. \end{aligned}$$

(43)

Here: variables describe radially-averaged plasma magnitudes, but we again omit modifying the symbols for them; the cathode is modeled as an emission layer of cold electrons of thickness $\ell_c$ and volumetric emission $S_c$, yielding a discharge current $I_d=\int_{\ell_c} eAS_c dz$; the three source terms with $S_w$ corresponds to losses at the lateral walls, with $\delta _s$ the secondary electron emission yield of the wall, defined in the Appendix; $\mathcal {E}_p$ is the effective energy per ionization-created electron [43]; $\mathcal {E}_w$, obtained from Eq. (78) of the sheath model, is the effective energy per primary electron lost at the wall; and we assumed $\nu _e \varvec{j}_{c}\ll \nu _e^* \varvec{j}_{ e}$ and $S_p+S_c\ll n_e\nu _e^*$. The equations for the quasineutral discharge are completed with an anode sheath AB. Boundary conditions for the equations are set at (i) the edge B of the anode sheath and (ii) the far downstream plume. In addition, the discharge voltage $V_d$ is set between the anode and the cathode center.

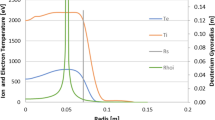
The left side of Eq. (41) represents electron azimuthal convection, while electron axial convection is always negligible in Eq. (40), as commented above. The inclusion of azimuthal convection also permits to take into account wall collisionality effects in Eqs. (41)-(42) as source terms due to the exchange of magnetized primary electrons by unmagnetized secondary ones. To be consistent, the azimuthal energy is included in Eq. (42). Figure 3, obtained from a full-fluid model [49], depicts an example of the stationary solution on electrons from the anode to the far plume, comparing the cases with and without azimuthal inertia. The region around the cathode is quasineutral, avoiding the non-physical sheaths created when the cathode is considered as a boundary. One limitation of the 1Dz model is that the whole ion beam intersects the cathode layer and is directly affected by it (in contrast for instance to the 2D discharge of Fig. 1). This and the remaining magnetic field around the cathode, generate exaggerated bumps of electric potential and temperature downstream of the cathode. The profile of $u_{\theta e}$, Fig. 3(a), shows: the magnetization of electrons when emitted, the posterior demagnetization of the electron beam moving downstream, and the relevance of azimuthal inertia there. Inertia can also be relevant near the anode and in fact it bounds $u_{\theta e}$ to $O(c_e)$ [50]. This bound is observed when ion currents and plasma density are very low there, leading to $-u_{ze}\chi ^*\le O(c_e)$ and eventually to the transition from a ‘normal’ to an ‘inverse’ anode sheath [51].

Fig. 3

Axial, stationary profiles for electron magnitudes in a HET channel and plume, based on the 1Dz fluid model of [49]: a azimutal velocity, b axial velocity, c electric potential, and d temperature. Red curves are for the full model and blue ones for the model without electron inertia. The anode sheath edge B is at $z=0$, E is the channel exit, C is the center of the cathode layer, extending ±2.5 mm. The jumps of axial velocity and potential in the anode sheath are not plotted

In Fig. 3(b), $u_{ze}$ changes sign across the cathode region; it becomes equal to the ion fluid velocity in the current-free plume, and it is mildly affected by azimuthal inertia between anode and cathode. The profiles of $\phi$ and $T_e$, Fig. 3(c)-(d), are little affected by electron inertia. The second peak of $T_e$ downstream the cathode is caused by the remaining magnetic field and the anomalous heating prescribed there (an aspect requiring further research).

The 1Dz model is useful to test quickly the sensitivity of HET performances to different conditions and physics. It is therefore a very valuable tool to complement the previous 2D(z, r) electron model, which typically takes two orders of magnitude more of computational time (e.g. minutes versus tens of hours). For instance, including azimuthal inertia in the 2D(z, r) electron model is expensive computationally and complicates numerical convergence. Instead, the 1Dz model has justified (at least partially) to implement

$$\begin{aligned} u_{\theta e}=\min (-\chi ^* u_{ze}, 2 c_e) \end{aligned}$$

in HYPHEN, avoiding regions with nonphysical values $u_{\theta e}\gg c_e$. The 1Dz model is also being helpful to fit quickly the turbulent function $\alpha_a(z)$ and to assess downstream boundary conditions on the electron energy flux.

Nonetheless, the 1Dz model has the penalty of requiring expressions for the extra source terms due to non-axial physics. Unavoidably, this introduces a certain degree of arbitrariness which cannot be dismissed when extracting conclusions from this model. Furthermore, a 1Dz model makes sense in a HET with a quasi-radial magnetic topology, but is much less suitable for a MS-HET. In the case of an EPT with a quasi-axial magnetic topology, there is a stronger coupling between 1D axial and radial models [52].

Fluid models from 1D fully kinetic solutions

Solutions from kinetic models can show which are the macroscopic equations fulfilled by the plasma in a thruster chamber and plume, and thus define kinetically-consistent fluid models. Attention must be paid mainly to the expressions for the pressure tensor, the heat flux vector, and boundary conditions. This procedure has been completed satisfactorily with the two 1D kinetic models commented next.

1D-radial kinetic model for HETs

A 1D radial (1Dr) fully kinetic model of the radial plasma response in a cross-section of an annular HET with a radial magnetic field and dielectric walls has been developed in [53,54,55,56]. Ions and electrons are treated as PIC macroparticles while (very-slow) neutrals constitute just a background population, with the neutral density adjusted to maintain a stationary discharge. The kinetic solution shows that the electron VDF, Fig. 4(a), presents a large depletion of the radial velocity tail caused by the incomplete replenishment of wall-collected electrons, through secondary electron emission, volumetric collisions, and wave-based effects. This tail depletion implies anisotropy, with the electron radial temperature, $T_{re}$, (i.e. parallel to the magnetic field) lower than the perpendicular temperature, $T_{\perp e} (=T_{ze}=T_{\theta e})$.

Fig. 4

1D radial results for a cross-section of a HET, based on the kinetic model of Ref. [56]. a Normalized electron VDF along $v_z$ and $v_r$ at mid channel M: $\hat{f}_e^{(r)} \propto \int f_e \text {d}v_\theta \text {d}v_z$, $\hat{f}_e^{(z)} \propto \int f_e \text {d}v_\theta \text {d}v_r$. Radial profiles of macroscopic variables: b $n_e/\bar{n}_e$ with $\bar{n}_e$ the radially-averaged value, and $\phi /\phi _M$ referenced to $\phi _{W_2}=0$; c $j_{ze}$ and its mean valued indicated by the dashed line; and d $P''_{re}$ and its 3 main contributions, in W/cm$^2$. Points Q1 and Q2 mark the (approximate) transitions to the Debye sheaths. Wave-based turbulence here is modeled as isotropic collision events with frequency $0.01 \omega _{ce}$

Figure 4(b) plots the radial profiles of the electric potential and the electron density. Integral moments of the electron VDF at the steady state satisfy the azimuthal momentum equation (in cylindrical coordinates)

$$\begin{aligned} \frac{1}{r^2} \frac{\partial }{\partial r}[r^2(m_e n_eu_{re}u_{\theta e}+p_{r\theta e})]= j_{ze}B_r +F_{\theta c}+F_{\theta a}, \end{aligned}$$

(44)

which can be compared with Eq. (41) for a fluid 1Dz model. The term $p_{r\theta e}$ corresponds to the non-diagonal, gyroviscous part of the pressure tensor $\bar{\bar{p}}_e$. It is much smaller than the diagonal terms, but it is the only pressure term contributing to the azimuthal momentum balance and, indeed, it can be larger than the azimuthal inertia term. The radial profile of $p_{r\theta e}$ is undulated, caused by the collective remain of the gyromotion of individual electrons and their reflections within the lateral sheaths. That gyroviscous term is responsible of the radial undulations of $j_{ze}$ in Fig. 4(c), which scale with the electron Larmor radius and resemble the experimentally reported near-wall-conductivity phenomenon [57].

The radial flux of electron energy in this 1Dr plasma turns out to be

$$\begin{aligned} P''_{re}\simeq h_{re} + q_{re} + p_{r\theta e}u_{\theta e}, \end{aligned}$$

(45)

where the right side is the standard macroscopic decomposition into enthalpy flux

$$\begin{aligned} h_{re}=\left( 3T_{re}/2 + T_{\perp e}\right) n_e u_{re}, \end{aligned}$$

heat flux $q_{re}$ (parallel to the magnetic field), and gyrosviscous energy flux $p_{r\theta e}u_{\theta e}$. This last term matters because of the ordering $u_{\theta e}\gg u_{re}, u_{ze}$. Figure 4(d) depicts the radial profiles of the three contributions to $P''_{re}$, showing that all are important. Furthermore, the radial heat flux is found to be approximately proportional to the enthalpy flux,

$$\begin{aligned} q_{re}\propto h_{re}, \end{aligned}$$

(46)

whereas it is uncorrelated with temperature gradients. This suggests a convective character instead of a diffusive one for that flux, a behavior already observed in other near-collisionless plasmas, such as laser-induced ones [58], tokamak’s divertors [59], and the magnetized plume model discussed in 1D-axial kinetic model of a paraxial plume section.

Therefore, the 1Dr kinetic model provides relevant information to validate and upgrade the electron fluid model. Some upgrades are affordable, other might have a too-high computational cost for the improvements in results they bring with. For instance, the use of a mixed convective-diffusive model for the heat flux is affordable, as commented in a later section. On the contrary, to include two temperatures and a gyroviscous tensor would be a major complication and should be avoided except in fundamental studies (or 1D ones). In fact, the 1Dr model provides two partial justifications to maintain a single scalar pressure. The first one is that the radially-undulating gyroviscous term in Eq. (44) becomes marginal when integrated radially [56]. The second one is that the parallel and perpendicular temperatures isotropize quite fast when the magnetic field is curved with respect to the wall normal [60, 61]. The 1Dr kinetic model has also stood out the differences between planar and annular channels. In the last case, cylindrical effects due to centrifugal forces and magnetic mirror can generate important radial asymmetries, as Fig. 4(c) and (d) confirm.

Another important output of the 1Dr kinetic model is the validation of the two-scale spatial approach adopted by electron fluid models, i.e. the clean separation between the quasineutral plasma bulk and the very thin Debye sheaths. This is well illustrated in Fig. 4(b) for $\phi (r)$, where points Q1 and Q2 are the transition points between the plasma bulk and the sheaths, which here are set where the relative electric charge, defined as $1-n_e/n_i$, is a 2%, which coincides very well with a radial ion Mach number close to 1, as prescribed by the sonic Bohm criterion at a Debye sheath entrance. Finally, the kinetic computation of the electron fluxes towards each wall allowed us [55, 56] to determine the values of parameters $\sigma _{rp}$ and a in Eqs. (73) and (77), which measure, for electron fluxes, the deviation of the electron VDF from a Maxwellian one. For magnetic fields perpendicular to the wall, the replenishment factor $\sigma _{rp}$ is rather low, between 0.05 and 0.20. However, for curved magnetic fields, $\sigma _{rp}$ is much larger and the temperature anisotropy lower [61].

1D-axial kinetic model of a paraxial plume

A second plasma configuration admitting a kinetic solution (for both ions and electrons) and thus the study of macroscopic equations for electrons is the expansion of a fully-magnetized plasma in a paraxial (i.e. quasi-1D) magnetic nozzle, a study relevant to EPTs. The paraxial model describes the dynamics of magnetized electrons (and ions) along the nozzle axis. The study has been developed along several works [62,63,64,65], which have addressed the problem under different perspectives (steady-state versus time-dependent models, collisionless versus partially-collisional ones, convergent-divergent MNs versus divergent-only ones, integral versus differential formulations).

A coil or solenoid creates a magnetic field with convergent-divergent lines, constituting the MN guiding the plasma; the field strength is maximum at the magnetic throat. The plasma source upstream of the MN is assumed to inject Maxwellian electrons and ions upstream of the MN (although other types of VDFs were studied too). For the purposes here, the attention is focused on the electron kinetic and macroscopic properties in the divergent region of the MN. In that region, the magnetic field B(z) decreases and the (self-consistent) electric potential, $\phi (z)$, is found to decrease monotonically too. Therefore, the (inverse) magnetic mirror effect makes electrons to gain parallel velocity as they move downstream the MN throat, while $\phi (z)$ makes then to lose it. As a result, most electrons from the source are reflected back electrostatically to it. Only a small fraction of them is ‘free’, having enough energy to flow downstream with the (supersonic) ion population, in order that the plasma plume be current-free. Indeed, the total potential fall along the MN controls the amount of free electrons needed to satisfy the plasma current-free condition (in a similar way as a sheath potential fall next to a dielectric wall does, but here the potential fall is ambipolar and extends along the whole divergent region) [64]. In addition, the opposing electrostatic and magnetic-mirror forces lead to the existence of a third population of doubly-trapped electrons, bouncing back and forth between two spatial locations. These electrons are unconnected to the upstream source (and to infinity downstream), and their steady-state density depends on the scarce electron-electron collisionality events [65] or the formation period of the MN (in a collisionless scenario)[63]. The amount of doubly-trapped electrons affects much the electric potential profile in the MN, as Fig. 5 (a) shows. The presence of this doubly-trapped population of electrons has been identified in other near-collisionless plasma configurations, such as Langmuir probes [66].

Fig. 5

1D axial profiles for electrons in a paraxial MN, based on the kinetic model of Ref. [65]. In a-b The vertical dash-dot line is the location of the magnetic throat. In a-c: $T_{e0}$ and $n_{e0}$ are upstream values; $\bar{\nu }_{ee}$= 0.1 (solid), 0.01 (dashed,) 0 (dashed-dot), with $\bar{\nu }_{ee}$ the electron-electron collision frequency nondimensionalized with a typical electron transit time. In c the line with asterisks is the polytropic relation with $\gamma -1=0.23$. In d $h_e=(3T_{\parallel e}/2+T_{\perp e})n_eu_{\parallel e}$ and the curve is for $\bar{\nu }_{ee}$= 0.1

The macroscopic behavior of the electrons is obtained from integrating in the particle velocity space the kinetic solution. In spite of the rather different characteristics of the three subpopulations, the whole electron population is found to satisfy the simple paraxial equations

$$\begin{aligned} {n_eu_{\parallel e}}/B=\text {const}, \end{aligned}$$

(47)

$$\begin{aligned} en_e\frac{d\phi }{dz}-\frac{dp_{\parallel e}}{dz}+(p_{\parallel e}-p_{\perp e}) \frac{d\ln B}{dz}=0, \end{aligned}$$

(48)

$$\begin{aligned} \left( -e\phi +\frac{3}{2}T_{\parallel e}+T_{\perp e}\right) \frac{n_eu_{\parallel e}}{B}+\frac{q_{\parallel e}}{B}=\text {const}, \end{aligned}$$

(49)

$$\begin{aligned} \frac{n_eT_{\perp e}u_{\parallel e}+q_{T\parallel e}}{B^2}=\text {const}, \end{aligned}$$

(50)

where: 1/B is proportional to the effective cross-section area of the plasma beam, and the integration constants are obtained at the upstream boundary of the domain. Equation (47) expresses the electron flux conservation. Equation (48) is the momentum equation which includes the macroscopic magnetic mirror force, and the pressure tensor follows Eq. (4). Equation (49) is the conservation of the total electron energy, including the parallel heat flux and the electric potential energy; the perpendicular heat flux, $\varvec{q}_{\perp e}$, is zero at the MN axis. Equation (50) is the conservation of the electron perpendicular energy at the axis, with $q_{T\parallel e}$ the parallel flux of transverse heat [67]. Observe that these fluid equations are collisionless: collisions of electrons with neutrals and ions are not considered and electron-electron collisions shape the pressure tensor and the heat fluxes.

The kinetic solution of this MN model shows that electron temperature anisotropy develops in the divergent MN, and both $T_{\parallel e}$ and $T_{\perp e}$ decrease, Fig.5 (b). Downstream, $T_{\perp e}$ goes to zero due to the inverse magnetic mirror on individual electrons, while $T_{\parallel e}$ decreases to an asymptotic nonzero value, $T_{\parallel e \infty }$. The electron cooling is due to regions in the VDF velocity space becoming progressively empty or void (see Fig. A2 in [64]). The temperature anisotropy yields the magnetic mirror force in the momentum Eq. (48), but this contribution is generally smaller than the one from the gradient of $p_{\parallel e}$.

To close consistently the macroscopic model, equations for $q_{T\parallel e}$ and $q_{\parallel e}$ based on lower-moment magnitudes are needed [67]. No simple expressions for them and valid in the whole MN have been found yet or even exist. Only the far plume region admits approximate expressions. First, the factor $B^{-2}$ in Eq. (50) explains that $q_{T\parallel e}\rightarrow 0$ downstream, together with $T_{\perp e}$. Then, Fig. 5(c) suggests to take [64]

$$\begin{aligned} q_{\parallel e}\approx \alpha _q n_eT_{\parallel e}u_{\parallel e}, \end{aligned}$$

(51)

with $\alpha _q$ a constant (dependent on the electron-electron collisionality). This ‘convective’ behavior of the parallel heat flux is very similar to the one found in Eq. (46) in the 1Dz HET kinetic model. Using Eq. (51) and defining

$$\begin{aligned} \gamma =(3+2\alpha _q)/(1+2\alpha _q), \end{aligned}$$

Equation (49) becomes

$$\begin{aligned} -e\phi + \gamma T_{\parallel e}/(\gamma -1)=\text {const}. \end{aligned}$$

(52)

Thus, in the far paraxial plume, the collisionless electron fluid behaves as an adiabatic gas with an specific heat ratio $\gamma$, and the electron cooling can be explained macroscopically as the enthalpy drop caused by the increment in electric potential energy. This is a surprisingly simple behavior for the combination of the three subpopulations of electrons. Using Eq. (48) with $p_{\perp e}=0$ to eliminate $\phi$, Eq. (52) yields a B-dependent polytropic equation of state for the parallel temperature,

$$\begin{aligned} T_{\parallel e}\left( {B}/{n_e}\right) ^{\gamma -1} =\text {const}. \end{aligned}$$

(53)

In summary, the algebraic Eqs. (47) and (51)-(53) constitute the macroscopic model for electrons in the far plume of the MN.

So far in this subsection, a magnetized paraxial plume has been considered. Reference [68] carried out a similar direct-Vlasov analysis for an unmagnetized paraxial plume. An equivalent kinetic solution was found, by just exchanging the magnetic moment of magnetized electrons by an action integral on unmagnetized electrons. Hence, the macroscopic behavior of the unmagnetized plume features temperature anisotropy and cooling too, suggesting them to be robust properties in the expansion of collisionless plumes, either magnetized or not. A particle-based formulation of unmagnetized paraxial plumes led to similar results [69]. Plume cooling has been verified experimentally in EPTs [70,71,72] and in HETs [73, 74]; still, detecting experimentally the temperature anisotropy continues to be challenging.

Electron fluid models for large plumes

The behavior of the plasma discharge in the plume region of a thruster presents some differences with respect to the one inside the thruster channel. As shown in the last subsection, the lack of wall confinement further reduces plasma collisionality and foments non-Maxwellian features in electrons, which are no simple to include in fluid models. In addition, plasma plumes are much larger regions than a thruster channel and this raises additional numerical challenges. The next two subsections confront these theoretical and numerical problems.

2D collisionless plume in a magnetic nozzle

The collisionless, fully- kinetic model of a paraxial MN of 1D-axial kinetic model of a paraxial plume section was extended in Ref. [75] to a fully-2D MN in the limit of cold, fully-magnetized ions. In that configuration, electron Eqs. (47)-(50) apply along each magnetic line with line-dependent constants. However, the case of interest in EPTs, with weakly magnetized (heavy) ions and reproducing the beam-nozzle detachment has been tackled so far only with a fully-fluid 2D model and assuming an isotropic electron pressure. A set of papers have discussed the different physical phenomena in that scenario [3, 76,77,78,79,80,81].

They consider the full-2D expansion of a collisionless plasma plume in an axisymmetric, divergent MN, shaped by a longitudinal magnetic field $\varvec{B} (z,r)$. Magnetic streamtubes are surfaces $\psi (z,r)=$const with $\psi$ the magnetic streamfunction, defined by

$$\begin{aligned} \nabla \psi =rB\varvec{1}_\top . \end{aligned}$$

(54)

The electron submodel uses the continuity and momentum Eqs. (1) and (6) in the stationary, collisionless limit, and completes them with a simple polytropic law for the scalar pressure,

$$\begin{aligned} {\nabla \ln p_e} =\gamma {\nabla \ln n_e}. \end{aligned}$$

(55)

After straightforward manipulations, the electron fluid turns out to satisfy the set of algebraic equations

$$\begin{aligned} j_{\top e}=0, \end{aligned}$$

(56)

$$\begin{aligned} {j_{\parallel e}}/{B}=G_e(\psi ), \end{aligned}$$

(57)

$$\begin{aligned} \phi -\frac{\gamma }{\gamma -1}\frac{T_{e}}{e}= \Phi _p(\psi ), \end{aligned}$$

(58)

$$\begin{aligned} u_{\theta e}/r= d\Phi _p/d\psi . \end{aligned}$$

(59)

The two first ones state that, for full magnetization, magnetic streamtubes are electron streamtubes, and the electron current inside each tube remains constant and equal to the upstream value $G_e(\psi )$. Equation (58) is a polytropic Boltzmann relation along each streamtube, with $T_e(n_e)$ provided by Eq. (55) and $\Phi _p$ a thermalized potential apt for polytropic (i.e. non isothermal) electrons.

The most novel equation in this 2D scenario is (59), which asserts that the electron fluid isorotates in each streamtube, implying that any azimuthal electron current must be created before entering the collisionless magnetic nozzle. This equation was obtained by applying Eq. (54) to

$$\begin{aligned} j_{\theta e}B =- en_e\nabla _\top \Phi _p, \end{aligned}$$

(60)

this one stating that the azimuthal drift is the combination of the $E\times B$ and diamagnetic drifts. Observe that a relevant feature of this collisionless model is the determination of  $\varvec{j}_e$ without having resource to an Ohm’s law.

The combination of this algebraic model for electrons with a fluid model for supersonic ions yields an hyperbolic set of differential equations for the ions. This set is solved with the method of characteristics lines [76], which is very suitable to construct the plume solution from the MN throat to infinity, getting past the turning points of the magnetic lines. The two-fluid model has been very successful in: explaining the 2D plume expansion and the magnetic thrust [76], the effects due to electron inertia [78] and hot ions [80], the change of nozzle shape due to the induced magnetic field [77, 81], and the plasma detachment from the MN via ion demagnetization [79].

The isotropic and polytropic relation (55) is adequate to reproduce the observed electron cooling but it omits the development of pressure anisotropy found in the 1Dz kinetic model. To include pressure anisotropy would imply, first, to substitute the algebraic Eqs. (58) and (59) by the differential ones,

$$\begin{aligned} 0=-\nabla _\parallel p_{\parallel e}+ (p_{\parallel e}-p_{\perp e})\nabla _\parallel \ln B +en_e \nabla _\parallel \phi , \end{aligned}$$

(61)

$$\begin{aligned} -j_{\theta e}B=-\nabla _\top p_{\perp e} + (p_{\perp e}-p_{\parallel e})\nabla _\top \ln B +en_e \nabla _\top \phi , \end{aligned}$$

(62)

where the last one includes now the B-curvature drift. Second, closure relations on the two temperatures are needed. From the 1Dr kinetic solution, $T_{\perp }/B=$const and Eq. (53) for $T_{\parallel e}$ could be valid choices. This extended 2D fluid model with partially-magnetized ions has not been deeply analyzed yet. It remains to be proven that it is numerically affordable with the method of characteristic lines. Otherwise, the more general treatment of the next subsection could be more convenient.

2D and 3D weakly-collisional plumes

Simulations and experiments have made evident that the electron fluid cools down in plasma plumes. However, the simulations with 2D hybrid codes do not always reproduce this. For instance, in the EPT case of Fig. 2 with the plume domain extending 3-4 times the channel width, plot (b) shows that there is practically no cooling along the magnetic lines. That short plume size is adequate to study the plasma discharge inside the thruster channel and near the exit, but it is clearly insufficient to analyze the plume expansion into the free space or within a large vacuum chamber. More recent simulations of an EPT with HYPHEN [41] demonstrate that a short plume domain can miscalculate thruster performances because of the large range of the electromagnetic force and the incomplete electron cooling and demagnetization. However, to simulate a large plume is both costly and challenging computationally, due to the additional orders of inhomogeneity in $n_e$ along the whole discharge, the increasing irregularity of cells (mainly if an MFAM is used, as observed in Fig. 1), and the possible presence of non-neutral regions. Furthermore, in order to achieve a reliable solution with a relatively compact plume domain, it is crucial to define physically-consistent conditions at the downstream and lateral boundaries of the domain [41, 69].

In a weakly-collisional, current-free plume, where transport along magnetic lines is not local, boundary conditions on electron currents and energy fluxes for a finite plume region are not obvious. In general, 2D hybrid codes have imposed a zero electric current density at each boundary point [27, 30, 38, 82], as if the plume were surrounded by a dielectric wall. A better approach is to consider the plume surrounded by a metallic wall of potential $\phi _V$. If the plasma beam is current-free, $\phi _V$ is determined by setting to zero the total electric current across the plume boundary [83]. Applying Eq. (74), this implies that the wall potential satisfies the integral equation

$$\begin{aligned} \int _{\partial S_p} dS \ \varvec{j}_{i}\cdot \varvec{n}=\int _{\partial S_p} dS\ \sigma _{rp} \frac{en_e\bar{c}_e}{4} \exp \frac{e(\phi _V-\phi )}{T_e}, \end{aligned}$$

(63)

with $\partial S_p$ and $\varvec{n}$ the contour and the outwards normal of the plume boundary.

Figure 6 compares, for the case of Fig. 1, the electric current loops when applying either local or global conditions in the plume. While the main plasma region, between the anode and the cathode, is only slightly affected by the plume boundary conditions, the electric currents in the plume region are rather different. These current loops are much more affected by the plume size in the case of local boundary conditions [83]. Thus, the global boundary condition is a more robust one, and also $\phi _V$ is rather unaffected by the plume extension (while the local sheath between the plume boundary P and the wall V, shrinks with plume size increasing). Hence, the use of the global condition allows working with rather compact plume sizes and provides the single downstream potential $\phi _V$; also, the electron energy fluxes outward the plume can be computed from the expressions in the Appendix.

Fig. 6

Electric current density in a meridian plane for the case of Fig.1. Comparison of electric current when applying different boundary conditions in the plume: a Local conditions with $j_{ne}=j_{ni}$; b global conditions

In the case of the plasma plume expanding into free space, the global condition is the correct approach too: it can be postulated that the wall V is the infinity, and the layer between the plume boundary P and V would mimic the plume region not been simulated. This is the first step to define a model of a ‘global downstream matching layer’[83], with a whole set of boundary conditions for both (confined) electrons and (nearly free-expanding) ions between P and infinity.

Turning to heat fluxes, different closures can be postulated for weakly-collisional, magnetized plumes. It has already been evidenced that the Fourier’s law (21) fails along the magnetic lines. Several alternatives are being considered. A first, empirical one, is to modify that Fourier’s law component, introducing an anomalous parallel collisionality $\nu _q$:

$$\begin{aligned} q_{\parallel e} = -\frac{5p_e}{2m_e(\nu _e+\nu _q)}\nabla _\parallel T_e. \end{aligned}$$

(64)

For instance, Ref. [41] recovers the observed parallel cooling in an EPT with $\nu _q/\nu _e \sim 10-100$. Notice that this anomalous parallel cooling, motivated by the emptying of VDF regions and existing even in unmagnetized plumes [68], has a different nature than the perpendicular anomalous transport, due to turbulence (i.e. the contribution $\alpha _a\omega _{ce}$ to $\nu _e^*$).

A second, better physically-based alternative, under present assessment within HYPHEN, is to keep the conductive Fourier’s law for the perpendicular heat flux, $q_{\perp e}$ and use a convective law for the parallel heat flux, $q_{\parallel e}$. An issue to be solved here is that boundary conditions can be imposed only on $q_{\perp e}$, while the magnetic lines are oblique to the boundary in general.

A third alternative is to implement a convective-only heat flux, which is equivalent to express the flux of electron energy, Eq. (8), as

$$\begin{aligned} \varvec{P}''_e=\frac{\gamma }{\gamma -1}n_eT_e \varvec{u}_e. \end{aligned}$$

(65)

Since the electron energy Eq. (7) can be expressed as

$$\begin{aligned} \nabla \cdot \left( \varvec{P}''_e-e n_e \varvec{u}_e\phi\right) = (-\nabla \cdot \varvec{j}_i +S_c)\phi + Q_{c}+Q_a- \frac{\partial }{\partial t} \left( \frac{3}{2} p_e\right) , \end{aligned}$$

(66)

the total electron energy (included the electric potential contribution) is conserved in the sourceless, stationary, collisionless case. Since $\nabla \cdot \varvec{j}_i=0$ in that situation too, it is straightforward to obtain, with the aid of the momentum Eq. (6), a polytropic equation of state along the electron streamlines,

$$\begin{aligned} (\varvec{u}_e\cdot \nabla )\ln p_e=\gamma (\varvec{u}_e\cdot \nabla ) \ln n_e, \end{aligned}$$

(67)

which yields Eq. (55) if conditions are uniform upstream. These results generalize (within the isotropic temperature framework) 1D results of the previous section.

EP2PLUS is a simulation code based on a hybrid 3D model to study weakly-collisionless plumes [84]. 3D scenarios are of interest to study, for instance, asymmetric thruster configurations (e.g. a HET with a lateral cathode) or the plume interaction with the surroundings of the thruster and nearby objects [85]. The code applies the 4-moment electron model with the polytropic closure (55). Being 3D, turbulence is included through the empirical model of Eq. (18). Thus, the electron model consists of

$$\begin{aligned} n_e=n_i+(\epsilon _0/e)\nabla ^2\phi , \end{aligned}$$

(68)

$$\begin{aligned} \nabla \cdot \varvec{j}_e=- \nabla \cdot \varvec{j}_i+S_c-\partial \rho _{el}/\partial t, \end{aligned}$$

(69)

$$\begin{aligned} \varvec{j}_e= \bar{\bar{\mu }}_e^* \cdot (-e n_e\nabla \Phi _p - \mu _e^{-1}\varvec{j}_c), \end{aligned}$$

(70)

where $\Phi _p$ is the thermalized potential of Eq. (58) and $\rho _{el}$ is the electric charge. An important capability of EP2PLUS is to deal with non-neutral subregions. In the quasineutral subregions, Eqs. (69) and (70) yield $\Phi _p$ and $\varvec{j}_e$, and then $\phi$ is obtained from Eq. (58). In the non-neutral subregions, the elliptic Poisson Eq. (68) for $\phi$ is coupled to an elliptic equation for $\Phi _p$ [29].

Figure 7 presents an application of EP2PLUS to the unmagnetized plume of a gridded ion thruster, when turbulent transport is absent, and the polytropic closure (67) is more plausible. Figure 7(b) depicts well the non-neutral region around the grids. Figure 7(c) shows the paths of the electron beam emitted by the cathode, while Fig. 7(d) plots the paths of the electric current and its complete cancellation downstream the cathode.

Fig. 7

Neutralization of electric charge and current in the 3D near plume of an ion thruster, based on [86]. In grey, the 3x5-hole grids simulated with EP2PLUS. The black box at the top is the cathode, which emits electrons. a Ion density from the PIC module; b relative electric charge; c electron current density emitted from the cathode; and d electric current density

In a 3D magnetized scenario, a 3D MFAM is not a practical option. Also, an MFAM is unapplicable if a time-dependent induced magnetic field is included, as in some MN studies. EP2PLUS uses a 3D Cartesian mesh, but this can present problems of numerical diffusion and convergence when $\chi ^*\gg 1$ and the tensor $\bar{\bar{\mu }}_e^*$ is stiff [87]. At present, the code is able to provide reliable solutions for $\chi ^*$ up to 50-100 (depending on the particular plasma scenario). Recent achievements of EP2PLUS with magnetized plumes are the following. Reference [29] determines the 3D structure of an initially axisymmetric plume under the influence of an oblique geomagnetic field. Reference [88] analyzes the 3D electron currents in the near plume of a HET with a lateral cathode, their quick azimuthal symmetrization, their division in up-bound and down-bound beams, and the neutralization of the ion beam current by the second electron beam. Along with these valuable results, Ref. [29] made also evident the inadequacy of applying a polytropic law in the near region of a HET, where the right side of Eq. (66) is far from being negligible.

While the 4-moment model is satisfactory to study the electron currents and to fit an empirically observed electron cooling, it misses to model correctly the physical evolution of the electron energy. The change of the electron fluid model of EP2PLUS from a 4-moment to an 8-moment one implies to apply Eqs. (69) and (66) for the divergences of $\varvec{j}_e$ and $\varvec{P}''_e$, while these variables satisfy generalized conductive-convective laws in terms of $\Phi$ and $T_e$ [89],

$$\begin{aligned} \varvec{j}_e= -en_e\bar{\bar{\mu }}_e^* \cdot \nabla \Phi +n_e \Big (1- \ln \frac{n_e}{n_0} \Big ) \bar{\bar{\mu }}_e^* \cdot \nabla T_e - \frac{\bar{\bar{\mu }}_e^*}{\mu _e^*}\cdot \varvec{j}_c, \end{aligned}$$

(71)

$$\begin{aligned} \varvec{P}''_e=\frac{5}{2} T_en_e \Big (\varvec{u}_e-\frac{\bar{\bar{\mu }}_e^*}{e} \cdot \nabla T_e \Big ). \end{aligned}$$

(72)

In the quasineutral and non-neutral zones, $\phi$ is obtained from Eqs. (34) and (68), respectively.

Summary and conclusions

Slow-dynamics of weakly-collisional magnetized electrons in plasma thrusters are amenable to fluid modeling, but present uncertainties on: the pressure tensor; the heat flux; fluxes to walls; and time-correlated effects caused by high-frequency oscillations (either forced or self-driven) and responsible of wave-based electron transport and heating.

The discussion has been focused in a one-temperature, drift-diffusive model with classical conductive heat flux closures and an empirical model for wave-based effects (from either turbulence or EM emission). This is the most prevalent model today for HETs, EPTs, and similar thrusters. In magnetized, axisymmetric scenarios, the large anisotropy of the mobility tensor $\bar{\bar{\mu }}_e$ leads to very different electron transport properties along each spatial direction. Suitable ways to deal with them have been discussed, including the convenience of using magnetic field aligned meshes and thermalized potentials. Simulations providing detailed 2D maps of electron macroscopic variables have illustrated the capabilities of the above electron model.

1D axial fluid models have been proposed for quick parametric analyses and testing of complementary physics. It has been highlighted the relevant role of azimuthal inertia, not only for high-voltage operation, but around the anode and the cathode, and at the far plume of a HET discharge.

The plasma-wall interaction in a thruster channel has a central role on the discharge and the performances. Since the plasma is quasineutral, Debye sheaths define that interaction. Sheath models providing consistent fluxes of particles, momentum, and energy to the walls for different types of walls are found central to determine performances associated to the discharge physics. Transition to a positive sheath and to charge saturation conditions can have a large effect on these fluxes.

Peculiarities of electron models for plasma plumes, caused by their lower collisionality and expansion physics have been stood out. An axisymmetric, stationary, semianalytic fluid model for a magnetic nozzle configuration has been presented to explain the electron response in a fully-collisionless scenario and the reduction, in that case, of the set of electron differential equations to an algebraic one. For a weakly-collisional, 3D scenario, the differences between 4-moment and 8-moment models (with different heat flux closures) have been discussed. Also the limited size of the simulated plume and, therefore, the importance of defining consistent boundary conditions has been highlighted. Global current-free conditions are found, in general, more robust and physical than local conditions, and provide a good estimate of the far-downstream electric potential.

Two 1D kinetic electron models have been used to derive kinetically-consistent fluid models, and to help characterizing the pressure tensor and the heat flux vector. In the two cases, an anisotropic pressure tensor and a parallel heat flux of convective type were found. The inclusion of a non-scalar pressure tensor in a fluid model is a major challenge for the simulation of the full 2D or 3D discharge. On the contrary, to consider a convective parallel heat flux is equivalent to assume an adiabatic response for a poliatomic gas (with an intermediate specific heat ratio).

In conclusion, slow-dynamics electron models are being very useful to understand the electron transport and the whole plasma discharge in HETs and EPTs, but there is still much room for improvement in physical modeling, boundary conditions, and numerical implementation. However, the key challenge for a solid reliability of the slow dynamics model continues to be the achievement of physically-consistent expressions for the correlated effects of the high-frequency dynamics in, at least, the momentum and energy equations of the 8-moment slow-dynamics model.

Appendix: The Debye sheath model

In the zero Debye length limit, the quasineutral plasma discharge is coupled to the thruster walls by infinitely-thin, unmagnetized, collisionless Debye sheaths. The sheath local solution can thus be expressed as an integral function on the ion and electron VDFs. This function depends on the local electric potential in the sheath, the VDFs at the sheath entrance, and the electric and material properties of the wall.

The plasma sheath transition is defined by the Bohm criterion on the ion and electron VDFs [90]. For fluid electrons and normal sheaths (i.e. with the wall potential lower than the plasma potential) Ref. [91] expressed the Bohm criterion as a sonic-supersonic condition, based on a ‘Mach-Bohm number’ on the ion population. Furthemore, for a PIC formulation on ions, it showed the need to impose a Bohm forcing algorithm at the quasineutral boundary of the discrete PIC mesh in order to attain the correct plasma fluxes.

For the purposes here, only electron magnitudes are discussed next. Some surfaces, such as ceramics or thermioinic materials, can present strong secondary electron emission (SEE). In order to deal with this, the sheath model must distinguish between these secondary (s) electrons and the primary (p) electrons coming from the quasineutral discharge, while the two populations are ‘merged’ into a single one (population e) within the quasineutral discharge [92]. Correct matching of fluxes is established at the sheath transition, considering the kinetic, 2-population electron model, inside the sheath, and the fluid, 1-population model, in the plasma bulk.

For a normal sheath, the (perpendicular) electron flux of primary electrons into the wall W can be expressed as

$$\begin{aligned} g_{np}(\phi _{WQ}) = (1-\delta _{r}) \sigma _{rp}\ \frac{n_{eQ}\overline{c}_{eQ}}{4}\exp {\frac{-e\phi _{WQ}}{T_{eQ}}}, \end{aligned}$$

(73)

where: subindex n in this Appendix means normal to the wall; $\phi _{WQ}=\phi_Q-\phi_W$ is the (positive) sheath potential fall between the sheath edge Q and the wall W; $\overline{c}_{e}=\sqrt{8T_{e}/\pi m_e}$; $\delta _{r}$ is the elastically reflected fraction of primary electrons; and $\sigma _{rp}$ is a replenishment factor of the VDF tail of collected electrons, equal to 1 if the electron VDF at the sheath edge Q is semi-Maxwellian.

If $\delta _s$ is the macroscopic yield of (true) SEE at the wall, $j_{ni}$ is the ion current density to the wall, and $j_n$ is the electric current density, the local current-voltage balance for the sheath is

$$\begin{aligned} j_n=j_{ni}-e(1-\delta _s)g_{np}(\phi _{WQ}). \end{aligned}$$

(74)

The parameters $\delta _r$ and $\delta _s$ depend on the impact energies of electrons and ions. They are marginal for the metallic surfaces of HETs and EPTs, but they can be large for ceramic walls, and, in any case, they depend on the particular material and the energy of primary electrons. In fact modeling the SEE with these two parameters is just a simplified version of more complete SEE models used in some kinetic simulations [11, 93].

For a dielectric wall, Eq. (74) plus $j_n=0$ determines the local sheath potential fall as

$$\begin{aligned} \frac{e\phi _{WQ}}{T_{eQ}}=\ln \sqrt{\frac{m_i}{2\pi m_e}}+\ln [(1-\delta _r)(1-\delta _s)\sigma _{rp}]-\ln \frac{j_{ni}}{en_{eQ}}\sqrt{\frac{m_i}{T_{eQ}}}. \end{aligned}$$

(75)

Since the first logarithm has a very large argument (around 200 for xenon), the effect of the second logarithm is relevant only if its argument is very small, which means either very low tail replenishment or a SEE yield close to 1; the last term on the right is marginal due to the Bohm criterion.

For the metallic anode of a HET, the integral relation between the anode potential $\phi _A$ and the discharge current is

$$\begin{aligned} I_d= \int _{\partial S_B} dS\ j_{ni}-\int _{\partial S_B} dS\ \sigma _{rp} \frac{en_e\bar{c}_e}{4}\exp \frac{e(\phi _A-\phi )}{T_e}, \end{aligned}$$

(76)

where the integral domain is the surface $\partial S_B$ of the anode sheath edge B.

Regarding electron energy fluxes, the net power density deposited by the whole electron population at W is

$$\begin{aligned} P''_{neW} \simeq g_{np} (aT_{eQ}+m_eu_{\theta eQ}^2/2-\delta _sE_s), \end{aligned}$$

(77)

where: $E_s$ is the average emission energy of true SEE, $a=2$ for a Maxwellian VDF (and $a\sim 1.4-2$ in the kinetic model of [56]), and the azimuthal electron energy has been included for completeness. The electron power density at the sheath edge Q is

$$\begin{aligned} P''_{neQ}=P''_{neW}+e\phi _{WQ}(1-\delta _s)g_{np}, \end{aligned}$$

(78)

which is the boundary condition to be imposed to the quasineutral fluid model. Observe that the heat flux at Q is nonzero: $q_{neQ}=P''_{neQ}-(5/2)T_{eQ}n_{eQ}u_{neQ}$.

Since secondary electrons are emitted from a wall without (collective) azimuthal momentum, the net loss of azimuthal electron momentum at wall W (and sheath edge Q) is $m_eu_{\theta eQ}g_{np}$. In a ceramic wall with SEE, this loss amounts to $m_eu_{\theta eQ}j_{ni}/e(1-\delta _s)$, which, for $\delta _s\approx 1$, can be an important loss term in the azimuthal momentum Eq. (41) even if the convection terms are omitted. This effect is known as wall collisionality [43] or near-wall conductivity [26, 57]. In an inertialess electron model, as the spatial derivatives of $u_{\theta e}$ are neglected, a boundary condition on that variable cannot be imposed and this loss term cannot be taken properly into account. Some 2D(z, r) models include wall-collisionality effects as an additional contribution to the (volumetric) anomalous collisionality [13, 27]. Nonetheless, there is a certain consensus that wave-based turbulence is more relevant than wall-collisionality for electron anomalous transport in HETs.

Whereas stationary, normal sheaths are formed around most of the thruster surfaces, other situations can arise. For instance, a normal sheath at the anode requires ions flowing sonically to it. If the magnetic field near the anode is too high or the plasma density is too low, there is a limit when the ion flow cannot fulfill the Bohm criterion at the sheath edge [49, 94] and there is a transition from a normal to an inverse sheath. Ref. [95] observed it experimentally in HETs. Ref. [51] derived sheath edge conditions for a 1Dz full-fluid model dealing with both normal and inverse sheaths. These are

$$\begin{aligned} u_{zi}^2=\frac{T}{m_i}\frac{\eta ^2}{1+\eta ^2}, \qquad u_{ze}^2=\frac{T}{m_e}\frac{1}{1+\eta ^2}, \end{aligned}$$

with $T=T_e+T_i$, $\eta =|I_i/I_e|\sqrt{m_i/m_e}$, and the ion and electron axial velocities satisfying the generalized Bohm criterion $m_eu_{ze}^2 +m_i u_{zi}^2=T$. Expressions for the sheath potential fall can be found in [51] and the normal-to-inverse sheath transition happens for $\eta =\sqrt{T_i/T_e}$. Observe that this generalized sheath model requires to implement full inertia terms in the 1Dz electron equations.

For ceramic walls, as $\delta _s$ increases, the sheath potential fall decreases and the electric field at the wall too. Before the normal sheath collapses, this electric field vanishes, and the sheath enters into the the charge saturation limit (CSL) and regime [43, 96, 97], which is the scenario adopted in many HET simulations [27, 31, 43, 44]. Nonetheless, the exact sheath potential fall at the CSL is very sensitive to the ion and electron VDFs, and the classical result from Hobbs-Wesson [96] applies only to a fully replenished semi-Maxwellian VDF. This would explain that the CSL is very unstable numerically. Sheath instabilities and the development of an inverse sheath [98] are alternatives to the CSL scenario. Further investigation on these aspects is required.