1 Introduction

Control charts (CCs) are the tools used to monitor process quality. It is used to identify process deviations in any processes. The graphical representation of all the process data that CCs has gathered makes it simple to identify process variability and enable the organization to take the appropriate action to stop the source of variation. An under-control state is one in which all of the process data points fall between the upper control line (UCL) and lower control line (LCL) in the CCs; an out-of-control state occurs when any one of the data points falls outside the control lines. Two categories of CCs are offered for process monitoring, namely attribute and variable CCs. A process is considered to be variable if its inspection process is dependent on continuous data. A large number of variable CCs are made to track the process status. Shewhart x bar CCs are the most popular among them due to their simplicity. [13] suggested cumulative sum CCs, a plotting technique that shows the cumulative sums of deviations of sample values of a quality characteristic from a target value against time, as an alternative to Shewhart x bar CCs. When comparing the effectiveness of cumulative sum CCs and Shewhart x bar—CCs in identifying slight variations in the process average, [11] found that cumulative sum CCs are superior at doing so. [1] investigated the nonparametric adaptive cumulative sum CCs scheme for process location monitoring. In addition to outlining a process for creating geometric moving averages and contrasting the characteristics of CC tests based on moving averages [16], introduced exponentially weighted moving average CCs with average run lengths (ARL). Furthermore, [18] demonstrated that exponentially weighted moving average CCs will be a superior substitute because they are able to identify even minute variations in the process mean. [2] created effective memory-style charts by combining several auxiliary data sources. [3] investigated the Poisson adaptive exponentially weighted moving average CCs for shift range monitoring in more detail. [21] expanded upon the exponentially weighted moving average ideas by introducing new neutrosophic double and triple CCs.

Conversely, CCs are categorized as attribute CCs when the quality check is based on whether the product meets specific requirements. Attribute CCs are preferred for monitoring processes with non-normal distributions. In the single sampling scheme literature,the implementation of CCs through industrial application was explained by [9] who studied attribute CCs based on the inverse Weibull distribution. [15] developed attribute CCs based on exponentiated half logistic distribution with a known or unknown shape parameter and observed a declining trend in the ARL values. [4], analysed CC performance using a generalized exponential distribution and stated that they are a useful tool for estimating the mean life of power system equipment. Moving average CCs were studied by [5] for Rayleigh and inverse Rayleigh distributions, and the ARLs examined the CCs' performance for a range of parameter settings at varying shift sizes. It is found that CCs detects a shift in the process more effectively. [17] looked into attribute CCs using a log-logistic distribution and suggested using them to mentor non-conforming products in the electronic appliance industry. [14] discovered a declining trend in the values of ARLs as the shift constant increased, assuming that the manufactured goods' lifetime follows a log logistic distribution. [23] investigated CCs for a few widely used distributions, namely, Burr X and XII, inverse Gaussian, and exponential lifetime distributions. Based on ARL values, a comparison of the performances reveals that the inverse Gaussian distribution performs better than all others.

Process shifts are also identified using sequential sampling schemes like repetitive sampling. A particular sample from the lot is taken and examined under a repetitive sampling scheme in order to determine whether or not to accept the lot. If the results of the test indicate that it should be rejected, another sample is chosen, and so on, until the lot is approved or rejected in accordance with the necessary specifications. [7] studied CCs under repeated sampling schemes for both attribute and variable CCs, and found that when ARL0 stays constant for both charts, the suggested CCs provide smaller values of ARL1 than CCs based on a single sampling scheme. The study also concludes that, in terms of ARL values, CCs based on repetitive sampling schemes outperform conventional np-CCs and X-bar CCs. [22] proposed X-bar CCs under a repeated sampling scheme based on the inverse Rayleigh distribution and found that they are more effective than the conventional Shewhart X-bar CCs. [8] studied CCs based on the Birnbaum – Saunders distribution under repetitive sampling scheme and concluded that CCs based on repetitive sampling scheme performs better than CCs based on single sampling scheme. Through the use of out-of-control ARL to compare performance, [6] designed CCs for the Rayleigh distribution based on repetitive sampling scheme. Their findings demonstrate that the CCs based on repetitive sampling scheme perform better than single sampling scheme in terms of ARL. [19] suggested that the control chart using repetitive sampling should be designed such that the fixed sample size is the same as the average sample number.

In order to analyze the lifetime data, [12] introduced a probability distribution that alternates between the gamma and exponential distributions in the appropriate ratio. While gamma and exponential distributions are widely used in statistics and have been extensively researched, the Lindley distribution has not received much attention since its introduction. [10] subsequently investigated the Lindley distribution's characteristics, the Lindley distribution gained popularity for data modelling. Moreover, numerous authors have applied the Lindley distribution in a variety of fields. This paper, following a thorough review of the literature, suggests attribute CCs for the Lindley distribution through repeated sampling under time-truncated life tests.

The Lindley distribution is defined in Section 2, the design of attribute CCs using repetitive sampling under time-truncated life tests based on the Lindley distribution is stated in Section 3, and the recital is examined with the aid of under control and out of control ARL. The results for the suggested CCs are described and explained in Section 4. In Section 5, the effectiveness of the suggested CCs is examined through the application of the CC to both simulated and real data sets. Based on ARL values, the suggested CCs performance is compared with single sampling CCs in Section 6. The findings of this investigation are presented in Section 7.

2 Lindley Distribution

The cumulative distribution function of the Lindley distribution, is defined as

$$F\left(t\right)=1-\frac{\psi +1+\psi t}{\psi +1}\mathit{exp}\left(-\psi t\right),\text{ where }t>0, \, \psi >0$$
(1)

The corresponding probability density function is

$$f\left(t\right)=\frac{{\psi }^{2}}{\psi +1}\left(1+t\right)\mathit{exp}\left(-\psi t\right),\text{ where }t>0, \, \psi >0$$
(2)

The rth moment about the origin of the Lindley distribution is

$$E\left({X}^{r}\right)=\frac{r !\left(\psi +r+1\right)}{{\psi }^{r}\left(\psi +1\right)}, \, r=\text{1,2},...$$
(3)

Hence the mean of the Lindley distribution is given by

$$\frac{\psi +2}{\psi \left(\psi +1\right)}$$
(4)

3 Design of Attribute CCS for Lindley Distribution

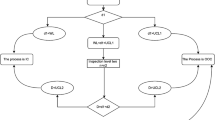
It is assumed that the failure time probability of the product is based on the Lindley distribution with probability, so the attribute CCs under time-truncated life tests for the Lindley distribution are designed as follows.

$$p=1-\frac{\psi +1+\psi t}{\psi +1}\mathit{exp}\left(-\psi t\right)$$
(5)
  1. 1)

    From the process, based on random sample, n products are to be selected.

  2. 2)

    Conduct life test on the randomly selected product and test is terminated at a time \({t}_{0}\) whose termination time is fixed based on average life of the product and it is given by \({t}_{0}=a{\mu }_{0}\) where ‘a’ is called as the truncation constant and \({\mu }_{0}\) is referred as the average life of the product.

Hence \({t}_{0}=a\frac{\psi +2}{\psi \left(\psi +1\right)}\).

Therefore

$${p}_{0}=1-\frac{\psi +1+a\left(\frac{\psi +2}{\psi +1}\right)}{\psi +1}\mathit{exp}\left(-a\frac{\psi +2}{\psi +1}\right)$$
(6)

Number of failed product \({X}_{i}\) is counted. Here it is assumed that \({X}_{i}\)= np0 follows Binomial distribution with parameters \(B\left(n,{p}_{0}\right)\), where n- sample size and \({p}_{0}\)- probability of failure before \({t}_{0}\).

The proposed CCs is designed based on two inner and outer control limits.

The inner control limits are UCL2 and LCL2 are

$$UC{L}_{2}=n{p}_{0}+{k}_{2}\sqrt{n{p}_{0}{q}_{0}}$$
(7a)
$$LC{L}_{2}=n{p}_{0}-{k}_{2}\sqrt{n{p}_{0}{q}_{0}}$$
(7b)

Outer control limits are UCL1 and LCL1 are

$$UC{L}_{1}=n{p}_{0}+{k}_{1}\sqrt{n{p}_{0}{q}_{0}}$$
(8a)
$$LC{L}_{1}=n{p}_{0}-{k}_{1}\sqrt{n{p}_{0}{q}_{0}}$$
(8b)

where \({q}_{0}=1-{p}_{0}\), k1 and k2 are control limits, where \(\left({k}_{1}>{k}_{2}\right)\) whose values are based on the desired under control ARL0.

  1. (1)

    if \({X}_{i}\)> UCL1 or \({X}_{i}\)< LCL1 the process is declared as out of control.

  2. (2)

    if LCL2 ≤ \({X}_{i}\)≤ UCL2, then it is under control

  3. (3)

    if UCL2 ≤ \({X}_{i}\)≤ UCL1 or LCL1 ≤ \({X}_{i}\)≤ LCL2, then step 1 is to be repeated.

3.1 Under Control Average Run length for Proposed CCs

From step (4), the out-of-control probability, when the process is in under control state is given by:

$$\begin{array}{c}P_{OoC(0)}=P\left(X_i>UCL_1\right)+P\left(X_i<LCL_1\right)\\=\sum\nolimits_{f=UCL_{1+1}}^n\begin{pmatrix}n\\f\end{pmatrix}p_0^fq_0^{\left(n-f\right)}+\sum\nolimits_{f=0}^{LCL_1}\begin{pmatrix}n\\f\end{pmatrix}p_0^fq_0^{\left(n-f\right)}\end{array}$$
(9)

Where p0 is given by Eq. 6.

Then from step (6), the repetition probability when the process is under control, if

$$\begin{array}{c}{P}_{rep(0)}=P\left(UC{L}_{2}<{X}_{i}<UC{L}_{1}\right)+P\left(LC{L}_{1}<{X}_{i}<LC{L}_{2}\right)\\ ={\sum }_{f=LC{L}_{1}+1}^{LC{L}_{2}}\left(\begin{array}{c}n\\ f\end{array}\right){{p}_{0}}^{f}{{q}_{0}}^{\left(n-f\right)}+{\sum }_{f=UC{L}_{2}+1}^{UC{L}_{1}}\left(\begin{array}{c}n\\ f\end{array}\right){{p}_{0}}^{f}{{q}_{0}}^{\left(n-f\right)}\end{array}$$
(10)

where p0 is given by Eq. 6.

When the process is under control under repetitive scheme, the out-of-control probability is defined as:

$${P}_{OoC}=\frac{{P}_{OoC(0)}}{1-{P}_{rep(0)}}$$
(11)

The performances of the CCs are evaluated based on the under control ARL0 and the average sample size (ASS0) as suggested by (Adeoti O. A., 2022)] which is defined as follows

$$AR{L}_{0}=\frac{1}{{P}_{OoC}}$$
(12)
$$AS{S}_{0}=\frac{n}{1-{P}_{rep(0)}}$$
(13)

3.2 Out of Control Average Run Length for Proposed CCs

If the process is shifted to a new scale parameter \({t}_{0}=c\mu\) where c shifting constant, and the process is declared as out of control. The failure probability \({p}_{1}\) that a product failed before the time \({t}_{0}\) is defined as:

$${p}_{1}=1-\frac{\psi +1+c\left(\frac{\psi +2}{\psi +1}\right)}{\psi +1}\mathit{exp}\left(-\frac{\psi +2}{\psi +1}c\right)$$
(14)

Based on this, out of control probability for the shifted process is defined as

$$\begin{array}{c}{P}_{OoC(1)}=P\left({X}_{i}>UC{L}_{1}\right)+P\left({X}_{i}<LC{L}_{1}\right)\\ ={\sum }_{f=UC{L}_{1}+1}^{n}\left(\begin{array}{c}n\\ f\end{array}\right){{p}_{1}}^{f}{{q}_{1}}^{\left(n-f\right)}+{\sum }_{f=0}^{LC{L}_{1}}\left(\begin{array}{c}n\\ f\end{array}\right){{p}_{1}}^{f}{{q}_{1}}^{\left(n-f\right)}, \text{where }{p}_{1}\text{is given by Eqn}.14\end{array}$$
(15)

Similarly, the repetition probability for the shifted process is:

$$\begin{array}{c}{P}_{rep(1)}=P\left(UC{L}_{2}<{X}_{i}<UC{L}_{1}\right)+P\left(LC{L}_{1}<{X}_{i}<LC{L}_{2}\right)\\ ={\sum }_{f=LC{L}_{1}+1}^{LC{L}_{2}}\left(\begin{array}{c}n\\ f\end{array}\right){{p}_{1}}^{f}{{q}_{1}}^{\left(n-f\right)}+{\sum }_{f=UC{L}_{2}+1}^{UC{L}_{1}}\left(\begin{array}{c}n\\ f\end{array}\right){{p}_{1}}^{f}{{q}_{1}}^{\left(n-f\right)},\text{ where }{p}_{1}\text{is given by Eqn}.14\end{array}$$
(16)

The out-of-control ARL1 and ASS1 as suggested by (Adeoti O. A., 2022) are defined as

$$AR{L}_{1}=\frac{1}{{P}_{OoC(1)}}$$
(17)
$$AS{S}_{1}=\frac{n}{1-{P}_{rep(1)}}$$
(18)

The parameters of the CCs \(\left({k}_{1},{k}_{2},a\right)\), the inner and outer control limits for desired ARL0 and for different shifts c are calculated based on the following algorithm:

  1. 1)

    Specify ARL0 and the sample size n

  2. 2)

    Calculate the CCs parameters \(\left({k}_{1},{k}_{2},a\right)\)

  3. 3)

    Determine the ARL1 and ASS1 for different shift constants.

In the proposed CCs, ARL1 and ASS1 are obtained based on the above algorithm for different shifts C and different ARL0. The results obtained are presented in Tables 1, 2, 3, 4 and 5. For sample sizes n = 25, 30, 35, and 40, we reported ARL1 and ASS1 of the proposed CC in Tables 1 through 4 for target in-control ARL0 = 200, 250, 300, and 370 with varying shifts for Lindley distribution when ψ = 1. Table 2 is created for the suggested CC by varying ψ = 1.5, 2, 2.5, and 3 and fixing sample size n = 30 and ARL0 = 370. The following patterns in ARL1 and ASN1 are observed from Tables 1, 2, 3, 4 and 5.

  1. 1)

    A decreasing trend in ARL1 is observed for the same values of n, k1, and k2, as c changes from 1 to 4.

  2. 2)

    When n increases, ARL1 also increases for the same values of c.

  3. 3)

    ASN1 rises first and then decreases and finally reaches sample size n as c increases to 4.

Table 1 Value of ARL1 and ASS1 for different shifts for Lindley distribution when ARL0 = 200 and \(\uppsi =1\)
Full size table
Table 2 Value of ARL1 and ASS1 for different shifts for Lindley distribution when ARL0 = 250 and \(\uppsi =1\)
Full size table
Table 3 Value of ARL1 and ASS1 for different shifts for Lindley distribution when ARL0 = 300 and \(\uppsi =1\)
Full size table
Table 4 Value of ARL1 and ASS1 for different shifts for Lindley distribution when ARL0 = 370 and \(\uppsi =1\)
Full size table
Table 5 Value of ARL1 and ASS1 for different shifts for Lindley distribution when ARL0 = 370 and n = 30
Full size table

4 Description of Results

Let us assume that a manufacturing unit with an average life of 100 h and a failure time probability that follows the Lindley distribution with \(\psi =1\) is using the suggested CCs in real time as follows.

In the following ways, the tables are used: First fix the ARL0 and let it be fixed as 250, let us take sample size n = 25. From Table 2, the CCs parameters are k1 = 2.694, k2 = 1.362 and a = 1.295. The control limits are obtained as UCL1 = 24, UCL2 = 21, LCL1 = 11 and LCL2 = 14. Now the \({t}_{0}=0.6544*100\approx 65\) Hence the CCs to be set up is as follows: Number of failures for the truncated time \({t}_{0}=65\) is counted and.

  1. a.

    If \({X}_{i}>24\text{ or }{X}_{i}<11\) the process is declared as out of control

  2. b.

    If \(14\le {X}_{i}\le 21\), the process is declared as under control

  3. c.

    If \(21<{X}_{i}<24\text{ or }11<{X}_{i}<14\), the process is repeated.

5 Application of Proposed CC

5.1 Simulation Study

This section demonstrates the application of the proposed CC through simulated data. The data are generated from Lindley distribution when the process is in-control with parameters ψ = 1. We take into account a random sample of size 30 observations with a subgroup size of 15. For shifting c = 1.2, for the Lindley distribution with ψ = 1.2 generates an additional 15 subgroup sample data. We found that, after fixing ARL0 = 300, from Table 3, the CCs parameters for n = 30 are obtained as k1 = 2.871, k2 = 1.736, a = 1.326 with LCL1 = 14, LCL2 = 17, UCL1 = 28, and UCL2 = 26. The mean of the simulated data is calculated as 21.065. With this information, the test time is calculated as t0 = a*µ = 1.326* 21.065 = 28. This led to the test being administered for t0 = 28, and the item count that fails before that time is denoted by Xi. In Fig. 1, the CCs with these control limits are plotted for the simulated data. Figure 1 demonstrates that even though the process is under control, a change in the 17th and 24th items in the process causes disruptions. As a result, it is evident that the suggested CC was successful in finding the process modification.

Fig. 1
figure 1

CC for simulated data set when ARL0 = 300 and n = 30

Full size image

Simulated data:

18.87

17.64

24.02

23.62

21.22

18.34

19.84

22.42

19.74

23.46

3.53

18.15

24.89

19.17

22.85

18.75

27.10

23.94

22.45

23.50

22.21

22.18

24.74

15.88

17.12

22.13

17.55

17.69

22.49

17.6

5.2 Real Life Example

Using precise information from a study that looked at the prevalence of lung cancer in 44 US states is used for CC analysis and the data is available at www.calvin.edu/stob/data/cigs.csv. [20] are among the researchers who have previously looked through this data set. The Lindley distribution describes the distribution of the data, with mean 19.65 and ψ = 0.20632. Fixing ARL0 = 370, n = 44, the value of a = 1.021. We use Eq. 6 to find the value of P0 as 0.606 and by using Eq. 7 (a and b) and 8 (a and b), we determine the values of LCL1 = 11, UCL1 = 28, LCL2 = 12, and UCL2 = 26 when k1 = 2.750 and k2 = 2.4 respectively.

The data set is given below:

17.05

19.80

15.98

22.07

22.83

24.55

27.27

23.57

13.58

22.80

20.30

16.59

16.84

17.71

25.45

20.94

26.48

22.04

22.72

14.20

15.60

20.98

19.50

16.70

23.03

25.95

14.59

25.02

12.12

21.89

19.45

12.11

23.68

17.45

14.11

17.60

20.74

12.01

21.22

20.34

20.55

15.53

15.92

25.88

    

The CC for the data is given in Fig. 2 and the following steps explain how the chart functions:

Fig. 2
figure 2

CC for real data set when ARL0 = 300 and n = 44 for the proposed plan

Full size image

  • Step 1: A random selection of 44 items is made from the Lindley distribution using a scale parameter ψ = 0.20632.

  • Step2: The truncated time is calculated as t0 = 20. for which these items are placed, the number of failed items Xi is counted during the test.

  • Step 3: Declare the process as under control, if 12 ≤ \({X}_{i}\)  ≤ 26.

  • Step 4: The procedure is considered to be out of control, if \({X}_{i}\) > 28 or \({X}_{i}\)< 11.

  • Step 5: If not, the procedure is carried out again until the status of the process is established.

For the Lindley distribution single sampling plan with ψ = 0.20632, the CCs parameters for n = 44 are calculated by fixing ARL0 = 370 in order to determine the effectiveness of the repetitive sampling plan. The value obtained are k = 2.9079, a = 1.1197 with P0 as 0.6520 and UCL = 38 and LCL = 19. Every data point falls inside the control limits, as shown by the CC for the data in Fig. 3. From this, we can find the effectiveness of the repetitive sampling plan as that plan suggests for repetitive sampling.

Fig. 3
figure 3

CC for real data set when ARL0 = 300 and n = 44 for the single sampling plan

Full size image

6 Comparative Study

A comparative study is done between the proposed repeated sampling CC under time-truncated life tests with the CC using single sampling scheme. Under time-truncated life tests for the Lindley distribution, CCs with the single sampling scheme are not documented in the literature; instead, they are evaluated for comparison’s sake. The values of ARL1 for the proposed CCs and single sampling CCs are tabulated in Table 6 along with values obtained for various shifts for the Lindley distribution time-truncated life tests when \(\uppsi =1, 2 and 3\), ARL0 = 370 and n = 30. Figure 4 illustrates how the proposed CCs have lower ARL values for each shift than the CC using single sampling scheme. For instance, when \(\uppsi =1\) the ARL1 for the CC using single sampling scheme is 115.99, whereas the proposed CCs ARL1 is 75.36 for shift c = 1.1. Because of this, the suggested scheme performs better than the Lindley distribution's CCs using single sampling scheme based on ARL values.

Table 6 ARL1 for the proposed CC and CC using Single sampling for different shifts for Lindley distribution when ARL0 = 370 and n = 30
Full size table
Fig. 4
figure 4

Comparison of ARL1 for the proposed CC with single sampling CC for different shifts for Lindley distribution when \(\uppsi =1,\) ARL0 = 370 and n = 30

Full size image

7 Conclusions

In this paper, attribute CCs under a truncated life test is presented for repeated sampling scheme using Lindley distribution. The purpose of creating the suggested CCs structure was to assess its efficacy through the utilization of ARL values. Tables for different quality parameters are provided for practical purposes. Through application to both simulation and real-world data sets, the proposed CCs effectiveness was investigated. It is determined from the simulation study that the suggested CC was effective in identifying the process modification. Using data sets on the prevalence of lung cancer in 44 US states, the suggested chart's performance is evaluated in a real-world scenario. When the identical data is used for single sampling CC, it is discovered that repetitive sampling CC perform better than single sampling CCs. A comparative study is performed between the suggested CC and the single sampling CC based on the ARL values and it is found that suggested CC performs better than CCs using single sampling scheme based on Lindley distribution. Hence, CCs using repeated sampling scheme under Lindley distribution is recommended. The proposed control chart has the limitation that it can be applied only when the data follows the Lindley distribution. The suggested CCs can be expanded for future research by utilizing various sample schemes. Similarly, an attribute CCs design within the framework of neutrosophic statistics may be the subject of a subsequent investigation.