1 Introduction

The derivative-type nonlinear Schrödinger equations have several applications in plasma physics and nonlinear fiber optics. In plasma physics, the equation (also called DNLS-I)

$$\begin{aligned} \textrm{i}q_{t}+q_{xx}+\textrm{i}(|q|^{2}q)_{x}=0 \end{aligned}$$
(1)

describes small-amplitude nonlinear Alfvén waves propagating parallel to the ambient magnetic field [9, 13]. In nonlinear optics, the modified NLS i.e. the equation (1) plus the nonlinear term \(|q|^2{q}\) describes the case of subpicosecond optical pulses [3, 6]. Recently Moses et al. has experimentally demonstrated that the equation (also called DNLS-II)

$$\begin{aligned} \textrm{i}q_{t}+q_{xx}+\textrm{i}|q|^{2}q_{x}=0 \end{aligned}$$
(2)

describes the propagation of the self-steepening optical pulses without self-phase modulation [14]. In the view of inverse scattering theory they are gauge equivalent [23] to the following equation [7] (also called DNLS-III)

$$\begin{aligned} \textrm{i}q_{t}+q_{xx}-\textrm{i}q^{2}q^{*}_{x}+\frac{1}{2}|q|^4{q}=0, \end{aligned}$$
(3)

where the asterisk denotes the complex conjugate, so we take DNLS-III as an example to present our work. The above derivative-type equations are important integrable models. In addition, there are more general integrable generalizations, such as the high-order Kaup–Newell equation [18], the generalized mixed nonlinear Schrödinger equation [19], Kundu equation [11], Kundu–Eckhaus equation [5, 11]. Much research has been conducted for them, here we will not dwell on a detailed exposition of various results. The Eq. (3) are the compatible condition of the following linear differential equations

$$\begin{aligned} \psi _x=X\psi ,\qquad \psi _t=T\psi , \end{aligned}$$
(4)

where

$$\begin{aligned} \begin{aligned} X=&-\textrm{i}\lambda ^{2}\sigma _3+\lambda {Q}+\frac{\textrm{i}}{2}{|q|^2}\sigma _3,\\ T=&-2\textrm{i}\lambda ^{4}\sigma _3+2\lambda ^3Q+\textrm{i}\lambda ^{2}{|q|^2}\sigma _3+\textrm{i}\lambda \sigma _3Q_x+\frac{\textrm{i}}{4}{|q|^4}\sigma _3-\frac{1}{2}(QQ_x-Q_xQ) \end{aligned} \end{aligned}$$

and the potential matrix

$$\begin{aligned} Q(x,t)=\left( \begin{array}{cc} 0 &{}\quad q \\ -q^{*} &{}\quad 0 \\ \end{array} \right) , \end{aligned}$$

\(\sigma _3\) is one of the Pauli matrices

$$\begin{aligned} \sigma _1=\left( \begin{array}{cc} 0 &{}\quad 1 \\ 1 &{}\quad 0 \\ \end{array} \right) ,\quad \sigma _2=\left( \begin{array}{cc} 0 &{}\quad -\textrm{i} \\ \textrm{i} &{}\quad 0 \\ \end{array} \right) ,\quad \sigma _3=\left( \begin{array}{cc} 1 &{} 0 \\ 0 &{} -1 \\ \end{array} \right) . \end{aligned}$$

It is known that Zakharov first given higher-order solitons for the NLS equation corresponding to a double pole [24]. Subsequently higher-order solitons have also been studied for the modified KdV equation [22], the sine-Gordon equation [21] and so on. So far various methods have been developed to deal with higher-order solitons, for example the usual Riemann–Hilbert (RH) method [20], generalized Darboux transform [8, 12], \(\bar{\partial }\)-method [10], robust inverse scattering transform [4] et al.. In this paper, to avoid the difficulty of calculating residue conditions with multiple poles, different from the work [25, 26] we generalize Olmedilla’s idea [16] to the framework for RH method and arbitrary higher-order soliton solutions for the derivative nonlinear Schrödinger equation can be directly obtained.

This paper is arranged as follows. In Sect. 2, we summary the inverse scattering method for DNLS-III. In Sect. 3, we derive the explicit determinant form of a higher-order soliton which corresponds to one pth order pole. In Sect. 4, the interaction related to one simple pole and the other one double pole is displayed.

2 Summary of the Inverse Scattering Method for the DNLS Equation

Firstly, we summarize the already well-known results [15] for the DNLS-III that will be used in our study. In this section we solve the initial value problem for the DNLS-III with the following zero boundary condition (ZBC) at \(x\rightarrow \infty\):

$$\begin{aligned} \lim _{x \rightarrow \pm \infty }{q(x,t)}=0, \end{aligned}$$
(5)

meanwhile the complex function q(x) satisfies

$$\begin{aligned} \int _{-\infty }^{\infty }|x^{n}||q(x)|dx<\infty . \end{aligned}$$

2.1 The Direct Scattering Problem

2.1.1 Jost Solution and Analyticity

For the oriented curve \(\Sigma =\mathbb {R}\bigcup {\textrm{i}\mathbb {R}}\) (see Fig. 1) in complex \(\lambda\)-plane, we define \(J_{\pm }\) as the Jost solutions of the Lax representation (4) which obey the boundary conditions

$$\begin{aligned} J_{\pm }(x,\lambda )\rightarrow {e^{-\textrm{i}\lambda ^{2}x\sigma _3}},\quad x\rightarrow \pm \infty . \end{aligned}$$
(6)

Let

$$\begin{aligned} U_{\pm }(x,\lambda )=J_{\pm }(x,\lambda )e^{\textrm{i}\lambda ^{2}x\sigma _3}, \end{aligned}$$

then

$$\begin{aligned} \begin{aligned}&U_{\pm {x}}=-\textrm{i}\lambda ^{2}[\sigma _3,U_{\pm }]+\lambda {Q}U_{\pm }+\frac{\textrm{i}}{2}|q|^2\sigma _3{U_{\pm }},\\&U_{\pm }(x,\lambda )\rightarrow {\mathbb {I}},\quad x\rightarrow \pm \infty , \end{aligned} \end{aligned}$$
(7)

which is equivalent to Volterra integral equation

$$\begin{aligned} U_{\pm }(x,\lambda )=\mathbb {I}+\int _{\pm \infty }^{x}e^{-\textrm{i}\lambda ^{2}\hat{\sigma }_3(x-y)}(\lambda {Q(y)}+\frac{\textrm{i}}{2}|q|^2\sigma _3)U_{\pm }(y,\lambda )dy. \end{aligned}$$
(8)
Fig. 1
figure 1

The complex \(\lambda\)-plane, showing the regions \(D_{\pm }\) where \(\Re (\lambda )\Im (\lambda )>0\) (grey) and \(\Re (\lambda )\Im (\lambda )<0\) (white), respectively

Full size image

Denoting \(D_{\pm }=\{\lambda \in \mathbb {C}|\pm {\Re (\lambda )\Im (\lambda )>0}\}\), as shown in Fig. 1. By performing the Neumann series (cf. [1]) on the Volterra integral equations (8), we know that \(U_{-1}(J_{-1})\) and \(U_{+2}(J_{+2})\) can be analytically extended to \(D_{+}\) and continuously extended to \(D_{+}\bigcup \Sigma\), while \(U_{+1}(J_{+1})\) and \(U_{-2}(J_{-2})\) can be analytically extended to \(D_{-}\) and continuously extended to \(D_{-}\bigcup \Sigma\), where the subscripts 1 and 2 identify matrix columns, i.e., \(U_{\pm }=(U_{\pm 1},U_{\pm 2})\).

2.1.2 Scattering Matrix

Abel’s theorem implies that for any solution \(\psi (x,\lambda )\) of the Lax representation (4) one has \(\partial _{x}(\det {\psi })=0\). Since \(\mathop {\textrm{lim}}\nolimits _{x\rightarrow \pm \infty }{J_{\pm }}e^{\textrm{i}\lambda ^{2}\sigma _3{x}}=I\) for \(\lambda \in {\Sigma }\), we have

$$\begin{aligned} \det {J_{\pm }(x,\lambda )}=1. \end{aligned}$$

It follows that \(\forall \lambda \in \Sigma\) both \(J_{+}\) and \(J_{-}\) are two fundamental matrix solutions of the scattering problem (4). Define the scattering matrix S(k)

$$\begin{aligned} J_{-}(x,\lambda )=J_{+}(x,\lambda )S(\lambda ), \end{aligned}$$
(9)

where \(S=\{s_{ij}\}\). Rewrite it by component

$$\begin{aligned} J_{-1}(x,\lambda )= & {} s_{11}(\lambda )J_{+1}(x,\lambda )+s_{21}(\lambda )J_{+2}(x,\lambda ), \end{aligned}$$
(10)
$$\begin{aligned} J_{-2}(x,\lambda )= & {} s_{12}(\lambda )J_{+1}(x,\lambda )+s_{22}(\lambda )J_{+2}(x,\lambda ). \end{aligned}$$
(11)

Furthermore we obtain

$$\begin{aligned} s_{11}(\lambda )=W(J_{-1},J_{+2}),\quad s_{22}(\lambda )=W(J_{+1},J_{-2}), \end{aligned}$$

where W(f, g) is the Wronskian of f and g and reflection coefficients

$$\begin{aligned} \rho (\lambda )=\frac{s_{21}}{s_{11}},\quad \tilde{\rho }(\lambda )=\frac{s_{12}}{s_{22}}. \end{aligned}$$

From the analytic property of Jost solutions, \(s_{11}(\lambda )\) can be analytically extended to \(D_{+}\) and continuously extended to \(D_{+}\bigcup \Sigma\), while \(s_{22}(\lambda )\) can be analytically extended to \(D_{-}\) and continuously extended to \(D_{-}\bigcup \Sigma\).

2.1.3 Symmetry Conditions and Discrete Spectrum

By virtue of the uniqueness of the Jost solutions, we have the following symmetry conditions

$$\begin{aligned} J_{\pm }(\lambda )=\sigma _3J_{\pm }(-\lambda )\sigma _3,\quad J_{\pm }(\lambda )=\textrm{i}\sigma _2J_{\mp }^{*}(\lambda ^{*})(\textrm{i}\sigma _2)^{-1}. \end{aligned}$$
(12)

So

$$\begin{aligned} \begin{aligned} s_{11}(\lambda )&=s_{11}(-\lambda ),\quad s_{12}(\lambda )=-s_{12}(-\lambda ),\quad s_{21}(\lambda )=-s_{21}(-\lambda ), \\ s_{22}(\lambda )&=s_{22}(-\lambda ),\quad s_{11}(\lambda )=s_{22}^{*}(\lambda ^{*}),\quad s_{12}(\lambda )=-s_{21}^{*}(\lambda ^{*}) \end{aligned} \end{aligned}$$
(13)

and

$$\begin{aligned} \rho (\lambda )=-\rho (-\lambda ),\quad \tilde{\rho }(\lambda )=-\rho ^{*}(\lambda ^{*}). \end{aligned}$$
(14)

If \(s_{11}(\lambda _{n})=0, n=1,\ldots ,N\), the eigenfunctions \(J_{-1}(x,\lambda )\) and \(J_{+2}(x,\lambda )\) at \(\lambda =\lambda _n\) must be proportional, i.e.

$$\begin{aligned} J_{-1}(x,\lambda _n)=\gamma _n{J_{+2}(x,\lambda _n)}, \end{aligned}$$
(15)

where \(\gamma _{n}\) is a complex valued constant. Owing to the relations (13), we have

$$\begin{aligned} s_{11}(\lambda )=0\Longleftrightarrow {s}_{11}(-\lambda )=0\Longleftrightarrow {s}_{22}(-\lambda ^{*})=0 \Longleftrightarrow {s}_{22}(\lambda ^{*})=0, \end{aligned}$$

then

$$\begin{aligned} \begin{aligned} J_{-1}(-\lambda _n)&=\hat{\gamma }_n{J_{+2}(-\lambda _n)},\\ J_{-2}(-\lambda ^{*}_{n})&=\check{\gamma }_n{J_{+1}(-\lambda ^{*}_{n})},\\ J_{-2}(\lambda ^{*}_{n})&=\tilde{\gamma }_n{J_{+1}(\lambda ^{*}_{n})}, \end{aligned} \end{aligned}$$
(16)

where \(\hat{\gamma }_n=-\gamma _n, \check{\gamma }_n=\gamma _n^{*}, \tilde{\gamma }_n=-\gamma _n^{*}\). That is, the discrete spectrum is the set

$$\begin{aligned} Z=\{\lambda _{n},-\lambda _{n},\lambda ^{*}_{n},-\lambda ^{*}_{n}\}. \end{aligned}$$

This distribution is shown in Fig. 1.

2.1.4 Asymptotics as \(\lambda \rightarrow \infty\)

The Wentzel–Kramers–Brillouin (WKB) expansion can be used to derive the asymptotic of modified Jost solutions. In fact, we know that \(U_{\pm }\) are analytic in \(\mathbb {C}/\Sigma\), then we can write an asymptotic expansion for \(U_{\pm }\) when \(\lambda \rightarrow \infty\)

$$\begin{aligned} U_{\pm }(x,\lambda )=U_{\pm ,0}+\frac{U_{\pm ,1}}{\lambda }+\frac{U_{\pm ,2}}{\lambda ^{2}}+O\left(\frac{1}{\lambda ^{3}}\right). \end{aligned}$$
(17)

Substituting the above expansion into the Eq. (7) and utilizing the expressions for \(s_{11}\) and \(s_{22}\), we have

$$\begin{aligned} U_{\pm }(x,\lambda )\longrightarrow {I},\quad |\lambda |\longrightarrow \infty \end{aligned}$$

and

$$\begin{aligned} s_{11}(\lambda )\rightarrow {1},\quad s_{22}(\lambda )\rightarrow {1}. \end{aligned}$$

2.2 The Inverse Scattering Problem

2.2.1 Riemann–Hilbert Problem and Reconstruction Formula

In order to construct RH problem, introduce the sectionally meromorphic matrices

$$\begin{aligned} M_{+}(x,\lambda )=\left[ \frac{U_{-1}}{s_{11}},U_{+2}\right] ,\quad M_{-}(x,\lambda )=\left[ U_{+1},\frac{U_{-2}}{s_{22}}\right] . \end{aligned}$$

From the Eqs. (10) and (11) we obtain the jump condition

$$\begin{aligned} M_{+}(x,\lambda )=M_{-}(x,\lambda )(I+G(\lambda )), \end{aligned}$$

where

$$\begin{aligned} G(\lambda )=\left( \begin{array}{cc} -\rho (\lambda ){\tilde{\rho }(\lambda )} &{}\quad \tilde{\rho }(\lambda )e^{-2\textrm{i}\lambda ^2{x}} \\ \rho (\lambda ){e^{2\textrm{i}\lambda ^2{x}}} &{}\quad 0 \\ \end{array} \right) . \end{aligned}$$

Recalling the asymptotic behavior of the scattering coefficients, it is easy to obtain that

$$\begin{aligned} M_{\pm }(x,\lambda )\rightarrow {I},\quad |\lambda |\rightarrow \infty . \end{aligned}$$

From the Eq. (7) we can reconstruct the potential q(x, t) from the solution of the RH problem as follow

$$\begin{aligned} q(x,t)=2\textrm{i}\lim _{\lambda \rightarrow \infty }{\lambda {[M(\lambda ;x,t)]_{12}}}. \end{aligned}$$
(18)

2.2.2 Residue Conditions and Solution for RHP

To solve the RHP, introduce the Cauchy projectors \(P^{\pm }\) over \(\Sigma\):

$$\begin{aligned} P^{\pm }[f](\lambda )=\frac{1}{2\pi {\textrm{i}}}\int _{\Sigma }\frac{f(\zeta )}{\zeta -(\lambda \pm {\textrm{i}0})}d\zeta . \end{aligned}$$

If \(f_{\pm }(\lambda )\) is analytic in the region \(D_{\pm }\) and \(f_{\pm }(\lambda )\rightarrow 0\) as \(|\lambda |\rightarrow \infty\), then

$$\begin{aligned} P^{\pm }(f_{\mp })(\lambda )=0,\quad P^{\pm }(f_{\pm })(\lambda )=\pm {f_{\pm }(\lambda )}. \end{aligned}$$
(19)

Furthermore, we can obtain the residue conditions from the equations (15) and (16)

$$\begin{aligned} \begin{aligned} \mathop {Res}\limits _{\lambda =\lambda _{n}}\left(\frac{U_{-1}}{s_{11}}\right)&=C_{n}e^{2\textrm{i}\lambda ^2_n{x}}U_{+2}(\lambda _n),\\ \mathop {Res}\limits _{\lambda =-\lambda _{n}}\left(\frac{U_{-1}}{s_{11}}\right)&=C_{n}e^{2\textrm{i}\lambda ^2_n{x}}U_{+2}(-\lambda _n),\\ \mathop {Res}\limits _{\lambda =\lambda _{n}^{*}}\left(\frac{U_{-2}}{s_{22}}\right)&={-C_{n}^{*}}e^{-2\textrm{i}\lambda ^{*{2}}_n{x}}U_{+1}(\lambda _n^{*}),\\ \mathop {Res}\limits _{\lambda =-\lambda _{n}^{*}}\left(\frac{U_{-2}}{s_{22}}\right)&={-C_{n}^{*}}e^{-2\textrm{i}\lambda ^{*{2}}_n{x}}U_{+1}(-\lambda _n^{*}) \end{aligned} \end{aligned}$$

where \(C_n=\frac{\gamma _{n}}{s^{\prime }_{11}(\lambda _n)}\).

Applying \(P^{-}\) to both sides of the expression (10) and \(P^{+}\) to both sides of the expression (11), meanwhile, taking advantage of the formulae (19) and the above residue conditions, we have

$$\begin{aligned} \begin{aligned} U_{+1}(\lambda )=&\left( \begin{array}{c} 1 \\ 0 \\ \end{array} \right) +\sum _{n=1}^{N}\frac{C_{n}e^{2\textrm{i}\lambda ^2_n{x}}U_{+2}(\lambda _n)}{\lambda -\lambda _n}\\&+\sum _{n=1}^{N}\frac{C_{n}e^{2\textrm{i}\lambda ^2_n{x}}U_{+2}(-\lambda _n)}{\lambda +\lambda _n}+\frac{1}{2\pi {\textrm{i}}}\int _{\Sigma }\frac{\rho {e^{2\textrm{i}\zeta ^2{x}}}U_{+2}}{\zeta -(\lambda -{\textrm{i}0})}d\zeta ,\\ U_{+2}(\lambda )=&\left( \begin{array}{c} 0 \\ 1 \\ \end{array} \right) -\sum _{n=1}^{N}\frac{{C_{n}^{*}}e^{-2\textrm{i}\lambda ^{*{2}}_n{x}}U_{+1}(\lambda _n^{*})}{\lambda -\lambda _n^{*}}\\&-\sum _{n=1}^{N}\frac{{C_{n}^{*}}e^{-2\textrm{i}\lambda ^{*{2}}_n{x}}U_{+1}(-\lambda _n^{*})}{\lambda +\lambda _n^{*}}+\frac{1}{2\pi {\textrm{i}}}\int _{\Sigma ^{-}}\frac{\tilde{\rho }{e^{-2\textrm{i}\zeta ^2{x}}}U_{+1}}{\zeta -(\lambda +{\textrm{i}0})}d\zeta . \end{aligned} \end{aligned}$$
(20)

2.2.3 Time Evolution

The time evolution of the scattering data can be determined by the time part of the Lax representation (4). By the calculation (cf. [1] for details) we have

$$\begin{aligned} \begin{aligned} \lambda _{n}(t)&=\lambda _{n}, \quad \rho (t)=\rho {e^{4\textrm{i}{\lambda _{n}^4}t}}\\ \tilde{\rho }(t)&=\tilde{\rho }{e^{4\textrm{i}{\lambda _{n}^4}t}},\quad C_{n}(t)=C_{n}e^{4\textrm{i}{\lambda _{n}^4}t}. \end{aligned} \end{aligned}$$

2.3 The Soliton Solutions for the DNLS Equation

We now consider the potential q(x, t) for which the reflection coefficient \(\rho (\lambda )\) vanishes. As usual, in the case there is no jump from \(M_{+}\) to \(M_{-}\) across the continuous spectrum, and the Eq. (20) reduce to an algebraic system. Next we take 1-soliton solution as an example.

Let \(\rho (\lambda )=\tilde{\rho }(\lambda )=0\) and \(N=1\). From the Eq. (20) and the formula (18), we can obtain 1-soliton solution

$$\begin{aligned} q=-4|C_1|e^{-\textrm{i}\vartheta }Sech[2\eta (x+4\xi {t})+\mu +\textrm{i}\nu ]. \end{aligned}$$
(21)

where

$$\begin{aligned} \begin{aligned} \lambda _1^{2}&=\xi +\textrm{i}\eta ,\quad \frac{|C_1|}{\eta }\lambda _1=e^{-(\mu +\textrm{i}\nu )},\\ \vartheta&=\omega +2\xi {x}+4(\xi ^2-\eta ^2)t,\quad \omega =arg{(C_1)}. \end{aligned} \end{aligned}$$

Remark 1

If we consider N different zeros of \(s_{11}(\lambda )\), By observation and calculation we can obtain the determinant form of N-soliton solution which is similar to the expression (29), this procedure will be elaborated in the next section.

3 Higher-Order Soliton Solutions for the DNLS Equation

In this section we generalize Olmedilla’s idea to the framework for RH method. If the potential q(x) decay rapidly enough at infinity, so that \(\rho (\lambda )\) can be analytically continued above or below all poles \(\{{\pm \lambda _n}\}_{n=1}^{N}\) and \(\tilde{\rho }(\lambda )\) can be analytically continued below or above all poles \(\{{\pm \lambda _n^{*}}\}_{n=1}^{N}\) ( cf. [1, 2]). The Eq. (20) can be simplified by virtue of the residue theorem as follows:

$$\begin{aligned} \begin{aligned} U_{+1}(\lambda )&=\left( \begin{array}{c} 1 \\ 0 \\ \end{array} \right) +\frac{1}{2\pi {\textrm{i}}}\int _{\Gamma }\frac{\rho (\zeta ){e^{2\textrm{i}\theta }}U_{+2}(\zeta )}{\zeta -\lambda }d\zeta ,\\ U_{+2}(\lambda )&=\left( \begin{array}{c} 0 \\ 1 \\ \end{array} \right) +\frac{1}{2\pi {\textrm{i}}}\int _{\bar{\Gamma }}\frac{\tilde{\rho }(\zeta ){e^{-2\textrm{i}\theta }}U_{+1}(\zeta )}{\zeta -\lambda }d\zeta , \end{aligned} \end{aligned}$$
(22)

where \(\theta =\zeta ^2{x}+2\zeta ^4{t}\), \(\Gamma\) is the union of a contour from \(\infty\) to \(\textrm{i}\infty\) that passes above all poles \(\{\lambda _n\}_{n=1}^{N}\) and a contour from \(-\infty\) to \(-\textrm{i}\infty\) that passes below all poles \(\{-\lambda _n\}_{n=1}^{N}\), \(\bar{\Gamma }\) is the union of a contour from \(-\infty\) to \(\textrm{i}\infty\) that passes above all poles \(\{-\lambda ^{*}_n\}_{n=1}^{N}\) and a contour from \(\infty\) to \(-\textrm{i}\infty\) that passes below all poles \(\{\lambda ^{*}_n\}_{n=1}^{N}\) in the Fig. 1.

Supposing that \(\rho (\lambda )\) has a pth order pole, we consider the Laurent series expansion of \(\rho (\lambda )\) around the point \(\lambda _n\) in the region \(D_{+}\). From the symmetries (14), we have

$$\begin{aligned} \begin{aligned} \rho (\lambda )&=\rho _{0}(\lambda )+\sum _{k=1}^{p}\left[ \frac{\rho _{-k}}{(\lambda -\lambda _{n})^{k}} +(-1)^{p-1}\frac{\rho _{-k}}{(\lambda +\lambda _{n})^{k}}\right] ,\\ \tilde{\rho }(\lambda )&=\tilde{\rho }_{0}(\lambda )-\sum _{k=1}^{p}\left[ \frac{\rho _{-k}^{*}}{(\lambda -\lambda ^{*}_{n})^{k}} +(-1)^{p-1}\frac{\rho _{-k}^{*}}{(\lambda +\lambda _{n}^{*})^{k}}\right] , \end{aligned} \end{aligned}$$
(23)

where \(\rho _{0}(\lambda )\) and \(\tilde{\rho }_{0}(\lambda )\) are analytic and satisfy the symmetries (14), \(\rho _{-i}(i=1,2,\cdots ,p)\) is a constant. Plugging the expressions (23) into (22), the integral equations (22) can be rewritten as

$$\begin{aligned} \begin{aligned}&U_{+1}(\lambda )=\left( \begin{array}{c} 1 \\ 0 \\ \end{array} \right) -\sum _{k=1}^{p}\rho _{-k}\frac{\partial ^{(k-1)}\left(\frac{e^{2\textrm{i}\theta }U_{+2}(\zeta )}{\zeta -\lambda }\right)}{\partial {\zeta ^{k-1}}}|_{\zeta =\lambda _{n}}\\&-\sum _{k=1}^{p}(-1)^{k-1}\rho _{-k}\frac{\partial ^{(k-1)}\left(\frac{e^{2\textrm{i}\theta }U_{+2}(\zeta )}{\zeta -\lambda }\right)}{\partial {\zeta ^{k-1}}}|_{\zeta =-\lambda _{n}} +\frac{1}{2\pi {\textrm{i}}}\int _{\Sigma }\frac{\rho (\zeta ){e^{2\textrm{i}\theta }}U_{+2}(\zeta )}{\zeta -\lambda }d\zeta , \end{aligned} \end{aligned}$$
(24)
$$\begin{aligned} \begin{aligned}&U_{+2}(\lambda )=\left( \begin{array}{c} 0 \\ 1 \\ \end{array} \right) +\sum _{k=1}^{p}\rho ^{*}_{-k}\frac{\partial ^{(k-1)}\left(\frac{e^{-2\textrm{i}\theta }U_{+1}(\zeta )}{\zeta -\lambda }\right)}{\partial {\zeta ^{k-1}}}|_{\zeta =\lambda ^{*}_{n}}\\&+\sum _{k=1}^{p}(-1)^{k-1}\rho ^{*}_{-k}\frac{\partial ^{(k-1)}\left(\frac{e^{-2\textrm{i}\theta }U_{+1}(\zeta )}{\zeta -\lambda }\right)}{\partial {\zeta ^{k-1}}}|_{\zeta =-\lambda ^{*}_{n}} +\frac{1}{2\pi {\textrm{i}}}\int _{\Sigma }\frac{\tilde{\rho }(\zeta ){e^{-2\textrm{i}\theta }}U_{+1}(\zeta )}{\zeta -\lambda }d\zeta . \end{aligned} \end{aligned}$$
(25)

For the case of a reflectionless potential, i.e. \(\rho (\lambda )=\tilde{\rho }(\lambda )=0\) when \(\lambda \in \Sigma\), the integral equation (24) and (25) reduce to the system of linear equations. By calculation we have

$$\begin{aligned} \tilde{H}_{p}=\omega _{p}-\Omega _p{H_{p}},\quad H_{p}=\Omega ^{*}_p{\tilde{H}_{p}}, \end{aligned}$$
(26)

where \(\Omega =(F_{ij})_{p\times {p}}\) and \(F_{ij}\) is a \(2\times 2\) matrix. We denote

$$\begin{aligned} \begin{aligned} F_{ij}^{11}&=\sum _{k=j}^{p}C_{k-1}^{j-1}\rho _{-k}\frac{\partial ^{(k+i-j-1)}[(\zeta -\lambda )^{-1}e^{2\textrm{i}\theta }]}{\partial \lambda ^{i-1}\partial \zeta ^{k-j}}|_{\zeta =\lambda _n,\lambda =\lambda _n^{*}},\\ F_{ij}^{12}&=\sum _{k=j}^{p}C_{k-1}^{j-1}(-1)^{k-1}\rho _{-k}\frac{\partial ^{(k+i-j-1)}[(\zeta -\lambda )^{-1}e^{2\textrm{i}\theta }]}{\partial \lambda ^{i-1}\partial \zeta ^{k-j}}|_{\zeta =-\lambda _n,\lambda =\lambda _n^{*}},\\ F_{ij}^{21}&=\sum _{k=j}^{p}C_{k-1}^{j-1}\rho _{-k}\frac{\partial ^{(k+i-j-1)}[(\zeta -\lambda )^{-1}e^{2\textrm{i}\theta }]}{\partial \lambda ^{i-1}\partial \zeta ^{k-j}}|_{\zeta =\lambda _n,\lambda =-\lambda _n^{*}},\\ F_{ij}^{22}&=\sum _{k=j}^{p}C_{k-1}^{j-1}(-1)^{k-1}\rho _{-k}\frac{\partial ^{(k+i-j-1)}[(\zeta -\lambda )^{-1}e^{2\textrm{i}\theta }]}{\partial \lambda ^{i-1}\partial \zeta ^{k-j}}|_{\zeta =-\lambda _n,\lambda =-\lambda _n^{*}} \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \tilde{H}_{p}&=\left( \begin{array}{ccccc} U_{+11}(\lambda _n^{*}) &{}\quad U_{+11}(-\lambda _n^{*}) &{}\quad \frac{\partial {U_{+11}}}{\partial \lambda }(\lambda _n^{*}) &{}\quad \cdots &{}\quad \frac{\partial ^{(p-1)}U_{+11}}{\partial \lambda ^{p-1}}(-\lambda _n^{*}) \\ \end{array} \right) _{1\times {2p}}^{T},\\ H_{p}&= \left( \begin{array}{ccccc} U_{+21}(\lambda _n) &{}\quad U_{+21}(-\lambda _n) &{}\quad \frac{\partial {U_{+21}}}{\partial \lambda }(\lambda _n) &{}\quad \cdots &{}\quad \frac{\partial ^{(p-1)}U_{+21}}{\partial \lambda ^{p-1}}(-\lambda _n) \\ \end{array} \right) _{1\times {2p}}^{T},\\ \omega _p&=\left( \begin{array}{ccccccc} 1 &{}\quad 1 &{}\quad 0 &{}\quad 0&{}\quad \cdots &{}\quad 0&{}\quad 0 \\ \end{array} \right) _{1\times {2p}}^{T}. \end{aligned} \end{aligned}$$

From the formula (18), we have

$$\begin{aligned} q=-2\textrm{i}\Lambda _p{\tilde{H}_p}, \end{aligned}$$
(27)

where

$$\begin{aligned} \begin{aligned} \Lambda _p&=\left( \begin{array}{ccccccc} G_{1} &{}\quad \hat{G}_{1} &{}\quad G_{2} &{}\quad \hat{G}_{2}&{}\quad \cdots &{}\quad G_{{p}} &{}\quad \hat{G}_{{p}}\\ \end{array} \right) _{1\times {2p}},\\ G_{j}&=\sum _{k=j}^{p}C^{j-1}_{k-1}\rho ^{*}_{-k}\frac{\partial ^{(k-j)}(e^{-2\textrm{i}\theta })}{\partial \zeta ^{k-j}}|_{\zeta =\lambda _n^{*}},\\ \hat{G}_{j}&=\sum _{k=j}^{p}C^{j-1}_{k-1}(-1)^{k-1}\rho ^{*}_{-k}\frac{\partial ^{(k-j)}(e^{-2\textrm{i}\theta })}{\partial \zeta ^{k-j}}|_{\zeta =-\lambda _n^{*}}. \end{aligned} \end{aligned}$$

Using the expression (26) and (27), we obtain

$$\begin{aligned} q=-2\textrm{i}\Lambda _p(I+\Omega _p\Omega ^{*}_p)^{-1}\omega _p. \end{aligned}$$
(28)

The expression (28) can written into determinant form

$$\begin{aligned} q=2\textrm{i}\frac{\det {\tilde{\Phi }_{p}}}{\det {\Phi _{p}}}, \end{aligned}$$
(29)

where

$$\begin{aligned} \Phi _{p}=I+\Omega _p\Omega ^{*}_p,\quad \tilde{\Phi }_{p}=\left( \begin{array}{cc} 0 &{}\quad \Lambda _p \\ \omega _p &{}\quad \Phi _p \\ \end{array} \right) . \end{aligned}$$

Remark 2

If \(\rho (\lambda )\) has r different poles, \(\lambda _1,\lambda _2,\ldots ,\lambda _r\) in the region \(D_{+}\), and their order are \(p_1,p_2,\ldots ,p_r\) respectively. The process of dealing with the general case is similar to one pth order pole. To illustrate it we give an example of the interaction between one simple pole soliton and the other double pole soliton in the next section.

4 Example of the Solutions for DNLS Equation

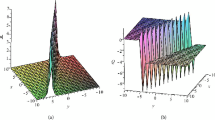
4.1 The Double Soliton Solution

In this subsection we consider the soliton solution related to one double pole. Let

$$\begin{aligned} \begin{aligned} \rho (\lambda )&=\rho _{0}+\frac{\rho _{-2}}{(\lambda -\lambda _1)^2}-\frac{\rho _{-2}}{(\lambda +\lambda _1)^2}+\frac{\rho _{-1}}{\lambda -\lambda _{1}}+\frac{\rho _{-1}}{\lambda +\lambda _{1}},\\ \tilde{\rho }(\lambda )&=\tilde{\rho }_{0}-\frac{\rho _{-2}^{*}}{(\lambda -\lambda _1^{*})^2}+\frac{\rho _{-2}^{*}}{(\lambda +\lambda _1^{*})^2}-\frac{\rho _{-1}^{*}}{\lambda -\lambda _{1}^{*}} -\frac{\rho _{-1}^{*}}{\lambda +\lambda _{1}^{*}}. \end{aligned} \end{aligned}$$
(30)

Substituting the expressions (30) into the Eqs. (24) and (25), we obtain

$$\begin{aligned} H_2=\omega _2+\Omega _2{\tilde{H}}_2,\quad \tilde{H}_2=-\Omega ^{*}_2{H_2}, \end{aligned}$$
(31)

where

$$\begin{aligned} \begin{aligned} \omega _2&=\left( \begin{array}{cccc} 1 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ \end{array} \right) ^{T},\quad \Omega _2 =\left( \begin{array}{cc} F_{11} &{}\quad F_{12} \\ F_{21} &{}\quad F_{22} \\ \end{array} \right) ,\\ H_2&= \left( \begin{array}{cccc} U_{+11}(\lambda _1^{*}) &{}\quad U_{+11}(-\lambda _1^{*}) &{}\quad \frac{\partial {U_{+11}}}{\partial \lambda }(\lambda _1^{*}) &{}\quad \frac{\partial {U_{+11}}}{\partial \lambda }(-\lambda _1^{*}) \\ \end{array} \right) ^{T},\\ \tilde{H}_2&= \left( \begin{array}{cccc} U_{+21}(\lambda _1) &{}\quad U_{+21}(-\lambda _1) &{}\quad \frac{\partial {U_{+21}}}{\partial \lambda }(\lambda _1) &{}\quad \frac{\partial {U_{+21}}}{\partial \lambda }(-\lambda _1) \\ \end{array} \right) ^{T}, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} F^{11}_{11}&=\left[ \frac{\rho _{-1}+\rho _{-2}(4\textrm{i}\lambda _1{x}+16\textrm{i}\lambda _1^3{t})}{\lambda _1-\lambda _1^{*}}-\frac{\rho _{-2}}{(\lambda _1-\lambda _1^{*})^2}\right] e^{2\textrm{i}\theta },\quad F^{22}_{11}=-F^{11}_{11},\\ F^{21}_{11}&=\left[ \frac{\rho _{-1}+\rho _{-2}(4\textrm{i}\lambda _1{x}+16\textrm{i}\lambda _1^3{t})}{\lambda _1+\lambda _1^{*}}-\frac{\rho _{-2}}{(\lambda _1+\lambda _1^{*})^2}\right] e^{2\textrm{i}\theta },\quad F^{12}_{11}=-F^{21}_{11},\\ F^{11}_{12}&=\frac{\rho _{-2}}{\lambda _1-\lambda _1^{*}}e^{2\textrm{i}\theta },\quad F^{21}_{12}=\frac{\rho _{-2}}{\lambda _1+\lambda _1^{*}}e^{2\textrm{i}\theta },\quad F^{12}_{12}=F^{21}_{12},\quad F^{22}_{12}=F^{11}_{12},\\ F^{11}_{21}&=\left[ \frac{\rho _{-1}+\rho _{-2}(4\textrm{i}\lambda _1{x}+16\textrm{i}\lambda _1^3{t})}{(\lambda _1-\lambda _1^{*})^2}-\frac{2\rho _{-2}}{(\lambda _1-\lambda _1^{*})^3}\right] e^{2\textrm{i}\theta },\quad F^{22}_{21}=F^{11}_{21},\\ F^{21}_{21}&=\left[ \frac{\rho _{-1}+\rho _{-2}(4\textrm{i}\lambda _1{x}+16\textrm{i}\lambda _1^3{t})}{(\lambda _1+\lambda _1^{*})^2}-\frac{2\rho _{-2}}{(\lambda _1+\lambda _1^{*})^3}\right] e^{2\textrm{i}\theta },\quad F^{12}_{21}=F^{21}_{21},\\ F^{11}_{22}&=\frac{\rho _{-2}}{(\lambda _1-\lambda _1^{*})^2}e^{2\textrm{i}\theta }, F^{21}_{22}=\frac{\rho _{-2}}{(\lambda _1+\lambda _1^{*})^{2}}e^{2\textrm{i}\theta },\quad F^{12}_{22}=-F^{21}_{22}, F^{22}_{22}=-F^{11}_{22}. \end{aligned} \end{aligned}$$

From the formula (29), we have

$$\begin{aligned} q=2\textrm{i}\frac{\det {\tilde{\Phi }_{2}}}{\det {\Phi _{2}}}, \end{aligned}$$
(32)

where

$$\begin{aligned} \begin{aligned} \Phi _{2}&=I+\Omega _2\Omega ^{*}_2,\quad \tilde{\Phi }_{2}=\left( \begin{array}{cc} 0 &{}\quad \Lambda _2 \\ \omega _2 &{}\quad \Phi _2 \\ \end{array} \right) ,\quad \chi =(4\textrm{i}\lambda _1{x}+16\textrm{i}\lambda _1^3{t}),\\ \Lambda _2&=\left( \begin{array}{cccc} \rho _{-1}^{*}-\rho _{-2}^{*}\chi &{}\quad \rho _{-1}^{*}-\rho _{-2}^{*}\chi &{}\quad \rho _{-2}^{*} &{}\quad -\rho _{-2}^{*} \\ \end{array} \right) . \end{aligned} \end{aligned}$$

As shown in Fig. 2.

Fig. 2
figure 2

\(\rho _{-1}=\textrm{i},\rho _{-2}=1,\lambda _1=1+\textrm{i},\) the left: the 3D image of \(|q|^2\), the right: the density image of \(|q|^2\)

Full size image

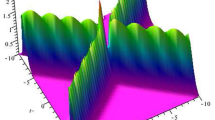
4.2 The Solution Related to One Simple Pole and the Other One Double Pole

In this subsection we consider the soliton solution related to one simplie pole and the other one double pole. Let

$$\begin{aligned} \begin{aligned} \rho (\lambda )&=\rho _{0}+\frac{\rho _{-2}}{(\lambda -\lambda _1)^2}-\frac{\rho _{-2}}{(\lambda +\lambda _1)^2} +\frac{\rho _{-1}}{\lambda -\lambda _{1}}+\frac{\rho _{-1}}{\lambda +\lambda _{1}} +\frac{\varrho _{-1}}{\lambda -\lambda _{2}}+\frac{\varrho _{-1}}{\lambda +\lambda _{2}},\\ \tilde{\rho }(\lambda )&=\tilde{\rho }_{0}-\frac{\rho _{-2}^{*}}{(\lambda -\lambda _1^{*})^2} +\frac{\rho _{-2}^{*}}{(\lambda +\lambda _1^{*})^2}-\frac{\rho _{-1}^{*}}{\lambda -\lambda _{1}^{*}} -\frac{\rho _{-1}^{*}}{\lambda +\lambda _{1}^{*}}-\frac{\varrho _{-1}^{*}}{\lambda -\lambda _{2}^{*}}-\frac{\varrho _{-1}^{*}}{\lambda +\lambda _{2}^{*}}. \end{aligned} \end{aligned}$$
(33)

Plugging the expressions (33) into the Eqs. (24) and (25), we have

$$\begin{aligned} H_{1,2}=\omega _{1,2}+\Omega _{1,2}{\tilde{H}}_{1,2},\quad \tilde{H}_{1,2}=-\Omega ^{*}_{1,2}{H_{1,2}}, \end{aligned}$$
(34)

where

$$\begin{aligned} \begin{aligned} \omega _{1,2}&=\left( \begin{array}{cccccc} 1 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 1 \\ \end{array} \right) ^{T},\quad \Omega _{1,2} =\left( \begin{array}{ccc} F_{11} &{}\quad F_{12} &{}\quad F_{13} \\ F_{21} &{}\quad F_{22} &{}\quad F_{23} \\ F_{31} &{}\quad F_{32} &{}\quad F_{33} \\ \end{array} \right) ,\\ H_{1,2}&= \left( \begin{array}{cccccc} H^{T}_2&{}\quad U_{+11}(\lambda _2^{*})&{}\quad U_{+11}(-\lambda _2^{*}) \\ \end{array} \right) ^{T},\\ \tilde{H}_{1,2}&= \left( \begin{array}{cccccc} \tilde{H}^{T}_2&{}\quad U_{+21}(\lambda _2) &{}\quad U_{+21}(-\lambda _2) \\ \end{array} \right) ^{T} \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} F^{11}_{13}&=\frac{\varrho _{-1}}{\lambda _2-\lambda _1^{*}}e^{2\textrm{i}\theta },\quad F^{21}_{13}=\frac{\varrho _{-1}}{\lambda _2+\lambda _1^{*}}e^{2\textrm{i}\theta }, \quad F^{12}_{13}=-F^{21}_{13},\quad F^{22}_{13}=-F^{11}_{13},\\ F^{11}_{23}&=\frac{\varrho _{-1}}{(\lambda _2-\lambda _1^{*})^2}e^{2\textrm{i}\theta },\quad F^{21}_{23}=\frac{\varrho _{-1}}{(\lambda _2+\lambda _1^{*})^2}e^{2\textrm{i}\theta },\quad F^{12}_{23}=F^{21}_{23},\quad F^{22}_{23}=F^{11}_{23},\\ F^{11}_{31}&=\left[ \frac{\rho _{-1}+\rho _{-2}(4\textrm{i}\lambda _1{x}+16\textrm{i}\lambda _1^3{t})}{\lambda _1-\lambda _2^{*}}-\frac{\rho _{-2}}{(\lambda _1-\lambda _2^{*})^2}\right] e^{2\textrm{i}\theta },\quad F^{22}_{31}=-F^{11}_{31},\\ F^{21}_{31}&=\left[ \frac{\rho _{-1}+\rho _{-2}(4\textrm{i}\lambda _1{x}+16\textrm{i}\lambda _1^3{t})}{\lambda _1+\lambda _2^{*}}-\frac{\rho _{-2}}{(\lambda _1+\lambda _2^{*})^2}\right] e^{2\textrm{i}\theta },\quad F^{12}_{31}=-F^{21}_{31},\\ F^{11}_{32}&=\frac{\rho _{-2}}{\lambda _1-\lambda _2^{*}}e^{2\textrm{i}\theta },\quad F^{21}_{32}=\frac{\rho _{-2}}{\lambda _1+\lambda _2^{*}}e^{2\textrm{i}\theta },\quad F^{12}_{32}=F^{21}_{22},\quad F^{22}_{32}=F^{11}_{32},\\ F^{11}_{33}&=\frac{\varrho _{-1}}{\lambda _2-\lambda _2^{*}}e^{2\textrm{i}\theta },\quad F^{21}_{33}=\frac{\varrho _{-1}}{\lambda _2+\lambda _2^{*}}e^{2\textrm{i}\theta },\quad F^{12}_{33}=-F^{21}_{33},\quad F^{22}_{33}=-F^{11}_{33}. \end{aligned} \end{aligned}$$

From the formula (29), we have

$$\begin{aligned} q=2\textrm{i}\frac{\det {\tilde{\Phi }_{1,2}}}{\det {\Phi _{1,2}}}, \end{aligned}$$
(35)

where

$$\begin{aligned} \begin{aligned} \Phi _{1,2}&=I+\Omega _{1,2}\Omega ^{*}_{1,2},\quad \tilde{\Phi }_{1,2}=\left( \begin{array}{cc} 0 &{}\quad \Lambda _{1,2} \\ \omega _{1,2} &{}\quad \Phi _{1,2} \\ \end{array} \right) ,\\ \Lambda _{1,2}&=\left( \begin{array}{cccccc} \rho _{-1}^{*}-\rho _{-2}^{*}\chi &{}\quad \rho _{-1}^{*}-\rho _{-2}^{*}\chi &{}\quad \rho _{-2}^{*} &{}\quad -\rho _{-2}^{*} &{}\quad \varrho _{-1}^{*} &{}\quad \varrho _{-1}^{*}\\ \end{array} \right) . \end{aligned} \end{aligned}$$

As shown in Fig. 3.

Fig. 3
figure 3

\(\rho _{-1}=\textrm{i},\rho _{-2}=1,\varrho _{-1}=-1,\lambda _1=1+\textrm{i},\lambda _2=2+\textrm{i}\), the left: the 3D image of \(|q|^2\), the right: the density image of \(|q|^2\)

Full size image

5 Conclusions and Discussions

We discussed the higher-order soliton solutions for DNLS-III equation by the improved Riemann–Hilbert method in detail. The main idea is to require the potentials q(x) decay rapidly enough at infinity so that the reflection coefficient \(\rho (\lambda )\) or \(\tilde{\rho }(\lambda )\) can be analytically extended to the region \(D_{\pm }\). For \(\rho (\lambda )\) has a pth order pole, by virtue of the Laurent series expansion of \(\rho (\lambda )\) we can obtain the explicit determinant form of higher-order soliton solutions. Moreover these results can be applied to the other derivative type NLS equations by gauge transform. In this paper the potentials q(x) is considered under the ZBC, we know that under the nonzero boundary condition (NZBC) it is more complicated to solve double soliton solutions by the usual RH method in the literature [17], in the near future we will generalize this idea to the NZBC case.