1 Introduction

Nonlinear integrable systems have become a very important research field in recent decades due to their complex structures and unpredictable dynamical properties appearing in different fields such as hydrodynamics, nonlinear optics, quantum physics and condensed matter physics. Up to now, new nonlinear equations are constantly being discovered, and some methods for solving equations are constantly being proposed such as Riemann–Hilbert method [1, 2], Hirota bilinear method [3,4,5,6,7,8], inverse scattering method [9,10,11,12], Darboux transformation method [13,14,15,16], Lie group method [17,18,19,20], Bäcklund transformation [21, 22] and so on. There are scholars have also analyzed the phase portraits of planar dynamical systems specifically through the bifurcation theory of dynamical systems and found richer traveling wave solutions [23, 24]. Recently, some researchers have been interested in multi-component integrable equations, such as four-component integrable partial differential equations (PDEs) and six-component integrable PDEs [25,26,27,28]. In Refs. [25, 26], the author has constructed the Hamiltonian structure for the four-component nonlinear Schrödinger (NLS) equations and modified Korteweg–de Vries (mKdV) equations utilizing the trace identity. In Refs. [27, 28], the six-component NLS equations and mKdV equations have been proposed by constructing the Liouville integrable hierarchy with the zero curvature formulation and the trace identity.

The Vakhnenko–Parkes (VP) equation

$$\begin{aligned} u u_{x x t}-u_{x} u_{x t}+u^{2} u_{t}=0, \end{aligned}$$
(1)

can model the propagation of high-frequency waves in a relaxed medium with periodic and isolated traveling wave solutions [29]. The inverse scattering transformation method and the Hirota method are successfully applied to VP Eq. (1) and N-soliton solutions have been found in Ref. [30]. In Ref. [31], the authors have introduced a modified VP equation for the first time and used the simplified Hirota method to find its real and complex soliton solutions. In Ref. [32], two generalized integrable extensions of the modified VP equations were proposed, and some exact explicit soliton solutions have been found by the inverse scattering method and Hirota bilinear method. In Refs. [33, 34], some soliton solutions, breather and mixed solutions of two generalized modified VP equations were obtained via the Hirota bilinear approach and auxiliary function method. To our knowledge, the bifurcation, traveling wave solutions, asymptotic analysis of soliton solutions and physical properties of the VP equation are still not carefully analyzed and studied, in order to better understand related physical properties of the VP equation, in this paper, we consider the following \((2+1)\)-dimensional extended Vakhnenko–Parkes (eVP) equation

$$\begin{aligned} u u_{x x t}-u_{x} u_{x t}+u^{2} u_{t}+\alpha u_{x}+\beta u_{y}=0. \end{aligned}$$
(2)

where \(\alpha\) and \(\beta\) are two arbitrary constants. When \(\alpha =\beta =0\), the \((2+1)\)-dimensional eVP equation is just the VP Eq. (1).

This paper is organized as below. In Sect. 2, based on the traveling wave transformation, we will study the dynamical behavior and bifurcation phenomena of Eq. (2), and obtain the phase portraits of the dynamical system for different parameters of Eq. (2). In Sect. 3, using the traveling wave transformation method, we will obtain Jacobi elliptic function double periodic traveling wave solution of Eq. (2). In Sect. 4, based on Hirota bilinear method, we will derive the analytical N-soliton solution of Eq. (2). As an application, we will investigate one-soliton, two-soliton and three-soliton solutions, whose structures are illustrated graphically. Moreover, the physical quantities and asymptotic properties of one-soliton and two-soliton solutions of Eq. (2) are also analyzed. The last section is our summary.

2 Bifurcation Theory Analysis

Substituting \(\xi =x+k y-c t\) into Eq. (2), then integrating it once, one can obtain

$$\begin{aligned} u u^{\prime \prime }-\left( u^{\prime }\right) ^{2}+\frac{1}{3} c u^{3}-\rho u=0, \end{aligned}$$
(3)

where \(\rho =\frac{\alpha +k \beta }{c}\). Let \(\frac{d u}{d \xi }=y\), Eq. (3) can be reduced to a plane differential system

$$\begin{aligned} \left\{ \begin{array}{l}\frac{d u}{d \xi }=y, \\ \frac{d y}{d \xi }=\frac{y^{2}-\frac{1}{3} u^{3}+\rho u}{u}.\end{array}\right. \end{aligned}$$
(4)

Let \(d \xi =u d \tau\), then system (4) has the same topological phase diagram as the following planar polynomial differential system except for \({\text {singular}}\ {\text {solution}}\ u=0\):

$$\begin{aligned} \left\{ \begin{array}{l} \frac{d u}{d \tau }=u y,\\ \frac{d y}{d \tau }=y^{2}-\frac{1}{3} u^{3}+\rho u, \end{array}\right. \end{aligned}$$
(5)

which is the first integral

$$\begin{aligned} H(u, y)=\frac{\frac{1}{3} u^{3}+\rho u+\frac{1}{2} y^{2}}{u^2}=h, \end{aligned}$$
(6)

where h is an integral constant. The following is the analysis of the singular points of system (5):

Case 1: If \(\rho <0, O(0,0)\) is the unique singular point of system (5). The Jacobi matrix \(J(0,0) \ne 0\), \({\text {det}} J(0,0)=0\), hence (0, 0) is the power-zero singular point. Setting \(v=\rho u\), we have

$$\begin{aligned} \left\{ \begin{array}{l} \frac{d v}{d \tau }=G(v, y), \\ \frac{d y}{d \tau }=v+F(v, y),\end{array}\right. \end{aligned}$$
(7)

where \(G(v,y)=\frac{1}{\rho ^{2}} v y,\ F(v,y)=y^{2}-\frac{1}{3 \rho ^{3}} v^{3}\). From \(v+F(v, y)=0\), \(v=-y^{2}+f(v, y)\) is obtained, and f(v, y) is a Higher Order Term. From the central manifold theorem, one can obtain

$$\begin{aligned} G(v, y)=\left. \frac{1}{\rho ^{2}} v y\right| _{v=-y^{2}+f(v, y)}=k y^{3}+g(v, y), \end{aligned}$$

where \(k=-\frac{1}{\rho ^{2}}<0\), which leads to

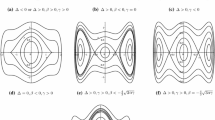
$$\begin{aligned} \phi (y)=\left. \left( \frac{\partial F}{\partial y}+\frac{\partial G}{\partial v}\right) \right| _{v=-y^{2}+f(v, y)} =\left( 2+\frac{1}{\rho ^{2}}\right) y=L y^{\lambda }. \end{aligned}$$

Since \(\lambda =1\) is odd, and \(\Delta =L^{2}+4 k(\lambda +1)=\left( 2-\frac{1}{\rho ^{2}}\right) \ge 0\), then from Proposition 2 in Ref. [35] it follows that O(0, 0) is an elliptical saddle point. The phase portrait of system (6) for \(\rho =-\frac{1}{3}\) is shown in Fig. 1a1.

Case 2: When \(\rho =0\), system (5) is rewritten as

$$\begin{aligned} \left\{ \begin{array}{l} \frac{d u}{d \tau }=u y, \\ \frac{d y}{d \tau }=y^{2}-\frac{1}{3} u^{3}, \end{array}\right. \end{aligned}$$
(8)

from which we easily know that O(0, 0) is a triple singular point of system (8). Let \(y=u x\), O(0, 0) is blown up to the x-axis of the xOu plane. The orbits of the uOy plane maps to the xOu plane symmetric about the u-axis when \(u<0\). Setting \(d t=u^{2} d \tau\), the system (8) is transformed into

$$\begin{aligned} \left\{ \begin{array}{l} \frac{d x}{d t}=\frac{1}{3}, \\ \frac{d u}{d t}=x, \end{array}\right. \end{aligned}$$
(9)

which has the first integral \(u=-\frac{3}{2} x^{2}+C\), and its trajectories are symmetric about the u-axis. The transformation \(d t=u^{2} d \tau\) keeps the image unchanged, and by \(y=u x\) the trajectories on the x axis are compressed to the origin. The phase portrait of system (6) for \(\rho =0\) is shown in Fig. 1a2.

Case 3: If \(\rho >0\), the singular points of system (5) are O(0, 0), \(E_1 (\sqrt{3 \rho }, 0)\) and \(E_2 (-\sqrt{3 \rho }, 0)\). For \(E_{1}\), \({\text {det}}J(E_{1})\) has two imaginary eigenvalues that means \(E_{1}\) is a focus or a center. Since that the trajectory of system (5) is symmetric about the v-axis, \(E_{1} (\sqrt{3 \rho }, 0)\) is a center. For \(E_{2}\), \({\text {det}}J(E_{2})\) has two real eigenvalues, and they are opposite numbers. Therefore, \(E_{2}\) is a saddle point. The phase portrait of system (6) for \(\rho =1\) is shown in Fig. 1a3.

Fig. 1
figure 1

Phase portrait of system (6) for (a1) \(\rho =-\frac{1}{3}\); (a2) \(\rho =0\); (a3) \(\rho =1\)

Full size image

3 Periodic Wave and Solitary Wave Solutions

In this section, we study the periodic wave and solitary wave solutions of Eq. (2) by using the traveling wave transformation method.

The first integral (6) with \(h=1\) can be expressed as follows

$$\begin{aligned} y=\sqrt{-\frac{2}{3} u\left( u-{\hat{u}}_{1}\right) \left( u-{\hat{u}}_{2}\right) }, \end{aligned}$$
(10)

where \({\hat{u}}_{2}< u< {\hat{u}}_{1}\), and \({\hat{u}}_{i}\ (i=1,2)\) are real roots of \(y=0\) in (10). Let the function \(u=u(\theta )\), and it satisfies the relation

$$\begin{aligned} u(\theta )={\hat{u}}_{1}+\left( {\hat{u}}_{2}-{\hat{u}}_{1}\right) \sin ^{2} \theta , \end{aligned}$$
(11)

Substituting (11) into Eq. (3), integrating both sides simultaneously yields

$$\begin{aligned} \int _{0}^{\theta } \frac{d \theta }{\sqrt{1-m \sin ^{2} \theta }}=\sqrt{\frac{{\hat{u}}_{1}}{6}}\left( \xi -\xi _{0}\right) , \end{aligned}$$
(12)

where \(m=\frac{{\hat{u}}_{1}-{\hat{u}}_{2}}{{\hat{u}}_{1}},\ \xi =x+k y-c t\), m (\(0\le m\le 1\)) stands for modulus. We can derive an elliptic cosine wave solution of Eq. (3)

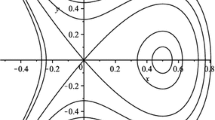
$$\begin{aligned} u={\hat{u}}_{2}+\left( {\hat{u}}_{1}-{\hat{u}}_{2}\right) {\text {cn}}^{2}\left( \sqrt{\frac{{\hat{u}}_{1}}{6}}\left( \xi -\xi _{0}\right) , m\right) , \end{aligned}$$
(13)

which is a Jacobian elliptic function periodic solution with period of 2K(m). Its amplitude is \({\hat{u}}_{1}-{\hat{u}}_{2}\), the wave number is \(\sqrt{\frac{{\hat{u}}_{1}}{6}}\), and the wavelength is \(2 K(m) \sqrt{\frac{6}{{\hat{u}}_{1}}}\). The double periodic structures of solution(13) with different modulus m are shown in Fig. 2a1–a3, from which we can clearly see that it displays different double periodic structures.

When \({\hat{u}}_{1} \rightarrow {\hat{u}}_{2}\), modulus \(m \rightarrow 0\), then \({\text {cn}} x \rightarrow \cos x\), solution (13) turns into

$$\begin{aligned} u={\hat{u}}_{2}+\left( {\hat{u}}_{1}-{\hat{u}}_{2}\right) \cos ^{2} \sqrt{\frac{{\hat{u}}_1}{6}}\left( \xi -\xi _{0}\right) \rightarrow {\hat{u}}_{2}, \end{aligned}$$

which is a constant solution.

When \({\hat{u}}_{2} \rightarrow 0\), modulus \(m \rightarrow 1\), then \({\text {cn}} x \rightarrow {\text {sech}} x\), solution (13) turns into

$$\begin{aligned} u={\hat{u}}_{2}+\left( {\hat{u}}_{1}-{\hat{u}}_{2}\right) {\text {sech}}^{2} \sqrt{\frac{{\hat{u}}_1}{6}}\left( \xi -\xi _{0}\right) , \end{aligned}$$
(14)

which is a bell-shaped soliton solution with amplitude \({\hat{u}}_{1}-{\hat{u}}_{2}\) and wavelength \(\sqrt{\frac{6}{{\hat{u}}_1}}\). The soliton structure of (14) with \(m=1\) is shown in Fig. 2a4, from which we can clearly see that it has the bell-shaped soliton structure.

Fig. 2
figure 2

Traveling wave solutions of Eq. (2) as \(h=k=1, c=2\): a1 \(m=\frac{1}{100}\); a2 \(m=\frac{2}{3}\); a3 \(m=\frac{298}{299}\); a4 \(m=1\)

Full size image

4 N-Soliton Solutions and Relevant Dynamical Behaviors

In this section, we will derive the N-soliton solution of Eq. (2) based on the Hirota bilinear method, and present the physical quantities and asymptotic analysis of one-soliton solution and two-soliton solution respectively to get a preliminary understanding of the dynamical behaviors.

Regarding the construction of N-solitons in (2+1)-dimensions, inspired by Refs. [4] and [34] and using the Hirota bilinear technique, we have the following theorem:

Theorem 1

If \(u=6(\ln f)_{x x}\) is the N-soliton solution of Eq. (2), then the function f has the following form as

$$\begin{aligned} \begin{aligned} f=&1+\sum _{j=1}^{N} \exp \left( \eta _{j}\right) +\sum _{j<l}^{N} A_{j l} \exp \left( \eta _{j}+\eta _{l}\right) +\sum _{j<l<k}^{N} A_{j l} A_{j k} A_{l k} \exp \left( \eta _{j}+\eta _{l}+\eta _{k}\right) \\&+\cdots +\left( \prod _{j<l} A_{j l}\right) \exp \left( \sum _{j=1}^{N} \eta _{j}\right) , \end{aligned} \end{aligned}$$
(15)

where \(\eta _{j}=a_{j} x+b_{j} y+\frac{\Omega _j}{a_{j}} t+\eta _{0 j}, \quad b_{j}=-\frac{\alpha a_{j}}{\beta }\),\(A_{j l}=-\frac{\left( a_{j}-a_{l}\right) ^{2}\left( a_{j}^{2}-a_{j} a_{l}+a_{l}^{2}\right) }{\left( a_{j}+a_{l}\right) ^{2}\left( a_{j}^{2}+a_{j} a_{l}+a_{l}^{2}\right) }, \quad (j, l=1,2, \cdots , N)\) with arbitrary constants \(a_{j}, b_{j}, \alpha , \beta\), \(\eta _{0_{j}}\) and \(\Omega _j=a_{1}^{2}a_{2}^{2}\cdots a_{j}^{2}\).

4.1 One-Soliton Solution and Related Physical Quantities

When \(N=1\), from (15) we have

$$\begin{aligned} f=1+e^{\eta _{1}}, \end{aligned}$$

with \(\eta _{1}=a_{1} x+b_{1} y+\frac{\Omega _1}{a_{1}} t,\ b_{1}=-\frac{\alpha }{\beta } a_{1}\), \(\Omega =a_{1}^{2}\). From \(u=6(\ln f)_{x x}\), we have the following exact one-soliton solution of Eq. (2) as

$$\begin{aligned} u=\frac{3 a_{1}^{2}}{2} {\text {sech}}^{2}\left( \frac{a_{1}}{2} x+\frac{a_{1}}{2} t-\frac{a_{1} \alpha }{2 \beta } y\right) , \end{aligned}$$
(16)

from which we can see the important physical quantities of one-soliton solution such as amplitude, width, velocity, wave number, initial phase and energy in both x-direction and y-direction as listed in Table 1.

Table 1 Physical quantities of one-soliton solution
Full size table

4.2 Two-Soliton, Breather Solution and Related Asymptotic State Analysis

When \(N=2\), from (15) we have

$$\begin{aligned} f=1+e^{\eta _{1}}+e^{\eta _{2}}+A_{12} e^{\eta _{1}+\eta _{2}}, \end{aligned}$$
(17)

with \(\eta _{i}=a_{i} x+b_{i} y+\frac{\Omega _2}{a_{i}} t+\eta _{0 i}, \ b_{i}=-\frac{\alpha }{\beta } a_{i} \ (i=1,2)\), \(\Omega _2=a_{1}^{2}a_{2}^{2}\), \(A_{j l}=-\frac{\left( a_{j}-a_{l}\right) ^{2}\left( a_{j}^{2}-a_{j} a_{l}+a_{l}^{2}\right) }{\left( a_{j}+a_{l}\right) ^{2}\left( a_{j}^{2}+a_{j} a_{l}+a_{l}^{2}\right) }, \ (j, l=1,2).\)

From \(u=6(\ln f)_{x x}\), we can give exact two-soliton solution of Eq. (2). In order to analyze its asymptotic properties, two-soliton solution can be rewritten as

$$\begin{aligned} \begin{aligned}&u=\frac{6\left( a_{1}^{2}+a_{1} a_{2}+a_{2}^{2}\right) \left( a_{1}+a_{2}\right) ^{2}\left[ 2 \sqrt{X_{1} X_{3}} \cosh \left( \eta _{2}+\frac{1}{2} \ln \left( \frac{X_{1}}{X_{3}}\right) \right) +2 \sqrt{X_{2} X_{4}} \cosh \left( \eta _{1}+\frac{1}{2} \ln \left( \frac{X_{2}}{X_{4}}\right) \right) +X_{5}\right] }{\left[ 2 Y_{1} \cosh \left( \frac{1}{2} \eta _{1}-\frac{1}{2} \eta _{2}\right) +2 \sqrt{Y_{1} Y_{2}} \cosh \left( \frac{1}{2} \eta _{1}+\frac{1}{2} \eta _{2}-\frac{1}{2} \ln \left( \frac{Y_{1}}{Y_{2}}\right) \right) \right] ^{2}}, \end{aligned} \end{aligned}$$
(18)

with

$$\begin{aligned} \begin{aligned}&\eta _{1}=\frac{a_{1}\left( \beta x-\alpha y+\beta a_{2}^{2} t\right) }{\beta },\ \eta _{2}=\frac{a_{2}\left( \beta x-\alpha y+\beta a_{1}^{2} t\right) }{\beta },\\&X_{1}=a_{1}^{2}\left( a_{1}^{2}-a_{1} a_{2}+a_{2}^{2}\right) \left( a_{1}-a_{2}\right) ^{2}, X_{2}=a_{2}^{2}\left( a_{1}^{2}-a_{1} a_{2}+a_{2}^{2}\right) \left( a_{1}-a_{2}\right) ^{2}, \\&X_{3}=a_{1}^{2}\left( a_{1}^{2}+a_{1} a_{2}+a_{2}^{2}\right) \left( a_{1}+a_{2}\right) ^{2}, \quad X_{4}=a_{2}^{2}\left( a_{1}^{2}+a_{1} a_{2}+a_{2}^{2}\right) \left( a_{1}+a_{2}\right) ^{2}, \\&X_{5}=2\left( a_{1}^{2}+a_{2}^{2}\right) \left( a_{1}-a_{2}\right) ^{2}\left( a_{1}+a_{2}\right) ^{2}, \quad Y_{1}=\left( a_{1}^{2}+a_{1} a_{2}+a_{2}^{2}\right) \left( a_{1}+a_{2}\right) ^{2}, \\&Y_{2}=\left( a_{1}^{2}-a_{1} a_{2}+a_{2}^{2}\right) \left( a_{1}-a_{2}\right) ^{2}. \end{aligned} \end{aligned}$$

Next, we will analyze the asymptotic properties of solution (18) and study its important physical quantities as listed in Table 2.

Table 2 Physical quantities of two-soliton solutions
Full size table

  • Before collision \((t \rightarrow -\infty )\),

    $$\begin{aligned} \begin{aligned}&u \rightarrow u_{1}^{-}=\frac{3 a_{2}^{2}}{2} {\text {sech}}^{2} \frac{\eta _{2}}{2}, \\&u \rightarrow u_{2}^{-}=\frac{3 a_{1}^{2}}{2} {\text {sech}}^{2} \frac{\eta _{1}}{2}, \end{aligned} \end{aligned}$$

    where \(u_{1}^{-}, u_{2}^{-}\)are the expressions for the asymptotic state before collision interaction.

  • After collsion \((t \rightarrow +\infty )\),

    $$\begin{aligned} \begin{aligned}&u \rightarrow u_{1}^{+}=\frac{3 a_{2}^{2}}{2} {\text {sech}}^{2}\left( \frac{\eta _{2}}{2}+\frac{1}{2} \ln \frac{Y_{2}}{Y_{1}}\right) , \\&u \rightarrow u_{2}^{+}=\frac{3 a_{1}^{2}}{2} {\text {sech}}^{2}\left( \frac{\eta _{1}}{2}+\frac{1}{2} \ln \frac{Y_{2}}{Y_{1}}\right) , \end{aligned} \end{aligned}$$

where \(u_{1}^{+}, u_{2}^{+}\)are the expressions for the asymptotic state after collision interaction.

Through the above analysis, it is not difficult to obtain some physical properties of the two-soliton solution: (i) The amplitudes, velocities, widths and wave numbers before and after interaction remain unchanged; (ii) The displacement of the two solitons before and after interaction is \(\frac{1}{2} \ln \frac{Y_{2}}{Y_{1}}\).

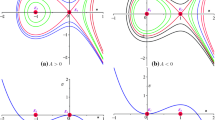
Case 1: If taking \(a_{1}=\frac{1}{2}, a_{2}=1, \alpha =30, \beta =1\), and \(\eta _{01}=\eta _{02}=0\), the solution (18) has parallel bell-shaped structure. Two line solitons propagate with different speeds along the same direction, and the soliton with the smaller amplitude propagates faster, at \(t=0\) the interaction of the two solitons overlaps, and then two solitons become farther apart. Dynamical behaviors of two parallel bell-shaped solitons of Eq. (2) at different time are shown in Fig. 3.

Fig. 3
figure 3

Dynamical behaviors of two-soliton solution of parallel bell-shaped structure of Eq. (2) at different time: a1 \(t=-5\); a2 \(t=-2\); a3 \(t=0\); a4 \(t=5\)

Full size image

Case 2: If taking \(a_{1}=a_{2}^{*}=k_{1}+m_{1} i, b_{1}=b_{2}^*=l_{1}+s_{1} i\), from (15) we have

$$\begin{aligned} f=1+2 e^{\mu } \cos (\sigma )+A_{12} e^{2 \mu }, \end{aligned}$$
(19)

with \(\eta _{1}=\eta _{2}{ }^{*}=\mu +\sigma i, \mu =k_{1} x+l_{1} y+\frac{k_{1} \Omega _2}{k_{1}^{2}+m_{1}^{2}} t, \sigma =m_{1} x+s_{1} y-\frac{m_{1} \Omega _2}{k_{1}^{2}+m_{1}^{2}} t, \eta _{01}=\eta _{02}=0, \quad A_{12}=-\frac{m_{1}^{2}\left( k_{1}^{2}-3 m_{1}^{2}\right) }{k_{1}^{2}\left( 3 k_{1}^{2}-m_{1}^{2}\right) }\).

From \(u=6(\ln f)_{x x}\) and solution (18), we can give a breather solution which has a periodic structure. When choosing the parameters \(k_{1}=1, m_{1}=1, \alpha =30, \beta =1\), and \(\eta _{01}=\eta _{02}=0\), the relevant structure and propagation process are shown in Fig. 4.

Fig. 4
figure 4

The propagation process of breather structure at different time: a1 \(t=-5\); a2 \(t=-2\); a3 \(t=0\); a4 \(t=5\)

Full size image

4.3 Three-Soliton and Soliton-Breather Interaction Solutions

When \(N=3\), from (15) we have

$$\begin{aligned} f=1+\sum _{i=1}^{3}e^{\eta _{i}}+\sum _{\begin{array}{c} j,l=1\\ j\ne l \end{array}}^{3}A_{jl} e^{\eta _{j}+\eta _{l}}+A_{123}\prod _{i=1}^{3}e^{\eta _{i}}, \end{aligned}$$
(20)

with \(\eta _{i}=a_{i} x+b_{i} y+\frac{\Omega _3}{a_{i}} t+\eta _{0 i}, b_{i}=-\frac{\alpha }{\beta } a_{i} \quad (i=1,2,3)\), \(\Omega _3=a_{1}^{2}a_{2}^{2}a_{3}^{2}\), \(A_{j l}=-\frac{\left( a_{j}-a_{l}\right) ^{2}\left( a_{j}^{2}-a_{j} a_{l}+a_{l}^{2}\right) }{\left( a_{j}+a_{l}\right) ^{2}\left( a_{j}^{2}+a_{j} a_{l}+a_{l}^{2}\right) },\ (j, l=1,2,3),\ A_{123}=A_{12}A_{13}A_{23}.\)

From \(u=6(\ln f)_{x x}\), we can give three-soliton and mixed soliton-breather interaction solutions.

Case 1: If taking \(a_1=\frac{3}{4}, a_2=\frac{1}{2}, a_3=1, \alpha =\beta =1\) and \(\eta _{01}=\eta _{02}=\eta _{03}=0\) in (20), from \(u=6(\ln f)_{x x}\), we can give the three-soliton solution of Eq. (2), whose structure is shown in Fig. 5, from which we can see three parallel bell-shaped solitons with different speeds move along the same direction, and the solution with the smallest amplitude move the fastest. From Fig. 5, we can see the collisions generated by these line solitons at \(t=0\). After the interaction, three line solutions get father apart due to different speeds, however, their velocities and shapes remain unchanged, which means that their interactions are elastic.

Fig. 5
figure 5

Propagation interaction process of three parallel solitons with parameters \(\alpha =\beta =1, a_1=\frac{3}{4},a_2=\frac{1}{2},a_3=1\) at different time: a1 \(t=-100\); a2 \(t=-50\); a3 \(t=0\); a4 \(t=100\)

Full size image

Case 2: If setting \(a_1=a_2^*=k_1+m_1 i, b_1=b_2^*=l_1+s_1i,\) \(a_3=k_2\), \(b_3=l_2,\) \(\eta _{01}=\eta _{02}=\eta _{03}=0\), then (20) become

$$\begin{aligned} f= 1+2 e^{\mu _1} \cos \left( \sigma _1\right) +A_2 e^{2\mu _1} +e^{\mu _2} \left[ 1+2 L e^{\mu _1} \cos \left( \sigma _1+\phi \right) +A_{12} L^2 e^{2 \mu _1}\right] \end{aligned}$$

where

$$\begin{aligned} \begin{aligned}&\mu _1=k_1 x+l_1 y+\frac{k_1 \Omega _3}{k_1^2+m_1^2} t, \quad \sigma _1=m_1 x+s_1 y-\frac{m_1 \Omega _3}{k_1^2+m_1^2} t, \ \ \mu _2=k_2 x+l_2 y+\frac{\Omega _3}{k_2} t, \\&L e^{i \phi }=A_{13}=-\frac{\left( k_1-k_2+m_1i\right) ^2\left( k_1^2-m_1^2+k_2^2-k_1 k_2+2 k_1 m_1i -k_2 m_1 i\right) }{\left( k_1+k_2+m_1 i\right) ^2\left( k_1^2-m_1^2+k_2^2+k_1 k_2+2 k_1 m_1 i+k_2 m_1i\right) }, \\&L e^{-i \phi }=A_{23}=A_{13}^*. \end{aligned} \end{aligned}$$

If taking \(k_1=\frac{24}{25}, m_1=1, \alpha =\beta =1, k_2=1\), a mixed soliton-breather interaction solution of a y-periodic soliton and a line soliton can be obtained. Figure 6 exhibits a bell-shaped soliton parallel to a breather, and two parallel structures propagate along x-axis with different speeds along the same direction. The line solution moves faster than the breather which finally overtake the breather and get farther apart from each other.

Fig. 6
figure 6

Dynamical behaviors of three-soliton solution at different time: a1 \(t=-20\); a2 \(t=-10\); a3 \(t=0\); a4 \(t=20\)

Full size image

5 Conclusion

This paper is concerned with the (2+1)-dimensional Eq. (2), which can describe the propagation of high-frequency waves in a relaxed medium. The main innovative results are as follows: Firstly, based on the traveling wave transformation method, we have investigated the bifurcation and Jacobi periodic traveling wave solution of Eq. (2). Based on the bifurcation, the singularities and periodic wave solutions of the system are analyzed graphically according to the bifurcation theory and the qualitative theory (see Figs. 1, 2). Secondly, using Hirota bilinear method, the analytical N-soliton solution of Eq. (2) has been obtained, and the asymptotic state analysis, physical properties and elastic interaction of soliton solutions as well as mixed soliton-breather interaction structures have been discussed. These results in this paper are discovered for the first time and might be helpful in explaining the propagation of high-frequency waves in a relaxed medium.