1 Introduction and the Statements of the Main Results

Homoclinic bifurcation is an important phenomenon to characterize the complex dynamic behavior of differential systems. Except for its theoretical significance, it has many important applications in mathematical biology [26, 27], laser physics [42], electronic engineering [23] and so on. Recently, a kind of homoclinic bifurcation of co-dimension two, called the homoclinic flip bifurcation, has been drawing much attention from the researchers. Unlike the celebrated Shilnikov bifurcation [36], which belongs to homoclinic bifurcation of co-dimension one and bifurcates to a saddle focus with complex eigenvalues, the homoclinic flip bifurcation corresponds to a real saddle and can generate infinitely many homoclinic bifurcations, saddle-node and period-doubling cascades, Smale-horseshoe dynamics and strange attractors [3, 12, 35]. As a crucial application, homoclinic flip bifurcations provide the theoretical explanation for the creation of spiking behavior in nonlinear models of neurons, see [27] for instance.

Consider a three-dimensional differential system with a real saddle equilibrium such that the equilibrium admits an unstable eigenvalue and two unequal real stable eigenvalues. Typically, when a real saddle equilibrium undergoes homoclinic bifurcations of co-dimension one, its two-dimensional stable manifold either shapes into a topological cylinder or a Möbius band along the flow of the homoclinic orbit [12]. The homoclinic flip bifurcation occurs when the two-dimensional stable manifold shifts from being orientable to nonorientable. There are three different unfoldings of the homoclinic flip bifurcation, denoted by cases A, B and C [12, 35]. This classification is based on the different constraints satisfied by eigenvalues at the real saddle equilibrium [27, 35]. In case A, a single attracting or repelling periodic orbit emerges from the unfolding. The unfolding in case B leads to the formation of multiple saddle periodic orbits and period-doubling bifurcation. Finally, the unfolding in case C brings about rich complex dynamics such as the period-doubling cascade, n-homoclinic orbits and Smale-horseshoe [12, 16]. Furthermore, case C can be divided into the inward twist case \(C_\textbf{in}\) and outward twist case \(C_\textbf{out}\), which are distinguished by global geometric properties of a two-dimensional manifold [10, 16]. In [35] Sandstede constructed a model which can exhibit all three cases A, B and \(C_\textbf{out}\) with homoclinic flip bifurcations for some suitable values of parameters. However, no explicit example of a model with homoclinic flip bifurcations of case \(C_\textbf{in}\) was found for a long time. Recently, Algaba et al. [3] studied homoclinic flip bifurcations of the inward twist case \(C_\textbf{in}\) and provided a first example of a system with the lowest number of parameters necessary, which exhibits such a degeneracy. The nonlinear differential system proposed by Algaba et al. reads

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}=a+yz,\\ \dot{y}=-y+x^2,\\ \dot{z}=b-4x, \end{array} \right. \end{aligned}$$
(1)

where x,  y and z are state variables and a, b are real parameters. Let us mention that system (1) unifies many other chaotic systems with only one equilibrium. For instance, system (1) becomes the well-known Sprott E system [37] in the case of \((a,b)=(0,1)\), and becomes the Wang-Chen system [41] in the case of \(b=1\).

Fig. 1
figure 1

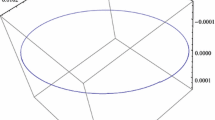
Chaotic attractor for system (1) with \(a=0,~b=2\)

Full size image

Numerical simulations show that system (1) has rich and complex dynamics in spite of its simple form [3, 6, 13, 30, 37, 41]. For example, it exhibits chaotic phenomena for suitable chosen values of parameters, see Fig. 1. This work aims to give some new interesting and fascinating properties of system (1) by a deeper investigation.

The integrability of a nonlinear system can help us understand the topological structures of its trajectories and quantitatively characterizing the distribution or trends of certain crucial physical quantities [18, 43]. As an initial step in our research, we make an integrability analysis of system (1) by using Darboux theory of integrability [9]. We show that system (1) does not have any polynomial, rational or Darboux first integrals, which means any search for a closed-form, analytical solution is bound to fail (cf Theorem 1).

Another facet of our study focuses on the dynamics of system (1). Understanding the stability of equilibrium points and bifurcations is crucial as they determine the long-term behavior and qualitative changes of dynamics of the considered system, providing insights into its potential transitions between different states [25, 44]. We systematically outline the stability of equilibrium points of system (1), classify all possible bifurcations of co-dimension one or two at isolated equilibrium points. Our results show that system (1) only undergoes Hopf bifurcation or Bautin bifurcation (cf Theorem 7).

By regarding system (1) as a geodesic in the Finsler space, we apply a geometric approach developed in [5, 7, 24] to examine the Jacobi stability of the trajectory of system (1) (cf Theorem 8). Finally, the dynamical behavior of system (1) on the Poincaré sphere at infinity is characterized by the Poincaré compactification (cf Theorem 9). The results in this work deepen our understanding of system (1) and may be helpful for further investigation into the phenomena of homoclinic flip bifurcations.

The work is organized as follows. In Sect. 2, the integrability analysis of system (1) is performed. The bifurcations at isolated equilibrium points and Jacobi stability of trajectories are studied in Sects. 3 and  4, respectively. In Sect. 5, the global dynamics of system (1) at infinity is investigated.

2 Integrability Analysis

We first recall some basic definitions. A nonconstant function \(\Phi (x,y,z)\) is called a first integral of system (1) if

$$\begin{aligned} (a+yz)\frac{\partial \Phi }{\partial x}+(-y+x^2)\frac{\partial \Phi }{\partial y}+\big (b-4x\big )\frac{\partial \Phi }{\partial z}=0. \end{aligned}$$

Furthermore, if the first integral \(\Phi (x,y,z)\) is a polynomial or rational function, then \(\Phi\) is called a polynomial or rational first integral of system (1).

A real polynomial \(F\in {\mathbb {R}}[x,y,z]\) is a Darboux polynomial of system (1) if there exists a polynomial \(K(x, y, z)\in {\mathbb {R}}[x,y,z]\), called the cofactor of F, such that

$$\begin{aligned} (a+yz)\frac{\partial F}{\partial x}+(-y+x^2)\frac{\partial F}{\partial y}+\big (b-4x\big )\frac{\partial F}{\partial z}=KF. \end{aligned}$$

Similarly, a nonconstant function \(E=\exp (g/h)\) with \(g,h\in {\mathbb {R}}[x,y,z]\) being coprime is an exponential factor of system (1) if

$$\begin{aligned} (a+yz)\frac{\partial E}{\partial x}+(-y+x^2)\frac{\partial E}{\partial y}+\big (b-4x\big )\frac{\partial E}{\partial z}=LE. \end{aligned}$$

for some polynomial \(L\in {\mathbb {R}}[x,y,z]\) with the degree at most one, called the cofactor of E. A function G of system (1) is called Darboux first integral if it is a first integral of the form

$$\begin{aligned} G=f_{1}^{\lambda _{1}}\cdots f_{p}^{\lambda _{p}}E_{1}^{\mu _{1}}\cdots E_{q}^{\mu _{q}}, \end{aligned}$$

where \(f_{1},\ldots ,f_{p}\) are Darboux polynomials, \(E_{1},\ldots ,E_{q}\) are exponential factors and \(\lambda _{i},\mu _{j}\in {\mathbb {R}}\), for \(i=1,\ldots ,p\) and \(j=1,\ldots ,q\).

Theorem 1

For any values of the parameters \(a,b\in {\mathbb {R}}\), system (1) has no polynomial, proper rational or Darboux first integrals.

Theorem 1 also implies that any search for a closed-form, analytical solution for system (1) is bound to fail. To prove it, we will utilize Darboux theory of integrability, which holds a significant position in the integrability of polynomial differential systems. This theory is of great importance and plays a crucial role in the understanding of the integrability of such systems [8, 9, 20, 31]. Compared with the differential Galois method [17, 19, 21, 32], Darboux theory of integrability allows us to obtain first integrals by identifying enough invariant algebraic surfaces (known as the Darboux polynomials) and exponential factors directly, see [29, 34, 38, 39] for instance.

To prove Theorem 1, we need the following lemmas.

Lemma 2

System (1) has no Darboux polynomials.

Proof

Suppose system (1) has a Darboux polynomial \(f(x,y,z)\in {\mathbb {R}}[x,y,z]\) with the cofactor \(K(x,y,z)\in {\mathbb {R}}[x,y,z]\), that is,

$$\begin{aligned} (a+yz)\frac{\partial f}{\partial x}+(x^2-y)\frac{\partial f}{\partial y}+\big (b-4x\big )\frac{\partial f}{\partial z}=Kf. \end{aligned}$$
(2)

By comparing the degrees of both sides of (2), we can see that the degree of K cannot exceed one. So, we can assume that \(K=k_0+k_1x+k_2y+k_3z\), where \(k_i\) are real numbers for \(i=0,1,2,3\). Now, (2) becomes

$$\begin{aligned} (a+yz)\frac{\partial f}{\partial x}+(x^2-y)\frac{\partial f}{\partial y}+\big (b-4x\big )\frac{\partial f}{\partial z}=(k_0+k_1x+k_2y+k_3z)f. \end{aligned}$$
(3)

We claim that \(k_2=k_3=0\). To do so, we express f(x, y, z) as \(\sum _{i=0}^m f_i(x,z)y^i\), where each \(f_i\) is a polynomial in x and z with real coefficients. Then substituting it into (3) yields

$$\begin{aligned} z\frac{\partial f_m(x,z)}{\partial x}=k_2f_m(x,z). \end{aligned}$$
(4)

Solving (4) leads to \(f_m=e^{\frac{k_2x}{z}}g_m(z)\) with \(g_m(\cdot )\) being a smooth function in z. Since \(f_m\) is a homogeneous polynomial in x,  z, we conclude that \(k_2=0\). Similarly, we write \(f(x,y,z)=\sum _{i=0}^{{\hat{m}}}{\hat{f}}_i(x,y)z^i\) with \({\hat{f}}_i\in {\mathbb {R}}[x,y]\), and conclude that \(k_3=0\).

Let \(f=f_n+f_{n-1}+\cdots +f_0\) with \(f_i=f_i(x,y,z)\) being a homogeneous polynomial of degree i. Without loss of generality we assume \(f_n\ne 0\). Comparing the terms of degree \(n+1\) in (3) leads to

$$\begin{aligned} yz\frac{\partial f_n}{\partial x}+x^2\frac{\partial f_n}{\partial y}=k_1xf_n. \end{aligned}$$
(5)

To solve (5), we take the change of variables

$$\begin{aligned} u=\frac{x^3}{3}-\frac{zy^2}{2},~~v=y,~~w=z. \end{aligned}$$
(6)

Correspondingly, the inverse transformation reads

$$\begin{aligned} x=\left( 3u+\frac{3wv^2}{2}\right) ^{\frac{1}{3}},~~y=z,~~z=w. \end{aligned}$$
(7)

From (5) we obtain

$$\begin{aligned} \left( 3u+\frac{3wv^2}{2}\right) ^{\frac{2}{3}}\frac{\partial f_n}{\partial v}=k_1\left( 3u+\frac{3wv^2}{2}\right) ^{\frac{1}{3}}f_n, \end{aligned}$$
(8)

which can be regarded as an ordinary differential equation of v if we fix the variables u,  w. Some computations yield

$$\begin{aligned} \int \frac{1}{(3u+\frac{3wv^2}{2})^{\frac{1}{3}}}dv=3^{-1/3}u^{-1/3}vF\left( \frac{1}{3},\frac{1}{2},\frac{3}{2},-\frac{wv^2}{2u}\right) , \end{aligned}$$

where

$$\begin{aligned} F(a,b,c,z)=\sum _{k=0}^{\infty }\frac{(a)_k(b)_kz^k}{(c)_kk!},~~(x)_k=x(x+1)\cdots (x+k-1), \end{aligned}$$

is the hypergeometric function [33, Chap. 60], and the constant of integration is omitted. Recall that the hypergeometric function F(a, b, c, x) can be equivalently represented as definite integrals

$$\begin{aligned} F(a,b,c,z)=\frac{\Gamma (c)}{\Gamma (b)\Gamma (c-b)}\int _{0}^1\frac{t^{b-1}}{(1-t)^{1+b-c}(1-xt)^a}dt, \end{aligned}$$

where \(c>b\) are positive and \(\Gamma (\cdot )\) is the gamma function. Then we have

$$\begin{aligned} f_n=e^{k_13^{-1/3}u^{-1/3}vF\left( \frac{1}{3},\frac{1}{2},\frac{3}{2},-\frac{wv^2}{2u}\right) }g_n(u,w), \end{aligned}$$
(9)

with \(g_n(u,w)\) is an arbitrary function in u and w. Since \(f_n\) is a homogeneous polynomial in x,  y and z we conclude that \(k_1=0\) and

$$\begin{aligned} f_n=g_n\left( \frac{x^3}{3}-\frac{zy^2}{2},z\right) =\sum _{l=0}^{[n/3]}a_l\left( \frac{x^3}{3}-\frac{zy^2}{2}\right) ^lz^{n-3l},~~a_l\in {\mathbb {R}}. \end{aligned}$$
(10)

We compute the terms of degree n in (3) and obtain

$$\begin{aligned} yz\frac{\partial f_{n-1}}{\partial x}+x^2\frac{\partial f_{n-1}}{\partial y}=k_0f_n+4x\frac{\partial f_{n}}{\partial z}+y\frac{\partial f_{n}}{\partial y}. \end{aligned}$$
(11)

Using (10), we convert (11) into

$$\begin{aligned} z\frac{{\partial f_{{n - 1}} }}{{\partial x}} + x^{2} \frac{{\partial f_{{n - 1}} }}{{\partial y}} & = \sum\limits_{{l = 0}}^{{[n/3]}} {a_{l} } k_{0} \left( {\frac{{x^{3} }}{3} - \frac{{zy^{2} }}{2}} \right)^{l} z^{{n - 3l}} \\ & - \sum\limits_{{l = 0}}^{{[n/3]}} 2 la_{l} \left( {\frac{{x^{3} }}{3} - \frac{{zy^{2} }}{2}} \right)^{{l - 1}} z^{{n - 3l}} xy^{2} + \sum\limits_{{l = 0}}^{{[n/3]}} 4 (n - 3l)a_{l} \left( {\frac{{x^{3} }}{3} - \frac{{zy^{2} }}{2}} \right)^{l} z^{{n - 3l - 1}} x \\ & - \sum\limits_{{l = 0}}^{{[n/3]}} l a_{l} \left( {\frac{{x^{3} }}{3} - \frac{{zy^{2} }}{2}} \right)^{{l - 1}} z^{{n - 3l + 1}} y^{2} . \\ \end{aligned}$$
(12)

Proceeding as above, we use (6)–(7) to solve (12), and get

$$\begin{aligned} f_{{n - 1}} & = g_{{n - 1}} (u,w) + \sum\limits_{{l = 0}}^{{[n/3]}} {a_{l} } k_{0} u^{l} w^{{n - 3l}} \int {\frac{{dv}}{{\left( {3u + \frac{{3wv^{2} }}{2}} \right)^{{\frac{2}{3}}} }}} - \sum\limits_{{l = 0}}^{{[n/3]}} 2 la_{l} u^{{l - 1}} w^{{n - 3l}} \int {\frac{{v^{2} dv}}{{\left( {3u + \frac{{3wv^{2} }}{2}} \right)^{{\frac{1}{3}}} }}} ; \\ & + \sum\limits_{{l = 0}}^{{[n/3]}} 4 (n - 3l)a_{l} u^{l} w^{{n - 3l - 1}} \int {\frac{{dv}}{{\left( {3u + \frac{{3wv^{2} }}{2}} \right)^{{\frac{1}{3}}} }}} - \sum\limits_{{l = 0}}^{{[n/3]}} l a_{l} u^{{l - 1}} w^{{n - 3l + 1}} \int {\frac{{v^{2} dv}}{{\left( {3u + \frac{{3wv^{2} }}{2}} \right)^{{\frac{2}{3}}} }}} . \\ \end{aligned}$$
(13)

Some direct computations yield

$$\begin{aligned}&\int {\frac{dv}{\left( 3u+\frac{3wv^2}{2}\right) ^{\frac{2}{3}}}}=3^{-2/3}u^{-2/3}vF\left( \frac{1}{2},\frac{2}{3},\frac{3}{2},-\frac{wv^2}{2u}\right) , \end{aligned}$$
(14)
$$\begin{aligned}&\int {\frac{v^2dv}{\left( 3u+\frac{3wv^2}{2}\right) ^{\frac{2}{3}}}}=3^{-2/3}u^{-2/3}\left( \frac{6vu}{5w}\left( 1+\frac{wv^2}{2u}\right) ^{1/3}-\frac{6vu}{5w}F\left( \frac{1}{2},\frac{2}{3},\frac{3}{2},-\frac{wv^2}{2u}\right) \right) ,\end{aligned}$$
(15)
$$\begin{aligned}&\int {\frac{dv}{\left( 3u+\frac{3wv^2}{2}\right) ^{\frac{1}{3}}}}=3^{-1/3}u^{-1/3}vF\left( \frac{1}{3},\frac{1}{2},\frac{3}{2},-\frac{wv^2}{2u}\right) ,\end{aligned}$$
(16)
$$\begin{aligned}&\int {\frac{v^2dv}{\left( 3u+\frac{3wv^2}{2}\right) ^{\frac{1}{3}}}}=3^{-1/3}u^{-1/3}\left( \frac{6uv}{7w}\left( 1+\frac{wv^2}{2u}\right) ^{2/3}-\frac{6uv}{7w}F\left( \frac{1}{3},\frac{1}{2},\frac{3}{2},-\frac{wv^2}{2u}\right) \right) . \end{aligned}$$
(17)

Substituting (14)–(17) into (13), we obtain

$$\begin{aligned} f_{n-1}=&g_{n-1}(u,w)-\frac{2}{5}\left( \frac{3}{2}\right) ^{\frac{1}{3}}{vu^{-1}(2u+wv^2)^{\frac{1}{3}}}\sum _{l=0}^{[n/3]}la_lu^lw^{n-3l}\\&-\frac{4}{7}\left( \frac{3}{2}\right) ^{2/3}{vu^{-1}(2u+wv^2)^{2/3}}\sum _{l=0}^{[n/3]}la_lu^lw^{n-3l-1}\\&+\frac{v}{3^{\frac{2}{3}}}F\left( \frac{1}{2},\frac{2}{3},\frac{3}{2},-\frac{wv^2}{2u}\right) \sum _{l=0}^{[n/3]}\left( k_0+\frac{6l}{5}\right) a_lu^{l-\frac{2}{3}}w^{n-3l}\\&+\frac{v}{3^{-\frac{1}{3}}}F\left( \frac{1}{3},\frac{1}{2},\frac{3}{2},-\frac{wv^2}{2u}\right) \sum _{l=0}^{[n/3]}\left( 4(n-3l)+\frac{12l}{7}\right) a_lu^{l-\frac{1}{3}}w^{n-3l-1}. \end{aligned}$$

Note that both functions \(F(\frac{1}{2},\frac{2}{3},\frac{3}{2},z)\) and \(F(\frac{1}{3},\frac{1}{2},\frac{3}{2},z)\) cannot be expressed in terms of elementary functions in the variable z and their integrals [22] and \(f_{n-1}\) is a homogeneous polynomial in x,  y and z. Then we conclude that

$$\begin{aligned} a_l(k_0+\frac{6l}{5})=0,~~a_l\left( 4(n-3l)+\frac{12l}{7}\right) =0,~~l=0,...,[n/3], \end{aligned}$$

which leads to \(a_l=0\) for \(l=0,...,[n/3].\) This contradicts with \(f_n\) being non-zero. \(\square\)

Next result gives the relationship between Darboux polynomials and polynomial first integrals, proper rational first integrals and exponent factors, see [11, 45] for the proof.

Lemma 3

For a polynomial vector field \({\mathcal {X}}\), the following statements hold.

  1. (i)

    It has a polynomial first integral if and only if it has a Darboux polynomial with the zero cofactor.

  2. (ii)

    It has a proper rational first integral \(\Phi =f/g\) with f, g being coprime if and only if both f, g are Darboux polynomials of \({\mathcal {X}}\) with the same non-zero co-factors.

  3. (iii)

    If it has an exponential factor \(E=\exp (g/h)\) with g, h being coprime and h being not constant, then h is a Darboux polynomial of \({\mathcal {X}}\).

Next result provides a complete classification of exponential factors for system (1).

Lemma 4

The generator of exponential factors of system (1) is \(E(x,y,z)=\exp (z)\) with the cofactor \(L(x,y,z)=b-4x\).

Proof

By Lemma 2 and the statement (iii) of Lemma 3, we can write the exponent factor \(E=\exp (g)\) with \(g\in {\mathbb {R}}[x,y,z]\) satisfying

$$\begin{aligned} (a+yz)\frac{\partial g}{\partial x}+ (-y+x^2)\frac{\partial g}{\partial y}+(b-4x)\frac{\partial g}{\partial z}=l_0+l_1x+l_2y+l_3z. \end{aligned}$$
(18)

Here \(L=l_0+l_1x+l_2y+l_3z,~l_i\in {\mathbb {R}}\) is the cofactor of E. Let \(g=g_m+g_{m-1}+\cdots +g_0\) with \(g_i=g_i(x,y,z)\) being a homogeneous polynomial of degree i and \(g_m\ne 0\).

In the case of \(m\ge 2\), comparing the terms of degree \(m+1\) and m yields

$$\begin{aligned}&yz\frac{\partial g_m}{\partial x}+x^2\frac{\partial g_m}{\partial y}=0, \end{aligned}$$
(19)
$$\begin{aligned}&yz\frac{\partial g_{m-1}}{\partial x}+x^2\frac{\partial g_{m-1}}{\partial y}=4x\frac{\partial g_{m}}{\partial z}+y\frac{\partial g_m}{\partial y}. \end{aligned}$$
(20)

Using the same arguments to prove (5) and (11), we conclude that \(g_m=0\) which is a contradiction.

In the case of \(m=1\), by direct computations we have \(g=a_0+a_1z\) and \(L=a_1(b-4x)\) where \(a_0,~a_1\) are arbitrary constants. Hence the exponent factor has the form \(E=\exp (g)=c_0\exp (a_1z)\) with \(c_0=\exp (a_0)\), which is generated by \(\exp (z)\). \(\square\)

Lemma 5

Assume a polynomial differential system has p Darboux polynomials \(f_{i}\) with cofactors \(K_{i}\) and q exponential factors \(E_{j}=\exp (g_{j}/h_{j})\) with cofactors \(L_{j}\), \(i=1,\ldots p\) and \(j=1,\ldots , q\). Then the function

$$\begin{aligned} f_{1}^{\lambda _{1}}\cdots f_{p}^{\lambda _{p}}E_{1}^{\mu _{1}}\ldots E_{p}^{\mu _{q}}, \end{aligned}$$

is a first integral of this system if and only if there are numbers \(\lambda _{i}\), \(\mu _{j}\in {\mathbb {R}}\) not all zero such that

$$\begin{aligned} \sum _{i=1}^{p}\lambda _{i}K_{i}+\sum _{j=1}^{q}\mu _{j}L_{j}=0. \end{aligned}$$

Proof

See [45, Proposition 3.5 in Chap. 3]. \(\square\)

Proof of Theorem 1:

By Lemma 2 and the statements (i,ii) of Lemma 3, we see that system (1) has neither polynomial first integrals nor proper rational first integrals. The non-existence of Darboux first integrals follows from Lemmas 2, 4 and 5.

3 Bifurcations of Co-dimensional One or Two

In this section we are concerned with the qualitative variation of the dynamical behaviors of system (1) in the vicinity of the isolated singularity. Next result gives the distribution of equilibrium points of system (1), whose proof is standard.

Proposition 6

The following statements hold for system (1).

(i) When \(b=0,~a=0\), system (1) has a family of non-isolated equilibrium \(E_{z}=(0,0,z)\), \(z\in {\mathbb {R}}\).

(ii) When \(b=0,~a\ne 0\), system (1) has no equilibrium.

(iii) When \(b\ne 0\), system (1) has and only has one equilibrium \(E_0=(\frac{b}{4},\frac{b^2}{16}, -\frac{16a}{b^2})\).

Now we turn to study all possible bifurcations of co-dimensional one and two at the isolated equilibrium \(E_0\). A necessary condition for the occurrence of bifurcations is that either a simple real eigenvalue approaches zero or a pair of simple complex eigenvalues reach the imaginary axis for some values of the parameter.

The characteristic polynomial at \(E_0\) is given by

$$\begin{aligned} P(\lambda )=\lambda ^3+\lambda ^2+\left( \frac{b^2}{4}+\frac{8a}{b}\right) \lambda +\frac{b^2}{4}=0. \end{aligned}$$
(21)

It is easy to check that \(P(\lambda )\) cannot have zero roots, which means the occurrence of fold, cusp, Bogdanov-Takens, fold-Hopf bifurcation is impossible. Our result shows the existence of the Hopf bifurcation and Bautin bifurcation. The Hopf bifurcation is a bifurcation near a critical equilibrium as the stability of the equilibrium changes due to the emergence of a pair of purely imaginary eigenvalues, which gives rise to the birth of a limit cycle. The Bautin bifurcation is a bifurcation near critical equilibrium when the equilibrium has a pair of purely imaginary eigenvalues and the first Lyapunov coefficient for the Hopf bifurcation vanishes, also called the generalized Hopf bifurcation, see [25, Chap. 3.5 and 8.7] for more details.

Theorem 7

The statements below are true for system (1).

  1. (i)

    It undergoes a supercritical Hopf bifurcation at \(E_0\) for parameter values \(a=0\) and either \(0<|b|<2(\sqrt{3}-\sqrt{2})\) or \(|b|>2(\sqrt{3}+\sqrt{2})\).

  2. (ii)

    It undergoes a subcritical Hopf bifurcation at \(E_0\) for parameter values \(a=0\) and \(2(\sqrt{3}-\sqrt{2})<|b|<2(\sqrt{3}+\sqrt{2})\).

  3. (iii)

    It undergoes a subcritical Bautin bifurcation at \(E_0\) for parameter values \(a=0\) and \(|b|=2(\sqrt{3}-\sqrt{2})\).

  4. (iv)

    It undergoes a supercritical Bautin bifurcation at \(E_0\) for parameter values \(a=0\) and \(|b|=2(\sqrt{3}+\sqrt{2})\).

Proof

We first assume \(b\ne 0\) so that system (1) can have the isolated equilibrium \(E_0\). Then we translate \(E_0\) to the origin by \((x_1,y_1,z_1)=(x-\frac{b}{4},y-\frac{b^2}{16},z+\frac{16a}{b^2})\) and rewrite (1) as

$$\begin{aligned} \dot{X}=F(X)=AX+\frac{1}{2}B(X,X),~~~X=(x_1,y_1,z_1)^T, \end{aligned}$$
(22)

where

$$\begin{aligned} A=\left( \begin{array}{ccc} 0&{}-\frac{16a}{b^2} &{} \frac{b^2}{16} \\ \frac{b}{2} &{} -1 &{} 0 \\ -4 &{} 0 &{} 0 \\ \end{array} \right) ,~~B(x_1,y_1,z_1,x_2,y_2,z_2)=\left( \begin{array}{c} y_1z_2+y_2z_1 \\ -2x_1x_2\\ 0 \\ \end{array} \right) . \end{aligned}$$

Clearly, the polynomial (21) has a pair of conjugate purely imaginary roots \(\lambda _{1,2}=\pm iw_0\) if and only if \(a=0\). And in the case of \(a=0\), we have \(w_0=b/2\).

In what follows, we assume \(a=0\) and use the centre manifold reduction to determine the type of bifurcations. The central manifold reduction is a technique employed in studying the dynamics of nonlinear systems near critical singularities. It identifies a low-dimensional invariant manifold, referred to as the central manifold, where intricate dynamical behavior of the considered system primarily occurs. Consequently, the central manifold reduction can reduces the dimension of the considered system, facilitating a more accessible analysis of its dynamics such as stability, bifurcations, and long-term behaviors [25, 44].

Define the vectors

$$\begin{aligned} q=\left( \begin{array}{c} -\frac{ib}{16} \\ -\frac{ib^2}{16ib+32}\\ \frac{1}{2} \\ \end{array} \right) ,~~~~ p=\left( \begin{array}{c} -\frac{8i}{b} \\ 0\\ 1 \\ \end{array} \right) , \end{aligned}$$

such that \(Aq=iw_0q,~A^Tp=-iw_0p\) and \(\langle p,q\rangle ={\overline{p}}^Tq=1\). The two-dimensional center manifold can be parameterized by \(w,{\overline{w}}\) through the immersion

$$\begin{aligned} X=H(w,{\overline{w}})=wq+{\overline{w}}{\overline{q}}+\sum _{2\le j+k\le 5}{\frac{1}{j!k!}h_{jk}w^{j}{\overline{w}}^k}+O(|w|^6),~~h_{jk}\in {\mathbb {C}}^3,~~{\overline{h}}_{jk}=h_{kj} \end{aligned}$$

and the system (22) restricted on the center manifold can be reduced to

$$\begin{aligned} \dot{w}=G(w,{\overline{w}})=iw_0w+\frac{1}{2}G_{21}w|w|^2+\frac{1}{12}G_{32}w|w|^4+O(|w|^6),~~G_{jk}\in {\mathbb {C}}. \end{aligned}$$

The unknown quantities \(h_{jk},~G_{21},~G_{32}\) are determined by the homological equation [44]

$$\begin{aligned} H_w(w,{{\overline{w}}})\dot{w}+H_{{{\overline{w}}}}(w,{{\overline{w}}})\dot{{{\overline{w}}}} =F(H(w,{{\overline{w}}})). \end{aligned}$$
(23)

We first consider the first Lyapunov coefficient

$$\begin{aligned} l_1=\frac{1}{2}\Re {G_{21}}. \end{aligned}$$

In our case we have

$$\begin{aligned} h_{11}=A^{-1}B(q,{\overline{q}})=\left( \begin{array}{c} 0 \\ \frac{b^2}{128} \\ \frac{b}{b^2+4} \\ \end{array} \right) ,\\ h_{20}=(2iw_0E_3-A)^{-1}B(q,q)=\left( \begin{array}{c} -\frac{b}{12(2+ib)} \\ -\frac{b^2(3ib+22)}{384(ib+1)(ib+2)} \\ -\frac{i}{3(ib+2)} \\ \end{array} \right) , \end{aligned}$$

and

$$\begin{aligned} G_{21}=\langle p, B({\overline{q}},h_{20})+2B(q,h_{11})\rangle , \end{aligned}$$

which yields

$$\begin{aligned} l_1=-\frac{b^2(b^4-40b^2+16)}{64(b^2+1)(b^2+4)^2}. \end{aligned}$$

Based on the expression of \(l_1\), we obtain the statements (i) and (ii) in Theorem 7.

When \(|b|=2(\sqrt{3}-\sqrt{2})\) or \(2(\sqrt{3}+\sqrt{2})\), the first Lyapunov coefficient \(l_1\) vanishes. To clarify the bifurcations, we need to calculate the second Lyapunov coefficient \(l_2\) defined by

$$\begin{aligned} l_2=\frac{1}{12}\Re {G_{32}}. \end{aligned}$$

We first consider \(|b|=2(\sqrt{3}-\sqrt{2})\). Recall that the third-order coefficients \(h_{30}\) and \(h_{21}\) are defined by

$$\begin{aligned} h_{30}=\left( 3 i \omega _{0} I_{n}-A\right) ^{-1}3 B\left( q, h_{20}\right) , \end{aligned}$$

and

$$\begin{aligned} \left( i \omega _{0} I_{n}-A\right) h_{21}=B\left( \bar{q},h_{20}\right) +2 B\left( q, h_{11}\right) -G_{21} q,~~\langle p,h_{21}\rangle =1. \end{aligned}$$

Some long and tedious computations lead to \(h_{30}\) and \(h_{21}\), see Appendix A for their expressions. Similarly, the fourth-order coefficients \(h_{40}\), \(h_{31}\) and \(h_{22}\) are given by

$$\begin{aligned} h_{40}&=\left( 4 i \omega _{0} I_{n}-A\right) ^{-1}\left[ 4 B\left( q, h_{30}\right) +3 B\left( h_{20},h_{20}\right) \right] \\&=\left( \frac{h^1_{401}}{h^2_{401}},\frac{h^1_{402}}{h^2_{402}},\frac{h^1_{403}}{h^2_{403}}\right) ^T,\\ h_{31}&=\left( 2 i \omega _{0} I_{n}-A\right) ^{-1} \left[ 3 B\left( h_{20}, h_{11}\right) +B\left( \bar{q}, h_{30}\right) +3 B\left( q, h_{21}\right) -3 G_{21} h_{20}\right] \\&=\left( \frac{h^1_{311}}{h^2_{311}},\frac{h^1_{312}}{h^2_{312}},\frac{h^1_{33}}{h^2_{313}}\right) ^T,\\ h_{22}&=-A^{-1}\left[ 2 B\left( h_{11}, h_{11}\right) +2 B\left( q, \bar{h}_{21}\right) +2 B\left( \bar{q},h_{21}\right) +B\left( \bar{h}_{20}, h_{20}\right) -2 h_{11}\left( G_{21}+\bar{G}_{21}\right) \right] \\&=\left( \frac{h^1_{221}}{h^2_{221}},\frac{h^1_{222}}{h^2_{222}},\frac{h^1_{223}}{h^2_{223}}\right) ^T, \end{aligned}$$

where the expressions of \(h^i_{40j},~h^i_{31j},~h^i_{22j}\),  \(i=1,2,j=1,2,3\) are given in Appendix A.

Finally, by the formula

$$\begin{aligned} G_{32}=\langle p, 6 B\left( h_{11}, h_{21}\right) +B\left( \bar{h}_{20}, h_{30}\right) +3 B\left( \bar{h}_{21}, h_{20}\right) +3 B\left( q, h_{22}\right) +2 B\left( \bar{q}, h_{31}\right) -6 G_{21} h_{21}-3 \bar{G}_{21} h_{21}\rangle , \end{aligned}$$

we obtain the second Lyapunov coefficient

$$\begin{aligned} l_2=\frac{m_1}{m_2}\approx 0.00094299>0, \end{aligned}$$

with

$$\begin{aligned} m_1=&9(66151620429820334886935496291647 \sqrt{3}-81018857855665520744724260783667 \sqrt{2}),\\ m_2=&32(2 \sqrt{3}-2 \sqrt{2})(\sqrt{3} \sqrt{2}-3)^{5}(79568 \sqrt{3} \sqrt{2}-194901)(812 \sqrt{3} \sqrt{2}-1989)^{3}(901 \sqrt{3} \sqrt{2}-2207)\\&(1044409530 \sqrt{3} \sqrt{2}-2558270431). \end{aligned}$$

Hence, system (1) undergoes a supercritical Bautin bifurcation when \(a=0,~b=2(\sqrt{3}-\sqrt{2})\). We prove the statement (iii) in Theorem 7.

Using the same arguments, we can show that if \(|b|=2(\sqrt{3}+\sqrt{2})\) the second Lyapunov coefficient

$$\begin{aligned} l_2=\frac{n_1}{n_2}\approx -0.384572<0, \end{aligned}$$

with

$$\begin{aligned} n_1=&-9(66151620429820334886935496291647 \sqrt{3}+81018857855665520744724260783667 \sqrt{2}),\\ n_2=&32((2 \sqrt{3}+2 \sqrt{2})(\sqrt{3} \sqrt{2}+3)^{5}(194901+79568 \sqrt{3} \sqrt{2})(1989+812 \sqrt{3}\sqrt{2})^{3}\\&(901 \sqrt{3} \sqrt{2}+2207)(2558270431+1044409530 \sqrt{3} \sqrt{2}). \end{aligned}$$

Then system (1) undergoes a supercritical Bautin bifurcation. We have proved the statement (iv) in Theorem 7.

\(\square\)

4 KCC Theory and Jacobi Instability

The KCC theory, or Jacobi stability analysis, uses a geometric approach to examine the stability of dynamical systems. This technique is credited to the work of Kosambi [24], Cartan [5], and Chern [7]. The KCC theory is an extension of geodesic flow stability analysis for a manifold in Finsler geometry to a differentiable manifold without metirc, and can be used effectively to investigate the robustness of a system of second-order differential equations [4, 15].

To analyze the Jacobi stability of system (1), we should convert (1) into a system of second-order differential equations. Indeed, from the third equation of (1), we have \(x=(b-\dot{z})/4\). Substituting it into the first equation of (1) yield

$$\begin{aligned} \ddot{z}+4yz+4a=0. \end{aligned}$$
(24)

Taking the derivative on both sides of the second equation of (1), one has

$$\begin{aligned} \ddot{y}=-\dot{y}+2x\dot{x}. \end{aligned}$$
(25)

Eliminating x and its derivative \(\dot{x}\) from (25) leads to

$$\begin{aligned} \ddot{y}+\frac{1}{2}yz\dot{z}+\frac{a}{2}\dot{z}-\frac{b}{2}yz-\frac{ab}{2}+\dot{y}=0. \end{aligned}$$
(26)

In what follows, the Einstein summation convention will be used. For convenience, we introduce \(z=X^1,~y=X^2,~x=X^3.\) Then (24) and (26) become

$$\begin{aligned} \left\{ \begin{array}{l} \frac{d^2}{dt^2}X^1+2G^1(X^1,X^2,Y^1,Y^2)=0,\\ \frac{d^2}{dt^2}X^2+2G^2(X^1,X^2,Y^1,Y^2)=0, \end{array} \right. \end{aligned}$$
(27)

where \(Y^k=dX^k/dt\) for \(k=1,2\) and

$$\begin{aligned} G^1=2X^1X^2+2a,~~~~G^2={\frac{1}{4}}{X^{{2}}X^{{1}}Y^{{1}}}+{\frac{a}{4}}Y^1-{\frac{b}{4}}X^1X^2-{\frac{ab}{4}}+{\frac{1}{2}}Y^2. \end{aligned}$$

Once \(X^1,~X^2\) are determined by (27), we can get \(X^3\) by \(X^3=(b-Y^1)/4\). Given a vector field \(\eta =\eta ^i\frac{\partial }{\partial X^i}\), the KCC-covariant differential of \(\eta\) associated with (27) is defined as

$$\begin{aligned} \frac{D}{dt}\eta ^i=\frac{d}{dt}\eta ^i+N^i_j \eta ^j, \end{aligned}$$

where \(N^i_j=\partial G^i/\partial X^j\) are coefficients of the nonlinear connection.

Below we derive the KCC invariants for system (27). The first KCC invariants are defined as

$$\begin{aligned} {e^1}&=-\frac{D}{dt}Y^1=2G^1-N^1_jY^j, \\&=4a+4X^1X^2, \\ {e^2}&=-\frac{D}{dt}Y^2=2G^2-N^2_jY^j, \\&=-\frac{ab}{2}+\frac{a}{4}Y^1+\frac{1}{2}Y^2-\frac{b}{2}X^1X^2+\frac{1}{4}X^1X^2Y^1. \end{aligned}$$

The variational equations along a trajectory \((X^1(t),X^2(t))\) of (27) are given by

$$\begin{aligned} \frac{d^2}{dt^2}\xi ^i+2N^i_j\frac{d}{dt}\xi ^i+2\frac{\partial G^i}{\partial X^j}\xi ^j=0,~~i=1,2, \end{aligned}$$
(28)

that is,

$$\begin{aligned} \left\{ \begin{array}{l} \frac{d^2}{dt^2}\xi ^1+4X^2\xi ^1+4X^1\xi ^2=0, \\ \frac{d^2}{dt^2}\xi ^2+\frac{X^1X^2+a}{2}\frac{d}{dt}\xi^1+\frac{d}{dt}\xi ^2 +\frac{X^2(Y^1-b)}{2}\xi ^1+\frac{X^1(Y^2-b)}{2}\xi^2=0. \end{array} \right. \end{aligned}$$
(29)

In terms of KCC-covariant differentials, (28) becomes

$$\begin{aligned} \frac{D^2}{dt^2}\xi ^i=P^i_j\xi ^j, \end{aligned}$$
(30)

where the deviation curvature tensor \(P^i_j\) are called the second KCC invariants and have the form

$$\begin{aligned}&P^1_1 = -\,4X^2,~~P^1_2=-4X^1,~~P^2_2=-\frac{1}{2}X^1Y^1+\frac{b}{2}X^1+\frac{1}{4}, \end{aligned}$$
(31)
$$\begin{aligned}&P^2_1=-\frac{1}{4}X^2Y^1+\frac{b}{2}X^2+\frac{1}{4}Y^2X^1+ +\frac{1}{8}X^1X^2+\frac{a}{8}. \end{aligned}$$
(32)

The third, fourth and fifth KCC invariants are defined as

$$\begin{aligned} P^i_{jk}=\frac{1}{3}\left( \frac{\partial P^i_j}{\partial Y^k} - \frac{\partial P^i_k}{\partial Y^j} \right) ,~~P^i_{jkl}=\frac{\partial P^i_{jk}}{\partial Y^l}, ~~D^i_{jkl}=\frac{\partial ^2 N^i_j}{\partial Y^kY^l}. \end{aligned}$$

For system (27), some simple computations give \(P^2_{12}=X^1/4,~P^2_{21}=X^1/4\) and the rest of third, fourth and fifth KCC invariants equal to zero.

Definition 1

[4] A trajectory of (27) is Jacobi stable if and only if the real parts of the eigenvalues of the deviation tensor \(P^i_j\) are strictly negative at each point on the trajectory.

By (31)–(32), the trace and determinant of the matrix \(P=(P^i_j)_{2\times 2}\) are given by

$$\begin{aligned} \textrm{tr} P={\frac{ \left( 2\,b-2\,Y^{{1}} \right) X^{{1}}}{4}}-4\,X^{{2}}+{\frac{1}{4}}, ~~ \textrm{det} P={\frac{ \left( X^{{2}}+2\,Y^{{2}} \right) {(X^{{1}})}^{2}}{2}}+{\frac{ \left( 2\,X^{{2}}Y^{{1}}+a \right) X^{{1}}}{2}}-X^{{2}}. \end{aligned}$$

Then by the classical Routh-Hurwitz criteria, we see that a trajectory of (27) is Jacobi stable if and only if \(\textrm{tr} P<0,~\textrm{det} P>0\) at each point on the trajectory.

There exist two quantities associated with the variational equations (28), which can be used to investigate the onset of chaos [15]. The first one is the deviation vector

$$\begin{aligned} \xi (t)=\sqrt{(\xi ^1(t))^2+(\xi ^2(t))^2}, \end{aligned}$$
(33)

where \((\xi ^1(t),\xi ^2(t))\) is the solution of (28) subject to the initial condition

$$\begin{aligned} (\xi ^1(0),\xi ^2(0),{\dot{\xi }}^1(0),{\dot{\xi }}^2(0))=(0,0,\xi _{10},\xi _{20}). \end{aligned}$$
(34)

The second one is the curvature of the deviation vector [15]

$$\begin{aligned} \kappa _0(t)=\frac{{\dot{\xi }}^1(t)\ddot{\xi }^2(t)-{\dot{\xi }}^2(t)\ddot{\xi }^1(t)}{\{ ({\dot{\xi }}^1(t))^2+({\dot{\xi }}^2(t))^2 \}^{3/2}}. \end{aligned}$$
(35)

Recall system (1) has a equilibrium point \(E_0=(\frac{b}{4},\frac{b^2}{16}, -\frac{16a}{b^2})\), which corresponds to the equilibrium point \({\hat{E}}_0=(X^1,X^2,Y^1,Y^2)=(-\frac{16a}{b^2},\frac{b^2}{16},0,0)\) of system (27). Below we perform a Jacobi stability analysis for such simplest trajectory, the equilibrium point \({\hat{E}}_0\) of system (27).

Theorem 8

The equilibrium point \({\hat{E}}_0\) of (27) is Jacobi unstable.

Proof

At the equilibrium point \({\hat{E}}_0\), the deviation curvature tensor is given by

$$P=\left[ \begin{array}{cc}P^1_1&P^1_2\\ P^2_1&{}P^2_2\end{array} \right] = \left[ \begin{array}{cc} -{\frac{{b}^{2}}{4}}&{}{\frac{64a}{{b}^{2 }}}\\ {\frac{{b}^{3}}{32}}&{}{\frac{b-32\,a}{4\,b}} \end{array} \right].$$

The determinant \({\det P}=-b^2/16<0\), which means P always has a positive root. The proof is completed.

\(\square\)

Using the equivalence of (1) and system (27), we say that \(E_0\) is also Jacobi unstable. On the other hand, it follows from (21) that \(E_0\) is Lyapunov stable (or linearly stable) if \(ab>0\). This indicates us that the stability criteria in the Jacobi sense does not completely align with the stability criteria in the Lyapunov sense. In comparison to Lyapunov stability, Jacobi stability focuses on the robustness of second-order differential equations concerning both internal parameter variations and environmental changes [1, 4], where robustness refers to the system’s insensitivity and adaptability to these alterations. Mathematically, Lyapunov stability is determined by the signs of eigenvalues of the linearized matrix at a singular point. In contrast, Jacobi stability relies on the signs of eigenvalues of the deviation curvature tensor at the same singular point. The role typically played by partial derivatives is replaced by covariant derivatives, resulting in the distinction between these two types of stability. For two-dimensional systems, there exist cases where singular points are Lyapunov stable but Jacobi unstable, and vice versa [4]. It was shown that for three-dimensional conservative systems, the Lyapunov stability and Jacobi stability may match exactly [1]. Our result presents a new example of a three-dimensional dissipative system where its singular point are Jacobi unstable, yet they can be either Lyapunov stable or unstable.

The variational equations (29) near equilibrium points read

$$\begin{aligned} \left\{ \begin{array}{l} \frac{d^2}{dt^2}\xi ^1+\frac{b^2}{4}\xi ^1-\frac{64a}{b^2}\xi ^2=0, \\ \frac{d^2}{dt^2}\xi ^2+\frac{d}{dt}\xi ^2 -\frac{b^3}{32}\xi ^1+\frac{8a}{b}{\xi ^2}=0. \end{array} \right. \end{aligned}$$
(36)

The series solutions of (36) subject to (34) are given by

$$\begin{aligned} \xi ^1(t)=&\xi _{10}\,t+{\frac{ \left( -{b}^{4}\xi _{10}+256\,a\xi _{20} \right) {t}^{3}}{24 \,{b}^{2}}}-{\frac{8\,a\xi _{20}\,{t}^{4}}{3\,{b}^{2}}}+o(t^4), \\ \xi ^2(t)=&\xi _{20}\,t-{\frac{\xi _{20}\,{t}^{2}}{2}}+{\frac{ \left( \left( -256\,a+ 32\,b \right) \xi _{20}+{b}^{4}\xi _{10} \right) {t}^{3}}{192\,b}}\\&+{\frac{ \left( \left( 512\,a-32\,b \right) \xi _{20}-{b}^{4}\xi _{10} \right) {t}^{4 }}{768\,b}}+o(t^4). \end{aligned}$$

By the formulas (33) and (35), one gets the deviation vector and its curvature:

$$\begin{aligned}&\xi (t)=a_1t+a_2t^2+a_3t^3+a_4t^4+o(t^4),\\&\kappa _0(t)=b_0+b_1t+b_2t^2+o(t^2), \end{aligned}$$

where

$$\begin{aligned} a_1=&\sqrt{{\xi _{10}}^{2}+{\xi _{20}}^{2}},~~a_2=-{\frac{{\xi _{20}}^{2}}{2}{\frac{1}{\sqrt{{\xi _{10}}^{2}+{\xi _{20}}^{2}}}}}, \\ a_3=&\sqrt{{\xi _{10}}^{2}+{\xi _{20}}^{2}} \left( -{\frac{-\xi _{10}\,\xi _{20}\,{b}^{5} +8\,{\xi _{10}}^{2}{b}^{4}+256\,a{\xi _{20}}^{2}b-56\,{\xi _{20}}^{2}{b}^{2}-2048 \,a\xi _{10}\,\xi _{20}}{192\,{b}^{2} \left( {\xi _{10}}^{2}+{\xi _{20}}^{2} \right) } }-{\frac{{\xi _{20}}^{4}}{8\, \left( {\xi _{10}}^{2}+{\xi _{20}}^{2} \right) ^{2} }} \right) , \\ a_4=&\sqrt{{\xi _{10}}^{2}+{\xi _{20}}^{2}} \bigg ( {\frac{\xi _{20}\, \left( -3\,{b}^ {5}\xi _{10}+1024\,ab\xi _{20}-96\,{b}^{2}\xi _{20}-2048\,a\xi _{10} \right) }{768\,{b }^{2} \left( {\xi _{10}}^{2}+{\xi _{20}}^{2} \right) }} \\&-{\frac{{\xi _{20}}^{2} \left( -\xi _{10}\,\xi _{20}\,{b}^{5}+8\,{\xi _{10}}^{2}{b}^{4}+256\,a{\xi _{20}}^{2} b-56\,{\xi _{20}}^{2}{b}^{2}-2048\,a\xi _{10}\,\xi _{20} \right) }{384\, \left( { \xi _{10}}^{2}+{\xi _{20}}^{2} \right) ^{2}{b}^{2}}}-{\frac{{\xi _{20}}^{6}}{16\, \left( {\xi _{10}}^{2}+{\xi _{20}}^{2} \right) ^{3}}} \bigg ) \end{aligned}$$

and

$$\begin{aligned} b_0=&-{\xi _{10}\,\xi _{20} \left( {\xi _{10}}^{2}+{\xi _{20}}^{2} \right) ^{-{\frac{3}{2}} }}, \\ b_1=&-{\frac{3\xi _{10}\,{\xi _{20}}^{3}}{ \left( {\xi _{10}}^{2}+{\xi _{20}}^{2} \right) ^{5/2}}}+{ \left( {\frac{\xi _{10}\, \left( \left( -256\,a+32\, b \right) \xi _{20}+{b}^{4}\xi _{10} \right) }{32\,b}}-{\frac{ \left( -{b}^{4 }\xi _{10}+256\,a\xi _{20} \right) \xi _{20}}{4\,{b}^{2}}} \right) \left( {\xi _{10}} ^{2}+{\xi _{20}}^{2} \right) ^{-{\frac{3}{2}}}}, \\ b_2=&-{\xi _{10}\,\xi _{20} } \bigg ( {\frac{-3\,\xi _{10}\,\xi _{20}\,{b}^{5}+24\,{\xi _{10}}^{2 }{b}^{4}+768\,a{\xi _{20}}^{2}b-192\,{\xi _{20}}^{2}{b}^{2}-6144\,a\xi _{10}\,\xi 20}{64\,{b}^{2} \left( {\xi _{10}}^{2}+{\xi _{20}}^{2} \right) }} \\&+{\frac{15\, {\xi _{20}}^{4}}{2\, \left( {\xi _{10}}^{2}+{\xi _{20}}^{2} \right) ^{2}}} \bigg ) \left( {\xi _{10}}^{2}+{\xi _{20}}^{2} \right) ^{-{\frac{3}{2}}} \\&+{\frac{3{\xi _{20}}^{2}}{ \left( {\xi _{10}}^{2}+{\xi _{20}}^{2} \right) ^{5/2} } \left( 1/32\,{\frac{\xi _{10}\, \left( \left( -256\,a+32\,b \right) \xi _{20}+{b}^{4}\xi _{10} \right) }{b}}-1/4\,{\frac{ \left( -{b}^{4}\xi _{10}+ 256\,a\xi _{20} \right) \xi _{20}}{{b}^{2}}} \right) } \\&+{ \left( {\frac{\xi _{10}\, \left( \left( 512\,a-32\,b \right) \xi _{20}-{b} ^{4}\xi _{10} \right) }{64\,b}}+{\frac{ \left( -{b}^{4}\xi _{10}+256\,a\xi _{20} \right) \xi _{20}}{8\,{b}^{2}}}+32\,{\frac{a{\xi _{20}}^{2}}{{b}^{2}}} \right) \left( {\xi _{10}}^{2}+{\xi _{20}}^{2} \right) ^{-{\frac{3}{2}}}}. \end{aligned}$$
Fig. 2
figure 2

Orientation of the local charts \(U_{i}\) and \(V_{i}\)(\(i = 1,2,3\)) in the endpoints of the x, y and z axis

Full size image

5 Dynamics at Infinity

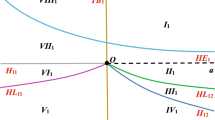
In this section, we turn to investigate the dynamics at infinity for system (1). Indeed, system (1) is a polynomial differential system that can be expanded to an analytic system within a closed ball of radius one known as the Poincaré ball. The boundary of this ball is invariant under the flow of the extended system and acts as its infinity [2, 40]. As shown in the Fig. 2, we will analyze the Poincaré compactification of system (1) in the local charts \(U_{i}\) and \(V_{i}\)(\(i = 1,2,3\)).

5.1 In the Local Charts \(U_1\)

  Taking the change of variables \((x,y,z)=(z_3^{-1},z_1z_3^{-1},z_2z_3^{-1})\) and the time \(\textrm{d}\tau =z_3^{-1}\textrm{d}t\), we obtain the Poincaré compactification p(X) in the local chart \(U_{1}\)

$$\begin{aligned} \left\{ \begin{array}{l} \frac{dz_1}{d\tau }=-az_1z_3^2-z_1^2z_2-z_1z_3+1,\\ \frac{dz_2}{d\tau }=-az_2z_3^2+bz_3^2-z_1z_2^2-4z_3,\\ \frac{dz_3}{d\tau }=-z_3(az_3^2+z_1z_2). \end{array} \right. \end{aligned}$$
(37)

Note that the \(z_{1}z_{2}\)-plane is invariant under the flow of system (37), which completely describes the dynamics on the sphere at infinity. For \(z_{3}=0\), system (37) can reduce to

$$\begin{aligned} \left\{ \begin{array}{l} \frac{dz_1}{d\tau }=-z_1^2z_2+1,\\ \frac{dz_2}{d\tau }=-z_1z_2^2.\\ \end{array} \right. \end{aligned}$$
(38)

System (38) has no equilibrium, but has a rational first integral

$$\begin{aligned} H_1(z_1,z_2)=\frac{z_2^3}{3z_1^2z_2-2}. \end{aligned}$$

With the help of \(H_1\), the global phase portrait of (38) is completely described as shown in the Fig. 3.

Fig. 3
figure 3

Phase portraits of system (38)

Full size image
Fig. 4
figure 4

Phase portraits of system (40)

Full size image

5.2 In the Local Charts \(U_2\)

  Similarly, we make change of variables \((x,y,z)=(z_1z_3^{-1},z_3^{-1},z_2z_3^{-1})\) and \(\textrm{d}{\tau }=z_3^{-1}\textrm{d}t\) to transform system (1) into

$$\begin{aligned} \left\{ \begin{array}{l} \frac{dz_1}{d\tau }=az_3^2-z_1^3+z_1z_3+z_2,\\ \frac{dz_2}{d\tau }=bz_3^2-z1^2z_2-4z_1z_3+z_2z_3,\\ \frac{dz_3}{d\tau }=-z_3(z_1^2-z_3). \end{array} \right. \end{aligned}$$
(39)

Note that the \(z_{1}z_{2}\)-plane is invariant under the flow of system (37), which completely describes the dynamics on the sphere at infinity. For \(z_{3}=0\), system (39) can reduce to

$$\begin{aligned} \left\{ \begin{array}{l} \frac{dz_1}{d\tau }=-z_1^3+z_2,\\ \frac{dz_2}{d\tau }=-z_1^2z_2.\\ \end{array} \right. \end{aligned}$$
(40)

As above, system (38) is also integrable and has a first integral \(H_2=\frac{M_1^3M_2^2}{M_3^3M_4^2}\) where

$$\begin{aligned} M_1&=2z_1^6-5z_1^3z_2+3z_2^2+\sqrt{(4z_1^6-4z_1^3z_2-3z_2^2)(z_1^3-z_2)^2}, \\ M_2&=-2z_1^6+3z_1^3z_2+\sqrt{(4z_1^6-4z_1^3z_2-3z_2^2)(z_1^3-z_2)^2}, \\ M_3&=-2z_1^6+5z_1^3z_2-3z_2^2+\sqrt{(4z_1^6-4z_1^3z_2-3z_2^2)(z_1^3-z_2)^2}, \\ M_4&=2z_1^3-3z_2. \end{aligned}$$

In addition, system (38) has a unique equilibrium \((z_1,z_2) = (0,0)\) which is a nilpotent point. By Theorem 3.5 in [11], we see that (0, 0) is a stable node. We also mention the origin is global asymptotically stable, which can easily follow from the Lyapunov function \(V(z_1,z_2)=z_1^6/6+2z_2^2\) and the Lasalle’s invariance principle. The dynamics on the local chart \(U_2\) is topologically equivalent to the one shown in the Fig. 4.

Fig. 5
figure 5

Phase portrait of system (42)

Full size image

5.3 In the Local Charts \(U_3\)

  Under the change of variables \((x,y,z)=(z_1z_3^{-1},z_2z_3^{-1},z_3^{-1})\) and \(\textrm{d}\tau =z_3^{-1}\textrm{d}t\), system (1) becomes

$$\begin{aligned} \left\{ \begin{array}{l} \frac{dz_1}{d\tau }=-bz_1z_3^2+az_3^2+4z_1^2z_3+z_2,\\ \frac{dz_2}{d\tau }=-bz_2z_3^2+4z_1z_2z_3+z_1^2-z_2z_3,\\ \frac{dz_3}{d\tau }=-z_3^2(bz_3-4z_1). \end{array} \right. \end{aligned}$$
(41)

Note that the \(z_{1}z_{2}\)-plane is invariant under the flow of system (37), which completely describes the dynamics on the sphere at infinity. For \(z_{3}=0\), system (41) can be reduced to

$$\begin{aligned} \left\{ \begin{array}{l} \frac{dz_1}{d\tau }=z_2,\\ \frac{dz_2}{d\tau }=z_1^2.\\ \end{array} \right. \end{aligned}$$
(42)

System (38) has a unique equilibrium \((z_1,z_2)=(0,0)\) and a polynomial first integral \(H(z_1,z_2)=3z_2^2-2z_1^3\). Then the phase portrait of system (42) is illustrated in the Fig. 5.

Finally, we mention that the flow of (1) in the local chart \(V_{i},~i=1,2,3\) is identical to the flow in \(U_{i}\), but with reversed time direction. Building on the previous discussion, we get a comprehensive overview of the global behavior of system (1) on the sphere at infinity \({\mathbb {S}}^2\).

Fig. 6
figure 6

Phase portrait of the system (1) on the Poincaré sphere at infinity

Full size image

Then by the Poincaré compactification [14, 28], we give a complete description of the dynamical behavior on the sphere at infinity for system (1).

Theorem 9

The phase portrait of the system (1) on the Poincaré sphere at infinity is as shown in the Fig. 6: there exist two nodes at the positive and negative endpoints of the y-axis, two cusp points at the positive and negative endpoints of the z-axis, and an unlimited set of heteroclinic orbits connecting these equilibrium points.

It should be pointed out that the dynamical behavior of the system at infinity is independent of the value of the parameters a,  b.

6 Conclusion

The work presents a qualitative analysis of a differential system in \({\mathbb {R}}^3\), focusing on the existence of homoclinic flip bifurcations of case C. Although this system is expressed in a simple form, we find that it possesses a wide range of intricate properties. The elementary method used in this study demonstrates the absence of closed-form, analytical solutions. We investigate the possible bifurcations at isolated equilibrium points, showing that only Hopf and Bautin bifurcations occur. Furthermore, we analyze the Jacobi instability of the system’s trajectory and discuss the behavior of the deviation vector near the equilibrium point. Lastly, we classify the system’s dynamical behavior on the Poincar’e sphere at infinity.