1 Introduction

Chaos is a highly intriguing and complex nonlinear phenomenon that has been extensively researched over the past 40 years by the scientific, Mathematical, and Engineering Communities. As a result, generating chaos has become a significant area of research. Many chaotic systems have been developed by taking inspiration from the famous Lorenz system [1,2,3,4,5]. There has been significant interest in generating chaotic systems that possess novel characteristics and many of these discoveries are based on equilibrium points which can be exhibit a range of characteristics, including chaotic behavior without any stable equilibria [6,7,8,9], stable equilibria [10,11,12,13], and even entire curves of equilibria [8, 14,15,16,17, 19], and surfaces of equilibria [20,21,22,23]. Such systems are useful for designing secure communication systems.

Since real systems are by their very nature fractional, it is not surprising that treating fractional order to describe system behaviour more accurately than integer methods. The mathematical discipline of fractional calculus [24,25,26,27] has now completely evolved, these mathematics have wide-ranging applications in the fields of nonlinear controls, electrical systems, and mechanical systems. etc. Many researchers have studied fractional chaotic systems, including those involving secure communication [28,29,30,31], image encryption [32, 33], random number generators [34,35,36,37], electronic circuit implementation [38, 39].

Building upon the aforementioned works, this paper explores the dynamic properties of the propose fractional-order chaotic system (FOCS). When the order q equals 0.97, the system displays attractors that are more intricate than a standard chaotic system with an integer value, making it well-suited for the development of highly secure communication systems. The FOCS is employed in a sound encryption scheme that comprises two levels of encryption, aimed at enhancing security levels. The security of the encrypted communication system has been verified by analyzing histograms, correlation coefficients, and spectrograms by using MATLAB software. Finally, a feasible electronic circuit for the new FOCS is realized.

The subsequent sections of the paper are structured as follows: Sect. 2 introduces the 3D chaotic system model with a curved equilibrium. Section 3 covers the calculus of fractional order systems, while Sect. 4 derives the fractional order model of the chaotic system. In Sect. 5, the dynamical behavior of the system is analyzed using techniques such as Lyapunov exponents, phase portraits, and bifurcation diagrams. Section 6 presents the electronic circuit implementation of the propose FOCS. In Sect. 7, a sound encryption algorithm based on the FOCS is developed. Section 8 presents a thorough analysis of the security of the communication scheme employed, with experimental results being presented in Sect. 9. Finally, the paper concludes in Sect. 10.

2 Model of the 3D Curved Equilibrium Chaotic System

[38] Proposed various equilibrium shapes of a chaotic system of the form.

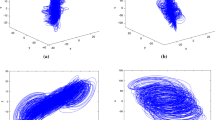
$$\begin{aligned} \begin{aligned}&\dot{x}=az \\&\dot{y}=-z\left( xz+{{y}^{2}} \right) \\&\dot{z}=z\left( c{{y}^{2}}-a{{z}^{2}}-b{{x}^{2}}+x \right) +f\left( x,y \right) \\ \end{aligned} \end{aligned}$$
(1)

where, x, y, and z are state variables and a, b, and c are parameters. A comprehensive model of system (1) having different equilibrium forms, as shown in Fig. 1, is provided with this article. The system is pronounced by Eq. (1) with a nonlinear function given in Table 1. The results obtained from the analysis of the system confirmed that it has a curved equilibrium.

Fig. 1
figure 1

The equilibrium points of system (1) for a CS-1 and b CS-2 are provided in Table 1

Full size image
Table 1 list of nonlinear function and the values of their parameters and initial conditions
Full size table

3 Fractional Order Preliminaries

The history of fractional calculus extends back more than three hundred years [24]. Elementary fractional-order operator in fractional calculus, the symbol denotes the generalization of integration and differentiation, where q and t are the operation’s limits. It can be used as a non-integer differentiator or integrator by selecting a positive or negative order q. As an example of the continuous-time fractional-order process, consider as:

$$\begin{aligned} D_{t}^{q}=\left\{ \begin{aligned}&\frac{{{d}^{q}}}{d{{t}^{q}}}\,\,\,\,\,\,\,\,\,\,\,\,:q\succ o, \\&1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,:q=0, \\&\int _{a}^{t}{{{\left( d\tau \right) }^{-q}}\,\,:q\prec 0.} \\ \end{aligned} \right. \end{aligned}$$
(2)

In the development of fractional calculus, there are three commonly used definitions of the fractional order differential operator, Grunwald-Letnikov, Riemann-Liouville, and Caputo [25,26,27]. The first definition is the Caputo, which is defined as

$$\begin{aligned} D_{t}^{q}f\left( t \right) ={{\left\{ \frac{1}{\Gamma \left( n-q \right) }\left( \frac{d}{dt} \right) \right. }^{n}}{{\int _{a}^{t}{\left( t-\tau \right) }}^{n-q-1}}{{f}^{n}}\left( \tau \right) d\tau \end{aligned}$$
(3)

where \(n-1\prec q\prec n\)

According to Anton Karl Grunwald and Aleksey Vasilievich Letnikov’s concept of the fractional order derivative, which is another common formulation used in fractional analysis is defined as

$$\begin{aligned} D_{t}^{q}f\left( t \right) =\underset{h\rightarrow 0}{\mathop {\lim }}\,{{h}^{-q}}\sum \limits _{j=0}^{\infty }{{{\left( -1 \right) }^{j}}\left( \begin{aligned}&q \\&j \\ \end{aligned} \right) f\left( t-jh \right) } \end{aligned}$$
(4)

and the Euler’s gamma function can be used to calculate binomial coefficients as,

$$\begin{aligned} \left( \begin{aligned}&q \\&j \\ \end{aligned} \right) =\frac{q!}{j!\left( q-j \right) !}=\frac{\Gamma \left( q+1 \right) }{\Gamma \left( q+1 \right) \Gamma \left( q-j+1 \right) } \end{aligned}$$
(5)

Among them, the Riemann–Liouville definition is more favoured than others, being the simplest definition and also the easiest one to use; the Riemann–Liouville definition is described by

$$\begin{aligned} \begin{aligned} \frac{d^qf(t)}{dt^q}= \frac{1}{ \Gamma (n-q)} \int _0^t \frac{f(\tau )}{ (t-\tau )^q-n+1} \,d\tau \end{aligned} \end{aligned}$$
(6)

Where q is a fractional order satisfying \(n-1\preceq q\preceq n\) and \(\Gamma (.)\) is the gamma function. If all initial values are assumed to be zero, the Laplace transform of the Riemann–Liouville fractional derivative can be represented as

$$\begin{aligned} \begin{aligned} L \left\{ \frac{d^qf(t)}{dt^q}\right\} =S^qL\left\{ f(t) \right\} \end{aligned} \end{aligned}$$
(7)

Hence, the transfer function that represents the fractional integral operator of order q, can be expressed as \(F(S)=\frac{1}{S^q}\) in the frequency domain.

4 New Fractional Order Chaotic System (FOCS)

This section is dedicated to deriving the fractional order of the chaotic system (1) model. Specifically, we will be defined as:

$$\begin{aligned} \begin{aligned} D^qx&= az \\ D^qy&= -z(xz+y^2) \\ D^qz&= f(x,y)+z(cy^2-az^2-bx^2+x) \end{aligned} \end{aligned}$$
(8)

Where q is the fractional order that satisfies \(0\preceq q\preceq 1\) and the parameter a,b and c.

Fig. 2
figure 2

Shows the behavior of the state variables in the chaotic system CS-1, with a fractional order of q=0.98. Specifically, a and b depict the signals of x and z respectively, although c presents the z–x plane phase portraits

Full size image

In this work, different methods can be used to show the oscillator is chaotic dynamics for the parameter and initial condition given in Table 1. When q = 0.97, the numerical simulation time series and phase portrait of the chaotic systems are shown in Fig. 2. The LEs of the oscillator in the mentioned parameters are calculated with a run time of 20,000 using Wolf’s algorithm [40] and modified wolf algorithms [41]. The largest positive Lyapunov exponent of the fractional order chaotic systems appears when q = 0.97. The LEs is obtained as shown in Table 2. The chaotic dynamic is dissipative since the sum of LEs is negative. As a result, the oscillator has dissipation; i.e., energy is losing when time goes to infinity.

5 Dynamic Analysis of FOCS

Generally, the phase portrait, bifurcation diagrams and Lyapunov spectrum are the basic dynamical tools that may be utilized to examine the dynamical behaviors of nonlinear chaotic systems [30].This part uses MATLAB to explore numerically the phase portrait, bifurcation diagrams and the Lyapunov exponents.

Table 2 Lyapunov exponents and the types of systems
Full size table

5.1 Phase Portrait

Using the parameter values and initial conditions provided in table 1, the chaotic oscillations of the curved equilibrium system (CS-2) begin at a fractional order of q = 0.967. I could observe during the order q = 0.94, Fig. 3a shows the phase portrait of the periodic oscillation till the order q = 0.952 we can see the period doubling range. Figure 3b shows 2 period oscillation of the order 0.97. Figure 3c shows the clear chaotic attractor for order q = 0.98.

Fig. 3
figure 3

Scenario of attractor for system (CS-2) a for q = 0.94 (periodic) b for q = 0.952 (period doubling), c for q = 0.97 (chaos)

Full size image

5.2 Bifurcation

In order to examine the system’s dynamical behavior, we utilized nonlinear functions CS-1 and CS-2 and studied the impact of parameter variations on the system. Figure 4 displays the obtained bifurcation diagrams for the system, with respect to parameters a, b, and a nonlinear function of CS-1 and CS-2, respectively. As seen in Fig. 4a, systems can form limit cycles, which are then driven to chaos via the period doubling process, as the values of b vary from 2 to 7.5 the CS-1 system shows chaotic regions for \(2.91 \prec b \prec 3, 3.15 \prec b \prec 3.35, 3.45 \prec b \prec 3.6, 3.62 \prec b \prec 3.8, 4.05 \prec b \prec 4.9,\) and \(4.98 \prec b \prec 7.1\).

Fig. 4
figure 4

Bifurcation diagram of x verses parameters of system (8) for a CS-1 and b CS-2

Full size image

Similarly as shown in Fig. 4b, as the values of a changes from 0.1 to 0.75 the CS-2 system exhibits areas of chaos for \(0.158 \prec a \prec 0.169, 0.18 \prec a \prec 0.2, 0.22 \prec a \prec 0.36, 0.38 \prec a \prec 0.45, 0.48 \prec a \prec 0.55,\) and \(0.56< a < 0.58.\)

5.3 Lyapunov Spectrum

Figure 5 demonstrates the equivalent Lyapunov spectrum of chaotic systems with various geometries of equilibrium. The Lyapunov spectrum is used to differentiate between chaotic, periodic, and stable system states.

Fig. 5
figure 5

Lyapunov spectra of system (8) verses parameters for a CS-1 and b CS-2

Full size image

6 Circuit Implementation of the FOCS of CS-1

The use of fractional operators in Engineering and circuit designs is limited due to the lack of an accepted definition for fractional differ-integrals but the Laplace transformation is used to solve linear differential equations precisely and in frequency response analysis techniques [43]. However, Ref. [44] it is proposed Approximating fractional operators using conventional integer-order operators is a feasible solution for this problem.

Fig. 6
figure 6

Chain circuit diagram of \(\frac{1}{S^{0.98}}\)

Full size image

Approximations of \(\frac{1}{S^q}\) with order of q is between 0.1and 0.9 with increment of 0.1 were provided at Table 1 of Ref. [45] with inaccuracies of about 2 dB. These approximations will be used for subsequent electronic circuit and simulation tests that follow. When q = 0.98, it can be calculated that the approximation formula of \(\frac{1}{S^{0.98}}\) is as follow:

$$\begin{aligned} \begin{aligned} \frac{1}{S^{0.98}}=\frac{1.2974(S+1125)}{(S+1423)(S+0.01125)} \end{aligned} \end{aligned}$$
(9)

Where s = jw, its complex frequency and their circuit diagram is display in Fig. 6. The transfer function of chain circuit diagram can be calculated as (10), by Taking \(C_o= 1\mu F\). Since \(H(S)C_o= \frac{1}{S^{0.98}}\)

$$\begin{aligned} \begin{aligned}&{{H}_{0.98}}\left( s \right) =\frac{{{R}_{1}}}{s{{R}_{1}}{{C}_{1}}+1}+\frac{{{R}_{2}}}{s{{R}_{2}}{{C}_{2}}+1} \\&\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\frac{1}{{{C}_{o}}}\frac{\left( \frac{{{c}_{o}}}{{{c}_{1}}}+\frac{{{c}_{o}}}{{{c}_{2}}} \right) [s+\frac{\frac{1}{{{R}_{1}}}+\frac{1}{{{R}_{2}}}}{{{c}_{1}}+{{c}_{2}}}]}{\left( s+\frac{1}{{{R}_{1}}{{C}_{1}}} \right) \left( s+\frac{1}{{{R}_{2}}{{C}_{2}}} \right) } \\ \end{aligned} \end{aligned}$$
(10)

In order to validate the theoretical models of FOCS (8) model with a nonlinear function CS-1, this part provides the MultiSIM design of an analogue circuit.The aim of this design is to achieve a practical implementation of the system and compare the theoretical outcomes of the state variable time series and phase portrait of the fractional-order chaotic system (8) using a nonlinear function CS-1, as shown in Fig. 2 for q = 0.98. The circuit design mainly consists of three integrators (U1, U3, U4), two inverters (U2, U5), fourteen multipliers AD633JN and operational amplifier is 741, and the supply power is \(\pm 15 V.\)

Fig. 7
figure 7

Electronic circuit implementation of the propose FOCS (8) of CS-1 for q = 0.98

Full size image

The value of electronic components used for the circuit elements were chosen as follows:\(R_1=R_2=R_4=R_6=R_7=R_8=R_{10}=R_{15}=100\,k\Omega ,V_1=1VDC,R_5=R_{12}=12.5\,k\Omega ,R_9=10\,k\Omega ,R_{11}=9.09\,k\Omega ,R_{13}=22.221\,k\Omega ,R_{14}=50\,k\Omega\) and Box A is shown in Fig. 6, has a value of \(R_1=R_2=500\,k\Omega ,C_1=C_2=1nF\). The circuit design for the FOCS is showed in Fig. 7 and the experimental circuit design on bread board is showed in Fig. 8 and the state variable signals and phase portrait obtained is shown in Fig. 9.

Fig. 8
figure 8

The experimental setup of the propose FOCS (8) of CS-1 for q = 0.98

Full size image
Fig. 9
figure 9

State variable signals obtained from the electronic circuit-based design of a fractional-order system (8) with CS-1 observed for a signals for variables x, b signals for variables y, and c phase portrait

Full size image

7 Sound Encryption Scheme Based on FOCS

A voice-based communication is becoming increasingly more common, the efficient and secure communication design is a new challenge for researcher to protect these signals from an unauthorized third party. Naturally the speech signal values and positions for neighboring samples are highly correlated. In order to break this correlation, there are literatures based on fractional order chaos based secured communication [29, 46,47,48]. In this article we propose FOCS based secure communication algorithm to breaks the correlation of samples of speech signals by using two levels of encryption techniques.

Figure 10. illustrates the architecture of the propose sound encryption scheme., First, the original sound signal is masked by using one of the key streams generated by using XOR operation of the random sequence generated from the FOCS (8) of CS-1 as stated in Algorithm 1, and then the masked signal using Algorithm 2 is again encrypted using key streams generated as shown in Fig. 10. The scrambled sound signal is then sent over an unreliable channel to the receiver.

Fig. 10
figure 10

The flowchart for the propose sound encryption method using CS-1 of system (8)

Full size image
Algorithm 1
figure a

Generation of the Pseudo-Random code

Full size image
Algorithm 2
figure b

Proposed a step-by-step sound encryption structure

Full size image

To recover the original sound signal, the decryption process follows the same flow chart and steps as the encryption process. The propose cryptographic algorithm is symmetric and uses the same key for both encryption and decryption of the audio signal. Figure 11 shows the sound decryption flow chart scheme.

Fig. 11
figure 11

The flowchart of the propose sound decryption using CS-1 of the system (8)

Full size image

8 Experimental Results and Security Analysis

The propose cryptosystem is used to encrypt a sound signal and the resulting figures are shown in Fig. 12. The original sound signal is represented by (a), while (b) displays the encrypted sound.

Fig. 12
figure 12

Original sound and encryption signal

Full size image

It is obvious that the encrypted and modulated sound signal is obviously similar to the noise, which indicates that no remaining unambiguousness that helps the hacker at the communication channel. It’s possible that encryption procedures were carried out successfully. However, security evaluations are necessary to determine whether encryption procedures are reliable or not because they are so easily decrypted, encrypted data with poor security analysis results will not be selected. Strong resistance to any quantifiable tests should characterize good encryption. The initial group of tests should include statistical analyses, such as (i) histogram, (ii) correlation, and (iii) spectrogram [49,50,51].

8.1 Histogram Analysis

A statistical method of describing the audio spreading is the histogram. In order to make the encrypted histogram flat and resistant to cipher attacks, algorithmic encryption is used to mask as many of its properties as feasible [50]. Figure 13c and d display the histograms for sound encryption and their corresponding encrypted histograms, respectively.

Fig. 13
figure 13

Sound signal: a original sound signal; b encrypted sound signal c original sound signal histogram d encrypted sound signal histogram

Full size image

8.2 Correlation Coefficient Analysis(CCA)

The cryptosystem put forth has the capability to assess the effectiveness of encryption against statistical attacks. By illustrating the correlation between the initial samples of segments in a sound signal and the encrypted samples of the same signal, the system can determine the success of the encryption process through the correlation coefficient of analysis (CCA), According to references [52, 53], a correlation coefficient of zero indicates that original signal and encrypted signal are entirely unrelated.

$$\begin{aligned} \begin{aligned} r_{xy} =\frac{Cov(x,y)}{ \sqrt{D(x)} \sqrt{D(y)}} \end{aligned} \end{aligned}$$
(11)

where cov (x, y) is the covariance between the original signal x and the encrypted signal y. D (x) and D (y) are the variances of the signals x and y.

Table 3 Displaying the correlation coefficient between original and encrypted sound
Full size table

Table 3 displays the correlation coefficient values of the original and encoded sound signals, as well as a comparison with other techniques. Compared to the methods currently in use [53, 54], this approach exhibits a lower correlation coefficient and stronger encryption techniques.

8.3 Spectrogram Analysis

The Fourier transform is utilized to generate a spectrum diagram of the time domain signal, which depicts how the audio frequency spectrum varies over time. This diagram employs time and frequency as two geometric dimensions to represent the spectrum. To generate a spectrogram, the sampled data is divided into overlapping blocks in the time domain, and the spectrum size of each block is calculated using the Fourier transform. The resulting spectrogram displays the decibels of audio signals at various frequencies and times using different colors [51, 52]. The spectrum diagrams of the encrypted sound signal, decrypted sound, and original sound are presented in Fig. 14. The spectrogram of the encrypted speech, depicted in Fig. 14, exhibits a uniform distribution across all frequencies, which is clearly distinguishable the spectrogram of the original signal.

Fig. 14
figure 14

Displaying the spectrogram of the a original sound signal, b encrypted sound signal, and c decrypted sound signal

Full size image

9 Conclusion

The article introduces a 3D fractional-order chaotic system (FOCS) that exhibits diverse equilibria shapes by incorporating nonlinear functions. The dynamics of the system are analyzed both analytically and numerically under different conditions and parameter values. The outcomes demonstrate that the system possesses a wide range of dynamic behavior and is suitable for sound encryption applications. Hardware compatibility is evaluated by implementing electronic circuitry. Simulation outcomes endorse the efficacy of the proposed 3D chaotic systems in encrypting and decrypting sound signals. To assess the security of the encryption system, histograms, correlation coefficients, and spectrograms are used. MATLAB software is engaged to prove the obtained outcomes.