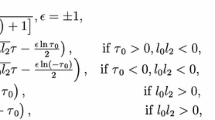1 Introduction

A variety of environmental and physical systems in different areas of science, including engineering, plasma physics, fluid dynamics and chemistry are described in terms of nonlinear partial differential equations (NLPDEs). Exact analytical solutions of NLPDEs in different fields of applied sciences play an important part in interpreting the qualitative nature of numerous processes and the appropriate modeling of associated processes. Additionally, exact solutions help the researchers to develop and perform studies to identify these parameters or functions by setting proper expected settings. Since many mathematical-physical models are also characterized by wave phenomena, a special class of analytical solutions for NLPDEs known as traveling waves is important. As a result, research into traveling wave solutions has become increasingly common in the study of nonlinear problems.

The extended \(\left(\frac{G'}{G^{2}}\right)\)-expansion method is a recently developed mathematical method to construct the traveling wave solutions of nonlinear problems in fluid dynamics, optics, engineering and others areas of science. The extended \(\left(\frac{G'}{G^{2}}\right)-\) expansion method provides a variety of useful traveling wave solutions. It is a modification of the well-known basic \(\left(\frac{G'}{G}\right)\)-expansion method. This novel technique has got the attention of mathematicians and physicists due to it simplicity, efficacy and applicability to handle various nonlinear problems. This manuscript aims to investigate the soliton and other traveling wave solutions of \((2+1)\) dimensional Zoomeron [9] and foam drainage equations [7] using the extended \(\left(\frac{G'}{G^{2}}\right)\)-expansion method.

Calogero and Degasperis [5] were the first to propose solitons that travel at varying speed and noted a correlation between their speed and polarisation effects. This resulted in the formation of a bilateral soliton, with one emerging from one side and coming from a great distance away, defined as a soliton accelerated boomerang to that side at the same speed in the far future, and the other revolving continually around the fixed point as somehow jostled in the direction of a spatial field shift. The coupled boomeron equation and additional unique integrable systems of coupled wave equations were derived from these well-known boomeron and trappon solitons, respectively, in [20]. The nonlinear Zoomeron equation is one of these particular examples of the boomeron equation. It is used to describe boomerons and trappons-related phenomena and shows how a single scalar field evolves.

The symmetry reductions and new group-invariant solutions of \((2+1)\) dimensional Zoomeron equation were presented by utilizing the classical Lie point symmetries [12, 13]. Also the authors in [13] constructed the conservation laws by applying the multiplier method. The integrability of this equation was presented by Painlevé property [14].

The solitary and the periodic wave solutions of \((2+1)\) dimensional Zoomeron equation were explored in [10] with enhanced \(\left(\frac{G'}{G}\right)\)-expansion method. In [1], Reza found some new periodic and soliton solutions using the \(\left(\frac{G'}{G}\right)\)- expansion method. The authors in [2] utilized the extended tanh, the exponential function and the \({sech^{p}}\)-\(tanh^{p}\) function methods to investigate the solutions of Zoomeron equation. Exact traveling wave solutions to the \((2+1)\) dimensional Zoomeron equation were obtained in [9] using modified simple equation method and the exp-function method.

The term foam refers to the solid or liquid formed by holding gas pockets together. Joseph Plateau, the famous physicist, observed this in the 19th century. A key application of NPDE is simulating foam formation. Various applications rely on foams and extensive research is being conducted on their properties in industry and other fields. Among the key questions raised in this area, Weaire et al. found some useful new insights in [18]. However, they did not answer all of the questions, so further studies are needed.

Several manufacturing products for industry contain foam, including personal care items, cosmetics, and cleaning products, as well as equipment used to dispensing and cleaning clothes and dishes. They can be found in acoustic cladding, lightweight mechanical components, and impact-absorbing pieces on automobiles, heat exchangers, and textured wallpapers, and even in cosmology. As in the honeycomb shape of the bees, bubbles or cells can form in a certain pattern or randomly. New types of foam include polymeric foams and metallic foams, which are mostly made of metals like aluminium.

Foams may be used in the listed industrial applications to clean up oil spills and lessen the impact of explosions. Polymeric foams, including those made of glass, ceramic, and metal, are also used in structural engineering and material science as a heat exchanger [3]. Foams are also used in the separation of essential products during the processing of minerals. Foams are used in geophysical applications to describe volcanic explosions.

The foam drainage (FD) equations are used to explain how the vertical foam density increases with gravity acceleration as a NPDE. These investigations are crucial because the FD equation is a straightforward model of the liquid flow in the channels and nodes between the bubbles under the capillarity and gravity influence [11, 17]. The foam drainage equation describes the drainage of liquid in foam for the foam density as a function of vertical position and time. Liquid foams are found all over the world and are formed when gas/liquid systems are used in industrial processes. Flow of liquid from is termed as foam drainage when it flows through the plateau’s boundaries under the action of capillarity and gravity. The symmetric group properties and conservation laws of the FD equation have been studied in [19].

The exact solutions of FD equation has been examined by \(\left(\frac{G'}{G}\right)-\) expansion method [4], the modified simple equation method, the exp-function method, the soliton ansatz method and the Riccati equation expansion method [21]. Combined approximative technique has also been applied to find a numerical solution of the foam drainage equation arising in various absorption and distillation processes [8].

In this work, the traveling wave behavior of the considered models will be examined using the extended \({\left(\frac{G'}{G^{2}}\right)-}\)expansion method. The organization of the manuscript is as follows: In Sect. 2, description of methods have been given. The exact solutions are obtained for NLPDE in Sect. 3. The physical interpretation is given in Sect. 4, and finally the concluding remarks are presented.

2 Outline of the Extended \(\mathbf {\left(\frac{G'}{G^{2}}\right)}\)—Expansion Method

The outline of the method is given as follows:

Step 1:

The general NLPDE with an unknown function \(v=v(x,y,t)\) can be expressed, as

$$\begin{aligned} P(v,v_{x}, v_{y}, v_{t}, v_{xx}, v_{xy}, . . .)=0. \end{aligned}$$
(1)

Equation (1) can be reduced to an ordinary differential equation (ODE), considering the traveling wave transformation

$$\begin{aligned} v(x,y,t)=v(\psi ), ~~~~~\psi =kx + ly\pm ct. \end{aligned}$$
(2)

The resulting ODE can be expressed in the form

$$\begin{aligned} H(v, kv_{\psi },lv_{\psi }, \pm cv_{\psi }, k^{2} v_{\psi \psi },l^{2}k^{2} v_{\psi \psi },...), \end{aligned}$$
(3)

for real constants k, l and c.

Step 2:

According to the extended \(\left(\frac{G'}{G^{2}}\right)\)-expansion method, the the trail solution for Eq. (3) is assumed, as

$$ v(\psi ) = a_{0} + \sum\limits_{{i = 1}}^{{i = n}} {\left[ {a_{i} \left( {\frac{{G^{\prime}}}{{G^{2} }}} \right)^{i} + b_{i} \left( {\frac{{G^{\prime}}}{{G^{2} }}} \right)^{{ - i}} } \right]} , $$
(4)

where \(G=G(\psi )\) satisfies

$$\begin{aligned} \bigg (\frac{G'}{G^{2}}\bigg )^{'}=\nu +\sigma \bigg (\frac{G'}{G^{2}}\bigg )^{2}. \end{aligned}$$
(5)

Here \(\sigma \ne 0\) and \(\nu \ne 1\) are integers, whereas the constants \(a_{i}, b_{i}\); \(i=0,1,2,...,n\) are to be calculated (\(a_{n}\) and \(b_{n}\) cannot be equal to zero simultaneously). The positive integer n can be obtained using the homogeneous balance method [16].

Step 3:

The general solution of Eq. (5) have three possibilities given, as follows:

  • If \(\sigma \nu >0\), then

    $$\begin{aligned} \frac{G'}{G^{2}}=\sqrt{\frac{\nu }{\sigma }}\bigg (\frac{D_{1}\cos (\sqrt{\sigma \nu }\psi )+D_{2}\sin (\sqrt{\sigma \nu }\psi )}{D_{2}\cos (\sqrt{\sigma \nu }\psi )-D_{1}\sin (\sqrt{\sigma \nu }\psi )}\bigg ). \end{aligned}$$
    (6)

  • If \(\sigma \nu <0\), then

    $$\begin{aligned} \frac{G'}{G^{2}}=-\sqrt{\frac{|\nu \sigma |}{\sigma }}\bigg (\frac{D_{1}\cosh (2\sqrt{|\sigma \nu |}\psi )+D_{1}\sinh (2\sqrt{|\sigma \nu |}\psi )+D_{2}}{D_{1}\cosh (2\sqrt{|\sigma \nu |}\psi )+D_{1}\sinh (2\sqrt{|\sigma \nu |}\psi )-D_{2}}\bigg ). \end{aligned}$$
    (7)

  • If \(\sigma \ne 0\) and \(\nu =0\), then

    $$\begin{aligned} \frac{G'}{G^{2}}=-\frac{D_{1}}{\sigma (D_{1}\psi +D_{2})}. \end{aligned}$$
    (8)

Here, \(D_1\) and \(D_2\) are arbitrary constants. The solutions are determined using the values of unknowns \(a_{i},~b_{i},~(i =0,1,2,3,...,n)\) and the general solution of Eq. (5) in Eq. (4).

3 Implementation of the Method

The following subsections present the construction of traveling wave solutions for the two considered models.

3.1 Application of Method to the Zoomeron Equation

The nonlinear \((2+1)\) dimensional Zoomeron equation is given, as

$$\begin{aligned} \bigg (\frac{v_{xy}}{v}\bigg )_{tt}-\bigg (\frac{v_{xy}}{v}\bigg )_{xx}+2(v^{2})_{xt}=0, \end{aligned}$$
(9)

where v(x, y, t) is the amplitude of the relative wave node. The transformation \(v(x,y,t)=v(\psi )\), \(\psi =x+y-wt\) is used to reduce Eq. (9) into an ODE, as

$$\begin{aligned} w^2(\frac{ v'' }{v})^{''}-(\frac{v''}{v})^{''}-2w(v^{2})^{''}=0. \end{aligned}$$
(10)

Integration of Eq. (10) with respect to \(\psi \) twice, yields

$$\begin{aligned} (w^2-1)v''-2wv^{3}+kv=0, \end{aligned}$$
(11)

where k is a constant. Application of the homogeneous balance principle gives \(n=1\). Hence the general solution of the Eq. (11) takes the form

$$\begin{aligned} v(\psi )=a_{0}+a_{1}\big (\frac{G'}{G^{2}}\big )+b_{1}\big (\frac{G'}{G^{2}}\big )^{-1}. \end{aligned}$$
(12)

Eqs. (5, 11 and 12) yields the following algebraic system of equations.

$$\begin{aligned} \left. \begin{array}{rrr} w^{2}b_{1}^2-2wb_{1}^{3}&{}=&{}0,\\ -6wa_{0} b_{1}^{2}&{}=&{}0, \\ (w^{2}-1)2b_{1}\sigma \nu -6 w a_{0}^{2} b_{1}-6wa_{1}b_{1}^{2}+kb_{1}&{}=&{}0, \\ -2wa_{0}^{3}-12wa_{0} b_{1} a_{1}+ka_{0}&{}=&{}0,\\ (w^{2}-1)2a_{1}\sigma \nu -6wa_{0}^{2} a_{1}-6wa_{1}^{2} b_{1}^{2}+ka_{1}&{}=&{}0, \\ -6wa_{0} a_{1}^{2}&{}=&{}0, \\ (w^{2}-1)2a_{1}\sigma ^{2}-2wa_{1}^{3}&{}=&{}0. \end{array}\right\} \end{aligned}$$
(13)

The following set of solutions are found for the system Eq. (13) using the Maple software.

Set 1:

$$\begin{aligned} a_{0}=\pm \frac{\sqrt{14wk}}{14w},~~~a_{1}=\frac{k}{14w},~~~b_{1}=1,~~~\sigma =\frac{k}{14\sqrt{w^{3}-w}},~~~\nu = -\sqrt{\frac{w^{3}-w}{w^{2}-1}}. \end{aligned}$$

Set 2:

$$\begin{aligned} a_{0}=\pm \frac{\sqrt{2wk}}{4w},~~~a_{1}=\frac{k}{16w},~~~b_{1}=1,~~~\sigma =\frac{k}{16\sqrt{w^{3}-w}},~~~\nu = \sqrt{\frac{w^{3}-w}{w^{2}-1}}. \end{aligned}$$

The following solutions are determined for Set 1:

Case 1: For \(\sigma \nu >0\), solutions in terms of trigonometric functions are obtained, as

$$\begin{aligned} v_{1}(x,y,t)= & {} \pm \frac{\sqrt{14wk}}{14w}+\frac{k}{14w}\sqrt{\frac{-14w}{k}}\bigg (\frac{D_{1}\cos (\sqrt{\nu \sigma }\psi )+D_{2}\sin (\sqrt{\nu \sigma }\psi )}{D_{2}\cos (\sqrt{\nu \sigma }\psi )-D_{1}\sin (\sqrt{\nu \sigma }\psi )}\bigg )\nonumber \\&+\sqrt{\frac{-k}{14w}}\bigg (\frac{D_{1}\cos (\sqrt{\nu \sigma }\psi )+D_{2}\sin (\sqrt{\nu \sigma }\psi )}{D_{2}\cos (\sqrt{\nu \sigma }\psi )-D_{1}\sin (\sqrt{\nu \sigma }\psi )}\bigg )^{-1}. \end{aligned}$$
(14)

Case 2: For \(\sigma \nu <0\), solutions in terms of hyperbolic functions are obtained, as

$$\begin{aligned} \begin{aligned} v_{2}(x,y,t)&=\pm \frac{\sqrt{14wk}}{14w}+\frac{k}{14w}\sqrt{\frac{-14w}{k}}\bigg (\frac{D_{1}\cosh (2\sqrt{|\nu \sigma |}\psi )+D_{1}\sinh (2\sqrt{|\nu \sigma |}\psi )+D_{2}}{D_{1}\cosh (2\sqrt{|\nu \sigma |}\psi )+D_{1}\sinh (2\sqrt{|\nu \sigma |}\psi )-D_{2}}\bigg ) \\ {}&+\sqrt{\frac{-k}{14w}}\bigg (\frac{D_{1}\cosh (2\sqrt{|\nu \sigma |}\psi )+D_{1}\sinh (2\sqrt{|\nu \sigma |}\psi )+D_{2}}{D_{1}\cosh (2\sqrt{|\nu \sigma |}\psi )+D_{1}\sinh (2\sqrt{|\nu \sigma |}\psi )-D_{2}}\bigg )^{-1}. \end{aligned} \end{aligned}$$
(15)

Case 3: For \(\nu =0\) and \(\sigma \ne 0\), solutions are determined, as

$$\begin{aligned} v_{3}(x,y,t)=\pm \frac{\sqrt{14wk}}{14w}+\frac{k}{14w}\bigg (\frac{-D_{1}}{\sigma (D_{1}\psi +D_{2})}\bigg )+\bigg (\frac{-D_{1}}{\sigma (D_{1}\psi +D_{2})}\bigg )^{-1}. \end{aligned}$$
(16)
Fig. 1
figure 1

a Graph of \(v_{1}(x, y, t)\), b Corresponding contour plot

Full size image
Fig. 2
figure 2

a Graph of \(v_{2}(x,y,t)\), b Corresponding contour plot

Full size image
Fig. 3
figure 3

a Graph of \(v_{3}(x,y,t)\), b Corresponding contour plot

Full size image

The following solutions are determined for Set 2 : 

Case 1: For \(\sigma \nu >0\), solutions in terms of trigonometric functions are obtained, as

$$\begin{aligned} v_{4}(x,y,t)= & {} \pm \frac{\sqrt{2wk}}{4w}+\frac{k}{4w}\sqrt{\frac{w}{k}}\bigg (\frac{D_{1}\cos (\sqrt{\nu \sigma }\psi )+D_{2}\sin (\sqrt{\nu \sigma }\psi )}{D_{2}\cos (\sqrt{\nu \sigma }\psi )-D_{1}\sin (\sqrt{\nu \sigma }\psi )}\bigg )\nonumber \\&+\frac{1}{4}\sqrt{\frac{k}{w}}\bigg (\frac{D_{1}\cos (\sqrt{\nu \sigma }\psi )+D_{2}\sin (\sqrt{\nu \sigma }\psi )}{D_{2}\cos (\sqrt{\nu \sigma }\psi )-D_{1}\sin (\sqrt{\nu \sigma }\psi )}\bigg )^{-1}. \end{aligned}$$
(17)

Case 2: For \(\sigma \nu <0\), solutions in terms of hyperbolic functions are obtained, as

$$\begin{aligned} \begin{aligned} v_{5}(x,y,t)&=\pm \frac{\sqrt{2wk}}{4w}+\frac{k}{4w}\sqrt{\frac{w}{k}}\bigg (\frac{D_{1}\cosh (2\sqrt{|\nu \sigma |}\psi )+D_{1}\sinh (2\sqrt{|\nu \sigma |}\psi )+D_{2}}{D_{1}\cosh (2\sqrt{|\nu \sigma |}\psi )+D_{1}\sinh (2\sqrt{|\nu \sigma |}\psi )-D_{2}}\bigg )\;\;\; \\ {}&+\frac{1}{4}\sqrt{\frac{k}{w}}\bigg (\frac{D_{1}\cosh (2\sqrt{|\nu \sigma |}\psi )+D_{1}\sinh (2\sqrt{|\nu \sigma |}\psi )+D_{2}}{D_{1}\cosh (2\sqrt{|\nu \sigma |}\psi )+D_{1}\sinh (2\sqrt{|\nu \sigma |}\psi )-D_{2}}\bigg )^{-1}. \end{aligned} \end{aligned}$$
(18)

Case 3: For \(\nu =0\) and \(\sigma \ne 0\), solutions are determined, as

$$\begin{aligned} v_{6}(x,y,t)=\pm \frac{\sqrt{2wk}}{4w}+\frac{k}{16w}\bigg (\frac{-D_{1}}{\sigma (D_{1}\psi +D_{2})}\bigg )+\bigg (\frac{-D_{1}}{\sigma (D_{1}\psi +D_{2})}\bigg )^{-1}. \end{aligned}$$
(19)
Fig. 4
figure 4

a Graph of \(v_{4}(x,y,t)\), b Corresponding contour plot

Full size image
Fig. 5
figure 5

a Graph of \(v_{5}(x,y,t)\), b Corresponding contour plot

Full size image
Fig. 6
figure 6

\(v_{6}(x,y,t):\) a 3D surface graph, b Corresponding contour plot

Full size image

3.2 Application of Method to Foam Drainage Equation

The nonlinear foam drainage equation can be expressed, as

$$\begin{aligned} \frac{\partial v}{\partial t}+\frac{\partial }{\partial x}\bigg (v^{2}-\frac{\sqrt{v}}{2}\frac{\partial v}{\partial x}\bigg )=0, \end{aligned}$$
(20)

where v shows the cross-section of a channel made at the point of intersection of three films. The transformation \(v(x,t)=v(\psi ), ~\psi =\gamma (x+\omega t)\) is used to reduce Eq. (20) into an ODE, as

$$\begin{aligned} \gamma \omega \frac{\partial v}{\partial \psi }+\gamma \frac{\partial }{\partial \psi }\bigg (v^{2}-\frac{\gamma }{2}\sqrt{v}\frac{\partial v}{\partial \psi }\bigg )=0, \end{aligned}$$
(21)

where \(\gamma \) and \(\omega \) are unknown constants. Integration of Eq. (21) yields

$$\begin{aligned} \gamma \omega v+ \gamma \bigg (v^{2}-\frac{\gamma }{2}\sqrt{v}\frac{\partial v}{\partial \psi }\bigg )=0, \end{aligned}$$
(22)

where the constant of integration is taken as zero. By substituting \(v(\psi )=v^{2}(\psi )\), the following relation is obtained.

$$\begin{aligned} \gamma \omega v^{2}+ \gamma \bigg (v^{4}-\frac{\gamma }{2}v(2vv^{'})\bigg )=0. \end{aligned}$$
(23)

Simplification of Eq. (23) yields

$$\begin{aligned} \omega -v^{2}+\gamma v^{'}=0. \end{aligned}$$
(24)

Using the homogeneous balance principle, the trail solution for Eq. (24) is considered, as

$$\begin{aligned} v(\psi )=a_{0}+a_{1}\big (\frac{G'}{G^{2}}\big )+b_{1}\big (\frac{G'}{G^{2}}\big )^{-1}. \end{aligned}$$
(25)

Eqs.(5, 24 and 25) provide the following of algebraic equations.

$$\begin{aligned} \left. \begin{array}{rrr} b_{1}^{2}+\gamma b_{1}\nu &{}=&{}0,\\ 2a_{0} b_{1}&{}=&{}0, \\ \omega +a_{0}^{2}+2b_{1} a_{1}-\gamma a_{1}\nu -\gamma b_{1} \sigma &{}=&{}0, \\ 2a_{0} a_{1}&{}=&{}0, \\ a_{1}^{2}+\gamma a_{1}\sigma &{}=&{}0. \end{array}\right\} \end{aligned}$$
(26)

The solution of the system Eq. (26) provides the following sets.

Set 1:

$$\begin{aligned} a_{0}=0,~~a_{1}= a_{1},~~ b_{1}=\frac{-\omega }{2a_1},~~\sigma =\frac{a_1}{\gamma },~~\nu =\frac{\omega }{2a_1\gamma }. \end{aligned}$$

Set 2:

$$\begin{aligned} a_{0}=a_{0},~~a_{1}= \sigma \gamma ,~~b_{1}=-\nu \gamma ,~~\sigma =\sigma ,~~\nu =\nu . \end{aligned}$$

Set 3:

$$\begin{aligned} a_{0}=0~~,a_{1}=\frac{-\sqrt{\sigma \omega }}{2\nu },~~ b_{1}=\sqrt{\frac{\nu \omega }{2\sigma }},~~\sigma =\sigma ,~~\nu =\nu ,~~\gamma =-\sqrt{\frac{\omega }{2\nu \sigma }}. \end{aligned}$$

Corresponding to Set 1, the following results are retrieved.

Case 1: The trigonometric function solutions are retrieved for \(\nu \sigma >0\), as

$$\begin{aligned} v_{7}(x,t)= & {} \sqrt{\frac{\omega }{2}}\bigg \{\bigg (\frac{D_{1}\cos (\sqrt{\nu \sigma }\psi )+D_{2}\sin (\sqrt{\nu \sigma }\psi )}{D_{2}\cos (\sqrt{\nu \sigma }\psi )-D_{1}\sin (\sqrt{\nu \sigma }\psi )}\bigg )\nonumber \\&-\bigg (\frac{D_{1}\cos (\sqrt{\nu \sigma }\psi )+D_{2}\sin (\sqrt{\nu \sigma }\psi )}{D_{2}\cos (\sqrt{\nu \sigma }\psi )-D_{1}\sin (\sqrt{\nu \sigma }\psi )}\bigg )^{-1}\bigg \}. \end{aligned}$$
(27)

Case 2: The hyperbolic function solutions are retrieved for \(\sigma \nu <0\), as

$$\begin{aligned} \begin{aligned} v_{8}(x,t)&=-\sqrt{\frac{\omega }{2}}\bigg \{\bigg (\frac{D_{1}\cosh (2\sqrt{|\nu \sigma |}\psi )+D_{1}\sinh (2\sqrt{|\nu \sigma |}\psi )+D_{2}}{D_{1}\cosh (2\sqrt{|\nu \sigma |}\psi )+D_{1}\sinh (2\sqrt{|\nu \sigma |}\psi )-D_{2}}\bigg ) \;\;\;\\ {}&-\bigg (\frac{D_{1}\cosh (2\sqrt{|\nu \sigma |}\psi )+D_{1}\sinh (2\sqrt{|\nu \sigma |}\psi )+D_{2}}{D_{1}\cosh (2\sqrt{|\nu \sigma |}\psi )+D_{1}\sinh (2\sqrt{|\nu \sigma |}\psi )-D_{2}}\bigg )^{-1}\bigg \}. \end{aligned} \end{aligned}$$
(28)

Case 3: The solutions in this case are retrieved for \(\nu =0\) and \(\sigma \ne 0\), as

$$\begin{aligned} v_{9}(x,t)=a_{1}\bigg (\frac{-D_{1}}{\sigma (D_{1}\psi +D_{2})}\bigg )-\frac{\omega }{2a_{1}}\bigg (\frac{-D_{1}}{\sigma (D_{1}\psi +D_{2})}\bigg )^{-1}. \end{aligned}$$
(29)
Fig. 7
figure 7

a Graph of \(v_{7}(x,t)\), b Corresponding contour plot

Full size image
Fig. 8
figure 8

a Graph of \(v_{8}(x,t)\), b Corresponding contour plot

Full size image
Fig. 9
figure 9

a Graph of \(v_{9}(x,t)\), b Corresponding contour plot

Full size image

Corresponding to Set 2, the following results are retrieved.

Case 1: The trigonometric function solutions are retrieved for \(\nu \sigma >0\), as

$$\begin{aligned} v_{10}(x,t)=\; & {} a_{0}+\gamma \sqrt{\sigma \nu }\bigg \{\bigg (\frac{D_{1}\cos (\sqrt{\nu \sigma }\psi )+D_{2}\sin (\sqrt{\nu \sigma }\psi )}{D_{2}\cos (\sqrt{\nu \sigma }\psi )-D_{1}\sin (\sqrt{\nu \sigma }\psi )}\bigg )\nonumber \\&-\bigg (\frac{D_{1}\cos (\sqrt{\nu \sigma }\psi )+D_{2}\sin (\sqrt{\nu \sigma }\psi )}{D_{2}\cos (\sqrt{\nu \sigma }\psi )-D_{1}\sin (\sqrt{\nu \sigma }\psi )}\bigg )^{-1}\bigg \}. \end{aligned}$$
(30)

Case 2: The hyperbolic function solutions are retrieved for \(\sigma \nu <0\), as

$$\begin{aligned} \begin{aligned} v_{11}(x,t)&=a_{0}+\gamma \sqrt{\sigma \nu }\bigg \{\bigg (\frac{D_{1}\cosh (2\sqrt{|\nu \sigma |}\psi )+D_{1}\sinh (2\sqrt{|\nu \sigma |}\psi )+D_{2}}{D_{1}\cosh (2\sqrt{|\nu \sigma |}\psi )+D_{1}\sinh (2\sqrt{|\nu \sigma |}\psi )-D_{2}}\bigg ) \\ {}&-\bigg (\frac{D_{1}\cosh (2\sqrt{|\nu \sigma |}\psi )+D_{1}\sinh (2\sqrt{|\nu \sigma |}\psi )+D_{2}}{D_{1}\cosh (2\sqrt{|\nu \sigma |}\psi )+D_{1}\sinh (2\sqrt{|\nu \sigma |}\psi )-D_{2}}\bigg )^{-1}\bigg \}. \end{aligned} \end{aligned}$$
(31)

Case 3: The rational function solutions are retrieved for \(\nu =0\) and \(\sigma \ne 0\), as

$$\begin{aligned} v_{12}(x,t)=a_{0}+\sigma \gamma \bigg (\frac{-D_{1}}{\sigma (D_{1}\psi +D_{2})}\bigg )-\nu \gamma \bigg (\frac{-D_{1}}{\sigma (D_{1}\psi +D_{2})}\bigg )^{-1}. \end{aligned}$$
(32)
Fig. 10
figure 10

a Graph of \(v_{10}(x,t)\), b Corresponding contour plot

Full size image
Fig. 11
figure 11

a Graph of \(v_{11}(x,t)\), b Corresponding contour plot

Full size image
Fig. 12
figure 12

a Graph of \(v_{12}(x,t)\), b Corresponding contour plot

Full size image

Corresponding to Set 3, the following solutions are obtained.


Case 1: The trigonometric function solutions are retrieved for \(\nu \sigma >0\), as

$$\begin{aligned} v_{13}(x,t)= & {} -\sqrt{\frac{\omega }{2}}\bigg \{\bigg (\frac{D_{1}\cos (\sqrt{\nu \sigma }\psi )+D_{2}\sin (\sqrt{\nu \sigma }\psi )}{D_{2}\cos (\sqrt{\nu \sigma }\psi )-D_{1}\sin (\sqrt{\nu \sigma }\psi )}\bigg )\nonumber \\&-\bigg (\frac{D_{1}\cos (\sqrt{\nu \sigma }\psi )+D_{2}\sin (\sqrt{\nu \sigma }\psi )}{D_{2}\cos (\sqrt{\nu \sigma }\psi )-D_{1}\sin (\sqrt{\nu \sigma }\psi )}\bigg )^{-1}\bigg \}. \end{aligned}$$
(33)

Case 2: The hyperbolic function solutions are retrieved for \(\sigma \nu <0\), as

$$\begin{aligned} \begin{aligned} v_{14}(x,t)&=\sqrt{\frac{\omega }{2}}\bigg \{\bigg (\frac{D_{1}\cosh (2\sqrt{|\nu \sigma |}\psi )+D_{1}\sinh (2\sqrt{|\nu \sigma |}\psi )+D_{2}}{D_{1}\cosh (2\sqrt{|\nu \sigma |}\psi )+D_{1}\sinh (2\sqrt{|\nu \sigma |}\psi )-D_{2}}\bigg )\\&-\bigg (\frac{D_{1}\cosh (2\sqrt{|\nu \sigma |}\psi )+D_{1}\sinh (2\sqrt{|\nu \sigma |}\psi )+D_{2}}{D_{1}\cosh (2\sqrt{|\nu \sigma |}\psi )+D_{1}\sinh (2\sqrt{|\nu \sigma |}\psi )-D_{2}}\bigg )^{-1}\bigg \}. \end{aligned} \end{aligned}$$
(34)

Case 3: The rational function solutions are retrieved for \(\nu =0\) and \(\sigma \ne 0\), as

$$\begin{aligned} v_{15}(x,t)=-\sqrt{\frac{\sigma \omega }{2\nu }}\bigg (\frac{-D_{1}}{\sigma (D_{1}\psi +D_{2})}\bigg )-\bigg (\frac{-D_{1}}{\sigma (D_{1}\psi +D_{2})}\bigg )^{-1}. \end{aligned}$$
(35)
Fig. 13
figure 13

a Graph of \(v_{13}(x,t)\), b Corresponding contour plot

Full size image
Fig. 14
figure 14

a Graph of \(v_{14}(x,t)\), b Corresponding contour plot

Full size image

4 Physical Interpretation

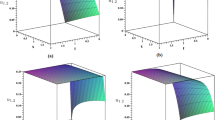
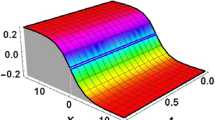
The graphs of the constructed traveling wave solutions demonstrate the properties of wave propagation that may arise in the dynamical framework of the governing equations. The constructed wave solutions are illustrated in Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14. The solutions obtained are rational, trigonometric and hyperbolic functions. For suitable choice of parameters kink, singular soliton, periodic soliton and lump-like soliton obtained using extended \(\left(\frac{G'}{G^{2}}\right)\)-expansion method. The plots depict the wave behavior as shown by the 3D surface graphs and the corresponding 2D contour plots. Contour graphics provide a complete 2D surface distribution, these graphics provide a more comprehensive data set. Solutions that are obtained for the considered nonlinear models show the effectiveness of the extended \(\left(\frac{G'}{G^{2}}\right)\)-expansion method. Figures 3(a), 6(a), 8(a), 11(a) and 14(a) show singular soliton solutions. Figures 2(a) and 5(a) show kink solutions. Figure 9(a) shows lump-like soliton. Figures 1(a), 4(a), 7(a), 10(a), 12(a) and 13(a) show periodic soliton solutions.

The obtained results are novel and provide deeper insight into the dynamical framework of the considered nonlinear equations as compared to the results available in literature. The established exact solitary wave solutions are important to induce new experiments to enhance the theory of foams and boomerons. These results can serve as a prototype to understand various other nonlinear differential equations and the governing physical systems.

A detailed review of the foam drainage equation, its various solutions and their physical relevance through experiments has been presented by Verbist et al. [15]. They considered a few known solitary wave solutions of the foam drainage equation. The authors reviewed the solutions and interpreted the analytical solutions by establishing their physical relevance through analysis and suggested experiments. Some interesting analytic results for the foam drainage equation have been presented by Cox et al. [6]. They also examined the solitary wave behavior of the foam drainage phenomena. The initial condition was taken by inclusion of the equilibrium distribution of the liquid fraction and the resulting solitary wave was examined. Some generalizations of the foam drainage equation were also proposed to account for the different physical systems involving liquid drainage through foam. In this manuscript, we have successfully retrieved a variety of traveling and solitary wave solutions of the foam drainage equation. The obtained results go beyond the ones discussed in [6] and [15]. The graphical simulations of the theoretical results indicate that different types of wave behavior is possible for the foam drainage. These solutions provide a basis for physicists to design new experimentations with suitable initial conditions as suggested by the obtained solution expressions.

Similarly, the solutions retrieved for the Zoomeron equation will be helpful to conduct new numerical and laboratory experiments for a deeper insight into the possible physical changes.

5 Conclusion

In this paper, the nonlinear \((2+1)\)-dimensional Zoomeron equation and foam drainage equation are investigated using the extended \(\left(\frac{G'}{G^{2}}\right)\)-expansion method. This approach is dependable and simple to use, and it offers a diverse range of options. The proposed technique is employed to retrieve the traveling wave solutions of the considered equations including hyperbolic, rational and trigonometric function solutions. These wave solutions are important to understand the wave behavior of nonlinear physical phenomena. It is worth-mentioning that the considered models are examined by employing the extended \(\left(\frac{G'}{G^{2}}\right)\)-expansion method for the first time in this work to the best of our knowledge. It is observed the proposed technique provides novel solutions as compared to the previously reported results. The graphical illustration of the obtained solutions shows a variety of soliton solutions. Khan examined periodic wave solutions and the bell-shaped profile by applying MSE method and exp-function method [9] and foam drainage equation is examined by Rani to obtain soliton solutions using \(\left(\frac{G'}{G}\right)\)-expansion method [4], whereas in this work new soliton solutions are obtained such as kink, lump-like soliton and singular soliton. The obtained soliton solutions may be helpful to provide a deeper insight into the nonlinear physical phenomena described by the governing equations. In future, the traveling wave solutions of higher order generalizations of the foam drainage equation suggested by Cox et al. [6] may be explored. The two-dimensional equation may be examined to understand the drainage of liquid through a two-dimensional slice of foam. The three-dimensional foam drainage equation will be useful to interpret the experiments conducted for foam drainage in circular tubes.