Numerical Solution of Reaction–Diffusion Equations with Convergence Analysis

Abstract

In this manuscript, we implement a spectral collocation method to find the solution of the reaction–diffusion equation with some initial and boundary conditions. We approximate the solution of equation by using a two-dimensional interpolating polynomial dependent to the Legendre–Gauss–Lobatto collocation points. We fully show that the achieved approximate solutions are convergent to the exact solution when the number of collocation points increases. We demonstrate the capability and efficiency of the method by providing four numerical examples and comparing them with other available methods.

1 Introduction

One of the special cases of partial differential equations (PDEs) is reaction diffusion equation (RDE) that has attracted the attention of many researchers, recently [1, 20, 28, 32, 33]. RDEs are the mathematical models which correspond with physical and chemical phenomena. Often, it is the change in space and time in viscosity of one and more chemical materials: chemical reactions in which the materials converted in each other, and diffusion which causes the materials to extend over a surface in space. RDEs are also applied in sciences such that biology [14], geology [15], ecology [20] and physics [23].

The general form of RDEs can be described as follows

$$\begin{aligned} u_{t}(t,x)=Ku_{xx}(t,x)+g(t,x,u(t,x)), \end{aligned}$$

(1)

and here we can consider the following initial and boundary conditions

$$\begin{aligned} {\left\{ \begin{array}{ll} u(t,0)=\varphi _{1}(t),\\ u(t,L)=\varphi _{2}(t), \quad (t,x)\in [0,T]\times [0,L],\\ u(0,x)=\varphi _{3}(x), \end{array}\right. } \end{aligned}$$

(2)

where K is the diffusion coefficient, $\varphi _{1}:[0,T]\rightarrow {{\mathbb {R}}}$, $\varphi _{2}:[0,T]\rightarrow {{\mathbb {R}}}$ and $\varphi _{3}:[0,L]\rightarrow {{\mathbb {R}}}$ are given sufficiently smooth functions. The target of this manuscript is to present an effective numerical method for solving the RDE (1) with conditions (2) and to analyze the convergence of the method.

There are several methods for solving this class of PDEs such as traveling wave method [19], finite elements [6], fixed-node finite-difference schemes [7] and spectral methods [4]. One of other methods for solving RDE presented by Reitz [22]. He applied different several methods for solving RDE. His methods had good numerical stability and can be used for multidimensional cases. Sharifi and Rashidian [24] applied an explicit finite difference associated with extended cubic B-spline collocation method for solving RDEs. Wang et al. [27] used the compact boundary value method (CBVM) for solving RDE. Their method is the combination of compact fourth-order differential method (CFODM) and P-order boundary value method (POBVM). This method is locally stable and have unique solution. Furthermore this method have fourth-order accuracy in space and P-order accuracy in place. Wu et al. [29] applied variational iteration method (VIM) for structuring integral equations to solve RDE. In this method, Lagrange multipliers and a discrete numerical integral formula are used to solve RDE. This method for first time was proposed by He [11]. Biazar and Mehrlatifan [3] solved RDE using the compact finite difference method. Diaz and Puri [8] applied the explicit positivity-preserving finite-difference method for solving RDE. Lee et al. [17] in their work investigated and found exact solutions of derivative RD system and next they showed some exact solutions of derivative nonlinear Schr$\ddot{\mathrm{o}}$dinger equation ( DNLS) via Hirota bilinearization method. Gaeta and Mancinelli [9] analyzed the asymptotic scaling properties of anomalous RDE. Their numerical results showed that for large t, well defined scaling properties. Another method for solving RDE is lifted local Galerkin which was presented by Xiao et al. [30]. Yi and Chen [31] introduced a new method based on repeated character maping of traveling wave for solving RDE. Toubaei et al. [26] represented one of the most applied functions of RDE in chemistry and biologic sciences in their paper and then they solved RDE by using collocation methods and finite differences methods. Koto [16] applied the implicit-explicit Range–Kutta method for RDE. Diaz [7] utilized a logarithmic numerical model. He considered the monotonousness, bounding and positiveness of approximations in following of his work and for first time he showed that the logarithmic designs are stable and convergent. The nonclassical symmetries method is used by Hashemi and Nucci [10] to solve the diffusion reaction equations. An et al. [2] suggested a method to compute the numerical approximation for both solutions and gradients, while the other methods can also compute the numerical solutions. Moreover, in this method they computed the element by element instead of solving the whole of system that this can decrease the expenses of computations.

Despite the existence of above-mentioned numerical methods , providing a numerical convergent method with simple structure and high accuracy, for solving RDEs, is still required. Hence, we extend a spectral collocation method to estimate the solution of RDEs. Spectral methods are one of the most powerful methods for solving the ordinary and partial differential equations [5, 25]. In this method, we apply a two-dimensional Lagrange interpolating polynomial to estimate the solution of the RDE. We apply the Legendre–Gauss–Lobatto (LGL) nodes as interpolating or collocation points and convert the RDE with its initial and boundary conditions into a system of algebraic equations. By solving this system, the coefficients of interpolating polynomial can be gained. We fully show that the approximate solutions are convergent to the exact solution when the number of collocation points tends to infinity. Note that spectral collocation methods have high accuracy and exponential convergence and, up to now many researchers utilized them to solve different continuous-time problems involving the ordinary and partial differential equations [12, 13, 18].

The paper is structured as follow: in Sect. 2, we implement the spectral collocation method for approximating the solution of RDE. In Sect. 3, we study the convergence of approximations to the exact solution of RDE. In Sect. 4, four numerical examples are given to show the efficiency and accuracy of methods comparing with those of others. Finaly, the conclusions and the suggestions are presented in Sect. 5.

2 Approximating the Solution by Spectral Collocation Method

We approximate the solution of system (1)–(2) as follows

$$\begin{aligned} u(t,x)\simeq u^{N}(t,x)= \sum _{i=0}^{N}\sum ^{N}_{j=0}{\tilde{u}}_{ij}L_{i}(t)L_{j}(x), \end{aligned}$$

(3)

where $L_{r}(t)$ and $L_{r}(x)$ are the Lagrange polynomials and defined as

$$\begin{aligned} L_{m}(t)=\prod _{r=0,r\ne m}^{N}\frac{t-t_{r}}{t_{m}-t_{r}},\quad L_{n}(x)=\prod _{r=0,r\ne n}^{N}\frac{x-x_{r}}{x_{n}-x_{r}}, \end{aligned}$$

(4)

where $\{x_{n}\}_{n=0}^{N}$ and $\{t_{m}\}_{m=0}^{N}$ are shifted LGL points [25] in intervals [0, L] and [0, T] , respectively, and are defined with the following relations

$$\begin{aligned} {\left\{ \begin{array}{ll} x_{n}=\frac{L}{2}(x^{1}_{n}+1), \quad n=0,1,\ldots ,N,\\ t_{m}=\frac{T}{2}(t^{1}_{m}+1),\quad m=0,1,\ldots ,N, \end{array}\right. } \end{aligned}$$

(5)

where $\{x^{1}_{n}\}_{n=0}^{N}$ and $\{t^{1}_{m}\}_{m=0}^{N}$ are the roots of the following polynomial

$$\begin{aligned} W(\zeta )=(1-\zeta ^{2})W'_{N}(\zeta );\quad \zeta \in [-1,1], \end{aligned}$$

where $W_{N}(.)$ is the Legendre polynomial [5] that is defined with the following recurrence formula

$$\begin{aligned} {\left\{ \begin{array}{ll} W_{N+1}(\zeta )=\frac{2N+1}{N+1} \zeta W_{N}(\zeta )-\frac{k}{k+1}W_{N-1}(\zeta ),\\ W_{0}(\zeta )=1,\qquad W_{1}(\zeta )=\zeta . \end{array}\right. } \end{aligned}$$

(6)

According to the approximation (3) we have

$$\begin{aligned} {\left\{ \begin{array}{ll} u_{t}(t,x)\simeq \sum _{i=0}^{N}\sum _{j=0}^{N}{\tilde{u}}_{ij}L'_{i}(t)L_{j}(x),\\ u_{xx}(t,x)\simeq \sum _{i=0}^{N}\sum _{j=0}^{N}{\tilde{u}}_{ij}L_{i}(t)L''_{j}(x). \end{array}\right. } \end{aligned}$$

(7)

The Lagrange polynomials satisfy

$$\begin{aligned} L_{i}(z_{j})={\left\{ \begin{array}{ll} 1, \quad i=j,\\ 0, \quad i\ne j. \end{array}\right. } \end{aligned}$$

(8)

So we can get

$$\begin{aligned} u(t_{m},x_{n})\simeq u_{mn},\quad m,n=0,1,\ldots , N, \end{aligned}$$

(9)

$$\begin{aligned} u_{t}(t_{m},x_{n}) \simeq \sum _{i=0}^{N}\sum _{j=0}^{N}{\tilde{u}}_{ij}L'_{i}(t_{m})L_{j}(x_{n})=\sum _{i=0}^{N}{\tilde{u}}_{in}D_{mi},\quad m,n=0,1,\ldots ,N, \end{aligned}$$

(10)

$$\begin{aligned} u_{xx}(t_{m},x_{n})\simeq \sum _{i=0}^{N}\sum _{j=0}^{N}{\tilde{u}}_{ij}L_{i}(t_{m})L''_{j}(x_{n})=\sum _{j=0}^{N}{\tilde{u}}_{mj}D^{(2)}_{nj};\quad m,n=0,1,\ldots ,N, \end{aligned}$$

(11)

where $D_{mi}$ and $D^{(2)}_{nj}$ are defined as follow

$$\begin{aligned} D_{mi}=L'_{i}(t_{m})={\left\{ \begin{array}{ll} -\frac{2}{T}\frac{N(N+1)}{4},&{} m=i=0,\\ \frac{W_{N}(t_{m})}{W_{N}(t_{i})}\frac{1}{t_{m}-t_{i}},&{} m\ne i,\\ 0,&{} 1\le m=i\le N-1,\\ \frac{2}{T}\frac{N(N+1)}{4},&{} m=i=N, \end{array}\right. } \end{aligned}$$

(12)

and

$$\begin{aligned} D_{nj}^{(2)}=\sum _{p=0}^{N}D_{np}D_{pj}. \end{aligned}$$

(13)

By replacing the relations (9), (10) and (11) in (1) we get

$$\begin{aligned} {\left\{ \begin{array}{ll} \sum _{i=0}^{N}{\tilde{u}}_{in}D_{mi}\simeq \sum _{j=0}^{N}{\tilde{u}}_{mj}D_{nj}^{(2)}+g(t_{m},x_{n},{\tilde{u}}_{mn}),\quad m=1,\ldots ,N, n=1,\ldots ,N-1,\\ {\tilde{u}}_{m0}=\varphi _{1} (t_{m}), {\tilde{u}}_{m1}=\varphi _{2}(t_{m}),\quad m=0,\ldots ,N, \\ {\tilde{u}}_{0n}=\varphi _{3}(x_{n}), n=1,\ldots N-1, \end{array}\right. } \end{aligned}$$

(14)

where ${\tilde{u}}_{mn}$ for $m,n= 0,1,\ldots ,N$ are the unknowns. By solving algebraic system (14), we achieve the point-wise approximate solutions ${\tilde{u}}_{mn}\ (m,n=0,1,\ldots ,N)$ and the continuous approximate solution $u^N(.,.)$ defined by (3).

3 Convergence Analysis

In this section we analyze the convergence of the proposed method. We assume $\Lambda =[0,T]\times [0,L]$ and $C^{k}(\Lambda )$ is the set of all continuously differentiable functions from order k. To check the convergence of the method, we initial with the following definition.

Definition 3.1

The continuous function $F:{{\mathbb {R}}}^{+}\rightarrow {{\mathbb {R}}}^{+}$ with the following properties is called modulus of continuity [21]

• 1. F is increasing,

• 2. $F(y)\rightarrow 0$ as $y\rightarrow 0$,

• 3. $F(y_{1}+y_{2})\le F(y_{1})+F(y_{2})$   for any $y_{1},y_{2}\in {{\mathbb {R}}}$,

• 4. $y\le aF(y)$    for some $a>0$ and $0<y\le 2$ .

A special case for modulus of continuity is

$$\begin{aligned} F(y)=y^{\vartheta }, \qquad 0<\vartheta \le 1. \end{aligned}$$

Here we consider that $O ^{2}$ is unit circle in ${{\mathbb {R}}}^{2}$. The continuous function f on $\Lambda$, accepts F(.) as modulus of continuity when the following is finite

$$\begin{aligned} \vert f(.,.)\vert _{F}=sup \Bigg \{\frac{\vert e(t_{1},x_{1})-e(t_{2},x_{2})\vert }{Y(\Vert (t_{1},x_{1})-(t_{2},x_{2})\Vert _{\infty })}: (t_{1},x_{1}),(t_{2},x_{2})\in \Lambda , (t_{1},x_{1})\ne (t_{2},x_{2}) \Bigg\}, \end{aligned}$$

(15)

where

$$\begin{aligned} \Vert (t_{1},x_{1})-(t_{2},x_{2})\Vert _{\infty }=max\{\vert t_{1}-t_{2}\vert , \vert x_{1}-x_{2}\vert \}. \end{aligned}$$

We utilize $C^{1}_{F}(O^{2})$ to show the set of the first continuously differentiable functions on the unit circle $O ^{2}$ and equippe it with the following norm

$$\begin{aligned} \Vert f(.,.)\Vert _{1,F}=\Vert f(.,.)\Vert _{\infty }+\Vert f_{t}(.,.)\Vert _{\infty }+\Vert f_{x}(.,.)\Vert _{\infty }+\vert f_{t}(.,.)\vert _{F}+\vert f_{x}(.,.)\vert _{F}. \end{aligned}$$

(16)

Now we define

$$\begin{aligned} \begin{aligned} C_{F}^{1}(\Lambda )=\{f(.,.)\in C^{1}(\Lambda ):\forall (t^{*},&x^{*})\in \Lambda , \exists \ map \Gamma :O^{2}\rightarrow \Lambda \ s.t\ (t^{*},x^{*})\in int(\Gamma (O^{2})) \\ and\ f\circ \Gamma (.,.)\in C_{F}^{1}(O ^{2})\}. \end{aligned} \end{aligned}$$

(17)

According to above if for some maps $\Gamma _{1}, \ldots , \Gamma _{n}$

$$\begin{aligned} \Lambda =\bigcup _{i=1}^{n}int(\Gamma _{i}(O^{2})), \end{aligned}$$

then $f(.,.)\in C^{1}_{F}(\Lambda )$ if and only if $f\circ \Gamma _{i}(.,.)\in C_{F}(O ^{2})$ for each $i=1,\ldots ,N$. Furthermore $C^{1}_{F}(\Lambda )$ is a Banach space with the norm

$$\begin{aligned} \Vert f(.,.)\Vert _{1,F}=\sum _{i=1}^{N}\Vert f\circ \Gamma _{i}(.,.) \Vert _{1,F}. \end{aligned}$$

(18)

We define $P(N,N,\Lambda )$, the space of all Polynomials, as

$$\begin{aligned} P(N,N,\Lambda )=\{\rho (t,x)=\sum _{i=0}^{N}\sum _{j=0}^{N}\tau _{ij}t^{i}x^{j}:\, (t,x)\in \Lambda , \tau _{ij}\in {{\mathbb {R}}}\}. \end{aligned}$$

(19)

Lemma 3.1

For any $f(.,.)\in C_{F}^{1}(\Lambda )$, exists a polynomial $\rho (.,.)\in P(N,N,\Lambda )$ such that

$$\begin{aligned} \Vert f(.,.)-\rho (.,.)\Vert _{\infty }\le \frac{\alpha _{0}\alpha _{1}}{2N}F\Big(\frac{1}{2N}\Big), \end{aligned}$$

(20)

where $\alpha _{1}=\Vert f(.,.)\Vert _{1,F}$ and constant $\alpha _{0}$ is independent of N.

Proof

The proof has been obtained from Theorem 2.1 in Ragozin [21]. $\square$

Related to the existence of solution, we convert system (14) into the following system

$$\begin{aligned} {\left\{ \begin{array}{ll} \left| \sum _{i=0}^{N}{\tilde{u}}_{in}D_{mi}- K\sum _{j=0}^{N}{\tilde{u}}_{mj}D_{nj}^{(2)}-g(t_{m},x_{n},{\tilde{u}}_{mn})\right| \le \frac{\sqrt{N}}{2N-1}F\Big(\frac{1}{2N-1}\Big),\quad m=1,\ldots ,N, n=1,\ldots ,N-1,\\ \vert {\tilde{u}}_{m0}-\varphi _{1} (t_{m})\vert \le \frac{\sqrt{N}}{2N-1}F\Big(\frac{1}{2N-1}\Big), \vert {\tilde{u}}_{mL}-\varphi _{2}(t_{m})\vert \le \frac{\sqrt{N}}{2N-1}F\Big(\frac{1}{2N-1}\Big),\quad m=0,\ldots ,N, \\ \vert {\tilde{u}}_{0n}-\varphi _{3}(x_{n})\vert \le \frac{\sqrt{N}}{2N-1}F\Big(\frac{1}{2N-1}\Big),\, n=0,1,\ldots N, \end{array}\right. } \end{aligned}$$

(21)

where N is enough large and F(.) is a function which satisfies Definition 3.1. Since $\lim _{N\rightarrow \infty }\frac{\sqrt{N}}{2N-1}F\Big(\frac{1}{2N-1}\Big)=0$, every ${\tilde{u}}_{mn}\ (m,n=0,1,\ldots ,N)$ in system (21) is a solution for system (14) as $N\rightarrow \infty$. We now define

$$\begin{aligned} \Phi (t,x,u,u_{xx})=Ku_{xx}(t,x)+g(t,x,u(t,x)), \end{aligned}$$

(22)

In the following, we show that system (21) is feasible.

Theorem 3.1

Suppose u(., .) is a solution for system (1)–(2) such that $u(.,.)\in C_{F}^{1}(\Lambda )$ then there is ${\bar{N}}>0$ such that for any $N\ge {\bar{N}}$ the relaxed system (21) has a solution as

$$\begin{aligned}{\tilde{u}}_{N}=({\tilde{u}}_{mn}; m,n=0,1,\ldots ,N),\end{aligned}$$

that satisfies

$$\begin{aligned} \vert u(t_{m},x_{n})-{\tilde{u}}_{mn}\vert \le \frac{\delta }{2N-1}F\Big(\frac{1}{2N-1}\Big),\quad m,n=0,1,\ldots , N, \end{aligned}$$

(23)

where constant $\delta >0$ is independent of N.

Proof

We suppose that $\rho (.,.)\in P(N-1,N,\Lambda )$ is the best approximation for $u_{t}(.,.)$. With the Lemma 1

$$\begin{aligned} \Vert u_{t}(t,x)-\rho (t,x)\Vert _{\infty }\le \frac{\kappa }{2N-1}F\Big (\frac{1}{2N-1}\Big ),\qquad (t,x)\in \Lambda , \end{aligned}$$

(24)

$\square$

where positive constant $\kappa$ is independent from N. Define

$$\begin{aligned} {\tilde{u}}(t,x)=u(0,x)+\int _{0}^{t}\rho (\upsilon ,x)d\upsilon ,\quad (t,x)\in \Lambda , \end{aligned}$$

(25)

and

$$\begin{aligned} {\tilde{u}}_{mn}={\tilde{u}}(t_{m},x_{n});\quad m,n=0,1,\ldots ,N. \end{aligned}$$

(26)

We want to prove that ${\tilde{u}}_{N} =({\tilde{u}}_{mn};\ m,n=0,1,\ldots ,N)$ satisfies system (21). By (24), (25) and (26) for $(t,x)\in \Lambda$ we have

$$\begin{aligned} \begin{aligned} \vert u(t,x)-{\tilde{u}}(t,x)\vert&= \vert \int _{0}^{t}(u_t(t,x)-\rho (\upsilon ,x)) d\upsilon \vert \le \int _{0}^{t}\vert (u_{t}(\upsilon ,x)-\rho (\upsilon ,x))\vert d\upsilon \\&\le \frac{\kappa }{2N-1}F\Big (\frac{1}{2N-1}\Big )\int _{0}^{t}d\upsilon \le \frac{\kappa T}{2N-1}F\Big (\frac{1}{2N-1}\Big ). \end{aligned} \end{aligned}$$

(27)

Now, according to the definition (25), the function ${\tilde{u}}(.,x) , x\in [0,L]$ is a polynomial of degree less than or equal to N. So,

$$\begin{aligned} \sum _{i=0}^{N}{\tilde{u}}_{in}D_{mi}={\tilde{u}}_t(t_{m},x_{n});\quad m,n=0,1,\ldots ,N. \end{aligned}$$

(28)

Therefore by (27) we have

$$\begin{aligned} \begin{aligned}&\Bigg \vert \sum _{i=0}^{N}{\tilde{u}}_{in}D_{mi}- \Phi \Bigg (t_{m}, x_{n}, {\tilde{u}}_{mn}, \sum _{j=0}^{N}{\tilde{u}}_{mj}D^{(2)}_{nj}\Bigg )\Bigg \vert \le \vert {\tilde{u}}_{t}(t_{m}, x_{n}) - u_{t}(t_{m}, x_{n})\vert \\&\qquad + \Bigg \vert u_{t}(t_{m}, x_{n})- \Phi \Bigg (t_{m}, x_{n}, {\tilde{u}}_{mn}, \sum _{j=0}^{N}{\tilde{u}}_{mj}D_{nj}^{(2)}\Bigg )\Bigg \vert =\vert \rho (t_{m},x_{n})-u_{t}(t_{m},x_{n})\vert \\&\qquad + \Bigg \vert \Phi (t_{m},x_{n}, u(t_m,x_n),u_{xx}(t_m,x_n))-\Phi \Bigg (t_{m},x_{n}, {\tilde{u}}_{mn}, \sum _{j=0}^{N}{\tilde{u}}_{mj}^{N}D_{nj}^{(2)}\Bigg )\Bigg \vert \\&\quad \leqslant \vert \rho (t_{m},x_{n})-u_{t}(t_{m},x_{n})\vert +M\vert u(t_m,x_n)-{\tilde{u}}_{mn}\vert \\&\quad \leqslant \frac{\kappa }{2N-1}F\Big (\frac{1}{2N-1}\Big )+M\frac{\kappa T}{2N-1}F\Big (\frac{1}{2N-1}\Big )\\&\quad =\frac{\kappa (1+MT)}{2N-1}F\Big (\frac{1}{2N-1}\Big ), \end{aligned} \end{aligned}$$

(29)

where M is the Lipschitz constant of function $\phi (.,.,.,.)$ with respect to the third component. Also, for bounded conditions we have for $m=0,\ldots , N$

$$\begin{aligned} \vert {\tilde{u}}_{m0}-\phi _{1}(t_{m})\vert \le \vert {\tilde{u}}_{m0}-u_{m0}\vert +\vert u_{m0}-\phi _{1} (t_{m})\vert \le \frac{\kappa T}{2N-1}F\Big(\frac{1}{2N-1}\Big), \end{aligned}$$

(30)

$$\begin{aligned} \vert {\tilde{u}}_{mL}-\phi _{2}(t_{m})\vert \le \vert {\tilde{u}}_{mL}-u_{mL}\vert +\vert u_{mL}-\phi _{2} (t_{m})\vert \le \frac{\kappa T}{2N-1}F\Big (\frac{1}{2N-1}\Big ), \end{aligned}$$

(31)

where $u_{mn}=u(t_m,x_n)$ for all $m,n=0,1,...,N.$ Moreover for $n=0,1,\ldots ,N$ we have

$$\begin{aligned} \vert {\tilde{u}}_{0n}-\phi _{3}(x_{n})\vert \le \vert {\tilde{u}}_{0n}-u_{0n}\vert +\vert u_{0n}-\phi _{3}(x_{n})\vert \le \frac{\kappa L}{2N-1}F\Big(\frac{1}{2N-1}\Big). \end{aligned}$$

(32)

Now we can choice ${\bar{N}}$ such that

$$\begin{aligned} max\{\kappa L, \kappa T, \kappa (1+MT)\}\le \sqrt{N}, \end{aligned}$$

for all $N\geqslant {\bar{N}}$ and this completes the proof.

Here we want to give the convergence theorem of solutions.

Theorem 3.2

Suppose $\{{\tilde{u}}_{mn}\};m,n=0,1,\ldots ,N\}_{N={\bar{N}}}^{\infty }$ is the sequence of the solutions of system (21) and $\{u^{N}(.,.)\}_{N={\bar{N}}}^{\infty }$ is the sequence of polynomials defined in (3). We assume that for any $x\in [0,L]$, the sequence $\{(u^{N}(0,x),u^{N}_{t}(.,.))\}_{N={\bar{N}}}^{\infty }$ has a subsequence $\{(u^{N_{i}}(0,x),u_{t}^{N_{i}}(.,.))\}_{i=0}^{\infty }$ such that converges to $(\psi ^{\infty }(x),p(.,.))$ uniformly, where $p(.,.)\in C^{2}(\Lambda )$, $\psi ^{\infty }(.)\in C^{2}([0,L])$ and $\lim _{i\rightarrow \infty } N_{i}=\infty$. Then

$$\begin{aligned} {\tilde{u}}(t,x)=\lim _{i\rightarrow \infty }u^{N_{i}}(t,x). \end{aligned}$$

(33)

satisfies the system (1)–(2).

Proof

Define

$$\begin{aligned} {\tilde{u}}(t,x)=\psi ^{\infty }(x)+\int _{0}^{t}\rho (\upsilon ,x)d\upsilon . \end{aligned}$$

(34)

We show that ${\tilde{u}}(.,.)$ satisfies system (1)–(2). Firstly, let ${\tilde{u}}(.,.)$ does not satisfy (1). So there is a $(\tau ,y)\in \Lambda$ such that

$$\begin{aligned} {\tilde{u}}_{t}(\tau ,y)-\Phi (\tau ,y,{\tilde{u}}(\tau ,y),{\tilde{u}}_{xx}(\tau ,y))\ne 0. \end{aligned}$$

(35)

We know the shifted LGL points $\{t_m\}_{m=1}^N$ and $\{x_m\}_{n=1}^N$ are dense in [0, T] and [0, L] , respectively, when $N\rightarrow \infty$. So there are subsequences $\{t_{m_{N_{i}}}\}_{i=1}^{\infty }$ and $\{x_{n_{N_{i}}}\}_{i=1}^{\infty }$ such that $0<m_{N_{i}}<N_{i}, 0<n_{N_{i}}<N_{i}$, $\lim _{i\rightarrow \infty }t_{m_{N_{i}}}=\tau , \; \lim _{i\rightarrow \infty }x_{n_{N_{i}}}=y$ and $\lim _{i\rightarrow \infty }N_i=\infty$. Hence, by (35) we get

$$\begin{aligned}&\lim _{i\rightarrow \infty }\big ({\tilde{u}}_{t}(t_{m_{N_{i}}},x_{n_{N_{i}}}) -\Phi \big (t_{m_{N_{i}}},x_{n_{N_{i}}},{\tilde{u}}_{m_{N_i},n_{N_i}},{\tilde{u}}_{xx} (t_{m_{N_{i}}},x_{n_{N_{i}}})\big )\big )\nonumber \\&\quad ={\tilde{u}}_{t}(\tau ,y)-\Phi (\tau ,y,{\tilde{u}}(\tau ,y),{\tilde{u}}_{xx}(\tau ,y))\ne 0. \end{aligned}$$

(36)

On the other hand, since $\lim _{i\rightarrow \infty }\frac{\sqrt{N_{i}}}{2N_{i}-1}F\Big(\frac{1}{2N_{i}-1}\Big)=0$, by (21) we get

$$\begin{aligned} \lim _{i\rightarrow \infty }\big ({\tilde{u}}_{t}(t_{m_{N_i}},x_{n_{N_i}})-\Phi \big (t_{m},x_{n}, {\tilde{u}}_{m_{N_i},n_{N_i}}, {\tilde{u}}_{xx} (t_{m_{N_i}},x_{n_{N_i}})\big )\big )=0, \end{aligned}$$

and this contradicts relation (36). So ${\tilde{u}}(.,.)$ satisfies the Eq. (1). Moreover, it is easy to show that ${\tilde{u}}(.,.)$ satisfies the initial and boundary conditions (2) and this completes the proof. $\square$

4 Examples

In this section, we have provided four of examples to illustrate the efficiency of method in solving RDEs. The first example is constructed by the authors to test the method. The next three examples show the comparison of the suggested method with other existing methods. We solve the corresponding system (14) using FSOLVE command in MATLAB software. The absolute error of gained estimate solution $u^{N}(.,.)$ is defined by

$$\begin{aligned} E^{N}(t,x)=| u(t,x)-u^{N}(t,x)| , \quad (t,x)=[0,1]\times [0,1]. \end{aligned}$$

Also, We calculate the $L_{2}$ and $L_{\infty }$ errors of approximations by the following relations

$$\begin{aligned} E_{2}^{N}=\Bigg (\sum _{i=0}^{N}\sum _{j=0}^{N}|u(t_{i},x_{j})-u^{N}(t_{i},x_{j})|^{2}\Bigg )^{\frac{1}{2}}, \\ E_{\infty }^{N}=max\{|u(t_{i},x_{j})-u^{N}(t_{i},x_{j})|: \ i,j=0,1,\ldots ,N\}. \end{aligned}$$

Example 4.1

Consider the RDE (1)–(2) with $g(t,x,u)=u+e^{t}sinx, K=1$ and the following conditions

$$\begin{aligned} {\left\{ \begin{array}{ll} u(t,0)=\varphi _{1}(t)=0,\\ u(t,1)=\varphi _{2}(t)=e^{t}sin1, \\ u(0,x)=\varphi _{3}(x)=sinx. \end{array}\right. } \end{aligned}$$

(37)

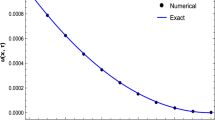
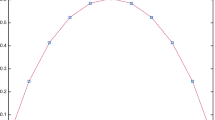
The accurate solution is $u(t,x)=e^tsinx,\ (t,x)\in [0,1]^2$. We solve this equation for N = 10 using suggested method. Figure 1 shows the obtained approximate solution and its absolute error. Also, Fig. 2 illustrates that by increasing N, the $L_{2}$ and $L_{\infty }$ errors decrease. This shows our presented method has good accuracy and stable treatment.

Example 4.2

Consider the RDE (1)–(2) with $g(t,x,u)=u-u^{2}+3e^{t-x}cos(t+x)+e^{2(t+x)}sin(t+x)^{2}, \; K=1$ and the following conditions

$$\begin{aligned} {\left\{ \begin{array}{ll} u(t,0)=\varphi _{1}(t)=e^{t}sint,\\ u(t,1)=\varphi _{2}(t)=e^{t-1}sin(t+1), \\ u(0,x)=\varphi _{3}(x)=e^{(-x)}sinx. \end{array}\right. } \end{aligned}$$

(38)

The accurate solution for this example is $u(t,x)=e^{t-x}sin(t+x),\ (t,x)\in [0,1]^2$. We illustrate the obtained approximate solution and its absolute error for N = 10 in Fig. 3. $E_{2}^{N}$ and $E_{\infty }^{N}$ errors are presented in Fig. 4. It can be seen that by increasing N, these errors decrease and our method is stable. Also we compare the presented method with IMEX Range–Kutta method [16], that are shown in Table 1. These results present that the $E_{2}^{N}$ error of suggested method is less than that of the method [16].

Example 4.3

Consider the RDE (1)–(2) with $g(t,x,u)=6u(1-u), \;K=1$ and the following conditions

$$\begin{aligned} {\left\{ \begin{array}{ll} u(t,0)=\varphi _{1}(t)=\frac{1}{(1+e^{-5t})^{2}},\\ u(t,L)=\varphi _{2}(t)=\frac{1}{(1+e^{1-5t})^{2}}, \\ u(0,x)=\varphi _{3}(x)=\frac{1}{(1+e^{x})^{2}}. \end{array}\right. } \end{aligned}$$

(39)

For this example, the accurate solution is $u(t,x)=\frac{1}{(1+e^{x-5t})^{2}},\ (t,x)\in [0,1]$. We solve this equation for N = 20 using our approach . Figure 5 shows the gained approximate solution and its absolute error. Also, Fig. 6 illustrates that by increasing N, the $E_{2}^{N}$ and $E_{\infty }^{N}$ errors decrease and the presented method has good accuracy. Then we compare with VIM method [29], that are shown in Table 2.

Example 4.4

Consider the RDE (1)–(2) with $g(t,x,u)=-0.5u$, $K=0.1$ and following conditions

$$\begin{aligned} {\left\{ \begin{array}{ll} u(t,0)=\varphi _{1}(t)=0,\\ u(t,L)=\varphi _{2}(t)=0, \\ u(0,x)=\varphi _{3}(x)=sin(\pi x), \end{array}\right. } \end{aligned}$$

(40)

The accurate solution is $u(t,x)=e^{(-0.5-0.1\pi ^{2})t}sin(\pi x),\ (t,x)\in [0,1]^{2}$. We illustrate the obtained results, for N = 9, in Fig. 7. $E_{2}^{N}$ and $E_{\infty }^{N}$ errors, for N = 9, are presented in Fig. 8. It can be seen that the errors decrease when N increases. We also give the absolute error of suggested method, compact finite difference method [3], explicit finite difference method [8] and collocation method [24] in the Table 3 . The results show that the error of suggested method is less than that of others.

Fig. 1

The estimate solution $U^N(.,.)$ and logarithm of $E^{N}(.,.)$ with $N=10$ for Example 4.1

Fig. 2

The logarithm of $E_{2}^{N}$ and $E_{\infty }^{N}$ for Example1

Fig. 3

The estimate solution $U^N(.,.)$ and logarithm of $E^{N}(.,.)$ with $N=10$ for Example 4.2

Fig. 4

The logarithm of $E_{2}^{N}$ and $E_{\infty }^{N}$ for Example 4.2

Table 1 The comparison for Example 4.2

Fig. 5

The estimate solution $U^N(.,.)$ and logarithm of $E^{N}(.,.)$ with $N=20$ for Example 4.3

Fig. 6

The logarithm of $E_{2}^{N}$ and $E_{\infty }^{N}$ for Example 4.3

Table 2 The comparison for Example 4.3

Fig. 7

The estimate solution $U^N(.,.)$ and logarithm of $E^{N}(.,.)$ with $N=9$ for Example 4.4

Fig. 8

The logarithm of $E_{2}^{N}$ and $E_{\infty }^{N}$ for Example 4.4

Table 3 The comparison of maximum of $E^{N}(.,.)$ for Example 4.4

5 Conclusions and Suggestions

In this text we showed that spectral collocation method can be utilized to find a solution for RDE with a simple structure. We analyzed the convergence of approximate solutions to the accurate solution by utilizing the theory of module of continuity and a normed space of polynomials. We presented two main theorem related to feasibility of obtained estimate solutions and their convergence. We solved some numerical examples and illustrated the capability of the presented method. For future work, we will utilize this powerful method and its convergence results for other types of PDEs involving delay and fractional derivatives.