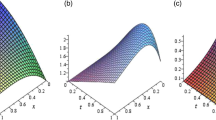
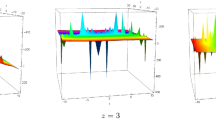
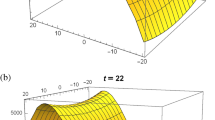
Abstract
The Lie symmetry analysis is adopted to the (2 + 1)-dimensional dispersionless B-type Kadomtsev–Petviashvili (dBKP) equation. The combination of symmetry analysis and symbolic computing methods proves that Lie algebra of infinitesimal symmetry of the dBKP equation depends on four independent arbitrary functions and one arbitrary parameter. The Lie algebra is reduced to four classes for deriving commutative relations, group invariant solutions of dBKP equation and conservation laws, and the optimal system of 1-dimensional subalgebras from one class is constructed. Based on the optimal system and other particular infinitesimal symmetries, plentiful symmetry reductions and invariant solutions are computed by using Lie group method. Six successive symmetries and conserved quantities of the dBKP equation are linked by the new conservation theorem. Besides, exact solution of the dBKP equation is constructed according to a conservation vector.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Non-linear partial differential equations (NLPDEs) are widely used to explain nonlinear physical phenomena in engineering sciences such as fluid dynamics, plasma physics and oceanography. Analysing mathematical properties of NLPDEs such as symmetry reductions, exact closed-form solutions and dynamic behavior of solutions is crucial to predict and utilize these phenomena. Lie symmetry analysis, a valid and concise approach to comprehend these properties of NLPDEs, was first presented by Lie in 1881 [1]. Based on transformative invariance of one-parameter Lie group, this method can reduce the number of independent variables. Since a Lie algebra of NLPDEs almost always contains infinite subalgebras, an optimal system should be found to avoid getting the equivalent group invariant solutions. In recent six decades, scholars such as Ovsyannikov, Olver, Ibragimov, Miao and Hu et al. [2,3,4,5,6] have sought to, but not limited to improve the way of searching optimal system. The impact of Lie symmetry’s thought simultaneously spread more widely [7,8,9].
Conservation law appears in NLPDEs related to areas such as water waves, foam, atmospheric flows, etc, its existence strongly proves the integrability of NLPDEs. Symmetries of NLPDEs could connect with conservation laws, Noether’s theorem in [10], partial Noether’s approach in [11] and multiplier approach in [12] are all highly effective for the derivation of conservation laws. The new conservation theorem is more widely utilized since there is no need for Lagrangian and relies only on the commutator table [13]. According to the fundamental notion of nonlinearly self-adjointness, corresponding conservation laws by self-adjointness can be generated by adjoint symmetry [14], which are examples of conservation laws by pairs of symmetries and adjoint symmetries [15]. In addition, exact solutions of NLPDEs could be constracted adopting particular conservation laws [16].
The significance has been realized recently to dispersionless limits of integrable hierarchies and equations, since they present in the research of various problems in applied mathematics and physics from the theory of conformal maps to the theory of quantum fields and strings [17,18,19]. In the quasi-classical \( {\overline{\partial }}- \)dressing scheme for dispersionless KP hierarchy, dispersionless B-type KP hierarchy is dispersionless KP hierarchy with even times frozen at zero plus symmetry, and the dBKP equation can be given by the compatibility condition for the first two Hamilton–Jacobi equations [20,21,22]
where \( w=w(x,y,t) \) denotes the unknown function of space variables x, y and time variable t, \( \partial ^{-1} \) means to integrate x. Substituting \(w=u_{x}\) into Eq. (1) to remove the integral symbol
Quantum W-infinity algebra, classical quantum torus structure and other discussions of dBKP hierarchy have been detailed in [21, 23, 24], yet mathematical properties of dBKP equation is just beginning to explore.
This paper explores new group invariant solutions of the dBKP equation by the Lie symmetry approach, the Lie point symmetries of dBKP equation are presented and discussed which have not been studied in previous literature. Lie symmetry method was applied to the dBKP equation and eight symmetry reductions were derived in 2021, but we derive twenty-five symmetry reductions. The invariant solutions are dissimilar since our research involves the general Lie algebra and its four reductive classifications, whereas the previous discussion was based on one reduction of the general Lie algebra. In the construction of optimal system, adjoint representation was adopted by previous research, yet we rely only on commutator table and its derivation process is given. Depending on the constracted optimal system, four indirectly solvable symmetry reductions with infinite number of solutions are given and discussed, which were not available in previous study. Although the new conservation theorem is both applied, the conservation laws are distinct for distinct Lie point symmetries, we further construct exact solution of the dBKP equation by a conservation law. The aim of this paper is to analyze the Lie algebra classifications, symmetry reductions and exact invariant solutions of the dBKP equation based on the Lie point symmetry, and to derive the conservation laws according to the new conservation theorem.
The whole structure can be divided into five main sections. In next section, we review the connection between the dBKP hierarchy and equation. Section 3 describes the Lie algebra with one-parameter transformation and their reductions for the dBKP equation under Lie symmetry analysis. Section 4 constructs an one-dimensional optimal system of subalgebras of dBKP equation. In Sect. 5, plentiful reduced equations and invariant solutions are derived. In Sect. 6, the new conservation theorem is utilized to link six successive symmetries and conserved quantities of the dBKP equation, besides, exact solution is constructed according to a set of conservation law. The last section gives conclusions and discussions.
2 The dBKP Hierarchy and the dBKP Equation
We begin with a brief review to the connection between the dBKP equation and dBKP hierarchy. The Lax function of dispersionless BKP hierarchy
in which \( \kappa \) is a conjugate variable of x, and \( \varGamma \) is odd Laurent series of \( \kappa .\) \( \varGamma \) can be written as
the form of the dressing function is as
Definition 2.1
The dispersionless BKP hierarchy are composed of flows in the Lax pair [20]
in which “\( + \)” represents the nonnegative projection about \( \kappa \) and “\( - \)” represents the negative projection. Eq. (1) is the simplest nontrivial flow in the dBKP hierarchy.
3 Lie Algebra Classifications
In this section, the Lie symmetry analysis to Eq. (2) starts at considering following one-parameter Lie group of infinitesimals transformation
where \( \xi ^{x} , \xi ^{t} , \xi ^{y} , \varPhi \) are functions of x, t, y, u and \(\varsigma > 0\) is a sufficiently small one-parameter, the vector field relevant to (7) is
The following second prolongation holds
with
in which \({D_p},~ (p=x, y, t) \) are the total derivatives respectively about p .
Above deterministic Eq. (10) can be produced under constant condition
with \(\Delta = 3u_{xt}+15u_{x}^{2}u_{xx}-5u_{x}u_{xy}-5u_{xx}u_{y}-\frac{5}{3}u_{yy}=0.\) According to Eq. (11), the following equation holds
The form of the coefficient function is obtained by calculating the standard symmetry group
where c is an arbitrary constant, \({f_1}, {f_2}, {f_3}\) and \({f_4}\) are arbitrary functions about t. Consequently, the vector field of Eq. (2) can be determined by below infinitesimal symmetries
This set of vectors form a Lie algebra under commutative operations \([{V_i},{V_j}] = {V_i}{V_j} - {V_j}{V_i},\) which is skew symmetric with each diagonal term being zero. One can give the commutator table of system (2) (see Table 1).
The following four cases are convenient for calculating the commutative relations of infinitesimal symmetries and deriving invariant solutions of Eq. (2), if arbitrary functions \( f_{i}\) \( (i=1,\ldots ,4) \) are defined as
Case 1. \( f_{1}=\cdots =f_{4}=1 \) The infinitesimal symmetries of Eq. (2) form the five-dimensional Lie algebra \( L^{5} \) are spanned by the following independent operators
Then the commutative relations of above operators can be given in Table 2.
The following one-parameter \( \varsigma \) symmetry groups \({\tau _i}\ (1,~\ldots ~,5)\) generated by the correlating infinitesimal symmetries \({V_i}~(i=1~\ldots ~,5)\) hold
where \({\tau _1}\) is a translation of time, \({\tau _2},\ {\tau _3}\) are translations about space, \({\tau _{4}}\) is a dependent variable translation, \({\tau _5}\) is a translation of scale. (16) implies that if \(u = f(x,y,t)\) is a solution of Eq. (2), so are \({u^{(j)}}\ (1 \le j \le 5)\)
Case 2. \( f_{1}=\cdots =f_{4}=t+1 \)
The infinitesimal symmetries are shown as follows
Case 3. \( f_{1}=f_{2}=t+1,~ f_{3}=f_{4}=(t+1)^{2} \)
With the infinitesimal symmetries
Case 4. \( f_{1}=f_{2}=1,~f_{3}=f_{4}=e^{t} \)
With the infinitesimal symmetries
The commutative operations of infinitesimal symmetries in cases 2, 3, 4 are presented in the Appendix 1.
4 Optimal System
In this section, we construct an optimal system of one-dimensional subalgebras of case 1 for Eq. (2) with the method of Ibragimov in [6], which has the advantage of relying only on the commutator table (see Table 2), Supposing that any vector field can be written as
utilizing the following generators to find linear transformations of the vector \( (R_{1}, R_{2}, R_{3}, R_{4}, R_{5}) \)
where \(P_{ij}^{\gamma }\) are represented by the formula \([\text{V}_{{i}},\text{V}_{{j}}] =\text{P}_{ij}^{\gamma }.\)
Theorem 4.1
The following operators provide an optimal system of one-dimensional subalgebras of the Lie algebra spanned by \( V_{1}, ~V_{2},~ V_{3},~ V_{4}, ~V_{5} \)
Proof
According to (22) and the Table 2, \( \varXi _{1}, \varXi _{2}, \varXi _{3}, \varXi _{4} \) and \(\varXi _{5} \) can be written as
for the generators \(\varXi _{i} ,\) \(c _{i} \) with the initial condition \( {\tilde{R}}|_{c_{i}=0}=R \) \( (i=1,\ldots ,5) \) are written as
and the solutions of Eq. (25) give the transformations
It is necessary to construct the optimal system to simplify the vector
Since the rank of a matrix \(\Vert \mathbf{P}_{\mathbf{ij}}^{\varvec{\gamma }}{} \mathbf{R}_{\mathbf{j}}\Vert (\gamma =1,\ldots ,5) \) of the coefficients of the operators (24) is three, which means that the matrix has two functionally independent invariants \( R^{m}\) \( (m=1,~2) .\) Integrating the equation
following invariants hold
Since whether the invariant is 0 or not affects the combinations of generators, the process of constructed optimal system can only be divided into two cases. \(\square \)
Case 1. \( R_{5}\ne 0 \)
Respectively taking \( c_{2}=-\frac{R_{2}}{R_{5}} ,\) \( c_{3}=-2\frac{R_{3}}{R_{5}} ,\) \( c_{4}=-3\frac{R_{4}}{R_{5}} \) in \( T_{3},~T_{4}, ~T_{5} \) and simplify the vector (27) to the form
(1.1) \( R_{1}=0 \)
Providing the operator
(1.2) \( R_{1}\ne 0 \)
Without losing generality, assuming \( R_{1}=1,R_{5}=\pm 1 \) in the vector (27), providing the operator
Case 2. \( R_{5}=0 \)
(2.1) \( R_{1}\ne 0 \)
The vector (27) is reduced to the form
that cannot be reduced, taking all possible linear combinations, the following representatives are given
(2.2) \( R_{1}=0 \)
Taking into account all combinations, we obtain the following representatives
The optimal system is provided by collecting subalgebras (31), (32), (34) and (35), thus the proof is completed.
5 Symmetry Reductions and Invariant Solutions
In this section, the Lie group of point transformation method is employed in the dBKP equation. The subalgebras in (14), the obtained optimal system and cases 2–4 are selected to acquire symmetry reductions and group invariant solutions of dBKP equation, which can been realized through solving associated Lagrange characteristic equation
Subalgebra \( V_{3}(f_{3})=f_{3}\partial _{x}-\frac{3}{5}yf_{3t}\partial _{u} \)
Associated Lagrange equation is
Then, the following similarity form holds
Substituting above variables from Eq. (38) into Eq. (2), then Eq. (2) is reduced to
therefore, solutions of Eq. (1) are
Subalgebra \( V_{3}(f_{3})+V_{4}(f_{4})= f_{3}\partial _{x}-\frac{3}{5}yf_{3t}\partial _{u}+V_{4}(f_{4})=f_{4}\partial _{u} \)
By solving the associated characteristic equation, the similarity variables yield
Substituting these variables into Eq. (2), one has
therefore, we get solutions of Eq. (1)
The concrete results in optimal system and cases 2–4 are presented in Tables 3 and 4 by repeating the Lie group method
The exact solutions of Eq. (1) can be acquired by determining certain arbitrary functions.
Subalgebra \( V_{2}=\partial _{y} \) Taking \( F_{1}(z)=\dfrac{1}{3}(c_{1}z+c_{2}), \) where \( c_{1} \) and \( c_{2} \) are arbitrary constants, we get following binary equation
solving Eq. (44), a solution of Eq. (1) is derived as
Subalgebra \( V_{2}+V_{4}=\partial _{y}+\partial _{u} \)
Taking \( F_{1}(z)=lnz, \) we get the following binary equation
a solution of Eq. (1) can be obtained by solving Eq. (46)
Subalgebra \( V_{2}+V_{3}=\partial _{y}+\partial _{x} \)
Taking \( F_{1}(z)=0, \) solving the following binary equation
we acquire solutions of Eq. (1)
Subalgebra \( V_{2}-V_{3}+V_{4}=\partial _{y}-\partial _{x}+\partial _{u} \)
Taking \( F_{1}(z)=0, \) solving the following binary equation
solutions of Eq. (1) can be given as
6 Construction of Conservation Laws of the dBKP System
6.1 Nonlinear Self-Adjointness
In this subsection, we will introduce certain symbols and theorems from [13, 14]. For a kth-order system of PDEs with n-independent variables \( \mathbf{x}=(x^{1},x^{2},\ldots ,x^{n}) \) and m-dependent variables \( \mathbf{u}=(u^{1},u^{2},\ldots ,u^{m}) \)
where \( {{\textbf {u}}}_{(r)} \) represents the set of derivatives of order r \( (r=1,\ldots ,m),\) the system of adjoint equations for system (52) is as follows
where
The formal Lagrangian and Euler–Lagrange operator are defined as
in which \( D_{i} \) is total derivative operator with respect to \( x^{i} .\)
Definition 6.1
A nonlinear system is nonlinear self-adjoint if its adjoint system satisfies
where \({\varvec{\Theta }}_{{\varvec{\alpha }}}^{{\varvec{\beta }}}(\mathbf{x},\mathbf{u})\ne \mathbf{0}\) is undecided, \( {\varvec{\Theta }}=(\theta ^{1},\ldots ,\theta ^{m}) \) is a n-dimension vector.
Theorem 6.1
For symmetry generator admitted by system (52)
the adjoint equations (53) conserve symmetry above, which means the following adjoint symmetry must be admitted by the system of adjoint equations (53),
where \( Y(F_{\alpha })=\lambda _{\alpha }^{\beta } F_{\alpha } ,\) with \( \lambda _{\alpha }^{\beta } \) is a constant that needs to be determined.
Theorem 6.2
(New conservation theorem) Every Lie point symmetry, Lie–Bäcklund symmetry and nonlocal symmetry X admitted by the system of (52) can give the conservation law of the system consisting of Eq. (52) and the adjoint equations (53), its conservation vector \( \mathbf{C}= (C^{1}, C^{2}, \ldots ) \) has the form
where \( W^{\alpha }=\eta ^{\alpha }-\zeta ^{j}u^{\alpha }_{j},~\alpha =1,2,\ldots ,m. \)
Theorem 6.3
If a vector \( \mathbf{C} = (C^{x}, C^{y}, C^{t}) \) satisfies the conservation equation
it is called a conserved vector for Eq. (2).
6.2 Construction of Conservation Laws Using Symmetries
According to the definition and theorems mentioned in Sect. 6.1, for system
we write the formal Lagrangian in symmetric form
with L satisfies
Therefore
here \( \rho _{i} \) are arbitrary functions of t.
The next step is to use particular symmetries obtained in Sect. 3 to construct conservation laws.
Symmetry generator \( X_{1}=\frac{\partial }{\partial x} \)
We derive the corresponding Lie characteristic functions \( W^{1}=-u_{x}\) and \( W^{2}=-v_{x}, \) hence the conserved vector is composed of
Symmetry generator \( X_{2}=\frac{\partial }{\partial y} \)
The corresponding Lie characteristic functions are \( W^{1}=-u_{y}\) and \( W^{2}=-v_{y}, \) then conserved vector is composed of
It can be calculated and verified
Symmetry generator \( X_{3}=\frac{\partial }{\partial t} \)
In this case, we have the corresponding Lie characteristic functions \( W^{1}=-u_{t}\) and \( W^{2}=-v_{t}, \) and conserved vector is composed of
We can verify that
Symmetry generator \( X_{4}=(t+1)\frac{\partial }{\partial x}-\frac{3y}{5}\frac{\partial }{\partial u} \)
We can get the Lie characteristic functions \( W^{1}=-\frac{3y}{5}-(t+1)u_{x}\) and \( W^{2}=-(t+1)v_{x}, \) then following conserved component vectors hold
Symmetry generator \( X_{5}=2x\frac{\partial }{\partial x}+y\frac{\partial }{\partial y}+3u\frac{\partial }{\partial u} \)
The coefficients of \( X_{5} \)’s extension can be calculated
An adjoint symmetry is generated
the corresponding Lie characteristic functions are \( W^{1}=3u-2xu_{x}-yu_{y}\) and \( W^{2}=-4v-yv_{y}-2xv_{x}, \) and following conserved component vectors hold
Conservation law can be verified
Symmetry generator \( X_{6}=(t+1)\frac{\partial }{\partial t}+\frac{x}{5}\frac{\partial }{\partial x}+\frac{3y}{5}\frac{\partial }{\partial y}-\frac{u}{5}\frac{\partial }{\partial u} \)
The coefficients of \( X_{6} \)’s extension can be calculated
and one gives adjoint symmetry
the corresponding Lie characteristic functions are \( W^{1}=-\frac{u}{5}-(t+1)u_{t}-\frac{x}{5}u_{x}-\frac{3y}{5}u_{y}\) and \( W^{2}=-\frac{2v}{5}-(t+1)v_{t}-\frac{3y}{5}v_{y} ,\) then following conserved component vectors
can be obtained. Conservation law can be verified
6.3 Constructing Solution of the dBKP Equation by Conserved Vector (66)
We know the conserved component vectors obtained of symmetry generator \( X_{1} \)
Taking
and assuming
then
Substituting the relationships of (81) into Eq. (2), one has
only the last two terms \( 9GH_{x}, -G_{y} \) may contain independent variable y, thus the calculations can be shorten significantly if we consider two special cases.
Case 1. \( H_{x}=0 \)
Under this circumstance, the following relationship holds
Then Eq. (84) becomes
using the constant coefficient variation method, we obtain
where a is an arbitrary constant, Eq. (83) can be written as
Integrating the system (88), we get
where l, m are arbitrary functions of t.
Case 2. \( G(t,y)=g(t) \)
Equation (84) becomes
if taking
the following formula is calculated
where k is an arbitrary functions of z, a solution of Eq. (84) can be acquired if we make \( k(z)=lnz \) .
Hence one of solutions of Eq. (1) is
7 Conclusions and Discussions
In summary, the authors study the dBKP equation using the Lie symmetry method and Ibragimov’s adjoint symmetry approach. The important results are that the Lie point symmetries of the dBKP equation are reduced to four classes, the rich symmetry reductions and new group invariant solutions are derived based on the above reduced symmetries. Except for particular complex symmetries themselves tend to generate still complex reduced equations, these main results prove that the reduction of the infinite-dimensional Lie algebra of symmetries to four classes is effective. For the symmetry reductions of subalgebras \( V_{2},~ V_{2}+V_{4},~ V_{2}+V_{3}\) and \( V_{2}-V_{3}+V_{4} \) contain infinite solutions which can not be obtained directly, we obtain the exact solutions by determining arbitrary functions. The traveling wave solutions can not be acquired since the dBKP system has the characteristic that each term contains the first power factor of the same order without dispersion term. Compared with other published papers on the study related to B-type equations [25,26,27,28], the current paper adds the application of symmetry analysis on the dispersionless B-type equation. Further research on obtained Lie point symmetries and special symmetry reductions by \( \mu \)-symmetry [29], Laplace transform [30] and PT-symmetry [31] are worth trying in the future.
Data Availability
Not applicable.
Abbreviations
- NLPEDs:
-
Non-linear partial differential equations
- dBKP equation:
-
(2 + 1)-Dimensional dispersionless B-type Kadomtsev–Petviashvili equation
References
Lie, S.: On integration of a class of linear partial differential equations by means of definite integrals. Arch. Math. 6(3), 328–368 (1881)
Ovsyannikov, L.V.: Group properties of differential equations. Siberian Branch, USSR Academy of Sciences, Novosibirsk (1962)
Olver, P.J.: Applications of Lie groups to differential equations. Springer Science, Business Media (2000)
Miao, Q., Hu, X., Chen, Y.: ONEOptimal: a Maple package for generating one-dimensional optimal system of finite dimensional Lie algebra. Commun. Theor. Phys. 61(2), 160 (2014)
Hu, X., Li, Y., Chen, Y.: A direct algorithm of one-dimensional optimal system for the group invariant solutions. J. Math. Phys. 56(5), 053504 (2015)
Grigoriev, Y.N., Ibragimov, N.H., Kovalev, V.F., et al.: Symmetries of integro-differential equations: with applications in mechanics and plasma physics. Springer, New York (2010)
Niwas, M., Kumar, S., Kharbanda, H.: Symmetry analysis, closed-form invariant solutions and dynamical wave structures of the generalized (3+1)-dimensional breaking soliton equation using optimal system of Lie subalgebra. J. Ocean Eng. Sci. 7(2), 188–201 (2022)
Zhao, Z., Han, B.: On optimal system, exact solutions and conservation laws of the Broer-Kaup system. Eur. Phys. J. Plus. 130(11), 1–15 (2015)
Liu, M., Li, X., Zhao, Q.: Exact solutions to Euler equation and Navier-Stokes equation. Angew. Math. Phys. 70(2), 1–13 (2019)
Noether, E.: Invariant variation problems. Transp. Theory Stat. Phys. 1(3), 186–207 (1971)
Kara, A.H., Mahomed, F.M.: Noether-type symmetries and conservation laws via partial Lagrangians. Nonlinear Dynam. 45(3), 367–383 (2006)
Naz, R.: Conservation laws for some compacton equations using the multiplier approach. Appl. Math. Lett. 25(3), 257–261 (2012)
Ibragimov, N.H.: A new conservation theorem. J. Math. Anal. Appl. 333(1), 311–328 (2007)
Ibragimov, N.H.: Nonlinear self-adjointness and conservation laws. J. Phys. A: Math. Theor. 44(43), 432002 (2011)
Ma, W.: Conservation laws by symmetries and adjoint symmetries. Discrete Contin. Dyn. Syst. Ser. S. 11(4), 707–721 (2018)
Ibragimov, N.H., Avdonina, E.D.: Nonlinear self-adjointness, conservation laws, and the construction of solutions of partial differential equations using conservation laws. Russ. Math. Surveys. 68(5), 889 (2013)
Wiegmann, P.B., Zabrodin, A.: Conformal maps and integrable hierarchies. Commun. Math. Phys. 213(3), 523–538 (2000)
Krichever, I.: The dispersionless Lax equations and topological minimal models. Commun. Math. Phys. 143(2), 415–429 (1992)
Mineev-Weinstein, M., Wiegmann, P.B., Zabrodin, A.: Integrable structure of interface dynamics. Phys. Rev. Lett. 84(22), 5106 (2000)
Bogdanov, L.V., Konopelchenko, B.G.: On dispersionless BKP hierarchy and its reductions. J. Non-Linear. Math. Phys. 12(sup1), 64–73 (2005)
Takasaki, K.: Quasi-classical limit of BKP hierarchy and W-infinity symmetries. Lett. Math. Phys. 28(3), 177–185 (1993)
Konopelchenko, B., Martínez Alonso, L.: Dispersionless scalar integrable hierarchies, Whitham hierarchy, and the quasiclassical \( {\overline{\partial }}- \)dressing method. J. Math. Phys. 43(7), 3807–3823 (2002)
Li, C.: Dispersionless and multicomponent BKP hierarchies with quantum torus symmetries. J. Geom. Phys. 119, 103–111 (2017)
Chen, Y., Tu, M.: A note on the dispersionless BKP hierarchy. J. Phys. A: Math. Gen. 39(24), 7641 (2006)
Ma, W., Yong, X., Lü, X.: Soliton solutions to the B-type Kadomtsev-Petviashvili equation under general dispersion relations. Wave Motion. 103, 102719 (2021)
Ma, W.: N-soliton solution of a combined pKP-BKP equation. J. Geom. Phys. 165, 104191 (2021)
Kumar, S., Jadaun, V., Ma, W.: Application of the Lie symmetry approach to an extended Jimbo-Miwa equation in (3+1) dimensions. Eur. Phys. J. Plus. 136(8), 1–30 (2021)
Ali, M., Ma, W., Sadat, R.: Lie Symmetry Analysis and Wave Propagation in Variable-Coefficient Nonlinear Physical Phenomena. East Asian J. Appl. Math. 12(1), 201–212 (2022)
Cicogna, G., Gaeta, G., Morando, P.: On the relation between standard and \( \mu \)-symmetries for PDEs. J. Phys. A: Math. Gen. 37(40), 9467 (2004)
Craddock, M., Platen, E.: Symmetry group methods for fundamental solutions. J. Different. Equat. 207(2), 285–302 (2004)
Ma, W.: Nonlocal PT-symmetric integrable equations and related Riemann-Hilbert problems. Partial Differ. Equ. Appl. Math. 4, 100190 (2021)
Funding
Partial financial support was received from the National Nature Science Foundation of China (no. 11701334) and the “Jingying” Project of Shandong University of Science and Technology.
Author information
Authors and Affiliations
Contributions
QZ conceived the study and the manuscript design as well as classified the Lie algebras of the dBKP equation. HW constructed the one-dimensional optimal system and computed the symmetry reductions of dBKP equation. XL constructed conservation laws and acquired a solution of the dBKP equation from a constructed conservation vector. CL introduced the applications and theories of the dispersionless hierarchies and equations.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no competing interests.
Ethics approval and consent to participate
The authors approve and consent to participate.
Consent for publication
The authors agree to publication.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhao, Q., Wang, H., Li, X. et al. Lie Symmetry Analysis and Conservation Laws for the (2 + 1)-Dimensional Dispersionless B-Type Kadomtsev–Petviashvili Equation. J Nonlinear Math Phys 30, 92–113 (2023). https://doi.org/10.1007/s44198-022-00073-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s44198-022-00073-6