1 Introduction

Pattern is a kind of non-uniform macrostructure with certain regularity in space or time, which exists widely in nature. All kinds of pattern structures constitute a colorful and charming world. Therefore, it is of great significance to understand the cause and mechanism of pattern formation for revealing the mystery of nature formation. In order to understand its formation mechanism, many scholars turned their work to study various mathematical models with different factors, such as delay [14, 16, 36], noise [19], network [25, 28, 34], season [29] and so on, among which, the reaction-diffusion equation was often used in [1, 22] and the references therein.

In particular, nonlocal effect has attracted more and more attention because it can describe a variety of morphogenetic phenomena. Then, how does the nonlocal effect play an important role in the formation of patterns? Actually, the research on the nonlocal model can be traced back to Britton [5, 6]. He found that introducing nonlocal effects into a single reaction diffusion equation would lead to the change of stability about the positive equilibrium point and the disturbance around it (it should be noted that when considering spatiotemporal patterns, the instability of the equilibrium point and the appearance of branches are often accompanied). Subsequently, scholars further considered this problem in a limited region, and studied the Neumann boundary condition [10] and Dirichlet boundary condition [27]. Recently, Guo [11, 12] and Yang and Xu [32] investigated the spatiotemporal patterns for a single species reaction diffusion equation. Of course, the introduction of nonlocal has great influence not only on the dynamics of patterns, but also on the traveling wave solution [3, 4, 17] and the well posedness about the solution of Cauchy problem [15, 16, 33].

The above considerations are the influence of nonlocal effect on the single population reaction-diffusion model, so a very natural question, how does it affect the pattern dynamics of reaction-diffusion system? In this paper, we consider the influence of nonlocal effect on the pattern dynamics of Lotka–Volterra cooperative system. Specifically, we will study the following model

$$\begin{aligned} {\left\{ \begin{array}{ll} u_t(x,t)=\Delta u(x,t)+u(x,t)(1-(\phi **u)(x,t)+a_1v(x,t)),\\ v_t(x,t)=d\Delta v(x,t)+rv(x,t)(1-v(x,t)+a_2u(x,t)), \end{array}\right. } \end{aligned}$$
(1.1)

where

$$\begin{aligned} (\phi **u)(x,t)=\int _{-\infty }^{t}\int _{{\mathbb {R}}^2}\phi (x-y,t-s)u(y,s)dyds, \end{aligned}$$

and

$$\begin{aligned} \phi (x,t)=\frac{1}{4\pi t}e^{-\frac{|x|^2}{4 t}}\frac{1}{\tau }e^{-\frac{t}{\tau }}, \end{aligned}$$
(1.2)

for \((x,t)\in {\mathbb {R}}^2\times (0,\infty )\). Here, u and v indicate the population density of two species. d an r denote the diffusion coefficient and the natural growth rate of species v respectively. And \(a_1, a_2\) represent the intensity of interaction between two species. In addition, the coefficients \(d, r, a_1, a_2, \tau \) and the population density are both positive. For more biological interpretation about model (1.1), we can refer to [20, 23, 24].

Obviously, system (1.1) has at least three equilibrium points (0, 0), (0, 1), (1, 0). And there is a fourth equilibrium point

$$\begin{aligned} (u^*, v^*)=\left( \frac{1+a_1}{1-a_1a_2}, \frac{1+a_2}{1-a_1a_2}\right) , \end{aligned}$$

when \(a_1a_2<1\). The appearance of the fourth equilibrium point means that two groups finally will reach the state of coexistence, so from the biological point of view, we always assume that \(a_1a_2<1\). In addition, we know that the classic Lotka–Volterra cooperative system corresponding to system (1.1) will not have Turing patterns under normal conditions. Under the influence of Predator-Prey and Lotka–Volterra competition system, we will study whether and what kind of patterns will appear in system (1.1) after introducing nonlocal effect?

In fact, the study of nonlocal effect on the pattern dynamics of Predator-Prey and Lotka–Volterra competition systems is a hot topic in recent years. Xu et al. [30] considered the following Predator-Prey system

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial u}{\partial t}=d\Delta u+ru\left( 1+\alpha u-\beta u^2-(1+\alpha -\beta ) \int _{-\infty }^t\int _{{\mathbb {R}}^2}\phi (x-y,t-s)u(s,y)dsdy\right) -uv,\\ \frac{\partial v}{\partial t}=\Delta v+av(u-b), \end{array}\right. } \end{aligned}$$
(1.3)

and gave the possible Turing patterns about system (1.3) by using stability analysis and numerical simulation. Following, Chen and Yu [8] researched the model with nonlocal intraspecific competition of prey for resources, and found the steady state can lose the stability when conversion rate passes through some Hopf bifurcation and the bifurcating periodic solutions near such bifurcation value can be spatially nonhomegeneous. It should be pointed out that this is very different from the classic results. Guo and Yan [13] investigated the following Lotka–Volterra competition system with nonlocal delay effect

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial u}{\partial t}(x,t)=d\Delta u(x,t)+\lambda u(x,t)(1-(A_{11}*u)(x,t-\tau )-(A_{12}*v)(x,t-\tau )),\\ \frac{\partial v}{\partial t}(x,t)=d\Delta v(x,t)+\lambda v(x,t)(1-(A_{21}*u)(x,t-\tau )-(A_{22}*v(x,t-\tau ))), \end{array}\right. } \end{aligned}$$

where

$$\begin{aligned} A_{ij}*f=\int _{\Omega }A_{ij}(x,y)f(y,t)dy, \ \ i, j= 1,2. \end{aligned}$$

By means of Lyapunov–Schmidt reduction, the normal form theory and the center manifold reduction, the existence and stability of spatially nonhomogeneous steady-state solutions and bifurcation direction of Hopf bifurcating periodic orbits are given. Then, Yan and Guo [31] further extended the above conclusion to Lotka–Volterra model with cross-diffusion and delay effect. And Han and Wang [14] also studied the following Lotka–Volterra competition diffusion system with nonlocal term

$$\begin{aligned} {\left\{ \begin{array}{ll} u_t=\Delta u+u(1-\phi **u+a_1v),\\ v_t=d\Delta v+rv(1-\phi **v+a_2u), \end{array}\right. } \end{aligned}$$
(1.4)

where \(\phi **u\) and \(\phi **v\) are similar to model (1.1) with (1.2). Through using the multi-scale analysis and numerical simulation, they obtained the pattern of system (1.4) under what conditions and gave the verification. For more research about the influence of nonlocal (or delay) effects on the system, see [2, 7, 17, 18, 21, 35].

However, we find that few studies consider the influence of nonlocal effect on Lotka–Volterra cooperative system. It may be that in a general sense, people think that branch is more likely to occur in predator-prey or competing relationship, which leads to the appearance of Turing patterns. Of course, from a mathematical point of view, it is easier to deal with the first two cases than the cooperative system. In this paper, we will try to study the pattern dynamics of model (1.1). Specifically, we always assume \(a_1a_2<1\) in this paper. Firstly, by analyzing the characteristic equation of the corresponding system, the conditions of Turing bifurcation are obtained. Further, according to these conditions, we give Turing space which is made up of diffusion coefficient d and time delay \(\tau \) by numerical simulation. Secondly, through multi-scale analysis, we get the amplitude equations, and moreover with the help of some transformation and solving steady-state solution, we obtain all possible pattern structures of system (1.1). Finally, through numerical simulation, we give two different patterns of system (1.1).

The remainder of the paper is arranged as follows. In Sect. 2, we discuss the conditions of Turing bifurcation caused by nonlocal effect in Lotka–Volterra cooperative system, and give Turing space by numerical simulation. Then we use multi-scale analysis, stability analysis and so on to give the possible pattern of system (1.1), and through numerical simulation , two kinds of specific pattern forms in Sect. 3 are given. Finally, a brief discussion is drawn in Sect. 4.

2 Turing Bifurcation

In this section, we research the Turing bifurcation of (1.1) and seek out the corresponding Turing space. It’s worth noting that here we mainly consider the influence of nonlocal effect. Firstly, we prove that the equilibrium \((u^*, v^*)\) of the classic Lotka–Volterra cooperative system is stable. Then, we show that \((u^*, v^*)\) will become unstable after the introduction of nonlocal effect. Lastly, by analyzing the characteristic equations of diffusion and non diffusion, some conditions for Turing bifurcation occurring near the positive equilibrium point \((u^*, v^*)\) are given.

By linearizing the classic Lotka–Volterra cooperative system

$$\begin{aligned} {\left\{ \begin{array}{ll} u_{t}=\Delta u+u\left( 1- u+a_{1} v\right) , \\ v_{t}=d \Delta v+r v\left( 1-v+a_{2} u\right) , \end{array}\right. } \end{aligned}$$

near \((u^*, v^*)\), we can get

$$\begin{aligned} {\left\{ \begin{array}{ll} u_{t}=\Delta u-\frac{1+a_{1}}{1-a_{1} a_{2}} u+a_{1} \frac{1+a_{1}}{1-a_{1} a_{2}} v, \\ v_{t}=d \Delta v+r a_{2} \frac{1+a_{2}}{1-a_{1} a_{2}} u-r \frac{1+a_{2}}{1-a_{1} a_{2}} v. \end{array}\right. } \end{aligned}$$
(2.1)

Select the following test functions

$$\begin{aligned} \left( \begin{array}{l} u \\ v \end{array}\right) =\sum _{k=1}^{\infty }\left( \begin{array}{l} C_{k}^{1} \\ C_{k}^{2} \end{array}\right) e^{\lambda t+i \kappa \cdot \gamma }, \end{aligned}$$
(2.2)

where i is the imaginary number unit, \(\lambda \) is the growth rate of the disturbance in time t, \(\kappa \cdot \kappa =k^2\) and k is the wave number, \(\gamma =(X,Y)\) is the two-dimensional space vector. By substituting Eq. (2.2) into Eq. (2.1), we can get the characteristic equation

$$\begin{aligned} \left| \begin{array}{ll} -\lambda -k^{2}-\frac{1+a_{1}}{1-a_{1} a_{2}} &{} a_{1} \frac{1+a_{1}}{1-a_{1} a_{2}} \\ r a_{2} \frac{1+a_{2}}{1-a_{1} a_{2}} &{} -\lambda -d k^{2}-r \frac{1+a_{2}}{1-a_{1} a_{2}} \end{array}\right| =0, \end{aligned}$$

which is equivalent to

$$\begin{aligned} \begin{array}{c} \lambda ^{2}+\left( (d+1) k^{2}+\frac{1+a_{1}+r\left( 1+a_{2}\right) }{1-a_{1} a_{2}}\right) \lambda +d k^{4}+\frac{d\left( 1+a_{1}\right) +r\left( 1+a_{2}\right) }{1-a_{1} a_{2}} k^{2}+\frac{r\left( 1+a_{2}\right) \left( 1+a_{1}\right) }{1-a_{1} a_{2}}=0. \end{array} \end{aligned}$$
(2.3)

It is obviously that the characteristic Eq. (2.3) has two negative characteristic roots, so the system is stable near the equilibrium point \((u^*,v^*)\). Next, we consider the influence of nonlocal effect. In order to simplify our research system, let \(w(x,t)=(\phi **u)(x,t)\), the system (1.1) is able to be converted to the following form

$$\begin{aligned} {\left\{ \begin{array}{ll} u_{t}=\Delta u+u\left( 1-w+a_{1} v\right) , \\ v_{t}=d \Delta v+r v\left( 1-v+a_{2} u\right) , \\ w_{t}=\Delta w+\frac{1}{\tau }(u-w). \end{array}\right. } \end{aligned}$$
(2.4)

Similar to the above discussion, the system (2.4) has three equilibrium points (0, 0, 0), (0, 1, 0), (1, 0, 1). And when \(a_1a_2<1\), the system (2.4) has the fourth equilibrium point

$$\begin{aligned} (u^*,v^*,w^*)=\left( \frac{1+a_1}{1-a_1a_2},\frac{1+a_2}{1-a_1a_2}, \frac{1+a_1}{1-a_1a_2}\right) . \end{aligned}$$

Next, linearize the system (2.4) near the equilibrium point \((u^*,v^*,w^*)\), and we can obtain

$$\begin{aligned} \left\{ \begin{array}{l} u_{t}=\Delta u+a_{11} u+a_{12} v+a_{13} w, \\ v_{t}=d \Delta v+a_{21} u+a_{22} v+a_{23} w ,\\ w_{t}=\Delta w+a_{31} u+a_{32} v+a_{33} w, \end{array}\right. \end{aligned}$$
(2.5)

where

$$\begin{aligned} (a_{i j})=\left( \begin{array}{ccc}0 &{} a_{1} u^{*} &{} -u^{*} \\ r a_{2} v^{*} &{} -r v^{*} &{} 0 \\ \frac{1}{\tau } &{} 0 &{} -\frac{1}{\tau }\end{array}\right) . \end{aligned}$$

Select the following test functions

$$\begin{aligned} \left( \begin{array}{l} u \\ v \\ w \end{array}\right) =\sum _{k=1}^{\infty }\left( \begin{array}{l} C_{k}^{1} \\ C_{k}^{2} \\ C_{k}^{3} \end{array}\right) e^{\lambda t+i \kappa \cdot \gamma }, \end{aligned}$$
(2.6)

where i is the imaginary number unit, \(\lambda \) is the growth rate of the disturbance in time t, \(\kappa \cdot \kappa =k\) and k is the wave number, \(\gamma =(X,Y)\) is the two-dimensional space vector. By substituting Eq. (2.6) into equation (2.5), we can get the characteristic equation

$$\begin{aligned} {\text {det}}(A)=\left| \begin{array}{ccc} a_{11}-k^{2}-\lambda &{} a_{12} &{} a_{13} \\ a_{21} &{} a_{22}-d k^{2}-\lambda &{} a_{23} \\ a_{31} &{} a_{32} &{} a_{33}-k^{2}-\lambda \end{array}\right| =0, \end{aligned}$$

which is equivalent to

$$\begin{aligned} \lambda ^{3}+b_{1}(k) \lambda ^{2}+b_{2}(k) \lambda +b_{3}(k)=0, \end{aligned}$$
(2.7)

where

$$\begin{aligned} \begin{aligned}&b_{1}(k)=(d+2) k^{2}+r v^{*}+\frac{1}{\tau },\\&b_{2}(k)=(2 d+1) k^{4}+\left( 2 r v^{*}+\frac{d+1}{\tau }\right) k^{2}+\frac{u^{*}}{\tau }+\frac{r v^{*}}{\tau }-r a_{1} a_{2} u^{*} v^{*}, \\&b_{3}(k)=d k^{6}+\left( \frac{d}{\tau }+r v^{*}\right) k^{4}+\left( \frac{r v^{*}}{\tau }+\frac{d u^{*}}{\tau }-r a_{1} a_{2} u^{*} v^{*}\right) k^{2}+\frac{r\left( 1-a_{1} a_{2}\right) u^{*} v^{*}}{\tau }. \end{aligned} \end{aligned}$$

Obviously, from the characteristic Eq. (2.7), we can see that the eigenvalue is not always negative, which further shows that under the influence of nonlocal delay, the system (2.4) may lose stability near the positive equilibrium point \((u^*,v^*,w^*)\).

Next, with the help of analysis the characteristic equation for non-diffusion and diffusion, we look for some conditions of Turing bifurcation arising around \((u^*,v^*,w^*)\).

When the system (2.4) has no diffusion term, its characteristic equation is as follows

$$\begin{aligned} \lambda ^{3}+b_{1}(0) \lambda ^{2}+b_{2}(0) \lambda +b_{3}(0)=0, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} b_{1}(0)&=r v^{*}+\frac{1}{\tau },\\ b_{2}(0)&=\frac{u^{*}}{\tau }+\frac{r v^{*}}{\tau }-r a_{1} a_{2} u^{*} v^{*}, \\ b_{3}(0)&= \frac{r\left( 1-a_{1} a_{2}\right) u^{*} v^{*}}{\tau }. \end{aligned} \end{aligned}$$

So, we can get the proposition below.

Proposition 1

The positive equilibrium point \((u^*,v^*,w^*)\) of system (2.4) is stable only when these conditions are satisfied:

$$\begin{aligned} \left\{ \begin{array}{l} b_{1}(0)>0, b_{3}(0)>0, \\ b_{1}(0) b_{2}(0)>b_{3}(0), \end{array}\right. \end{aligned}$$
(2.8)

Proof

According to the ordinary differential equations, we know that the necessary and sufficient conditions for the stability of equilibrium point \((u^*,v^*,w^*)\) are: \(Re(\lambda _i)<0\) ( i=1, 2, 3). Then, according to the Routh–Hurwitz criterion, we can get \(Re(\lambda _i)<0\) only when the above conditions are satisfied. This completes the proof. \(\square \)

When the system (2.4) has diffusion term, similar to Proposition 1, we can obtain that the positive equilibrium point \((u^*,v^*,w^*)\) of (2.4) is stable only when these conditions are satisfied:

  1. (1)

    \(b_{1}(k)>0\);

  2. (2)

    \(b_{3}(k)>0\);

  3. (3)

    \(b_{1}(k) b_{2}(k)>b_{3}(k).\)

When any of these conditions is broken, the coexistence equilibrium state of (2.4) will become unstable. In the next step, we will analyze the characteristic Eq. (2.7) to obtain the necessary condition for Turing bifurcation. Under this condition, the system will appear spatiotemporal pattern. Therefore, we consider the following three cases:

Case 1.:

The existence of \(k\in {\mathbb {R}}\) makes \(b_{1}(k)\le 0\) hold. Let \(b_1(k)=G(k^2)=(d+2) k^{2}+r v^{*}+\frac{1}{\tau }\). Because d and \(k^2\) are both positive numbers, then, as long as \(b_1 (0) > 0\) is established, \(b_1 (k) > 0\) will be established. Therefore, under the condition (2.8), there is no \(k\in {\mathbb {R}}\), which makes \(b_{1}(k)\le 0\).

Case 2.:

The existence of \(k\in {\mathbb {R}}\) makes \(b_{3}(k)\le 0\) hold.

Let \(b_3(k)=F(k^2)\) and \(z=k^2\), we can obtain

$$\begin{aligned} F(z)=f_1 z^3+f_2 z^2+f_3 z+f_4, \end{aligned}$$

where

$$\begin{aligned} f_{1}&=d, \\ f_2&=\frac{d}{\tau }+r v^{*},\\ f_3&=\frac{r v^{*}}{\tau }+\frac{d u^{*}}{\tau }-r a_{1} a_{2} u^{*} v^{*},\\ f_4&=\frac{r\left( 1-a_{1} a_{2}\right) u^{*} v^{*}}{\tau }. \end{aligned}$$

Obviously, we can observe that \(f_{1}>0\), \(f_{2}>0\), and

$$\begin{aligned} f_{4}=\frac{r\left( 1-a_{1} a_{2}\right) u^{*} v^{*}}{\tau }=\frac{r(1+a_{1})(1+a_{2})}{\tau (1-a_{1} a_{2})} >0, \end{aligned}$$

therefore, Turing bifurcation can only appear under the condition of \(f_3 < 0\). Furthermore, we can know the following properties about F(z).

  1. (1)

    When \(z\rightarrow \infty \), \(F(z)\rightarrow \infty \).

  2. (2)

    The first derivative of F(z) is

    $$\begin{aligned} \frac{d F(z)}{d z}=3 f_{1} z^{2}+2 f_{2}z+f_{3}, \end{aligned}$$

    because \(\frac{d F(z)}{d z}\) is a quadratic function, and \(\Delta > 0\), so F(z) has two poles:

    $$\begin{aligned} z_{1}&=\frac{-f_{2}+\sqrt{f_{2}^{2}-3 f_{1} f_{3}}}{3 f_{1}}, \\ z_{2}&=\frac{-f_{2}-\sqrt{f_{2}^{2}-3 f_{1} f_{3}}}{3 f_{1}}. \end{aligned}$$

    The second derivative of F(z) is

    $$\begin{aligned} \frac{d^2 F(z)}{d z^2}=6 f_{1} z+2f_{2}, \end{aligned}$$

    because \(f_{1}>0, f_{2}>0\), when z is large, F(z) is a concave function.

  3. (3)

    If \(z_{1}, z_{2}\) are the poles, we can see that the maximum value of the equation is keeps to the left of the minimum value, that is, \(z_{max}<z_{min}\), so \(z_{min}=z_1\).

According to the previous discussion and analysis, we can obtain that when \(b_3(k)\le 0\) and the condition (2.8) is true, Turing bifurcation will appear in system (2.4). Therefore, we can obtain the conclusion below.

Conclusion 1 If the condition (2.8) is true, Turing bifurcation will be produced only when the following conditions

$$\begin{aligned} \left\{ \begin{array}{l} f_{3}<0, \\ F\left( z_{1}\right) \le 0, \end{array}\right. \end{aligned}$$

are established.

Proof

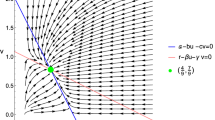
From the above analysis, \(f_3 < 0\) is necessary. Then, from the properties of F(z), we can easily get \(z _1 > 0\), and \(z _1\) is the minimum point (for the convenience of understanding, we drew the sketches of \(\frac{d F(z)}{d z}\) and F(z), as shown in Fig. 1). Therefore, the condition of \(F\left( z_{1}\right) \le 0\) is necessary. \(\square \)

Fig. 1
figure 1

This graph shows the general trend of \(\frac{dF(z)}{dz}\) and F(z)

Full size image
Case 3.:

The existence of \(k\in {\mathbb {R}}\) makes \(b_{1}(k) b_{2}(k)\le b_{3}(k)\) hold.

Let \(b_{1}(k) b_{2}(k)-b_{3}(k)=H(k^2)\) and \(z=k^2\), we can obtain

$$\begin{aligned} H(z)=h_1 z^3+h_2 z^2+h_3 z+h_4, \end{aligned}$$

where

$$\begin{aligned} h_{1}&=2(d+1)^{2}, \\ h_{2}&=\frac{(d+1)(d+3)}{\tau }+4 r(d+1) v^{*}, \\ h_{3}&=\frac{2 r(d+2) v^{*}}{\tau }+\frac{2 u^{*}}{\tau }+\frac{d+1}{\tau ^{2}}-r(d+1) a_{1} a_{2} u^{*} v^{*}, \\ h_{4}&=\frac{r^{2} v^{* 2}}{\tau }+\frac{u^{*}+r v^{*}}{\tau ^{2}}-r^{2} a_{1} a_{2} u^{*} v^{* 2}. \end{aligned}$$

Obviously we can get that \(h_{1}>0\), \(h_{2}>0\). Similar to the discussion of F(z), we can know the following properties about H(z).

  1. (1)

    When \(z\rightarrow \infty \), \(H(z)\rightarrow \infty \).

  2. (2)

    The first derivative of H(z) is

    $$\begin{aligned} \frac{d H(z)}{d z}=3 h_{1} z^{2}+2 h_{2} z+h_{3}. \end{aligned}$$

    Obviously, \(\frac{d H(z)}{d z}\) is a quadratic function. So if \(\Delta \le 0\), then \(\frac{d H(z)}{d z}\ge 0\) is constant, and H(z) is an increasing function. If \(\Delta > 0\), then H(z) has two poles:

    $$\begin{aligned} z_{1}&=\frac{-h_{2}+\sqrt{h_{2}^{2}-3 h_{1} h_{3}}}{3 h_{1}}, \\ z_{2}&=\frac{-h_{2}-\sqrt{h_{2}^{2}-3 h_{1} h_{3}}}{3 h_{1}}, \end{aligned}$$

    The second derivative of H(z) is

    $$\begin{aligned} \frac{d^2 H(z)}{d z^2}=6 h_{1} z+2h_{2}, \end{aligned}$$

    because \(h_{1}>0, h_{2}>0\), when z is large, H(z) is a concave function.

  3. (3)

    If \(z_{1}, z_{2}\) are the poles, we can see that the maximum value of the equation is keeps to the left of the minimum value, that is, \(z_{max}<z_{min}\), so \(z_{min}=z_1\).

According to the previous discussion and analysis, we can obtain that when \(b_{1}(k) b_{2}(k)\le b_{3}(k)\) and the condition (2.8) is true, Turing bifurcation will appear in the system. Therefore, we can obtain the conclusion below.

Conclusion 2 If the condition (2.8) is true, Turing bifurcation will be produced only when the following conditions are true

$$\begin{aligned} \left\{ \begin{array}{l} h_{3}<0, \\ H\left( z_{1}\right) \le 0. \end{array}\right. \end{aligned}$$

Proof

It can be seen from the condition (2.8) that \(h_1> 0, h_2>0, h_4>0\), therefore,Turing bifurcation can only appear under the condition of \(h_3 < 0\). So \(h_3 < 0\) is necessary. Then, from the properties of H(z), we can easily get \(z _1 > 0\), and \(z_1\) is the minimum point (for the convenience of understanding, we drew the sketches of \(\frac{d H(z)}{d z}\) and H(z), as shown in Fig. 2). Therefore,the condition of \(H\left( z_{1}\right) \le 0\) is necessary. \(\square \)

Fig. 2
figure 2

This graph shows the general trend of \(\frac{dH(z)}{dz}\) and H(z)

Full size image

Obviously, we can see that the conditions for conclusions 1 and 2 are a little complex. For the convenience of understanding, we have plotted Fig. 3, which directly shows the overview of these conditions. The green area indicate the value range of the parameters that may appear Turing bifurcation. In other words, if we set the values of r , \(a_1\) , \(a_2 \) to 0.1, 0.8 and 0.9, and use the conditions in conclusion 1 and conclusion 2, we can obtain the Turing space composed of parameters d and \(\tau \), as shown in Fig. 3.

Fig. 3
figure 3

The shaded area indicates Turing bifurcation space composed of parameters d and \(\tau \). The left graph shows the results under the conclusion 1 and the right graph shows the results under the conclusion 2

Full size image

It should be noted that w(x, t) satisfies the third formula in system (2.4) when \(\phi (x)\) with form (1.2). In this case, the system (1.1) and the system (2.4) are completely equivalent, and the local stability about the equilibrium point is completely equivalent by using the characteristic method, that is to say, the stability of \((u^*, v^*, w^*)\) in system (2.4) is same with the stability of \((u^*,v^*)\) in system (1.2). This is different from the stability of traveling wave in article [20]. Furthermore, even if we consider the global stability (including the influence of initial value), since the initial of w(x, t) in system (2.4) can be calculated by the initial of u(x, t) in system (2.4) (see P1977 in [17] or P16 in [16]), system (1.1) and system (2.4) both only need the initial values of u and v. Therefore, to a certain extent, we can use system (2.4) to study system (1.1), so as to overcome the difficulties caused by nonlocal effects.

3 Multiple Scale Analysis and Conclusions

In this section, we plan to make use of the multiple scale analysis method to acquire the amplitude equations that form the different Turing patterns. Then, by analyzing the stability of the amplitude equations, we can obtain the sufficient conditions for the appearance of different Turing patterns, so that different Turing patterns can be constructed by numerical simulation.

Since the coexistence equilibrium will not be stable until the wave number disturbance approaches the critical value \(k=k_T\), the multiple scale analysis method is mostly used near the bifurcation threshold. Therefore, the multiple scale analysis method is widely applied and becomes an effective method to obtain the amplitude equations. Specifically, we will first expand the nonlinear term N, variable U and control parameters \(\tau \) with a small parameter \(\varepsilon \). Then we can substitute them into the equation and compare the coefficients of \(\varepsilon \), \(\varepsilon ^2 \), \(\varepsilon ^3 \) to obtain three new equations. And then using Fredholm solvability conditions, we will acquire the amplitude equations. Finally, we will explore the stability of amplitude equations in order to construct different Turing patterns.

In the next, we first look for the amplitude equations of the system (1.1). Because in the vicinity of \(\tau =\tau _T\), the eigenvalues are close to zero near the critical modules, we can know that they are slowly changing modules. However, those modules that deviate from the critical mode will soon relax. Therefore, we are supposed to consider the perturbations of k in the vicinity of \(k_T\). To do this, we first look for \(k_T\). Therefore, we are supposed to find the extreme point of \(b _3 (k) = F(k ^ 2)\) for \(k^2\), that is, we are supposed to obtain the solution of \(\frac{d F(z)}{d z}= 3f _ 1z ^ 2 +2f _ 2z + f _ 3\). From the discussion in section 2, we can get:

$$\begin{aligned} z_1=(k_T)^2=\frac{-f_{2}+\sqrt{f_{2}^{2}-3 f_{1} f_{3}}}{3 f_{1}}. \end{aligned}$$

Substituting \(k = k _ T\) into \(b_ 3 (k) = 0\), the value of \(\tau _T\) can be obtained. It should be noted that \(k_T\) and \(\tau _T\) do not need to give a specific formulas. We only need to give the values of parameters \(a _1, a _ 2, d \) and r to get the values of \(k_T\) and \(\tau _T\) .

Next, we rewrite the system (2.4) near the equilibrium point \((u^*,v^*,w^*)\) to the following form

$$\begin{aligned} \left\{ \begin{array}{l} u_{t}=\Delta u+a_{11} u+a_{12} v+a_{13} w+N_{1}(u, v, w), \\ v_{t}=d \Delta v+a_{21} u+a_{22} v+a_{23} w+N_{2}(u, v, w), \\ w_{t}=\Delta w+a_{31} u+a_{32} v+a_{33} w+N_{3}(u, v, w), \end{array}\right. \end{aligned}$$
(3.1)

where

$$\begin{aligned} N_{1}(u, v, w)&=a_{1} u v-u w, \\ N_{2}(u, v, w)&=r a_{2} u v-r v^{2}, \\ N_{3}(u, v, w)&=0. \end{aligned}$$

Since close to onset \(\tau =\tau _{T}\), the solutions of system (2.4) are able to be represented as

$$\begin{aligned} U=U_{s}+\sum _{j=1}^{3} U_{o}\left[ {A}_{j} e^{i \mathrm {k}_{j} \cdot r}+{\bar{A}}_{j} e^{-i \mathrm {k}_{j} \cdot \mathrm {r}}\right] , \end{aligned}$$
(3.2)

where \(\left| k_{j}\right| =k_{T} \) and \(k_{j}\), \(-k_{j}\ ( j=1, 2, 3)\) are a couple of oscillatory wave vectors with different directions. Analogously, the solutions of system (3.1) are able to expand to (3.2) as follows

$$\begin{aligned} U^{0}=\sum _{j=1}^{3} U_{0}\left[ {A}_{j} e^{i \mathrm {k}_{j} \cdot r}+{\bar{A}}_{j} e^{-i \mathrm {k}_{j} \cdot \mathrm {r}}\right] , \end{aligned}$$

where \( U_{s} \) indicates the homogeneous steady state and \(U_{0}= (l_1, l_2, 1)^{T}\) (the value of \(l_1\), \(l_2\) will be determined below) is the characteristic value of the linearized operator. \(A_{j}\) and the conjugate \({\bar{A}}_{j}\) are the amplitudes integrated with the modes \(\mathrm {k}_{j} \) and \(-\mathrm {k}_{j}\), respectively. Let \(U=(u, v, w)^T\), \(N=(N_1, N_2, N_3)^T\), the system (3.1) is equivalent to the form below

$$\begin{aligned} \frac{\partial U}{\partial t}=LU+N, \end{aligned}$$
(3.3)

where

$$\begin{aligned} L= &\,\left( \begin{array}{ccc}a_{11}+\Delta &{} a_{12} &{} a_{13} \\ a_{21} &{} a_{22}+d \Delta &{} a_{23} \\ a_{31} &{} a_{32} &{} a_{33}+\Delta \end{array}\right) , \\ N= &\,\left( \begin{array}{c}a_{1} u v-u w \\ r a_{2} u v-r v^{2} \\ 0\end{array}\right) . \end{aligned}$$

Let

$$\begin{aligned} L=L_{T}+\left( \tau _{T}-\tau \right) M, \end{aligned}$$
(3.4)

where

$$\begin{aligned} L_{T}= &\,\left( \begin{array}{ccc}a_{11}^{*}+\Delta &{} a_{12}^{*} &{} a_{13}^{*} \\ a_{21}^{*} &{} a_{22}^{*}+d \Delta &{} a_{23}^{*} \\ a_{31}^{*} &{} a_{32}^{*} &{} a_{33}^{*}+\Delta \end{array}\right) , \\ M= &\,\left( \begin{array}{lll}b_{11} &{} b_{12} &{} b_{13} \\ b_{21} &{} b_{22} &{} b_{23} \\ b_{31} &{} b_{32} &{} b_{33}\end{array}\right) , \end{aligned}$$

and

$$\begin{aligned} a_{11}^{*}&=0,\quad a_{12}^{*}=\frac{a_{1}\left( 1+a_{1}\right) }{1-a_{1} a_{2}},\quad a_{13}^{*}=-\frac{\left( 1+a_{1}\right) }{1-a_{1} a_{2}},\\ a_{21}^{*}&=\frac{r a_{2}\left( 1+a_{2}\right) }{1-a_{1} a_{2}},\quad \ a_{22}^{*}=-\frac{r\left( 1+a_{2}\right) }{1-a_{1} a_{2}},\quad a_{23}^{*}=0,\\ a_{31}^{*}&=\frac{1}{\tau _{T}}, \quad a_{32}^{*}=0,\quad a_{33}^{*}=-\frac{1}{\tau _{T}},\\ b_{11}^{*}&=\frac{a_{11}-a_{11}^{*}}{\tau _{T}-\tau },\quad b_{12}^{*}=\frac{a_{12}-a_{12}^{*}}{\tau _{T}-\tau },\quad b_{13}^{*}=\frac{a_{13}-a_{13}^{*}}{\tau _{T}-\tau },\\ b_{21}^{*}&=\frac{a_{21}-a_{21}^{*}}{\tau _{T}-\tau },\quad \ b_{22}^{*}=\frac{a_{22}-a_{22}^{*}}{\tau _{T}-\tau },\quad b_{23}^{*}=\frac{a_{23}-a_{23}^{*}}{\tau _{T}-\tau },\\ b_{31}^{*}&=\frac{a_{31}-a_{31}^{*}}{\tau _{T}-\tau },\quad b_{32}^{*}=\frac{a_{32}-a_{32}^{*}}{\tau _{T}-\tau },\quad b_{33}^{*}=\frac{a_{33}-a_{33}^{*}}{\tau _{T}-\tau }. \end{aligned}$$

Using the multiple scale method, we can expand the nonlinear term N, the variable U and the control parameter \(\tau \) in the following forms with a small parameter \(\varepsilon \).

$$\begin{aligned} \tau _{T}-\tau= &\,\varepsilon \tau _{1}+\varepsilon ^{2} \tau _{2}+\varepsilon ^{3} \tau _{3}+o\left( \varepsilon ^{4}\right) , \end{aligned}$$
(3.5)
$$\begin{aligned} U= &\,\left( \begin{array}{l}u \\ v \\ w\end{array}\right) =\varepsilon \left( \begin{array}{l}u_{1} \\ v_{1} \\ w_{1}\end{array}\right) +\varepsilon ^{2}\left( \begin{array}{l}u_{2} \\ v_{2} \\ w_{2}\end{array}\right) +\varepsilon ^{3}\left( \begin{array}{l}u_{3} \\ v_{3} \\ w_{3}\end{array}\right) +o\left( \varepsilon ^{4}\right) , \end{aligned}$$
(3.6)
$$\begin{aligned} N= &\,\varepsilon ^{2} h_{1}+\varepsilon ^{3} h_{2}+o\left( \varepsilon ^{4}\right) , \end{aligned}$$
(3.7)
$$\begin{aligned} \frac{\partial }{\partial t}= &\,\frac{\partial }{\partial T_{0}}+\varepsilon \frac{\partial }{\partial T_{1}}+\varepsilon ^{2} \frac{\partial }{\partial T_{2}}+o\left( \varepsilon ^{3}\right) , \end{aligned}$$
(3.8)
$$\begin{aligned} \frac{\partial A}{\partial t}= &\,\varepsilon \frac{\partial A}{\partial T_{1}}+\varepsilon ^{2} \frac{\partial A}{\partial T_{2}}+o\left( \varepsilon ^{3}\right) , \end{aligned}$$
(3.9)

where \(h^{2}\) and \( h^{3}\) express the second and the third order of \(\varepsilon \) in the expansion of the nonlinear term N, respectively, and \(T_{0}=t\), \(T_{1}=\varepsilon t\), \(T_{2}=\varepsilon ^2t\), A is the amplitude.

Then from (3.3) and (3.4), we can get

$$\begin{aligned} \frac{\partial U}{\partial t}=L U+N=\left( L_{T}+\left( \tau _{T}-\tau \right) M\right) U+N=L_{T} U+\left( \tau _{T}-\tau \right) M U+N. \end{aligned}$$
(3.10)

By substituting (3.5)–(3.8) into (3.10), we can get

$$\begin{aligned}&\frac{\partial }{\partial t}\left( \varepsilon \begin{pmatrix} u_{1} \\ v_{1} \\ w_{1}\\ \end{pmatrix} +\varepsilon ^{2} \begin{pmatrix} u_{2} \\ v_{2} \\ w_{2}\\ \end{pmatrix} +\varepsilon ^{3} \begin{pmatrix} u_{3} \\ v_{3} \\ w_{3}\\ \end{pmatrix}\right) \nonumber \\&\quad =L_{T}\left( \varepsilon \begin{pmatrix} u_{1} \\ v_{1} \\ w_{1}\\ \end{pmatrix} +\varepsilon ^{2} \begin{pmatrix} u_{2} \\ v_{2} \\ w_{2}\\ \end{pmatrix}+\varepsilon ^{3} \begin{pmatrix} u_{3} \\ v_{3} \\ w_{3}\\ \end{pmatrix}\right) +\left( \varepsilon \tau _{1}+ \varepsilon ^{2} \tau _{2}+\varepsilon ^{3} \tau _{3}\right) M\nonumber \\&\qquad \times \left( \varepsilon \begin{pmatrix} u_{1} \\ v_{1} \\ w_{1}\\ \end{pmatrix}+\varepsilon ^{2} \begin{pmatrix} u_{2} \\ v_{2} \\ w_{2}\\ \end{pmatrix}+\varepsilon ^{3} \begin{pmatrix} u_{3} \\ v_{3} \\ w_{3}\\ \end{pmatrix}\right) +\varepsilon ^{2} h_{1}+\varepsilon ^{3} h_{2}+o(\varepsilon ^{4}), \end{aligned}$$
(3.11)

where

$$\begin{aligned}&\frac{\partial }{\partial t}\left( \varepsilon \begin{pmatrix} u_{1} \\ v_{1} \\ w_{1}\\ \end{pmatrix} +\varepsilon ^{2}\begin{pmatrix} u_{2} \\ v_{2} \\ w_{2}\\ \end{pmatrix} +\varepsilon ^{3}\begin{pmatrix} u_{3} \\ v_{3} \\ w_{3}\\ \end{pmatrix}\right) \\&\quad =\varepsilon ^{2} \frac{\partial }{\partial T_{1}}\begin{pmatrix} u_{1} \\ v_{1} \\ w_{1}\\ \end{pmatrix}+\varepsilon ^{3} \frac{\partial }{\partial T_{1}} \begin{pmatrix} u_{2} \\ v_{2} \\ w_{2}\\ \end{pmatrix}+\varepsilon ^{3} \frac{\partial }{\partial T_{2}} \begin{pmatrix} u_{1} \\ v_{1} \\ w_{1}\\ \end{pmatrix} +o\left( \varepsilon ^{4}\right) . \end{aligned}$$

Compare the coefficients of \(\varepsilon \) on both sides of the Eq. (3.11), we can get

$$\begin{aligned} L_{T}\left( \begin{array}{c}u_{1} \\ v_{1} \\ w_{1}\end{array}\right) =0. \end{aligned}$$
(3.12)

Compare the coefficients of \(\varepsilon ^2\) on both sides of the Eq. (3.11), we can get

$$\begin{aligned} \frac{\partial }{\partial T_{1}}\left( \begin{array}{l} u_{1} \\ v_{1} \\ w_{1} \end{array}\right) =L_{T}\left( \begin{array}{l} u_{2} \\ v_{2} \\ w_{2} \end{array}\right) +\tau _{1} M\left( \begin{array}{l} u_{1} \\ v_{1} \\ w_{1} \end{array}\right) +h_{1}. \end{aligned}$$
(3.13)

Compare the coefficients of \(\varepsilon ^3\) on both sides of the Eq. (3.11), we can get

$$\begin{aligned} \frac{\partial }{\partial T_{1}}\left( \begin{array}{l} u_{2} \\ v_{2} \\ w_{2} \end{array}\right) +\frac{\partial }{\partial T_{2}}\left( \begin{array}{l} u_{1} \\ v_{1} \\ w_{1} \end{array}\right) =L_{T}\left( \begin{array}{l} u_{3} \\ v_{3} \\ w_{3} \end{array}\right) +\tau _{1} M\left( \begin{array}{l} u_{2} \\ v_{2} \\ w_{2} \end{array}\right) +\tau _{2} M\left( \begin{array}{l} u_{1} \\ v_{1} \\ w_{1} \end{array}\right) . \end{aligned}$$
(3.14)

For the first order of \(\varepsilon \) as (3.12), because \(L_{T}\) is the linear operator close to the onset in the system, \( (u_{1}, v_{1}, w_1) ^{T}\) is the linear combination of characteristic vector corresponding to the characteristic value 0. Solving (3.12), we can get

$$\begin{aligned} \left( \begin{array}{l} u_{1} \\ v_{1} \\ w_{1} \end{array}\right) =\left( \begin{array}{l} l_{1} \\ l_{2} \\ 1 \end{array}\right) \left( W_{1} e^{i k_{1} \gamma }+W_{2} e^{i k_{2} \gamma }+W_{3} e^{i k_{3} \gamma }+c . c .\right) , \end{aligned}$$
(3.15)

where

$$\begin{aligned} l_{1}&= \frac{2}{3}-\frac{r v^{*} \tau _{T}}{3 d}, \\ l_{2}&= \frac{1}{a_{1}}+\frac{r^{2} v^{* 2} \tau _{T}^{2}-d r v^{*} \tau _{T}-2 d^{2}}{9 d^{2} a_{1} u^{*} \tau _{T}}, \\ \left| k_{j}\right|&=k_{T}, \end{aligned}$$

\(W_{j} \) represents the amplitude about the mode \( e^{i k_{1} r}\ (j = 1, 2, 3)\) of the system on the first order perturbation, and c.c. represents the conjugate of the previous term. Its form is determined by the perturbation terms of the higher order.

For the second order of \(\varepsilon \) as (3.13), we have

$$\begin{aligned} L_{T} \begin{pmatrix} u_{2} \\ v_{2} \\ w_{2}\\ \end{pmatrix}&=\frac{\partial }{\partial T_{1}} \begin{pmatrix} u_{1} \\ v_{1} \\ w_{1}\\ \end{pmatrix} -\tau _{1} M \begin{pmatrix} u_{1} \\ v_{1} \\ w_{1}\\ \end{pmatrix}-h_{1}\nonumber \\&=\frac{\partial }{\partial T_{1}} \begin{pmatrix} u_{1} \\ v_{1} \\ w_{1}\\ \end{pmatrix} -\tau _{1} \begin{pmatrix} b_{11} u_{1}+b_{12} v_{1}+b_{13} w_{1} \\ b_{21} u_{1}+b_{22} v_{1}+b_{23} w_{1} \\ b_{31} u_{1}+b_{32} v_{1}+b_{33} w_{1}\\ \end{pmatrix}- \begin{pmatrix} a_{1} u_{1} v_{1}-u_{1} w_{1} \\ r a_{2} u_{1} v_{1}-r v_{1}^{2}\\ 0 \end{pmatrix}\nonumber \\&=\begin{pmatrix} F_{u} \\ F_{v} \\ F_{w} \end{pmatrix}. \end{aligned}$$
(3.16)

In order to make sure the existence of the nontrivial solution of this Eq. (3.16), let the adjoint operator of \(L_{T}\) be \(L_{T}^{*}\). And then according to the Fredholm solubility conditions, we can know that the vector-valued function on the right hand side of (3.16) need be orthogonal with the zero characteristic vector of operator \(L_{T}^{*}\). In this system, the zero eigenvector of \(L_{T}^{*}\) is

$$\begin{aligned} \begin{pmatrix} 1\\ l_{1}^{\prime } \\ l_{2}^{\prime } \end{pmatrix}+c.c., ( j=1, 2, 3), \end{aligned}$$

where

$$\begin{aligned} l_{1}^{\prime }&=\frac{d-2 r v^{*} \tau _{T}}{2 d r a_{2} v^{*} \tau _{T}}, \\ l_{2}^{\prime }&=-\frac{3}{4}+\frac{r v^{*} \tau _{T}}{2 d}. \end{aligned}$$

Therefore, we can obtain

$$\begin{aligned} \left( 1, l_{1}^{\prime }, l_{2}^{\prime }\right) \left( \begin{array}{l}F_{u}^{i} \\ F_{v}^{i} \\ F_{w}^{i}\end{array}\right) =0, \end{aligned}$$
(3.17)

where \(F_{u}^{j}\), \(F_{v}^{j}\) and \(F_{w}^{j}\) correspond to the coefficients of \( e^{i k_{j} r}\) in \(F_{u}\), \(F_{v}\) and \(F_{w}\), respectively, it means that

$$\begin{aligned} \left( \begin{array}{l} F_{u} \\ F_{v} \\ F_{w} \end{array}\right) =\left( \begin{array}{l} F_{u}^{1} \\ F_{v}^{1} \\ F_{w}^{1} \end{array}\right) e^{i k_{1} \gamma }+\left( \begin{array}{l} F_{u}^{2} \\ F_{v}^{2} \\ F_{w}^{2} \end{array}\right) e^{i k_{2} \gamma }+\left( \begin{array}{c} F_{u}^{3} \\ F_{v}^{3} \\ F_{w}^{3} \end{array}\right) e^{i k_{3} \gamma }. \end{aligned}$$

According to (3.15) and (3.16), we can get

$$\begin{aligned} \left( \begin{array}{c} F_{u}^{1} \\ F_{v}^{1} \\ F_{w}^{1} \end{array}\right)= &\,\left( \begin{array}{c} l_{1} \frac{\partial W_{1}}{\partial T_{1}} \\ l_{2} \frac{\partial W_{1}}{\partial T_{1}} \\ \frac{\partial W_{1}}{\partial T_{1}} \end{array}\right) -\tau _{1}\left( \begin{array}{c} l_{1} b_{11}+l_{2} b_{12}+b_{13} \\ l_{1} b_{21}+l_{2} b_{22}+b_{23} \\ l_{1} b_{31}+l_{2} b_{32}+b_{33} \end{array}\right) W_{1}\nonumber \\&-\left( \begin{array}{c} 2 a_{1} l_{1} l_{2}-2 l_{1} \\ 2 r a_{2} l_{1} l_{2}-2 r l_{2}^{2}\\ 0\end{array}\right) \overline{W_{2}}\cdot \overline{ W_{3}}= 0, \end{aligned}$$
(3.18)
$$\begin{aligned} \left( \begin{array}{c} F_{u}^{2} \\ F_{v}^{2} \\ F_{w}^{2} \end{array}\right)= &\,\left( \begin{array}{c} l_{1} \frac{\partial W_{2}}{\partial T_{1}} \\ l_{2} \frac{\partial W_{2}}{\partial T_{1}} \\ \frac{\partial W_{2}}{\partial T_{1}} \end{array}\right) -\tau _{1}\left( \begin{array}{c} l_{1} b_{11}+l_{2} b_{12}+b_{13} \\ l_{1} b_{21}+l_{2} b_{22}+b_{23} \\ l_{1} b_{31}+l_{2} b_{32}+b_{33} \end{array}\right) W_{2}\nonumber \\&-\left( \begin{array}{c} 2 a_{1} l_{1} l_{2}-2 l_{1} \\ 2 r a_{2} l_{1} l_{2}-2 r l_{2}^{2}\\ 0\end{array}\right) \overline{W_{1}}\cdot \overline{ W_{3}}= 0, \end{aligned}$$
(3.19)
$$\begin{aligned} \left( \begin{array}{c} F_{u}^{3} \\ F_{v}^{3} \\ F_{w}^{3} \end{array}\right)= &\,\left( \begin{array}{c} l_{1} \frac{\partial W_{3}}{\partial T_{1}} \\ l_{2} \frac{\partial W_{3}}{\partial T_{1}} \\ \frac{\partial W_{3}}{\partial T_{1}} \end{array}\right) -\tau _{1}\left( \begin{array}{c} l_{1} b_{11}+l_{2} b_{12}+b_{13} \\ l_{1} b_{21}+l_{2} b_{22}+b_{23} \\ l_{1} b_{31}+l_{2} b_{32}+b_{33} \end{array}\right) W_{3}\nonumber \\&-\left( \begin{array}{c} 2 a_{1} l_{1} l_{2}-2 l_{1} \\ 2 r a_{2} l_{1} l_{2}-2 r l_{2}^{2}\\ 0\end{array}\right) \overline{W_{1}}\cdot \overline{ W_{2}}= 0. \end{aligned}$$
(3.20)

Using the Fredholm solubility condition and taking (3.18)–(3.20) into (3.17), we can get the following results

$$\begin{aligned} {\left\{ \begin{array}{ll} \left( l_{1}+l_{1}^{\prime } l_{2}+l_{2}^{\prime }\right) \frac{\partial W_{1}}{\partial T_{1}}&{}=\tau _{1} W_{1}\left[ l_{1} b_{11}+l_{2} b_{12}+b_{13}+l_{1}^{\prime }\left( l_{1} b_{21}+l_{2} b_{22}+b_{23}\right) \right. \\ &{}\quad +\left. l_{2}^{\prime }\left( l_{1} b_{31}+l_{2} b_{32}+b_{33}\right) \right] +\left[ 2 a_{1} l_{1} l_{2}-2 l_{1}+l_{1}^{\prime }(2 r a_{2} l_{1} l_{2} \right. \\ &{}\quad \left. -2 r l_{2}^{2})\right] \overline{W_{2}}\cdot \overline{ W_{3}}, \\ \left( l_{1}+l_{1}^{\prime } l_{2}+l_{2}^{\prime }\right) \frac{\partial W_{2}}{\partial T_{1}}&{}=\tau _{1} W_{2}\left[ l_{1} b_{11}+l_{2} b_{12}+b_{13}+l_{1}^{\prime }\left( l_{1} b_{21}+l_{2} b_{22}+b_{23}\right) \right. \\ &{}\quad +\left. l_{2}^{\prime }\left( l_{1} b_{31}+l_{2} b_{32}+b_{33}\right) \right] +\left[ 2 a_{1} l_{1} l_{2}-2 l_{1}+l_{1}^{\prime }(2 r a_{2} l_{1} l_{2}\right. \\ &{}\quad \left. -2 r l_{2}^{2})\right] \overline{W_{1}}\cdot \overline{ W_{3}},\\ \left( l_{1}+l_{1}^{\prime } l_{2}+l_{2}^{\prime }\right) \frac{\partial W_{3}}{\partial T_{1}}&{}=\tau _{1} W_{3}\left[ l_{1} b_{11}+l_{2} b_{12}+b_{13}+l_{1}^{\prime }\left( l_{1} b_{21}+l_{2} b_{22}+b_{23}\right) \right. \\ &{}\quad +\left. l_{2}^{\prime }\left( l_{1} b_{31}+l_{2} b_{32}+b_{33}\right) \right] +\left[ 2 a_{1} l_{1} l_{2}-2 l_{1}+l_{1}^{\prime }(2 r a_{2} l_{1} l_{2}\right. \\ &{}\quad \left. -2 r l_{2}^{2})\right] \overline{W_{1}}\cdot \overline{ W_{2}}. \end{array}\right. } \end{aligned}$$
(3.21)

By substituting (3.15) into (3.16), we can get

$$\begin{aligned} \begin{aligned} \left( \begin{array}{l} u_{2} \\ v_{2} \\ w_{2} \end{array}\right)&=\left( \begin{array}{l} U_{0} \\ V_{0} \\ W_{0} \end{array}\right) +\sum _{i=1}^{3}\left( \begin{array}{l} U_{i} \\ V_{i} \\ W_{i} \end{array}\right) e^{i k_{i} \gamma }+\sum _{i=1}^{3}\left( \begin{array}{c} U_{i i} \\ V_{i i} \\ W_{i i} \end{array}\right) e^{i 2 k_{i} \gamma }+\left( \begin{array}{l} U_{12} \\ V_{12} \\ W_{12} \end{array}\right) e^{i\left( k_{1}-k_{2}\right) \gamma }\\&\quad +\left( \begin{array}{l} U_{23} \\ V_{23} \\ W_{23} \end{array}\right) e^{i\left( k_{2}-k_{3}\right) \gamma }+\left( \begin{array}{c} U_{31} \\ V_{31} \\ W_{31} \end{array}\right) e^{i\left( k_{3}-k_{1}\right) \gamma }+c . c . \end{aligned}. \end{aligned}$$
(3.22)

At the same time, we can obtain the coefficients in (3.22) through solving the linear equations about \( e^{0}\), \( e^{i k_{j} r}\), \( e^{i 2k_{j} r}\), \( e^{i (k_{j}-k_{m}) r}\), and we can know

$$\begin{aligned}&\begin{pmatrix} U_{0} \\ V_{0} \\ Y_{0}\\ \end{pmatrix} =\begin{pmatrix} u_{0} \\ v_{0} \\ y_{0}\\ \end{pmatrix}\left( \left| W_{1}\right| ^{2}+\left| W_{2}\right| ^{2} +\left| W_{3}\right| ^{2}\right) ,\quad U_{i}=l_{1} Y_{i},\ V_{i}=l_{2} Y_{i}, \\&\begin{pmatrix} U_{i i} \\ V_{i i} \\ Y_{i i}\\ \end{pmatrix} = \begin{pmatrix} u_{11} \\ v_{11} \\ y_{11}\\ \end{pmatrix} W_{i}^{2}, \quad \begin{pmatrix} U_{i j} \\ V_{i j} \\ Y_{i j}\\ \end{pmatrix}=\begin{pmatrix} u_{12} \\ v_{12} \\ y_{12}\\ \end{pmatrix} W_{i} {\overline{W}}_{j}, \end{aligned}$$

where

$$\begin{aligned} \begin{pmatrix} u_{0} \\ v_{0} \\ y_{0}\\ \end{pmatrix}&=\begin{pmatrix} \frac{-a_{12}^{*}\left( 2 r a_{2} l_{1} l_{2}-2 r l_{2}^{2}\right) +a_{22}^{*}\left( 2 a_{1} l_{1} l_{2}-2 l_{1}\right) }{a_{12}^{*} a_{21}^{*}-a_{22}^{*} a_{13}^{*}} \\ \frac{-a_{21}^{*}\left( 2 a_{1} l_{1} l_{2}-2 l_{1}\right) +a_{13}^{*}\left( 2 r a_{2} l_{1} l_{2}-2 r l_{2}^{2}\right) }{a_{12}^{*} a_{21}^{*}-a_{22}^{*} a_{13}^{*}} \\ u_{0} \end{pmatrix},\\ \begin{pmatrix} u_{11} \\ v_{11} \\ y_{11}\\ \end{pmatrix}&=\begin{pmatrix} \left( 1+4 k_{T}^{2} \tau _{T}\right) y_{11} \\ \frac{a_{21}^{*}\left( 1+4 k_{T}^{2} \tau _{T}\right) \left( a_{1} l_{1} l_{2}-l_{1}\right) +\left( r a_{2} l_{1} l_{2}-r l_{2}^{2}\right) \left[ \left( 1+4 k_{T}^{2} \tau _{T}\right) 4 k_{T}^{2}-a_{13}^{*}\right] }{\left( 4 d k_{T}^{2}-a_{22}^{*}\right) \left[ \left( 1+4 k_{T}^{2} \tau _{T}\right) 4 k_{T}^{2}-a_{13}^{*}\right] -a_{12}^{*} a_{21}^{*}\left( 1+4 k_{T}^{2} \tau _{T}\right) } \\ \frac{\left( 4 d k_{T}^{2}-a_{22}^{*}\right) \left( a_{1} l_{1} l_{2}-l_{1}\right) +a_{12}^{*}\left( r a_{2} l_{1} l_{2}-r l_{2}^{2}\right) }{\left( 4 d k_{T}^{2}-a_{22}^{*}\right) \left[ \left( 1+4 k_{T}^{2} \tau _{T}\right) 4 k_{T}^{2}-a_{13}^{*}\right] -a_{12}^{*} a_{21}^{*}\left( 1+4 k_{T}^{2} \tau _{T}\right) }\\ \end{pmatrix},\\ \begin{pmatrix} u_{12} \\ v_{12} \\ y_{12}\\ \end{pmatrix}&=\begin{pmatrix} \left( 1+3 k_{T}^{2} \tau _{T}\right) y_{12} \\ \frac{a_{21}^{*}\left( 1+3 k_{T}^{2} \tau _{T}\right) \left( 2 a_{1} l_{1} l_{2}-2 l_{1}\right) +\left( 2 r a_{2} l_{1} l_{2}-2 r l_{2}^{2}\right) \left[ \left( 1+3 k_{T}^{2} \tau _{T}\right) 3 k_{T}^{2}-a_{13}^{*}\right] }{\left( 3 d k_{T}^{2}-a_{22}^{*}\right) \left[ \left( 1+3 k_{T}^{2} \tau _{T}\right) 3 k_{T}^{2}-a_{13}^{*}\right] -a_{12}^{*} a_{21}^{*}\left( 1+3 k_{T}^{2} \tau _{T}\right) } \\ \frac{\left( 3 d k_{T}^{2}-a_{22}^{*}\right) \left( 2 a_{1} l_{1} l_{2}-2 l_{1}\right) +a_{12}^{*}\left( 2 r a_{2} l_{1} l_{2}-2 r l_{2}^{2}\right) }{\left( 3 d k_{T}^{2}-a_{22}^{*}\right) \left[ \left( 1+3 k_{T}^{2} \tau _{T}\right) 3 k_{T}^{2}-a_{13}^{*}\right] -a_{12}^{*} a_{21}^{*}\left( 1+3 k_{T}^{2} \tau _{T}\right) }\\ \end{pmatrix}. \end{aligned}$$

For the third order of \(\varepsilon \) as (3.14), we have

$$\begin{aligned} \begin{aligned}&L_{T}\left( \begin{array}{c} u_{3} \\ v_{3} \\ w_{3} \end{array}\right) = \frac{\partial }{\partial T_{1}}\left( \begin{array}{c} u_{2} \\ v_{2} \\ w_{2} \end{array}\right) +\frac{\partial }{\partial T_{2}}\left( \begin{array}{c} u_{1} \\ v_{1} \\ w_{1} \end{array}\right) -\tau _{1}\left( \begin{array}{c} b_{11} u_{2}+b_{12} v_{2}+b_{13} w_{2} \\ b_{21} u_{2}+b_{22} v_{2}+b_{23} w_{2} \\ b_{31} u_{2}+b_{32} v_{2}+b_{33} w_{2} \end{array}\right) \\&\quad -\tau _{2}\left( \begin{array}{c} b_{11} u_{1}+b_{12} v_{1}+b_{13} w_{1} \\ b_{21} u_{1}+b_{22} v_{1}+b_{23} w_{1} \\ b_{31} u_{1}+b_{32} v_{1}+b_{33} w_{1} \end{array}\right) +\left( \begin{array}{c} u_{1} w_{2}+u_{2} w_{1}-a_{1}\left( u_{1} v_{2}+u_{2} v_{1}\right) \\ 2 r v_{1} v_{2}-r a_{2}\left( u_{1} v_{2}+u_{2} v_{1}\right) \\ 0 \end{array}\right) =\left( \begin{array}{c} H_{u} \\ H_{v} \\ H_{w} \end{array}\right) . \end{aligned} \end{aligned}$$
(3.23)

Similar to the above discussion, taking coefficients of \( e^{i k_{j} r}, (j=1, 2, 3)\) of \(H_{u}\), \(H_{v}\) and \(H_{w}\) in Eq. (3.23), we can attain

$$\begin{aligned} \begin{pmatrix} H_{u}^{1} \\ H_{v}^{1} \\ H_{w}^{1}\\ \end{pmatrix}&=\begin{pmatrix} l_{1} \frac{\partial W_{1}}{\partial T_{2}} \\ l_{2} \frac{\partial W_{1}}{\partial T_{2}} \\ \frac{\partial W_{1}}{\partial T_{2}}\\ \end{pmatrix} +\begin{pmatrix} l_{1} \frac{\partial Y_{1}}{\partial T_{1}} \\ l_{2} \frac{\partial Y_{1}}{\partial T_{1}} \\ \frac{\partial Y_{1}}{\partial T_{1}}\\ \end{pmatrix}-\tau _{1}\begin{pmatrix} l_{1} b_{11}+l_{2} b_{12}+b_{13} \\ l_{1} b_{21}+l_{2} b_{22}+b_{23} \\ l_{1} b_{31}+l_{2} b_{32}+b_{33}\\ \end{pmatrix} Y_{1}\nonumber \\&\quad -\tau _{2} \begin{pmatrix} l_{1} b_{11}+l_{2} b_{12}+b_{13} \\ l_{1} b_{21}+l_{2} b_{22}+b_{23} \\ l_{1} b_{31}+l_{2} b_{32}+b_{33}\\ \end{pmatrix} W_{1} +\begin{pmatrix} G_{11}\left| W_{1}\right| ^{2}+G_{12}\left( \left| W_{2}\right| ^{2}+\left| W_{3}\right| ^{2}\right) \\ G_{21}\left| W_{1}\right| ^{2}+G_{22}\left( \left| W_{2}\right| ^{2}+\left| W_{3}\right| ^{2}\right) \\ 0 \end{pmatrix} W_{1}\nonumber \\&\quad +\begin{pmatrix} 2 l_{1}-2 a_{1} l_{1} l_{2} \\ 2 r l_{2}^{2}-2 r a_{2} l_{1} l_{2}\\ 0 \end{pmatrix} \left( \overline{W_{2}} \cdot {\overline{Y}}_{3}+\overline{Y_{2}}\cdot \overline{W_{3}}\right) , \end{aligned}$$
(3.24)
$$\begin{aligned} \begin{pmatrix} H_{u}^{2} \\ H_{v}^{2} \\ H_{w}^{2} \end{pmatrix}&= \begin{pmatrix} l_{1} \frac{\partial W_{2}}{\partial T_{2}} \\ l_{2} \frac{\partial W_{2}}{\partial T_{2}} \\ \frac{\partial W_{2}}{\partial T_{2}} \end{pmatrix} +\begin{pmatrix} l_{1} \frac{\partial Y_{2}}{\partial T_{1}} \\ l_{2} \frac{\partial Y_{2}}{\partial T_{1}} \\ \frac{\partial Y_{2}}{\partial T_{1}} \end{pmatrix}-\tau _{1} \begin{pmatrix} l_{1} b_{11}+l_{2} b_{12}+b_{13} \\ l_{1} b_{21}+l_{2} b_{22}+b_{23} \\ l_{1} b_{31}+l_{2} b_{32}+b_{33} \end{pmatrix} Y_{2}\nonumber \\&\quad -\tau _{2}\begin{pmatrix} l_{1} b_{11}+l_{2} b_{12}+b_{13} \\ l_{1} b_{21}+l_{2} b_{22}+b_{23} \\ l_{1} b_{31}+l_{2} b_{32}+b_{33} \end{pmatrix} W_{2} +\begin{pmatrix} G_{11}\left| W_{1}\right| ^{2}+G_{12}\left( \left| W_{2}\right| ^{2}+\left| W_{3}\right| ^{2}\right) \\ G_{21}\left| W_{1}\right| ^{2}+G_{22}\left( \left| W_{2}\right| ^{2}+\left| W_{3}\right| ^{2}\right) \\ 0 \end{pmatrix} W_{2}\nonumber \\&\quad +\begin{pmatrix} 2 l_{1}-2 a_{1} l_{1} l_{2} \\ 2 r l_{2}^{2}-2 r a_{2} l_{1} l_{2}\\ 0 \end{pmatrix} \left( \overline{W_{1}}\cdot {\overline{Y}}_{3}+\overline{Y_{1}}\cdot \overline{W_{3}}\right) , \end{aligned}$$
(3.25)
$$\begin{aligned} \begin{pmatrix} H_{u}^{3} \\ H_{v}^{3} \\ H_{w}^{3}\\ \end{pmatrix}&=\begin{pmatrix} l_{1} \frac{\partial W_{3}}{\partial T_{2}} \\ l_{2} \frac{\partial W_{3}}{\partial T_{2}} \\ \frac{\partial W_{3}}{\partial T_{2}}\\ \end{pmatrix}+ \begin{pmatrix} l_{1} \frac{\partial Y_{3}}{\partial T_{1}} \\ l_{2} \frac{\partial Y_{3}}{\partial T_{1}} \\ \frac{\partial Y_{3}}{\partial T_{1}}\\ \end{pmatrix}-\tau _{1} \begin{pmatrix} l_{1} b_{11}+l_{2} b_{12}+b_{13} \\ l_{1} b_{21}+l_{2} b_{22}+b_{23} \\ l_{1} b_{31}+l_{2} b_{32}+b_{33}\\ \end{pmatrix} Y_{3}\nonumber \\&\quad -\tau _{2}\begin{pmatrix} l_{1} b_{11}+l_{2} b_{12}+b_{13} \\ l_{1} b_{21}+l_{2} b_{22}+b_{23} \\ l_{1} b_{31}+l_{2} b_{32}+b_{33}\\ \end{pmatrix} W_{3} +\begin{pmatrix} G_{11}\left| W_{1}\right| ^{2}+G_{12}\left( \left| W_{2}\right| ^{2}+\left| W_{3}\right| ^{2}\right) \\ G_{21}\left| W_{1}\right| ^{2}+G_{22}\left( \left| W_{2}\right| ^{2}+\left| W_{3}\right| ^{2}\right) \\ 0 \end{pmatrix} W_{3}\nonumber \\&\quad +\begin{pmatrix} 2 l_{1}-2 a_{1} l_{1} l_{2} \\ 2 r l_{2}^{2}-2 r a_{2} l_{1} l_{2}\\ 0 \end{pmatrix}\left( \overline{W_{1}} \cdot {\overline{Y}}_{2}+\overline{Y_{1}}\cdot \overline{W_{2}}\right) , \end{aligned}$$
(3.26)

where

$$\begin{aligned} G_{11}&=l_{1}\left( y_{0}+y_{11}\right) +\left( u_{0}+u_{11}\right) -a_{1}l_{1}\left( v_{0}+v_{11}\right) -a_{1} l_{2}\left( u_{0}+u_{11}\right) , \\ G_{12}&=l_{1}\left( y_{0}+y_{12}\right) +\left( u_{0}+u_{12}\right) -a_{1} l_{1}\left( v_{0}+v_{12}\right) -a_{1} l_{2}\left( u_{0}+u_{12}\right) , \\ G_{21}&=2 r l_{2}\left( v_{0}+v_{11}\right) -r a_{2} l_{1}\left( v_{0}+v_{11}\right) -r a_{2} l_{2}\left( u_{0}+u_{11}\right) , \\ G_{22}&=2 r l_{2}\left( v_{0}+v_{12}\right) -r a_{2} l_{1}\left( v_{0}+v_{12}\right) -r a_{2} l_{2}\left( u_{0}+u_{12}\right) , \end{aligned}$$

Again making use of the Fredholm solubility condition and combining (3.24)–(3.26), we can get

$$\begin{aligned}&\left( l_{1}+l_{1}^{\prime } l_{2}+l_{2}^{\prime }\right) \left( \frac{\partial W_{1}}{\partial T_{2}}+\frac{\partial Y_{1}}{\partial T_{1}}\right) \nonumber \\&\quad =\left( \tau _{1} Y_{1}+\tau _{2} W_{1}\right) \left[ l_{1} b_{11}+l_{2} b_{12}+b_{13}+l_{1}^{\prime }\left( l_{1} b_{21}+l_{2} b_{22}+b_{23}\right) \right. \nonumber \\&\qquad \left. +l_{2}^{\prime }\left( l_{1} b_{31}+l_{2} b_{32}+b_{33}\right) \right] -\left[ G_{11}\left| W_{1}\right| ^{2} +G_{12}\left( \left| W_{2}\right| ^{2}+\left| W_{3}\right| ^{2}\right) \right] W_{1}\nonumber \\&\qquad -l_{1}^{\prime }\left[ G_{21}\left| W_{1}\right| ^{2}+G_{22}\left( \left| W_{2}\right| ^{2} +\left| W_{3}\right| ^{2}\right) \right] W_{1} \nonumber \\&\qquad -\left[ 2 l_{1}-2 a_{1} l_{1} l_{2}+l_{1}^{\prime }\left( 2 r l_{2}^{2}-2 r a_{2} l_{1} l_{2}\right) \right] \left( \overline{W_{2}} {\overline{Y}}_{3}+{\overline{Y}}_{2} \overline{W_{3}}\right) , \end{aligned}$$
(3.27)
$$\begin{aligned}&\left( l_{1}+l_{1}^{\prime } l_{2}+l_{2}^{\prime }\right) \left( \frac{\partial W_{2}}{\partial T_{2}}+\frac{\partial Y_{2}}{\partial T_{1}}\right) \nonumber \\&\quad =\left( \tau _{1} Y_{2}+\tau _{2} W_{2}\right) \left[ l_{1} b_{11}+l_{2} b_{12}+b_{13}+l_{1}^{\prime }\left( l_{1} b_{21}+l_{2} b_{22}+b_{23}\right) \right. \nonumber \\&\qquad \left. +l_{2}^{\prime }\left( l_{1} b_{31}+l_{2} b_{32}+b_{33}\right) \right] -\left[ G_{11}\left| W_{2}\right| ^{2}+G_{12}\left( \left| W_{1}\right| ^{2} +\left| W_{3}\right| ^{2}\right) \right] W_{2}\nonumber \\&\qquad -l_{1}^{\prime }\left[ G_{21}\left| W_{2}\right| ^{2}+G_{22}\left( \left| W_{1}\right| ^{2}+\left| W_{3}\right| ^{2}\right) \right] W_{2} \nonumber \\&\qquad -\left[ 2 l_{1}-2 a_{1} l_{1} l_{2}+l_{1}^{\prime }\left( 2 r l_{2}^{2}-2 r a_{2} l_{1} l_{2}\right) \right] \left( \overline{W_{1}} {\overline{Y}}_{3}+{\overline{Y}}_{1} \overline{W_{3}}\right) , \end{aligned}$$
(3.28)
$$\begin{aligned}&\left( l_{1}+l_{1}^{\prime } l_{2}+l_{2}^{\prime }\right) \left( \frac{\partial W_{3}}{\partial T_{2}}+\frac{\partial Y_{3}}{\partial T_{1}}\right) \nonumber \\&\quad =\left( \tau _{1} Y_{3}+\tau _{2} W_{3}\right) \left[ l_{1} b_{11}+l_{2} b_{12}+b_{13}+l_{1}^{\prime }\left( l_{1} b_{21}+l_{2} b_{22}+b_{23}\right) \right. \nonumber \\&\qquad \left. +l_{2}^{\prime }\left( l_{1} b_{31}+l_{2} b_{32}+b_{33}\right) \right] -\left[ G_{11}\left| W_{3}\right| ^{2}+G_{12}\left( \left| W_{1}\right| ^{2} +\left| W_{2}\right| ^{2}\right) \right] W_{3}\nonumber \\&\qquad -l_{1}^{\prime }\left[ G_{21}\left| W_{3}\right| ^{2} +G_{22}\left( \left| W_{1}\right| ^{2}+\left| W_{2}\right| ^{2}\right) \right] W_{3}\nonumber \\&\qquad -\left[ 2 l_{1}-2 a_{1} l_{1} l_{2}+l_{1}^{\prime }\left( 2 r l_{2}^{2}-2 r a_{2} l_{1} l_{2}\right) \right] (\overline{W_{1}} \overline{Y_{2}}+\overline{Y_{1}} \overline{W_{2}}). \end{aligned}$$
(3.29)

Let

$$\begin{aligned} \left( \begin{array}{l}A_{i}^{u} \\ A_{i}^{v} \\ A_{i}^{w}\end{array}\right) =\varepsilon \left( \begin{array}{l}l_{1} \\ l_{2} \\ 1\end{array}\right) W_{i}+\varepsilon ^{2}\left( \begin{array}{l}l_{1} \\ l_{2} \\ 1\end{array}\right) Y_{i}+o\left( \varepsilon ^{3}\right) , (i=1,2,3). \end{aligned}$$
(3.30)

By multiplying (3.21) and (3.27)–(3.29) by \(\varepsilon , \ \varepsilon ^{2}\), respectively, and combining variables with (3.9) and (3.30)at the same time, we can acquire the amplitude equations as follows

$$\begin{aligned} {\left\{ \begin{array}{ll} {s_{0} \frac{\partial A_{1}}{\partial t}=\mu A_{1}+h {\bar{A}}_{2} {\bar{A}}_{3}-\left[ g_{1}\left| A_{1}\right| ^{2}+g_{2}\left( \left| A_{2}\right| ^{2} +\left| A_{3}\right| ^{2}\right) \right] A_{1}}, \\ {s_{0} \frac{\partial A_{2}}{\partial t}=\mu A_{2}+h {\bar{A}}_{1} {\bar{A}}_{3}-\left[ g_{1}\left| A_{2}\right| ^{2}+g_{2}\left( \left| A_{1}\right| ^{2} +\left| A_{3}\right| ^{2}\right) \right] A_{2}}, \\ {s_{0} \frac{\partial A_{3}}{\partial t}=\mu A_{3}+h {\bar{A}}_{1} {\bar{A}}_{2}-\left[ g_{1}\left| A_{3}\right| ^{2}+g_{2}\left( \left| A_{1}\right| ^{2} +\left| A_{2}\right| ^{2}\right) \right] A_{3}}, \end{array}\right. } \end{aligned}$$
(3.31)

where

$$\begin{aligned} {\left\{ \begin{array}{ll} B=\left( l_{1} b_{11}+l_{2} b_{12}+b_{13}\right) +l_{1}^{\prime }\left( l_{1} b_{21}+l_{2} b_{22}+b_{23}\right) +l_{2}^{\prime }\left( l_{1} b_{31}+l_{2} b_{32}+b_{33}\right) , \\ s_{0}=\frac{\left( l_{1}+l_{1}^{\prime } l_{2}+l_{2}^{\prime }\right) }{\tau _{T} B},\quad \mu =\frac{\tau _{T}-\tau }{\tau _{T}}, \\ h=\frac{2 a_{1} l_{1} l_{2}-2 l_{1}+l_{1}^{\prime }\left( 2 r a_{2} l_{1} l_{2}-2 r l_{2}^{2}\right) }{\tau _{T} B}, \\ g_{1}=\frac{G_{11}-l_{1}^{\prime } G_{21}}{\tau _{T} B},\quad g_{2}=\frac{G_{12}-l_{1}^{\prime } G_{22}}{\tau _{T} B}. \end{array}\right. } \end{aligned}$$

After that we analyze the stability of the amplitude equations, and according to the analysis, we are able to obtain different Turing patterns. Obviously, each amplitude in (3.31) can be decomposed to a phase angle \(\varphi _{j}\) and a mode \(\rho _{j}=|A_{j}|\). Next, taking \(A_{i}=\rho _{i} e^{i\varphi _{i}}\) into (3.31) and then separating the imaginary part from the real part. As a consequence, we can obtain the following equations of the real variables

$$\begin{aligned} \left\{ \begin{array}{l}{s_{0} \frac{\partial \varphi }{\partial t}=-h \frac{\rho _{1}^{2} \rho _{2}^{2}+\rho _{1}^{2} \rho _{3}^{2}+\rho _{2}^{2} \rho _{3}^{2}}{\rho _{1} \rho _{2} \rho _{3}} \sin \varphi }, \\ {s_{0} \frac{\partial \rho _{1}}{\partial t}=\mu \rho _{1}+h \rho _{2} \rho _{3} \cos \varphi -g_{1} \rho _{1}^{3}-g_{2} \rho _{2}^{2} \rho _{3}^{2} \rho _{1}}, \\ {s_{0} \frac{\partial \rho _{2}}{\partial t}=\mu \rho _{2}+h \rho _{1} \rho _{3} \cos \varphi -g_{1} \rho _{2}^{3}-g_{2} \rho _{1}^{2} \rho _{3}^{2} \rho _{2}}, \\ {s_{0} \frac{\partial \rho _{3}}{\partial t}=\mu \rho _{3}+h \rho _{1} \rho _{2} \cos \varphi -g_{1} \rho _{3}^{3}-g_{2} \rho _{1}^{2} \rho _{2}^{2} \rho _{3}},\end{array}\right. \end{aligned}$$
(3.32)

where \(\varphi =\varphi _{1}+\varphi _{2}+\varphi _{3}\). The equation (3.32) has five kinds of stationary solutions:

  1. (a)

    The uniform steady state solution

    $$\begin{aligned} \rho _{1}=\rho _{2}=\rho _{3}=0. \end{aligned}$$
  2. (b)

    A strip pattern

    $$\begin{aligned} \rho _{1}=\sqrt{\frac{\mu }{g_{1}}}, \quad \rho _{2}=\rho _{3}=0. \end{aligned}$$
  3. (c)

    Two spots patterns

    $$\begin{aligned} \rho _{1}=\rho _{2}=\rho _{3}=\frac{|h| \pm \sqrt{h^{2}+4 \mu \left( g_{1}+2 g_{2}\right) }}{2\left( g_{1}+2 g_{2}\right) }. \end{aligned}$$

    They exist under the following conditions: \(\mu >\mu _{1}=\frac{-h^{2}}{4\left( g_{1}+2 g_{2}\right) } \).

  4. (d)

    A mixed structure solution

    $$\begin{aligned} \rho _{1}=\frac{|h|}{g_{2}-g_{1}}, \quad \rho _{2}=\rho _{3}=\sqrt{\frac{\mu -g_{1} \rho _{1}^{2}}{g_{1}+g_{2}}}, \end{aligned}$$

    with \(g_{2}>g_{1}\).

Then several different Turing patterns of Eq. (1.1) are given by numerical simulation. These simulation results reflect the spatiotemporal distribution of these studied species, and the associated spatiotemporal patterns are shown here. For this, we consider the Neumann boundary conditions. We set the values of parameter as follows: \(a_1=0.8, a_2=0.9, r=0.1\) and take the size of the space area as \(1000\times 1000\), space steps as \(\Delta x=1,\ \Delta y=1\) and time steps as \(\Delta t=0.05\). In addition, we consider that the individual species are evenly distributed in the spatial domain at the beginning. With the evolution of time, individual species spread out in space, and the distribution of individual species finally constitutes different patterns. For all numerical simulations, we can show different spatiotemporal patterns of species u and v.

Fig. 4
figure 4

Snapshots of contour plot of the temporal evolution of u at different moments with \(d=5, \tau =1.9\) in Turing space. \(u-a, u-b, u-c, u-d\) respectively indicate the images at times \(t=10, t=100, t=1000, t=100{,}000\)

Full size image

Next, we will take different parameters \(d=5, \tau =1.9\) and \(d=0.2, \tau =1.5\) and observe the possible Turing patterns of u and v, see Figs. 4, 56 and 7.

Fig. 5
figure 5

Snapshots of contour plot of the temporal evolution about v at different moments with \(d=5, \tau =1.9\) in Turing space. \(v-a, v-b, v-c, v-d\) respectively indicate the images at times \(t=10, t=100, t=1000, t=100{,}000\)

Full size image
Fig. 6
figure 6

Snapshots of contour plot of the temporal evolution about u at different moments with \(d=0.2, \tau =1.5\) in Turing space. \(u-a, u-b, u-c, u-d\) respectively indicate the images at times \(t=10, t=100, t=1000, t=100{,}000\)

Full size image

From the above numerical simulation, we find that system (1.1) will appear strip pattern (see Figs. 4, 5) and spot pattern (see Figs. 6, 7) under certain conditions. In addition, these patterns also show that in real life, the distribution of species is uneven and affected by many factors. In particular, in this paper we consider the combined effect of the diffusion coefficient of species v and time delay. From Figs. 4 and 5, we find that the system (1.1) will produce strip pattern under the combined effect of d and \(\tau \), that is to say, in some areas, the population density over (or falls below) the maximum (or minimum) value. This phenomenon is similar to the distribution of forest after desertification control (see [26]). From Figs. 6 and 7, we find that the system (1.1) finally appeared spot pattern. In the spots pattern (see [9]), we find that the population density about species u and v may has maximum (or minimum) values in some places. Obviously, because we only consider the effect of d and \(\tau \), the results obtained are often simpler than those in real nature.

Fig. 7
figure 7

Snapshots of contour plot of the temporal evolution about v at different moments with \(d=0.2, \tau =1.5\) in Turing space. \(v-a, v-b, v-c, v-d\) respectively indicate the images at times \(t=10, t=100, t=1000, t=100{,}000\)

Full size image

4 Discussion

In this paper, we systematically study the effect of diffusion coefficient d and time delay \(\tau \) on the pattern of nonlocal Lotka–Volterra cooperative system (1.1). It should be noted that in order to simplify the calculation and learn more about the influence of nonlocal effects on Lotka–Volterra cooperative system, we only consider nonlocal effects on species u here. In fact, there are nonlocal effects on species u and species v, and the research ideas are basically similar.

In addition, the study of this paper breaks our inherent thinking. Generally, we think that the pattern is generated in the competition or predation process, but through the study of this paper, we found that pattern can also appear in the nonlocal Lotka–Volterra system. The research in this paper enriches the theory of pattern dynamics to some extent. We know that many natural phenomena can be explained by using the theory of pattern dynamics. Here we just make a preliminary attempt. In the future, we will further study this aspect and expect to use our theory to explain more natural phenomena.