1 Introduction

The COVID-19 pandemic has resulted in a significant number of deaths. Owing to the sudden onset of this catastrophic event, the healthcare system was unprepared to provide services to the massive influx of patients, leading to many fatalities due to the lack of available treatment and prevention facilities [14]. Similarly, many people lost their lives in Iran, where the government, like others worldwide, did not anticipate the pandemic. At the onset of COVID-19 in Iran, there were only 1,788 beds available. During the peak of the pandemic, the number of cases in Iran reached approximately 59,000 [68]. Assuming that 10% of these individuals required hospitalization, the hospitals’ capacity would be overwhelmed, rendering them unable to provide adequate treatment.

Many scholars assert that the delivery of healthcare services positively impacts customer behavior, including patient satisfaction and potentially reducing mortality [22]. Providing high-quality healthcare to older patients is particularly important, with responsiveness in the hospital environment being a key aspect [7]. Furthermore, patient satisfaction, appropriate therapeutic outcomes, and compliance with treatment routines are essential for improving overall service delivery [9]. A critical component of a healthcare system is its responsiveness to the population’s changing needs, which the World Health Organization (WHO) highlighted in 2000 as one of the frameworks for healthcare systems. This dynamic ability requires tools for evaluating nonclinical healthcare services to assess the health system. The nonclinical dimension of quality is defined as “the way in which the health system responds to nonmedical needs” [23]. This dimension encompasses two categories: respect for people’s rights, including dignity, autonomy, confidentiality of information, and communication [78], and customer service, which includes the right to choose, prompt listening, access to necessities, and social support.

To measure the quality of services that companies provide for customers, service quality has become a popular framework [71]. Several approaches have been proposed in the literature to explore service quality. Initially, qualitative methods were used to develop a model for measuring service quality [31]. In one approach, service quality is divided into three dimensions: performance quality, functional quality, and organizational image [12]. Some studies suggest that performance quality is more significant than technical quality in differentiating one’s service from competitors [19]. Performance quality refers to how the service is provided and utilized, while the organization’s image also influences customer perception. In service quality literature, SERVPERF and SERVQUAL are popular and considered straightforward for evaluating service quality [18]. These models consist of various factors (or criteria) and subfactors (or subcriteria) used to determine the level of service quality provided to customers, primarily measured as the difference between expectations and actual service delivery.

The utility of SERVQUAL in healthcare applications has been espoused in recent studies. The common thread of these studies highlights the straightforward application of SERVQUAL in evaluating the gap between patients’ expectations and actual delivery. Goula et al. [24] adopted the five dimensions of the SERVQUAL model to evaluate the quality of health services in public Greek hospitals. Pekkaya et al. [57] reported a similar application in evaluating the outpatient department of a Turkish hospital. AlOmari [6] utilized SERVQUAL to gauge patients’ perspectives on performance gaps across all SERVQUAL dimensions, taking five private hospitals in Syria as the case study. In Saudi Arabian public and private hospitals, Al‐Borie et al. [5] conducted an empirical study evaluating healthcare services using SERVQUAL, considering some demographic variables. Li et al. [44] carried out a large-scale analysis of hospitals in nine Chinese cities, encompassing both in-patient and outpatient facilities. Aghamolaei et al. [1] examined the service quality gap of a main hospital in a Southern Iranian province. Al-Neyadi et al. [3] conducted a case study in public and private hospitals in the United Arab Emirates to identify which SERVQUAL dimensions most impact patients’ satisfaction with healthcare services. Separate studies by Ali et al. [4] and Kansra and Jha [36] explored the use of the SERVQUAL gap model in some hospitals in India. Rahim et al. [60] introduced an innovation in generating evaluations within SERVQUAL. Instead of survey questionnaires, they applied machine learning topic classification of patient sentiments on Facebook, identifying the association of these sentiments with the SERVQUAL dimensions.

Due to the challenges in operationalizing the SERVQUAL model, various extensions have been proposed [82], as evidenced by numerous studies. Some scholars utilized statistical extensions [62, 70, 75], while others applied multicriteria decision analysis (MCDA) methods [2, 28, 53]. Various MCDA methods have been employed in different contexts [54, 73] under conditions of certainty or recognized uncertainty. The concept of fuzzy SERVQUAL was implemented for service quality evaluation in a physiotherapy and rehabilitation hospital in Turkey [11] and in outpatient services across three hospitals in Taiwan [28]. The rationale for using fuzzy SERVQUAL is its ability to handle fuzzy evaluations, which are pertinent in real-world scenarios. However, despite the growing number of studies adopting SERVQUAL in healthcare, systematic evaluation approaches have not received adequate attention in the literature. Some research, such as Khan Mohammadi et al. [37], has begun to address this gap, highlighting the lack of service quality evaluations in Iranian hospitals during COVID-19 and introducing a novel methodology, making it a noteworthy project.

The influx of patients to hospitals has surged due to infectious diseases like the COVID-19 pandemic, leading to increased health service delivery by specific organizations. Poor health services can result in customer attrition, both directly and indirectly if they fail to meet high-quality standards. High-quality health services are crucial for satisfying customer needs. Moreover, system-based quality improvements can enhance customer satisfaction while reducing shift work time and costs. With various health centers offering similar services, patient satisfaction, referrals, and reuse are influenced by the perceived quality of healthcare. The importance of maintaining good health cannot be overstated. A lack of understanding of health service quality may deter people from seeking care. Given the global significance of this issue, there is an urgent need for clarity on the actions to be taken. Numerous methods, including multicriteria decision making (MCDM), have been utilized globally to facilitate informed decision-making. After a series of mathematical computations, the analysis results are presented in a manner that prioritizes options or criteria based on their analytical outcomes. These methods have been widely adopted in research across various sectors due to their ability to manage diverse data sets.

However, a scarcity of studies has emerged in view of their applications in the healthcare sector during the global COVID-19 pandemic. Thus, this study demonstrates a holistic evaluation of the service quality of hospitals using an integrated MCDM method. The evaluation framework is driven by a customized SERVQUAL model consisting of four criteria with corresponding subcriteria. The analytic hierarchy process (AHP), first proposed by Saaty [64], assigns the priority weights of the criteria and subcriteria, representing the importance degree of the subcriteria on service quality. The AHP is a widely popular weighting method due to its rigor in measuring the importance degrees of a given set of elements (e.g., criteria, subcriteria) with respect to a higher-level element, e.g., the goal of the evaluation problem. Schmidt et al. [66] reported a comprehensive literature review of the applications of the AHP in healthcare research, demonstrating its uses in addressing several sector-related problems. Furthermore, unlike other MCDM methods that integrate SERVQUAL, our proposed method considers each criterion of the customized SERVQUAL as a separate hierarchical MCDM problem. For each criterion, the evaluation of the hospitals is carried out using the weighted aggregated sum product assessment (WASPAS) developed by Zavadskas et al. [86]. The WASPAS method integrates the weighted sum model and the weighted product model, thereby overcoming the limitations of each model and consequently increasing the capability of the WASPAS to discriminate the performance of alternatives. Owing to its efficacy in handling MCDM problems, it has seen significant applications five years after its introduction, prompting Mardani et al. [48] to report a literature review of its advances. Recent studies demonstrated its applications in the healthcare sector, almost exclusively within the subdomain of healthcare waste management [15, 49, 50], implying its potential in other subdomains.

Nevertheless, implementing both AHP and WASPAS methods, especially in eliciting judgments by decision makers, has inherent ambiguity, which Pelissari et al. [58] described as well handled by fuzzy set theory and its extensions. Fuzzy set theory, first proposed by Zadeh [83], offers a robust mathematical framework to address nonprobabilistic uncertainty. Instead of binary membership introduced in the classical set theory, fuzzy set theory assigns a membership grade of an element to a set. Its massive relevance gives rise to the proliferation of fuzzy set extensions, with each extension promising better capability to handle more uncertain information [34]. These extensions include intuitionistic fuzzy sets [10], bipolar fuzzy sets [87], neutrosophic sets [72], Pythagorean fuzzy sets [80], picture fuzzy sets [17], Fermatean fuzzy sets [67], \(q\)-rung orthopair fuzzy sets [81], linear Diophantine fuzzy sets [61], and spherical fuzzy sets (SFS) [8, 38]. Their integrations with MCDM methods become an agenda of increasing attention in the literature [32, 47, 58]. Among the fuzzy set extensions, SFS overcomes the limitations of picture fuzzy sets and Pythagorean fuzzy sets in two aspects: (1) introducing four membership grades instead of two in Pythagorean fuzzy sets, which can handle more information about the fuzziness of the sets, and (2) allowing for inconsistencies in the membership degrees, which is the main drawback of picture fuzzy sets. The membership functions of SFS are defined as spherical surfaces, which permit a broader range of parameters to be assigned compared to other fuzzy set extensions.

Thus, to leverage the use of SFS, its integration with AHP, coined as SF-AHP [40], and with WASPAS, denoted as SF-WASPAS [39], is adopted in this work. Such an integration addresses the ambiguity brought about by the imprecise concepts represented by the subcriteria, which would result in imprecise judgments in estimating the ratios of the importance among subcriteria and evaluating hospitals in the different subcriteria. Given the different rankings generated in the different criteria, the proposed methodological approach in this work incorporates the strengths of two voting systems in social choice theory: the Borda and Copeland methods. Integrating these methods aggregates the different rankings of the hospitals and generates a final evaluation ranking. Succinctly, this work answers the following research questions:

(R1) What are the most critical subcriteria within each criterion of the SERVQUAL in maintaining the quality of hospital services?

(R2) How do we determine the hospital with the most preferred service quality?

This research contributes in two main ways. Firstly, there is the contextual contribution. This study aims to enhance service quality in Semnan, an Iranian state affected by COVID-19 and provides insights that could guide private hospitals in improving patient care. Despite Semnan state having only five hospitals, determining and prioritizing service quality is vital due to the interest from investors in competing with public hospitals. Secondly, the methodological contribution demonstrates the integration of SF-AHP and SF-WASPAS in a real-world application, particularly during the COVID-19 pandemic when many information details are uncertain. This paper contributes by employing spherical fuzzy numbers to improve data quality, contrasting with previous papers that assumed a precise environment. The notion of treating each criterion of SERVQUAL as a separate MCDM problem and using an integrated Borda−Copeland as an aggregator of the rankings associated with the different criteria is an important departure that this work offers.

This paper is structured into seven parts. Section 2 evaluates prior research and relevant methodologies. Section 3 presents some preliminary concepts of SFS, SF-AHP, and SF-WASPAS. Section 4 outlines the case study that constitutes the MCDM problem. The weights of the SERVQUAL subcriteria resulting from the application of SF-AHP, the rankings of the hospitals in the different criteria using the SF-WASPAS, and the aggregation of the different rankings with an integrated Borda−Copeland method are all detailed in Sect. 5. The discussion of the results and findings is described in Sect. 6. It ends with concluding remarks and some future works in Sect. 7.

2 Literature Review

In this section, previous studies in healthcare performance evaluation are reviewed. This research categorizes the literature into two segments: before and after the COVID-19 pandemic.

According to Habib et al. [26], it has been demonstrated that linear Diophantine fuzzy statistical aggregation operators are among the best algorithms for evaluating healthcare supply chain performance in Industry 4.0. The novelty, reliability, and efficiency of the proposed methodology were validated through a credibility test, sensitivity analysis, and comparative analysis. Haakenstad et al. [25] assessed the performance of healthcare centers across 204 countries. Peykani et al. [59] introduced a credibility-based fuzzy window data envelopment analysis approach as a novel method for dynamic evaluation of hospital performance during various periods, considering linguistic variables and data ambiguity. Utilizing the Sustainable Development Goals as a framework, Umar et al. [77] analyzed the performance of the Chinese healthcare system. Özdemir and Çağlayan [56] evaluated the performance of intensive care units in hospitals affected by the COVID-19 pandemic using the hesitant fuzzy Multiattribute Border Approximation Area Comparison (MABAC) method. During the COVID-19 pandemic in Iran, Malekzadeh et al. [46] evaluated the performance of intensive care units in hospitals affiliated with Mazandaran University of Medical Sciences. Ismail et al. [29] proposed a proactive preparedness real-time system incorporating artificial intelligence that selects a learning model based on the evolution of an infection over time. This system integrates a novel methodology for determining the appropriate learning model into the forecast algorithm, resulting in an accurate, autonomous algorithm. Shanbehzadeh et al. [69] evaluated and compared some decision tree classification algorithms using validated clinical features to predict COVID-19, assessing their efficiency and performance. Kyritsi et al. [41] conducted an evaluation of a local manufacturer of Rapid Test Ag 2019-nCoV (PROGNOSIS, BIOTECH, Larissa, Greece) to determine its accuracy in clinical settings and mass screenings. Wagenhäuser et al. [79] carried out a prospective performance evaluation study in a hospital setting, comparing quantitative reverse transcription polymerase chain reaction with rapid diagnostic tests from three manufacturers for the detection of SARS-CoV-2. By integrating game theory with differential equation analysis, Zare et al. [84] measured the effectiveness of health centers. Omrani et al. [55] developed a method for measuring hospital performance in various provinces by clustering data envelopment analysis under uncertain conditions for decision-making units. Kang et al. [35] concluded that many emergency departments could improve their performance by reengineering their processes based on the application of data envelopment analysis for performance evaluations.

Chen et al. [16] demonstrated that hospital performance declined following a recession, highlighting the impact economic downturns have on hospital operations. Johannessen et al. [30] suggested that hospitals could improve performance by providing greater consideration to employees with multiple skills. Sun et al. [74] aimed to examine the efficiency of national health systems using longitudinal country-level data on health spending per capita for 173 countries from 2004 to 2011. They constructed data envelopment analyses to evaluate efficiency and regression models to examine the determinants of efficiency. Table 1 provides a summary of previous studies.

Table 1 Summary of previous evaluation methods
Full size table

3 Preliminaries

Here, we present some preliminary concepts of SFS, SF-AHP, and SF-WASPAS to achieve a self-contained discussion of the proposed methodology.

3.1 Spherical Fuzzy Sets

In the literature, two variants of SFS emerged, published almost simultaneously, one proposed by Kutlu Gündoğdu and Kahraman [38] and the other by Ashraf et al. (2019). In this study, we subscribed to the definition of Kutlu Gündoğdu and Kahraman [38]. Regardless of the variant, SFS is considered a direct generalization of the Pythagorean fuzzy set and picture fuzzy set.

Definition 1

[38]. Let \(\mathcal{U}\) be a reference set. Then, an SFS \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{S}\) defined over \(\mathcal{U}\) is given by

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{S} = \left\{ {\left. {x,\left( {\mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{S} }} \left( x \right),v_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{S} }} \left( x \right),\pi_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{S} }} \left( x \right)} \right)} \right|x \in {\mathcal{U}}} \right\},$$
(1)

where \(\mu _{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{S} }} :{\mathcal{U}} \to \left[ {0,1} \right],~v_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{S} }} :{\mathcal{U}} \to \left[ {0,1} \right],\) and \(\pi _{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{S} }} :{\mathcal{U}} \to \left[ {0,1} \right]\),

and

$$0 \le \mu_{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{S}}^{2} \left( x \right) + v_{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{S}}^{2} \left( x \right) + \pi_{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{S}}^{2} \left( x \right) \le 1.$$
(2)

For each \(x\in \mathcal{U}\), \(\mu _{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{S} }} \left( x \right)\), \(v_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{S} }} \left( x \right)\), and \(\pi _{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{S} }} \left( x \right)\) refer to the membership, non-membership, and hesitancy degrees of \(x\) to \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{S}\), respectively.

For convenience, we denote \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{S} = \left( {\mu _{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{S} }} ,v_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{S} }} ,\pi _{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{S} }} } \right)\) as a spherical fuzzy number (SFN).

Definition 2

[38]. Suppose \({\mathcal{S}}_{1}=\left({\mu }_{{\mathcal{S}}_{1}},{v}_{{\mathcal{S}}_{1}},{\pi }_{{\mathcal{S}}_{1}}\right)\), \({\mathcal{S}}_{2}=\left({\mu }_{{\mathcal{S}}_{2}},{v}_{{\mathcal{S}}_{2}},{\pi }_{{\mathcal{S}}_{2}}\right)\), and \(\mathcal{S}=\left({\mu }_{\mathcal{S}},{v}_{\mathcal{S}},{\pi }_{\mathcal{S}}\right)\) be any three SFNs and \(\lambda >0\). Then, the operations of SFNs are given as follows:

$${\mathcal{S}}_{1}\oplus {\mathcal{S}}_{2}=\left({\left({\mu }_{{\mathcal{S}}_{1}}^{2}+{\mu }_{{\mathcal{S}}_{2}}^{2}-{\mu }_{{\mathcal{S}}_{1}}^{2}{\mu }_{{\mathcal{S}}_{2}}^{2}\right)}^{1/2}, {v}_{{\mathcal{S}}_{1}}{v}_{{\mathcal{S}}_{2}},{\left(\left(1-{\mu }_{{\mathcal{S}}_{2}}^{2}\right){\pi }_{{\mathcal{S}}_{1}}^{2}+\left(1-{\mu }_{{\mathcal{S}}_{1}}^{2}\right){\pi }_{{\mathcal{S}}_{2}}^{2}-{\pi }_{{\mathcal{S}}_{1}}^{2}{\pi }_{{\mathcal{S}}_{2}}^{2}\right)}^{1/2}\right)$$
(3)
$${\mathcal{S}}_{1}\otimes {\mathcal{S}}_{2}=\left({\mu }_{{\mathcal{S}}_{1}}{\mu }_{{\mathcal{S}}_{2}},{\left({v}_{{\mathcal{S}}_{1}}^{2}+{v}_{{\mathcal{S}}_{2}}^{2}-{v}_{{\mathcal{S}}_{1}}^{2}{v}_{{\mathcal{S}}_{2}}^{2}\right)}^{1/2},{\left(\left(1-{v}_{{\mathcal{S}}_{2}}^{2}\right){\pi }_{{\mathcal{S}}_{1}}^{2}+\left(1-{v}_{{\mathcal{S}}_{1}}^{2}\right){\pi }_{{\mathcal{S}}_{2}}^{2}-{\pi }_{{\mathcal{S}}_{1}}^{2}{\pi }_{{\mathcal{S}}_{2}}^{2}\right)}^{1/2}\right)$$
(4)
$$\lambda \mathcal{S}=\left({\left(1-{\left(1-{\mu }_{\mathcal{S}}^{2}\right)}^{\lambda }\right)}^{1/2},{v}_{\mathcal{S}}^{\lambda },{\left({\left(1-{\mu }_{\mathcal{S}}^{2}\right)}^{\lambda }-{\left(1-{\mu }_{\mathcal{S}}^{2}-{\pi }_{\mathcal{S}}^{2}\right)}^{\lambda }\right)}^{1/2}\right)$$
(5)
$${\mathcal{S}}^{\lambda } = \left( {\mu_{{\mathcal{S}}}^{\lambda } ,\left( {1 - \left( {1 - v_{{\mathcal{S}}}^{2} } \right)^{\lambda } } \right)^{1/2} ,\left( {\left( {1 - v_{{\mathcal{S}}}^{2} } \right)^{\lambda } - \left( {1 - v_{{\mathcal{S}}}^{2} - \pi_{{\mathcal{S}}}^{2} } \right)^{\lambda } } \right)^{1/2} } \right)$$
(6)

Definition 3

[38]. Let \({\mathcal{S}}_{k}= \left({\mu }_{{\mathcal{S}}_{k}},{v}_{{\mathcal{S}}_{k}},{\pi }_{{\mathcal{S}}_{k}}\right)\), \(k=\mathrm{1,2},\dots ,K\), be any collection of SFNs. Then, the spherical weighted arithmetic mean (SWAM) is defined as follows:

$${\text{SWAM}}\left({\mathcal{S}}_{1},\dots ,{\mathcal{S}}_{K}\right)=\sum_{k=1}^{K}{w}_{k}{\mathcal{S}}_{k}=\left({\left(1-\prod_{k=1}^{K}{\left(1-{\mu }_{{\mathcal{S}}_{k}}^{2}\right)}^{{w}_{k}}\right)}^{1/2},\prod_{k=1}^{K}{v}_{{\mathcal{S}}_{k}}^{{w}_{k}},{\left(\prod_{k=1}^{K}{\left(1-{\mu }_{{\mathcal{S}}_{k}}^{2}\right)}^{{w}_{k}}-\prod_{k=1}^{K}{\left(1-{\mu }_{{\mathcal{S}}_{k}}^{2}-{\pi }_{{\mathcal{S}}_{k}}^{2}\right)}^{{w}_{k}}\right)}^{1/2}\right) ,$$
(7)

where \(w=\left({w}_{1}, ..., {w}_{K}\right)\) is the weight vector of \({\mathcal{S}}_{k}\), with \({w}_{k}\ge 0\) and\({\sum }_{k=1}^{K}{w}_{k}=1\).

Definition 4

[38]. Let \(\mathcal{S}=\left({\mu }_{\mathcal{S}},{v}_{\mathcal{S}},{\pi }_{\mathcal{S}}\right)\) be a SFN. The score function over \(\mathcal{S}\) is a mapping \({\mathbb{S}}\):\(\mathcal{S}\to {\mathbb{R}}\), defined by

$${\mathbb{S}}\left(\mathcal{S}\right)={\left({\mu }_{\mathcal{S}}-{\pi }_{\mathcal{S}}\right)}^{2}-{\left({v}_{\mathcal{S}}-{\pi }_{\mathcal{S}}\right)}^{2}$$
(8)

Definition 5

[38]. Let \(\mathcal{S}=\left({\mu }_{\mathcal{S}},{v}_{\mathcal{S}},{\pi }_{\mathcal{S}}\right)\) be a SFN. The accuracy function over \(\mathcal{S}\) is a mapping \({\mathbb{H}}\):\(\mathcal{S}\to {\mathbb{R}}\), defined by

$${\mathbb{H}}\left(\mathcal{S}\right)={\mu }_{\mathcal{S}}^{2}+{v}_{\mathcal{S}}^{2}+{\pi }_{\mathcal{S}}^{2}$$
(9)

Theorem 1

[38]. Let \({\mathcal{S}}_{1}=\left({\mu }_{{\mathcal{S}}_{1}},{v}_{{\mathcal{S}}_{1}},{\pi }_{{\mathcal{S}}_{1}}\right)\) and \({\mathcal{S}}_{2}=\left({\mu }_{{\mathcal{S}}_{2}},{v}_{{\mathcal{S}}_{2}},{\pi }_{{\mathcal{S}}_{2}}\right)\) be two SFNs. Then, the following hold:

  1. (i)

    \({\mathcal{S}}_{1}<{\mathcal{S}}_{2}\Leftrightarrow {\mathbb{S}}\left({\mathcal{S}}_{1}\right)<{\mathbb{S}}\left({\mathcal{S}}_{2}\right)\),

  2. (ii)

    \({\mathcal{S}}_{1}>{\mathcal{S}}_{2}\Leftrightarrow {\mathbb{S}}\left({\mathcal{S}}_{1}\right)>{\mathbb{S}}\left({\mathcal{S}}_{2}\right)\),

  3. (iii)

    \({\mathcal{S}}_{1}={\mathcal{S}}_{2}\), then

    $$\begin{gathered} {\mathbb{H}}\left( {{\mathcal{S}}_{1} } \right) < {\mathbb{H}}\left( {{\mathcal{S}}_{2} } \right) \Rightarrow {\mathcal{S}}_{1} < {\mathcal{S}}_{2} , \hfill \\ {\mathbb{H}}\left( {{\mathcal{S}}_{1} } \right) > {\mathbb{H}}\left( {{\mathcal{S}}_{2} } \right) \Rightarrow {\mathcal{S}}_{1} > {\mathcal{S}}_{2} , \hfill \\ {\mathbb{H}}\left( {{\mathcal{S}}_{1} } \right) = {\mathbb{H}}\left( {{\mathcal{S}}_{2} } \right) \Rightarrow {\mathcal{S}}_{1} = {\mathcal{S}}_{2} . \hfill \\ \end{gathered}$$

3.2 Spherical Fuzzy Analytic Hierarchy Process

In the domain of MCDM, the AHP is a theory of measurement where criteria and alternatives are weighted based on both objective values and subjective opinions, resulting in a decision that incorporates both values and opinions as part of the process [64]. AHP is widely used in several applications [27, 76] and is increasingly adopted to assist in decision-making for problems based on the human judgments. However, it is essential to note that expert judgments contain ambiguity. To address this issue, integrating AHP and fuzzy set theory has been a popular agenda in the last decade [45], allowing for subjective judgments based on the fuzzy sets and qualitative evaluations [85]. Fuzzy set theory is renowned for its emphasis on the rationality of uncertainty caused by ambiguity, which can be managed by using linguistic variables to handle uncertainty resulting from incomplete information. Fuzzy AHP is becoming more popular as they are integrated with other MCDM methods, as shown in the review of Kahraman et al. [33], with several variants available. AHP can be utilized to compare values based on the fuzzy criteria within a range of values. Among the several fuzzy AHP variants, Kutlu Gündoğdu and Kahraman [40] introduced the spherical fuzzy AHP (SF-AHP) as an extension to the traditional AHP, incorporating the notion of SFS. In most MCDM studies, the SF-AHP is mainly utilized to determine the weights of the fuzzy selection criteria. Using fuzzy criteria enhances decision-making when dealing with multicriteria problems, facilitating more effective decisions. The algorithm of the SF-AHP can be outlined as follows:

Step 1: Develop the hierarchical structure of the model. This hierarchy usually consists of three levels: At Level 1, the overall goal of the decision problem is positioned. Level 2 consists of a set of \(n\) criteria with defined criterion functions. Finally, at Level 3, the set of \(m\) nondominated decision alternatives is defined, which eventually addresses the goal.

Step 2: Perform pairwise comparisons using the evaluation scale in Table 2. Suppose each score is represented as \({\widetilde{a}}_{\varphi }\), \(\varphi =\mathrm{1,2},3,\dots\), the corresponding score indices are calculated based on the SI function, defined as follows:

$${\text{SI}}\left( {\tilde{a}_{\varphi } } \right) = \sqrt {\left| {100{*}\left[ {\left( {\mu_{{\tilde{a}_{\varphi } }} - \pi_{{\tilde{a}_{\varphi } }} } \right)^{2} - \left( {v_{{\tilde{a}_{\varphi } }} - \pi_{{\tilde{a}_{\varphi } }} } \right)^{2} } \right]} \right|} .$$
(10)

for the linguistic score AMI, VHI, HI, SMI, and EI. On the other hand,

$$\frac{1}{{\text{SI}}\left({\widetilde{a}}_{\varphi }\right)}=\frac{1}{\sqrt{\left|100*\left[{\left({\mu }_{{\widetilde{a}}_{\varphi }}-{\pi }_{{\widetilde{a}}_{\varphi }}\right)}^{2}-{\left({v}_{{\widetilde{a}}_{\varphi }}-{\pi }_{{\widetilde{a}}_{\varphi }}\right)}^{2}\right]\right|}}$$
(11)

for the linguistic scores EI, SLI, LI, VLI, and ALI. This step generates a pairwise comparison matrix with crisp (nonfuzzy) scores.

Table 2 Linguistic evaluation scale with corresponding spherical fuzzy numbers [40]
Full size table

Step 3: Calculate the consistency of each pairwise comparison matrix. From the pairwise comparison matrix with linguistic scores, construct the corresponding pairwise comparison matrix with the equivalent SI values. This step requires solving an eigenvalue problem. Consider the resulting matrix \(A={\left({a}_{ij}\right)}_{n\times n}\), where \({a}_{ij}={\text{SI}}\left({\widetilde{a}}_{ij}\right)\) is the corresponding SI value of a linguistic evaluation \({\widetilde{a}}_{ij}\), which represents the importance ratio of the \(i\) th element over the \(j\) th element, \(i,j=1,\dots ,n\). Then, the following problem obtains the maximum eigenvalue \({\lambda }_{{\text{max}}}\):

$$Aw={\lambda }_{{\text{max}}}w$$
(12)

where \(w\) is the principal eigenvector associated with \({\lambda }_{max}\). The consistency ratio CR becomes

$${\text{CR}}=\frac{{\text{CI}}}{{\text{RI}}}$$
(13)

where RI is the random consistency index generated from a sufficiently large number of matrices of the same size, and CI is the consistency index computed as follows:

$${\text{CI}}=\frac{{\lambda }_{{\text{max}}}-n}{n-1}$$
(14)

For an acceptable CR value, \({\text{CR}}\le 0.10\). Otherwise, decision makers must revise their pairwise comparison matrix.

Step 4: Determine the spherical fuzzy local weights of the criteria and alternatives. Consider the sets of \(n\) criteria and \(m\) alternatives. Consider also a spherical fuzzy pairwise comparison matrix that evaluates the criteria set with respect to the goal in the form \(\widetilde{\mathcal{C}}={\left({\widetilde{\mathcal{c}}}_{jk}\right)}_{n\times n}\), where \({\widetilde{\mathcal{c}}}_{jk}=\left({\mu }_{{\widetilde{\mathcal{c}}}_{jk}},{\nu }_{{\widetilde{\mathcal{c}}}_{jk}},{\pi }_{{\widetilde{\mathcal{c}}}_{jk}}\right)\) is a SFN representing the ratio estimate of the importance of the \(j\) th criterion over the \(k\) th criterion with scale shown in Table 1. The spherical fuzzy local weight of the \(j\) th criterion, denoted as \({\widetilde{w}}_{j}\), is obtained using the SWAM operator in Definition 3.

$$\tilde{w}_{j} = {\text{SWAM}}\left( {\tilde{c}_{j1} , \ldots ,\tilde{c}_{jn} } \right) = \left( {\left( {1 - \mathop \prod \limits_{k = 1}^{n} \left( {1 - \mu_{{\tilde{c}_{jk} }}^{2} } \right)^{{w_{k} }} } \right)^{1/2} ,\mathop \prod \limits_{k = 1}^{n} v_{{\tilde{c}_{jk} }}^{{w_{k} }} ,\left( {\mathop \prod \limits_{k = 1}^{n} \left( {1 - \mu_{{\tilde{c}_{jk} }}^{2} } \right)^{{w_{k} }} - \mathop \prod \limits_{k = 1}^{n} \left( {1 - \mu_{{\tilde{c}_{jk} }}^{2} - \pi_{{\tilde{c}_{jk} }}^{2} } \right)^{{w_{k} }} } \right)^{1/2} } \right)\quad (\forall j),$$
(15)

where \({w}_{k}=\frac{1}{n}\).

Consider also the spherical fuzzy pairwise comparison matrix that evaluates the alternatives with respect to the \(j\)th criterion in the form \({\widetilde{\mathcal{A}}}^{j}={\left({\widetilde{\mathcal{a}}}_{ik}^{j}\right)}_{m\times m}\). Similarly, the spherical fuzzy local weight of the \(i\)th alternative with respect to the \(j\) th criterion, denoted as \({\widetilde{w}}_{ij}\), is calculated as follows:

$$\tilde{w}_{ij} = {\text{SWAM}}\left( {\tilde{a}_{i1}^{j} , \ldots ,\tilde{a}_{im}^{j} } \right) = \left( {\left( {1 - \mathop \prod \limits_{k = 1}^{m} \left( {1 - \mu_{{\tilde{a}_{ik}^{j} }}^{2} } \right)^{{w_{k} }} } \right)^{1/2} ,\mathop \prod \limits_{k = 1}^{m} v_{{\tilde{a}_{ik}^{j} }}^{{w_{k} }} ,\left( {\mathop \prod \limits_{k = 1}^{m} \left( {1 - \mu_{{\tilde{a}_{ik}^{j} }}^{2} } \right)^{{w_{k} }} - \mathop \prod \limits_{k = 1}^{m} \left( {1 - \mu_{{\tilde{a}_{ik}^{j} }}^{2} - \pi_{{\tilde{a}_{ik}^{j} }}^{2} } \right)^{{w_{k} }} } \right)^{1/2} } \right)\quad (\forall i,j)$$
(16)

where, in this case,\({w}_{k}=\frac{1}{m}\).

Step 5: Obtain the global weights. The information about the global weights is obtained through hierarchical layer sequencing. We employ a hierarchical structure to aggregate the spherical fuzzy weights at each level of the hierarchy, simplifying the computations. Currently, there are two methods available for this process. The first option is to compute the nonspherical fuzzy weight of each criterion using the score function \({\text{SI}}\). Let \({\widetilde{w}}_{j}=\left({\mu }_{{\widetilde{w}}_{j}},{v}_{{\widetilde{w}}_{j}},{\pi }_{{\widetilde{w}}_{j}}\right)\), then

$${\text{SI}}\left( {\tilde{w}_{j} } \right) = \sqrt {\left| {100*\left[ {\left( {3\mu_{{\tilde{w}_{j} }} - \frac{{\pi_{{\tilde{w}_{j} }} }}{2}} \right)^{2} - \left( {\frac{{v_{{\tilde{w}_{j} }} }}{2} - \pi_{{\tilde{w}_{j} }} } \right)^{2} } \right]} \right|} \quad (\forall j)$$
(17)

The normalized weight \(w_{j}\) is determined using:

$$w_{j} = \frac{{{\text{SI}}\left( {\tilde{w}_{j} } \right)}}{{\mathop \sum \nolimits_{j = 1}^{n} {\text{SI}}\left( {\tilde{w}_{j} } \right)}}\quad (\forall j)$$
(18)

The spherical fuzzy global weight of the \(i\) th alternative, represented as \(w_{i}\), yields

$$\tilde{w}_{i} = w_{1} \tilde{w}_{i1} \oplus w_{2} \tilde{w}_{i2} \oplus \cdots \oplus w_{n} \tilde{w}_{in} \quad (\forall i)$$
(19)

with the scalar multiplication and \(\oplus\) operations defined in Definition 2. Alternatively, the second option is to perform the following:

$$\tilde{w}_{i} = \left( {\tilde{w}_{1} \otimes \tilde{w}_{i1} } \right) \oplus \left( {\tilde{w}_{2} \otimes \tilde{w}_{i2} } \right) \oplus \ldots \oplus \left( {\tilde{w}_{n} \otimes \tilde{w}_{in} } \right)$$
(20)

where the operations \(\otimes\) and \(\oplus\) are found in Definition 2.

Step 6: Defuzzify the \({\widetilde{w}}_{i}\) (\(\forall i\)) values using the function SI.

Step 7: Rank the alternatives according to the decreasing value of \({\text{SI}}\left({\widetilde{w}}_{i}\right)\). The alternative with the largest value is the most preferred.

3.3 Spherical Fuzzy WASPAS

The SFS extension of WASPAS was proposed by Kutlu Gündoğdu and Kahraman [39]. The steps are outlined as follows:

Step 1: Create a spherical fuzzy decision matrix in the given form:

$$\hat{A}^{k} = \left( {\hat{\alpha }_{{ij}}^{k} } \right)_{{m \times n}}$$
(21)

where \({\widehat{\alpha }}_{ij}^{k}\) is spherical fuzzy evaluation of alternative \({a}_{i}\) (\(i=1,\dots ,m\)) with respect to a criterion \({c}_{j}\) (\(j=1,\dots ,n\)), assessed by the decision maker \({{\text{DM}}}_{k}\) (\(k=1,\dots ,K\)). Here, \({\widehat{\alpha }}_{ij}^{k}\) is expressed as a SFS in the form

$$\hat{\alpha }_{ij}^{k} = \left( {\mu_{{\hat{\alpha }_{ij}^{k} }} ,\nu_{{\hat{\alpha }_{ij}^{k} }} ,\pi_{{\hat{\alpha }_{ij}^{k} }} } \right)$$
(22)

Step 2: Aggregate the spherical fuzzy decision matrices from \(K\) decision makers. The aggregate spherical fuzzy decision matrix is denoted by \(\widehat{\mathrm{\rm A}}={\left({\widehat{a}}_{ij}\right)}_{m\times n}\), where

$${\widehat{a}}_{ij}={\text{SWAM}}\left({\widehat{\alpha }}_{ij}^{1},\dots ,{\widehat{\alpha }}_{ij}^{K}\right)=\sum_{k=1}^{K}{w}_{k}{\widehat{\alpha }}_{ij}^{k}=\left({\left(1-\prod_{k=1}^{K}{\left(1-{\left({\mu }_{{\widehat{\alpha }}_{ij}^{k}}\right)}^{2}\right)}^{{w}_{k}}\right)}^{1/2},\prod_{k=1}^{K}{\left({\nu }_{{\widehat{\alpha }}_{ij}^{k}}\right)}^{{w}_{k}},{\left(\prod_{k=1}^{K}{\left(1-{\left({\mu }_{{\widehat{\alpha }}_{ij}^{k}}\right)}^{2}\right)}^{{w}_{k}}-\prod_{k=1}^{K}{\left(1-{\left({\mu }_{{\widehat{\alpha }}_{ij}^{k}}\right)}^{2}-{\left({\pi }_{{\widehat{\alpha }}_{ij}^{k}}\right)}^{2}\right)}^{{w}_{k}}\right)}^{1/2}\right)$$
(23)

where \({w}_{k}\) is the weight assigned to the \(k\) th decision maker, \(0\le {w}_{k}\le 1\), and \({\sum }_{k=1}^{K}{w}_{k}=1\).

Step 3: Obtain the priority weights of the criteria. Each criterion \({c}_{j}\) is assigned a weight \({w}_{j}\), for \(j=1,\dots ,n\). Kutlu Gündoğdu and Kahraman [39] outlined a process of generating criteria weights. For brevity, we skipped such a discussion. Suppose \({w}_{j}\) is exogenously determined or is obtained by any weighting process, e.g., SF-AHP.

Step 4: Calculate the weighted sum model (WSM), represented as \({\widehat{Q}}_{i}^{\left(1\right)}\), in the form

$$\hat{Q}_{i}^{\left( 1 \right)} = \mathop \sum \limits_{j = 1}^{n} w_{j} \hat{a}_{ij} = w_{1} \hat{a}_{i1} \oplus \cdots \oplus w_{n} \hat{a}_{in} ,\quad \forall i$$
(24)

where the scalar multiplication and \(\oplus\) operations are defined in Definition 2.

Step 5: Similarly, calculate the weighted product model (WPM), represented as \({\widehat{Q}}_{i}^{\left(2\right)}\), in the form

$$\hat{Q}_{i}^{\left( 2 \right)} = \mathop \prod \limits_{j = 1}^{n} \left( {\hat{a}_{ij} } \right)^{{w_{j} }} = \left( {\hat{a}_{i1} } \right)^{{w_{1} }} \otimes \ldots \otimes \left( {\hat{a}_{in} } \right)^{{w_{n} }} \quad \forall i$$
(25)

where the power and \(\otimes\) operations are likewise presented in Definition 2.

Step 6: Assign a value to the parameter \(\lambda\), \(0\le \lambda \le 1\), and calculate the following:

$$\lambda \hat{Q}_{i}^{\left( 1 \right)} = \left( {\left( {1 - \left( {1 - \mu_{{\hat{Q}_{i}^{\left( 1 \right)} }}^{2} } \right)^{\lambda } } \right)^{1/2} ,v_{{\hat{Q}_{i}^{\left( 1 \right)} }}^{\lambda } ,\left( {\left( {1 - \mu_{{\hat{Q}_{i}^{\left( 1 \right)} }}^{2} } \right)^{\lambda } - \left( {1 - \mu_{{\hat{Q}_{i}^{\left( 1 \right)} }}^{2} - \pi_{{\hat{Q}_{i}^{\left( 1 \right)} }}^{2} } \right)^{\lambda } } \right)^{1/2} } \right),\;\forall i$$
(26)
$$\left( {1 - \lambda } \right)\hat{Q}_{i}^{\left( 2 \right)} = \left( {\left( {1 - \left( {1 - \mu_{{\hat{Q}_{i}^{\left( 2 \right)} }}^{2} } \right)^{{\left( {1 - \lambda } \right)}} } \right)^{1/2} ,v_{{\hat{Q}_{i}^{\left( 2 \right)} }}^{{\left( {1 - \lambda } \right)}} ,\left( {\left( {1 - \mu_{{\hat{Q}_{i}^{\left( 2 \right)} }}^{2} } \right)^{{\left( {1 - \lambda } \right)}} - \left( {1 - \mu_{{\hat{Q}_{i}^{\left( 2 \right)} }}^{2} - \pi_{{\hat{Q}_{i}^{\left( 2 \right)} }}^{2} } \right)^{{\left( {1 - \lambda } \right)}} } \right)^{1/2} } \right),\;\forall i$$
(27)

Step 7: Having obtained the WSM and WPM, perform the following:

$$\hat{Q}_{i} = \lambda \hat{Q}_{i}^{\left( 1 \right)} \oplus \left( {1 - \lambda } \right)\hat{Q}_{i}^{\left( 2 \right)}$$
(28)

Step 8: Generate the corresponding crisp score of \(\hat{Q}_{i}\) by performing

$${\mathbb{S}}\left( {\hat{Q}_{i} } \right) = \left( {\mu_{{\hat{Q}_{i} }} - \pi_{{\hat{Q}_{i} }} } \right)^{2} - \left( {v_{{\hat{Q}_{i} }} - \pi_{{\hat{Q}_{i} }} } \right)^{2}$$
(29)

4 Research methodology

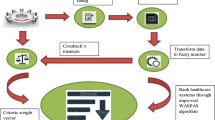
In this study, we evaluate the hospitals in Semman, Iran, based on the quality of services they provided during the COVID-19 pandemic. The customized SERVQUAL model identifies four factors, hereby referred to as criteria in our proposed model, along with their corresponding subcriteria. Table 3 presents the lists of criteria and subcriteria derived from the customized SERVQUAL model. In the proposed approach, the SF-AHP method assigns priority weights of the criteria and subcriteria, eventually generating the final weights of the subcriteria relative to the priority weights of their parent criterion. The computational processes within SFS obtain these final weights. The sets of weights of the subcriteria are then integrated into the SF-WASPAS to obtain the priority ranking of the hospitals for each criterion, resulting in four different rankings. Finally, an integrated Borda−Copeland method is utilized to aggregate these rankings and generate the final evaluation ranking of the hospitals. Figure 1 illustrates the general procedure of the proposed integrated method.

Table 3 Criteria and subcriteria derived from customized SERVQUAL model
Full size table
Fig. 1
figure 1

The proposed methodological framework

Full size image

5 Data analysis

5.1 Implementation of the SF-AHP

First, a spherical fuzzy pairwise comparison matrix was constructed for comparing the four customized SERVQUAL criteria with respect to the goal of evaluating the service quality of hospitals. These criteria include reliability, responsiveness, assurance and tangibility, and empathy. The same process of constructing the spherical fuzzy pairwise comparison matrices was implemented for comparing the subcriteria with respect to their parent criterion. For instance, a spherical fuzzy pairwise comparison matrix containing the subcriteria RE1, RE2, RE3, RE4, RE5, RE6, RE7, and RE8 as elements was created to compare pairwise the ratios of the importance of any two subcriteria with respect to their parent criterion (i.e., reliability). Utilizing the SF-AHP with the computational procedure outlined in Sect. 3.2. generates the spherical fuzzy weights of the criteria elements. Likewise, the weights of the subcriteria with respect to their parent criterion were obtained. Then, the product of the spherical fuzzy weight of a criterion and the spherical fuzzy weights of its subcriteria under the \(\otimes\) operator in Definition 2 was obtained to generate the final spherical fuzzy weights of the subcriteria.

In the reliability criterion, subcriteria such as accountability in obtaining feedback, availability of information, timely service delivery, trustworthiness of staff, sufficient knowledge of staff, workers’ knowledge of the use of technology, proper service, and customer satisfaction are considered. Table 4 demonstrates the ranking of these subcriteria. The resulting \({\text{CR}}=0.0899\) indicates acceptable consistency.

Table 4 Reliability subcriteria evaluation using SF-AHP
Full size table

Meanwhile, Table 5 shows the results of the SF-AHP implementation of the subcriteria of the responsiveness criterion. These include responsiveness to customer inquiries, employee technological proficiency, quality of service, customer satisfaction, staff cleanliness, modern transportation facilities, suitable brochures, and hospital layout. The results suggest that neatness of employees (RES5), suitable brochure (RES7), and customer satisfaction (RES4) yield the most critical subcriteria for the reliability criterion. As indicated in Table 5, the results also demonstrate a CR value of 0.0479, below the threshold of 0.10.

Table 5 Responsiveness subcriteria evaluation using SF-AHP
Full size table

In the assurance and tangibility criterion, the following nine subcriteria contribute to SERVQUAL, including employee neatness, modern transport vehicles, suitable brochures, hospital layout, instilling confidence in customers through employee behavior, attentiveness to customer needs and demands, nondiscrimination toward customers, 24/7 convenience services, and staff attentiveness to customers. Table 6 displays the final ranking of the assurance and tangibility subcriteria. The results suggest that imparting confidence in customers based on the behavior of employees (AT5), paying attention to needs and demands (AT6), and attention of staff to customers (AT9) yield the most critical subcriteria.

Table 6 Assurance and tangibility subcriteria evaluation using SF-AHP
Full size table

In the empathy criterion, which emphasizes building customer confidence through employee behavior, subcriteria such as attention to customer needs and demands, nondiscrimination, providing 24/7 convenience, responsiveness to customer requests, complaint resolution, staff willingness to provide timely service, readiness to assist and guide, and commitment to timely and appropriate service are among the ten subcriteria included in the parent criterion empathy. As shown in Table 7, these subcriteria are ranked by their importance, resulting in the identification of providing convenient services around the clock (E4), imparting confidence in customers based on the behavior of employees (E1), and nondiscrimination toward customers (E3) as the most important subcriteria. The CR value for the corresponding pairwise comparison matrix yields 0.0624, which falls below the threshold of 0.10, indicating acceptable consistency in the judgments of decision makers.

Table 7 Empathy subcriteria evaluation using SF-AHP
Full size table

5.2 Implementation of the SF-WASPAS

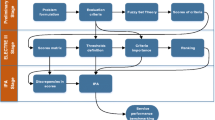
With the priority weights of the respective subcriteria, the rankings of the alternatives (i.e., five hospitals) were obtained through the implementation of the SF-WASPAS. The weights generated by SF-AHP were inputs to Step 4 of Sect. 3.3. Four different rankings were established given the four criteria, each corresponding to a criterion. The reliability criterion yields the ranking of alternatives in Table 8. Succeeding rankings for the responsiveness, assurance and tangibility, and empathy criteria are shown in Tables 9, 10, and 11, respectively. Figure 2 summarizes the rankings of the alternative in the four different criteria of the customized SERVQUAL model. It elucidates that A1 is consistently on top of the ranking in all criteria under consideration, while A5 is also at the bottom. The integrated Borda−Copeland method is adopted to gain insights into the aggregate evaluation of the hospitals.

Table 8 Final ranking of reliability subcriteria for hospitals
Full size table
Table 9 Final ranking of responsiveness subcriteria for hospitals
Full size table
Table 10 Final ranking of assurance and tangibility subcriteria for hospitals
Full size table
Table 11 Final ranking of empathy subcriteria for hospitals
Full size table
Fig. 2
figure 2

Rankings of the hospitals in the four criteria of the customized SERVQUAL model

Full size image

5.3 Implementation of the Integrated Borda−Copeland Method

This step of the proposed computational framework aggregates the rankings of the five hospitals according to the four criteria of the customized SERVQUAL model. The aggregation process follows the integration of Borda and Copeland methods. Several studies adopted the Borda and Copeland methods to determine the final ranking of alternatives given the rankings generated by different MCDM methods; see, for instance, Moghimi and Yazdi [51], Lestari et al. [43], Mohebali et al. [52],De Carvalho et al. [20], Firouzi et al. [21], and Şahin [65]. In particular, we adopted the approach outlined by Şahin [65] and Firouzi et al. [21]. Here, we present the steps we implemented to determine the aggregate ranking of the five hospitals.

The Borda method is a positional voting system within the social choice theory that determines the winner in an election or competition, initially proposed by Borda [13]. Analogously, instead of voters, in the context of this study, consider the voters as the customized SERVQUAL criteria. One of the earliest studies outlining the use of the Borda method within the MCDM domain can be traced back to Lansdowne and Woodward [42]. As outlined in Şahin [65] and Firouzi et al. [21], the implementation of the Borda method involves the following:

Step 1: Construct the following matrix

$$M={\left({m}_{ik}\right)}_{m\times m}$$
(30)

with rows and columns consisting of the alternatives (i.e., hospitals), where \({m}_{ik}=1\) if \({\#}_{j=1}^{n}\left({r}_{ij}\succcurlyeq {r}_{kj}\right)>\frac{n}{2}\), \({r}_{ij}\), \({r}_{kj}\) is the rank of the alternative \({a}_{i}\), \({a}_{k}\) in the criterion \({c}_{j}\), \(m\) is the number of alternatives, and \(n\) is the number of criteria. This condition implies that if the number of times that \({a}_{i}\) ranks over alternative \({a}_{k}\) with the criteria as voters is more than the majority (i.e., \(\frac{n}{2}\)), then \({a}_{i}\) wins over \({a}_{k}\). Otherwise, \({m}_{ik}=0\). The population of matrix \(M\) generates the Borda counts, as shown in Table 12.

Table 12 The Borda counts
Full size table

Step 2: Obtain the row and column sums of \(M\). The row sums (\(\sum_{k=1}^{m}{m}_{ik}\)) of \(M\) indicate the number of times an alternative won over other alternatives. Conversely, the column sums (\(\sum_{i=1}^{m}{m}_{ik}\)) represent the number of times an alternative loses to other alternatives. The information on row and column sums is shown in Table 12.

First characterized by Saari and Merlin [63], the Copeland method is a voting system that is an extension of a Condorcet winner. The Copeland method performs pairwise comparisons of all alternatives. Let

$${s}_{ik}=\left\{\begin{array}{cc}1& {\text{if}} \, {a}_{i} \, {\text{beats}} \, {a}_{k}\\ 0& {\text{if}} \, {a}_{i} \, {\text{and}} { \, a}_{k} \, \text{are tied} \\ -1& {\text{if}} \, {a}_{i} \, \text{loses to} \, {a}_{k}\end{array}\right.$$
(31)

then,

$${\text{Copeland}}\left({a}_{i}\right)=\sum_{k=1}^{m}{s}_{ik}$$
(32)

Step 3: Determine the Copeland scores. By construction, the row and column sums of matrix \(M\) provide information for the Copeland scores. Let \({m}_{i,r}=\sum_{k=1}^{m}{m}_{ik}\) and \({m}_{i,c}=\sum_{i=1}^{m}{m}_{ik}\) be the row and column sums, respectively. Then,

$${\text{Copeland}}\left( {a_{i} } \right) = \mathop \sum \limits_{k = 1}^{m} m_{ik} - \mathop \sum \limits_{i = 1}^{m} m_{ik} = m_{i,r} - m_{i,c} \quad \forall i$$
(33)

Table 13 illustrates the Copeland scores.

Table 13 Copeland scores
Full size table

Step 4: Rank the alternatives (i.e., hospitals) based on Copeland scores. Based on Table 13, the following obtains the aggregate evaluation of the hospitals:

$$A1{ \succcurlyeq }A3 \approx A4{ \succcurlyeq }A2{ \succcurlyeq }A5.$$

6 Discussion

This study aims to evaluate the quality of service in Iran’s hospitals during the COVID-19 pandemic. Several viral mutations of COVID-19 have emerged in Iran, bringing new insights to Iranian hospitals and the healthcare industry. The number of hospitals in Iran is increasing in both the private and public sectors; however, the number in other states, particularly smaller ones, is deficient due to the lack of necessary infrastructure. Consequently, patients usually have two options: travel to a state with more facilities, potentially spreading the illness more quickly, or go to their local hospital. Thus, the quality of services in these hospitals is critical to prevent the spread of illnesses and minimize mortality rates. Failure to implement quality improvement processes can result in institutions not taking proactive measures to improve service quality. This may lead to a deterioration of trust, potentially affecting their reputation, health, and finances in an adverse manner. The way healthcare facility employees engage with patients and their relatives during service delivery is an essential aspect of quality characteristics. In this study, we proposed an integrated approach that evaluates the service quality of hospitals based on the SERVQUAL model. The SERVQUAL model comprises five criteria and 22 subcriteria. In this work, a customized SERVQUAL model has been adopted to measure hospital quality. The customized model adopted four main criteria: reliability, responsiveness, assurance and tangibility, and empathy. The reliability criterion has eight subcriteria, responsiveness has eight subcriteria, and assurance and tangibility have nine subcriteria, while the empathy criterion has ten subcriteria. The implementation of the SF-AHP determines the priority weights of the criteria and subcriteria under a platform that handles uncertainty in the judgment elicitation process within the AHP. Within the reliability criterion, ‘sufficient knowledge of staff’ received the highest priority. In the responsiveness criterion, ‘responding to customers rapidly’ and ‘instilling confidence in customers based on the employee behavior’ yielded the highest priority. In the empathy criterion, providing convenient services around the clock was the highest priority subcriterion. In all subcriteria, with the implementation of SF-WASPAS to address uncertainty within an MCDM framework, hospital 1 (A1) demonstrates the highest service quality. According to the Borda and Copeland methods, hospitals 3 and 4 had the second-highest priority, while hospital 2 had the fourth and hospital 5 had the lowest priority among them. The findings on the priority subcriteria allow the case hospitals to design initiatives that improve their service quality. Furthermore, the ranking of the hospitals provides them with information for benchmarking best practices, particularly those observed by hospital 1.

7 Conclusion and Future Work

When making inferences about a hospital’s system or when taking precautions about what to expect, the quality of its service is a crucial factor to consider. While technological advances have enabled medical facilities to serve patients and their relatives more efficiently, they still face numerous problems in providing these services. The literature presents various methods for measuring patient benefits from hospital services and assessing the quality of those services. Based on the data sets containing inevitably qualitative information, several methodologies can reflect the uncertainty in the data, an important consideration when interpreting the results. During the COVID-19 pandemic, many people worldwide lost their lives. Hospitals were unprepared for this unprecedented challenge, and Iran was no exception. Iran experienced multiple waves of COVID-19, which strained the country’s healthcare industry. They faced difficulties in providing essential resources such as doctors, nurses, and treatment facilities to handle the surge in patients.

This study aims to assess the performance of hospitals during the COVID-19 pandemic in Semnan Province, Iran, using the SERVQUAL model and integrated MCDM methods. Several methods exist when it comes to measuring service quality in various organizations. One such method is SERVQUAL, which comprises five criteria and 24 subcriteria, providing insights into the quality of services organizations provide. MCDM methods, on the other hand, help identify the factors or healthcare companies with the highest priority in terms of service quality. In this work, a comprehensive decision-making structure is constructed by analyzing related studies that analyze SERVQUAL for both state and private hospitals. The evaluation of the constructed structure has been performed using an integrated decision-making procedure, namely the SF-AHP for the identification of priority weights of the SERVQUAL subcriteria and SF-WASPAS for the evaluation of the hospitals under the different criteria, both of which are spherical fuzzy set extensions that allow inconsistent judgments and address more information about their ambiguity. As an important departure offered in our proposed methodology, the generation of different rankings associated with the SERVQUAL criteria is leveraged by the use of an integrated Borda-Copeland method for the final ranking of hospitals.

The contribution of this research lies in its innovative use of the MCDM methods in an uncertain environment and the revision of the service quality measurement model, which has resulted in a new approach to evaluating hospitals during the COVID-19 era. This model can serve as a benchmark not only for hospitals in other countries but also for hospitals facing similar challenges and seeking guidance from the best-performing hospitals in similar situations. As part of further research, the applied methodology could be used to assess the service quality of temporary hospitals, which may be considered a new hospital concept when the number of patients is very high, and the capacity of existing hospitals is insufficient to meet these patients’ needs. The most significant limitation is the lack of experts capable of evaluating criteria and alternatives. Despite these limitations, a detailed and systematic hierarchy for comparing the service performance of significant hospitals in the pandemic area has been successfully implemented.