Inspection of the Production Lot Using Two Successive Occasions Sampling Under Neutrosophy

Abstract

The efficiency of the measuring tools and operators is a significant part of lot sentencing decisions. These tools have to pass some pre-specified quality levels to avoid problems during the quality assessment scenarios. These measurements have a serious risk to be encountered with any extent of ambiguity, doubt, or indeterminacy due to any of the factors like variation among the operating regimes, warming effects in the hot climatic conditions, the operators’ casual attitude, and so on. These factors as the most significant sources of extraneous variations can deeply affect the efficacy of lot sentencing decisions. Hence, the decision when based on the measurement through the operating tools and these tools have to pass which have fulfilled some adequate standards only then lot sentencing may avoid or save from the rejection of a good lot. The authors have put their focus on dealing with the factors that arise by measuring variability among the measured or determined values despite having the normal population distribution. In this study, the auxiliary information is used to estimate the variable of interest over the two successive occasions under the neutrosophic interval numbers and proved helpful to overcome this issue. The presented approach has discussed that in blurred, doubted, uncertain and undetermined datasets partially or completely, the efficacy of the decision for the whole lot cannot be decided on the single point crisped value. But the range of values around such a single crisp point in the form of neutrosophic theory is proved far better. In this context, the neutrosophic interval number successive sampling-based sampling plan is proposed which is the major contribution to the existing literature. It is explained in terms of operating characteristic function and the plan parameters are determined through the neutrosophic non-linear optimization approach. The comparative analysis is presented with the existing sampling plans and found efficient. Moreover, a real-life industrial dataset is used as an application of the concept.

1 Introduction

Today, industries are at greater risk due to final products efficiency and the specificity of the warranty time for a company. A sale product is a final product that comes out with no further processing. Decisions about acceptance or rejection of a lot are a matter of one or two minute which depends upon the quality of the measuring tools and the operators/operating systems. That is why a minute inspection of these final products is an important part of the successful specified warranty time to increase revenue. In simple words, the operating systems are responsible for the core issues. In real practice, the respective operating system and operators take a few minutes to complete the whole lot sentencing procedure. So, the accuracy of the measuring tools plays a major role in this case. The operating acceptance sampling plans which are implemented to evaluate the lot sentencing procedures must be minutely selected by keeping warranty time and the revenue increase for the company in mind.

Hence, tools assessment is vital to get accurate, to the point, and desired quality levels as these tools can be the major cause for manipulating the product quality variation due to the effect of these extraneous factors in the lot sentencing procedures. First, Azam et al. [1] have discussed this situation in statistical process control over the two successive occasions and designed a successive sampling-based acceptance sampling plan. According to them, the lot sentencing matter should not be solely dependent on the current time recorded observations when the products are facing constantly the effects of the production process environment in the form of temperature, labor and others, etc. Azam et al. [1] involve some prior or recorded information as auxiliary data to measure the extent or the degree of variation more accurately and prove it efficient. Azam et al. [1] introduced the estimation over the two successive occasions for estimating the average change in the current occasion, the total average change in the 2nd occasion is treated as an estimate of the variable under study. The prior occasion measurement from the same object is observed at the 1st occasion is treated as the auxiliary dataset. As real-life dataset always possessed variation itself about the variable of interest, then a sampling plan based on the current data without any prior knowledge may not efficiently provide a reliable clue about the rate of change in nature or the effect of any factor which may have some serious effects on the process (Miranda [2]). After the efficient approach in the construction of the acceptance sampling plan, this concept has successfully gained its place in the area of quality control mean monitoring charts. Azam et al. [3] introduced the successive sampling over the two successive occasions approach in the designing of the control chart and proved it efficient than the existing one. Again, Arshad et al. [4] used this concept with repetitive sampling and designed a successive sampling over the two successive occasions-based control chart and found it better.

The neutrosophic numbers have gained a remarkable place in statistical quality control, as they have become a tool to treat datasets with uncertainty whether it is at a partial level or a complete level. To date, the literature of statistical process control has been quite enriched with neutrosophic numbers-based sampling plans and the control charts, i.e., Kanagawa and Ohta [5] have designed an attribute sampling plan based on the fuzzy set theory and proved it efficient for handling uncertain and ambiguous dataset. Tamaki et al. [6] presented a fuzzy design for the lot sentencing procedures using the attributes. Cheng et al. [7] in the construction of fuzzy testings’ adapted the neutrosophic numbers and found them efficient. Aslam [8] has introduced an acceptance sampling plan using the neutrosophic process loss function and found it better than the existing single sampling-based sampling plan and the neutrosophic sampling plan. After this, Aslam [9] utilized the neutrosophic numbers to handle the uncertainty in the dataset, which follows the exponential distribution behavior, and constructed the acceptance sampling plan. Aslam and Arif [10] extended the neutrosophic numbers with the Weibull distribution for the construction of the testing of the grouped products. Aslam and Raza [11] designed the sampling plan of the neutrosophic numbers for the industries facing the multiple manufacturing lines with uncertainty and Again Aslam [12] developed an attribute sampling plan with the single sampling scheme and found them better than existing ones. Aslam [13] considered the concept of product-moment with the measurement in the adaptation of neutrosophic numbers in the construction of its methodology. Aslam [14] proposed the variable acceptance sampling plan in the adaptation of neutrosophic interval numbers and used it as a comparison paper in this study.

The control charts are designed using the neutrosophic interval numbers to get more sensitive control charts for the small shifts when uncertainty is involved like; Zarandi et al. [15] and Alaeddini et al. [16] has forwarded neutrosophic numbers in control charts using adaptive sampling scheme with run rules method and a hybrid control chart with statistical clustering for the both fixed and the variable sampling methods.

The motivation behind the presented work is discussed by considering the partially or completely uncertainty element raising doubts in some kind of the blurred dataset. In such scenarios, the sampling plans based on the crisp and determined single point values will not fulfill the purpose and may have a serious risk of rejecting a good lot. So, the authors are motivated in the presented study to deal with the sudden variation element of data sets with the successive sampling over the two successive occasions estimation procedure and the crisp and determined values scenarios with the neutrosophic interval numbers. The efficacy of the concept is explained through the operating characteristic function. The upcoming Sect. 2 and Sect. 3 will explain the theory of neutrosophic interval numbers and the proposed methodology with determined parametric results. Section 4 and Sect. 5 are comprised of results discussion and the comparative study analysis with existing sampling plans. The similarities and differences of the research are also discussed in Sect. 6, whereas Sect. 7 is based on real-life application using some industrial dataset as an example and Sect. 8 has discussed the limitations of the proposed study. The last section is wrapped up with the concluding remarks and further research perspectives.

2 Neutrosophic Interval Number Statistics Theory

The neutrosophic logic is considered as the generalization of fuzzy logic environment and considered to handle the measures of indeterminacy, see Smarandache [17]. Based on this logic, Smarandache [18] gave the idea of neutrosophic statistics. This statistic is an extension of classical statistics and applied under an uncertain environment. Neutrosophic statistics is more flexible, effective, and informative than classical statistics. The applications of neutrosophic statistics in some other fields are also widely used; Chen et al. [19] have given the scale effect and anisotropy analysis with the neutrosophic numbers for the rock joint roughness coefficient and again Chen et al. [20] have expressed the rock joint roughness coefficient in the adaptation of the neutrosophic interval statistics numbers. Moreover, neutrosophic numbers are widely used in decision-making theory like Garg [21] has proposed the single value-based algorithm with neutrosophic decision-making based on the COPRAS (complex proportional assessment method) and the aggregate operators with some new modified information measures, Nancy and Garg [22] developed a divergence measure with single-valued neutrosophic set and explained the TOPSIS (Technique for the order preference with similarity to deal with the situation) method I adaptation of multi-criteria decision-making procedures, Garg and Nancy [23] have given the concept of non-linear programming using the neutrosophic interval set for handling the multi-criteria decision-making. Garg & Nancy [24] have given some new laws and their applications based on the single-valued neutrosophic numbers to deal with the multi-attribute decision-making environment, and again Garg and Nancy [25] have introduced some new modified aggregation operators, which are linguistically prioritized to deal with the multi-attribute group decision-making environment. After this, Garg and Nancy [26] extended it to develop hybrid weighted average aggregation operators in the adaptation of neutrosophic set numbers to handle a multi-criteria decision-making environment. Recently, Jana and Pal [27] gave robust single-valued neutrosophic soft aggregation operators in multi-criteria decision-making, Jana et al. [28] introduced the trapezoidal operators with their implementation on multi-attribute decision-making, Jana et al. [29] presented the multi-attribute decision-making problems based on the SVTNH methods, again Jana and Karaaslan [30] introduced the Dice and Jaccard similarity measures based expected intervals trapezoidal neutrosophic fuzzy numbers with their application in multi-criteria decision-making as well. Moreover, Jana et al. [31] designed a multi-criteria decision-making approach based on the SVTrN dombi aggregation functions methodology and Jana and Pal [32] introduced a multi-criteria decision-making dealing with the single-valued neutrosophic dombi power aggregation operators.

Neutrosophic interval statistics represents a set of data, with partial or complete indeterminacy when statistical tools are used to deal with the situation. The only difference between the classical and neutrosophic statistics is the nature of the classical statistics dataset which deals with the crisp and the determined values. The neutrosophic interval numbers are developed to measures are developed to measure the degree or extent of indeterminacy in the dataset as the interval of numbers around those crisp values. It is very important to differentiate indeterminacy which comes from the randomness of the dataset, as randomness is the characteristic of classical statistics. Both the randomness and indeterminacy are handled with neutrosophic interval number statistics. Smarandache [18] has explained that if in a dataset with neutrosophic approach values are isolated points then can be expressed as the $A=6+b$ with $b\in \left[\mathrm{0,1}\right], \mathrm{7,26}+c,$ where $c\in [\mathrm{3,5}]$. Hence, the resulting number will represent the neutrosophic number (detail can be seen in Smarandache [18]) in a specific interval format, i.e., when there are 100 balls and each ball can be expressed in an interval format $\left[a,b\right]\, \forall a,b\in \{\mathrm{1,2},3,\dots ,100\}$ and $a\le b$ if $a=b,$ then result will give a crisp number $\left[a,a\right]=a.$ Then, it will be explained as instead of the random sequence of the crisp values, it will be the random sequence of interval values and the classical statistics formulas are converted from crisp variable to the neutrosophic variable (i.e., the variable with values as a set).

3 The Proposed Acceptance Sampling Plan

Usually, the existing studies put their emphasis on utilizing the measured crisped, determined, pointed values to construct a sampling plan. At times, it does not seem practical to have such scenarios as various extraneous factors are constantly causing serious wear and tear of the measuring instruments on which the lot sentencing procedure is mainly relying. So, the novelty in the presented research is to use the range of values around these crisped, determined, and pointed values. The presented concept gives a more precise and accurate picture of the problem under study which closely predicts the scenario.

The proposed sampling plan is a two occasions-based estimation design and correlation value between two occasions has significant importance in estimating the variable under study with the neutrosophic interval numbers. The variable under study ${Y}_{Ni}=\left\{{Y}_{Li},{Y}_{Ui}\right\}$ represents the current occasion information under neutrosophic interval numbers the prior occasion information ${X}_{Ni}=\left\{{X}_{Li},{X}_{Ui}\right\}$ which is collected from the same object for the same characteristic of interest, as the 1st occasion information. The correlation between them is explained by ${\rho }_{{X}_{N}{Y}_{N}}=\left\{{\rho }_{{X}_{L}{Y}_{L}},{\rho }_{{X}_{U}{Y}_{U}}\right\}$. The dataset is binary, over the two successive occasions to gather information from the same object or unit named as two successive occasions with the single sampling unit.

To get an efficient estimated average change over the recent occasion ${Y}_{Ni}$ with the explored prior occasion information ${X}_{Ni}$, in the presence of high value of the correlation between two occasions Mukhopadhyay [33] suggested a best linear unbiased estimator for estimating the average change in the variable of interest over the two occasions ${\mu }_{{Y}_{Ni}}$ which is provided in Eq. (1). Moreover, it provides minimum variance estimation among existing linear unbiased estimators. The estimator for ${\mu }_{{Y}_{Ni}}$ is given as follows:

$$\widehat{{\mu }_{{Y}_{Ni}}}={a}_{N}{\overline{x} }_{{u}_{Ni} }+{b}_{N}{\overline{x} }_{{m}_{Ni} } +{c}_{N}{\overline{y} }_{{m}_{Ni} }+ {d}_{N}{\overline{y} }_{{u}_{Ni.}}$$

(1)

Let ${n}_{N}=\left\{{n}_{L},{n}_{U}\right\}$ and each ${n}_{N}={m}_{N}+{u}_{N},$ where ${m}_{N}=\left\{{m}_{L},{m}_{U}\right\}$ and ${u}_{N}=\left\{{u}_{L},{u}_{U}\right\}. {n}_{N}$ units are drawn at successive occasions and ${\overline{x} }_{{m}_{Ni}}$, ${\overline{y} }_{{m}_{Ni}}$, ${\overline{x} }_{{u}_{Ni}}$ and ${\overline{y} }_{{u}_{Ni}}$ are the sample means. Here, ${m}_{Ni}$ stands for the matched units and ${u}_{Ni}$ for the unmatched units at both the occasions, with ${a}_{N}, {b}_{N},{c}_{N}$ and ${d}_{N}$ as the fixed quantities which imply that ${a}_{N}+{b}_{N }=0$ and ${{c}_{N}+d}_{N}=1$. Both the occasions’ population have an equal variation on both occasions, i.e., ${\sigma }_{{X}_{Ni}}^{2}={\sigma }_{{Y}_{Ni}}^{2}={\sigma }^{2}$. The constant terms are estimated as

$${a}_{N}=\frac{{\mu }_{N}{\lambda }_{N}{\rho }_{{X}_{N}{Y}_{N}}}{1-{{\mu }_{N}}^{2}{\rho }_{{X}_{N}{Y}_{N}}^{2}},$$

(2)

$${c}_{N}=\frac{{\lambda }_{N}}{1-{{\mu }_{N}}^{2}{\rho }_{{X}_{N}{Y}_{N}}^{2}},$$

(3)

${\lambda }_{N}=\frac{{m}_{Ni}}{{n}_{N}}, {\mu }_{N}=\frac{{u}_{Ni}}{{n}_{N}}$ as the matched and the unmatched elements, proportion implies that ${\upmu }_{N}+{\lambda }_{N}=1$.

The optimum way to get unmatched units proportion and the variance of ${\mu }_{{Y}_{Ni}}$ is as follows:

$${\mu }_{N\mathrm{opt}}=\frac{1}{1+\sqrt{1-{\rho }_{{X}_{N}{Y}_{N}}^{2}}},$$

(4)

$${Var(\widehat{{\mu }_{{Y}_{Ni}}})}_{\mathrm{opt}}= \frac{{\sigma }^{2}}{2{n}_{N}} \left(1+ \sqrt{1-{\rho }_{{X}_{N}{Y}_{N}}^{2}}\right).$$

(5)

In the presented neutrosophic statistical interval numbers approach, the respective population mean and variance of ${\mu }_{{Y}_{N}}$ can be explained as ${\mu }_{{Y}_{N}}=\left\{{\mu }_{{Y}_{L}},{\mu }_{{Y}_{U}}\right\}$ and ${\sigma }_{{Y}_{N}}^{2}=\left\{{\sigma }_{{Y}_{L}}^{2},{\sigma }_{{Y}_{U}}^{2}\right\}$. Here, it is assumed that these population parametric values are prior data to study the current occasion variable behavior for estimating ${\mu }_{{Y}_{N}}$. A detailed discussion about successive sampling over two occasions-based acceptance sampling plans can be seen in Azam et al. [1].

The proposed plan is being designed under the following steps:

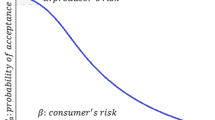
Step 1: Two kinds of risks must be stated (producer’s and consumer’s risks) with respective quality levels such as acceptable quality level (AQL) and the limiting quality level (LQL).

Step 2: Select a simple random sample with a size ${n}_{N}=\left\{{n}_{L},{n}_{U}\right\}$ from the population of size ${N}_{N}=\left\{{N}_{L},{N}_{U}\right\}$ and compute the estimator $\widehat{{\mu }_{{Y}_{Ni}}}$ and the acceptance statistic will be as follows:

$${V}_{N}=\frac{{USL}_{N}-\widehat{{\mu }_{{Y}_{Ni}}}}{{\sigma }_{{Y}_{N}}}.$$

(6)

Step 3: Understudy, production lot will be accepted if and only if the condition ${V}_{N }\ge$ ${C}_{N}$ fulfilled, or otherwise, it will be rejected. Here, ${C}_{N}=\left\{{C}_{L},{C}_{U}\right\}$ is characterized as the neutrosophic acceptance number.

Hence, the proposed sampling plan has five basic parameters, ${n}_{N}=\left\{{n}_{L},{n}_{U}\right\}$ and ${C}_{N}=\left\{{C}_{L},{C}_{U}\right\}$ along with the ${\rho }_{{X}_{N}{Y}_{N}} ,$ ${p}_{1}$ and ${p}_{2}$ and upper neutrosophic specified limit as ${USL}_{N}=\left\{{USL}_{L},{USL}_{U}\right\}$ and follows the normal distribution. It is considered that $\widehat{{\mu }_{{Y}_{Ni}}}$ exhibits normal distribution behavior according to (Duncan [34]) as $\widehat{{\mu }_{{Y}_{Ni}}} \sim N\left[{\mu }_{{Y}_{Ni}} , \frac{{{\sigma }_{Y}^{2}}_{N}}{2{n}_{N}} \left(1+ \sqrt{1-{\rho }_{{X}_{N}{Y}_{N}}^{2}}\right)\right]$ with mean values as$E\left(\widehat{{\mu }_{{Y}_{Ni}}}\right)= {\mu }_{{Y}_{Ni}}$, where ${\mu }_{{Y}_{Ni}}$ is the neutrosophic population mean of the study variable and variance as$Var\left(\widehat{{\mu }_{{Y}_{Ni}}}\right)= \frac{{{\sigma }_{Y}^{2}}_{N}}{2{n}_{N}} \left(1+ \sqrt{1-{\rho }_{{X}_{N}{Y}_{N}}^{2}}\right)$. Here, two cases are discussed based on the availability of ${\sigma }_{{Y}_{N}}$ population standard deviation. Case A: when the population standard deviation ${\sigma }_{{Y}_{N}}$ is known. Case B: when the population standard deviation ${\sigma }_{{Y}_{N}}$ is not known. The following discussion has been presented for the proposed neutrosophic operating mechanism of the characteristic (NOC) function in the proposed scenario:

3.1 Case A: When ${\sigma }_{{Y}_{N}}$ is Known

By assuming the upper specification limit ${USL}_{N}=\left\{{USL}_{L},{USL}_{U}\right\}$ for the $\widehat{{\mu }_{{Y}_{Ni}}}$ when the value of ${\sigma }_{{Y}_{N}}$ is known, the probability of acceptance for a lot is given below

$${P}_{aN}=P\left({ V}_{N} \ge { C}_{N}\right),$$

(7)

$${P}_{aN}=P\left(\widehat{{\mu }_{{Y}_{Ni}}} +{ C}_{N}{\sigma }_{{Y}_{N}}\le {USL}_{N}\right).$$

(8)

According to Duncan [34], the estimator will become

$$\widehat{{\mu }_{{Y}_{Ni}}} +{ C}_{N}{\sigma }_{{Y}_{N}} \sim N\left[{\mu }_{{Y}_{Ni}}+{ C}_{N}{\sigma }_{{Y}_{N}} , \frac{{{\sigma }_{Y}^{2}}_{N}}{2{n}_{N}} \left(1+ \sqrt{1-{\rho }_{{X}_{N}{Y}_{N}}^{2}}\right)\right].$$

(9)

It has been noted that $\widehat{{\mu }_{{Y}_{Ni}}} +{ C}_{N}{\sigma }_{{Y}_{N}}$ follows the standard normal distribution, so the above equation becomes

$$ P_{aN} = P\left[ {\frac{{\left( {\widehat{{\mu_{{Y_{Ni} }} }} + C_{N} \sigma_{{Y_{N} }} } \right) - \left( {\mu_{{Y_{Ni} }} + C_{N} \sigma_{{Y_{N} }} } \right)}}{{\sqrt { \frac{{\sigma_{{Y_{N} }}^{2} }}{{2n_{N} }} \left( {1 + \sqrt {1 - \rho_{{X_{N} Y_{N} }}^{2} } } \right)} }} \le \frac{{USL_{N} - \left( {\mu_{{Y_{Ni} }} + C_{N} \sigma_{{Y_{N} }} } \right)}}{{\sqrt { \frac{{\sigma_{{Y_{N} }}^{2} }}{{2n_{N} }} \left( {1 + \sqrt {1 - \rho_{{X_{N} Y_{N} }}^{2} } } \right)} }}} \right], $$

(10)

where

$$\frac{\left(\widehat{{\mu }_{{Y}_{Ni}}}+{ C}_{N}{\sigma }_{{Y}_{N}}\right) -\left({\mu }_{{Y}_{Ni}}+{ C}_{N}{\sigma }_{{Y}_{N}}\right)}{\sqrt{ \frac{{{\sigma }_{Y}^{2}}_{N}}{2{n}_{N}} \left(1+ \sqrt{1-{\rho }_{{X}_{N}{Y}_{N}}^{2}}\right)}}={z}_{p}.$$

(11)

Finally, the OC function for the known standard deviation $\left({\sigma }_{{Y}_{N}}\right)$ is given below

$$ P_{aN} \left( p \right) = {\Phi }\left[ {\frac{{\left( {Z_{p} - C_{N} } \right)}}{{\sqrt { \frac{1}{{2n_{N} }} \left( {1 + \sqrt {1 - \rho_{{X_{N} Y_{N} }}^{2} } } \right)} }}} \right]. $$

(12)

Here, ${\Phi \left(.\right)\,\mathrm{ and }\, Z}_{p}$ are cumulative density function (CDF) and the ${p}^{th}$ percentile value of the standard normal distribution correspondingly.

$$ L_{N} \left( {p_{1} } \right) \ge 1 - \alpha \,{\text{and}}\,\,L_{N} \left( {p_{2} } \right) \le \beta $$

(13)

Now, the proposed plan parametric values are computed such that specified producer’s risk value $\alpha$ and consumer’s risk value $\beta$ are justified. These two risks are satisfied when the $NOC$ curve passed over two particular points $(\alpha ,{p}_{1})$ and $(\beta ,{p}_{2})$ one-to-one. It is justified only if ${n}_{N}$ is minimized. To determine plan parametric values of the proposed sampling plan, the following non-linear optimization rule is used:

Minimized ${n}_{N}$ such that

$$ P_{aL} \left( {p_{1} } \right) = {\Phi }\left[ {\frac{{\left( {Z_{p} - C_{L} } \right)}}{{\sqrt { \frac{1}{{2n_{L} }} \left( {1 + \sqrt {1 - \rho_{{X_{N} Y_{N} }}^{2} } } \right)} }}} \right] \ge 1 - \alpha ,\,P_{aU} \left( {p_{1} } \right) = {\Phi }\left[ {\frac{{\left( {Z_{p} - C_{U} } \right)}}{{\sqrt { \frac{1}{{2n_{U} }} \left( {1 + \sqrt {1 - \rho_{{X_{N} Y_{N} }}^{2} } } \right)} }}} \right] \ge 1 - \alpha , $$

(14)

$$ P_{aL} \left( {p_{2} } \right) = {\Phi }\left[ {\frac{{\left( {Z_{p} - C_{L} } \right)}}{{\sqrt { \frac{1}{{2n_{L} }} \left( {1 + \sqrt {1 - \rho_{{X_{N} Y_{N} }}^{2} } } \right)} }}} \right] \le \beta \,{\text{and}}\,P_{aU} \left( {p_{2} } \right) = {\Phi }\left[ {\frac{{\left( {Z_{p} - C_{U} } \right)}}{{\sqrt { \frac{1}{{2n_{U} }} \left( {1 + \sqrt {1 - \rho_{{X_{N} Y_{N} }}^{2} } } \right)} }}} \right] \le \beta . $$

(15)

To get these concepts in the discussion concerning the simulation, a brief code is provided in Algorithm 1.

3.2 Case B: When ${\sigma }_{{Y}_{N}}$ Is Not Known

Usually, in real practice, ${\sigma }_{{Y}_{N}}$ is not available. In this situation, ${\sigma }_{{Y}_{N}}$ has to be estimated with the help of some prior information or dataset by the sample standard deviation ${S}_{{Y}_{N}}$. The operating characteristic (OC) function of the designed plan when the standard deviation ${\sigma }_{{Y}_{N}}$ is not available with the acceptance probability of a lot, given below

$${P}_{aN}^{*}=P\left({V}_{N }^{*}\ge { C}_{N}\right),$$

(16)

$${P}_{aN}^{*}=P\left(\frac{{ USL}_{N} - \widehat{{\mu }_{{Y}_{Ni}}} }{{S}_{{Y}_{N}} }\ge { C}_{N}\right),$$

(17)

$${P}_{aN}^{*}=P\left(\widehat{{\mu }_{{Y}_{Ni}}} +{ C}_{N}{S}_{{Y}_{N}} \le { USL}_{N}\right).$$

According to Duncan [34] approach:

$\widehat{{\mu }_{{Y}_{Ni}}} +{ C}_{N}{S}_{{Y}_{N}}$, follows a standard normal distribution as follows:

$$\widehat{{\mu }_{{Y}_{Ni}}} +{ C}_{N}{S}_{{Y}_{N}}\sim N\left[{\mu }_{{Y}_{Ni}} +{ C}_{N} E\left({S}_{{Y}_{N}}\right), \frac{{{\sigma }_{Y}^{2}}_{N}}{{n}_{N}} + {{ C}_{N}}^{2} Var\left({S}_{{Y}_{N}}\right)\right].$$

(18)

We know that

$$ c_{4} = \sqrt {\frac{2}{{ n_{N} - 1}}} \cdot \frac{{\Gamma \left( {\frac{{ n_{N} }}{2}} \right)}}{{\Gamma \left( {\frac{{ n_{N} - 1}}{2}} \right)}}. $$

(19)

As we know that the mean and variance of ${S}_{{Y}_{N}}$ are as follows: $E({S}_{{Y}_{N}})={c}_{4 }{\sigma }_{{Y}_{N}}$ and $Var({S}_{{Y}_{N}})={{\sigma }_{Y}^{2}}_{N}\left(1- {c}_{4}^{2}\right)$. Now, the proposed OC function can be written as.

$$ P\left( {V_{aN }^{*} \ge C_{N} } \right) = P\left[ {\frac{{\left( {\widehat{{\mu_{{Y_{Ni} }} }} - C_{N} S_{{Y_{N} }} } \right) - \left( {\mu_{{Y_{Ni} }} + C_{N} .c_{4} \sigma_{{Y_{N} }} } \right)}}{{\sqrt {\left[ {\frac{{\sigma_{{Y_{N} }}^{2} }}{{n_{N} }} + C_{N}^{2} \sigma_{{Y_{N} }}^{2} \left( {1 - c_{4}^{2} } \right)} \right]} }} \le \frac{{ USL_{N} - \left( {\mu_{{Y_{Ni} }} + C_{N} .c_{4} \sigma_{{Y_{N} }} } \right)}}{{\sqrt {\left[ {\frac{{\sigma_{{Y_{N} }}^{2} }}{{n_{N} }} + C_{N}^{2} \sigma_{{Y_{N} }}^{2} \left( {1 - c_{4}^{2} } \right)} \right]} }}} \right]. $$

(20)

After some mathematical simplifications, it will become:

$${P}_{aN}\left(p\right)=\Phi \left[\frac{{Z}_{P}-{ C}_{N}{c}_{4} }{\sqrt{\left[\frac{1}{{ n}_{N}} + {{ C}_{N}}^{2}\left(1- {c}_{4}^{2}\right)\right]}} \right].$$

(21)

Similar to the ${\sigma }_{{Y}_{N}}$ known case, we will find proposed plan parameters using the optimization scheme such as.

Minimized ${n}_{N}$

$${P}_{aN}\left({p}_{1}\right)=\Phi \left[\frac{{Z}_{{p}_{1}}-{ C}_{N}{c}_{4} }{\sqrt{\left[\frac{1}{{ n}_{N}} + {{ C}_{N}}^{2}\left(1- {c}_{4}^{2}\right)\right]}} \right]\ge 1-\alpha ,$$

(22)

$${P}_{aN}\left({p}_{2}\right)=\Phi \left[\frac{{Z}_{{p}_{2}}-{ C}_{N}{c}_{4} }{\sqrt{\left[\frac{1}{{ n}_{N}} + {{ C}_{N}}^{2}\left(1- {c}_{4}^{2}\right)\right]}} \right]\le \beta .$$

(23)

To get this concept in a discussion concerning the simulation, a brief code is provided in Algorithm 2.

The advantage of the proposed methodology following the neutrosophic theory is to grab those deficiencies and overcome the discrepancies which are not able to do in the crisped, determined, and pointed values of the lot acceptance numbers. In the above-mentioned plan, the neutrosophic interval numbers assign a range around the crisped values to minimize the chance of rejecting a good lot. Hence, the proposed methodology will prove an efficient effort when already the uncertainty, and doubt in the measurements are expected. The lot sentencing procedure has a dependence on the performance of the measuring tool and they may face any kind of wear and tear so, by keeping lots of issues in mind, it is better to provide an interval instead of a single point value to decide about the future of the whole lot.

4 Results and Discussion

After the completion of the optimization process, the determined results are expressed extensively in Tables 1, 2, 3, 4, 5, 6, 7, 8 for two respective cases, explained in Sect. 3. The parametric values are determined by the simulation process in the adaptation of specified AQL and LQL values as per justification of the points $(\alpha =0.05,{ p}_{1})$ and $(\beta =0.10,{ p}_{2})$ in the optimization process. The respective discussion is being explained for both the cases sigma ${\sigma }_{{Y}_{N}}$ known and unknown, as follows:

Table 1 Plan parameters for the existing neutrosophic plan, when ${\sigma }_{{Y}_{N}}$ is known and ${\rho }_{{X}_{N}{Y}_{N}}=0$

Table 2 Plan parameters for proposed plan, when ${\sigma }_{{Y}_{N}}$ is known and ${\rho }_{{X}_{N}{Y}_{N}} = 0.50$

Table 3 Plan parameters for proposed plan, when ${\sigma }_{{Y}_{N}}$ is known and ${\rho }_{{X}_{N}{Y}_{N}} = 0.75$

Table 4 Plan parameters for the proposed plan, when ${\sigma }_{{Y}_{N}}$ is known and ${\rho }_{{X}_{N}{Y}_{N}} = 0.95$

Table 5 Plan parameters for the existing neutrosophic plan, when ${\sigma }_{{Y}_{N}}$ is unknown and ${\rho }_{{X}_{N}{Y}_{N}} = 0$

Table 6 Plan parameters for the proposed plan, when ${\sigma }_{{Y}_{N}}$ is unknown and ${\rho }_{{X}_{N}{Y}_{N}} = 0.50$

Table 7 Plan parameters for the proposed plan, when ${\sigma }_{{Y}_{N}}$ is unknown and ${\rho }_{{X}_{N}{Y}_{N}} = 0.75$

Table 8 Plan parameters for the proposed plan, when ${\sigma }_{{Y}_{N}}$ is unknown and ${\rho }_{{X}_{N}{Y}_{N}} = 0.95$

4.1 Results Discussion for ${{\varvec{\sigma}}}_{{{\varvec{Y}}}_{{\varvec{N}}}}$ Known Case

The computed parametric values of the proposed plan with sigma known case are mentioned in Tables 2, 3, 4 extensively. A detailed analysis along with different values of the ${\rho }_{{X}_{N}{Y}_{N}}$ is given below:

• The determined $AQL$ value shows a dropping trend in the ${n}_{N}$ values as $LQL$ increases. For example, from Table 2, it can be seen that when$AQL =0.001$, ${n}_{N}=\{69, 77\}$ for$LQL=0.003$. But ${n}_{N} =\{8, 9\}$ for $=0.02$.

• An inclined trend can be easily observed for a fixed value of $LQL$, the ${n}_{N}$ increases as $AQL$ increases. For example, from Table 2, it can be seen that when $LQL =0.015$, ${n}_{N}=\{10, 12\}$ for $AQL=0.001$. But ${n}_{N} =\{20, 26\}$ for $AQL=0.0025$, and ${n}_{N} =\{50, 65\}$ for $AQL=0.005$.

• For the fixed values of $AQL$ and $LQL$, a dropping behavior can be seen in the ${n}_{N}$ values as ${\rho }_{{X}_{N}{Y}_{N}}$ increase. For example, for $AQL =0.001$ & $LQL=0.006$ at ${\rho }_{{X}_{N}{Y}_{N}}=0.50$, ${n}_{N}=\{24, 31\}$ from Table 2, ${n}_{N} =\{22, 27\}$ for ${\rho }_{{X}_{N}{Y}_{N}}=0.75$ from Table 3, and ${n}_{N} =\{17, 22\}$ for ${\rho }_{{X}_{N}{Y}_{N}}=0.95$ from Table 4.

4.2 Results Discussion for ${{\varvec{\sigma}}}_{{{\varvec{Y}}}_{{\varvec{N}}}}$ Unknown Case

In this section, a detailed analysis is presented for unknown sigma ${\sigma }_{{Y}_{N}}$, at the points of $(\alpha =0.05,{p}_{1})$ & $(\beta =0.10,{p}_{2})$ along with various values of ${\rho }_{{X}_{N}{Y}_{N}}$. The parametric computational results are shown in extensive Tables 6, 7, 8 for the specified combinations of $AQL$ and $LQL$ values, and the following trend is being observed:

• The $AQL$ value shows a dropping trend in respective computed sample sizes ${n}_{N}$ values as $LQL$ values increases. For example, in Table 6 when $AQL =0.001$, it is observed that ${n}_{N}=\{87, 97\}$ for $LQL=0.008$. But ${n}_{N} =\{34, 40\}$ for $AQL=0.02$.

• An inclined trend can be easily observed for the sample ${n}_{N}$ when the values of $LQL$ are fixed, as $AQL$ increases. For example, from Table 6 when $LQL =0.015$, ${n}_{N}=\{44, 47\}$ for $AQL=0.001$. But ${n}_{N} =\{85, 100\}$ for $AQL=0.0025$, and ${n}_{N} =\{198, 232\}$ for $AQL=0.005$.

• For the same $AQL$ and $LQL$ computations, a dropped downtrend can also be seen in the ${n}_{N}$ values as ${\rho }_{{X}_{N}{Y}_{N}}$ increases. For example, for $AQL =0.001$ & $LQL=0.006$ at ${\rho }_{{X}_{N}{Y}_{N}}=0.50$ & ${n}_{N}=\{126, 138\}$ from Table 6, ${n}_{N} =\{122, 137\}$ for ${\rho }_{{X}_{N}{Y}_{N}}=0.75$ from Table 7, and ${n}_{N} =\{117, 129\}$ for ${\rho }_{{X}_{N}{Y}_{N}}=0.95$ from Table 8.

4.3 Key Findings

The observed key findings from the two respective sections of the Case A and Case B are as follows:

• For both the ${\sigma }_{{Y}_{N}}$ known and unknown cases as ${n}_{N}$ and ${C}_{N}$ decreases as the respective $AQL$ and the $LQL$ values go on increases.

• For both the ${\sigma }_{{Y}_{N}}$ known and unknown cases as $AQL, {n}_{N}$ and ${C}_{N}$ increases at the fixed $LQL$ value.

• For both the ${\sigma }_{{Y}_{N}}$ known and unknown cases ${n}_{N}$ and ${C}_{N}$ decreases at the respective $AQL$ and the $LQL$ fixed values

Moreover, the presented sampling plan perform under the five respective parameter values of $AQL, LQL, \alpha ,\beta$ and ${\rho }_{{X}_{N}{Y}_{N}}$.

5 Comparative Study

The comparison study has been made with Azam et al. [1] and Aslam [14] and found that the proposed plan is better than the existing sampling plans. First, the comparison is discussed in detail with Azam et al. [1]. The proposed sampling plan can be transformed into the single sampling neutrosophic acceptance sampling plan when ${\rho }_{{X}_{N}{Y}_{N}}=0$; the correlation between prior and current occasion information becomes zero, as a generalization of the proposed plan for ${\rho }_{{X}_{N}{Y}_{N}}=0$. The tabulated results are provided in Table 1 and Table 5, respectively, for both sigma known and unknown cases with the corresponding sample size ${n}_{N}=\left\{{n}_{L},{n}_{U}\right\}$ & the lot rejection number ${C}_{N}=\left\{{C}_{L},{C}_{U}\right\}$. The proficiency of any acceptance sampling plan can be evaluated in terms of the least determined sample value in its magnitude necessary for lot inspection. Moreover, sample size with its least possible value in magnitude can be used as a point of demarcation at specified quality measures of $AQL$ and $LQL$. Whereas the lower limit of the proposed concept can represent Azam et al. [1] and the proposed concept is based on the neutrosophic interval dataset. Before doing comparative analysis in terms of finding the most efficient one, it has to be understood by this basic difference. Now it can be easily observed that the proposed plan gives the lower value of neutrosophic sample size whereas the difference is due to the different ${\rho }_{{X}_{N}{Y}_{N}}$ values and because of the simulation process. The observed analysis is as follows:

• For the $AQL=0.001$ and $LQL= 0.003, 0.020$ at sigma known case from Table 9, the existing plan gives a sample size ${n}_{N}=\left\{75, 100\right\}, \{\mathrm{8,10}\}$, and for $AQL=0.0025$ and for $LQL= 0.010, 0.020$ gives neutrosophic sample size ${n}_{N}=\left\{38, 44\right\}, \left\{\mathrm{16,19}\right\},$ whereas proposed one gives minimum value of ${n}_{N}=\left\{\mathrm{62,78}\right\},\{\mathrm{7,8}\}$ and ${n}_{N}=\left\{\mathrm{32,40}\right\},\{\mathrm{13,16}\}$ at ${\rho }_{{X}_{N}{Y}_{N}}=0.75$ and ${n}_{N}=\left\{\mathrm{49,60}\right\},\{\mathrm{6,7}\}$ and ${n}_{N}=\left\{\mathrm{25,31}\right\},\{\mathrm{10,13}\}$ at ${\rho }_{{X}_{N}{Y}_{N}}=0.95,$ respectively.

• For the $AQL=0.001$ and $LQL= 0.008, 0.020$ at sigma unknown case from Table 10, the existing plan neutrosophic sample sizes are ${n}_{N}=\left\{89, 98\right\}, \{\mathrm{34,39}\}$, and for $AQL=0.0025$ and $LQL= 0.015, 0.025$ gives ${n}_{N}=\left\{86, 106\right\}, \{\mathrm{46,50}\}$ whereas the presented concept gives least value of ${n}_{N}=\left\{\mathrm{86,96}\right\},\{\mathrm{33,39}\}$ and ${n}_{N}=\left\{\mathrm{83,90}\right\},\{\mathrm{44,52}\}$ at ${\rho }_{{X}_{N}{Y}_{N}}=0.75$ and ${n}_{N}=\left\{\mathrm{82,93}\right\},\{\mathrm{32,36}\}$ and ${n}_{N}=\left\{\mathrm{80,90}\right\},\{\mathrm{42,47}\}$ at ${\rho }_{{X}_{N}{Y}_{N}}=0.95,$ respectively.

Table 9 Comparison for ${\sigma }_{{Y}_{N}}$ known case

Table 10 Comparison for ${\sigma }_{{Y}_{N}}$ unknown case

Second, the comparison is made with Aslam [14]. As the results were compared in detail concerning the proposed $AQL$ and $LQL$ levels in the determination of parametric values then these were found improved concerning the Aslam [14] to get more sensitive and sophisticated sampling plans to ensure saving time and resources. A brief description has been explained as follows:

• For the $AQL=0.001$ and $LQL= 0.003, 0.020$ for sigma known case, the existing plan of Aslam[14] gives a sample size ${n}_{N}=\left\{213, 268\right\}, \{50, 80\}$, and for $AQL=0.0025$ and $LQL= 0.030, 0.050$ gives neutrosophic sample size ${n}_{N}=\left\{143, 233\right\}, \left\{\mathrm{138,213}\right\},$ whereas proposed one gives a minimum value of sample size like; ${n}_{N}=\left\{\mathrm{62,78}\right\},\{\mathrm{7,8}\}$ and ${n}_{N}=\left\{\mathrm{9,11}\right\},\{\mathrm{6,7}\}$ at ${\rho }_{{X}_{N}{Y}_{N}}=0.75$ and ${n}_{N}=\left\{\mathrm{49,60}\right\},\{\mathrm{6,7}\}$ and ${n}_{N}=\left\{\mathrm{7,8}\right\},\{\mathrm{5,6}\}$ at ${\rho }_{{X}_{N}{Y}_{N}}=0.95$ respectively.

The robustness and validation of the proposed sampling plan results can be viewed from Tables 11 and 12 that when $AQL$ and $LQL$ are fixed then by changing the ${\rho }_{{X}_{N}{Y}_{N}}$ which is the most significant parameter of the plan. For example as ${\rho }_{{X}_{N}{Y}_{N}}$ changes from 0.5 to 0.75 for the fixed values of $AQL=0.001$ and $LQL=0.002$ the value of determining sample size will become ${n}_{N}=\left\{\mathrm{8,9}\right\},\{\mathrm{7,8}\}$. Similarly, for the fixed values of $AQL=0.0025$ and $LQL=0.050$ the value of the optimized sample sizes will become ${n}_{N}=\left\{\mathrm{6,7}\right\},\{\mathrm{6,7}\}$.

Table 11 Comparison with Aslam [14]

Table 12 Data for gauge capability assessment application

The innovative objective of the proposed plan is to introduce the interval-based criteria for the lot sentencing following the range of the numbers around the crisped, determined values in some uncertain situations where uncertainty or doubts about the arising numbers. The authors are inspired to deal with successive sampling over the two successive occasions obtained information under the neutrosophic interval numbers as successive sampling is itself a big data technique with a high degree of correlation among the values recorded over the prescribed occasions.

6 Similarities and Differences

It has significant importance to discuss the similarities and differences of the proposed sampling plan in the adaptation of the neutrosophic numbers with the existing acceptance sampling plan before moving ahead. The similarity is the utilization of the neutrosophic numbers in case of independence over the two occasions or the two occasions information exists without any correlation between them. The difference occurs as the correlation over the occasions shows its existence from moderate to some higher values like; ${\rho }_{{X}_{N}{Y}_{N}}=0.50, 0.75\, \mathrm{and}\, 0.95$. The successive sampling scheme refers to cases with a higher value of the correlation between the two occasions. That is why when the value of correlation is less than 0.5, the proposed concept does not exhibit a significant result than the existing plan. Hence, the discussion is based on the cases related to a higher tendency of the correlation. It is also important to describe that real-life datasets always possessed a high degree of correlation as a natural tendency, otherwise, the smaller value-based dataset is normally generated using some controlled methods of random numbers generation as lab study. Hence, it can be further concluded that the proposed concept has a greater tendency to handle real-life problems in case of uncertain situations with maximum accuracy and precision despite the partial or complete indeterminacy levels.

7 Application

To present the real-life application of the proposed concept, the dataset is taken from Azam et al. [1], comprised of 20 objects which are studied over the two successive occasions mentioned in Table 11. The problem under study is to deal with an ambiguous situation under neutrosophic methods, which are proved better to take two-point values over the range at some point rather than a single crisp value. In this example, there are two operators considered to inspect the lot successively each operator at a time, and operators for the inspected lot items take measurements with the gauge (measuring tool) fitness for acceptance or rejection of the lot.

The statistic of the neutrosophic successive sampling plan developed in Sect. 3 is applied by considering the units at 1st (taken $x$ as some prior information) and 2nd (taken $y$ as the study variable) over two occasions successively, by the gauge is recorded for the two respective sample sizes ${n}_{N}=\left\{{n}_{L}=14,{n}_{U}=15\right\}$ with ${C}_{N}=\left\{{C}_{L}=1.8653,{C}_{U}=1.8473\right\}$ under ${\rho }_{{X}_{N}{Y}_{N}}=0.95$ between two occasions population dataset as $X$ and $Y$ is shown in Table 8 with the assumption that population standard deviation is unknown. The type I and type II error values are fixed as $\alpha =5\%$, $\beta =10\%$, with $AQL=0.005$, $LQL=0.10$ as two limiting quality levels, the decision about these values is based on the consensus between fabricator and purchaser. The neutrosophic acceptance sampling plan for successive two occasions will operate as follows:

Step 1The respective random samples of sizes ${n}_{N}=\left\{{n}_{L}=14,{n}_{U}=15\right\}$ are selected at the first occasion, amongst them ${m}_{N}=\left\{{m}_{L}={m}_{U}=11\right\}$ has been retained for the second occasion as matched units (Detail description is mentioned in Table 12 and Table 13) and they are measured at the second occasion.

Table 13 Sampling procedure over two successive occasions

Step 2On the second occasion unmatched units ${u}_{N}=\left\{{u}_{L}=3,{u}_{U}=4\right\}$ are also selected as fresh units. The units, which are not selected on 1st occasion from remaining units as an information source (also mentioned in Table 13).

Step 3 Computational results are as follows: ${\widehat{{\mu }_{Y}}}_{N}=\left\{{\widehat{{\mu }_{Y}}}_{L}=22.85369,{\widehat{{\mu }_{Y}}}_{U}=22.21237\right\}$ the proposed neutrosophic estimator is computed for the average change estimation in current occasion over the two occasions with neutrosophic proposed plan constants computed by the equations mentioned in Sect. 3 as follows: ${a}_{N}=\left\{{a}_{L}=0.16621,{a}_{U}=0.19717\right\}$,${b}_{N}=\left\{{b}_{L}=-0.16621,{b}_{U}=-0.19717\right\}$,${c}_{N}=\left\{{c}_{L}=0.81942,{c}_{U}=0.78298\right\}$, ${d}_{N}=\left\{{d}_{L}=0.89572,{d}_{U}=0.217013\right\}$ and now the pooled variance of the matched and unmatched units ${s}_{pN}^{2}=\left\{{s}_{pL}^{2}=12.88889,{s}_{pU}^{2}=0.21701\right\}$ so ${s}_{pN}^{2}=\frac{1}{{n}_{N}-2}\left[\left(m-1\right){s}_{ymN}^{2}+\left(u-1\right){s}_{yuN}^{2}\right]$ Moreover, correlation is being computed between the matched 1st and 2nd occasions units as ${r}_{mN}=\left\{{r}_{mL}=0.94657\cong 0.95,{r}_{mU}=0.94434\cong 0.95\right\}$ $.$

Now the proposed plan statistic is calculated as ${V}_{tN}^{*}=\left\{{V}_{tL}^{*}=10.3468,{V}_{tU}^{*}=10.1964\right\}$, where ${USL}_{N}=\left\{{USL}_{L}={USL}_{U}=60\right\}$ is used as given information in the example.

Step 4After the computations, it is observed that computed ${V}_{tN}^{*}\ge {C}_{N}$; as $\left\{{{V}_{tL}^{*}=10.3468\ge C}_{L}=1.8653,{V}_{tU}^{*}=10.1964{\ge C}_{U}=1.8473\right\}$ so it is decisively concluded that usage of the gauge capability measuring instrument is an efficient instrument for the lot inspection procedure with the help of two operators one for each recorded dataset and as per results, the under study lot is accepted.

8 Limitations of the Study

Samarandache [18] has explained that the neutrosophic numbers are not necessarily only the sets with intervals but these may also be any real numbers, discrete or continuous, a pointed single value, a finite or an infinite, or vice versa. The same is the case is discussed in the presented study in the adaptation of the neutrosophic number statistics to analyze the truth of the in-determinant and uncertain values with the help of neutrosophic numbers, neutrosophic logic, set, probability, and the neutrosophic statistics collectively. The work cannot handle a dataset with partial or complete indeterminacies or to overcome doubts, uncertainties, and ambiguities for precise accurate, and reliable results. If the dataset is based on the pointed crisp values and frees off the uncertainties, then this logic and its utilization can mislead the procedures.

9 Concluding Remarks and Future Recommendations

In this study, a variable acceptance sampling plan based on the neutrosophic interval numbers over two successive occasions is presented. The proposed concept is discussed for two aspects: population standard deviation is known and unknown cases where the variable of interest follows the normal distribution. Moreover, the parametric values are obtained using a non-linear optimization approach for the various possible values of the population correlation with specified different values of $LQL$ and $AQL$ and ${n}_{N}$ and ${C}_{N}$ are determined. The comparison has been made with the existing single sampling neutrosophic acceptance sampling plan given by Azam et al. [1], as a special case of the proposed concept and with Aslam [14]. The proposed plan was found far better than the existing plans to get precise, efficient, determinant, reliable in terms of reducing the chance of rejecting a good lot. Moreover, the proposed argument is strengthened with the real-life implementation of the plan by taking an industrial dataset from Azam et al. [1] and the sensitivity of the plan is proved far better to handle the ambiguity of the matters by giving reliable lot sentencing in real-life practices. The proposed plan can be applied in automobile, aerospace and milk industries. From further research perspectives, the presented work can be extended in other dimensions such that with other sampling procedures like; repetitive sampling, multiple dependent state sampling, resubmitted sampling and resubmitted repetitive sampling schemes, etc. This concept can also be extended by considering neutrosophic interval numbers at multiple occasions’ auxiliary information for the computation of the variable under study. The concept of the exponentially weighted moving average (EWMA), hybrid EWMA, and double EWMA can also be adopted with estimators like; ratio, product, and regression as an extension of the proposed sampling plan to deal with the diverse variety of the lots as an efficient decision-making methodology.