1 Introduction

With the advantages of safety, efficiency and standardization, container liner shipping has become the most important mode of transportation in current international trade. Affected by the economic crisis in 2008, the shipping industry remains in the downturn. Nowadays, with the larger-scale trend of containership, the shipping capacity provided by liner shipping companies is significantly greater than the demand in the shipping market, which leads to fierce competition among liner shipping companies. Most liner shipping companies face operating losses or meager profits in the long-term downturn of the shipping market. This makes liner shipping companies consider reducing total operating costs which is the sum of total bunker consumption cost and total vessel operating cost.

IMO pays more attention to the marine ecosystem, which leads to higher requirements for the quality of bunker fuel, and the rising price of bunker fuel has become the main theme. The increase in bunker price has led to a larger proportion of bunker fuel consumption cost in the total operating cost of liner shipping companies. Bunker fuel consumption costs usually account for 60% of the total operating costs (Golias et al. 2009), or even more than 75% (Ronen 2011). The high bunker fuel cost put huge operating pressure on liner shipping companies. Therefore, according to previous studies (Lashgari et al. 2021), optimizing sailing speed can greatly reduce bunker fuel consumption cost, thereby reducing the total operating cost of liner shipping companies.

The heterogeneity of ships is mainly reflected in the different fuel consumption functions and operation costs of ships. Vessels with the same capacity have different fuel consumption costs and maintenance costs due to factors such as the manufacturing process, the number of years in service, and the state of operation and maintenance. The relationship between the fuel consumption and the sailing speed may also differ between different legs due to differences in the specific marine environment. The relationships between speed and fuel consumption for two ships deployed on the same route are calibrated based on historical data and are shown in Fig. 1. We can see that the difference in fuel consumption rates can be as high as 48.1% (when sailing at 10 knots).

Fig. 1
figure 1

Fuel consumption function of two ships on the same shipping leg

Full size image

In addition, for a shipping route of a liner shipping company, sailing speed will affect the round-trip time. Slow steaming may prolong the round-trip time, make the goods in transit longer, reduce the time value of the goods, and decrease the service quality of liner shipping companies. Service quality is the core competitiveness for liner shipping companies in a competitive shipping market. Moreover, service frequency is an important factor to measure service quality. In order to maintain the weekly service frequency, the fleet deployment plan should be adjusted while optimizing the speed to minimize the total operating cost of the liner shipping company.

Based on the above considerations, this paper investigates how to optimize the sailing speed and select vessels to deploy on the specific route for container ships with bunker fuel consumption heterogeneity to obtain the minimum total operating cost while maintaining the weekly service frequency. This can be referred to as the fleet deployment and sailing speed optimization (FDSSO) problem for container ships with bunker fuel consumption heterogeneity. We consider this problem from two aspects:

  1. (i)

    (Speed optimization) We need to determine the optimal sailing speed because slow steaming will significantly reduce the bunker consumption cost. This paper considers two cases where the bunker consumption rates for each ship on different shipping legs are the same and different. In view of the same bunker fuel consumption function on different legs, the optimal sailing speed across the shipping route is studied. When the fuel consumption function is different on different legs, the optimal sailing speed of each shipping leg on the specific route is obtained.

  2. (ii)

    (Fleet deployment) Given a group of candidate ships with different operating costs and bunker fuel consumption but with the same capacity, on the premise of maintaining the weekly service frequency of liner transportation companies, the FDSSO problem chooses the optimal ship to enter the route, adjusts the fleet deployment plan and optimizes the speed, in order to balance the ship operating cost and bunker consumption cost.

The above two questions are interrelated. In order to maintain the weekly service frequency, the sailing speed optimization and fleet deployment plan need to be simultaneously considered for liner shipping companies. According to the two scenarios with the same and different fuel consumption functions on different legs on the specific route, we describe the FDSSO problem as two mixed integer nonlinear programming models. According to the characteristics of the two models, we develop a tailored exact algorithm and outer approximation algorithm to solve the two models respectively. Finally, numerical experiments are conducted to verify the validity of the two models.

1.1 Literature review

This paper mainly includes two parts: one is the research on ship sailing speed optimization, and the other is the research on fleet deployment. Therefore, the literature review focuses on these two aspects.

1.1.1 Sailing speed optimization

Adjusting the speed will impact the bunker consumption cost, and it also influences the transit time of goods, and the service level of liner shipping companies. Ronen (2011) found that fuel consumption is approximately proportional to the cube of sailing speed of the container ships. Through numerical experiments, it is concluded that when the ship sailing speed is reduced by 20%, the daily fuel consumption will be reduced by 50%. Many researches (Hu et al. 2014; Fagerholt et al. 2015; Wang et al. 2015, 2019; Aydin et al. 2017; Zheng et al. 2019; Adland et al. 2020) consider cutting down bunker fuel consumption cost by optimizing sailing speed to decrease the total operating cost of liner shipping companies. Wang and Meng (2012) confirmed that the fuel consumption is approximately proportional to the third power of the speed by linear regression method based on real data. For the mixed integer nonlinear programming model, an outer approximation algorithm is developed to optimize the sailing speed of each leg and obtain the optimal number of ships deployed on each route in the shipping network. Wen et al. (2016) proposed a branch-and-price algorithm and column generation heuristic algorithm for a mixed integer linear programming model to simultaneously optimize the routing and sailing speed for full-load tramp ships. Through the sensitivity analysis of the bunker price, it is concluded that the fuel price has a significant impact on the ship average sailing speed and total shipping profit. In order to minimize bunker consumption, Kim et al. (2016) developed a mixed integer nonlinear programming to study how to optimize the sailing speed of tramp ships with time window constraints, and proposed a recursive partition algorithm to find the optimal solution effectively. Aydin et al. (2017) proposed a dynamic programming model for the optimization of sailing speed and bunking problem with uncertain port time and time windows. Numerical experiments are carried out with the actual data of a liner transportation company. The results show that the vessel sailing speed decision considering the stochastic port time and time windows has a significant influence on cutting down the bunker consumption cost. Considering varying river streamflow speed and the stochastic dam traversing time, Tan et al. (2018) optimized the sailing speed and designed the ship sailing schedule by analyzing the relationship between the service level, the vessel sailing speed and the round-trip time of inland river shipping. Since some emission control areas require expensive low-sulfur fuel, Ma et al. (2020) studied minimizing the navigation cost of shipping companies by optimizing the ship route and speed.

1.1.2 Fleet deployment

Fleet deployment is one of the important strategic decisions for liner shipping companies, which needs to consider the feasibility and economic rationality of ship technology and operation. Boffey et al. (1979) investigated the problem of fleet deployment for container liners, and used the Atlantic route as an example to carry out numerical experiments. Bue due to the limitation of computation capability, it cannot solve the problem of liner ship deployment efficiently. Evans and Marlow (2001) analyzed several cost types that exist in the fleet deployment problem, and then compared them quantitatively using numerical experiments. The paper concluded that fuel cost is the largest proportion of the total operating costs of liner ships. Therefore, reducing the fuel consumption of a ship can control the total operating cost of the ship and help to increase the revenue of the liner shipping company. Alvarez (2009) find out the best transport route and the optimal fleet deployment scheme. A multi-objective optimization model is formulated to solve both fleet deployment and container routing problems simultaneously. This model not only reflects the revenue and operating costs of liner companies. An optimization algorithm is designed to solve them according to the characteristics of the model. Bakkehaug et al. (2016) proposed an adaptive large neighborhood search heuristic algorithm to solve the ship routing deployment problem with voyage separation requirements. Gu et al. (2019) reduced the bunker consumption and CO2 emissions by formulating a mixed-integer linear programming model which adjusts the composition and deployment of the fleet. Karbassi Yazdi et al. (2020) studied the ships transporting liquefied natural gas, and proposed a meta-heuristic binary PSO algorithm to solve the ship routing and fleet deployment problem.

1.1.3 Joint optimization between vessel speed and fleet deployment

There is also a lot of research (Wang and Meng 2012; Karsten et al. 2018; Kim et al. 2019; Yang and Xing 2020) focusing on the joint sailing speed optimization and fleet deployment. Meng and Wang (2011) established a mathematical optimization model with equilibrium constraints to design the intermodal network. This model comprehensively considers the cargo transshipment, and optimizes the actual shipping speed and economic fleet size. Xia et al. (2015) comprehensively considered the influence of sailing speed and load when designing bunker consumption functions. Combined with the general bunker consumption function, a mixed integer nonlinear programming model is established at the strategic level to comprehensively optimize the ship routing, cargo allocation, fleet deployment and sailing speed. An iterative search algorithm based on column generation is proposed to solve the model and obtain the optimal solution. The bunker consumption and carbon dioxide (CO2) emissions of vessels are affected by the sailing speed of vessels and the environment of the voyage. With the emphasis on the marine environment and the establishment of emission control areas (ECA), Sheng et al. (2019) studied the optimal ship speed and fleet size for shipping services to comply with the ECA regulation. A mixed-integer convex minimum cost model is formulated to minimize the total annual fleet cost, including the fleet operating costs and in-transit inventory costs. Research has shown that the inventory cost of in-transit cargo can affect the speed of a ship. Given a set of service routes and candidate ships, Zhuge et al. (2021) proposed a mixed integer nonlinear programming model to jointly optimize the ship path, deployment and sailing speed problems. Combining a dynamic programming approach, a tailored method was developed to determine the number of ships deployed on each route, the sailing speed of each leg and voyage paths. Sensitivity analysis of bunker prices shows that the total cost of all routes with emission reduction measures is much higher than without emission reduction.

However, the above article does not consider the fuel consumption heterogeneity of ships. They assumed that the bunker fuel consumption costs, operation costs and maintenance costs of vessels with the same capacity are the same. This article considers the heterogeneity of ships. Ships with the same capacity have different fuel consumption functions because of their load and sea environment. This paper will establish two mixed integer nonlinear programming models. One considers that a ship has one bunker consumption function on the entire route, and the other considers that a ship has different bunker consumption functions on each leg of the designed route.

1.2 Contributions

Different from the studies reviewed above, this paper establishes two mixed integer nonlinear programming models for the joint optimization of ship speed and deployment problem under the scenarios that the same and different fuel consumption function on each leg of the specific route. The contributions of this paper are threefold: first, we consider a problem that jointly optimizes the sailing speed and fleet deployment of container ships with fuel consumption heterogeneity while maintaining the weekly service frequency. Second, this paper considers two cases, the same and different fuel consumption functions on different legs of the specific route. Third, two tailored exact algorithms are developed for these two cases to select the optimal number of ships on the route and obtain the optimal sailing speed on the route or on each leg.

The rest of the paper is organized as follows. Section 1.2 develops two mix-integer nonlinear models to state the fleet deployment and sailing speed optimization problem for container ships with bunker consumption heterogeneity. Section 2 develops two tailored algorithms to obtain the global optimal solution for the proposed two models. Section 3 conducts numerical experiments to demonstrate the validity of the model and the efficiency of the algorithm. Section 4 summarizes this paper.

2 Model formulation

A liner shipping company operates a route with multiple ports, these ports are represented by set P. Let the set \(\xi\) denote the total number of ports of call on the specific shipping route, and the sequence can be expressed as: \(p_{1} \to p_{2} \to \cdots \to p_{\left| \xi \right|} \to p_{1}\). According to the sequence of ports called by the containership, the voyage between two adjacent ports (such as \(p_{i}\) and \(p_{i + 1}\)) is called a shipping leg, and the set \(I = \{ i|i:p_{i} \to p_{i + 1} ,p_{i} \in \xi \}\) represents the legs on the specific route. The route information of the liner shipping company such as the service frequency, service quality and operation cost of each ship is given. This section focuses on selecting the optimal vessels from candidate vessels with similar capacity on the specific route and determining the optimal sailing speed. Two mixed integer nonlinear programming models are formulated to maintain the weekly service frequency and minimize the total operating cost, which is consist of bunker consumption cost and ship operating cost. The notations are listed in Table 1 below.

Table 1 Notations
Full size table

2.1 Sailing speed and weekly service frequency

The sailing speed of ships on each leg shall be between the economic sailing speed \(\left[ {v_{i}^{\min } ,v_{i}^{\max } } \right]\). The round-trip time on a specific route consists of the sailing time on all legs of the route and the total berthing time at all ports. The sailing speed of the fleet will affect the round-trip time of this specific route, because the sailing time is related to the sailing speed of the vessels and the distance of the legs. We use \(t_{i}\) represents the berthing time at each port, which is composed of the waiting time of ships and handling time of the goods. From this, we can conclude that the total sailing time (hour) on the specific route is:

$$\sum\limits_{i \in I} {\left( {{{L_{i} } \mathord{\left/ {\vphantom {{L_{i} } {v_{i} + t_{i} }}} \right. \kern-\nulldelimiterspace} {v_{i} + t_{i} }}} \right)}$$
(1)

The round-trip time (week) \(w\) that the vessel sails on the specific route is:

$$\sum\limits_{{i \in {\text{I}}}} {{{\left( {{{L_{i} } \mathord{\left/ {\vphantom {{L_{i} } {v_{i} + t_{i} }}} \right. \kern-\nulldelimiterspace} {v_{i} + t_{i} }}} \right)} \mathord{\left/ {\vphantom {{\left( {{{L_{i} } \mathord{\left/ {\vphantom {{L_{i} } {v_{i} + t_{i} }}} \right. \kern-\nulldelimiterspace} {v_{i} + t_{i} }}} \right)} {168}}} \right. \kern-\nulldelimiterspace} {168}}}$$
(2)

where 168 refers to the ship on the specific route in a week of sailing time (hour), calculated by the expression 168 = 24 * 7.

As liner shipping companies maintain a weekly service frequency on a specific route, the number of vessels deployed on the specific route is related to the round-trip time (or total sailing time). For example, the round-trip time is 56 days, in order to maintain weekly service frequency, eight ships should be deployed on that specific route. The decision variable \(m\) represents the number of ships deployed on the specific route. To ensure the weekly service frequency, we have the following constraint:

$$\sum\limits_{{i \in {\text{I}}}} {\left( {{{L_{i} } \mathord{\left/ {\vphantom {{L_{i} } {v_{i} + t_{i} }}} \right. \kern-\nulldelimiterspace} {v_{i} + t_{i} }}} \right)} \le 168m$$
(3)

2.2 Vessel deployment

The fleet consists of a series of ships with simialr capacity. The number of ships deployed in the route is equal to the number of ships that can maintain the weekly service frequency for liner shipping companies. The constraint on the number of ships sailing on this route are as follows:

$$\sum\limits_{s \in S} {x_{s} } = m$$
(4)

2.3 Two mixed-integer nonlinear programming model

2.3.1 Same fuel consumption function on different legs

According to the existing research (Ronen 2011; Wang and Meng 2012) on speed optimization, the daily bunker consumption of the ship is proportional to the third power of its sailing speed. We study the daily fuel consumption of a series of ships with similar capacity and use the set \({\text{S}}\) to represent the series of ships. It is assumed that the speed of ships with similar capacity on the specific route is \(v\) (knot). The daily fuel consumption on the specific route is \(f^{s} (v)\) (ton/day). The daily fuel consumption function of each ship on the specific route is:

$$f^{s} (v) = \alpha_{s} v^{{\beta_{s} }} ,\forall s \in S$$
(5)

where \(\alpha_{s}\) and \(\beta_{s}\) are coefficients to be calibrated from the operation data of linear shipping companies.

The objective function in the model is to minimize the total operating cost, in which the total operating cost is composed of ship fuel consumption cost and operation cost. Since the fuel consumption function depends on the voyage speed, \(f^{s} (v_{i} )\) (ton/day) represents the fuel consumption of the vessel \({\text{s}} \in S\) on the leg \({\text{i}}\). The fuel price is \(c^{bunk}\) ($/ton), and the total operating cost of one ship is expressed as:

$$c^{bunk} {{\alpha_{s} v_{i}^{{\beta_{s} - 1}} L_{i} } \mathord{\left/ {\vphantom {{\alpha_{s} v_{i}^{{\beta_{s} - 1}} L_{i} } {24 + c_{s}^{oper} }}} \right. \kern-\nulldelimiterspace} {24 + c_{s}^{oper} }}$$
(6)

The objective function in this model is:

$$\min c^{bunk} \sum\limits_{s \in S} {\sum\limits_{i \in I} {{{\alpha_{s} L_{i} v_{i}^{{\beta_{s} - 1}} x_{s} } \mathord{\left/ {\vphantom {{\alpha_{s} L_{i} v_{i}^{{\beta_{s} - 1}} x_{s} } {24}}} \right. \kern-\nulldelimiterspace} {24}}} } + \sum\limits_{s \in S} {c_{s}^{oper} x_{s} }$$
(7)

where \(x_{s}\) is a binary variable, which is used to decide whether the ship \(s\) enter the specific route.

The shipping company maintains the weekly service frequency, selects the optimal number of ships to enter the designated route and determines the sailing speed in each leg of the route to minimize the total operating cost which includes the bunker consumption cost and the operating cost of the ship. Therefore, the fleet deployment and speed optimization problem are expressed as a nonlinear mixed integer programming model, which is as follows:


[MINLP1]

$$\min c^{bunk} \sum\limits_{s \in S} {\sum\limits_{i \in I} {{{\alpha_{s} L_{i} v_{i}^{{\beta_{s} - 1}} x_{s} } \mathord{\left/ {\vphantom {{\alpha_{s} L_{i} v_{i}^{{\beta_{s} - 1}} x_{s} } {24}}} \right. \kern-\nulldelimiterspace} {24}}} } + \sum\limits_{s \in S} {c_{s}^{oper} x_{s} }$$
(8)

Subject to:

$$\sum\limits_{{i \in {\text{I}}}} {\left( {{{L_{i} } \mathord{\left/ {\vphantom {{L_{i} } {v_{i} + t_{i} }}} \right. \kern-\nulldelimiterspace} {v_{i} + t_{i} }}} \right)} \le 168m$$
(9)
$$\sum\limits_{s \in S} {x_{s} } = m$$
(10)
$$v_{i} \in \left[ {v_{i}^{\min } ,v_{i}^{\max } } \right],\forall i \in I$$
(11)
$$x_{s} \in \{ 0,1\} ,\forall s \in S$$
(12)
$$m \in Z_{ + }$$
(13)

2.3.2 Different fuel consumption function on different legs

In this section, we assume that the fuel consumption functions of the candidate ships are different on different legs of a specific route. The sailing speed on leg \(i \in I\) of the specific route is \(v_{i}\), and the daily fuel consumption on this leg is \(f_{i}^{s} (v_{i} )\) (ton/day). Therefore, we get the expression of the daily fuel consumption of each ship \({\text{s}} \in S\) on leg \(i \in I\) of the specific route as follows:

$$f_{i}^{s} (v_{i} ) = \alpha_{i}^{s} v_{i}^{{\beta_{i}^{s} }} ,\forall s \in S,i \in I.$$
(14)

where \(\alpha_{i}^{s}\) and \(\beta_{i}^{s}\) are coefficient calibrated according to the operation data of linear shipping companies.

Since the fuel consumption function is related to the vessel speed on each leg, \(f_{i}^{s} (v_{i} )\) is used to represent the fuel consumption of the ship \(s \in S\) on the leg \(i\) of a specific route. The total operating cost of each ship on the leg \(i\) is:

$$c^{bunk} a_{i}^{s} v_{i}^{{\beta_{i}^{s} - 1}} L_{i} /24 + c_{s}^{oper}$$
(15)

The total operating cost of this route is:

$$\min \, c^{bunk} \sum\limits_{s \in S} {\sum\limits_{i \in I} {{{a_{i}^{s} v_{i}^{{\beta_{i}^{s} - 1}} L_{i} x_{s} } \mathord{\left/ {\vphantom {{a_{i}^{s} v_{i}^{{\beta_{i}^{s} - 1}} L_{i} x_{s} } {24}}} \right. \kern-\nulldelimiterspace} {24}}} } + \sum\limits_{s \in S} {c_{s}^{oper} } x_{s}$$
(16)

On the designated route, the bunker consumption is different on different legs. In this case, a mixed-integer nonlinear programming model is established to solve the problem of the fleet deployment and speed optimization, which is expressed as follows:


[MINLP2]

$$\min \, c^{bunk} \sum\limits_{s \in S} {\sum\limits_{i \in I} {{{a_{i}^{s} v_{i}^{{\beta_{i}^{s} - 1}} L_{i} x_{s} } \mathord{\left/ {\vphantom {{a_{i}^{s} v_{i}^{{\beta_{i}^{s} - 1}} L_{i} x_{s} } {24}}} \right. \kern-\nulldelimiterspace} {24}}} } + \sum\limits_{s \in S} {c_{s}^{oper} } x_{s}$$
(17)

Subject to:

$$\sum\limits_{i \in I} {\left( {{{L_{i} } \mathord{\left/ {\vphantom {{L_{i} } {v_{i} + t_{i} }}} \right. \kern-\nulldelimiterspace} {v_{i} + t_{i} }}} \right)} \le 168m$$
(18)
$$\sum\limits_{s \in S} {x_{s} } = m$$
(19)
$$v_{i} \in \left[ {v_{i}^{\min } ,v_{i}^{\max } } \right],\forall i \in I$$
(20)
$$x_{s} \in \{ 0,1\} ,\forall s \in S$$
(21)
$$m \in Z_{ + }$$
(22)

3 Solution algorithm

3.1 A tailored algorithm for the model MINLP1

In Sect. 2.3.1, the fuel consumption functions are the same in each leg, and establish a non-convex mixed-integer nonlinear programming model, which cannot be solved directly by the existing solvers such as Gurobi. Therefore, we develop a tailored method to obtain the global optimal solution of the model MINLP1.

Firstly, the model has the following properties:

Proposition 1

In the optimal solution, \(v_{1} = v_{2} = \cdots = v_{\left| I \right|} = v*,\) that is, the speed of the ship on each leg is the same.

Proof

Suppose that a feasible solution is \(v_{i} \ne v_{j}\) for two different shipping legs i and j, that is, the speeds on leg \({\text{i}}\) and leg \({\text{j}}\) are different. We consider a sailing speed

$$\tilde{v} = {{\left( {L_{i} + L_{j} } \right)} \mathord{\left/ {\vphantom {{\left( {L_{i} + L_{j} } \right)} {\left( {{{L_{i} } \mathord{\left/ {\vphantom {{L_{i} } {v_{i} }}} \right. \kern-\nulldelimiterspace} {v_{i} }} + {{L_{j} } \mathord{\left/ {\vphantom {{L_{j} } {v_{j} }}} \right. \kern-\nulldelimiterspace} {v_{j} }}} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {{{L_{i} } \mathord{\left/ {\vphantom {{L_{i} } {v_{i} }}} \right. \kern-\nulldelimiterspace} {v_{i} }} + {{L_{j} } \mathord{\left/ {\vphantom {{L_{j} } {v_{j} }}} \right. \kern-\nulldelimiterspace} {v_{j} }}} \right)}}$$
(23)

Obviously, Eq. (23) can be transformed as \((L_{i} + L_{j} )/\tilde{v} = L_{i} /v_{i} + L_{j} /v_{j} ,\) and the value \(\tilde{v}\) satisfies the constraint (9). We have,

$$\tilde{v} - v_{i} = {{L_{j} v_{i} \left( {v_{j} - v_{i} } \right)} \mathord{\left/ {\vphantom {{L_{j} v_{i} \left( {v_{j} - v_{i} } \right)} {\left( {L_{i} v_{j} + L_{j} v_{i} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {L_{i} v_{j} + L_{j} v_{i} } \right)}}$$
(24)
$$\tilde{v} - v_{j} = {{L_{i} v_{j} \left( {v_{i} - v_{j} } \right)} \mathord{\left/ {\vphantom {{L_{i} v_{j} \left( {v_{i} - v_{j} } \right)} {\left( {L_{i} v_{j} + L_{j} v_{i} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {L_{i} v_{j} + L_{j} v_{i} } \right)}}$$
(25)

Therefore, \(\min \{ v_{i} ,v_{j} \} \le \tilde{v} \le \max \{ v_{i} ,v_{j} \}\) is obtained, and the variable \(\tilde{v}\) also satisfies the constraint (11). According to the above analysis, \(\tilde{v}\) is the feasible solution of model [MINLP1] in Sect. 2.3.1.

According to the objective function of the model [MINLP1], we assume that \(f(v) = v^{{\beta^{s} - 1}}\), where \(\beta^{s} \ge 1\), \(f({\text{v}})\) is a convex function. According to Jensen inequality of convex function:

$$f\left( {\lambda_{i} v_{i} + \lambda_{j} v_{j} } \right) \le \lambda_{i} f\left( {v_{i} } \right) + \lambda_{j} f\left( {v_{j} } \right)$$
(26)

Taking the reciprocal of \(v\), and assume that \(f\left( \frac{1}{v} \right) = \left( \frac{1}{v} \right)^{{1 - \beta^{s} }}\), where \(\beta^{s} \ge 1\). \(f\left( \frac{1}{v} \right)\) is also a convex function. Jensen inequality can be transformed into the following equivalent form

$$f\left( {\frac{{\lambda_{i} }}{{v_{i} }} + \frac{{\lambda_{j} }}{{v_{j} }}} \right) \le \lambda_{i} f\left( {\frac{1}{{v_{i} }}} \right) + \lambda_{j} f\left( {\frac{1}{{v_{j} }}} \right)$$
(27)

where \(\lambda_{i} = \frac{{L_{i} }}{{L_{i} + L_{j} }},\) \(\lambda_{j} = \frac{{L_{j} }}{{L_{i} + L_{j} }}.\)

Then we have:

$$\lambda_{i} f\left( {\frac{1}{{v_{i} }}} \right) + \lambda_{j} f\left( {\frac{1}{{v_{j} }}} \right) = \frac{{L_{i} }}{{L_{i} + L_{j} }}\left( {\frac{1}{{v_{i} }}} \right)^{{1 - \beta_{s} }} + \frac{{L_{j} }}{{L_{i} + L_{j} }}\left( {\frac{1}{{v_{j} }}} \right)^{{1 - \beta_{s} }} = \frac{{L_{i} }}{{L_{i} + L_{j} }}\left( {v_{i} } \right)^{{1 - \beta_{s} }} + \frac{{L_{j} }}{{L_{i} + L_{j} }}\left( {v_{j} } \right)^{{1 - \beta_{s} }}$$
(28)
$$f\left( {\frac{{\lambda_{i} }}{{v_{i} }} + \frac{{\lambda_{j} }}{{v_{j} }}} \right) = f\left( {\frac{{L_{i} }}{{L_{i} + L_{j} }} \cdot \frac{1}{{v_{i} }} + \frac{{L_{j} }}{{L_{i} + L_{j} }} \cdot \frac{1}{{v_{j} }}} \right) = \left( {\frac{{L_{i} }}{{L_{i} + L_{j} }} \cdot \frac{1}{{v_{i} }} + \frac{{L_{j} }}{{L_{i} + L_{j} }} \cdot \frac{1}{{v_{j} }}} \right)^{{1 - \beta_{s} }} = \left( {\frac{{L_{i} /v_{i} + L_{j} /v_{j} }}{{L_{i} + L_{j} }}} \right)^{{1 - \beta_{s} }}$$
(29)

According to the Jensen inequality, we have

$$\frac{{L_{i} }}{{L_{i} + L_{j} }}\left( {v_{i} } \right)^{{\beta_{s} - 1}} + \frac{{L_{j} }}{{L_{i} + L_{j} }}\left( {v_{j} } \right)^{{\beta_{s} - 1}} \ge \left( {\frac{{L_{i} /v_{i} + L_{j} /v_{j} }}{{L_{i} + L_{j} }}} \right)^{{1 - \beta_{s} }} = \left( {\frac{{L_{i} + L_{j} }}{{L_{i} /v_{i} + L_{j} /v_{j} }}} \right)^{{\beta_{s} - 1}} = \tilde{v}^{{\beta^{s} - 1}}$$
(30)

Therefore, we have \(c^{bunk} \alpha^{s} L_{i} v_{i}^{{\beta^{s} - 1}} /24 + c^{bunk} \alpha^{s} L_{j} v_{j}^{{\beta^{s} - 1}} /24 \ge c^{bunk} \alpha^{s} \left( {L_{i} + L_{j} } \right)\tilde{v}^{{\beta^{s} - 1}} /24\), this means that when \(v_{i} = v_{j}\), the value of the objective function is smaller. □

The above proposition shows that we can replace decision variable \(v_{i} ,i \in I\) with variables \(v\) equivalently, and the value of the optimal objective function remains unchanged. Based on this, we design the tailored algorithm:

Algorithm 1. Tailored algorithm for the model MINLP1

Step 1.

(Initialize) \(m = 1\)

Step 2.

(Calculate the sailing speed \(v\)) According to the constraint (9) and the value of \(m\), calculate \(v = \sum\limits_{i \in I} {{{L_{i} } \mathord{\left/ {\vphantom {{L_{i} } {\left( {168m - \sum\limits_{i \in I} {t_{i}^{p} } } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {168m - \sum\limits_{i \in I} {t_{i}^{p} } } \right)}}}\)

Step 3.

(Calculate total cost) If the value of \(v\) does not meet the constraint (11), discard the situation, return to step 2 with \(m = m + 1.\) If \(v \in \left[ {v_{\min } ,v_{\max } } \right]\), calculate the total operation cost \(c^{bunk} \sum\limits_{i \in I} {{{\alpha^{{\text{s}}} L_{i} v^{{\beta^{s} - 1}} } \mathord{\left/ {\vphantom {{\alpha^{{\text{s}}} L_{i} v^{{\beta^{s} - 1}} } {24 + c_{s}^{oper} }}} \right. \kern-\nulldelimiterspace} {24 + c_{s}^{oper} }}}\) of each ship according to the value of \(v\) and fuel consumption function \(f^{s} (v) = \alpha_{s} v^{{\beta_{s} }} ,\forall s \in S\)

Step 4.

(Sort) Using the bubble sorting algorithm, arrange total operation cost of all ships in set \(S\) in ascending order

Step 5.

(Select ships) The value of the decision variable \(x_{s}\) corresponding to the first \({\text{m}}\) ships equal to 1, otherwise, equal to zero. Calculate the total operation cost of the first \({\text{m}}\) ships

Step 6.

(Termination conditions) If \(m \le |S|\), set m = m + 1, go back to step 2. Otherwise, go to Step 7

Step 7.

(Output) Select the optimal m with the lowest total operating cost together with its fleet deployment plan

*\(|{\text{S|}}\): the total number of candidate ship

The following proposition shows that the algorithm obtains the optimal solution of the model in polynomial time.

Proposition 2

The running time of the above algorithm is up to \(O(\left| S \right|^{3} ).\)

Proof

In algorithm 1, for each value of \({\text{m}}\), the bubble sorting method needs to be used to arrange the total operation cost of each ship. The running time of bubble sorting is \(O(\left| S \right|^{2} )\). Since algorithm 1 will traverse \(m = 1,2, \ldots ,|S|,\) then the total running time is \(O\left( {\left| S \right|^{2} \times \left| S \right|} \right){ = }O\left( {\left| S \right|^{3} } \right).\) □

3.2 Outer-approximation algorithm

For the case with different bunker consumption rates in different shipping legs, the model [MINLP2] cannot be solved by the algorithm in Sect. 2.1 as the sailing speeds in different legs are different. We thus solve this model using an outer linear approximation method.

3.2.1 Alternative decision variables and convexity of the objective function

Firstly, new decision variables \(u_{i} = 1/v_{i} ,\forall i \in I\) are defined to replace the decision variables \(v_{i},\forall i \in I\). The constraints of these new decision variables are written as:

$$1/v_{i}^{\max } = u_{i}^{\min } \le u_{i} \le u_{i}^{\max } = 1/v_{i}^{\min } ,\forall i \in I$$

Then all expressions containing \(v_{i}\) are expressed by \(u_{i}\), and the objective function and constraints can be expressed as:

$$\min \, \sum\limits_{s \in S} {\left( {\sum\limits_{i \in I} {{{c^{bunk} a_{i}^{s} u_{i}^{{1 - \beta_{i}^{s} }} L_{i} } \mathord{\left/ {\vphantom {{c^{bunk} a_{i}^{s} u_{i}^{{1 - \beta_{i}^{s} }} L_{i} } {24 + c^{oper} }}} \right. \kern-\nulldelimiterspace} {24 + c^{oper} }}} } \right)} x_{s}$$
(31)
$$\sum\limits_{i \in I} {(L_{i} u_{i} + t_{i} )} \le 168m$$
(32)
$$u_{i} \in \left[ {u_{i}^{\min } ,u_{i}^{\max } } \right],\forall i \in I$$
(33)

where the constraint (32) becomes a linear constraint. The objective function (31) is still nonlinear. Therefore, the auxiliary variables \(f_{i}^{s},\forall i \in I,\forall s \in S\) and \(C_{s},\forall s \in S\) are introduced, and the objective function and constraints are written as:

$$Min\sum\limits_{s \in S} {C_{s} } x_{s}$$
(34)
$$C_{s} \ge \sum\limits_{i \in I} {f_{i}^{s} } + c_{s}^{oper} ,\forall s \in S$$
(35)
$$f_{i}^{s} \ge c^{bunk} \alpha_{i}^{s} u_{i}^{{1 - \beta_{i}^{s} }} L_{i} /24,\forall i \in I,s \in S$$
(36)

Constraints (35) are linear constraints, and Constraints (36) can be approximated by the method of outer approximation and translates to linear constraints. The objective function (34) is still a nonlinear function. Therefore, we further transform and introduce auxiliary variables \(A_{s},\forall s \in S\), including:

$$Min\sum\limits_{s \in S} {A_{s} }$$
(37)
$$A_{s} \ge C_{s} + M(x_{s} - 1),\forall s \in S$$
(38)
$$A_{s} \ge 0,\forall s \in S$$
(39)

where \(M\) is a large constant. The original model has been transformed into a mixed-integer nonlinear programming model with convex constraints:

$$Min\sum\limits_{s \in S} {A_{s} }$$
(40)

subject to:

$$A_{s} \ge C_{s} + M(x_{s} - 1),\forall s \in S$$
(41)
$$C_{s} \ge \sum\limits_{i \in I} {f_{i}^{s} } + c_{s}^{oper} ,\forall s \in S$$
(42)
$$f_{i}^{s} \ge c^{bunk} \alpha_{i}^{s} u_{i}^{{1 - \beta_{i}^{s} }} L_{i} /24,\forall i \in I,s \in S$$
(43)
$$\sum\limits_{i \in I} {(L_{i} u_{i} + t_{i} )} \le 168m$$
(44)
$$\sum\limits_{s \in S} {x_{s} } = m$$
(45)
$$u_{i} \in \left[ {u_{i}^{\min } ,u_{i}^{\max } } \right],\forall i \in I$$
(46)
$$x_{s} \in \{ 0,1\} ,\forall s \in S$$
(47)
$$m \in Z_{ + }$$
(48)
$$A_{s} \ge 0,\forall s \in S$$
(49)

3.2.2 Outer-approximation algorithm

After the above transformation, constraints (43) are convex. The Outer-approximation algorithm is an effective method to linearize the convex constraint. So the piecewise linear functions are used to approximate the constraints (43). We divide the definition domain of the function into N equal parts. Clearly, the error of the approximation decreases as the value of N increases. We carry out the following steps to solve the MINLP2 and realize the algorithm of outer linear approximation:

Algorithm 2. Outer-approximation algorithm for the model MINLP2

Input: N

Step 1.

(Initialize) Set \(k = u_{\min } ,s = 0\)

Step 2.

(Iteration) Set \(k = k + ({\text{u}}_{\max } - {\text{u}}_{\min } )/N\)

Step 3.

(Piecewise-linear convex function) Rewrite inequality (43) as \(h_{i}^{s} (u_{i} ) = c^{bunk} \alpha_{i}^{s} u_{i}^{{1 - \beta_{i}^{s} }} L_{i} /24\). The derivative equation is \({h_{i}^{s}}^{\prime } (u_{i} ) = c^{bunk} (1 - \beta_{i}^{s} )\alpha_{i}^{s} u_{i}^{{ - \beta_{i}^{s} }} L_{i} /24,u_{i} \in \left[ {u_{i}^{\min } ,u_{i}^{\max } } \right]\). According to the principle of external approximation, we get that the linear equation used for approximation at certain point \(k\) is: \(g_{i}^{s} (u_{i} ) = {h_{i}^{s}} ^{\prime}(k)*(u_{i} - k) + h_{i}^{s} (k)\). We rewrite it into the form of \(y = nx + b\) to obtain the expression of \(g_{i}^{s} (u_{i} ) = {h_{i}^{s}}^{\prime} (k)*u_{i} + h_{i}^{s} (k) - k* {h_{i}^{s}} ^{\prime}(k)\). That is, at the point \(k\), the coefficient value of the tangent equation is: \(b = h_{i}^{s} (k) - k* {h_{i}^{s}} ^{\prime}(k),\)\(n = {h_{i}^{s}} ^{\prime}(k)\)

Step 4.

(Outer approximation) We obtain a series of approximate functions of a ship, and the convex function can be expressed by these piecewise linear functions \(\overline{{h_{i}^{s} (u_{i} )}} = \max \left\{ {g_{i}^{s} (u_{k} ),k = u_{\min } , \ldots ,u_{\max } } \right\},\forall i \in I,\forall s \in S\)

Step 5.

(Termination conditions) If \(k = 1/{\text{v}}_{\min }\), end the iteration, otherwise, go back to step 2

So far, we have transformed the mixed integer nonlinear programming model into a mixed integer linear programming problem. The software Gurobi can be used to calculate the optimal solution of the model [MINLP2].

4 Numerical experiments

4.1 Data description

We demonstrate the applicability of the model with real data from a global liner shipping company. We select a route and take 9 ships with 8000-TEU capacity sailing on this route. It is assumed that the capacity of this liner shipping company can meet the transportation requirements on the route. We do not need to consider chartering ships. In this paper, we deploy optimal ships to enter the route and optimize the speed to reduce the total operating cost of liner shipping companies.

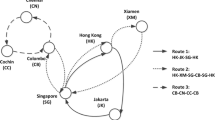
Figure 2 shows the route studied in this paper. The distance and berthing time of each leg on the designated route are shown in Table 2. The economic speed and fixed operating cost of each ship are given in Table 3.

Fig. 2
figure 2

Schematic diagram of designated route

Full size image
Table 2 Basic information of the designated route
Full size table
Table 3 Relevant data of 8000-TEU ship
Full size table

4.2 Result analysis

4.2.1 Same fuel consumption function on different legs

The bunker fuel consumption-sailing speed functions are fitted through the real data provided by the liner tfransportation company. In this section, the values of the coefficients \(\alpha_{s}\) and \(\beta_{s}\) in fuel consumption functions are shown in Table 4.

Table 4 Bunker fuel consumption function of 9 ships
Full size table

We use the tailored method in Sect. 2.1 to conduct numerical experiments. The solution results are shown in Table 5. It can be seen that the tailored method substitutes the appropriate number of ships into the model for the solutions, and then records the total operating cost. We should ensure that the fleet should sail within the economic speed range. We can directly discard the ship deployment plan if the speed is not within economic speed range (e.g., when the number of ships is below 5). For the fleet deployment plan within the economic speed range, we use bubble sorting method to rank the operating costs of all ships, and choose the speed and fleet deployment plan with the lowest total operating cost. When the price of bunker fuel is $600 and the economic speed of the ship is between [10, 25], the minimum total operating cost is $4.5601 × 106. In this scheme, 7 ships are selected to enter the route. The numbers of the 7 ships are 1, 2, 3, 4, 5, 7 and 8 respectively. The optimal speed of the fleet is 13.48 knots.

Table 5 Optimal sailing speed and optimal fleet deployment plan
Full size table

We also investigate the effect of the bunker fuel price on the model solution. As shown in Table 6, when the price of the bunker fuel is low, liner shipping companies tend to have a higher ship sailing speed and deploy fewer ships on this route. However, with the rise of the bunker fuel price, liner shipping companies will reduce the sailing speed to reduce the fuel consumption cost and appropriately increase the fleet size to maintain the weekly service frequency. For example, when the bunker fuel price is 100 USD/ton, the liner shipping company chooses 5 ships to enter the route, and the optimal sailing speed is 20.39 knots. But when the bunker price rises to 900 USD/ton, 8 routes are deployed on the route, and the average sailing speed is 11.53 knots. In addition, the proportion of bunker consumption cost in the total operating cost will increase with the increase of the fuel price. Through the sensitivity analysis of bunker fuel price, it can be concluded that bunker fuel price has an important impact on the number of ships deployed on the route and sailing speed.

Table 6 Comparison of ship costs under different fuel prices
Full size table

4.2.2 Different fuel consumption function on different legs

The bunker fuel consumption-sailing speed functions are fitted based on the real historical data provided by the liner shipping company. In this section, the values of the coefficients \(\alpha_{{\text{i}}}^{s}\) and \(\beta_{{\text{i}}}^{s}\) in fuel consumption functions are fitted through the historical data provided by the liner transportation company, and are shown in Table 7.

Table 7 Bunker fuel consumption functions of 9 ships on each leg of the specific route
Full size table

We divide each nonlinear convex constraint into 150 piecewise linear convex constraints. That is, the input N in the Outer approximation algorithm is designed to be 150. We use Python software and call Gurobi to solve the model. After 21,954 simplex iterations, we obtain the global optimal solution. We conclude that the lowest cost in this numerical experiment is 3.4984 × 106 $ per week. The optimal sailing speed and fleet deployment plan on the specific route are shown in Tables 8 and 9 respectively.

Table 8 Sailing speed of fleet in each leg
Full size table
Table 9 Fleet deployment plan on the route
Full size table

Tables 8 and 9 show the sailing speed of the fleet on each leg and the number of ships deployed on the specific route. Because the fuel consumption function of each leg is different, the optimal speed of the ship on each leg is also different. When the fuel price is $600, optimal sailing speeds on legs are between 12.72 and 17.18 knots, and 7 ships need to be deployed on the route. The numbers of these 7 ships are No. 1, No. 2, No. 3, No. 4, No. 5, No. 7 and No. 8 respectively. In this case, liner transportation companies can minimize the total operating cost while ensuring the weekly service frequency.

Table 10 shows the changes in the total operating costs, fuel consumption costs, the average fleet sailing speed and the fleet size when the fuel price increases from 100 USD/ton to 900 USD/ton. When bunker prices rise, liner shipping companies adjust the composition of their fleet even if they keep fleet size unchanged. For example, when the bunker price rose from 300 to 400 USD/ton, liner shipping companies deploy 6 ships on the route, but replaced the No. 5 ship with the No. 8 ship. This allows liner shipping companies to adjust their fleet composition when bunker prices change, so as to reduce bunker fuel consumption costs. Furthermore, when the price of the bunker fuel is very low, the proportion of ship bunker fuel consumption cost in the total operating cost is low. Liner shipping companies will tend to sail at higher speeds with fewer ships. However, with the rising price of the bunker fuel, the total bunker fuel consumption cost accounts for an increasing proportion in the total operating expenses of shipping companies. Liner shipping companies are considering reducing the speed of ships and increasing the size of their fleets.

Table 10 Comparison of ship costs under different fuel prices
Full size table

4.2.3 Comparison between homogeneous and heterogeneous vessels

To further investigate the value of our models with heterogenous ships, we compare it with the model with homogenous ships. Without considering the heterogeneity of the ships, the fuel consumption function and the operation cost are the same for all ships, and equal to the average of the corresponding parameters in our heterogeneous ship models. In this case, we only need to determine the number of ships deployed on the specific route and the sailing speed of the fleet. We compare the results between the homogeneous scenario and the heterogeneous one of the models [MINLP1] and [MINLP2]. It is assumed that the liner shipping company has nine ships to choose from and the bunker price is 600$/ton. The optimal solutions are shown in Table 11.

Table 11 Comparison between models with homogeneous and heterogeneous vessels
Full size table

It can be seen that considering heterogeneous ships in our model results in a smaller fleet size (7 vs. 9) and lower total operating costs (4.5601 × 106 vs. 4.7431 × 106 and 3.4984 × 106 vs. 4.148 × 106) compared to models with the homogeneous scenario. Due to the smaller fleet size, in order to maintain the weekly service frequency, ships sail at higher speeds in the heterogeneity models (13.48 vs. 10.06 and 14.17 vs. 10.19). Although the speed is higher, the fuel consumption cost is lower (3.7258 × 106 vs. 3.7810 × 106 and 2.6641 × 106 vs. 3.0861 × 106). This is because fewer ships consume the bunker fuel, which shows that the heterogeneity model can better deploy the fleet size and the sailing speed of the fleet to be able to use the lowest cost to provide services.

5 Conclusions

The shipping market has been in a downturn for a long time. Although slow steaming can effectively reduce bunker consumption and decreases the total operating cost of liner shipping companies, it prolongs the round-trip time and cut down their service quality. Therefore, this paper needs to consider how to optimize the sailing speed and fleet deployment on the premise of maintaining the weekly service frequency. This paper considers the two cases of the same and different fuel consumption-sailing speed functions in different legs of the route. A problem that arises here is the fleet deployment and sailing speed optimization (FDSSO) problem for containership with bunker fuel consumption heterogeneity.

In order to solve this problem, two mixed-integer nonlinear programming models are established in this paper. Under the same fuel consumption-sailing speed function on different legs, we obtain the optimal sailing speed and fleet size on this route, and select the optimal ship entering the route. When the fuel consumption-sailing speed function is different in different legs, we also obtain the optimal fleet size and select the optimal ship entering the route. Different from the first model, we give the optimal sailing speed of each leg on the route.

Because these models are nonlinear, we can't solve them directly with Cplex or Gurobi. Therefore, we develop two exact algorithms to solve the two models respectively, i.e., an algorithm that combines the enumeration and bubble sorting for MINLP1 and the outer approximation algorithm for MINLP2. Finally, we use numerical experiments to verify the effectiveness of the two models and the efficiency of the algorithm.

According to the relationship between bunker price, sailing speed and fleet size, we draw the following conclusions. Due to the increasing bunker fuel price, the bunker cost takes up an increasing proportion of total operating cost of the liner shipping companies. Liner shipping companies will adopt the strategies, such as slow steaming to reduce the bunker consumption, and deploy more ships to the route to increase the fleet size, in order to achieve the purpose of reducing the total operating costs of liner shipping companies on the premise of maintaining the weekly service frequency. We also compare the proposed model with ship heterogeneity with that without considering ship heterogeneity. Results show that considering ship heterogeneity gives a better fleet deployment strategy with lower ship operating cost, fuel consumption cost and thus the total fleet operating cost.

 There are still many limitations that need further research.

  1. 1.

    The fleet deployment and speed optimization model in this paper considers the effect of speed on the service frequency of ships, voyage time, the number of ships deployed on the route, and the daily fuel consumption. It is assumed that the ship is fully loaded and can meet the shipping demand of the route. However, the capacity of the ships and the container shipping demand volume are not considered in these models. Future studies can discuss how the capacity of ships affects the volume of shipping demand satisfied by the shipping company.

  2. 2.

    This paper only considers the effect of the speed changes on fuel costs for container ships. But the change in speed also affects the opportunity cost of liner companies and the penalty cost of voyage time, which can be incorporated in future studies.

  3. 3.

    It is assumed that the ship sails at a constant speed throughout the whole journey, which is not realistic. Therefore, a dynamic speed in future studies would be more conducive to a better fleet deployment plan.