A Unified Treatment of Families of Partition Functions

Abstract

We present a unified framework of combinatorial descriptions, and the analogous asymptotic growth of the coefficients of two general families of functions related to integer partitions. In particular, we resolve several conjectures and verify several claims that are posted on the On-Line Encyclopedia of Integer Sequences. We perform the asymptotic analysis by systematically applying the Mellin transform, residue analysis, and the saddle point method. The combinatorial descriptions of these families of generalized partition functions involve colorings of Young tableaux, along with their “divisor diagrams”, denoted with sets of colors whose sizes are controlled by divisor functions.

1 Introduction

Given a triple of nonnegative integers (i, j, k) with $i+j+k\ge 1$, we consider the generating functions

$$\begin{aligned} P(z) = P^{\langle i,j,k\rangle }(z)&= \prod (1-z^{n_1\ldots n_{i}d_{1}\ldots d_{j}e_{1}\ldots e_{k}})^{-n_1\ldots n_i/d_{1}\ldots d_{j}} \end{aligned}$$

(1)

and

$$\begin{aligned} Q(z) = Q^{\langle i,j,k\rangle }(z)&= \prod (1+z^{n_1\ldots n_{i}d_{1}\ldots d_{j}e_{1}\ldots e_{k}})^{n_1\ldots n_i/d_{1}\ldots d_{j}} \end{aligned}$$

(2)

with the $(i+j+k)$-fold product taken over all positive integers n’s, d’s, and e’s. The n’s refer to the indices occurring in the exponent as numerators; the d’s refer to indices occurring in the exponent as denominators; and the e’s are extra indices. We say that any such infinite product represented by the triple (i, j, k) is admissible.

1.1 Integer Partitions, and Integer Partitions with Distinct Summands

The triple $(i,j,k) = (0, 0, 1)$ yields the most well-known specific case of this family of generating functions:

$$\begin{aligned} P(z) = \prod \limits _{k=1}^\infty \frac{1}{1-z^k}&= \sum \limits _{n=0}^\infty {P_n}z^n \end{aligned}$$

(3)

and

$$\begin{aligned} Q(z) = \prod \limits _{k=1}^\infty (1+z^k)&= \sum \limits _{n=0}^\infty {Q_n}z^n. \end{aligned}$$

(4)

In this case, the generating function P(z) enumerates the combinatorial class ${\mathcal {P}}$ of integer partitions, i.e., $P_n$ is the number of partitions of n. Similarly, the generating function Q(z) enumerates the combinatorial class ${\mathcal {Q}} \subset {\mathcal {P}}$ of integer partitions with distinct summands, or equivalently, $Q_n$ is the number of partitions of n with distinct summands.

As unlabelled structures, the product formulas in Eqs. (3) and (4) are combinatorially justified by viewing ${\mathcal {P}}$ as a multiset of positive integers and ${\mathcal {Q}}$ as a powerset of positive integers. In other words, these classes can be defined by the well-known combinatorial specifications

$$\begin{aligned} {\mathcal {P}} \triangleq \textsc {MSet}\big (\textsc {Seq}_{\ge 1}({\mathcal {Z}})\big ) \end{aligned}$$

and

$$\begin{aligned} {\mathcal {Q}} \triangleq \textsc {PSet}\big (\textsc {Seq}_{\ge 1}({\mathcal {Z}})\big ), \end{aligned}$$

with ${\mathcal {Z}}$ denoting the atomic class. In this context, P(z) and Q(z) can be referred to as multiset and powerset partition functions, respectively. (See [1] for a broad general background on analytic combinatorics.) The genesis of the study of partition functions goes back to the work of Euler [2]. The so called “partition problem” consists of finding the asymptotic growth of the coefficients of functions like P(z) and Q(z). The coefficients of the function P(z) in fact result from what we now know as the Euler transform of the sequence $a(n) = 1$, which is defined in general as

$$\begin{aligned} \prod \limits _{n \ge 1} \frac{1}{(1-z^n)^{a(n)}}. \end{aligned}$$

The celebrated and well-known works of Hardy and Ramanujan are considered the first main contributions to the partition problem (see [3, 4]). In particular, for the triple $(i,j,k) = (0, 0, 1)$, they showed that

$$\begin{aligned} P_n \sim \frac{e^{\pi \sqrt{2n/3}}}{4\sqrt{3}\!\ n} \qquad \text {and} \qquad Q_n \sim \frac{e^{\pi \sqrt{n/3}}}{4\cdot 3^{1/4}\!\ n^{3/4}}. \end{aligned}$$

The main method they used is nowadays known as the “circle method” and is based on the representation of the coefficients of power series by means of the integral Cauchy formula. One of our goals is to solve the partition problem (first order asymptotics) for the more general class of partition functions of the forms given in Eqs. (1) and (2).

1.2 A Unified Framework

Several other particular cases have also been previously considered by other authors. We endeavor to introduce a framework to systematically classify these families of combinatorial classes and their analogous generating functions.¹ Table 1 shows a list of entries that appear in the On-Line Encyclopedia of Integer Sequences (OEIS) that correspond to certain triples (i, j, k). We will see that, in general, what we are dealing with now is what we called the “cyclic” Euler transform of a sequence a(n) which we now define as the sequence of coefficients of the function

$$\begin{aligned} \prod _{n\ge 1} \exp \left( \sum \limits _{\ell =1}^\infty \frac{z^{n \ell }}{n\ell } \right) ^{a(n)}. \end{aligned}$$

Among the cases that we identified in the OEIS, some contain an asymptotic analysis, and some give a combinatorial description, but we endeavor to handle all such cases systematically. Several claims about the asymptotic growth of the coefficients of the generating functions are stated only as conjectures without proofs, all due to Kotĕs̆ovec. We aim to present a more general treatment and a unifying framework for the combinatorial specifications of the labelled classes, as well as a systematic study of the asymptotic analysis of the number of these combinatorial objects.

1.3 On Kot$\breve{\textrm{e}}{\breve{\textrm{s}}}$ovec’s Conjectures

We are able to resolve all of Kotĕs̆ovec’s conjectures about these families of combinatorial classes and their generating functions. We are delighted to discover that all of his conjectures are true, with one exception: In the case of the admissible triple $(i,j,k) = (0,1,0)$, Kotĕs̆ovec’s conjecture about the asymptotic growth of the logarithm of coefficients is incorrect. We provide proofs of all of his conjectures. In the case of the erroneous conjecture about (0, 1, 0), we first explain the likely source of the confusion (likely due to numerical error), and we provide the corrected asymptotic analysis for this case as well.

Table 1 A list of 25 sequences and the analogous OEIS entries corresponding to the generating functions in Eqs. (1) and (2)

Because the erroneous conjecture led us to study this family of combinatorial objects, generating functions, and their asymptotic analysis, we start with Kotĕs̆ovec’s slightly erroneous conjecture about the case (0, 1, 0):

Conjecture 1

(Kotĕs̆ovec, Sep. 2018, see A028342 in OEIS) Let

$$\begin{aligned} P(z) \triangleq \prod _{d=1}^\infty (1-z^d)^{-1/d} = \sum _{n=0}^\infty \frac{p_n}{n!}z^n. \end{aligned}$$

(5)

The coefficients of P(z) have the asymptotic growth rate

$$\begin{aligned} \log \frac{p_n}{n!} \sim \frac{\log 2}{2}\log ^2 n. \end{aligned}$$

(6)

In order to explain the correct asymptotic behavior, and the likely source of the erroneous asymptotics, we need some well-known constants. For every $n \ge 0$, let $\gamma _n$ denote the nth Stieltjes number. In particular, let $\gamma \triangleq \gamma _0$ be the Euler–Mascheroni constant. Also, let ${\text {W}}(z)$ denote the Lambert ${\text {W}}$ function. Theorem 1 is the corrected version of Conjecture 1. It is also an exemplary prototype of the style of asymptotic results that can be deduced from our analysis.

Theorem 1

(Combinatorial description and asymptotic behavior for (0, 1, 0), see A028342) Let P(z) and $\{p_n\}_{n\ge 0}$ be given as in Eq. (5).

• (Combinatorial description) The sequence $\{p_n\}_{n\ge 0}$ enumerates the class of colored permutations by number of divisors, that is, permutations that after decomposing them into a product of cycles, each cycle carries a label that is a divisor of its corresponding length (see 3.3.1).

• (Asymptotic behavior) Furthermore, let $c \triangleq \pi ^2/12 - \gamma ^2/2-2\gamma _1$ and $w_n \triangleq {\text {W}}(e^{\gamma }n)$. Then (see Theorem 15)

  $$\begin{aligned} \frac{p_n}{n!}&\sim \frac{(w_n/n)^{1-\gamma }}{\sqrt{2\pi \log (w_n/n)}} \exp \left( c+w_n + \frac{\log ^2 (w_n/n)}{2}\right) . \end{aligned}$$

  (7)

  In particular,

  $$\begin{aligned} \log \frac{p_n}{n!} \sim \frac{\log ^2n}{2}. \end{aligned}$$

  (8)

Let us discuss a possible explanation why Kotĕs̆ovec made his conjecture in Eq. (6), which differs by a factor of $\log 2$ from the true asymptotic behavior given in Eq. (8). First, consider Fig. 1, which illustrates the three different estimates of $\log (p_n/n!)$ given by:

• (a) Kotĕs̆ovec’s conjecture in Eq. (6),

• (b) the logarithm of the very accurate estimate from Eq. (7), and

• (c) the accurate (but much slower to converge) estimate from Eq. (8).

Fig. 1

The three different estimates of $a(n) = \log p_n/n!$. The graphs corresponds to the plots of $a(n)/\theta (n)$, where $\theta (n)$ is a Kotĕs̆ovec’s estimate in Eq. (6), b the logarithm of the very accurate estimate from of Eq. (7), and c the accurate (but much slower to converge) estimate from Eq. (8)

In the illustration, the central item (b) shows that Eq. (7) gives a very accurate estimation. Furthermore, at first sight, the left item (a) shows that the estimation given by Eq. (6) is intuitively compatible with Kotĕs̆ovec’s conjecture 1, whereas the right item (c) shows that the estimation with Eq. (8) is slow to converge (but, perhaps surprisingly, will eventually converge to 1).

Computationally, obtaining the exact numerical values of the coefficients of P(z) is very challenging for indices of order greater that $10^3$. Indeed, the OEIS entry A028342 has a table (attributed to Kotĕs̆ovec) that lists only the first 455 values of $a_n$. For these reasons, it is likely that Kotĕs̆ovec simply based his asymptotic estimate on a relatively small number of terms. It is also likely that he was not aware of the precise estimation given by Eq. (7).

We leverage the fact that the numeric value of $w_n$ can be obtained for very large values of n. It is easy to see that the logarithm of Eq. (7) is asymptotically equivalent to $w_n^2/2$, and the later is asymptotically equivalent to $(\log ^2 n)/2$; however, this asymptotic convergence is extremely slow. In Table 2, we illustrate values of $w_n^2/\log ^2n$ for indices $n \le 10^3$, and we emphasize that (in this range) they mainly exhibit a decreasing behavior, so it is easy to be misled about their asymptotic growth.

Table 2 List of values of $w_n^2/\log ^2n$ for some $n \le 10^3$

If we divide the last entry in this table by $\log 2$, then we obtain $\frac{w_{1000}^2}{(\log 2) \log ^2 1000} = 0.9954$, which may have led Kotĕs̆ovec to mistakenly include $\log {2}$ in his conjecture in Eq. (6), based on numerical evidence.² However, in Table 3 we can look at the same values of $w_n^2/\log ^2n$, for much larger indices $n\ge 10^4$. This allows us to see the slow asymptotic convergence that justifies that both estimates in Theorem 1 are accurate. Taken together with our proof (see Theorem 15), we confirm our numerical estimate of Theorem 1.

Table 3 List of values of $w_n^2/\log ^2n$ for some $n \ge 10^4$

The rest of the paper is organized as follows. In Sect. 2 we present a brief background on the study of partition functions. In Sect. 3 we describe, as labeled classes, the combinatorial structures enumerated by the (exponential) generating functions (1) and (2). In Sect. 4, we discuss the asymptotic analysis of these generating functions: First, we compute the Mellin transforms, which can be derived in a systematic way across the (i, j, k) families. In contrast, the residue analysis needs to be customized for each triple parameter, though some generalities can be developed. The final asymptotic growth is obtained through saddle point method. With this methodology, we can resolve the conjectures about the asymptotic growth of the 6 sequences marked with (b) or (c) in Table 1. Additionally, we discover the asymptotic growth of the 9 sequences in OEIS that are marked with (d) in Table 1, and we provide the proofs.

2 Background

2.1 The Partition Problem

Ever since the work of Hardy and Ramanujan, there has been a continued and intensive development of the study of partition functions, there is a vast and diverse literature on the subject, the standard general reference is the book of Andrews [7] from 1984 and the references therein. The area has continued developing and we can only mention a brief list of some more recent works that are related, up to certain extends, to our context, like [8,9,10,11,12,13,14], works with more probabilistic points of view include [15,16,17,18,19], connexions with cellular automata can be found in [20], for other similar frameworks with q-series see [10], and so forth. There are several ways to generalizations, and in the literature several kinds of classes of functions are so called “weighted partitions”. For example, one kind arises by locating a sequence $(b_n)_{n=1}^\infty$ of “weights” as coefficients, namely, products of the form

$$\begin{aligned} P(z)=\prod \limits _{n\ge 1}\frac{1}{1-b_nz^n} \qquad \text { and } \qquad Q(z)=\prod \limits _{n\ge 1}(1+b_nz^n) \end{aligned}$$

(see e.g. [11, 13, 21,22,23,24,25]). Another kind arises by locating a sequence $(a_n)_{n\ge 1}$ of “weights” as exponents, namely, products of the form

$$\begin{aligned} P(z)=\prod \limits _{n\ge 1}\left( \frac{1}{1-z^n}\right) ^{a_n} \qquad \text { and } \qquad Q(z)=\prod \limits _{n\ge 1}(1+z^n)^{a_n} \end{aligned}$$

(see e.g. [6, 16, 26,27,28,29,30,31,32]). A third kind could arise when putting the previous two kinds together, namely, products of the form

$$\begin{aligned} P(z)=\prod \limits _{n\ge 1}\left( \frac{1}{1-b_nz^n}\right) ^{a_n} \qquad \text { and } \qquad Q(z)=\prod \limits _{n\ge 1}(1+b_nz^n)^{a_n}, \end{aligned}$$

etc. In this paper, products of the second kind arise when $j=0$ (see Theorem 3), and also when the triple is $(i,j,k) = (0,1,0)$ (see Theorem 2), thus, in these cases there are certain sequences of weights as exponents. There have been several works that, under some general hypothesis, resolve the partition problem for families of sequences of weights as exponents (at least the first order asymptotic growth, and mostly focused, in fact, in the ${\mathcal {P}}$-form rather than the $\mathcal Q$-form). Probably the most famous result for sequences of weights as exponents is Meinardus’ Theorem [29] from 1954, which is also explained in depth in Theorem 6.2 of [7, Chapter 6, pp. 88]. Even before Meinardus, there are other works, such as Brigham [28] in 1950, that consider weighted partitions as a general framework for many types of partition problems. For example, he mentions well-known works of Wright [26, 27] from 1931 and 1934 as particular cases. Meinardus’ Theorem has been generalized, as in [33], see also [31], and for further works in this context see e.g. [30, 34, 35]. Nevertheless, the immense generalities make many cases to fall beyond the assumptions of well-known results like Meinardus’ Theorem and its generalizations, and some open conjectures on several partition problems that have been considered remain, as far as we know, unsolved, for instance see A028342 and A318413 in OEIS. For example, in the case of the former, which is when $(i,j,k) = (0,1,0)$, what fails in Meinardus’ Theorem is the fact that a pole of $\zeta (s+1)$ is located at 0. In the case of the later, or more generally, when the triple is (i, 0, k), then it is necessary to analyze the Dirichlet series $\sum _{n\ge 1}\frac{\psi (n)}{n^s}$, where $\psi (n)$ is defined in Theorem 2. The Meinardus style of argument is designed for the case of partitions of integers, that is, when the triple is $(i,j,k) = (0,0,1)$ (for this case, see again [7, Chapter 6]).

Furthermore, several other instances of open conjectures that fall within the scope of Eqs. (1) and (2) are found in A168243, A107742, A280541, A318414, and we will present their resolutions. In virtue of Theorem 2, the general form of the “weighted partition function” that we are considering here has the form

$$\begin{aligned} \prod \limits _{n\ge 1}\exp \left( \frac{1}{n}\log \frac{1}{1-z^n}\right) ^{a_n} \end{aligned}$$

(the sequence $(a_n)$ that yields Eqs. (3) and (4) is $a_n=n$). Thus one of our goals here is to resolve the conjectures regarding the partition problem in all these cases, in addition to verifying all claims.

2.2 Divisor Functions

Recall that the well-known sum of divisors is the divisor function defined for every $n \ge 1$ by

$$\begin{aligned} \sigma _{x}(n):= \sum _{d\mid n} d^{x}. \end{aligned}$$

For example, $\sigma _0(n)$ is the number of divisors of n and $\sigma (n):= \sigma _1(n)$ is the sigma function, i.e. the sum of the positive divisors of n. Also, for every $k\ge 1$, the k-fold number of divisors is the divisor function defined by

$$\begin{aligned} \tau _{k}(n) := \sum _{d_1\ldots d_k=n} 1. \end{aligned}$$

In particular, $\tau _1(n)= 1$ and $\tau (n):=\tau _2(n)=\sigma _0(n)$ (we let $\tau _0(n):=1$). Observe that

$$\begin{aligned} \tau _{k+1}(n) := \sum _{d\mid n} \tau _{k}(n/d). \end{aligned}$$

Divisor functions are central in analytic number theory, in particular because of the well-known identity

$$\begin{aligned} \zeta (s)^k = \sum \limits _{n\ge 1} \frac{\tau _k(n)}{n^s}, \end{aligned}$$

i.e., $\zeta (s)^k$ is the Dirichlet series of $\big (\tau _k(n)\big )_{n\ge 1}$. For some recent developments see [36,37,38,39].

3 Combinatorial Specifications

In this section we present the general combinatorial specifications that yield the exponential generating functions given in Eqs. (1) and (2). We will focus on the combinatorial class ${\mathcal {P}}$ and at the end of the section we will discuss the corresponding class ${\mathcal {Q}}$. When $j=0$ (i.e. there are no denominators), we get two alternative specifications that yield the same exponential generating functions, hence we obtain two isomorphic kinds of labeled combinatorial classes. We will describe several particular examples. We will be interested in coloring several objects with a countable set of different colors, as depicted in Fig. 2. But first let us start with descriptions of certain basic classes in a way that will be useful throughout.

Fig. 2

A countable list of different colors, labelled by $\{1, 2, 3, 4, 5, 6, 7, \ldots \}$

3.1 Permutations, Integer Partitions, Young Tableaux, and Divisor Diagrams

The combinatorial class ${\mathcal {S}}$ of all permutations can be specified as sets of labelled cycles, i.e.

$$\begin{aligned} {\mathcal {S}}({\mathcal {Z}}) = {\textsc {Set}}\big ( {\textsc {Cyc}}({\mathcal {Z}})\big ), \end{aligned}$$

(9)

which translates into the exponential generating function

$$\begin{aligned} \exp \left( \log \frac{1}{1-z}\right) = \frac{1}{1-z}. \end{aligned}$$

For example, a permutation like

$$\begin{aligned} \left( \begin{array}{cccccccccccccccccc} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16 & 17 & 18 \\ 5 & 10 & 19 & 18 & 27 & 8 & 12 & 32 & 15 & 16 & 9 & 31 & 34 & 11 & 29 & 13 & 17 & 22 \end{array}\right. \\ \left. \begin{array}{cccccccccccccccc} 19 & 20 & 21 & 22 & 23 & 24 & 25 & 26 & 27 & 28 & 29 & 30 & 31 & 32 & 33 & 34\\ 30 & 2 & 14 & 23 & 4 & 26 & 28 & 33 & 1 & 24 & 6 & 21 & 7 & 3 & 25 & 20 \end{array}\right) \end{aligned}$$

decomposes as a set of cycles coming from its decomposition as a product of cycles, namely,

$$\begin{aligned}&(1 5 27) (2 10 16 13 34 20) (3 19 30 21 14 11 9 15 29 6 8 32) \\&(4 18 22 23) (7 12 31) (17) (24 26 33 25 28). \end{aligned}$$

In general, we write cycles starting with the “leader”, and we can always “re-accommodate” the product of cycles monotonically in a unique way according to their lengths and, within cycles of equal length, according to the leader. For example,

$$\begin{aligned}&(3 19 30 21 14 11 9 15 29 6 8 32) (2 10 16 13 34 20) \nonumber \\&(24 26 33 25 28) (4 18 22 23) (1 5 27) (7 12 31) (17). \end{aligned}$$

(10)

Any permutation is associated to an integer partition of its size, namely the lengths of its cycles, e.g. for the permutation above we have the partition $34 = 12 + 6 + 5 + 4 + 3 + 3 + 1$. It is customary to represent integer partitions as Young diagrams, i.e. as monotone arrangements of horizontal blocks formed by consecutive boxes with lengths according to the summands in the partition. See item (a) in Fig. 3 for the example above (observe that, for reference, the associated partition is written to the left of the Young diagram). A Young tableau on a Young diagram of size n is a well-labelling of the boxes of the Young diagram with the set $\{1, \ldots , n\}$ (then, all the n symbols are required to be used exactly once). For example, (b) in Fig. 3 is the unique representation (described before) of the partition given as in Eq. (10). In fact, every Young tableau has an associated permutation which has the labelled rows as its decomposition in cycles. Thus, different labelling of Young diagrams can yield Young tableaux that have the same associated permutation, for example in Fig. 3, items (b) and (c) differ only because some rows were shifted cyclically, that is, the permutation remains invariant under the action $\alpha$ by cyclic shifts, that is, $\alpha (a_1,\ldots , a_n) = (a_2, \ldots a_{n}, a_1)$ for every cycle $(a_1, \ldots ,a_n)$. A class of Young tableaux is modular if its elements are regarded as equivalence classes of the equivalence relation defined by the $\alpha$-orbits. Similarly, in Fig. 3, items (b) and (d) differ only by a permutation of the two rows of length three, the other generic instance that make two different Young tableaux induce the same permutation. Thus there is also an action $\sigma$ that for every $n\ge 1$ acts by permutations on the set of n-blocks, and the original permutation is also invariant under this $\sigma$-action. A class of Young tableaux is symmetric if its elements are regarded as equivalence classes of the orbital equivalence relation induced by the $\sigma$-action. Thus for example, the class ${\mathcal {S}}$ of all permutations is represented by the class of modular and symmetric Young tableaux.

Fig. 3

Young Tableaux: a A Young diagram. b A Young tableau. c A Young tableau obtained from (b) by cyclically shifting some rows. d A Young tableau obtained from (b) by switching rows of the same size

The divisor diagram associated to a Young diagram is again an arrangement of blocks of boxes arranged as rows beside the Young diagram in a way that blocks of length n in the Young diagram correspond to blocks of length $\tau (n)$ in the divisor diagram (it is like the “image” of the Young diagram under the number of divisor function $\tau (n)$, thus, in general, the arrangement in the divisor diagram is not monotone). See Fig. 4.

Fig. 4

A Young diagram together with its divisor diagram

Henceforth, the divisors of a positive integer n will be written as $1=p_1<\cdots < p_{\tau (n)}=n$.

3.2 General Combinatorial Specifications for ${\mathcal {P}}$

Let us formally give the two main global combinatorial specifications.

Theorem 2

For every admissible triple (i, j, k), define for every positive integer n the arithmetic function

$$\begin{aligned} \chi (n):= {\left\{ \begin{array}{ll} n^2\cdot \tau _i(n) \quad & \text {for } (i\ge 1,0,0) \\ n \sum \limits _{\ell =1}^{\tau (n)} p_\ell \cdot \tau _i(p_\ell ) \cdot \tau _k(n/p_\ell ) \quad & \text {for } (i\ge 1,0,k \ge 1) \\ \sum \limits _{\ell =1}^{\tau (n)} p_\ell ^2 \cdot \tau _i(p_\ell ) \cdot \tau _j(n/p_\ell ) \quad & \text {for } (i\ge 1,j\ge 1, 0) \\ \sum \limits _{\ell =1}^{\tau (n)} \sum \limits _{m=1}^{\tau (n/p_{\ell })} p_\ell ^2 q_m \cdot \tau _i(p_\ell ) \cdot \tau _k(q_m) \cdot \tau _j\big (n/(p_\ell q_m)\big ) \quad & \text {for } (i\ge 1,j\ge 1,k \ge 1) \\ n\cdot \tau _k(n) \quad & \text {for } (0,0,k \ge 1) \\ \sum \limits _{\ell =1}^{\tau (n)} p_\ell \cdot \tau _k(p_\ell ) \cdot \tau _j(n/p_\ell ) \quad & \text {for } (0,j\ge 1,k \ge 1) \\ \tau _j(n) \quad & \text {for } (0,j\ge 1,0) \\ \end{array}\right. } \end{aligned}$$

where $q_m \mid \frac{n}{p_\ell }$ for $m=1,\ldots ,\tau (n/p_\ell )$ are the divisors of $n/p_\ell$. Then P(z) is the cyclic Euler transform of $\chi (n)$, that is,

$$\begin{aligned} P(z) = \prod _{n\ge 1} \left( \exp \left( \sum \limits _{\ell =1}^\infty \frac{z^{n \ell }}{n\ell } \right) \right) ^{\chi (n)}. \end{aligned}$$

(11)

Proof

We have

$$\begin{aligned} P(z)&= \prod \left( \frac{1}{1-z^{n_1\ldots n_{i}d_{1}\ldots d_{j}e_{1}\ldots e_{k}}} \right) ^{n_1\ldots n_i/d_{1}\ldots d_{j}} \\&= \prod \exp \left( \log \left( \left( \frac{1}{1-z^{n_1\ldots n_{i}d_{1}\ldots d_{j}e_{1}\ldots e_{k}}} \right) ^{n_1\ldots n_i/d_{1}\ldots d_{j}} \right) \right) \\&= \prod \exp \left( \frac{1}{d_1\ldots d_j}\log \left( \frac{1}{1-z^{n_1\ldots n_{i}d_{1}\ldots d_{j}e_{1}\ldots e_{k}}} \right) \right) ^{n_1\ldots n_i}\\&= \prod \exp \left( \frac{1}{d_1\ldots d_j} \sum \limits _{\ell =1}^\infty \frac{z^{n_1\ldots n_{i}d_{1}\ldots d_{j}e_{1}\ldots e_{k} \ell }}{\ell } \right) ^{n_1\ldots n_i}\\&= \prod \exp \left( n_1\ldots n_{i}e_{1}\ldots e_{k} \sum \limits _{\ell =1}^\infty \frac{z^{n_1\ldots n_{i}d_{1}\ldots d_{j}e_{1}\ldots e_{k} \ell }}{n_1\ldots n_{i}d_{1}\ldots d_{j}e_{1}\ldots e_{k}\ell } \right) ^{n_1\ldots n_i}\\&= \prod \exp \left( \sum \limits _{\ell =1}^\infty \frac{z^{n_1\ldots n_{i}d_{1}\ldots d_{j}e_{1}\ldots e_{k} \ell }}{n_1\ldots n_{i}d_{1}\ldots d_{j}e_{1}\ldots e_{k}\ell } \right) ^{(n_1\ldots n_i)^2\cdot e_{1}\ldots e_{k}} \end{aligned}$$

and hence the result follows. $\square$

Corollary 1

The exponential generating function in Eq. (1) comes from the specification

$$\begin{aligned} {\mathcal {P}}({\mathcal {Z}}) = \prod \limits _{n=1}^\infty {\textsc {Seq}}_{\chi (n)}\left( {\textsc {Set}}\left( \bigcup _{\ell = 1}^{\infty }{\textsc {Cyc}}_{n\ell } ({\mathcal {Z}})\right) \right) . \end{aligned}$$

(12)

Only when $j>0$ we are forced to consider cycles. Thus the case $j=0$ deserves its own attention. In fact we will see now, in the result that follows, that in this case ${\mathcal {P}}$ admits a specification that translates into a representation of P(z) with the form given in Meinardus’ Theorem (thus the later could be applied if all its hypothesis are satisfied); the proof of this result and the next two that follow are now straightforward.

Theorem 3

For every positive integer n, let

$$\begin{aligned} \psi (n):= {\left\{ \begin{array}{ll} n \cdot \tau _i(n) \quad & \text {for } (i \ge 1, 0, 0) \\ \tau _k(n) \quad & \text {for } (0, 0, k\ge 1) \\ \sum \limits _{\ell =1}^{\tau (n)} p_\ell \cdot \tau _i(p_\ell ) \cdot \tau _k(n/p_\ell ) \quad & \text {for } (i\ge 1, 0, k\ge 1). \end{array}\right. } \end{aligned}$$

If $j=0$, then P(z) is the Euler transform of $\psi (n)$, that is,

$$\begin{aligned} P(z)&= \prod \left( \frac{1}{1-z^{n_1\ldots n_{i}e_{1}\ldots e_{k}}} \right) ^{n_1\ldots n_i} = \prod _{n\ge 1} \left( \frac{1}{1-z^{n}} \right) ^{\psi (n)} . \end{aligned}$$

Corollary 2

The exponential generating function in Eq. (2) comes from the specification

$$\begin{aligned} {\mathcal {P}}({\mathcal {Z}}) = \prod \limits _{n=1}^\infty {\textsc {Seq}}_{\psi (n)}\big ({\textsc {Seq}}({\mathcal {Z}}^n)\big ). \end{aligned}$$

(13)

Proposition 4

Given an admissible triple (i, 0, k), the combinatorial classes defined by Eqs. (12) and (13) are isomorphic.

3.3 Examples

So, let us now see several examples to better understand the labeled structures defined by Eqs. (12) and (13). Let us start with the cases that force an exponential context, i.e. when $j\ge 1$. Actually, in virtue of Theorem 2, analyzing the first few cases suffices to understand the whole class described in Eq. (12).

3.3.1 Colored Permutations by Number of Divisors: (0, 1, 0)

Consider the case $(i,j,k) = (0,1,0)$. This is the case of Theorem 1. In this case, the specification in Eq. (12) becomes

$$\begin{aligned} {\mathcal {P}} ({\mathcal {Z}}) = \prod _{n=1}^{\infty }{\textsc {Set}}\Big (\bigcup _{\ell = 1}^\infty {\textsc {Cyc}}_{n\ell }({\mathcal {Z}})\Big ) \end{aligned}$$

(compare with (9)). It represents the class of permutations, but now they carry a label on each cycle which is a divisor of that cycle’s length. For instance,

$$\begin{aligned}&\overbrace{(3 19 30 21 14 11 9 15 29 6 8 32)}^{3\mid 12} \overbrace{(2 10 16 13 34 20)}^{2\mid 6} \nonumber \\&\overbrace{(24 26 33 25 28)}^{1\mid 5} \overbrace{(4 18 22 23)}^{4\mid 4} \overbrace{(1 5 27)}^{3\mid 3} \overbrace{(7 12 31)}^{1\mid 3} \overbrace{(17)}^{1\mid 1}. \end{aligned}$$

(14)

Any such set of labels showing an example divisor of each cycle length is suitable. For instance, another element of size 34 is

$$\begin{aligned}&\overbrace{(3 19 30 21 14 11 9 15 29 6 8 32)}^{12\mid 12} \overbrace{(2 10 16 13 34 20)}^{3\mid 6}\nonumber \\&\overbrace{(24 26 33 25 28)}^{5\mid 5} \overbrace{(4 18 22 23)}^{2\mid 4} \overbrace{(1 5 27)}^{1\mid 3} \overbrace{(7 12 31)}^{1\mid 3} \overbrace{(17)}^{1\mid 1} \end{aligned}$$

(15)

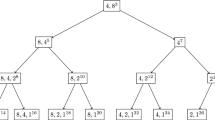
We emphasize that any label of the form $p\mid l$ above a cycle of length l is valid. In other words, an element of ${\mathcal {P}}$ is completely determined by the structure of the cycles in that permutation, and the choice of one divisor (indeed, any divisor p) of each cycle length. The choice of divisors is equivalent to coloring each row of length n of the corresponding Young diagram with $\tau (n)$ colors, e.g. see Fig. 5. So in this case the structure is the class of colored permutations with divisor function $\tau (n)$, that is, colored permutations by number of divisors. Its first elements are shown in Fig. 6.

Fig. 5

Colored permutations by number of divisors (the numbering on the right of each row corresponds to the color number). a Coloring according to Eq. (14) b Coloring according to Eq. (15). c Another legal coloring

Fig. 6

The first elements of colored permutations by number of divisors

3.3.2 Colored Permutations by Number of Divisors with Rooted Colorings of Divisor Diagrams by Number of Divisors: (0, 2, 0)

Consider the case $(i,j,k) = (0,2,0)$. In this case we obtain the specification

$$\begin{aligned} {\mathcal {P}} ({\mathcal {Z}}) = \prod _{n=1}^{\infty }{\textsc {Seq}}_{\tau (n)}\left( {\textsc {Set}}\left( \bigcup \limits _{\ell =1}^\infty {\textsc {Cyc}}_{n\ell }(\mathcal Z)\right) \right) . \end{aligned}$$

(16)

Fig. 7

A colored permutation by number of divisors together with four instances of rooted colorings of its divisor diagram by number of divisors. a A colored partition in a Young diagram. b, c, d Three different rooted colorings of the divisor diagram associated to the Young diagram in (a)

Keeping in mind the case (0, 1, 0) in Sect. 3.3.1, we see that again we get colored permutations by number of divisors, but now, in addition, each block in the Young diagram carries an additional label, namely, for each block of length n, if we list the divisors of n as $1=p_1< \cdots < p_{\tau (n)}=n$ and then pick one divisor $p_l$, then the label is a color chosen from a set of colors of size $\tau (p_l)=l$, and this can be pictured as colorings of rooted divisor diagrams by size. So in this case, if the lth box of a block is the root, then the size of the set of colors is l. See Fig. 7 for instance, it shows a colored permutation and four instances of rooted colorings of its divisor diagram by number of divisors. If the first box is chosen as the root for all blocks, then there is only one coloring, the monochromatic, and this is the case shown in item (b) in this figure. Items (c), (d) and (e) show other possible rooted colorings of the divisor diagram.

3.3.3 Colored Permutations by Number of Divisors with Rooted Colorings of Divisor Diagram with Divisor Function $\chi (n)$: (i, j, k)

With the two previous examples on mind, now we can understand the general case in Eq. (12) because it only differs from the specification in Eq. (16) by the divisor function $\chi (n)$ instead of the divisor function $\tau (n)$ in the sequence operator. Thus, the structure is essentially the same, that is, the class consists again of colored permutations by number of divisors, and the difference is that the coloring of the rooted divisor diagram is now determined by the divisor function $\chi (n)$. To be precise, if the lth box in a block of the divisor diagram that is associated to an n-block in the Young diagram has been chosen as the root, and if the divisors of n are written as $1=p_1<\cdots <p_{\tau (n)}=n$, then the block of the divisor diagram is colored with a set of colors of size $\chi (p_l)$. Note that in the general case, if two distinct boxes in the lth column of the divisor diagram are chosen as roots of their corresponding blocks, then the blocks may be colored with sets of colors of distinct cardinalities.

Now it is turn to analyze the specification given in Eq. (13).

3.3.4 Ordered Colorings of Young Tableaux by Size: (1, 0, 0)

Now consider the triple $(i,j,k) = (1,0,0)$. In this case, P(z) is known to be the ordinary generating function of the plane partitions, studied by Wright (see [26]). In a labelled universe, the class consists of well colorings of plane partitions and is combinatorially isomorphic to the (isomorphic) classes that result from the specifications given in Eqs. (12) and (13). The later becomes

$$\begin{aligned} {\mathcal {P}}({\mathcal {Z}}) = \prod _{n=1}^{\infty }{\textsc {Seq}}_n\left( {{\textsc {Seq}}({\mathcal {Z}}^n)}\right) \end{aligned}$$

(17)

and it translates into

$$\begin{aligned} P(z) = \prod _{n=1}^{\infty } \frac{1}{(1-z^n)^n}. \end{aligned}$$

In this case, the labelled class ${\mathcal {P}}$, as specified in Eq. (17), consists of colorings of Young tableaux by size, i.e. the blocks of size n are colored with n distinct colors. See Fig. 8 for examples. Note the difference with the colored permutations by number of divisors from Sect. 3.3.1 in that here the Young tableaux are colored by size and they are not modular nor symmetric. Furthermore, in this case we also have $\chi (n)=n^2\tau _{1}(n)=n^2$, thus, according to Proposition 4, the class of colored Young tableaux by size is isomorphic to the class of colored permutations by number of divisors with rooted colorings of divisor diagrams by size squared.

Fig. 8

Colored Young tableaux by size. Each row of length n is colored with a set of colors of size n. a A colored Young tableau by size function. b Another colored Young tableau, it differs from (a) not only from the coloring, but also the labelling of the rows of size three have been permuted, i.e. the Young tableaux are not symmetric. c Another colored Young tableau, it differs from (a) not only from the coloring, but also a row has been cyclically shifted, i.e. the Young tableaux are not modular. d Another coloring of another Young tableau

3.3.5 Colored Young Tableaux by Divisor Function $\psi (n)$: (i, 0, k)

The specification in Eq. (13) for the general case of triples (i, 0, k) differs from the previos example in that $\psi (n)$ now replaces the size function n. In other words, we get again colored Young tableaux like in Sect. 3.3.4, the only difference is that now the size of the set of colors used to color the set of n-blocks is the divisor function $\psi (n)$ (indeed, when $i=1$ and $k=0$, $\psi (n)=n$, i.e. $\psi (n)$ is the size). Again we recall that this class is isomorphic to the class of colored permutations by number of divisors with with rooted colorings of divisor diagrams with divisor function $\chi (n)$.

3.4 The Class ${\mathcal {Q}}$

With the two global combinatorial perspectives for ${\mathcal {P}}$ given by the specifications in Eq. (12) and (13), we can give a general description of the corresponding class ${\mathcal {Q}}$ with markers and bivariate (exponential) generating functions as follows. First consider a weighted version of Eq. (12), namely, the specification

$$\begin{aligned} \widehat{{\mathcal {P}}}({\mathcal {Z}} , {\mathcal {V}}) = \prod \limits _{n=1}^\infty {\textsc {Seq}}_{\chi (n)}\left( {\textsc {Set}}\left( \bigcup _{\ell = 1}^{\infty } \mathcal V^{\ell + 1}{\textsc {Cyc}}_{n\ell } ({\mathcal {Z}})\right) \right) . \end{aligned}$$

The corresponding bivariate (exponential) generating function ${\widehat{P}}(z,v)$ is therefore

$$\begin{aligned} {\widehat{P}}(z,v) = \prod _{n=1}^{\infty }\exp \left( \sum _{\ell = 1}^\infty v^{\ell +1}\frac{z^{n\ell }}{n\ell }\right) ^{\chi (n)}. \end{aligned}$$

In the case $v=1$, we have already seen (in Eq. (11)) that ${\widehat{P}}(z,1)=P(z)$. Now set the weight $v=-1$ and follow the proof of Theorem 2 backwards to get

$$\begin{aligned} {\widehat{P}}(z,-1)&= \prod _{n=1}^{\infty }\exp \left( \sum _{\ell =1}^{\infty } (-1)^{\ell +1}\frac{z^{n\ell }}{n\ell }\right) ^{\chi (n)} \\&= \prod \exp \left( -\sum \limits _{\ell =1}^\infty \frac{(-z^{n_1\ldots n_{i}d_{1}\ldots d_{j}e_{1}\ldots e_{k}})^ \ell }{n_1\ldots n_{i}d_{1}\ldots d_{j}e_{1}\ldots e_{k}\ell } \right) ^{(n_1\ldots n_i)^2\cdot e_{1}\ldots e_{k}} \\&= \prod \exp \left( -\sum \limits _{\ell =1}^\infty \frac{(-z^{n_1\ldots n_{i}d_{1}\ldots d_{j}e_{1}\ldots e_{k}})^ \ell }{\ell } \right) ^{n_1\ldots n_i/ d_{1}\ldots d_{j}} \\&= \prod \exp \left( - \log \frac{1}{1+z^{n_1\ldots n_{i}d_{1}\ldots d_{j}e_{1}\ldots e_{k}}} \right) ^{n_1\ldots n_i / d_{1}\ldots d_{j}} \\&= Q(z). \end{aligned}$$

More generally, however, if we fix the value of the weights v, we get

$$\begin{aligned} P_{n}^{(v)}&= [z^{n}]{\widehat{P}}(z,v) = [z^{n}]\prod _{n=1}^{\infty }\exp \left( \sum _{\ell = 1}^\infty v^{\ell +1}\frac{z^{n\ell }}{n\ell }\right) ^{\chi (n)} \\&= [z^{n}]\prod _{\delta =1}^{\infty }\exp \Bigg (\sum _{\begin{array}{c} \ell \ge 1\\ \textrm{with }\!\ \delta \mid \ell \end{array}}^\infty v^{\frac{\ell }{\delta }+1}\frac{z^{\ell }}{\ell }\Bigg )^{\chi (\delta )}. \end{aligned}$$

As seen above, the coefficients $Q_{n} = [z^{n}]Q(z)$ can be calculated as a sum of weighted terms (with weights $+1$ and $-1$) of coefficients from P(z). Since $v=1$ yields ${\widehat{P}}(z,1) = P(z)$ and $v=-1$ yields ${\widehat{P}}(z,-1) = Q(z)$, it would be interesting to explore other exponential generating functions of the form ${\widehat{P}}(z,v)$ for other roots of unity $v=e^{i\theta }$ on the unit circle. We leave such explorations as open problems.

4 Asymptotic Analysis

The asymptotic analysis is carried out in a similar way as in [1]. Let us start with the substitution $z\triangleq e^{-t}$. Let $L_{P}(t) = \log \big (P(e^{-t})\big )$ and $L_{Q}(t) = \log \big (Q(e^{-t})\big )$. Also, let L(t) denote either $L_P(t)$ or $L_Q(t)$.

4.1 Mellin Transforms

Recall that the Mellin transform of a function $f:\mathbb R_{>0} \rightarrow \infty$ is the complex-variable function $\mathcal M(f;s)\ \triangleq \int _0^\infty f(x)x^{s-1}dx$ defined in the fundamental strip $\langle \alpha , \beta \rangle \triangleq \{ z = a + bi \ : \ a \in (\alpha , \beta ) \}$, where $\alpha$ and $\beta$ are such that

$$\begin{aligned} f(x) = \left\{ \begin{array}{lcl} O(x^\alpha ) & \qquad & x \rightarrow 0 \\ O(x^\beta ) & & x \rightarrow \infty . \end{array} \right. \end{aligned}$$

For references to the Mellin transform and its properties, see [40, 41, Ch. 8.8], [42, 43] also [44, Ch. 9].

Proposition 5

(Mellin transform for ${\mathcal {P}}$ and ${\mathcal {Q}}$) Let $L_{P}^{*}(s) := {\mathcal M}[L_{P}(t); s]$ and $L_{Q}^{*}(s) := {{\mathcal {M}}}[L_{Q}(t); s]$ be the Mellin transforms of $L_{P}(t)$ and $L_{Q}(t)$, respectively. These Mellin transforms have the succinct forms

$$\begin{aligned} L_{P}^{*}(s) = \zeta (s-1)^i\zeta (s+1)^{j+1}\zeta (s)^{k}\Gamma (s) \end{aligned}$$

(18)

and

$$\begin{aligned} L_{Q}^{*}(s) = (1-2^{-s})\zeta (s-1)^i\zeta (s+1)^{j+1}\zeta (s)^{k}\Gamma (s). \end{aligned}$$

(19)

Proof

Since $L_{P}(t) = \log \big (P(e^{-t})\big )$, the the definition of P and the fact that the log of the product equals the sum of the logs imply

$$\begin{aligned} L_{P}(t)&= \log \prod (1-e^{-tn_1\ldots n_id_1\ldots d_j e_1 \ldots e_k})^{-n_1\ldots n_i/d_1\ldots d_j} \\&=\sum \frac{n_1\ldots n_i}{d_{1}\ldots d_{j}} \log (1/(1-e^{-tn_1\ldots n_id_1\ldots d_j e_1 \ldots e_k})). \end{aligned}$$

Then we can expand the log as a series, and exchange the order of the summations, to obtain

$$\begin{aligned} L_{P}(t) = \sum _{j=1}^{\infty }\frac{1}{j}\sum \frac{n_1\ldots n_i}{d_{1}\ldots d_{j}}e^{-tn_1\ldots n_id_1\ldots d_j e_1 \ldots e_kj}. \end{aligned}$$

By linearity of the Mellin transform, we have

$$\begin{aligned} L_{P}^{*}(s) = \sum _{j=1}^{\infty }\frac{1}{j}\sum \frac{n_1\ldots n_i}{d_{1}\ldots d_{j}}{{\mathcal {M}}}\left[ e^{-tn_1\ldots n_id_1\ldots d_j e_1 \ldots e_kj}; s\right] . \end{aligned}$$

Using scaling for the Mellin transform [44, equation (9.5)], we have

$$\begin{aligned} {{\mathcal {M}}}\left[ e^{-tn_1\ldots n_id_1\ldots d_j e_1 \ldots e_kj}; s\right] = (n_1\ldots n_id_1\ldots d_j e_1 \ldots e_kj)^{-s}{\mathcal M}\left[ e^{-t}; s\right] . \end{aligned}$$

It is well known that ${{\mathcal {M}}}\left[ e^{-t} ; s\right] = \Gamma (s)$ and that, in this case, the fundamental strip is $\langle 0, \infty \rangle$. So it follows that

$$\begin{aligned} L_{P}^{*}(s) = \sum _{l=1}^{\infty }\frac{1}{l}\sum \frac{n_1\ldots n_i}{d_{1}\ldots d_{j}} \cdot (n_1\ldots n_id_1\ldots d_j e_1 \ldots e_k l)^{-s}\Gamma (s), \end{aligned}$$

which simplifies to

$$\begin{aligned} L_{P}^{*}(s) = \zeta (s-1)^i\zeta (s+1)^{j+1}\zeta (s)^{k}\Gamma (s). \end{aligned}$$

The analysis for $L_{Q}(t)$ is similar. First we have

$$\begin{aligned} L_{Q}(t) = \log \prod (1+e^{-tn_1\ldots n_id_1\ldots d_j e_1 \ldots e_k})^{n_1\ldots n_i/d_{1}\ldots d_{j}}. \end{aligned}$$

Then we expand as before, and we get

$$\begin{aligned} L_{Q}(t) = \sum _{l=1}^{\infty }\frac{(-1)^{l+1}}{l}\sum \frac{n_1\ldots n_i}{d_{1}\ldots d_{j}}e^{-tn_1\ldots n_id_1\ldots d_j e_1 \ldots e_kl}. \end{aligned}$$

Again using linearity and scaling, it follows that

$$\begin{aligned} L_{Q}^{*}(s) = \sum _{l=1}^{\infty }\frac{(-1)^{l+1}}{l}\sum \frac{n_1\ldots n_i}{d_{1}\ldots d_{j}} \cdot (n_1\ldots n_id_1\ldots d_j e_1 \ldots e_k l)^{-s}\Gamma (s), \end{aligned}$$

which simplifies to

$$\begin{aligned} L_{Q}^{*}(s) = \eta (s+1)\zeta (s-1)^i\zeta (s+1)^{j}\zeta (s)^{k}\Gamma (s), \end{aligned}$$

where $\eta (s) = \sum _{n=1}^{\infty }\frac{(-1)^{n+1}}{n^s}$ is the Dirichlet eta function. For symmetry with the equation for $L_{P}^{*}(s)$, we transform this to:

$$\begin{aligned} L_{Q}^{*}(s) = (1-2^{-s})\zeta (s-1)^i\zeta (s+1)^{j+1}\zeta (s)^{k}\Gamma (s). \end{aligned}$$

In both the P(z) and the Q(z) cases, if $i > 0$, then the fundamental strip is $\langle 2, \infty \rangle$. Otherwise, if $i=0$ and $k > 0$, then the fundamental strip is $\langle 1, \infty \rangle$. Finally, if $i=k=0$, then the fundamental strip is $\langle 0, \infty \rangle$. $\square$

4.2 Singularity Analysis

Henceforth let $L^*(s)$ denote the analytic continuation of either $L^*_P(s)$ or $L_Q^*(s)$ to the entire complex plane, except for singularities. We make a handful of singularity analysis observations.

Proposition 6

$L^*(s)$ is meromorphic. Furthermore, the following hold:

• 1. If $i\ge 1$, then $L^*(s)$ has a singularity at $s=2$ generated by $\zeta (s-1)^{i}$. It is a pole of order $i\ge 1$, because the remaining terms in Eqs. (18) and (19) are nonzero at $s=2$.

• 2. If $k \ge 1$, then $L^*(s)$ has a singularity at $s=1$ generated by $\zeta (s)^k$. It is a pole of order $k\ge 1$ because the remaining terms terms in Eqs. (18) and (19) are nonzero at $s=1$.

• 3. Both $L_P^*(s)$ and $L_Q^*(s)$ have a singularity at $s=0$ generated by $\zeta (s+1)^{j+1}\Gamma (s)$. The singularity of $L_P^*(s)$ at $s=0$ is a pole of order $j+2 \ge 2$ because the remaining terms in (18) are nonzero at $s=0$. In contrast, since $1-2^{-s}$ has a simple zero at $s=0$, then the singularity of $L_Q^*(s)$ at $s=0$ is a pole of order $j+1 \ge 1$ because the remaining terms in (19) are nonzero at $s=0$.

• 4. If $i=0$, then $L^*(s)$ has a singularity at $s=-1$ generated by $\Gamma (s)$. It is a simple pole because the remaining terms in (18) and (19) are nonzero at $s=-1$. On the other hand, if $i\ge 1$, then the simple pole at $s=-1$ generated by $\Gamma (s)$ is cancelled by the zero of order $i\ge 1$ in $\zeta (s-1)^i$.

• 5. If $k=0$, then $L^*(s)$ has a singularity at $s=-2n$ for each $n\ge 1$, generated by $\Gamma (s)$. It is a simple pole because the remaining terms in (18) and (19) are nonzero at $s=-2n$. On the other hand, if $k\ge 1$, then the singularity at $s=-2n$ is cancelled by the zero of order $k\ge 1$ in $\zeta (s)^k$.

• 6. For each $n\ge 1$, the simple pole at $s = -(2n+1)$ generated by $\Gamma (s)$ is cancelled by the zero of order $j+1\ge 1$ in $\zeta (s+1)^{j+1}$.

4.3 Residue Analysis

Proposition 7

For all $i\ge 1$ and $j\ge 0$ and $k\ge 0$, there is a computable polynomial $a(t)=a_0+\cdots + a_{i-1}t^{i-1}$ such that

$$\begin{aligned} {{\text {Res}}}\big (L^*(s)t^{-s}\big )_{s=2} = \frac{a(\log t)}{t^2}. \end{aligned}$$

For $L_P^*(s)$ and $L_Q^*(s)$ respectively, the values of $a_{i-1}$ are

$$\begin{aligned} \frac{(-1)^{i-1}\zeta (3)^{j+1}\pi ^{2k}}{6^{k}(i-1)!} \qquad \text {and} \qquad \frac{(3) (-1)^{i-1}\zeta (3)^{j+1}\pi ^{2k}}{(4)(6^{k})(i-1)!}. \end{aligned}$$

(20)

We use $a_{i-1}$ very often in the following discussion, so we define $A:= a_{i-1}$ (so that the dependence on the values of i and j and k is implicit; we also treat the relationship to P or Q as implicit).

Proof

We first note that ${{\text {Res}}}\big (\zeta (s+1)^i t^{-s}\big )_{s=0}$ is a polynomial in $\log {t}$ of degree $i-1$, with leading coefficient $\frac{(-1)^{i-1}}{(i-1)!}$. So we have

$$\begin{aligned} {{\text {Res}}}\big (\zeta (s+1)^i t^{-s}\big )_{s=0} = \frac{(-1)^{i-1}}{(i-1)!}(\log {t})^{i-1} + o((\log {t})^{i-1}). \end{aligned}$$

At $s=0$, we note that $\zeta (s+3)^{j+1}$, $\zeta (s+2)^{k}$, and $\Gamma (s+2)$ are all smooth, and also that $\zeta (2) = \pi ^{2}\!/6$ and $\Gamma (2) = 1$. It follows that

$$\begin{aligned} {{\text {Res}}}\big ( \zeta (s+1)^i \zeta (s+3)^{j+1} \zeta (s+2)^{k} \Gamma (s+2) t^{-s}\big )_{s=0} \\ = \frac{(-1)^{i-1}\zeta (3)^{j+1}\pi ^{2k}}{6^{k}(i-1)!}(\log {t})^{i-1} + o((\log {t})^{i-1}). \end{aligned}$$

Shifting s by 2, the LHS becomes ${{\text {Res}}}\big ( \zeta (s-1)^i \zeta (s+1)^{j+1} \zeta (s)^{k} \Gamma (s) t^{-(s-2)}\big )_{s=2} = t^{2}{{\text {Res}}}\big ( L_P^*(s)t^{-s}\big )_{s=2}$ so we obtain

$$\begin{aligned} {{\text {Res}}}\big ( L_P^*(s)t^{-s}\big )_{s=2} = \frac{1}{t^{2}}\bigg (\frac{(-1)^{i-1}\zeta (3)^{j+1}\pi ^{2k}}{6^{k}(i-1)!}(\log {t})^{i-1} + o((\log {t})^{i-1})\bigg ). \end{aligned}$$

At $s=2$, we also note that $1 - 2^{-s} = 3/4$, so we obtain

$$\begin{aligned} {\text {Res}}\big ( L_Q^*(s)t^{-s}\big )_{s=2} = \frac{1}{t^{2}}\bigg (\frac{(3)(-1)^{i-1}\zeta (3)^{j+1}\pi ^{2k}}{(4)(6^{k})(i-1)!}(\log {t})^{i-1} + o((\log {t})^{i-1})\bigg ). \end{aligned}$$

$\square$

Proposition 8

For all $i\ge 0$ and $j\ge 0$ and $k\ge 1$, there is a computable polynomial $b(t)=b_0+\cdots + b_{k-1}t^{k-1}$ such that

$$\begin{aligned} {{\text {Res}}}\big (L^*(s)t^{-s}\big )_{s=1} = \frac{b(\log t)}{t}. \end{aligned}$$

For $L_P^*(s)$ and $L_Q^*(s)$ respectively, the values of $b_{k-1}$ are

$$\begin{aligned} \frac{(-1)^{i+k-1}\pi ^{2(j+1)}}{6^{j+1}2^{i}(k-1)!} \qquad \text {and} \qquad \frac{(-1)^{i+k-1}\pi ^{2(j+1)}}{6^{j+1}2^{i+1}(k-1)!}. \end{aligned}$$

(21)

We define $B:= b_{k-1}$ (the dependence on i, j, k and on P or Q is implicit).

Proof

Using exactly the same observation as from the previous proposition, we first note that ${{\text {Res}}}\big (\zeta (s+1)^k t^{-s}\big )_{s=0}$ is a polynomial in $\log {t}$ of degree $k-1$, with leading coefficient $\frac{(-1)^{k-1}}{(k-1)!}$. So we have

$$\begin{aligned} {{\text {Res}}}\big ( \zeta (s+1)^{k} t^{-s}\big )_{s=0} = \frac{(-1)^{k-1}}{(k-1)!}(\log {t})^{k-1} + o((\log {t})^{k-1}). \end{aligned}$$

At $s=0$, we note that $\zeta (s)^{i}$, $\zeta (s+2)^{j+1}$, and $\Gamma (s+1)$ are all smooth, and also that $\zeta (0) = -1/2$ and $\zeta (2) = \pi ^{2}\!/6$ and $\Gamma (1) = 1$. It follows that

$$\begin{aligned}&{{\text {Res}}}\big ( \zeta (s)^i \zeta (s+2)^{j+1} \zeta (s+1)^{k} \Gamma (s+1) t^{-s}\big )_{s=0} \\&\quad = \frac{(-1)^{i+k-1}\pi ^{2(j+1)}}{6^{j+1}2^{i}(k-1)!}(\log {t})^{k-1} + o((\log {t})^{k-1}). \end{aligned}$$

Shifting s by 1, the LHS becomes ${{\text {Res}}}\big ( \zeta (s-1)^i \zeta (s+1)^{j+1} \zeta (s)^{k} \Gamma (s) t^{-(s-1)}\big )_{s=1} = t{{\text {Res}}}\big ( L_P^*(s)t^{-s}\big )_{s=1}$ so we obtain

$$\begin{aligned} {{\text {Res}}}\big ( L_P^*(s)t^{-s}\big )_{s=1} = \frac{1}{t}\bigg (\frac{(-1)^{i+k-1}\pi ^{2(j+1)}}{6^{j+1}2^{i}(k-1)!}(\log {t})^{k-1} + o((\log {t})^{k-1})\bigg ). \end{aligned}$$

At $s=1$, we also note that $1 - 2^{-s} = 1/2$, so we obtain

$$\begin{aligned} {{\text {Res}}}\big ( L_Q^*(s)t^{-s}\big )_{s=1} = \frac{1}{t}\bigg (\frac{(-1)^{i+k-1}\pi ^{2(j+1)}}{6^{j+1}2^{i+1}(k-1)!}(\log {t})^{k-1} + o((\log {t})^{k-1})\bigg ). \end{aligned}$$

$\square$

Proposition 9

For all nonnegative i, j, k, there is a computable polynomial $c(t)=c_0+\cdots + c_{j+1}t^{j+1}$ such that

$$\begin{aligned} {{\text {Res}}}\big (L_P^*(s)t^{-s}\big )_{s=0} = c(\log t) \end{aligned}$$

and the value of $c_{j+1}$ is

$$\begin{aligned} \frac{(-1)^{i+j+k+1}}{2^{k}(j+1)!\!\ 12^{i}}. \end{aligned}$$

(22)

We define $C:= c_{j+1}$ (the dependence on i, j, k and on P is implicit).

Proof

We first note that ${{\text {Res}}}\big (\zeta (s+1)^{j+1}\Gamma (s)t^{-s}\big )_{s=0}$ is a polynomial in $\log {t}$ of degree $j+1$, with leading coefficient $\frac{(-1)^{j+1}}{(j+1)!}$. So we have

$$\begin{aligned} {{\text {Res}}}\big ( \zeta (s+1)^{j+1}\Gamma (s) t^{-s}\big )_{s=0} = \frac{(-1)^{j+1}}{(j+1)!}(\log {t})^{j+1} + o((\log {t})^{j}). \end{aligned}$$

At $s=0$, we note that $\zeta (s-1)^{i}$ and $\zeta (s)^{k}$, are both smooth, and also that $\zeta (-1) = -1/12$ and $\zeta (0) = -1/2$. It follows that

$$\begin{aligned}&{{\text {Res}}}\big ( L_P^*(s)t^{-s}\big )_{s=0} = {{\text {Res}}}\big ( \zeta (s-1)^i \zeta (s+1)^{j+1} \zeta (s)^{k} \Gamma (s) t^{-s}\big )_{s=0} \\&\quad = \frac{(-1)^{i+j+k+1}}{2^{k}(j+1)!\!\ 12^{i}}(\log {t})^{j+1} + o((\log {t})^{j}). \end{aligned}$$

$\square$

We define $D:= d_{j}$ (the dependence on i, j, k and on Q is implicit).

Proposition 10

For all nonnegative i, j, k, there is a computable polynomial $d(t)=d_0+\cdots + d_{j}t^{j}$ such that

$$\begin{aligned} {{\text {Res}}}\big (L_Q^*(s)t^{-s}\big )_{s=0} = d(\log t) \end{aligned}$$

and the value of $d_{j}$ is

$$\begin{aligned} \ln (2)\frac{(-1)^{i+j+k}}{2^{k}j!\!\ 12^{i}}. \end{aligned}$$

(23)

Proof

We first note that ${{\text {Res}}}\big ((1-2^{-s})\zeta (s+1)^{j+1}\Gamma (s)t^{-s}\big )_{s=0}$ is a polynomial in $\log {t}$ of degree j, with leading coefficient $\ln (2)\frac{(-1)^{j}}{j!}$. So we have

$$\begin{aligned} {{\text {Res}}}\big ( (1-2^{-s})\zeta (s+1)^{j+1} \Gamma (s)t^{-s}\big )_{s=0}\\ = \ln (2)\frac{(-1)^{j}}{j!}(\log {t})^{j} + o((\log {t})^{j-1}). \end{aligned}$$

At $s=0$, we note that $\zeta (s-1)^{i}$ and $\zeta (s)^{k}$, are both smooth, and also that $\zeta (-1) = -1/12$ and $\zeta (0) = -1/2$. It follows that

$$\begin{aligned} {{\text {Res}}}\big ( L_Q^*(s)t^{-s}\big )_{s=0}&= {{\text {Res}}}\big ( (1-2^{-s})\zeta (s-1)^i \zeta (s+1)^{j+1} \zeta (s)^{k} \Gamma (s)t^{-s}\big )_{s=0}\\&= \ln (2)\frac{(-1)^{i+j+k}}{2^{k}j!\!\ 12^{i}}(\log {t})^{j} + o((\log {t})^{j-1}). \end{aligned}$$

$\square$

Proposition 11

Fix an admissible triple (i, j, k). Then the following hold:

• If $i=0$, then ${{\text {Res}}}\big (L^*(s)t^{-s}\big )_{s=-1}$ is a computable linear monomial in t (that depends on whether we are analyzing ${\mathcal {P}}$ or ${\mathcal {Q}}$).

• Let $n \ge 1$. If $k=0$, then ${{\text {Res}}}\big (L^*(s)t^{-s}\big )_{s=-2n}$ is a computable degree 2n monomial in t (that depends on whether we are analyzing ${\mathcal {P}}$ or ${\mathcal {Q}}$).

When necessary, we will add a subscript in the polynomials a(t) and b(t) to indicate which class we are considering, that is, we will write $a_P (z)$, $a_Q (z)$, $b_P (z)$ and $b_Q (z)$. Only in four exceptional cases we will be able to find the asymptotic growth of the coefficients of P(z) namely when the admissible triple is (1, 0, 0), (0, 1, 0), (0, 0, 1), and (1, 0, 1), and similarly, only in five exceptional cases we will be able to find the asymptotic growth of the coefficients of Q(z), namely when the admissible triple is one of the previous four, and, in addition, when the admissible triple is (0, 2, 0). For all these cases, we will need all the coefficients of the corresponding polynomials, and so Tables 4 and 5 show the polynomials in Propositions 7, 8, 9 and 10.

Table 4 Polynomials in Propositions 7, 8 and 9 associated to the first admissible triples for the class ${\mathcal {P}}$

Table 5 Polynomials in Proposition 7, 8 and 10 associated to the first admissible triples for the class ${\mathcal {Q}}$

We briefly explain the usefulness of the Mellin transform, following the notation from [44, Ch. 9]. Consider a function f(x), with Mellin transform $f^{*}(s)$ that is a meromorphic function. The asymptotic properties of f(x) stem from its analytic properties. In our case, our meromorphic function is $f^*(s) = L^*(s)$. We have provided a detailed description of the set of singularities of $L^*(s)$, and we utilize this well-known methodology. Suppose that a function f(x) admits a Mellin transform $f^*(s)$ with fundamental strip $\langle \alpha , \beta \rangle$. Moreover, suppose that $f^*(s)$ admits a meromorphic extension to the whole complex plane. If f has the property that, for every $M \ge \beta$, the set of poles ${\mathcal {K}}_M$ in $\langle \alpha , M \rangle$ of $f^*(s)$ is finite, it follows that, as $x \rightarrow \infty$,

$$\begin{aligned} f(x) = -\sum _{\lambda \in {\mathcal {K}}_M}{{\text {Res}}}\big ( f^*(s)x^{-s} \big )_{s=\lambda } +O(x^{-M}). \end{aligned}$$

Similarly, if for every $N \le \alpha$, the set of poles $\mathcal {K}_N$ in $\langle N, \beta \rangle$ of the Mellin transform $f^*(s)$ is finite, then, as $x \rightarrow 0$,

$$\begin{aligned} f(x) = -\sum _{\lambda \in \mathcal {K}_N}{{\text {Res}}}\big ( f^*(s)x^{-s} \big )_{s=\lambda } +O(x^{N}). \end{aligned}$$

The above results follow from Cauchy’s residue theorem, when integrating (clockwise) along rectangles with bi-infinite vertical sides that cross the real line at $c \in (\alpha , \beta )$ and at M (or at N). These infinite rectangles are approximated by finite rectangles with horizontal sides, as illustrated in general in Fig. 9a and in particular for the admissible triple (0, 1, 0) in Fig. 9b (see Theorem 15). Then the following result follows:

Fig. 9

a The fundamental strip of $f^*(s)$ (shaded gray) and the integration contour. b The case of $L^*(s)$ for the admissible triple (0, 1, 0)

Proposition 12

Let g(z) be equal to either c(z) or d(z) depending on whether we are analyzing ${\mathcal {P}}$ or ${\mathcal {Q}}$, respectively, and also let h(z) be the series formed by the sum of the residues at $s=-1$ and at $s=-2n$ with $n\ge 1$ (note that $h(z) = 0$ if $i>0$ and $k>0$, see 4 and 5 in Prop. 6). As $t\rightarrow 0$ the following hold:

• If $i\ge 1$, then $L(t) \sim \frac{a(\log t)}{t^2} + \frac{b(\log t)}{t} + g(\log t) + h(t)$.

• If $i=0$ and $k\ge 1$, then $L(t) \sim \frac{b(\log t)}{t} + g(\log t)+ h(t)$.

• If $i=k=0$, then $L(t) \sim g(\log t) + h(t)$.

Henceforth we will systematically divide our analysis according to the following three types of admissible triples: $(i\ge 1, j, k)$, $(0,j,k\ge 1)$ and $(0,j\ge 1, 0)$.

4.4 Saddle Point Equations

Let F(z) denote either P(z) or Q(z). Now using $t=-\log z$ as $z \rightarrow 1$ yields

$$\begin{aligned}&F(z) \sim \exp \Biggl ( \frac{a\big (\log (-\log z)\big )}{(-\log z)^2} + \frac{b\big (\log (-\log z)\big )}{-\log z} \nonumber \\&\quad + g\big (\log (-\log z) \big ) + h(-\log z)\big ) \Biggr ) . \end{aligned}$$

(24)

Let $f(z):=\log F(z)-n\log (z)$. The saddle is located at radius “r” with $rf'(z) = r\frac{F'(r)}{F(r)}=n$. We have the following elementary result that gives a general form:

Proposition 13

As $z\rightarrow 1$ we have

$$\begin{aligned} z\frac{F'(z)}{F(z)}&\sim \frac{1}{\log ^3(1/z)} \cdot \left( 2a\big ( \log \log (1/z)\big ) - a'\big ( \log \log (1/z)\big ) \right) \end{aligned}$$

(25)

$$\begin{aligned}&\quad + \frac{1}{\log ^2(1/z)} \cdot \left( b\big ( \log \log (1/z)\big ) - b'\big ( \log \log (1/z)\big ) \right) \nonumber \\&\quad - \frac{1}{\log (1/z)} \cdot g'\big ( \log \log (1/z)\big ) \nonumber \\&\quad -h'\big ( \log (1/z)\big ). \end{aligned}$$

(26)

Proof

From Eq. (24), it is straightforward to calculate the asymptotic growth of $F^{\prime }(z)$, and the proposition follows immediately. $\square$

In general, all the terms numbered as (25)–(26) need to be taken into account in order to determine the asymptotic growth of the coefficients of F(z). We can neglect the contribution of h(z). Consequently, as we have already mentioned, only in a very few cases we can explicitly solve the saddle point equation

$$\begin{aligned} r\frac{F'(r)}{F(r)}=n \end{aligned}$$

and thus it is only in these cases that an explicit expression for the asymptotic growth of the coefficients of F(z) can be obtained. Let us precisely identify the cases we can resolve:

Corollary 3

We have the following:

• If the admissible triple is either (1, 0, 0), (1, 0, 1), (0, 0, 1), or (0, 1, 0), then $r\frac{P'(r)}{P(r)}=n$ becomes a polynomial in $-\log r$ of degree at most 3 and thus it can be solved.

• If the admissible triple is either (1, 0, 0), (1, 0, 1), (0, 0, 1), (0, 1, 0), or (0, 2, 0), then $r\frac{Q'(r)}{Q(r)}=n$ becomes a polynomial in $-\log r$ of degree at most 3 and thus it can be solved.

Proof

All follow from Propositions 7, 8, 9, 10 and 11. $\square$

Nevertheless, as we will see, it is possible to obtain the asymptotic growth of the logarithm of the coefficients for every admissible triple. The next section contains the case studies where we solve the saddle point equation and deduce the asymptotic growth of the coefficients for all the cases in Corollary 3. Then in section 6 we present the general result that gives the asymptotic growth of the logarithm of the coefficients for every admissible triple.

5 Case Studies: First-Order Asymptotic Approximation

In this section we deduce the asymptotic growth of the coefficients in all the cases in Corollary 3 that are not known (Table 6 shows the current status of this estimates in OEIS).

Table 6 Status in OEIS of the asymptotic behavior of the coefficient for the cases in Corollary 3

In the cases below and in the next section we need to apply the saddle point method. Such usage of the saddle point method is justified, because all the generating functions that we consider in this work are Hayman admissible, also referred to as H-admissible. We follow [1, section VIII.5] for context, and we check the three conditions listed there.

Proposition 14

For every admissible triple, both P(z) and Q(z) are H-admissible.

Proof

The key is to analyze the form of the ratio $R_{P}(z) \triangleq P^{\prime }(z)/P(z)$. To obtain it we differentiate P(z) term-by-term using the product rule and get the $(i+j+k)$-fold sum

$$\begin{aligned} R_{P}(z) = \sum {(n_1\ldots n_i)^{2}(e_{1}\ldots e_{k}) z^{n_1\ldots n_{i}d_{1}\ldots d_{j}e_{1}\ldots e_{k}-1}\over 1-z^{n_1\ldots n_{i}d_{1}\ldots d_{j}e_{1}\ldots e_{k}}}. \end{aligned}$$

Similarly, if we define $R_{Q}(z) \triangleq Q^{\prime }(z)/Q(z)$, it follows that

$$\begin{aligned} R_{Q}(z) = \sum {(n_1\ldots n_i)^{2}(e_{1}\ldots e_{k}) z^{n_1\ldots n_{i}d_{1}\ldots d_{j}e_{1}\ldots e_{k}-1}\over 1+z^{n_1\ldots n_{i}d_{1}\ldots d_{j}e_{1}\ldots e_{k}}}. \end{aligned}$$

We readly note that $\lim \limits _{r\rightarrow 1}r\frac{P'(r)}{P(r)} = \lim \limits _{r\rightarrow 1} rR_{P}(r) = +\infty$, and also

$$\begin{aligned} \lim _{r\rightarrow 1}\left( r \frac{P'(r)}{P(r)} + r^2\frac{P''(r)}{P(r)} - r^2 \left( \frac{P'(r)}{P(r)}\right) ^2 \right) =\lim _{r\rightarrow 1} \big ( rR(r) + r^2R'(r)\big ) = +\infty , \end{aligned}$$

so the capture condition holds for P (and for Q as well). For the locality and decay condition, we consider the Taylor series expansion

$$\begin{aligned} \log P(re^{i\theta }) = \log P(r) + \sum \limits _{k=1}^\infty \alpha _k(r)\frac{(i\theta )^k}{k!} \end{aligned}$$

(27)

and observe that the second and third coefficients are $\alpha _2(r) = rR(r) + r^2R'(r)$ and $\alpha _3(r)= rR(r)+3r^2R'(r) + r^3R''(r)$. By saddle-point dimensioning heuristic we let $\theta _0(r) \triangleq \big (rR(r)\big )^{-5/12}$. It follows that $\alpha _2(r)\theta _0(r)^2 \rightarrow \infty$ and $\alpha _3(r)\theta _0(r)^3 \rightarrow 0$ as $r\rightarrow 1$, and also together with (27) we have

$$\begin{aligned} \frac{P(re^{i\theta }) \sqrt{rR(r)+r^2R'(r)}}{P(r)} \rightarrow 0 \qquad \text {as} \ r\rightarrow 1 \end{aligned}$$

uniformly for $\theta$ in the range $\theta _0(r) \le |\theta |< \pi$. (Similarly, we check the same for Q.) $\square$

For Theorem 15, we also recall that W(z) denotes the Lambert W function. We use the following property of W(z):

Remark 1

The solution to $x = be^{cx}$ is $x = - \frac{1}{c}{\text {W}}(-bc)$, and it is also the solution to $\log x = \log b + cx$.

Theorem 15

If the admissible triple is (0, 1, 0), then

Proof

From Table 4, we have $c(z) =\frac{\pi ^2}{12}-\frac{\gamma ^2}{2} - 2\gamma _1 - \gamma z + \frac{1}{2}z^2$. Then the saddle point equation becomes $-\log (\log (1/z))/\log (1/z) + \gamma /\log (1/z) = n$, which is equivalent to $\log u = \log e^\gamma -nu$ with $u=\log (1/z)$. Thus, with Remark 1, we obtain the saddle point $r = \exp \left( -{\text {W}}(e^\gamma n)/n\right)$ and with it we get

$$\begin{aligned}&\frac{1}{2\pi }e^{\log P(r) - n\log r} \sim \frac{1}{2\pi } \exp \left( \frac{\log ^{2}( {\text {W}}(e^\gamma n)/n )}{2}\right) ( {\text {W}}(e^\gamma n)/n )^{-\gamma }\nonumber \\&\cdot e^{\pi ^{2}\!/12 - \gamma ^{2}\!/2 - 2\gamma _{1}}\exp \big ( {\text {W}}(e^\gamma n) \big ) \end{aligned}$$

and

$$\begin{aligned} \int _{-\pi }^\pi \exp \left( \frac{f''(r)}{2!}(re^{i\theta } - r)^2 + \ldots \right) d\theta&\sim \frac{{\text {W}}(e^\gamma n)}{n}\sqrt{\frac{2\pi }{\log \big ({\text {W}} (e^\gamma n)/n)\big )}}. \end{aligned}$$

Putting together the last two estimates above, since ${\text {W}}(x) = \log x -\log \log x + o(x)$, we get, after simplifications, the desired result. $\square$

Theorem 16

If the admissible triple is (0, 1, 0), then

$$\begin{aligned} [z^n]Q(z) \sim \frac{2^{\gamma -(\log 2)/2+1/2}}{ \sqrt{\pi }(\log 2)^{\log 2-1/2}}\cdot n^{\log 2-1}. \end{aligned}$$

Proof

In this case, from Table 5 we get $d(z) = \gamma \log 2 - \frac{\log ^22}{2}-(\log 2)z$. Then the saddle point equation $(\log 2)/\log (1/z) = n$ yields the asymptotic saddle point $r = \exp \left( -(\log 2)/n\right)$ and with it we get

$$\begin{aligned} \frac{1}{2\pi }e^{\log Q(r) - n\log r} \sim \frac{e^{\gamma \log 2 - \frac{\log ^22}{2}}}{2\pi (\log 2)^{\log 2}}\cdot n^{\log 2} \cdot 2 \end{aligned}$$

and

$$\begin{aligned} \int _{-\pi }^\pi \exp \left( \frac{f''(r)}{2!}(re^{i\theta } - r)^2 + \ldots \right) d\theta&\sim \frac{\sqrt{2\pi \log 2}}{n} \end{aligned}$$

Putting together the last two estimates above and simplifying yields the desired result. $\square$

Theorem 17

If the admissible triple is (0, 2, 0), then

$$\begin{aligned} [z^n]Q(z)&\sim \frac{e^{d_0+d_1\log \theta (n)+d_2\log ^2\theta (n)-d_1}}{2\sqrt{\pi } \sqrt{d_2\log \Big (\frac{2d_2}{n}\log \big ( \frac{ne^{-d_1/(2d_2)}}{2d_2} \big )\Big )} } \biggl (\frac{2d_2}{n}\log \Big ( \frac{ne^{-d_1/(2d_2)}}{2d_2} \Big )\biggr )^{1-2d_2} \end{aligned}$$

where $\theta (n) = \frac{2d_2}{n}{\text {W}}\big ( \frac{ne^{-d_1/(2d_2)}}{2d_2} \big )$.

Proof

The saddle point equation $-2d_2\log \log (1/z)/\log (1/z) - d_1/\log (1/z) = n$ is equivalent to $\log u = -\frac{d_1}{2d_2}-\frac{n}{2d_2} u$ with $u=\log (1/z)$, thus we get the asymptotic saddle point $r = \exp \big (-\frac{2d_2}{n}{\text {W}}\big ( e^{-d_1/(2d_2)}\cdot \frac{n}{2d_2} \big ) \big )$ and with it, letting $s = -\log r$, we get

$$\begin{aligned} \frac{1}{2\pi }e^{\log Q(r) - n\log r} \sim \frac{e^{d_0+d_1\log \theta (n)+d_2\log ^2 \theta (n)}}{2\pi } \cdot e^{n\theta (n)} \end{aligned}$$

and

$$\begin{aligned} \int _{-\pi }^\pi \exp \left( \frac{f''(r)}{2!}(re^{i\theta } - r)^2 + \ldots \right) d\theta&\sim \sqrt{\frac{\pi }{d_2\log \theta (n)}} \cdot \theta (n) \end{aligned}$$

Putting together the last two estimates above and simplifying yields the desired result. $\square$

6 First-Order Asymptotic Approximation of Logarithmic Growth

Despite the fact that the saddle point equation above can be solved explicitly only in a few cases, to determine the asymptotic growth of the logarithm of the coefficients, the following slower asymptotic saddle points suffice. (Again we use the notation F(z) to represent either P(z) or Q(z).)

Proposition 18

The saddle point equation $rf'(r)=r F^{\prime }(r) / F(r) - n = 0$ yields the following weak asymptotic saddle points $r = \exp (-\exp (\alpha (n)))$ along the positive real axis:

$$\begin{aligned} \alpha (n) = {\left\{ \begin{array}{ll} -\log \big ( \frac{n}{2A} \big )^{1/3} & \text {if} i=1\\ - \frac{i-1}{3} {\text {W}}\big ( - \frac{3}{i-1} \big (\frac{n}{2A }\big )^{1/(i-1)} \big ) & \text {if} \ i> 1\\ -\log \big ( \frac{n}{B } \big )^{1/2} & \text {if} \ i=0\ \text {and} \ k=1\\ - \frac{k-1}{2} {\text {W}}\big ( - \frac{2}{k-1} \big (\frac{n}{B}\big )^{1/(k-1)} \big ) & \text {if} \ i=0\ \text {and} \ k> 1\\ -j\!\ {\text {W}}\big ( - \frac{1}{j} \big (\frac{n}{-(j+1)C }\big )^{1/j} \big ) & \text {if} \ i=0\ \text {and} \ k=0\ \text {and} \ j\ge 1\\ & \text {and} \ F(z)=P(z) \\ \log ( {-D/n} ) & \text {if} \ i=0\ \text {and} \ k=0\ \text {and} \ j=1\\ & \text {and} \ F(z)=Q(z) \\ -(j-1) {\text {W}}\big ( - \frac{1}{j-1} \big (\frac{n}{-jD}\big )^{1/(j-1)} \big ) & \text {if} \ i=0\ \text {and} \ k=0\ \text {and} \ j> 1\\ & \text {and} \ F(z)=Q(z). \\ \end{array}\right. } \end{aligned}$$

Proof

If $i \ge 1$, then the saddle point location is the same in the P(z) and Q(z) cases.

$$\begin{aligned} P(z) \sim \exp \left( \frac{A \log ^{i-1} (-\log z)}{(-\log z)^2} \big (1+o(1)\big ) \right) . \end{aligned}$$

(28)

The saddle is located at radius “r” with $r\frac{P'(r)}{P(r)}=n$, so using the approximation in (28) we get

$$\begin{aligned} \frac{P'(r)}{P(r)} \sim \frac{1}{r} \left( \frac{2A \log ^{i-1}(-\log r)}{(-\log r)^3} - \frac{(i-1)A \log ^{i-2}(-\log r)}{(-\log r)^3} \right) . \end{aligned}$$

(29)

If $i=1$, this simplifies to $2A/(-\log r)^3 = n$, so the location of the saddle point r is:

$$\begin{aligned} r = \exp \bigg ( - \bigg ( \frac{2A}{n} \bigg )^{1/3}\bigg ). \end{aligned}$$

If $i>1$, because we only want a first-order solution of (29), we want to solve

$$\begin{aligned} \frac{2A \log ^{i-1}(-\log r)}{(-\log r)^3} = n. \end{aligned}$$

Taking a power of $1/(i-1)$ throughout yields

$$\begin{aligned} (2A )^{1/(i-1)}\log (-\log r) = n^{1/(i-1)}(-\log r)^{3/(i-1)}. \end{aligned}$$

Taking logarithms and solving for $\log \log (-\log r)$ yields:

$$\begin{aligned} \log \log (-\log r) = \log \bigg (\frac{n}{2A }\bigg )^{1/(i-1)} + \frac{3}{i-1} \log (-\log r). \end{aligned}$$

We know that $\log {x} = \log {b} + cx$ has solution $x = -(1/c){\text {W}}(-bc)$. Using $x = \log (-\log {r})$ and $b = \big (\frac{n}{2A }\big )^{1/(i-1)}$ and $c = 3/(i-1)$, it follows that

$$\begin{aligned} \log (-\log {r}) = - \frac{i-1}{3} {\text {W}}\left( - \frac{3}{i-1} \left( \frac{n}{2A }\right) ^{1/(i-1)} \right) . \end{aligned}$$

and it follows immediately that

$$\begin{aligned} r = \exp \bigg ( -\exp \bigg ( - \frac{i-1}{3} {\text {W}}\bigg ( - \frac{3}{i-1} \bigg (\frac{n}{2A }\bigg )^{1/(i-1)} \bigg ) \bigg ) \bigg ). \end{aligned}$$

If $i=0$ and $k \ge 1$, the saddle point location is the same in the P(z) and Q(z) cases. We have

$$\begin{aligned} P(z) \sim \exp \left( \frac{B \log ^{k-1} (-\log z)}{-\log z} \big (1+o(1)\big ) \right) . \end{aligned}$$

(30)

The saddle is located at radius “r” with $r\frac{P'(r)}{P(r)}=n$, so using the approximation in (30) we get

$$\begin{aligned} \frac{P'(r)}{P(r)} \sim \frac{1}{r} \left( \frac{B \log ^{k-1}(-\log r)}{(-\log r)^2} - \frac{(k-1)B \log ^{k-2}(-\log r)}{(-\log r)^2} \right) . \end{aligned}$$

(31)

If $k=1$, this simplifies to $B /(-\log r)^2 = n$, so the location of the saddle point r is:

$$\begin{aligned} r = \exp \bigg ( - \bigg ( \frac{B }{n} \bigg )^{1/2}\bigg ). \end{aligned}$$

If $k>1$, because we only want a first-order solution of (31), we want to solve

$$\begin{aligned} \frac{B \log ^{k-1}(-\log r)}{(-\log r)^2} = n. \end{aligned}$$

Taking a power of $1/(k-1)$ throughout yields

$$\begin{aligned} (B )^{1/(k-1)}\log (-\log r) = n^{1/(k-1)}(-\log r)^{2/(k-1)}. \end{aligned}$$

Taking logarithms and solving for $\log \log (-\log r)$ yields:

$$\begin{aligned} \log \log (-\log r) = \log \bigg (\frac{n}{B}\bigg )^{1/(k-1)} + \frac{2}{k-1}\log (-\log r). \end{aligned}$$

We know that $\log {x} = \log {b} + cx$ has solution $x = -(1/c){\text {W}}(-bc)$. Using $x = \log (-\log {r})$ and $b = \big (\frac{n}{B}\big )^{1/(k-1)}$ and $c = 2/(k-1)$, it follows that

$$\begin{aligned} \log (-\log {r}) = - \left( \frac{k-1}{2}\right) {\text {W}}\left( - \frac{2}{k-1} \left( \frac{n}{B}\right) ^{1/(k-1)} \right) \end{aligned}$$

and it follows immediately that

$$\begin{aligned} r = \exp \bigg ( -\exp \bigg ( - \bigg (\frac{k-1}{2}\bigg ) {\text {W}}\bigg ( - \frac{2}{k-1} \bigg (\frac{n}{B}\bigg )^{1/(k-1)} \bigg ) \bigg ) \bigg ). \end{aligned}$$

If $i=0$ and $j \ge 1$ and $k=0$, then

$$\begin{aligned} P(z)&\sim \exp \left( C \log ^{j+1} (-\log z) \big (1+o(1)\big ) \right) ,\nonumber \\ Q(z)&\sim \exp \left( D \log ^{j} (-\log z) \big (1+o(1)\big ) \right) . \end{aligned}$$

(32)

The saddle is located at radius “r” with $r\frac{P'(r)}{P(r)}=n$, so using the approximation in (32) we get

$$\begin{aligned} \frac{P'(r)}{P(r)}&\sim \frac{1}{r} \left( - \frac{(j+1)C \log ^{j}(-\log r)}{-\log r} \right) , \end{aligned}$$

(33)

$$\begin{aligned} \frac{Q'(r)}{Q(r)}&\sim \frac{1}{r} \left( - \frac{jD \log ^{j-1}(-\log r)}{-\log r} \right) . \end{aligned}$$

(34)

In the case $j=1$, when analyzing the saddle point for Q(z), we have simply $\frac{Q'(z)}{Q(z)} \sim \frac{1}{z} \frac{D}{\log z}$, so the location of the saddle point r satisfies $\frac{D}{\log r} = n$, and thus $r = \exp (D/n)$.

If $j\ge 1$ (or if $j>1$ in the Q case), because we only want a first-order solution of (33) and (34), we want to solve

$$\begin{aligned} \frac{-(j+1)C \log ^{j}(-\log r)}{-\log r} = n \qquad \text {and} \qquad \frac{-jD \log ^{j-1}(-\log r)}{-\log r} = n. \end{aligned}$$

Taking a power of 1/j or $1/(j-1)$ (respectively) throughout yields

$$\begin{aligned} (-(j+1)C )^{1/j}\log (-\log r) = n^{1/j}(-\log r)^{1/j} \end{aligned}$$

and

$$\begin{aligned} (-jD )^{1/(j-1)}\log (-\log r) = n^{1/(j-1)}(-\log r)^{1/(j-1)}. \end{aligned}$$

Taking logarithms and solving for $\log \log (-\log r)$ yields:

$$\begin{aligned} \log \log (-\log r) = \log \bigg (\frac{n}{-(j+1)C }\bigg )^{1/j} + \frac{1}{j}\log (-\log r) \end{aligned}$$

and

$$\begin{aligned} \log \log (-\log r) = \log \bigg (\frac{n}{-jD}\bigg )^{1/(j-1)} + \frac{1}{j-1}\log (-\log r). \end{aligned}$$

We know that $\log {x} = \log {b} + cx$ has solution $x = -(1/c){\text {W}}(-bc)$. Using $x = \log (-\log {r})$ and $b = \big (\frac{n}{-(j+1)C }\big )^{1/j}$ or, respectively, $b = \big (\frac{n}{-jD}\big )^{1/(j-1)}$, and using $c = 1/j$ or, respectively, $c=1/(j-1)$, it follows that the locations of the saddle point r satisfy, respectively:

$$\begin{aligned} \log (-\log {r}) = -j\!\ {\text {W}}\left( - \frac{1}{j} \left( \frac{n}{-(j+1)C }\right) ^{1/j} \right) \end{aligned}$$

and

$$\begin{aligned} \log (-\log {r}) = -(j-1)\!\ {\text {W}}\left( - \frac{1}{j-1} \left( \frac{n}{-jD}\right) ^{1/(j-1)} \right) \end{aligned}$$

and it follows immediately that

$$\begin{aligned} r = \exp \bigg ( -\exp \bigg ( - j\!\ {\text {W}}\bigg ( - \frac{1}{j} \bigg (\frac{n}{-(j+1)C }\bigg )^{1/j} \bigg ) \bigg ) \bigg ) \end{aligned}$$

and

$$\begin{aligned} r = \exp \bigg ( -\exp \bigg ( - (j-1)\!\ {\text {W}}\bigg ( - \frac{1}{j-1} \bigg (\frac{n}{-jD}\bigg )^{1/(j-1)} \bigg ) \bigg ) \bigg ) . \end{aligned}$$

$\square$

6.1 Central Approximation

We are using $f(z) = \log F(z) - n\log {z}$, as explained immediately below Eq. (24). We have

$$\begin{aligned} [z^{n}]F(z)&\sim \frac{1}{2\pi }F(r)r^{-n} \int \limits _{-\pi }^{\pi } \exp \left( \frac{1}{2}f''(r)(re^{i\theta }-r)^2 \right) d \theta \nonumber \\&\sim \frac{1}{2\pi }\exp \Biggl ( \frac{a\big (\alpha (n)\big )}{\exp (2\alpha (n))} + \frac{b\big (\alpha (n)\big )}{\exp (\alpha (n))} + g\big (\alpha (n)\big )\nonumber \\&\quad + h\big (\exp (\alpha (n))\big ) \Biggr ) \cdot e^{n\exp (\alpha (n))}\sqrt{\frac{-2\pi }{f''(r)r^{2} }} . \end{aligned}$$

(35)

It follows from Proposition 18 that

$$\begin{aligned} n e^{\alpha (n)} \sim {\left\{ \begin{array}{ll} (2A)^{1/3}n^{2/3} & \text {if i=1} \\ n\exp \big ( - \frac{i-1}{3} {\text {W}}\big ( - \frac{3}{i-1} \big (\frac{n}{2A }\big )^{1/(i-1)} \big ) \big ) & \text {if} \ i>1\\ (Bn)^{1/2} & \text {if} \ i=0, k=1\\ n\exp \big (-\frac{k-1}{2} {\text {W}}\big ( - \frac{2}{k-1} \big (\frac{n}{B}\big )^{1/(k-1)} \big )\big ) & \text {if} \ i=0, k> 1\\ n\exp \big (-j\!\ {\text {W}}\big ( - \frac{1}{j} \big (\frac{n}{-(j+1)C }\big )^{1/j} \big )\big ) & \text {if} \ i=k=0, j\ge 1\\ & \text {and} \ F(z)=P(z) \\ -D & \text {if} \ i=k=0, j=1\\ & \text {and} \ F(z)=Q(z) \\ n\exp \big (-(j-1) {\text {W}}\big ( - \frac{1}{j-1} \big (\frac{n}{-jD }\big )^{1/(j-1)} \big )\big ) & \text {if} \ i=k=0, j> 1\\ & \text {and} \ F(z)=Q(z). \end{array}\right. }\nonumber \\ \end{aligned}$$

(36)

It also follows from Proposition 18 that

$$\begin{aligned} \log \Big (\sqrt{\frac{1}{r^{2}}}\!\ \Big ) = -\log (r) = \exp (\alpha (n)) \end{aligned}$$

so

$$\begin{aligned} \log \Big (\sqrt{\frac{1}{r^{2}}}\!\ \Big ) \sim {\left\{ \begin{array}{ll} (2A)^{1/3}n^{-1/3} & \text {if} \ i=1\\ \exp \big ( - \frac{i-1}{3} {\text {W}}\big ( - \frac{3}{i-1} \big (\frac{n}{2A }\big )^{1/(i-1)} \big ) \big ) & \text {if} \ i>1\\ B^{1/2}n^{-1/2} & \text {if} \ i=0, k=1\\ \exp \big (-\frac{k-1}{2} {\text {W}}\big ( - \frac{2}{k-1} \big (\frac{n}{B}\big )^{1/(k-1)} \big )\big ) & \text {if} \ i=0, k> 1\\ \exp \big (-j\!\ {\text {W}}\big ( - \frac{1}{j} \big (\frac{n}{-(j+1)C }\big )^{1/j} \big )\big ) & \text {if} \ i=k=0, j\ge 1\\ & \text {and} \ F(z)=P(z) \\ -D/n & \text {if} \ i=k=0, j=1\\ & \text {and} \ F(z)=Q(z) \\ \exp \big (-(j-1) {\text {W}}\big ( - \frac{1}{j-1} \big (\frac{n}{-jD }\big )^{1/(j-1)} \big )\big ) & \text {if} \ i=k=0, j> 1\\ & \text {and} \ F(z)=Q(z). \end{array}\right. }\nonumber \\ \end{aligned}$$

(37)

We also use Proposition 18 to compute

$$\begin{aligned} \frac{a\big (\alpha (n)\big )}{\exp (2\alpha (n))}&\sim {\left\{ \begin{array}{ll} (\frac{1}{2})(2A)^{1/3}n^{2/3} & \text {if} \ i=1 \\ A\big ( - \frac{i-1}{3} {\text {W}}\big ( - \frac{3}{i-1} \big (\frac{n}{2A }\big )^{1/(i-1)} \big )\big )^{i-1} & \text {if} \ i>1\\ \cdot \exp \big (2\big (\frac{i-1}{3}\big ) {\text {W}}\big ( - \frac{3}{i-1} \big (\frac{n}{2A }\big )^{1/(i-1)} \big ) \big ) \end{array}\right. } \nonumber \\ \frac{b\big (\alpha (n)\big )}{\exp (\alpha (n))}&\sim {\left\{ \begin{array}{ll} (Bn)^{1/2} & \text {if} \ i=0, k=1 \\ B\big ( - \frac{k-1}{2} {\text {W}}\big ( - \frac{2}{k-1} \big (\frac{n}{B}\big )^{1/(k-1)} \big ) \big )^{k-1} & \text {if} \ i=0, k> 1 \\ \cdot \exp \big (\frac{k-1}{2} {\text {W}}\big ( - \frac{2}{k-1} \big (\frac{n}{B}\big )^{1/(k-1)} \big )\big ) \end{array}\right. }\nonumber \\ g\big (\alpha (n)\big )&\sim {\left\{ \begin{array}{ll} C\big ( -j\!\ {\text {W}}\big ( - \frac{1}{j} \big (\frac{n}{-(j+1)C }\big )^{1/j} \big ) \big )^{j+1} & \text {if} \ i=k=0, j\ge 1 \\ & \text {and} \ F(z) = P(z) \\ D\log ( {-D/n} ) & \text {if} \ i=k=0, j= 1\\ & \text {and} \ F(z) = Q(z) \\ D\big ( -(j-1) {\text {W}}\big ( - \frac{1}{j-1} \big (\frac{n}{-jD}\big )^{1/(j-1)} \big ) \big )^{j} & \text {if} \ i=k=0, j> 1 \\ & \text {and} \ F(z) = Q(z). \end{array}\right. } \end{aligned}$$

(38)

Finally, we compute $f^{\prime \prime }$, using $f(z)=\log \big (F(z)\big )-n\log (z)$.

Proposition 19

From (24), the following hold:

• For $i > 0$,

  $$\begin{aligned} f^{\prime \prime }(r) = \left\{ \begin{array}{ll} 6Ae^{-4\alpha (n)} + \Theta (e^{-3\alpha (n)} ) & \text {if} \ i=1 \\ 6A\alpha (n)^{i - 1}e^{-4\alpha (n)} + \Theta (\alpha (n)^{i - 2}e^{-4\alpha (n)} ) & \text {if} \ i>1 \end{array} \right. . \end{aligned}$$

• For $i=0$ and $k > 0$,

  $$\begin{aligned} f^{\prime \prime }(r) = \left\{ \begin{array}{ll} -2Be^{-3\alpha (n)} + \Theta (e^{-2\alpha (n)} ) & {k=1} \\ -2B\alpha (n)^{k - 1}e^{-3\alpha (n)} + \Theta (\alpha (n)^{k-2}e^{-3\alpha (n)} ) & {k>1} \end{array} \right. . \end{aligned}$$

• For $i=0$ and $k=0$ and $j \ge 1$, in the P(z) case, we have

  $$\begin{aligned} f^{\prime \prime }(r) = -(j+1)C\alpha (n)^{j}e^{-2\alpha (n)} + \Theta (\alpha (n)^{j-1}e^{-2\alpha (n)} ). \end{aligned}$$

• For $i=0$ and $k=0$ and $j > 1$, in the Q(z) case, we have

  $$\begin{aligned} f^{\prime \prime }(r) = \left\{ \begin{array}{ll} -D\!\ e^{-2\alpha (n)} + \Theta (e^{-\alpha (n)} ) & \text {if} \ j=1 \\ -jD\alpha (n)^{j-1}e^{-2\alpha (n)} + \Theta (\alpha (n)^{j-2}e^{-2\alpha (n)} ) & \text {if} \ j>1 \end{array} \right. \end{aligned}$$

It follows that

$$\begin{aligned} \log \Big (\sqrt{\frac{1}{f^{\prime \prime }(r)}}\!\ \Big ) \sim {\left\{ \begin{array}{ll} 2\alpha (n) & \text {if} \ i\ge 1\\ \frac{3}{2}\alpha (n) & \text {if} \ i=0, k\ge 1\\ \alpha (n) & \text {if} \ i=k=0, j\ge 1, F(z)=P(z)\\ \alpha (n) & \text {if} \ i=k=0, j\ge 1, F(z)=Q(z). \end{array}\right. } \end{aligned}$$

(39)

Theorem 20

Let F(z) denote P(z) or Q(z). We have

$$\begin{aligned} \log {[z^{n}]F(z)} \sim {\left\{ \begin{array}{ll} (3/2)(-3)^{-(i-1)/3}(2A)^{1/3}(\ln {n})^{(i-1)/3}n^{2/3} & \text {if} \ i\ge 1 \\ (2)(-2)^{-(k-1)/2}B^{1/2}(\ln {n})^{(k-1)/2}n^{1/2} & \text {if} \ i=0, k\ge 1 \\ (-1)^{j+1}(C)(\ln {n})^{j+1} & \text {if} \ i=k=0, j\ge 1 \\ & \text {and} \ F(z)=P(z) \\ (-1)^{j}(D)(\ln {n})^{j} & \text {if} \ i=k=0, j\ge 1\\ & \text {and} \ F(z)=Q(z). \end{array}\right. } \end{aligned}$$

where, as defined in (20), we have

$$\begin{aligned} A = {\left\{ \begin{array}{ll}\frac{(-1)^{i-1}\zeta (3)^{j+1}\pi ^{2k}}{6^{k}(i-1)!} & \text {in the} \ F(z)=P(z)\ \text {case} \\ \frac{(3) (-1)^{i-1}\zeta (3)^{j+1}\pi ^{2k}}{(4)(6^{k})(i-1)!} & \text {in the} \ F(z)=Q(z)\ \text {case} \end{array}\right. } \end{aligned}$$

and as defined in (21), we have

$$\begin{aligned} B = {\left\{ \begin{array}{ll} \frac{(-1)^{i+k-1}\pi ^{2(j+1)}}{6^{j+1}2^{i}(k-1)!} & \text {in the} \ F(z)=P(z)\ \text {case} \\ \frac{(-1)^{i+k-1}\pi ^{2(j+1)}}{6^{j+1}2^{i+1}(k-1)!} & \text {in the} \ F(z)=Q(z)\ \text {case} \\ \end{array}\right. } \end{aligned}$$

and, finally, as in (22) and (23) respectively, we have

$$\begin{aligned} C = \frac{(-1)^{i+j+k+1}}{2^{k}(j+1)!\!\ 12^{i}}\quad \text {in the} \ F(z) = P(z)\ \text {case,} \end{aligned}$$

and

Proof

We are using the framework from Eq. (35). Assembling the contributions from (36) and (38), and noting that (37) and (39) do not contribute to the first-order asymptotics of the logarithm of the coefficients, we put these contributions together and in (35), taking the logarithm, we obtain these first order approximations:

Now we use ${\text {W}}(z) = \ln (z) - \ln \ln (z) + o(1)$ to simplify everything. The case for $i>1$ simplifies to $(3/2)(-3)^{-(i-1)/3}(2A)^{1/3}(\ln {n})^{(i-1)/3}n^{2/3}$, which agrees with the case $i=1$. The case for $i=0$, $k>1$ simplifies to $(2)(-2)^{-(k-1)/2}B^{1/2}(\ln {n})^{(k-1)/2}n^{1/2}$, which agrees with the case $i=0$, $k=1$. The case for $i=0$, $k=0$, $j\ge 1$, with $F(z)=P(z)$, simplifies to $(-1)^{j+1}(j+1)(C)(\ln {n})^{j} + (-1)^{j+1}(C)(\ln {n})^{j+1}$, which then simplifies to $(-1)^{j+1}(C)(\ln {n})^{j+1}$. The case for $i=0$, $k=0$, $j > 1$, with $F(z)=Q(z)$, simplifies to $(-1)^{j}(j)(D)(\ln {n})^{j-1} + (-1)^{j}(D)(\ln {n})^{j}$, which further simplifies to $(-1)^{j}(D)(\ln {n})^{j}$, which agrees with the case $i=0$, $k=0$, $j=1$, with $F(z)=Q(z)$. Theorem 20 follows as a result of these simplifications.$\square$