New insights into MHD squeezing flows of reacting-radiating Maxwell nanofluids via Wakif's–Buongiorno point of view

Abstract

This work presents a computational investigation of a squeezing nanofluid flow under the influence of thermal radiation, magnetohydrodynamics (MHD), and chemical process in a constrained parallel-wall geometry. In this study, the non-Newtonian behavior of a rate-type (Maxwell) nanofluid is captured by rheological expressions that serve as the foundation for the flow formulation. This kind of thinking makes it possible to simulate the intricate nanofluid behavior that incorporates the elastic and viscous responses, which are useful in a variety of situations related to nanofluid dynamics, rheology, and materials science. Additionally, the transport equations are modeled properly using Wakif's–Buongiorno nanofluid model. The equations reflecting the dynamics of the nanofluid and heat-mass transport are developed based on admissible physical assumptions, such as the negligible viscous dissipation as well as the lower magnetic Reynolds number. After that, several similarity variables are introduced in these equations to get the dimensionless formulation form. Akbari–Ganji's method is used to carry out extensive computational simulations. Our results show that the increased squeezing parameters lead to larger horizontal and vertical velocities. On the other hand, the temperature showed a reverse relationship with the increasing squeezing parameters and exhibiting a cooling impact.

1 Introduction

Squeezing flow elaborates the dynamic behavior of a fluid as it travels between two tightly aligned surfaces. Stefan's groundbreaking work [1] on using the lubrication approximation to squeeze flow was a major turning point, and this part has been used for many years. Modern engineers and researchers have been focusing more and more on studying these flows in recent times because of the numerous industrial applications of fluid flows confined between two parallel surfaces, including in polymer processing, hydrodynamical systems, solidity and injection design, food processing, foam production, accelerators, lubrication equipment, and power transmission damping devices. Taking into account the applications, a range of methods and configurations have been used to extensively analyze the squeezed flow dynamics. This has consequences for both fundamental science and real-world engineering environments.

Noor et al. [2] studied the properties of a magnetized squeezed Casson nanomaterial with a heat source and radiative flux. Their research showed that an increase in the fluid’s velocity and temperature distribution occurs when the plates move inward. A dual-stratified compressed nanofluid was examined by Farooq et al. [3] using a Maxwell rheological model set up with parallel permeable plates. The results showed that the velocity profile displays a crossflow behavior when the material parameter increases. Sobamowo et al. [4] investigated squeezed flow analysis of third-grade magnetized nanofluid configured by parallel disks susceptible to radiative flux and porous medium. Based on better estimations of the Prandtl number, the obtained results showed a decrease in temperature. This phenomena is caused by the lower diffusivity of the third-grade material. Convective-stratified characteristics of squeezed flow were analyzed by Khan et al. [5] while taking inclined rheology into account. They reported a decrease in concentration and thermal fields that were influenced by a greater stratification parameter (solutal, thermal). Famakinwa et al. [6] developed squeezed nanofluid incompressible flow taking alumna and copper oxide nanoparticles and water base fluid into consideration.

Non-Newtonian fluids are recognized by having a viscosity that varies according to the rate of stress or applied shear, unlike Newtonian fluids, which maintain a consistent viscosity. An illustrative example of a non-Newtonian fluid is the Maxwell fluid, often employed to represent the rheological behavior of complex fluids such as polymers, suspensions, and emulsions [7]. The time-dependent shear stress, as explained by this model, arises from the relaxation of the elastic component in a non-Newtonian fluid, characterized by both elastic and viscous components. Given the occurrence of non-Newtonian fluid behavior in various applications such as biological fluids and industrial processes, it has garnered significant attention from the scientific community. Several research endeavors have reported the flow features of Maxwell fluids in different scenarios, including flows with directional stress, stretching flow, and rhythmic flow, employing a blend of experimental and computational approaches. The results obtained from these studies have significantly advanced our comprehension of the fundamental physical mechanisms governing the behavior of these fluids. Additionally, they have played a key role in the creation of novel models and simulation strategies for forecasting and comprehending the characteristics of non-Newtonian fluids, such as the Maxwell fluid [8, 9] Several authors have written in-depth comments regarding the significance of non-Newtonian Maxwell fluid. This type of fluid’s potential manufacturing uses have been discussed in a number of places [10,11,12,13]. A form of fluid called Maxwell fluid is created by adding electrically conductive particles to a base fluid. Particles scattered in Maxwell fluids typically range in size from a few nanometers to a few microns and often consist of metals like Copper (Cu) or Silver (Ag). Maxwell fluids could be used in a variety of applications, including electronic cooling and heat transfer, by altering the thermal and electrical properties of the basic fluid by adding these particles. A growing body of research is being done to better understand and improve the performance of Maxwell nanofluids because of the unique characteristics they display. Many authors have studied the behavior of Maxwell fluid flow because of its significance, introducing the effect of many physical and mass transfer phenomena, as confirmed by literature work [14,15,16,17].

Squeezed fluid has become a novel sort of fluid in recent years and attracted a lot of curiosity. The squeezed fluid is generated through the compression of a base fluid containing suspended nanoparticles, resulting in reduced particle size and increased concentration. This pression operation imparts unique properties to the squeezed fluid, such as enhanced thermal conductivity and superior heat transfer capabilities [18]. One of the main advantages of compressed fluids is their ability to improve the efficiency of heat transfer systems. By elevating the nanoparticle concentration of the fluid, squeezed fluid augments thermal conductivity, enabling more performance heat transmission. That’s particularly beneficial in applications such as electronic cooling, in which achieving efficient thermal dispersion is crucial to maintaining optimum system functionality. Numerous research endeavors have delved into exploring the flow and thermal features of squeezed fluids in diverse forms and configurations [19,20,21]. Knowledge gained from such investigations plays an essential role in understanding the behavior of compressed fluid flow, helping to optimize and improve the efficiency of devices using such flow.

Examining the Maxwell nanomaterial squeezed flow by radiatively fluxed parallel stratified walls is the goal of this work. The upper plate exhibits a certain time-dependent velocity distribution as it approaches the lower plate, while the lower plate stays stationary. Thermal radiation, chemical processes, and magnetohydrodynamics (MHD) are all aspects of mathematical modeling. Equations that elaborate on the dynamics of heat, mass transport, and fluid movement are developed and converted into a dimensionless form through the use of similarity variables. Numerical simulations employ the Akbari–Ganji method (AGM) and Runge–Kutta (RK). Tables and graphs are used to examine the effects of various flow parameters on dimensionless quantities (temperature, velocity, concentration, and heat-mass transference rate).

2 Mathematical modeling

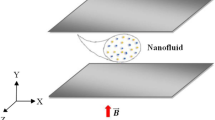
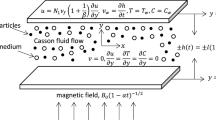
Let us define the Maxwell nanofluid that conducts electricity and contains nanoparticles that are contained by parallel plates that are layered. It is assumed that the formulated flow is two-dimensional, laminar, incompressible, and unstable. With a stretching velocity of ${U}_{w}=\frac{ax}{1-\gamma t}$, the lower plate, fixed at $y = 0$, is moving inside its plane in the positive x direction. Assuming that the lower plate $\left(y=0\right)$ is porous. The nanofluid can flow there at an injection (or suction) velocity of $\frac{-{V}_{0}}{1-\gamma t}$. With a vertical velocity of ${v}_{h}=\frac{dh\left(t\right)}{dt}$, where${v}_{h}=\frac{-\gamma }{2}\sqrt{\frac{\nu }{a\left(1-\gamma t\right)}}$. The upper plate, situated at$y = h(t)$, is traveling in the direction of the lower plate. The distance $h\left(t\right)=\sqrt{\frac{\nu \left(1-\gamma t\right)}{a}}$ is on the plates. It’s also important to remember that the lower plate has linear stretchability in addition to rigidity. Assuming a reduced magnetic Reynolds number and an applied magnetic field of  $\frac{{B}_{0}}{\sqrt{1-\gamma t}}$, magneto-hydrodynamic effects are considered. Additionally, we make use of a Cartesian coordinate system $(x, y)$, in which the stretching sheet’s $x$-axis is parallel to its normal. Figure 1 shows a schematic illustration of the flow geometry. The following is a concise, point-by-point summary of the fundamental assumptions underpinning the problem:

• A squeezing Maxwell nanofluid flow  is considered between parallel, horizontally positioned plates under a magnetic field effect.

•  Wakif's-Buongiorno approach is adopted theoretically as a realistic nanofluid model.

• The interactions between thermal radiation and thermal sources disclose the characteristics of heat transfer.

• A chemical reaction process is taken into account when evaluating the mass transfer.

Fig. 1

Physical model of the problem

The following are the governing formulations that describe the flow with heat-mass transfer:

• The continuity equation of the nanofluid

The continuity equation is also known as mass conservative law which depicts that mass can neither be created nor destroyed.

Mathematically, it can be displayed as:

$$\frac{\partial \rho }{\partial t}+\nabla .\left(\rho \mathbf{V}\right)=0$$

(1)

where the nanofluid density is represented by $\rho$, while  ${\varvec{V}}$ designates the velocity field.

Balance of mass for incompressible nanofluids reduces to:

$$\nabla .\mathbf{V}=0$$

(2)

In Cartesian coordinates:

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$$

(3)

• The equation of momentum for Maxwell nanofluid

This law comes from Newton’s second law and addresses the conservation of the total linear momentum of the given system. It is mathematically stated as follows:

$$\rho \frac{D{\varvec{V}}}{Dt}=\rho {\varvec{g}}+\nabla .\overline{\upsigma }+{\varvec{J}}\times {\varvec{B}}$$

(4)

Here, in Eq. (4), the term on the left-hand side denotes inertial forces whereas the surface forces are designated by the term $\nabla .\overline{\upsigma }$ and the second term depicts body forces per unit volume. In the above illustration, density is expressed symbolically as $\rho$, and substantial derivative is represented by $\frac{D}{Dt}$. ${\varvec{V}}$ reflects the velocity field and $\rho {\varvec{g}}$ represents the gravitational body force, it is assumed negligible in our problem, ${\varvec{J}}\times {\varvec{B}}$ is electromagnetic with ${\varvec{J}}=\sigma \left[{\varvec{E}}+\left({\varvec{V}}\times {\varvec{B}}\right)\right]$ which due to small magnetic Reynolds, ${\varvec{E}}$ is negligible, so ${\varvec{J}}=\sigma \left({\varvec{V}}\times {\varvec{B}}\right)$, ${\varvec{V}}=\left(u,v\right)$

we have:

$${\varvec{J}}=\upsigma \left({\varvec{V}}\times {\varvec{B}}\right)=\upsigma \left(u{{\varvec{e}}}_{{\varvec{x}}}+v{{\varvec{e}}}_{{\varvec{y}}}\right)\times \left(\frac{{B}_{0}}{\sqrt{1-\upgamma t}} {{\varvec{e}}}_{{\varvec{y}}}\right)=\upsigma \left(u\frac{{B}_{0}}{\sqrt{1-\upgamma t}} \right)\left({{\varvec{e}}}_{{\varvec{x}}}\times {{\varvec{e}}}_{{\varvec{y}}}\right)+\upsigma \left(v\frac{{B}_{0}}{\sqrt{1-\upgamma t}} \right)\left({{\varvec{e}}}_{{\varvec{y}}}\times {{\varvec{e}}}_{{\varvec{y}}}\right),$$

$$\left({{\varvec{e}}}_{{\varvec{y}}}\times {{\varvec{e}}}_{{\varvec{y}}}\right)=0,$$

$$\left({{\varvec{e}}}_{{\varvec{x}}}\times {{\varvec{e}}}_{{\varvec{y}}}\right)={{\varvec{e}}}_{{\varvec{z}}},$$

$${\varvec{J}}=\left(u\frac{\sigma {B}_{0}}{\sqrt{1-\gamma t}} \right){{\varvec{e}}}_{{\varvec{z}}},$$

$${\varvec{J}}\times {\varvec{B}}=\sigma \left[\left(u\frac{{B}_{0}}{\sqrt{1-\gamma t}} \right){{\varvec{e}}}_{{\varvec{z}}}\right]\times \left({B}_{0}{{\varvec{e}}}_{{\varvec{y}}}\right)=\sigma \left(u\frac{{B}_{0}}{\sqrt{1-\gamma t}} \right)\left(\frac{{B}_{0}}{\sqrt{1-\gamma t}} \right)\left({{\varvec{e}}}_{{\varvec{z}}}\times {{\varvec{e}}}_{{\varvec{y}}}\right),$$

${{\varvec{e}}}_{{\varvec{z}}}\times {{\varvec{e}}}_{{\varvec{y}}}=-{{\varvec{e}}}_{{\varvec{x}}}$.

So, we find that: ${\varvec{J}}\times {\varvec{B}}=- \frac{\sigma{B}_{0}^{2}}{1-\gamma t}{u}{\varvec{e}}_{{\varvec{x}}}$.

$\overline{\upsigma }$ denotes the Cauchy stress tensor. For the flow of an incompressible nanofluid, the Cauchy stress tensor addresses as:

$$\overline{\upsigma }=-P{\varvec{I}}+{\varvec{S}}$$

(5)

Here, ${\varvec{I}}$ denotes the identity tensor, $P$ is the pressure, and ${\varvec{S}}$ denotes the extra stress tensor. So, we find:

$$\nabla .\overline{\upsigma }=-\nabla P+\nabla .{\varvec{S}}$$

(6)

Equation (4) becomes:

$$\rho \frac{D{\varvec{V}}}{Dt}=-\nabla P+\nabla .{\varvec{S}}- \frac{\upsigma{B}_{0}^{2}}{1-\upgamma t}u{{\varvec{e}}}_{{\varvec{x}}}$$

(7)

• Maxwell nanofluid

It exhibits a non-Newtonian nature categorizes as a subclass of rate-type nanofluids. It can predict viscoelastic features and elaborate only on the relaxation time. Maxwell nanofluids are polymer solutions having a low molecular weight. The constitutive equation of Maxwell nanofluid in terms of tensor is:

$$\left(1+\lambda \frac{D}{Dt}\right){\varvec{S}}=\upmu {{\varvec{A}}}_{1}$$

(8)

Here, $\mu$ depicts the dynamic viscosity, $\frac{D}{Dt}$ designates the covariant derivative, the relaxation time is symbolized by $\lambda$, ${{\varvec{A}}}_{1}$ is the first Rivlin-Ericksen tensor and denotes the rate of deformation. First Rivlin-Ericksen is described as:

$${{\varvec{A}}}_{1}=grad\boldsymbol{ }{\varvec{V}}+{\left(grad\boldsymbol{ }{\varvec{V}}\right)}^{+}$$

(9)

Here, $\left(+\right)$ and ${\varvec{V}}$ denote, respectively, the transpose and velocity field.

In the Cartesian coordinates system, the gradient of the velocity field and the first Rivlin–Ericksen tensor are depicted as follows:

$$grad\boldsymbol{ }{\varvec{V}}=\left(\begin{array}{cc}\frac{\partial u}{\partial x}& \frac{\partial u}{\partial y}\\ \frac{\partial v}{\partial x}& \frac{\partial v}{\partial y}\end{array}\right),\quad \boldsymbol{ }{\left(grad\boldsymbol{ }{\varvec{V}}\right)}^{+}=\left(\begin{array}{cc}\frac{\partial u}{\partial x}& \frac{\partial v}{\partial x}\\ \frac{\partial u}{\partial y}& \frac{\partial v}{\partial y}\end{array}\right)$$

(10)

$${{\varvec{A}}}_{1}=\left(\begin{array}{cc}\frac{\partial u}{\partial x}& \frac{\partial u}{\partial y}\\ \frac{\partial v}{\partial x}& \frac{\partial v}{\partial y}\end{array}\right)+\left(\begin{array}{cc}\frac{\partial u}{\partial x}& \frac{\partial v}{\partial x}\\ \frac{\partial u}{\partial y}& \frac{\partial v}{\partial y}\end{array}\right)=\left(\begin{array}{cc}2\frac{\partial u}{\partial x}& \frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\\ \frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}& 2\frac{\partial v}{\partial y}\end{array}\right)$$

(11)

Covariant derivatives of a tensor ${\varvec{S}}$, a vector ${\varvec{B}},$ and a scalar $W$ are defined by:

$$\frac{D{\varvec{S}}}{Dt}=\frac{\partial {\varvec{S}}}{\partial t}+\left({\varvec{V}}.\nabla \right){\varvec{S}}$$

(12)

$$\frac{D{\varvec{B}}}{Dt}=\frac{\partial {\varvec{B}}}{\partial t}+\left({\varvec{V}}.\nabla \right){\varvec{B}}$$

(13)

$$\frac{DW}{Dt}=\frac{\partial W}{\partial t}+\left({\varvec{V}}.\nabla \right)W$$

(14)

to obtain the equation of momentum of the Maxwell nanofluid we introduce the following operator $\left[1+\lambda \frac{D}{Dt}\right]$ in Eq. (7) we get:

$$\rho \left[1+\lambda \frac{D}{Dt}\right]\left(\frac{D{\varvec{V}}}{Dt}\right)=-\left[1+\lambda \frac{D}{Dt}\right]\left(\nabla P\right)+\left[1+\lambda \frac{D}{Dt}\right]\left(\nabla .{\varvec{S}}\right)-\left[1+\lambda \frac{D}{Dt}\right]\left( \frac{\upsigma{B}_{0}^{2}}{1-\upgamma t}{u}{\varvec{e}}_{{\varvec{x}}}\right)$$

(15)

After applying

$$\left[1+\lambda \frac{D}{Dt}\right]\left(\nabla .\right)$$

(16)

and invoking the value of ${\varvec{S}}$ (Eq. 8), we get:

$$\rho \left[1+\lambda \frac{D}{Dt}\right]\left(\frac{D{\varvec{V}}}{Dt}\right)=-\left[1+\lambda \frac{D}{Dt}\right]\left(\nabla P\right)+\upmu \left(\nabla .{{\varvec{A}}}_{1}\right)-\left[1+\lambda \frac{D}{Dt}\right]\left( \frac{\upsigma{B}_{0}^{2}}{1-\upgamma t}{u}{\varvec{e}}_{{\varvec{x}}}\right)$$

(17)

where:

$$\frac{D{\varvec{V}}}{Dt}=\frac{\partial {\varvec{V}}}{\partial t}+u\frac{\partial {\varvec{V}}}{\partial x}+v\frac{\partial {\varvec{V}}}{\partial y}=\left(\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}\right){{\varvec{e}}}_{{\varvec{x}}}+\left(\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}\right){{\varvec{e}}}_{{\varvec{y}}}$$

(18)

$\nabla .{{\varvec{A}}}_{1}$ represent divergence of the first Rivlin-Ericksen tensor given by:

$$\nabla .{{\varvec{A}}}_{1}=\left(\begin{array}{c}\frac{\partial {{A}_{1}}_{{\varvec{x}}{\varvec{x}}}}{\partial x}+\frac{\partial {{A}_{1}}_{{\varvec{x}}{\varvec{y}}}}{\partial y}\\ \frac{\partial {{A}_{1}}_{{\varvec{y}}{\varvec{x}}}}{\partial x}+\frac{\partial {{A}_{1}}_{{\varvec{y}}{\varvec{y}}}}{\partial y}\end{array}\right)=\left(\begin{array}{c}2\frac{{\partial }^{2}u}{\partial {x}^{2}}+\frac{{\partial }^{2}u}{\partial {y}^{2}}+\frac{{\partial }^{2}v}{\partial x\partial y}\\ \frac{{\partial }^{2}u}{\partial y\partial x}+\frac{{\partial }^{2}v}{\partial x\partial y}+2\frac{{\partial }^{2}v}{\partial {y}^{2}}\end{array}\right)=\left(\begin{array}{c}\frac{{\partial }^{2}u}{\partial {x}^{2}}+\frac{{\partial }^{2}u}{\partial {y}^{2}}\\ \frac{{\partial }^{2}v}{\partial {x}^{2}}+\frac{{\partial }^{2}v}{\partial {y}^{2}}\end{array}\right)$$

(19)

The components of the unsteady two-dimensional flow of Maxwell nanofluid are established in Eq. (20) and Eq. (21):

$$\left(\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}\right)+\lambda \left(\frac{{\partial }^{2}u}{\partial {t}^{2}}+2u\frac{{\partial }^{2}u}{\partial t\partial x}+2v\frac{{\partial }^{2}u}{\partial t\partial y}+2uv\frac{{\partial }^{2}u}{\partial x\partial y}+{v}^{2}\frac{{\partial }^{2}u}{\partial {y}^{2}}\right)=-\frac{1}{\rho }\frac{\partial P}{\partial x}-\frac{\lambda }{\rho }\left(\frac{{\partial }^{2}p}{\partial t\partial x}+u\frac{{\partial }^{2}P}{\partial {x}^{2}}+v\frac{{\partial }^{2}p}{\partial x\partial y}-\frac{\partial u}{\partial x}\frac{\partial P}{\partial x}\right)+\upnu \left(\frac{{\partial }^{2}u}{\partial {x}^{2}}+\frac{{\partial }^{2}u}{\partial {y}^{2}}\right)-\frac{\upsigma {{B}_{0}}^{2}}{{\rho }(1-\upgamma t)}u-\frac{\upsigma {{B}_{0}}^{2}}{{\rho }(1-\upgamma t)}\lambda \left(\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}\right)$$

(20)

$$\left(\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}\right)+\lambda \left(\frac{{\partial }^{2}v}{\partial {t}^{2}}+2u\frac{{\partial }^{2}v}{\partial t\partial x}+2v\frac{{\partial }^{2}v}{\partial t\partial y}+2uv\frac{{\partial }^{2}v}{\partial x\partial y}+{v}^{2}\frac{{\partial }^{2}v}{\partial {y}^{2}}\right)=-\frac{1}{\rho }\frac{\partial P}{\partial x}-\frac{\lambda }{\rho }\left(\frac{{\partial }^{2}P}{\partial t\partial x}+u\frac{{\partial }^{2}P}{\partial {x}^{2}}+v\frac{{\partial }^{2}p}{\partial x\partial y}-\frac{\partial v}{\partial y}\frac{\partial P}{\partial x}\right)+\upnu \left(\frac{{\partial }^{2}v}{\partial {x}^{2}}+\frac{{\partial }^{2}v}{\partial {y}^{2}}\right)$$

(21)

• The energy equation of Maxwell nanofluid

First thermodynamics law is utilized to derive the energy equation (balance of energy). Physically, it describes the total energy in a system that remains constant. Mathematically, it is defined as:

$$\rho {c}_{p}\left(\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}\right)=-\left(\nabla .{{\varvec{q}}}_{{\varvec{f}}}\right)-\left(\nabla .{{\varvec{q}}}_{{\varvec{r}}{\varvec{a}}{\varvec{d}}}\right)+\frac{{D}_{B}}{{\delta }_{W}}\boldsymbol{ }\nabla T.\nabla C+\frac{{ D}_{T}}{{ T}_{h}}\nabla T.\nabla T$$

(22)

where ${{\varvec{q}}}_{{\varvec{f}}}$ and ${{\varvec{q}}}_{{\varvec{r}}{\varvec{a}}{\varvec{d}}}$ describe radiative and thermal fluxes respectively. Stefan Boltzman and conventional Fourier’s law are utilized to describe radiative and thermal heat fluxes respectively.

$${{\varvec{q}}}_{{\varvec{f}}}=-k\nabla \boldsymbol{ }\boldsymbol{ }T$$

(23)

where $k$ is the thermal conductivity. Utilizing Rosse-land approximation for radiation we have:

$${{\varvec{q}}}_{{\varvec{r}}{\varvec{a}}{\varvec{d}}}=-\left(\frac{4\upsigma }{3{k}_{1}}\right)\frac{\partial T^4}{\partial y}{{\varvec{e}}}_{{\varvec{y}}}$$

(24)

where $\sigma$ is the Stefan–Boltzmann constant and ${k}_{1}$ is the mean absorption coefficient of the nanofluid. Moreover, we suppose that the temperature difference within the flow is such that ${T}^{4}$ may be expanded in a Taylor series. Hence, expanding ${T}^{4}$ about ${T}_{\infty }$ and ignoring higher-order terms we get:

$${T}^{4}=4{T}_{\infty }^{3}T-3{T}_{\infty }^{4}$$

(25)

We have:

$$\nabla .{{\varvec{q}}}_{{\varvec{r}}{\varvec{a}}{\varvec{d}}}=-\left(\frac{4\upsigma }{3{k}_{1}}\right)\frac{{\partial }^{2}{T}^{4}}{\partial {y}^{2}}=-\left(\frac{4\upsigma }{3{k}_{1}}\right)\frac{{\partial }^{2}\left(4{T}_{\infty }^{3}T-3{T}_{\infty }^{4}\right)}{\partial {y}^{2}}=-\frac{16\upsigma {{T}_{\infty }}^{3}}{3{k}_{1}\rho {C}_{p}}\frac{{\partial }^{2}T}{\partial {y}^{2}}$$

(26)

For two-dimensional the energy equation takes the form:

$$\left(\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}\right)=\alpha \left(\frac{{\partial }^{2}T}{\partial {x}^{2}}+\frac{{\partial }^{2}T}{\partial {y}^{2}}\right)+\uptau \frac{{D}_{B}}{{\delta }_{W}}\left(\frac{\partial C}{\partial x}\frac{\partial T}{\partial x}+\frac{\partial C}{\partial y}\frac{\partial T}{\partial y}\right)+\uptau \frac{{ D}_{T}}{{ T}_{h}}\left[{\left(\frac{\partial T}{\partial x}\right)}^{2}+{\left(\frac{\partial T}{\partial y}\right)}^{2}\right]-\frac{16\upsigma {{T}_{\infty }}^{3}}{3{k}_{1}\rho {C}_{p}}\frac{{\partial }^{2}T}{\partial {y}^{2}}$$

(27)

• The concentration equation of Maxwell nanofluid

According to this law, the change in concentration with respect to time is equal to net mass flux. Second Fick’s law is adopted to derive the mass transport equation. With chemical reaction, Brownian, and thermophoresis diffusion effects This law can be expressed mathematically as:

$$\left(\frac{\partial C}{\partial t}+u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}\right)=-\frac{1}{\rho }_{p}\nabla .{\varvec{J}}-{k}_{2}\left(C-{C}_{h}\right)$$

(28)

From first Fick’s law, we have : ${\varvec{J}}=-{{\rho}_{p}}\left(\frac{{D}_{B}}{{\delta }_{W}}\nabla C+\frac{{ D}_{T}}{{ T}_{h}}\nabla T\right)$

Here, ρ_p represents the density of nanoparticles. Accordingly, the concentration equation becomes:

$$\left(\frac{\partial C}{\partial t}+u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}\right)={D}_{B}\left(\frac{{\partial }^{2}C}{\partial {x}^{2}}+\frac{{\partial }^{2}C}{\partial {y}^{2}}\right)+\frac{{ {\delta }_{W}D}_{T}}{{ T}_{h}}\left(\frac{{\partial }^{2}T}{\partial {x}^{2}}+\frac{{\partial }^{2}T}{\partial {y}^{2}}\right)-{k}_{2}\left(C-{C}_{h}\right)$$

(29)

The following are the boundary conditions:

$${at}\quad {y=0},\quad u={U}_{w}=\frac{ax}{1-\gamma t},\quad v=\frac{-{V}_{0}}{1-\gamma t} ,\quad k{\left.\frac{\partial T}{\partial y}\right|}_{y=0}=-{h}_{f}\left({T}_{f}-T\right),\quad {D}_{B}{\left.\frac{\partial C}{\partial y}\right|}_{y=0}=-{{h}^{*}}_{f}\left({C}_{f}-C\right)$$

(30)

$${at}\quad {y=h}\left(t\right),\quad u=0,\quad v={v}_{h}=\frac{dh\left(t\right)}{dt}=\frac{-\upgamma }{2}\sqrt{\frac{\upnu }{a\left(1-\upgamma t\right)}},\quad T={T}_{h},\quad C={C}_{h}$$

(31)

Here, $\rho$ represents the nanofluid density, $\lambda$ is the relaxation period, and $(u, v)$ represent the components of the velocity in the $(x, y)$ directions. $\nu =\frac{\mu }{\rho }$ represents the kinematic viscosity, $P$ is the pressure, ${B}_{0}$ for a constant applied magnetic field, $(T, C)$ are used for the temperature and the concentration,  $\tau$ represents the proportion of the nanofluid’s heat capacity to the effective heat capacity of the nanoparticles. $\left({h}_{f} , {{h}^{*}}_{f}\right)$ are the convective heat and mass transmission coefficients. $\alpha$ is the thermal diffusivity, ${T}_{0}$ is designated as a reference temperature, $\sigma$ is used for the electric conductivity, $\left({D}_{B}, {D}_{T}\right)$ are the Brownian and the thermophoresis diffusive coefficients, ${T}_{f}$ and ${C}_{f}$ refer to the temperature and the concentration of the convective nanofluid, $\gamma$ is a positive dimensional constant, ${C}_{0}$ is reference concentration, ${V}_{0}<0$ specifies the injection case, ${V}_{0}>0$ reflects the suction case, ${T}_{h}$ and ${C}_{h}$ correspond to the temperature and concentration values of the upper plate, $a$ is a constant, $k$ is used to show the thermal conductivity. Considering the subsequent transformations:

$$\eta =\frac{y}{h\left(t\right)},\quad u={U}_{w}{f}^{{\prime}}\left(\eta \right),\quad v=-\sqrt{\frac{a\upnu }{a\left(1-\upgamma t\right)}}f\left(\eta \right),\quad \theta \left(\eta \right)=\frac{T-{T}_{h}}{{T}_{f}-{T}_{0}},\quad \phi \left(\eta \right)=\frac{C-{C}_{h}}{{C}_{f}-{C}_{0}}$$

(32)

Eliminating the pressure gradient term from Eqs. (20) and (21) and in view of Eq. 30, and Eq. 31, the following non-dimensionalized forms of the governing equations and related boundary conditions for this squeezing problem are given:

$${f}^{{\prime}{\prime}{\prime}{\prime}}+f{f}^{{\prime}{\prime}{\prime}}-{f}^{{\prime}}{f}^{{\prime}{\prime}}-\frac{{S}_{q}}{2}\left(3{f}^{{\prime}{\prime}}+{\eta f}^{{\prime}{\prime}}\right)-\beta \left[{\left(\frac{{S}_{q}}{2}\right)}^{2}\left(15{f}^{{\prime}{\prime}}+14\eta {f}^{{\prime}{\prime}{\prime}}+{\eta }^{2}{f}^{{\prime}{\prime}{\prime}{\prime}}\right)+{S}_{q}\left(2{f}^{{\prime}}{f}^{{\prime}{\prime}}+\eta {\left({f}^{{\prime}{\prime}}\right)}^{2}-\delta \left(3f{f}^{{\prime}{\prime}}+\eta {f}^{{\prime}{\prime}}\right)\right)-\left(2f{\left({f}^{{\prime}{\prime}}\right)}^{2}+2{\left({f}^{{\prime}}\right)}^{2}{f}^{{\prime}{\prime}}-{f}^{2}{f}^{{\prime}{\prime}{\prime}{\prime}}\right)\right]-{M}^{2}\left[\left({f}^{{\prime}{\prime}}+\beta \left(\frac{{S}_{q}}{2}\left(3{f}^{{\prime}{\prime}}+\eta {f}^{{\prime}{\prime}{\prime}}\right)-{f}^{{\prime}}{f}^{{\prime}{\prime}}-f{f}^{{\prime}{\prime}{\prime}}\right)\right)\right]=0$$

(33)

$$\left(1+R\right){\theta }^{{\prime}{\prime}}+{P}_{r}f{\theta }^{{\prime}}-{P}_{r}{S}_{q}\theta -\frac{{P}_{r}{S}_{q}}{2}\eta {\theta }^{{\prime}}+{P}_{r}{N}_{b}{\theta }^{{\prime}}{\phi }^{{\prime}}+{P}_{r}{N}_{t}{\theta }^{{\prime}^{2}}=0$$

(34)

$$\phi^{{\prime}{\prime}} + P_{r} L_{e} f\phi^{{\prime}} - P_{r} L_{e} S_{q} \phi - \frac{{P_{r} L_{e} S_{q} }}{2}\eta \phi^{{\prime}} + \frac{{N_{t} }}{{N_{b} }}\theta^{{\prime}{\prime}} - K_{r} L_{e} \phi = 0$$

(35)

with boundary conditions:

$$f\left(0\right)=S,\quad f\left(1\right)=\frac{{S}_{q}}{2},\quad {f}^{{\prime}}\left(0\right)=1, \quad{f}^{{\prime}}\left(1\right)=0,\quad {\theta }^{{\prime}}\left(0\right)=-{\gamma }_{1}\left[1-\theta \left(0\right)\right],\quad \theta \left(1\right)=0,\quad {\phi }^{{\prime}}\left(0\right)=-{\upgamma }_{2}\left[1-\phi \left(0\right)\right],\quad \phi \left(1\right)=0$$

(36)

Here $\delta =\sqrt{\frac{\nu \left(1-\gamma t\right)}{ax}}$ denotes length parameter, $M=\frac{\sigma {{B}_{0}}^{2}}{{\rho }a\left(1-\gamma t\right)}$ the Hartman number, ${P}_{r}=\frac{\nu }{\alpha }$ the Prandtl number, ${L}_{e}=\frac{\alpha }{{D}_{B}}$ the Lewis number, $R=\frac{16\sigma {{T}_{\infty }}^{3}}{3{kk}_{1}}$ the radiation parameter, ${N}_{b}=\frac{\tau { D}_{B}\left({C}_{f}-{C}_{0}\right)}{\nu {\delta }_{W}}$ the Brownian motion parameter, $S=\frac{{V}_{0}}{ah\left(t\right)}$ the injection/suction parameter, ${\gamma }_{1}=\frac{{h}_{f}}{K}\sqrt{\frac{\nu \left(1-\gamma t\right)}{a}}$ the thermal Biot number, $\beta =\frac{a\lambda }{1-\gamma t}$ the Deborah number, ${N}_{t}=\frac{\tau { D}_{T}\left({T}_{f}-{T}_{0}\right)}{\nu {T}_{H}}$ the thermophoresis parameter, ${S}_{q}=\frac{\gamma }{a}$ the squeezing parameter, ${K}_{r}=\frac{{k}_{2}\left(1-\gamma t\right)}{a}$ the chemical reaction and ${\gamma }_{2}=\frac{{{h}^{*}}_{f}}{{D}_{B}}\sqrt{\frac{\nu \left(1-\gamma t\right)}{a}}$ the mass Biot number.

It is important to clarify here that ${\delta }_{W}$ is a corrective concentration coefficient, which is called as Wakif’s concentration coefficient [22,23,24,25].The value of ${S}_{q}$ can be used to characterize the movement of parallel plates. When ${S}_{q}$ is positive, it means that the sheets are traveling in the direction of each other, whereas when ${S}_{q}$ is negative, it means that the sheets are moving outward. The following formulas are used to calculate the rates of mass and heat transmission:

$${Nu}_{x}=\frac{-x\left(k+\frac{16\upsigma {{T}_{\infty }}^{3}}{3{k}_{1}}\right){\left.\frac{\partial T}{\partial y}\right|}_{y=h\left(t\right)}}{k\left({T}_{f}-{T}_{0}\right)}$$

(37)

$${Sh}_{x}=\frac{-x{D}_{B}{\left.\frac{\partial C}{\partial y}\right|}_{y=h\left(t\right)}}{{D}_{B}\left({C}_{f}-{C}_{0}\right)}$$

(38)

The form of Eqs. (37) and (38) in dimensionless forms is as follows:

$${\left({Re}_{x}\right)}^{-\frac{1}{2}}{Nu}_{x}=-\left(1+R\right){\theta }^{{\prime}}\left(1\right)$$

(39)

$${\left({Re}_{x}\right)}^{-\frac{1}{2}}{Sh}_{x}=-{\phi }^{{\prime}}\left(1\right)$$

(40)

${Re}_{x}$ is a local Reynolds number in this instance.

3 Akbari–Ganji’s method

The complete procedure has been spelled out in detail so that readers can understand the method used in this work.

In accordance with the boundary conditions, the general manner of a differential equation is as follows:

$$p_{k} {:}\;f\left( {u,\;u^{{\prime}},\;u^{{\prime}{\prime}}, \ldots ,u^{\left( m \right)} } \right) = 0;\quad u = u\left( x \right)$$

(41)

The following is taken into consideration for the nonlinear differential equation of $p$, which is a function of $u$, the parameter $u$, which is a function of $x$, and their derivatives:

Appropriate boundary conditions are given as:

$$\left\{\begin{array}{c}u\left(x\right)={u}_{0},\quad u^{{\prime}}\left(x\right)={u}_{1},\dots ,{u}^{\left(m-1\right)}\left(x\right)={u}_{m-1}\quad {at}\quad {x=0}\\ u\left(x\right)={{u}_{L}}_{0},\quad u^{{\prime}}\left(x\right)={{u}_{L}}_{1},\dots ,{u}^{\left(m-1\right)}\left(x\right)={{u}_{L}}_{m-1}\quad {at}\quad {x=L}\end{array}\right.$$

(42)

The series of letters in the polynomial function with constant coefficient of the differential equation is stated in the following form, which may be used to analyze the differential equation given in Eq. (41) using the AGM.

$$u\left(x\right)=\sum_{i=0}^{n}{a}_{i}{x}^{i}={a}_{0}+{a}_{1}{x}^{1}+{a}_{2}{x}^{2}+{a}_{3}{x}^{3}\dots +{a}_{n}{x}^{n}$$

(43)

It is important to note that the number of coefficients adopted in the Eq. (43) depends on the desired precision of accuracy. However, it is noted in common engineering problems five or six series are sufficient. Equation (41) is regarded as an answer function, regarding the series from degree $n$ there are $(n + 1)$ unknowns, which can be determined with the aid of the boundary conditions.

3.1 Applying the boundary conditions

The application of the boundary conditions are as follows:

$$when \quad x=0$$

(44)

$we \quad find:$:

$$\left\{\begin{array}{c}u\left(0\right)={a}_{0}={u}_{0}\\ u^{{\prime}}\left(0\right)={a}_{1}={u}_{1}\\ {u}^{{\prime}{\prime}}\left(0\right)={a}_{2}={u}_{2}\end{array}\right.$$

(45)

And when $x= L$:

$$\left\{\begin{array}{c}u\left(L\right)={a}_{0}+{a}_{1}L+{a}_{2}{L}^{2}+\dots +{a}_{n}{L}^{n}={u}_{{L}_{0}}\\ {u}^{{\prime}}\left(L\right)={a}_{1}+2{a}_{2}L+{3a}_{3}{L}^{2}+\dots +n{a}_{n}{L}^{n-1}={u}_{{L}_{1}}\\ {u}^{{\prime}{\prime}}\left(L\right)={2a}_{2}+6{a}_{3}L+{12a}_{4}{L}^{2}+\dots +n\left(n-1\right){a}_{n}{L}^{n-2}={u}_{{L}_{2}}\end{array}\right.$$

(46)

Upon substituting Eq. (43) into Eq. (41), the application of the boundary conditions to determine the unknown coefficients is proceeded as :

$$\genfrac{}{}{0pt}{}{{p}_{0} :f\left(u\left(0\right), {u}^{{\prime}}\left(0\right),{u}^{{\prime}{\prime}}\left(0\right),\dots \dots ,{u}^{\left(m\right)}\left(0\right)\right)}{\begin{array}{c}{p}_{1} :f\left(u\left(L\right), {u}^{{\prime}}\left(L\right),{u}^{{\prime}{\prime}}\left(L\right),\dots \dots ,{u}^{\left(m\right)}\left(L\right)\right)\end{array}}$$

(47)

Concerning the selection of n; $(n<m)$ sentences from Eq. (41) and the creation of a set of equations comprising of $(n+1)$ equations and $(n +1)$; unknowns, we encounter several extra unknowns, which coincidentally are the identical coefficients of Eq.(43). In order to solve this issue, we must first apply the boundary conditions to the aforementioned sets of differential equations and then deduce m times from Eq. (41) in accordance with the extra unknowns.

$$\genfrac{}{}{0pt}{}{{p}_{k}^{{\prime}} :f\left({u}^{{\prime}},{u}^{{\prime}{\prime}},{u}^{{\prime}{\prime}{\prime}},\dots \dots ,{u}^{\left(m+1\right)}\right)}{\begin{array}{c}{p}_{k}^{{\prime}{\prime}} :f\left( {u}^{{\prime}{\prime}},{u}^{{\prime}{\prime}{\prime}},{u}^{\left(IV\right)},\dots \dots ,{u}^{\left(m+2\right)}\right)\end{array}}$$

(48)

The differential equation ${p}_{k}$’s derivatives are subjected to the boundary conditions applied in Eq. (48) in the following manner:

$${P}_{k}^{{\prime}}{:}\; \left\{\begin{array}{c}\genfrac{}{}{0pt}{}{f\left({u}^{{\prime}}\left(0\right),{u}^{{\prime}{\prime}}\left(0\right),{u}^{{\prime}{\prime}{\prime}}\left(0\right),\dots \dots ,{u}^{\left(m+1\right)}\left(0\right)\right)}{f\left({u}^{{\prime}}\left(L\right),{u}^{{\prime}{\prime}}\left(l\right),{u}^{{\prime}{\prime}{\prime}}\left(L\right),\dots \dots ,{u}^{\left(m+1\right)}\left(L\right)\right)}\end{array}\right.$$

(49)

$${P}_{k}^{{\prime}{\prime}} : \left\{\begin{array}{c}\genfrac{}{}{0pt}{}{f\left({u}^{{\prime}{\prime}}\left(0\right),{u}^{{\prime}{\prime}{\prime}}\left(0\right),{u}^{\left(IV\right)}\left(0\right)\dots \dots ,{u}^{\left(m+2\right)}\left(0\right)\right)}{f\left({u}^{{\prime}{\prime}}\left(L\right),{u}^{{\prime}{\prime}{\prime}}\left(L\right),{u}^{\left(IV\right)}\left(L\right)\dots \dots ,{u}^{\left(m+1\right)}\left(L\right)\right)}\end{array}\right.$$

(50)

$(n+1)$ equations can be made from Eq. (45) to Eq. (50) so that $(n+1)$ unknown coefficients of Eq. (43) such as ${a}_{0}$, ${a}_{1}$, ${a}_{2}$....${a}_{n}$. Be computer. The solution of the nonlinear differential equation, Eq. (42) will be gained by determining the coefficients of Eq. (43). To comprehend the procedures of applying the following explanation we have presented the relevant process step by step in the following part.

3.2 Application of Akbari–Ganji’s method (AGM)

Based on the previously given coupled system of nonlinear differential equations and the fundamental concept of the approach, we rewrite Eqs. (33) through (35) in the following order:

$$F\left( {\upeta } \right) = f^{{\prime \prime \prime \prime} } + ff^{{\prime\prime\prime}} - f^{{\prime}}f^{{\prime\prime}} - \frac{{S_{q} }}{2}\left( {3f^{{\prime\prime}} + \eta f^{{\prime\prime}}} \right) - \beta \left[ {\left( {\frac{{S_{q} }}{2}} \right)^{2} \left( {15f^{{\prime\prime}} + 14\eta f^{{\prime\prime\prime}} + \eta^{2} f^{{\prime \prime \prime \prime} } } \right) + S_{q} \left( {2f^{{\prime}}f^{{\prime\prime}} + \eta \left( {f^{{\prime\prime}}} \right)^{2} - \delta \left( {3ff^{{\prime\prime}} + \eta f^{{\prime\prime}}} \right)} \right) - \left( {2f\left( {f^{{\prime\prime}}} \right)^{2} + 2\left( {f^{{\prime}}} \right)^{2} f^{{\prime\prime}} - f^{2} f^{{\prime \prime \prime \prime} } } \right)} \right] - M^{2} \left[ {\left( {f^{{\prime\prime}} + \beta \left( {\frac{{S_{q} }}{2}\left( {3f^{{\prime\prime}} + \eta f^{{\prime\prime\prime}}} \right) - f^{{\prime}}f^{{\prime\prime}} - ff^{{\prime\prime\prime}}} \right)} \right)} \right] = 0$$

(51)

$$G\left( {\upeta } \right) = \left( {1 + R} \right)\theta^{\prime\prime} + P_{r} f\theta^{{\prime}} - P_{r} S_{q} \theta - \frac{{P_{r} S_{q} }}{2}\eta \theta^{{\prime}} + P_{r} N_{b} \theta^{{\prime}}\phi^{{\prime}} + P_{r} N_{t} \theta^{{\prime^{2} }} = 0$$

(52)

$$Q\left( {\upeta } \right) = \phi^{{\prime\prime}} + P_{r} L_{e} f\phi^{{\prime}} - P_{r} L_{e} S_{q} \phi - \frac{{P_{r} L_{e} S_{q} }}{2}\eta \phi^{{\prime}} + \frac{{N_{t} }}{{N_{b} }}\theta^{{\prime\prime}} - K_{r} L_{e} \phi = 0$$

(53)

Owing to the fundamental principle of AGM, we have employed an appropriate trial function to solve the differential equation under consideration, which is a finite sequence of polynomials with constant coefficients, in the following manner:

$$f\left(\upeta \right)=\sum_{i=0}^{9}{a}_{i}{\upeta }^{i}={a}_{0}+{a}_{1}{\upeta }^{1}+{a}_{2}{\upeta }^{2}+{a}_{3}{\upeta }^{3}+{a}_{4}{x}^{4}+{a}_{5}{x}^{5}+{a}_{6}{x}^{6}+{a}_{7}{x}^{7}+{a}_{8}{x}^{8}+{a}_{9}{x}^{9}+\dots$$

(54)

$$\Theta \left(\upeta \right)=\sum_{i=0}^{9}{b}_{i}{\upeta }^{i}={b}_{0}+{b}_{1}{\upeta }^{1}+{b}_{2}{\upeta }^{2}+{b}_{3}{\upeta }^{3}+{b}_{4}{x}^{4}+{b}_{5}{x}^{5}+{b}_{6}{x}^{6}+{b}_{7}{x}^{7}+{b}_{8}{x}^{8}+{b}_{9}{x}^{9}+\dots$$

(55)

$$\Phi \left(\upeta \right)=\sum_{i=0}^{9}{c}_{i}{\upeta }^{i}={c}_{0}+{c}_{1}{\upeta }^{1}+{c}_{2}{\upeta }^{2}+{c}_{3}{\upeta }^{3}+{c}_{4}{x}^{4}+{c}_{5}{x}^{5}+{c}_{6}{x}^{6}+{c}_{7}{x}^{7}+{c}_{8}{x}^{8}+{c}_{9}{x}^{9}+\dots$$

(56)

3.3 Validation of numerical results

In this work, the unsteady MHD Maxwell nanofluid flow, heat, and mass transfer past between two parallel plates with the attendance of thermal radiation impacts, chemical reaction, Brownian, and thermophoresis diffusion effects considering the conventional Fourier’s heat flux model of heat conduction and from first Fick’s law for mass transport, are studied Semian-analytically by using the Akbari–Ganji’s Method (AGM). To verify the present analytical solution, we compared our results with results given by using Runge–Kutta. They are in excellent agreement as they have been demonstrated in Table 1 and Figs. 2, 3 and 4.

Table 1 Comparison of the present results with two different methods (AGM) and (RK) for $f\left(\eta \right)$, $\theta \left(\eta \right)$ and $\phi \left(\eta \right)$ when $\beta =S=\delta ={N}_{b}=0.3$, $M=0.5$, ${S}_{q}={L}_{e}=0.1$, $R = 0.2$, ${N}_{t} = 0.7$, $\beta =0.8$, ${K}_{r}=1.3$, ${\gamma }_{1}={\gamma }_{2}=1.4$ and ${P}_{r}=25.$

Fig. 2

Comparison between the results given by (RK) and (AGM) for $f\left(\eta \right)$ and $f^{{\prime}}\left(\eta \right)$

Fig. 3

Comparison between the results given by (RK) and (AGM) for $\theta \left(\eta \right)$ and ${\theta} ^{{\prime}}\left(\eta \right)$

Fig. 4

Comparison between the results given by (RK) and (AGM) for $\phi \left(\eta \right)$ and ${\phi}^{{\prime}}\left(\eta \right)$

4 Results and discussion

This section reveals the relationship between the flow parameters and many relevant characteristics, including temperature, velocity, and nanoparticle concentration. Plotting is done to this end in Figs. 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, and 20. The mass flow, heat, and squeezing phenomena representative parameters are used to build the graphical findings.

Fig. 5

Impact of S_q on $f(\eta )$

Fig. 6

Impact of ${S}_{q}$ on ${f}^{{\prime}}(\eta )$

Fig. 7

Impact of S on $f(\eta )$

Fig. 8

Impact of S on ${f}^{{\prime}}(\eta )$

Fig. 9

Impact of M on ${f}^{{\prime}}(\eta )$

Fig. 10

Impact of $\beta$ on ${f}^{{\prime}}(\eta )$

Fig. 11

Impact of ${S}_{q}$ on $\theta (\eta )$

Fig. 12

Impact of $R$ on $\theta (\eta )$

Fig. 13

Impact of ${N}_{b}$ on $\theta (\eta )$

Fig. 14

Impact of ${N}_{t}$ on $\theta (\eta )$

Fig. 15

Impact of ${\gamma }_{1}$ on $\theta (\eta )$

Fig. 16

Impact of ${L}_{e}$ on $\phi (\eta )$

Fig. 17

Impact of ${N}_{b}$ on $\phi (\eta )$

Fig. 18

Impact of ${N}_{t}$ on $\phi (\eta )$

Fig. 19

Impact of K_r on $\phi (\eta )$

Fig. 20

Impact of γ on $\phi (\eta )$

Figures 5 and 6 show the squeezing parameter $\left({S}_{q}\right)$ impact on the velocity components $f(\eta )$ and ${f}^{{\prime}}(\eta )$. It is observed that an increase in squeezing parameter $\left({S}_{q}\right)$ leads to an improvement in both horizontal and vertical velocities. Since the top plate’s movement toward the lower plate creates pressure, the squeezed nanoparticles flow quickly. The velocity distribution therefore increases.

The behavior of the injection/suction parameter $\left(S\right)$ on the vertical velocity $f(\eta )$ field is depicted in Fig. 7. With an increase in the suction/injection parameter, the velocity field rises. The addition of physical fluid particles improves the velocity profile in the system.

The behavior of injection/suction parameter $\left(S\right)$ on a horizontal ${f}^{{\prime}}(\eta )$ velocity profile is depicted in Fig. 8. Analysis shows that as the injection/suction parameter is increased, the velocity distribution diminishes. Compared to the vicinity of the lower porous stretchable plate, the velocity field decays more quickly near the top plate. The velocity field thus shows a drop.

Figure 9 addresses the response of the Hartman number $\left(M\right)$ on the velocity field. Increased resistance to the nanofluid's velocity is the result of interactions between the magnetic field and the conductive nanofluid. This resistance results in a decrease in ${f}^{{\prime}}(\eta )$. Stated differently, a reduction in ${f}^{{\prime}}(\eta )$ results from an increased Hartmann number $\left(M\right)$, which denotes a stronger magnetic field influence.

Higher Hartmann number $\left(M\right)$ leads to lower ${f}^{{\prime}}(\eta )$ because the magnetic field has a more significant retarding effect on the nanofluid motion; however, the opposite effects are observed in the second portion of the velocity curve. The magnetic field acts as a constraint, opposing the motion of the nanofluid and impeding its flow between the parallel plates.

The change in Deborah’s number $\left(\beta \right)$ on the horizontal velocity $f^{{\prime}}(\eta )$ is shown in Fig. 10. It is observed that the velocity profile gets stronger with an increase in $\left(\beta \right)$ in the region $0<\beta <0.6$, whereas in the region $0.6<\beta <1.0$, the velocity decreases as $\left(\beta \right)$ increases. Larger Deborah’s numbers correlate with longer relaxation times, which provide more resistance to the nanofluid flow. The velocity field so decays.

The impact of the squeezing parameter $\left({S}_{q}\right)$ on the temperature $\theta (\eta )$ is seen in Fig. 11 In this case, when the squeezing parameter $\left({S}_{q}\right)$ increases, $\theta (\eta )$ decreases. As a result of the upper plate movement’s squeezing impact, temperature is reduced. The squeezing force applied to the nanofluid lowers as $\left({S}_{q}\right)$ increases, which causes the flow temperature to drop in tandem.

The impact of radiation parameter $\left(R\right)$ versus temperature field $\theta (\eta )$ is shown in Fig. 12. Temperature $\theta (\eta )$ decreases as the radiation parameter $\left(R\right)$ increases. This is because the heat absorption coefficient’s effect on the working nanofluid decreases with increasing $\left(R\right)$, which causes the temperature field to drop.

The effect of the Brownian diffusion parameter $\left({N}_{b}\right)$ on the temperature distribution is seen in Fig. 13. A higher Brownian diffusion parameter raises the temperature of the nanofluid. The substantial dependency of the Brownian diffusion parameter on the Brownian diffusion coefficient is the reason for this relationship. The Brownian diffusion coefficient, which controls the nanofluid’s temperature distribution, rises in response to an increase in the Brownian motion parameter.

The impact of the thermophoresis variable $\left({N}_{t}\right)$ on the non-dimensional temperature $\theta (\eta )$ profile is seen in Fig. 14. In fact, a higher thermophoresis variable $\left({N}_{t}\right)$ causes the nanofluid’s thermophoresis force to rise. The nanofluid’s temperature is subsequently raised because of this increased thermophoresis force.

Figure 15 shows the temperature field $\theta (\eta )$ vs thermal Biot number $\left({\gamma }_{1}\right)$ curves. The coefficient of heat transmission increases with larger thermal Biot numbers $\left({\gamma }_{1}\right)$. The system’s temperature rises as a result of this increase in the heat transport coefficient.

The effect of the Lewis number $\left({L}_{e}\right)$ on particle concentration $\phi (\eta )$ is seen in Fig. 16, which indicates that a greater Lewis number causes the concentration distribution to drop. The inverse link between the Lewis number and the coefficient of Brownian diffusion is the reason for these phenomena. As the Lewis number rises, the coefficient of Brownian diffusion falls, which lowers the concentration profile.

Figure 17 shows the effect of the Brownian diffusion parameter $\left({N}_{b}\right)$ on the concentration distribution $\phi (\eta )$. The concentration profile here gets better for the dominating parameter of Brownian motion. The movement of the nanoparticles from the top plate to the nanofluid is responsible for the observed increase in concentration distribution.

The relationship between the concentration $\phi (\eta )$ field and the thermophoresis variable $\left({N}_{t}\right)$ is shown in Fig. 18. It is clear that resistance to mass diffusion generated by a greater $\left({N}_{t}\right)$ causes the concentration distribution to contract.

The fluctuation of concentration $\phi (\eta )$ vs chemical reaction $\left({K}_{r}\right)$ is shown in Fig. 19. It is evident that concentration $\phi (\eta )$ decreases as the chemical reaction $\left({K}_{r}\right)$ increases. For the concentration $\phi (\eta )$ vs the mass Biot number $\left({\gamma }_{2}\right)$, Fig. 20 is constructed. In this case, the mass Biot number $\left({\gamma }_{2}\right)$ is a function of concentration $\phi (\eta )$ rising. The mass Biot number is expressed in terms of the coefficient of mass-transference, which increases as $\left({\gamma }_{2}\right)$ increases. Consequently, $\phi (\eta )$ rises.

Using Tables 2 and 3, the characteristics of significant physical elements opposing Nusselt and Sherwood numbers are developed. We discovered that as the chemical reaction parameter, Brownian motion, and thermophoresis variables rise, so does the Nusselt number Table 2. while the Nusselt number decreases with higher numbers of the squeezing parameter.

Table 2 Numerical values of ${\left({Re}_{x}\right)}^{-\frac{1}{2}}{ Nu}_{x} \; \mathrm{ for } \; \beta =0.3, \; S=0.3, M=0.5, \; Pr=25, {L}_{e}=0.4, \;$ ${K}_{r}=0.7, \; {\gamma }_{1}={\gamma }_{2}=1.4, \; \delta =0.3$

Table 3 Numerical values of ${\left({Re}_{x}\right)}^{-\frac{1}{2}}{Sh}_{x} \; \mathrm{ for }\; \beta =0.3, \; S=0.3, \; M=0.5, \; Pr=25, \; {L}_{e}=0.4,$ ${K}_{r}=0.7, \; {\gamma }_{1}={\gamma }_{2}=1.4, \; {S}_{q}=0.1, R=0.2,\; {N}_{b}=0.3,\; {N}_{t}=0.7,\; \delta =0.3$

On the other hand, Table 3 shows that when ${L}_{e}$ values increase, the mass transfer rate increases as well, For the $\left({K}_{r}\right)$ parameter, however, the opposite effects are observed.

5 Conclusion and important remarks

The flow of magnetohydrodynamics Maxwell nanofluid squeezing flow under multi-physical assumptions in a constrained parallel-wall geometry is the main topic of this study. The conclusions of our investigation are summed up as follows:

• A higher Hartman, Deborah, and squeezing parameter all indicate increased velocity, however the suction/injection parameter shows the reverse trend.

• When suction/injection variables and squeezing are increased, vertical velocity increases.

• The temperature of the nanofluid increases with increasing radiation, thermophoresis, and thermal stratification factors, but decreases with increasing the squeezing parameter.

• Lower concentrations of nanoparticles are produced by a larger solutal stratification parameter, Lewis number, thermophoresis variable, chemical reaction parameter, and Brownian motion parameter; converse effects are noted for solutal Biot number.

• In contrast to the opposing trends observed for squeezing and radiation factors, the local Nusselt number increases as length, Brownian motion, and thermophoresis variables increase.

• Growing chemical reaction and solutal stratification characteristics cause a significant drop in the bulk transmission rate.