Numerical approximation of the typhoid disease model via Genocchi wavelet collocation method

Abstract

In this paper, we have considered the fractional typhoid disease model and obtained the numerical approximation of the model via the innovative wavelet scheme called the Genocchi wavelet collocation method (GWCM) with the help of Caputo fractional derivative for the fractional order. The approach under consideration is a powerful tool for obtaining numerical solutions to fractional-order nonlinear differential equations. The GWCM approach yields accurate solutions that are very close to exact solutions for highly nonlinear problems by avoiding data rounding and just computing a few terms. The Genocchi wavelet basis functions possess remarkable properties, including compact support, making them well-suited for approximating solutions to differential equations. The main benefit of this method lies in its capability to reduce the computational complexity associated with solving systems of ODEs, resulting in accurate and efficient solutions. The results of the developed technique, the RK4 method, and the ND solver have been compared. The numerical outcomes demonstrate that the implemented technique is incredibly effective and precise for solving the Typhoid model of fractional order. This paper contributes to numerical analysis by introducing the Genocchi wavelet method as a robust tool for solving biological models.

1 Introduction

Numerous variables must be analyzed and investigated worldwide, ranging from micro-host pathogen interactions to host-host interactions and contemporary ecological, social, economic, and demographic elements. Typhoid fever is one of the most severe infections in the world, caused by various Salmonella typhi bacteria. According to a WHO report, the sickness is most often caused by a lack of sanitation, in which the disease-causing bacterium enters the human body via contaminated food or drink. Typhoid fever has recently become widespread in developing countries [1]. According to the most recent global estimates, there are no less than 16 million new cases of Typhoid fever each year, with 600,000 deaths. Yearly incidence rates of 198 for every 100,000 in the Mekong Delta region of Vietnam and 980 for every 100,000 in Delhi, India, have recently been recorded [1]. Four epidemiologic types of S. typhi exposure were proposed in the 1960s [2].

Improving living conditions, such as sanitation and access to clean water, will reduce the risk of infection, resulting in fewer people becoming affected [3]. Mathematical modeling is a potent instrument for studying, investigating, and understanding the spread of various diseases and developing methods to manage them in society. Mathematical modeling makes understanding a disease's spread and defining the essential factors easier. Numerous biological models have been examined from different aspects in this regard. ODEs with suitable assumptions and parameters can represent these models. A mathematical model for typhoid transmission dynamics has been developed to examine vaccination's possible direct and indirect impacts [4]. Consideration that ordinary derivatives have been widely used in mathematical models of numerous diseases. However, the aforementioned differential operator has a local. As a result, researchers have focused their attention on fractional order differential operators. The stated branch has received a lot of attention in the recent few decades. Numerous researchers have offered various definitions for fractional derivatives and integrals, including Caputo-Fabrizio, Riemann–Liouville, Atangana-Baleanu, and Caputo fractional derivatives.

Fractional derivatives offer a fantastic tool for describing diverse materials and processes' memory and inherited characteristics. A more comprehensive range of behaviors can be modelled by switching from integer-order to fractional derivatives. Fractional order differential equations have attracted much research because they frequently arise in various biological applications, acoustics, robotics, signal processing, fluid mechanics, physics, engineering, and viscoelasticity. Understanding and using the precise solutions to physical events in actual scientific study is essential.

In the current study, we investigated the epidemiology model created by Peter et al. [5]. The following set of non-linear equations is used to describe this complex model. This Typhoid fever model is divided into five subclasses: susceptible individuals $S\left(\delta \right),$ carrier infectious individuals $Q\left(\delta \right)$, infectious individuals $I\left(\delta \right)$, recovered individuals $R\left(\delta \right)$, and environmental bacteria concentration $W\left(\delta \right)$. $N\left(\delta \right)=S\left(\delta \right)+Q\left(\delta \right)+I\left(\delta \right)+R\left(\delta \right)+W\left(\delta \right)$ denotes the total population number at time $\delta$.

$$\left.\begin{array}{l}\frac{dS(\delta )}{d\delta }=\lambda -\theta S\left(\delta \right) \left(\beta Q\left(\delta \right)+\gamma I\left(\delta \right)+\eta W\left(\delta \right)\right) \\ \frac{dQ(\delta )}{d\delta }=\mu S\left(\delta \right) \left(\beta Q\left(\delta \right)+\gamma I\left(\delta \right)+\eta W\left(\delta \right)\right)-\left(\nu +\varepsilon \right) Q\left(\delta \right) \\ \frac{dI(\delta )}{d\delta }=\left(1-\mu \right) S\left(\delta \right) \left(\beta Q\left(\delta \right)+\gamma I\left(\delta \right)+\eta W\left(\delta \right)\right)-\left(\xi +\sigma +\rho \right)I\left(\delta \right)\\ \frac{dR(\delta )}{d\delta }= \sigma I\left(\delta \right)-\tau R\left(\delta \right) \\ \frac{ dW(\delta )}{d\delta }= \varepsilon Q\left(\delta \right)+\rho I\left(\delta \right)-\kappa W\left(\delta \right)\end{array}\right\}$$

(1)

where $\lambda$ represents the rate of recruitment of susceptible people, the natural death rate is $\theta$, the disease-induced death rate and natural rate for class $Q$ class is $\nu$, the natural death rate for $I$ class is $\xi$, $\tau$ is the natural death rate, bacteria shedding rate for $Q$ is $\varepsilon$ whereas $\rho$ denotes bacteria shedding rate for $I$, the probability that newly infected individuals are asymptomatic is indicated by $\mu$, transmission rates between $S$ and $Q$ is $\beta$, between $S$ and $I$ is $\gamma$ and between $S$ and $W$ is $\eta$, $\sigma$ denotes recovery rate for infectious class and force of infection is predicted by $\kappa$.

Using the Caputo fractional operator of order $\alpha$ such that $\alpha \in (0, 1]$ and drawing inspiration from the work mentioned above, we examined the system of the nonlinear fractional differential equation provided by the typhoid model presented in Peter et al. [5].

$$\left.\begin{array}{l}\frac{{d}_{\delta }^{\alpha }S(\delta )}{d\delta }=\lambda -\theta S\left(\delta \right) \left(\beta Q\left(\delta \right)+\gamma I\left(\delta \right)+\eta W\left(\delta \right)\right) \\ \frac{{d}_{\delta }^{\alpha }S(\delta )}{d\delta }=\mu S\left(\delta \right) \left(\beta Q\left(\delta \right)+\gamma I\left(\delta \right)+\eta W\left(\delta \right)\right)-\left(\nu +\varepsilon \right) Q\left(\delta \right) \\ \frac{{d}_{\delta }^{\alpha }S(\delta )}{d\delta }=\left(1-\mu \right) S\left(\delta \right) \left(\beta Q\left(\delta \right)+\gamma I\left(\delta \right)+\eta W\left(\delta \right)\right)-\left(\xi +\sigma +\rho \right)I\left(\delta \right)\\ \frac{{d}_{\delta }^{\alpha }S(\delta )}{d\delta }= \sigma I\left(\delta \right)-\tau R\left(\delta \right) \\ \frac{{d}_{\delta }^{\alpha }S(\delta )}{d\delta }= \varepsilon Q\left(\delta \right)+\rho I\left(\delta \right)-\kappa W\left(\delta \right)\end{array}\right\}$$

(2)

With the initial conditions:$S\left(0\right)={a}_{1}, Q\left(0\right)={a}_{2} , I\left(0\right)={a}_{3}, R\left(0\right)={a}_{4}, W\left(0\right)={a}_{5}$.

Some of the significant work done on the Typhoid model are transmission dynamics of fractional Typhoid fever model [1], numerical solution by using Adam-bashforth method [6], the study of typhoid fever in five Asian countries [6], modelling and optimal control of the model [7], stochastic dynamical analysis of the model [8], fractional dynamics of typhoid fever transmission model [9], transmission dynamics of the disease by Differential transform method [9], series solution of the model by DTM [10], numerical solution by Adomian decomposition method [11], variational iteration method [12].

Wavelets comprise a family of functions created by the translation and dilation of a single function known as the mother wavelet. The mathematical analysis of Morlet, Meyer, Stromberg, Daubechies, and Grossmann has significantly advanced wavelet theory. Many scholars are drawn to it because of its distinctive characteristics, such as orthogonality, compactly supported, and multiresolution analysis. Numerous dynamical system problems have extensively used approximate solutions using an orthogonal family of functions. Using truncated orthogonal functions to approximate the various signals in the equation, one can approximate the underlying differential equation using orthogonal functions. Wavelet theory has drawn much interest recently due to its valuable applications in several fields, including numerical analysis, system analysis, signal analysis, and optimal control [12]. Wavelets are valuable because of their unique characteristics [13]. Several wavelet-based numerical approaches have been magnificently solved in the literature, including the following: Fibonacci wavelet approach [13, 14], Legendre wavelet collocation method [15], Hermite wavelet collocation scheme [16], Chebyshev wavelet collocation method [17], Laguerre wavelet collocation approach [18, 32], Bernoulli wavelet scheme [18,19,20], Haar wavelet method [21], Cardinal B-spline wavelet method [22], and sextic B-spline collocation scheme [33].

In recent years, Meyer and Morlet's wavelets have attracted the attention of many researchers working in various areas of mathematics. As a result, several articles have been done on these wavelets. A few of them are the Morlet wavelet neural network for solving a class of singular pantograph nonlinear differential models [34], numerical computing to solve the nonlinear corneal system of eye surgery using the capability of Morlet wavelet artificial neural networks [35], and the modified epidemiological model of computer viruses by using Fibonacci wavelets [36].

Genocchi wavelets are types of continuous wavelets. By utilising operational matrices to estimate the integrals, the following problem can be simplified to a set of algebraic equation.

Merits of Genocchi wavelet collocation method:

•In comparison to the Legendre polynomials ${L}_{m}\left(x\right)$, the Genocchi polynomials ${\mathcal{H}}_{m}(x)$ have fewer terms. Reducing CPU time is one of its benefits.

•The coefficient of individual terms in Genocchi polynomials ${\mathcal{H}}_{m}(x)$ is smaller than that of comparable terms in Legendre polynomials ${L}_{m}\left(x\right)$. This characteristic can be used to lower computational errors.

The Genocchi wavelet collocation method suits solutions with sharp edge/ jump discontinuities. By slightly modifying the method,

•An ordinary differential equation higher-order system can be solved using the Genocchi wavelet approach.

•It is possible to use this technique for PDEs and other mathematical models with various physical conditions.

•This method allows one to directly solve stiff systems, delay differential equations, and fractional differential equations without controlling parameters.

•The Genocchi wavelet approach is very accurate and has fast algorithms. In contrast to Chebyshev, Legendre, and Bernoulli wavelets, this approach is straightforward, precise, and requires fewer computing resources.

Demerits of Genocchi wavelet collocation method:

The proposed Genocchi wavelet collocation method is domain-restricted. i.e., It can’t be applied for the entire domain ${\mathbb{R}}$.

During our review of the literature, we discovered the following exceptional publications regarding the application of the Genocchi wavelet approach in solving some of the equations: fractional PDEs [23, 24], nonlinear fractional order delay differential equations [25], conformable fractional differential equations [26], different kind of differential equations [27], fractional Rosenau-Hyman equation [28]. These are the recent developments on the Genochhi wavelets.

The structure of this article is as follows: Wavelet definitions are given in "Preliminaries" of Sect. 2. OMI of Genocchi wavelets was completed in Sect. 3. Sections 4 and 5 describe the newly established strategy's application and solution methods. Ultimately, the article's conclusion is presented in Sect. 6.

2 Preliminaries of fractional derivative and Genocchi wavelets

Definition 1

The Caputo fractional derivative of $f\left(\delta \right)\in {C}_{\mu }$ is defined as [29]:

$$\frac{{d}^{\alpha }f\left(\delta \right)}{d{s}^{\alpha }}=\frac{1}{\Gamma (m-\alpha )} \underset{0}{\overset{\delta }{\int }}{\left(\delta -t\right)}^{m-\alpha -1} {f}^{(m)} (t) dt$$

For $m-1<\alpha \le m,$ $m$ is any positive integer, $\delta >0, f\left(\delta \right)\in {C}_{\mu }^{m} , \mu \ge -1.$

Definition 2: Genocchi wavelets

In the interval $[\mathrm{0,1})$ the Genocchi wavelets are defined as follows [25]:

$${\mathcal{H}}_{n, m}\left(\delta \right)=\left\{\begin{array}{c}{2 }^{\frac{k -1}{2}} {\widetilde{G}}_{m}\left({2}^{k}\delta -\widehat{n}\right), \frac{\widehat{n}}{{2}^{ k-1}}\le \delta <\frac{\widehat{n}+1}{ {2}^{ k-1}}\\ 0, Otherwise,\end{array}\right.$$

with

$${\widetilde{G}}_{m}\left({2}^{k}\delta -n+1\right)=\left\{\begin{array}{c} 1, m=1\\ \frac{1}{\sqrt{\frac{{ 2\left(-1\right) }^{m-1}{ \left(m !\right) }^{2}}{ \left(2m\right) !}{g}_{2m}}}{G}_{m}\left({2}^{k}\delta -n+1\right), m>1\end{array}\right.$$

where$m=0, 1 ,2 ,\dots , M-1, n=1, 2,\dots , {2}^{ k-1}$.

Theorem 1

Let $H$ be a Hilbert space and $W$ be a closed subspace of $H$ such that $\dim W < \infty$ and $\{ w_{1} ,w_{2} ,...,w_{n} \}$ is any basis for $W$. Let $g$ be an arbitrary element in $H$ and $g_{0}$ be the unique best approximation to $g$ out of $W$. Then [14]

$\left\| {g - g_{0} } \right\|_{2} = G_{g}$, Where $G_{g} = \left( {\frac{{Z(g,w_{1} ,w_{2} ,...w_{n} )}}{{Z(g,w_{1} ,w_{2} ,...w_{n} )}}} \right)^{\frac{1}{2}}$ and $Z$ is introduced in [14] as follows:

$$ Z\,(g,\,w_{1} ,\,w_{2} ,...\,w_{n} )\,\, = \,\,\,\left| {\,\,\begin{array}{*{20}c} {\, < g,g > } & { < g,w_{1} > } & {...} & { < g,w_{n} > } \\ { < w_{1} ,g > } & { < w_{1} ,w_{1} > } & {...} & { < w_{1} ,w_{n} > } \\ {...} & {...} & {...} & {...} \\ { < w_{n} ,g > } & { < w_{n} ,w_{1} > } & {...} & { < w_{n} ,w_{n} > } \\ \end{array} \,\,} \right| $$

Theorem 2

[30, 31]: Let ${L}^{2}[\mathrm{0,1}]$ be the Hilbert space generated by the Genocchi wavelet basis. Let $\eta \left(\delta \right)$ be the continuous bounded function in ${L}^{2}[\mathrm{0,1}]$. Then, the Genocchi wavelet expansion of $\eta (\delta )$ converges with it.

Proof

Let $\eta :[\mathrm{0,1}]\to R$ be a continuous function and $\left|\eta (\delta )\right|\le \mu$, where $\mu$ is any real number. Then Genocchi wavelet dilation of $y(\delta )$ can be expressed as,

$$\eta \left(\delta \right)={\sum\limits }_{n=1}^{{2}^{\frac{k -1}{2}}}{\sum\limits }_{m=0}^{M-1}{ a}_{n,m}{\mathcal{H}}_{n,m} (\delta ).$$

${a}_{n,m}=\langle \eta ( \delta ),{ \mathcal{H}}_{n,m} ( \delta )\rangle$ Denotes inner product. ${a}_{n,m}={\int }_{0}^{1}\eta (\delta ){\mathcal{H}}_{n,m}\left(\delta \right) d\delta$.

${a}_{n,m}={\int }_{I}\eta \left(\delta \right)\frac{{2}^{\frac{k-1}{2}}}{\sqrt{\frac{(-1{)}^{m-1}(m!{)}^{2}{\alpha }_{2m}}{\left(2m\right)!}}}{G}_{m}\left({2}^{k}\delta -n+1\right) d\delta ,$ where $I=\left[\frac{n -1}{{2}^{k-1}}\right., \left.\frac{n}{{2}^{k-1}}\right)$.

Then substitute ${2}^{k}\delta -n+1=y$ then we get, ${a}_{n,m}=\frac{{2}^{\frac{k-1}{2}}}{\sqrt{\frac{(-1{)}^{m-1}(m!{)}^{2}{\alpha }_{2m}}{\left(2m\right)!}}}{\int }_{0}^{1}\eta \left(\frac{y + n-1}{{2}^{k}}\right) {G}_{m}(y)\frac{dy}{{2}^{k}}$, ${a}_{n,m} =\frac{{2}^{\frac{-k-1}{2}}}{\sqrt{\frac{(-1{)}^{m-1}(m!{)}^{2}{\alpha }_{2m}}{\left(2m\right)!}}}{\int }_{.0}^{1}\eta \left(\frac{y + n-1}{{2 }^{k}}\right) {G}_{m}\left(y\right)dy$

By generalized mean value theorem,

${a}_{n,m} =\frac{{2 }^{\frac{-k+1}{2}}}{\sqrt{2m+1}} \eta \left(\frac{\xi +n-1}{{2 }^{k- 1}}\right){\int }_{0}^{1} {G}_{m}(y) dy$, for some $\xi \in (\mathrm{0,1})$

Since ${G}_{m}(y)$ is a bounded continuous function. Put ${\int }_{0}^{1} {G}_{m}(y) dy=h$, $\left|{a}_{n,m}\right| =\left|\frac{{2}^{\frac{-k-1}{2}}}{\sqrt{\frac{(-1{)}^{m-1}(m!{)}^{2}{\alpha }_{2m}}{\left(2m\right)!}}}\right|\left|\eta \left(\frac{\xi +n- 1}{{2}^{k}}\right)\right| h$

Since $\eta$ remains bounded.

Hence, $\left|{a}_{n,m}\right| =\left|\frac{{2}^{\frac{-k-1}{2}}}{\sqrt{\frac{(-1{)}^{m-1}(m!{)}^{2}{\alpha }_{2m}}{\left(2m\right)!}}} \mu h\right|,$ where $\mu =\eta \left(\frac{\delta +n- 1}{{2}^{k-1}}\right).$

Therefore, ${\sum\limits }_{n,m=0}^{\infty }{a}_{n,m}$ is absolutely convergent. Hence, the Genochhi wavelet series expansion $\eta (\delta )$ converges uniformly to it.

Remarks

Error estimation for continuous bounded function $\eta (\delta )$ by using the above theorem 2.

$\eta (\delta )$ is the exact solution and ${\eta }_{app}(\delta )$ is the Genochhi wavelet approximation.

Where, $\eta \left(\delta \right)={\sum\limits }_{n=1}^{\infty }{\sum\limits }_{m=0}^{\infty }{ a}_{n,m}{\mathcal{H}}_{n,m} \left(\delta \right)$ and ${\eta }_{app}\left(\delta \right)={\sum\limits }_{n=1}^{{2}^{\frac{k -1}{2}}}{\sum\limits }_{m=0}^{M-1}{ a}_{n,m}{\mathcal{H}}_{n,m} (\delta )$.

$$\eta \left(\delta \right)-{\eta }_{app}\left(\delta \right)={\sum\limits }_{n=1}^{\infty }{\sum\limits }_{m=0}^{\infty }{ a}_{n,m}{\mathcal{H}}_{n,m} \left(\delta \right)-{\sum\limits }_{n=1}^{{2}^{\frac{k -1}{2}}}{\sum\limits }_{m=0}^{M-1}{ a}_{n,m}{\mathcal{H}}_{n,m} \left(\delta \right) ={\sum }_{n={2}^{k}}^{\infty }{\sum }_{m=M}^{\infty }{ a}_{n,m}{\mathcal{H}}_{n,m} \left(\delta \right)$$

Now, ${\Vert {E}_{n}\Vert }^{2}={\Vert \eta \left(\delta \right)-{\eta }_{app}\left(\delta \right)\Vert }^{2}=\langle \eta \left(\delta \right)-{\eta }_{app}\left(\delta \right),\eta \left(\delta \right)-{\eta }_{app}\left(\delta \right)\rangle ,$ $\Rightarrow {\Vert {E}_{n}\Vert }^{2}=\underset{0}{\overset{1}{\int }}{\sum\limits }_{n={2}^{k}}^{\infty }{\sum\limits }_{m=M}^{\infty }{a}_{n,m }^{2}{\mathcal{H}}_{n,m}^{2} \left(\delta \right)$

But from the above theorem, we have, $\left|{a}_{n,m}\right| \le \left|\frac{{2}^{\frac{-k-1}{2}}}{\sqrt{\frac{(-1{)}^{m-1}(m!{)}^{2}{\alpha }_{2m}}{\left(2m\right)!}}} \mu h\right|,$

$$\Rightarrow {\Vert {E}_{n}\Vert }^{2}\le \underset{0}{\overset{1}{\int }}{\sum\limits }_{n={2}^{k}}^{\infty }{\sum\limits }_{m=M}^{\infty }\frac{{2}^{-k-1}}{\frac{(-1{)}^{m-1}(m!{)}^{2}{\alpha }_{2m}}{\left(2m\right)!}} {\mu }^{2} {h}^{2}{\mathcal{H}}_{n,m}^{2} \left(\delta \right).$$

Theorem 3

[29]: Let $I\subset R$ be a finite interval with length $m(I)$. Furthermore, $f(\delta )$ is an integrable function defined on $I$ and $\sum_{i=0}^{M-1}\sum_{j=1}^{{2}^{k-1}}{a}_{i,j}{\mathcal{H}}_{i,j}(\delta )$ be a good Genocchi wavelet approximation of $f$ on $I$ with for some $\epsilon >0$, $\left|f\left(\delta \right)-\sum_{i=0}^{M-1}\sum_{j=1}^{{2}^{k-1}}{a}_{i,j} {\mathcal{H}}_{i,j}(\delta )\right|\le \epsilon , \forall x \in I$. Then $-\epsilon m\left(I\right)+{\int }_{I}\sum \sum {a}_{i,j} {\mathcal{H}}_{i,j}(\delta ) d\delta \le$ ${\int }_{I}f\left(\delta \right)d\delta \le \epsilon m\left(I\right)+{\int }_{I}\sum \sum {a}_{i,j} {\mathcal{H}}_{i,j}(\delta ) d\delta$.

3 Operational matrix of integration (OMI)

The Genocchi wavelet basis at $k=1$ and $M=6$ are found in the following manner:

$${\mathcal{H}}_{\mathrm{1,0}}\left(\delta \right)=1$$

$${\mathcal{H}}_{\mathrm{1,1}}\left(\delta \right)=\sqrt{3}(-1+2\delta )$$

$${\mathcal{H}}_{\mathrm{1,2}}\left(\delta \right)=\sqrt{30}(-1+\delta )\delta $$

$${\mathcal{H}}_{\mathrm{1,3}}\left(\delta \right)=\sqrt{\frac{35}{17}} (1-6{\delta }^{2}+4{\delta }^{3})$$

$${\mathcal{H}}_{\mathrm{1,4}}\left(\delta \right)=3\sqrt{\frac{70}{31}} (\delta -2{\delta }^{3}+{\delta }^{4})$$

$${\mathcal{H}}_{\mathrm{1,5}}\left(\delta \right)=3\sqrt{\frac{154}{691}} (-1+2\delta ){(1+\delta -{\delta }^{2})}^{2}$$

$${\mathcal{H}}_{\mathrm{1,6}}\left(\delta \right)=2\sqrt{\frac{3003}{5461}} \delta (-3+5{\delta }^{2}-3{\delta }^{4}+{\delta }^{5})$$

$${\mathcal{H}}_{\mathrm{1,7}}\left(\delta \right)=3\sqrt{\frac{715}{929569}} (17-84{\delta }^{2}+70{\delta }^{4}-28{\delta }^{6}+8{\delta }^{7})$$

Once the first six bases mentioned above have been integrated with respect to the $\delta$ limit between 0 and $\delta$, the Genocchi wavelet bases can be expressed as a linear combination as follows:

$$\underset{0}{\overset{\delta }{\int }}{\mathcal{H}}_{\mathrm{1,0}}\left(\delta \right)d\delta =\left[\begin{array}{ccc}\frac{1}{2}& \frac{1}{2\sqrt{3}}& \begin{array}{ccc}0& 0& \begin{array}{cc}0& 0\end{array}\end{array}\end{array}\right] {\mathcal{H}}_{6}\left(\delta \right)$$

$$\underset{0}{\overset{\delta }{\int }}{\mathcal{H}}_{\mathrm{1,1}}\left(\delta \right)d\delta =\left[\begin{array}{cccccc}0& 0& \frac{1}{\sqrt{10}}& 0& 0& 0\end{array}\right]{\mathcal{H}}_{6}\left(\delta \right)$$

$$\underset{0}{\overset{\delta }{\int }}{\mathcal{H}}_{\mathrm{1,2}}\left(\delta \right)d\delta =\left[\begin{array}{cccccc}-\frac{\sqrt{\frac{5}{6}} }{2}& 0& 0& \frac{\sqrt{\frac{17}{42}} }{2}& 0& 0\end{array}\right]{\mathcal{H}}_{6}\left(\delta \right)$$

$$\underset{0}{\overset{\delta }{\int }}{\mathcal{H}}_{\mathrm{1,3}}\left(\delta \right)d\delta =\left[\begin{array}{cccccc}0& 0& 0& 0& \frac{\sqrt{\frac{31}{34}} }{3}& 0\end{array}\right]{\mathcal{H}}_{6}\left(\delta \right)$$

$$\underset{0}{\overset{\delta }{\int }}{\mathcal{H}}_{\mathrm{1,4}}\left(\delta \right)d\delta =\left[\begin{array}{cccccc}3\sqrt{\frac{7}{310}} & 0& 0& 0& 0& \frac{\sqrt{\frac{691}{1705}} }{2}\end{array}\right]{\mathcal{H}}_{6}\left(\delta \right)$$

$$\underset{0}{\overset{\delta }{\int }}{\mathcal{H}}_{\mathrm{1,5}}\left(\delta \right)d\delta =\left[\begin{array}{cccccc}0& 0& 0& 0& 0& 0\end{array}\right] {\mathcal{H}}_{6}\left(\delta \right)$$

$$\underset{0}{\overset{\delta }{\int }}\mathcal{H}\left(\delta \right) d\delta ={\hbox{B}}_{6\times 6}{ \mathcal{H}}_{6}\left(\delta \right)+{\overline{\mathcal{H}} }_{6}\left(\delta \right)$$

(3)

where,

$${\mathcal{H}}_{6}\left(\delta \right)\ne {\left[{\mathcal{H}}_{\mathrm{1,0}}\left(\delta \right),{ \mathcal{H}}_{\mathrm{1,1}}\left(\delta \right), {\mathcal{H}}_{\mathrm{1,2}}\left(\delta \right),{ \mathcal{H}}_{\mathrm{1,3}}\left(\delta \right), {\mathcal{H}}_{\mathrm{1,4}}\left(\delta \right),{ \mathcal{H}}_{\mathrm{1,5}}\left(\delta \right)\right]}^{T}$$

$${\hbox{B}}_{6\times 6}=\left[\begin{array}{cccccc}\frac{1}{2}& \frac{1}{2\sqrt{3}}& 0& 0& 0& 0\\ 0& 0& \frac{1}{\sqrt{10}}& 0& 0& 0\\ -\frac{\sqrt{\frac{5}{6}} }{2}& 0& 0& \frac{\sqrt{\frac{17}{42}} }{2}& 0& 0\\ 0& 0& 0& 0& \frac{\sqrt{\frac{31}{34}} }{3}& 0\\ 3\sqrt{\frac{7}{310}} & 0& 0& 0& 0& \frac{\sqrt{\frac{691}{1705}} }{2}\\ 0& 0& 0& 0& 0& 0\end{array}\right] , {\overline{\mathcal{H}} }_{6}\left(\delta \right)=\left[\begin{array}{c}\begin{array}{c}0\\ 0\\ 0\\ 0\\ 0\\ \sqrt{\frac{5461}{53898}} {\mathcal{H}}_{\mathrm{1,6}}\left(\delta \right)\end{array}\end{array}\right]$$

At $k=2$ and $M=6$, the Genocchi wavelet basis is investigated as follows:

$$\left.\begin{array}{c}{\mathcal{H}}_{\mathrm{1,0}}\left(\delta \right)=\sqrt{2}\\ {\mathcal{H}}_{\mathrm{1,1}}\left(\delta \right)=\sqrt{6}(-1+4\delta )\\ { \mathcal{H}}_{\mathrm{1,2}}\left(\delta \right)=4\sqrt{15} \delta (-1+2\delta )\\ { \mathcal{H}}_{\mathrm{1,3}}\left(\delta \right)=\sqrt{\frac{70}{17}} (1-24{\delta }^{2}+32{\delta }^{3})\\ {\mathcal{H}}_{\mathrm{1,4}}\left(\delta \right)=12\sqrt{\frac{35}{31}} (\delta -8{\delta }^{3}+8{\delta }^{4})\\ {\mathcal{H}}_{\mathrm{1,5}}\left(\delta \right)=6\sqrt{\frac{77}{691}} (-1+4\delta ){(1+2\delta -4{\delta }^{2})}^{2}\end{array}\right\}0\le \delta <\frac{1}{2}$$

$$\left.\begin{array}{c}{\mathcal{H}}_{\mathrm{2,0}}\left(\delta \right)=\sqrt{2}\\ {\mathcal{H}}_{\mathrm{2,1}}\left(\delta \right)=\sqrt{6}(-3+4\delta )\\ {\mathcal{H}}_{\mathrm{2,2}}\left(\delta \right)=4\sqrt{15}(1-3\delta +2{\delta }^{2})\\ {\mathcal{H}}_{\mathrm{2,3}}\left(\delta \right)=\sqrt{\frac{70}{17}} (-9+48\delta -72{\delta }^{2}+32{\delta }^{3})\\ {\mathcal{H}}_{\mathrm{2,4}}\left(\delta \right)=12\sqrt{\frac{35}{31}} (1-9\delta +24{\delta }^{2}-24{\delta }^{3}+8{\delta }^{4})\\ {\mathcal{H}}_{\mathrm{2,5}}\left(\delta \right)=6\sqrt{\frac{77}{691}} (-3+4\delta ){(1-6\delta +4{\delta }^{2})}^{2}\end{array}\right\}\frac{1}{2} \le \xi <1$$

$$\underset{0}{\overset{\delta }{\int }}\mathcal{H}\left(\delta \right) d\delta ={\hbox{B}}_{12\times 12}{ \mathcal{H}}_{12}\left(\delta \right)+{\mathcal{H}}_{12}\left(\delta \right)$$

(4)

where ${\mathcal{H}}_{12}\left(\delta \right)={[{\mathcal{H}}_{\mathrm{1,0}}\left(\delta \right),{\mathcal{H}}_{\mathrm{1,1}}\left(\delta \right),{\mathcal{H}}_{\mathrm{1,2}}\left(\delta \right),{\mathcal{H}}_{\mathrm{1,3}}\left(\delta \right),{ \mathcal{H}}_{\mathrm{1,4}}\left(\delta \right),{\mathcal{H}}_{\mathrm{1,5}}\left(\delta \right), { \mathcal{H}}_{\mathrm{2,0}}\left(\delta \right),{ \mathcal{H}}_{\mathrm{2,1}}\left(\delta \right),{\mathcal{H}}_{\mathrm{2,2}}\left(\delta \right),{\mathcal{H}}_{\mathrm{2,3}}\left(\delta \right),{\mathcal{H}}_{\mathrm{2,4}}\left(\delta \right),{\mathcal{H}}_{\mathrm{2,5}}\left(\delta \right)]}^{T}$

$${\hbox{B}}_{12\times 12} =\left[\begin{array}{cccccccccccc}\frac{1}{4}& \frac{1}{4\sqrt{3}}& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& \frac{1}{2\sqrt{10}}& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ -\frac{\sqrt{\frac{5}{6}} }{4}& 0& 0& \frac{\sqrt{\frac{17}{42}} }{4}& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& \frac{\sqrt{\frac{31}{34}} }{6}& 0& 0& 0& 0& 0& 0& 0\\ \frac{3\sqrt{\frac{7}{310}} }{2}& 0& 0& 0& 0& \frac{\sqrt{\frac{691}{1705}} }{4}& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& \frac{1}{4}& \frac{1}{4\sqrt{3}}& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& \frac{1}{2\sqrt{10}}& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& -\frac{\sqrt{\frac{5}{6}} }{4}& 0& 0& \frac{\sqrt{\frac{17}{42}} }{4}& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& \frac{\sqrt{\frac{31}{34}} }{6}& 0\\ 0& 0& 0& 0& 0& 0& \frac{3\sqrt{\frac{7}{310}} }{2}& 0& 0& 0& 0& \frac{\sqrt{\frac{691}{1705}} }{4}\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right] , \text{and} \quad {\overline{\mathcal{H}} }_{12}\left(\delta \right)=\left[\begin{array}{c}\begin{array}{c}0\\ 0\\ 0\\ 0\\ 0\\ \frac{\sqrt{\frac{5461}{53898}} }{2} {\mathcal{H}}_{\mathrm{1,6}}\left(\delta \right)\\ 0\\ 0\\ 0\\ 0\\ 0\\ \frac{\sqrt{\frac{5461}{53898}} }{2}{\mathcal{H}}_{\mathrm{2,6}}\left(\delta \right)\end{array}\end{array}\right]$$

The generalized first integration of $n$-wavelet basis at $k=2$ is defined as:

$$\underset{0}{\overset{\delta }{\int }}\mathcal{H}\left(\delta \right)d\delta ={\hbox{B}}_{2n\times 2n}\mathcal{H}\left(\delta \right)+{\overline{\mathcal{H}} }_{2n}\left(\delta \right).$$

4 Genocchi wavelet collocation method

This section describes the solution to an ODE system that represents the mathematical model of Typhoid disease via GWCM.

Assume that,

$$\left.\begin{array}{c}\frac{dS(\delta )}{d\delta }={A}^{T} H\left(\delta \right)\\ \frac{dQ(\delta )}{d\delta }={B}^{T }H\left(\delta \right)\\ \frac{dI(\delta )}{d\delta }={C}^{T} H\left(\delta \right)\\ \frac{dR(\delta )}{d\delta }={D}^{T} H\left(\delta \right)\\ \frac{dW(\delta )}{d\delta }={E}^{T} H\left(\delta \right)\end{array}\right\}$$

(5)

where,${A}^{T}=[ {a}_{\mathrm{1,0}},\dots {a}_{1, {\prime}M-1},{ a}_{\mathrm{2,0}},\dots {a}_{2,M-1},{a}_{{2}^{k-1},0},\dots .{a}_{{2}^{k-1},M-1}],$

$${B}^{T}=[{ b}_{\mathrm{1,0}},\dots {b}_{1,M-1}, {b}_{\mathrm{2,0}},\dots {b}_{2,M-1},{b}_{{2}^{k-1},0},\dots {b}_{{2}^{k-1},M-1}],$$

$${C}^{T}=[{ c}_{\mathrm{1,0}},\dots {c}_{1,M-1}, {c}_{\mathrm{2,0}},\dots {c}_{2,M-1},{c}_{{2}^{k-1},0},\dots {c}_{{2}^{k-1},M-1}],$$

$${D}^{T}=[{ d}_{\mathrm{1,0}},\dots {d}_{1,M-1}, {d}_{\mathrm{2,0}},\dots {d}_{2,M-1},{d}_{{2}^{k-1},0},\dots {d}_{{2}^{k-1},M-1}],$$

$${E}^{T}=[{ e}_{\mathrm{1,0}},\dots {e}_{1,M-1}, {e}_{\mathrm{2,0}},\dots {e}_{2,M-1},{e}_{{2}^{k-1},0},\dots {e}_{{2}^{k-1},M-1}],$$

$$\mathcal{H}\left(\delta \right)=[{\mathcal{H}\left(\delta \right)}_{\mathrm{1,0}},\dots {\mathcal{H}\left(\delta \right)}_{1,M-1},{\mathcal{H}\left(\delta \right)}_{\mathrm{2,0}},\dots {\mathcal{H}\left(\delta \right)}_{2,M-1},{\mathcal{H}\left(\delta \right)}_{{2}^{k-1},0},\dots {\mathcal{H}\left(\delta \right)}_{{2}^{k-1},M-1}]. $$

Computational algorithm

Step 1: Start.

Step 2: Input the wavelet functions $\mathcal{H}\left(\delta \right)$, and unknown coefficients A, B, C, D, and E.

Step 3: Assume $\frac{dS(\delta )}{d\delta }={A}^{T} \mathcal{H}\left(\delta \right)$, $\frac{dQ(\delta )}{d\delta }={B}^{T }\mathcal{H}\left(\delta \right)$, $\frac{dI(\delta )}{d\delta }={C}^{T} \mathcal{H}\left(\delta \right)$, $\frac{dR(\delta )}{d\delta }={D}^{T} \mathcal{H}\left(\delta \right)$ and $\frac{dW(\delta )}{d\delta }={E}^{T} \mathcal{H}\left(\delta \right)$.

Step 4: Input the operational matrices ${\hbox{B}}$ and $\overline{\mathcal{H} }(\delta )$.extracted from the wavelet functions.

Step 5: Integrate the set of equations assumed in Step 3 concerning the independent variable $\delta$ ranging from 0 to $\delta$.

Step 6: Replacing the integral terms of Step 5 with the operational matrices obtained in Step 3 and expressing the given initial conditions as wavelet functions, we obtain ${S\left(\delta \right)={F}^{T}\mathcal{H}\left(\delta \right) + A}^{T}\left[{\hbox{B}}\mathcal{H}\left(\delta \right) + \overline{\mathcal{H} }(\delta )\right],$

${Q\left(\delta \right)={G}^{T}\mathcal{H}\left(\delta \right)+ B}^{T}\left[{\hbox{B}} \mathcal{H}\left(\delta \right)+ \overline{\mathcal{H} }\left(\delta \right)\right]$, ${I\left(\delta \right)={H}^{T}\mathcal{H}\left(\delta \right)+ C}^{T}\left[{\hbox{B}} \mathcal{H}\left(\delta \right)+ \overline{\mathcal{H} }\left(\delta \right)\right]$, ${R\left(\delta \right)={K}^{T}\mathcal{H}\left(\delta \right)+ D}^{T}\left[{\hbox{B}} \mathcal{H}\left(\delta \right)+ \overline{\mathcal{H} }\left(\delta \right)\right]$ and ${W\left(\delta \right)={L}^{T}\mathcal{H}\left(\delta \right) + E}^{T}\left[{\hbox{B}} \mathcal{H}\left(\delta \right)+ \overline{\mathcal{H} }(\delta )\right]$.

Step 7: Differentiate Step 6 fractionally concerning $\delta$ using the Caputo-fractional derivative definition.

Step 8: Substitute Step 7, Step 6, and Step 3 in the considered model and collocate the system with the collocation points ${\delta }_{i}=\frac{2i-1}{{2}^{k}M}, i=1, 2\dots M$.

Step 9: Apply the Newton–Raphson method to solve the set of algebraic equations derived from Step 8 for the unknown coefficients.

Step 10: Replace the unknown coefficients obtained from Step 9 in Step 6 to obtain the wavelet solution of the considered system of FDEs.

Step 11: Stop.

Workflow diagram:

5 Numerical results and discussion

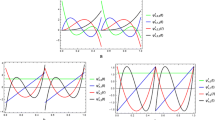
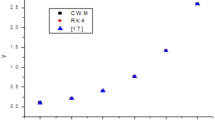
In general, today’s problems are not determinable but have stochastic influence, which offers an additional logical way to illustrate viral dynamics. Here, we employed the Genocchi wavelet collocation method to solve SFODEs. We found a suitable solution for the Typhoid model. Here, using the operational matrix from Sect. 2 as support, we applied the Genocchi wavelet collocation method to transform the set of nonlinear differential equations into a set of algebraic equations. Later, with the Newton–Raphson approach, the set of nonlinear algebraic equations is resolved, and the Genocchi wavelet coefficients and wavelet-based numerical solutions of $S\left(\delta \right), Q\left(\delta \right), I\left(\delta \right), R\left(\delta \right)$ and $W\left(\delta \right)$ are obtained for the model by substituting these coefficient values. Tables 1, 2, 3, 4 and 5 display the GWCM solutions produced for the integer order value of $\alpha =1$ which demonstrate that the suggested method solutions are relatively close to the NDSolve results when compared to the RK4 technique. The graphical representation of the solution compared with other techniques were carried out in Figs. 1, 2, 3, 4 and 5. The absolute error of the proposed method at diverse values of $M$ and $k$ are computed and listed in Table 6, 7, 8, 9 and 10. The numerical values of the model at $\alpha =0.2, 0.4, 0.6, 0.8,$ and 1.0 are calculated and tabulated in Table 11, 12, 13, 14 and 15. Figures 11, 12, 13, 14 and 15 provide the graphical depiction of the solution at $\alpha =0.2, 0.4, 0.6, 0.8,$ and $1.0,$ respectively. GWCM solutions are computed for a range of M and k values. Furthermore, increasing the values of M and k yields even more precision in the outcome, as seen in Figs. 6, 7, 8, 9 and 10. Therefore, based on graphical data, we may conclude that the model depends significantly on the order of fractional derivatives, which produces more biologically realistic outcomes. Additionally, we conclude that, compared to the analogous integer order Typhoid model, the suggested model under Caputo fractional order derivative offers more prosperous and flexible outcomes (Figs. 11, 12, 13, 14, 15).

Table 1 Comparison of numerical approximation and its Absolute error for $S(\delta )$

Table 2 Comparison of numerical approximation and its Absolute error for $Q(\delta )$

Table 3 Numerical comparison of the proposed technique with other techniques and its absolute error for $I(\delta )$

Table 4 Numerical comparison of the proposed technique with other techniques and its absolute error for $R(\delta )$

Table 5 Numerical comparison of the proposed technique with other techniques and its Absolute error for $W(\delta )$

Fig. 1

Approximate solutions of susceptible individuals $S(\delta )$

Fig. 2

Approximate solutions of susceptible individuals $Q(\delta )$

Fig. 3

Approximate solutions of susceptible individuals $I(\delta )$

Fig. 4

Approximate solutions of susceptible individuals $R(\delta )$

Fig. 5

Approximate solutions of susceptible individuals $W(\delta )$

Table 6 Comparision of absolute error for $S(\delta )$

Table 7 Comparision of absolute error for $Q(\delta )$

Table 8 Comparision of absolute error for $I(\delta )$

Table 9 Comparision of absolute error for $R(\delta )$

Table 10 Comparision of absolute error for $W(\delta )$

Table 11 Genocchi wavelet collocation method solution at diverse values of $\alpha$ for $S(\delta )$

Table 12 Genocchi wavelet collocation method solution at diverse values of $\alpha$ for $Q(\delta )$

Table 13 Genocchi wavelet collocation method solution at diverse values of $\alpha$ for $I(\delta )$

Table 14 Genocchi wavelet collocation method solution at various values of $\alpha$ for $R(\delta )$

Table 15 Genocchi wavelet collocation method solution at different values of $\alpha$ for $W(\delta )$

Fig. 6

Absolute error analysis of $S(\delta )$

Fig. 7

Absolute error analysis of $Q(\delta )$

Fig. 8

Absolute error analysis of $I(\delta )$

Fig. 9

Absolute error analysis of $R(\delta )$

Fig. 10

Absolute error analysis of $W(\delta )$

Fig. 11

Visual depiction of $S\left(\delta \right)$ with distinct values of $\alpha$

Fig. 12

Graphical depiction of $Q\left(\delta \right)$ with distinct values of $\alpha$

Fig. 13

Graphical depiction of $E\left(\delta \right)$ with distinct values of $\alpha$

Fig. 14

Graphical depiction of $R\left(\delta \right)$ with distinct values of $\alpha$

Fig. 15

Graphical depiction of $W\left(\delta \right)$ with distinct values of $\alpha$

6 Conclusion

In this study, we proposed a numerical approximation to the fractional order Typhoid disease model. The numerical solution was derived using the GWCM with the help of the Caputo fractional derivative. An innovative operational matrix is built based on the Genocchi wavelets at various resolutions (k) and used with the collocation approach to solve the model numerically. The solutions obtained from the developed strategy have been compared with techniques such as RK4 and ND Solver. Additionally, numerical examples support the idea that only a few Genocchi wavelets are required to attain suitable outcomes. Although the technique was easy to apply, the procedure produced an excellent result. The results that were obtained reinforced our belief that the method works well for managing highly nonlinear FDEs. The approach under discussion is straightforward, easy to apply, and requires less computing power. As a result, we concluded that the procedure under consideration is a prominent tool compared to RK4 to attain the numerical approximation of the mathematical models in the form of nonlinear FDEs.