Functional determinant approach investigations of heavy impurity physics

Abstract

In this brief review, we report some new development in the functional determinant approach (FDA), an exact numerical method, in the studies of a heavy quantum impurity immersed in Fermi gases and manipulated with radio-frequency pulses. FDA has been successfully applied to investigate the universal dynamical responses of a heavy impurity in an ultracold ideal Fermi gas in both the time and frequency domain, which allows the exploration of the renowned Anderson’s orthogonality catastrophe (OC). In such a system, OC is induced by the multiple particle-hole excitations of the Fermi sea, which is beyond a simple perturbation picture and manifests itself as the absence of quasiparticles named polarons. More recently, two new directions for studying heavy impurity with FDA have been developed. One is to extend FDA to a strongly correlated background superfluid background, a Bardeen–Cooper–Schrieffer (BCS) superfluid. In this system, Anderson’s orthogonality catastrophe is prohibited due to the suppression of multiple particle-hole excitations by the superfluid gap, which leads to the existence of genuine polaron. The other direction is to generalize the FDA to the case of multiple RF pulses scheme, which extends the well-established 1D Ramsey spectroscopy in ultracold atoms into multidimensional, in the same spirit as the well-known multidimensional nuclear magnetic resonance and optical multidimensional coherent spectroscopy. Multidimensional Ramsey spectroscopy allows us to investigate correlations between spectral peaks of an impurity-medium system that is not accessible in the conventional one-dimensional spectrum.

1 Introduction

An important approach to investigating polaron physics is to study the heavy impurity limit. Infinitely heavy impurity interacting with a Fermi sea represents one of the rare examples of exactly solvable many-body problems in the nonperturbative regime, which can serve as a benchmark for various approximations. Historically, this problem originated from the studies of the x-ray spectra in metals, where Mahan predicts the so-called Fermi edge singularities (FES), absorption edges in the spectra characterized by a power law divergence near the threshold [1]. The optical transition is determined by a highly spatial localized core-level hole that can be regarded as an impurity with infinite mass immersed in a Fermi sea of conduction electrons. The corresponding model Hamiltonian can be solved exactly and is often called MND Hamiltonian in the condensed matter community after the work of Mahan [2, 3] and Noziéres-De Dominicis [4].

FES is the first and one of the most important examples of nonequilibrium many-body physics. The underlying physics can be interpreted by the concept of Anderson’s orthogonality catastrophe (OC) [5], i.e., the many-particle states with and without impurity become orthogonal. FES has also been observed in current-voltage characteristics of resonant tunneling experiments dominated by localized states [6, 7] and has been proposed to be investigated in various systems, including quantum wires [8,9,10] and quantum dots [11]. In particular, a convenient and numerically exact method, namely the functional determinant approach (FDA) [12,13,14,15], has been developed to study FES in out-of-equilibrium Fermi gases [16,17,18] and open quantum dots [19]. Using FDA to investigate MND Hamiltonians has also been applied to study exciton-polarons in monolayer transition metal dichalcogenides (TMD), where the exciton serves as the impurity, and the itinerant excess electrons play the role of the background Fermi sea [20, 21]. However, the prediction can only be considered qualitative here, as the exciton mass is only about twice the electron mass in TMDs.

In recent years, ultracold quantum gases have emerged as an ideal testbed for impurity physics thanks to their unprecedented controllability. In the context of ultracold Fermi gases, the FES of an infinitely heavy impurity in an ideal Fermi gas has been quantitatively re-examined via the FDA [22, 23] and can be verified via Ramsey-interference-type experiments [24]. The Ramsey signals in the time domain are universal, i.e., fully determined by the impurity-medium scattering length and the Fermi wave vector of the medium Fermi gases, not only in the long-time limit (as their counterpart in solid-state systems) but also for all times. Corresponding spectra in the frequency domain obtained by Fourier transformation show FES and provide an insightful understanding of polaron physics. The exact results of the FDA can serve as benchmark calculations for various approximation calculations of Fermi polarons, such as Chevy’s ansatz or equivalently many-body T-matrix [25,26,27,28,29,30,31,32,33,34,35,36], and other exact methods, such as quantum Monte Carlo methods [37,38,39,40].

However, polaron, strictly speaking, does not exist in the infinitely heavy impurity limit, where the quasiparticle residue of polaron vanishes due to the presence of OC [22, 23]. On the other hand, the generalization of the FDA to finite impurity mass remains elusive. Nevertheless, FDA has been proven to be qualitatively accurate in describing heavy polarons in ultracold Fermi gases at a finite temperature, where thermal fluctuation is comparable with recoil energy [41, 42]. In addition, one can choose an impurity with very different polarizability from the background fermions. As a result, the impurity can be confined by a deep optical lattice or an optical tweezer without affecting the itinerant background fermions. In this case, the infinitely heavy mass limit becomes exact, and FDA calculations can serve as a critical meeting point for theoretical and experimental efforts to understand the complicated quantum dynamics of interacting many-particle systems. Inspired by the pioneer works [22, 23], a heavy impurity in Fermi gases has also been proposed to investigate spin transportation [43] and precise measurement of the temperature of noninteracting Fermi gases [44]. The exact finite-temperature free energy and Tan contact [45], as well as the exact dynamics of Tan contact of a heavy impurity in ideal Fermi gases, can be derived as a generalization of FDA [46]. Rabi oscillations of heavy impurities in an ideal Fermi gas can also be investigated via FDA [47]. Extensions of the FDA to the investigation of Rydberg impurities [48, 49] in Fermi [50] and Bose gases [51,52,53] have also been developed recently.

Here, we briefly review the formalism of the FDA and two recent developments. Firstly, FDA has been generalized to the system of a heavy impurity in a Bardeen–Cooper–Schrieffer (BCS) superfluid, where the strongly correlated superfluid background is described by a BCS mean-field wavefunction [54, 55]. In contrast to the ideal Fermi gas case, the pairing gap in the BCS superfluid prevents the OC and leads to genuine polaron signals in the spectrum even at zero-temperature. In addition, at finite temperature, additional features related to the subgap Yu-Shiba-Rusinov (YSR) bound state were predicted in the spectra of a magnetic impurity. Another recent development is to extend the FDA to multidimensional (MD) spectroscopy. In contrast to conventional one-dimensional (1D) spectroscopy which depends only on one variable, such as photon frequency, MD spectroscopy unfolds spectral information into several dimensions, revealing correlations between spectral peaks that the 1D spectrum cannot access.

2 Formalism

2.1 System setup

The basic setup of our system is shown in Fig. 1 a. We place a localized fermionic or bosonic impurity (the big black ball with a black arrow) with two internal pseudospins states $|\uparrow \rangle$ and $|\downarrow \rangle$ , which we will call spins for short from now on, in the background of ultracold Fermi gas (the red dots). In real experiments, there is usually more than one impurity, but the impurity density is prepared to be very low so that the interaction between impurities can be regarded as negligible. As mentioned before, the localization of impurity can be either achieved by confinement of a deep optical trap or treated as an approximation to an impurity atom with heavy mass. Unless specified otherwise, we are interested in the case where the interaction between the background Fermi gas and $|\downarrow \rangle$ is negligible, while the interaction with $|\uparrow \rangle$ is arbitrarily tunable by, e.g., Feshbach resonances. (It is straightforward to generalize to the case where both $|\uparrow \rangle$ and $|\downarrow \rangle$ interact with the background.) The spins states can be manipulated by radio-frequency (RF) pulses, which assume to be able to rotate the spins infinitely fast. In reality, the RF pulse length is usually comparable with the characteristic time scale $\tau _{F}=E_{F}^{-1}$ of the background Fermi gases, where $E_{F}$ is the Fermi energy, and we use unit $\hbar =1$ throughout this work. For example, in Ref. [41], the typical pulse length is about 10 $\mu$s, approximately 3.4 $\tau _{F}$ in their system. However, the optical control of Feshbach resonances in their experiment can be achieved very rapidly in less than 200 ns, which is about 0.08 $\tau _{F}$. As a result, one can switch off the interaction (for both spin states) in no time and rotate the spin without perturbing the background Fermi gas, which can be treated as an infinitely fast rotation theoretically. The interaction is switched back on after the rotation. In principle, one can rotate the spin in the Block sphere along an arbitrary axis, characterized by a unit vector $\vec {n}=(n_{x},n_{y},n_{z})$, for an arbitrary angle $\theta$. The rotation can be described by a unitary matrix in the spin basis as

$$\begin{aligned} R_{\vec {n}}(\theta )=\exp (-i\frac{\theta }{2}\vec {n}\cdot \vec {\sigma }), \end{aligned}$$

(1)

where $\vec {\sigma }=(\sigma _{x},\sigma _{y},\sigma _{z})$ and $\sigma _{x}$, $\sigma _{y}$, and $\sigma _{z}$ are Pauli matrices in the spin basis. A $\pi /2$-pulse along the $-\hat{y}$-axis gives $R_{-\hat{y}}(\pi /2)|\downarrow \rangle =(|\uparrow \rangle +|\downarrow \rangle )/\sqrt{2}$.

Fig. 1

a A sketch of the system setup for 1D Ramsey spectroscopy (injection scheme). b An interferometry interpretation of 1D Ramsey spectroscopy

The basic 1D Ramsey interferometric can be intuitively understood by the sketch in Fig. 1 (b). The effectively infinitely fast rotation allows one to prepare the system in a superposition state $|\Psi (0)\rangle =|\psi _{\text {FS}}\rangle \otimes (|\uparrow \rangle +|\downarrow \rangle )/\sqrt{2}$, where $|\psi _{\text {FS}}\rangle$ describes the zero-temperature ground state of the Fermi gas. For a single component Fermi gas, $|\psi _{\text {FS}}\rangle$ corresponds to all fermions occupying the lowest eigenenergy states, i.e., a Fermi sea. Here, we first briefly describe the general idea using pure and zero-temperature states. The detailed formalization and the straightforward generalization to finite-temperature density matrix description will be given later.

Since the two spin states interact differently with the Fermi sea, the associated time evolution operator after time t is different:

$$\begin{aligned} |\Psi (t)\rangle =\frac{1}{\sqrt{2}}(|\uparrow \rangle \otimes e^{-i\mathcal {H}_{\uparrow }t}|\psi _{\text {FS}}\rangle +|\downarrow \rangle \otimes e^{-i\mathcal {H}_{\downarrow }t}|\psi _{\text {FS}}\rangle ), \end{aligned}$$

(2)

where $\mathcal {H}_{\uparrow }$ and $\mathcal {H}_{\downarrow }$ are the Hamiltonian for a Fermi sea with an interacting and noninteracting impurity, respectively. The so-called many-body overlap function

$$\begin{aligned} S(t)\equiv \langle \psi _{\text {FS}}|e^{i\mathcal {H}_{\downarrow }t}e^{-i\mathcal {H}_{\uparrow }t}|\psi _{\text {FS}}\rangle \end{aligned}$$

(3)

can be measured via the interference

$$\begin{aligned} \text {Re}S(t)=\langle \sigma _{x}\rangle ,\ \text {Im}S(t)=-\langle \sigma _{y}\rangle , \end{aligned}$$

(4)

or equivalently $S(t)=\langle \sigma _{-}\rangle$ with $\sigma _{-}=\sigma _{x}-i\sigma _{y}$. Notice that for non-interacting $|\downarrow \rangle$, $\mathcal {H}_{\downarrow }|\psi _{\text {FS}}\rangle =E_{\text {FS}}|\psi _{\text {FS}}\rangle$ with $E_{\text {FS}}$ being the Fermi sea energy, i.e., the summation of eigenenergies of occupied states. Consequently, the overlap function $S(t)=e^{iE_{\text {FS}}t}\langle \psi _{\text {FS}}|e^{-i\mathcal {H}_{\uparrow }t}|\psi _{\text {FS}}\rangle$ takes the form of Loschmidt amplitude, the central object within the theory of dynamical quantum phase transitions [56].

A direct measurement of $\langle \sigma _{x}\rangle$ and $-\langle \sigma _{y}\rangle$ might not be as convenient as measuring $\langle \sigma _{z}\rangle =\left( N_{\uparrow }-N_{\downarrow }\right) /(N_{\uparrow }+N_{\downarrow })$, where $N_{\uparrow }$ and $N_{\downarrow }$ are the population of spin-up and spin-down impurities, respectively. (As mentioned above, there are usually a finite number of independent impurities in a realistic experiment.) Consequently, a standard protocol is to perform another rotation after the evolution time t. From the relation$R_{-\hat{y}}(\pi /2)^{-1}\sigma _{z}R_{-\hat{y}}(\pi /2)=\sigma _{x}$ and $R_{-\hat{x}}(\pi /2)^{-1}\sigma _{z}R_{-\hat{x}}(\pi /2)=-\sigma _{y}$, we can see that $\langle \sigma _{x}\rangle$ and $-\langle \sigma _{y}\rangle$ can be obtained by measuring $\sigma _{z}$ after rotation $R_{-\hat{y}}(\pi /2)$ and $R_{-\hat{x}}(\pi /2)$, respectively.

Since $|\uparrow \rangle$ and $|\downarrow \rangle$ correspond equivalently to the existence and absence of impurity in the single impurity case, we can therefore construct the creation operator $\hat{b}^{\dagger }$ and annihilation operator $\hat{b}$ for the impurity so that the full Hamiltonian can be written as

$$\begin{aligned} \hat{\mathcal {H}}=\hat{\mathcal {H}}_{\uparrow }|\uparrow \rangle \langle \uparrow |+\hat{\mathcal {H}}_{\downarrow }|\downarrow \rangle \langle \downarrow |=\hat{\mathcal {H}}_{\uparrow }\hat{b}^{\dagger }\hat{b}+\hat{\mathcal {H}}_{\downarrow }(1-\hat{b}^{\dagger }\hat{b}). \end{aligned}$$

(5)

The retarded Green’s function for the impurity can thus be written as

$$\begin{aligned} G_{I}(t)=-i\Theta (t)\langle \hat{b}(t)\hat{b}^{\dagger }\rangle , \end{aligned}$$

(6)

where $\hat{b}(t)=e^{i\hat{\mathcal {H}}t}\hat{b}e^{-i\hat{\mathcal {H}}t}$ in the Heisenberg picture. Tracing out the spin degree of freedom, we have the relationship between the retarded Green’s function and the many-body overlap function as

$$\begin{aligned} G_{I}(t)=-iS(t),\ t>0. \end{aligned}$$

(7)

As a result, the Fourier transformation

$$\begin{aligned} A(\omega )=\frac{1}{\pi }\int _{0}^{\infty }e^{i\omega t}S(t)dt=\frac{i}{\pi }\mathcal {G}_{I}(\omega ), \end{aligned}$$

(8)

is related to the retarded Green’s function in the frequency domain $\mathcal {G}_{I}(\omega )=\int _{0}^{\infty }e^{i\omega t}G_{I}(t)dt$, where the spectral function $\text {Re}A(\omega )=-\text {Im}\mathcal {G}_{I}(\omega )/\pi$ gives the absorption spectrum in the linear response regime. Throughout this work, $\text {Re}$ and $\text {Im}$ denote the real and imaginary parts of a complex number, respectively.

2.2 Functional determinant approach

In the previous section, we have given a general discussion of the underlying idea of 1D Ramsey responses of a heavy impurity and its relation to the absorption spectrum. Here, we show the detail of how to exactly solve the time-dependent problem nonperturbatively using the FDA. As a concrete example, we focus on the case where the background is a dilute single-component Fermi gas, which is considered to be noninteracting at ultracold temperature due to Pauli’s exclusion principle. As mentioned before, we assume only the background fermion only interacts with $|\uparrow \rangle$, which is dominated by the s-wave interaction that can be tuned via, e.g., Feshbach resonances. The corresponding Hamiltonian can be expressed in the form of Eq. 5, where

$$\begin{aligned} \hat{\mathcal {H}}_{\uparrow }=\hat{\mathcal {H}}_{\downarrow }+\sum _{\textbf{k},\textbf{q}}\tilde{V}(\textbf{k}-\textbf{q})\hat{c}_{\textbf{k}}^{\dagger }\hat{c}_{\textbf{q}}+\omega _{s},\ \hat{\mathcal {H}}_{\downarrow }=\sum _{\textbf{k}}\epsilon _{\textbf{k}}\hat{c}_{\textbf{k}}^{\dagger }\hat{c}_{\textbf{k}}. \end{aligned}$$

(9)

Here, $\omega _{s}$ denotes the energy differences between the two spin levels. $\hat{c}_{\textbf{k}}^{\dagger }$ and $\hat{c}_{\textbf{k}}$ are creation and annihilation operators of the background fermions with momentum $\textbf{k}$, respectively. $\epsilon _{\textbf{k}}=k^{2}/2m$ is the single-particle kinetic energy of the background fermions with mass m. $\tilde{V}(\textbf{k})$ is the Fourier transform of $V(\textbf{r})$, the interaction potential between $|\uparrow \rangle$ and the background fermions. The low-temperature physics is determined by the s-wave energy-dependent scattering length $a(E_{F})=-\tan \eta (k_{F})/k_{F}$ at the Fermi energy $E_{F}=k_{F}^{2}/2m$, with $\eta (E_{F})$ being an energy-dependent s-wave scattering phase-shift obtained from a two-body scattering calculation with potential $V(\textbf{r})$. For the simplicity of notation, we denote $a\equiv a(E_{F})$ hereafter.

For the example given here, we are interested in the so-called injection scheme where the spin is initially prepared in the noninteracting state $|\downarrow \rangle$. The initial density matrix of the system can therefore be written as $\rho _{i}=\rho _{\text {FS}}\otimes |\downarrow \rangle \langle \downarrow |$, where the thermal density matrix of the background fermion at a finite temperature $T^{\circ }$ is given by

$$\begin{aligned} \rho _{\text {FS}}=\prod _{\textbf{k}}\left[ n_{\textbf{k}}\hat{c}_{\textbf{k}}^{\dagger }\hat{c}_{\textbf{k}}+\left( 1-n_{\textbf{k}}\right) \hat{c}_{\textbf{k}}\hat{c}_{\textbf{k}}^{\dagger }\right] , \end{aligned}$$

(10)

with the occupation of the momentum state

$$\begin{aligned} n_{\textbf{k}}=\frac{1}{e^{\left( \epsilon _{\textbf{k}}-\mu \right) /k_{B}T^{\circ }}+1}. \end{aligned}$$

(11)

Here, $k_{B}$ is the Boltzman constant, $\mu \simeq E_{F}$ is the chemical potential determined by the number density of the background Fermi gas. We also define a diagonal matrix $\hat{n}$ with the matrix elements $n_{\textbf{k}}$, which will become useful later.

For the simple 1D Ramsey spectrum, we apply a $\pi /2$ RF pulse at $t=0$ that can be described in the spin-basis as

$$\begin{aligned} \hat{R}_{-\hat{y}}\left( \frac{\pi }{2}\right) \equiv \left( \begin{array}{cc} R_{\uparrow \uparrow }^{(\pi /2)}\textbf{1} &{} R_{\uparrow \downarrow }^{(\pi /2)}\textbf{1}\\ R_{\downarrow \uparrow }^{(\pi /2)}\textbf{1} &{} R_{\downarrow \downarrow }^{(\pi /2)}\textbf{1} \end{array}\right) =\frac{1}{\sqrt{2}}\left( \begin{array}{cc} \textbf{1} &{} \textbf{1}\\ -\textbf{1} &{} \textbf{1} \end{array}\right) , \end{aligned}$$

(12)

where $\textbf{1}$ represents the identity in the fermionic Hilbert space. For simplicity, we denote $\hat{\mathcal {R}}\equiv \hat{R}_{-\hat{y}}\left( \pi /2\right)$ hereafter. The total time evolution is determined by the unitary transformation

$$\begin{aligned} \hat{\mathcal {U}}(t)=\hat{U}(t)\hat{\mathcal {R}}, \end{aligned}$$

(13)

where

$$\begin{aligned} \hat{U}(t)=\left( \begin{array}{cc} e^{-i\hat{\mathcal {H}}_{\uparrow }t} &{} 0\\ 0 &{} e^{-i\hat{\mathcal {H}}_{\downarrow }t} \end{array}\right) \end{aligned}$$

(14)

is the free time evolution operator in the spin basis representation after the RF pulse. The final state of the system is thus given by $\rho _{f}=\mathcal {U}\rho _{i}\mathcal {U}^{\dagger }$. Recall that $S(t)=\langle \sigma _{-}\rangle$, we arrive at

$$\begin{aligned} S(t)=\text {Tr}\left( \sigma _{-}\rho _{f}\right) =\text {Tr}\left( e^{i\hat{\mathcal {H}}_{\downarrow }t}e^{-i\hat{\mathcal {H}}_{\uparrow }t}\rho _{\text {FS}}\right) \end{aligned}$$

(15)

that reduces to Eq. (3) at zero-temperature $k_{B}T^{\circ }=0$.

Since the complexity of the many-body Hamiltonians increases exponentially with the number of particles in the system, an exact calculation of S(t) is usually inaccessible. However, in the case that $H_{\uparrow }$ and $H_{\downarrow }$ are both fermionic, bilinear many-body operators as in Eq. (9), the overlap function can reduce to a determinant in single-particle Hilbert space. This approach, namely FDA, is based on a mathematical trace formula that has been elegantly proved by Klich [13]. (See Appendix A for details.) To proceed, we define $\hat{\mathcal {H}}_{\downarrow }\equiv \Gamma (h_{\downarrow })$ and $\hat{\mathcal {H}}_{\uparrow }\equiv \Gamma (h_{\uparrow })+\omega _{s}$. Here, $\Gamma (h)\equiv \sum _{\textbf{k},\textbf{q}}h_{\textbf{k}\textbf{q}}c_{\textbf{k}}^{\dagger }c_{\textbf{q}}$ is a bilinear fermionic many-body Hamiltonian in the Fock space, and $h_{\textbf{k}\textbf{q}}$ represents the matrix elements of the corresponding operator in the single-particle Hilbert space. Applying the Levitov’s formula, Eq. (58), gives $S(t)=e^{-i\omega _{s}t}\tilde{S}(t)$ where

$$\begin{aligned} \tilde{S}(t)=\text {det}[(\textbf{1}-\hat{n})+R(t)\hat{n}], \end{aligned}$$

(16)

and

$$\begin{aligned} R(t)=e^{ih_{\downarrow }t}e^{-ih_{\uparrow }t}. \end{aligned}$$

(17)

Correspondingly, the frequency domain spectrum can be obtained by a Fourier transformation

$$\begin{aligned} A(\omega )=\frac{1}{\pi }\int _{0}^{\infty }e^{i\omega t}S(t)dt=\frac{1}{\pi }\int _{0}^{\infty }e^{i\tilde{\omega }t}\tilde{S}(t)dt. \end{aligned}$$

(18)

Hereafter, unless specified otherwise, we denote $\tilde{\omega }=\omega -\omega _{s}$ for any frequency variable $\omega$. As one can see, $\omega _{s}$ has a simple effect as shifting the frequency origin of a 1D spectrum. Numerical calculations are carried out in a finite system confined in a sphere of radius R. Keeping the density constant, we increase R towards infinity until numerical results are converged. Other details of numerical calculations are described in the Appendix.

Figure 2 a and c show $\tilde{S}(t)$ for attractive ($k_{F}a=-2$) and repulsive impurity interaction ($k_{F}a=+2$), respectively. The zero-temperature (solid blue curves) asymptotic behavior of the Ramsey response at $t\rightarrow \infty$ is given by

$$\begin{aligned} \tilde{S}(t)\simeq{} & {} Ce^{-i\Delta Et}\left( \frac{1}{iE_{F}t+0^{+}}\right) ^{\alpha }\nonumber \\{} & {} +C_{b}e^{-i\left( \Delta E-E_{F}+E_{b}\right) t}\left( \frac{1}{iE_{F}t+0^{+}}\right) ^{\alpha _{b}}, \end{aligned}$$

(19)

where C and $C_{b}$ are both numerical constants independent with respect to $k_{F}a$ and $C_{b}=0$ for $a<0$. Here,

$$\begin{aligned} \alpha =\eta (E_{F})^{2}/\pi ^{2} \end{aligned}$$

(20)

and

$$\begin{aligned} \alpha _{b}=[1+\eta (E_{F})/\pi ]^{2} \end{aligned}$$

(21)

are determined by the s-wave scattering phase shifts $\eta (E_{F})$ at Fermi energy. $E_{b}$ is the binding energy of the shallowest bound state consisting of the impurity and a spin-up fermion for $a>0$. Furthermore, the change in energy can be understood as a renormalization of the Fermi sea by impurity scattering and is given by

$$\begin{aligned} \Delta E=\sum _{\nu =1}^{N}(E_{\nu }-\tilde{E}_{\nu }), \end{aligned}$$

(22)

where $E_{\nu }$ and $\tilde{E}_{\nu }$ are the lowest N eigenenergies of $\hat{h}_{\downarrow }$ and $\hat{h}_{\uparrow }$, respecitively, and the deeply bound states are excluded from $\tilde{E}_{\nu }$. Here N is the number of particles fixed by the chemical potential $\mu$.

Fig. 2

1D Ramsey spectroscopy for a, b attractive interaction $k_{F}a=-2$ and c, d repulsive interaction $k_{F}a=2$. a, c The overlap functions $\tilde{S}(t)$. b, d The spectral functions $\text {Re}A(\omega )$. Thick blue curves correspond to $k_{B}T^{\circ }=0$, thin red solid curves, and purple dashed curves correspond to $k_{B}T^{\circ }=0.03E_{F}$ and $k_{B}T^{\circ }=0.05E_{F}$, respectively

The corresponding spectral function $\text {Re}A(\omega )$ is shown in Fig. 2 b and d. The asymptotic behaviors of $\tilde{S}(t)$ translate into the threshold behaviors of spectra function at zero-temperature. For frequency $\tilde{\omega }\approx \Delta E$, we have a singularity $\text {Re}A(\omega )\propto \theta (\tilde{\omega }-\Delta E)|\tilde{\omega }-\Delta E|^{\alpha -1}$. If the impurity interaction is repulsive, an additional singularity shows up at $\tilde{\omega }\approx \omega _{b}=\Delta E-E_{F}+E_{b}$ as $\text {Re}A(\omega )\propto \theta (\tilde{\omega }-\omega _{b})|\tilde{\omega }-\omega _{b}|^{\alpha _{b}-1}$. These singularities are called FES and are closely related to the polaron resonances (see Fig. 4 for example): the spectrum only shows one peak for attractive impurity interaction and shows two peaks for repulsive interaction. We, therefore, name the FESs in Fig. 2 b and d as attractive or repulsive singularities, denoted by “A” and “R”, respectively. However, different than the polaron peaks that are Dirac delta functions or Lorentzians, the FESs are power-law singularities, which is a manifestation of OC: the quasiparticle resonances are rendered into power-law singularities by the multiple particle-hole excitations near the surface of Fermi sea. At a finite temperature, however, the thermal fluctuation leads to an exponential decay $\tilde{S}(t)$ and Lorentzian-shape broadening of singularities in $\text {Re}A(\omega )$, which allows FDA calculations to quantitatively predict the spectrum of mobile polaron if the thermal fluctuation is comparable to the recoil energy [41].

3 A BCS superfliuid as a background medium

This section extends the FDA to a strongly correlated superfluid background described by a standard BCS mean-field wavefunction [54, 55]. The purpose is twofold. First, we aim to construct an exactly solvable model for polaron with finite residue. This study shows that our system is suitable for an exact approach — an extended FDA. The presence of a pairing gap can efficiently suppress multiple particle-hole excitations and prevent Anderson’s OC. Therefore, our model provides a benchmark calculation of the polaron spectrum and rigorously examines all the speculated polaron features. We name our system “heavy crossover polaron” since the background Fermi gas can undergo a crossover from a Bose-Einstein condensation (BEC) to a BCS superfluid. Second, our prediction can be applied to investigate the background Fermi superfluid excitations, a long-standing topic in ultracold atoms. Polarons have already been realized in BEC and ideal Fermi gas experimentally, where the physics of these weakly interacting background gas is well understood. More recently, it has also been shown that polarons in BEC with a synthetic spin-orbit-coupling can reveal the nature of the background roton excitations [57]. Investigating polaron physics in a strongly correlated Fermi superfluid at the BEC-BCS crossover, namely crossover polaron, has also been proposed in several pioneering works with approximated approaches [58,59,60,61,62]. Our exact method in the heavy impurity limit allows us to apply the polaron spectrum to measure the Fermi superfluid excitation features, such as the pairing gap and sub-gap Yu-Shiba-Rusinov (YSR) bound states [63,64,65,66,67].

Our system consists of a localized impurity atom and a two-component Fermi superfluid with equal mass $m_{\Uparrow }=m_{\Downarrow }=m$. (Here, we use $|\Uparrow \rangle$ and $|\Downarrow \rangle$ to represent the two internal states of the background fermionic atoms, in contrast to the $|\uparrow \rangle$ and $|\downarrow \rangle$ for the impurity.) The interaction between unlike atoms in the two-component Fermi gas can be tuned by a broad Feshbach resonance and characterized by the s-wave scattering length $a_{F}$. At low temperatures T, these strongly interacting fermions undergo a crossover from a BEC to a BCS superfluid, which can be described by the celebrated BCS theory at a mean-field level. The full Hamiltonian can also be written in the form of Eq. 5, where $\hat{\mathcal {H}}_{\uparrow }=\hat{\mathcal {H}}_{\downarrow }+\omega _{s}+\hat{V}$,

$$\begin{aligned} \hat{V}=\sum _{\sigma =\Uparrow ,\Downarrow }\sum _{\textbf{k},\textbf{q}}\tilde{V}_{\sigma }(\textbf{k}-\textbf{q})c_{\textbf{k}\sigma }^{\dagger }c_{\textbf{q}\sigma }, \end{aligned}$$

(23)

with $\tilde{V}_{\sigma }(\textbf{k})$ being the Fourier transformation of the potential between impurity and $\sigma$-component fermion $V_{\sigma }(\textbf{r})$ that will eventually be characterized by the corresponding s-wave scattering length $a_{\sigma }$.

$$\begin{aligned} \hat{\mathcal {H}}_{\downarrow }=\hat{H}_{\text {BCS}}\equiv K_{0}+\sum _{\textbf{k}}\hat{\psi }_{\textbf{k}}^{\dagger }\underline{h_{\downarrow }(\textbf{k})}\hat{\psi }_{\textbf{k}}, \end{aligned}$$

(24)

is the standard BCS Hamiltonian for noninteracting impurity. Here, $\hat{\psi }_{\textbf{k}}^{\dagger }\equiv (c_{\textbf{k}\Uparrow }^{\dagger },c_{-\textbf{k}\Downarrow })$ is the Nambu spinor representation, with $c_{\textbf{k}\Uparrow }^{\dagger }$ ($c_{\textbf{k}\Downarrow }$) being the creation (annihilation) operator for a $\sigma$-component fermion with momentum $\textbf{k}$. $K_{0}\equiv -\mathcal {V}\Delta ^{2}/g+\sum _{\textbf{k}}(\epsilon _{\textbf{k}}-\mu )$, with $\mathcal {V}$ denoting the system volume and $\Delta$ being the pairing gap parameter. $\epsilon _{\textbf{k}}\equiv \hbar ^{2}k^{2}/2m$ is the single-particle dispersion relation, and $\mu$ is the chemical potential. We assume the populations of the two components are the same and fixed by $\mu$. The bare coupling constant g should be renormalized by the s-wave scattering length $a_{F}$ between the two components via $g^{-1}=m/4\pi a_{F}-\sum _{\textbf{k}}^{\Lambda }1/2\epsilon _{\textbf{k}}$, where $\Lambda$ is an ultraviolet cut–off. $\underline{h_{\downarrow }(\textbf{k})}$ can be regarded as a single-particle Hamiltonian $\hat{h}_{\downarrow }$ in momentum space and has a matrix form:

$$\begin{aligned} \underline{h_{\downarrow }(\textbf{k})}=\left[ \begin{array}{cc} \xi _{\textbf{k}} &{} \Delta \\ \Delta &{} -\xi _{\textbf{k}} \end{array}\right] , \end{aligned}$$

(25)

where $\xi _{\textbf{k}}\equiv \epsilon _{\textbf{k}}-\mu$. For a given scattering length $a_{F}$ and temperature $T^{\circ }$, $\Delta$ and $\mu$ are determined by a set of the mean-field number and gap equations [68].

To apply FDA, we need to express $\mathcal {H}_{\downarrow }$ and $\mathcal {H}_{\uparrow }$ in a bilinear form. It would be convenient to define $\hat{\psi }_{\textbf{k}}^{\dagger }=(c_{\textbf{k}\Uparrow }^{\dagger },c_{-\textbf{k}\Downarrow })\equiv (c_{\textbf{k}}^{\dagger },h_{\textbf{k}}^{\dagger })$ and rewrite $\hat{V}$ as

$$\begin{aligned} \hat{V}=\sum _{\textbf{kq}}\left[ \tilde{V}_{\Uparrow }(\textbf{k}-\textbf{q})c_{\textbf{k}}^{\dagger }c_{\textbf{q}}-\tilde{V}_{\Downarrow }(\textbf{q}-\textbf{k})h_{\textbf{k}}^{\dagger }h_{\textbf{q}}\right] +\sum _{\textbf{k}}\tilde{V}_{\Downarrow }(0), \end{aligned}$$

(26)

making the bilinear form apparent. We can also write the bilinear form of $\hat{\mathcal {H}}_{\uparrow }$ explicitly as

$$\begin{aligned} \hat{\mathcal {H}}_{\uparrow }=K_{0}+\omega _{0}+\omega _{s}+\sum _{\textbf{kq}}\hat{\psi }_{\textbf{k}}^{\dagger }\underline{h_{\uparrow }(\textbf{k},\textbf{q})}\hat{\psi }_{\textbf{q}}, \end{aligned}$$

(27)

where $\omega _{0}=\sum _{\textbf{k}}\tilde{V}_{\Downarrow }(0)$ and

$$\begin{aligned} \underline{h_{\uparrow }(\textbf{k},\textbf{q})}=\underline{h_{\downarrow }(\textbf{k})}\delta _{\textbf{k}\textbf{q}}+\left[ \begin{array}{cc} \tilde{V}_{\Uparrow }(\textbf{k}-\textbf{q}) &{} 0\\ 0 &{} -\tilde{V}_{\Downarrow }(\textbf{q}-\textbf{k}) \end{array}\right] \end{aligned}$$

(28)

can be regarded as a single-particle Hamiltonian $\hat{h}_{\uparrow }$ in momentum space and in a matrix form. We can see that $\hat{h}_{\uparrow }$ and $\hat{h}_{\downarrow }$ are the single-particle representative of $\hat{\mathcal {H}}_{\uparrow }$ and $\hat{\mathcal {H}}_{\downarrow }$ up to some constants, respectively.

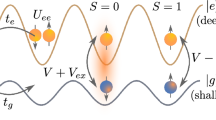
Diagonalizing $\underline{h_{\downarrow }(\textbf{k})}$ gives the well-known BCS dispersion relation $E_{\nu }=\pm \mathcal {E}_{\textbf{k}}=\pm \sqrt{\xi _{\textbf{k}}^{2}+\Delta ^{2}}$, where $\nu \equiv \{\pm ,\textbf{k}\}$ is a collective index. As sketched in Fig. 3 a, this spectrum consists of positive and negative branches separated by an energy gap. Since we prepare the impurity initially in the noninteracting state, the atoms occupy the eigenstates of $\underline{h_{\downarrow }(\textbf{k})}$ with a Fermi distribution $f(E_{\nu })=1/\left( e^{-E_{\nu }/k_{B}T}+1\right)$. At zero-temperature, the many-body ground state can be regarded as a fully filled Fermi sea of the lower branch and a completely empty Fermi sea of the upper branch. When the impurity interaction is on, eigenvalues $\tilde{E}_{\nu }$ of $\underline{h_{\uparrow }(\textbf{k})}$ still consists of two branches separated by the same gap, with each individual energy level shifted, as shown in Fig. 3 b. Moreover, when the impurity scattering is magnetic ($a_{\Uparrow }\ne a_{\Downarrow })$, a sub-gap YSR bound state exists [63,64,65,66,67].

Fig. 3

A sketch of the occupation and structure of the single-particle dispersion spectrum of a two-component superfluid Fermi gas with a positive chemical potential $\mu >0$ and the presence of a static impurity (black dot). a The spectrum when the impurity is in the noninteracting state (black arrow down) at zero-temperature. When the impurity is in the interacting polaron state (black arrow up), the spectrum is shown in b at zero and c at finite temperature. Reprinted with permission from [54]

It is worth noting that, in the many-body Hamiltonian $\hat{\mathcal {H}}_{\uparrow }$, we have assumed that the pairing order parameter $\Delta$ remains unchanged by introducing the interaction potential $V_{\sigma }(\textbf{r})$. For a non-magnetic potential ($V_{\Uparrow }=V_{\Downarrow }$) that respects time-reversal symmetry, this is a reasonable assumption, according to Anderson’s theorem [69]. For a magnetic potential ($V_{\Uparrow }\ne V_{\Downarrow }$), the local pairing gap near the impurity will be affected, as indicated by the presence of the YSR bound state. We will follow the typical non-self-consistent treatment of the magnetic potential in condensed matter physics [63, 69] and assume a constant pairing gap as the first approximation for simplicity.

Inserting the bilinear forms of Hamiltonian into the expression of overlap function in Eq. (15) and applying FDA gives $S(t)=e^{-i\omega _{s}t}\tilde{S}(t)$ where

$$\begin{aligned} \tilde{S}(t)=e^{-i\omega _{0}t}\text {det}[1-\hat{n}+e^{i\hat{h}_{\downarrow }t}e^{-i\hat{h}_{\uparrow }t}\hat{n}], \end{aligned}$$

(29)

with $\hat{n}$ is the occupation number operator. The corresponding spectral function in the frequency domain is given by Eq. (18).

Figure 4 shows numerical results for a magnetic impurity ($k_{F}a_{\Downarrow }=0$) immersed in the background BCS superfluid at the BCS side ($k_{F}a_{F}=-2$). In sharp contrast to the noninteracting Fermi gases, for cases with a nonzero pairing gap, the asymptotic behavior in the long-time limit shows that $|\tilde{S}(t\rightarrow \infty )|\propto t^{0}$ approaches a constant. These asymptotic constants are larger for larger $\Delta$. Further details can be obtained by an asymptotic form that fits our numerical calculations perfectly

$$\begin{aligned} \tilde{S}(t)\simeq D_{a}e^{-iE_{a}t}+D_{r}e^{-iE_{r}t}, \end{aligned}$$

(30)

where $D_{r}=0$ for $a_{\Uparrow }<0$. We obtain $D_{a}$, $D_{r}$, $E_{a}$, and $E_{r}$ from fitting and find that $E_{r}=\text {Re}E_{r}+i\text {Im}E_{r}$ is, in general, complex. In contrast, $E_{a}=\sum _{E_{\nu }<0}(E_{\nu }-\tilde{E}_{\nu })$ (where $\tilde{E}_{\nu }$ excludes the two-body deeply bound states) is purely real and can be explained as a renormalization of the filled Fermi sea.

Fig. 4

1D Ramsey spectroscopy of magnetic impurity ($k_{F}a_{\Downarrow }=0$) in a BCS superfluid at the BCS side ($k_{F}a_{F}=-2$) for a, b attractive impurity interaction $k_{F}a_{\Uparrow }=-2$ and c, d repulsive impurity interaction $k_{F}a_{\Uparrow }=2$. a, c The overlap functions $\tilde{S}(t)$. b, d The spectral functions $\text {Re}A(\omega )$. Thick blue curves correspond to $k_{B}T^{\circ }=0$, thin red solid curves, and purple dashed curves correspond to $k_{B}T^{\circ }=0.1E_{F}$ and $k_{B}T^{\circ }=0.15E_{F}$, respectively. A and R indicate the attractive and repulsive polaron resonances, respectively. DK and MH denote the dark continuum and molecule-hole continuum correspondingly. The green dashed and purple dash-dotted lines indicate the YSR features $E_{\text {RSR}}^{(-)}$ and $E_{\text {RSR}}^{(+)}$, respectively

The long-time asymptotic behavior of S(t) manifests itself as some characterized lineshape in the spectral function

$$\begin{aligned} A(\omega )\propto \left\{ \begin{array}{ll} Z_{a}\delta (\tilde{\omega }-E_{a}) &{} \tilde{\omega }\approx E_{a}\\ Z_{r}\frac{\left| \text {Im}E_{r}\right| /\pi }{(\tilde{\omega }-\text {Re}E_{r})^{2}+(\text {Im}E_{r})^{2}} &{} \tilde{\omega }\approx \text {Re}E_{r} \end{array}\right. , \end{aligned}$$

(31)

i.e., a $\delta$-function around $E_{a}$ and a Lorentzian around $\text {Re}E_{r}$. The existence of the $\delta$-function peak unambiguously confirms the existence of a well-defined quasiparticle — the attractive polaron with energy $E_{a}$. The Lorentzian, on the other hand, can be recognized as a repulsive polaron with finite width and hence finite lifetime. Here, $Z_{a}=|D_{a}|$ and $Z_{r}=|D_{r}|$ are the residues of attractive and repulsive polaron, correspondingly. Numerically, we find that $Z_{a}\propto (\Delta /E_{F})^{\alpha _{a}}$ and $Z_{r}\propto (\Delta /E_{F})^{\alpha _{r}}$ at small $\Delta$. The existence of finite residue of polarons indicates that the pairing gap suppresses multiple particle-hole excitations and prevents OC, which eventually leads to the survival of well-defined polarons.

We also find that the attractive polaron separates from a molecule-hole continuum (denoted as MH in Fig. 4) by a region of anomalously low spectral weight, namely the “dark continuum” (denoted as DK in Fig. 4). The existence of a dark continuum has been previously observed in spectra of other polaron systems. However, most of these studies apply various approximations, and only recently, a diagrammatic Monte Carlo study proves the dark continuum is indeed physical [39]. Here, our FDA calculation of the heavy crossover polaron spectrum gives exact proof of the dark continuum. By comparing Figs. 4 and 2, we expect that the dark continuum vanishes in the $\Delta \rightarrow 0$ limit and the attractive polaron merges into the molecule-hole continuum, forming a power-law singularity with the “wing”. Similar behavior also can be observed for the repulsive polaron, where the associated molecule-hole continuum is much less significant and cannot be visually seen in Fig. 4.

Finite-temperature results are indicated by the thin red solid (purple dashed) curves for $k_{B}T=0.1E_{F}\ (0.15E_{F})$ in Fig. 4. Some surprising features show up, other than the expected thermal broadening. An enhancement of spectral weight appears sharply at the energy $E_{\text {YSR}}^{(-)}=E_{a}-(\Delta -E_{\text {YSR}})$ below the attractive polaron. This spectral feature corresponds to the decay process highlighted by the purple arrow in Fig. (c), where an additional particle initially excited to the upper Fermi sea by thermal fluctuation is driven to the YSR state. For the case of $k_{F}a_{\Uparrow }>0$, a feature associated with the repulsive polaron appears at $E_{\text {YSR}}^{(+)}=\text {Re}(E_{r})-(E_{\text {YSR}}+\Delta )$, as indicated by the green arrow in Fig. 3 (c): an additional particle decays from the YSR state to the lower Fermi sea. The polaron spectrum can be applied to measure the superfluid gap $\Delta$ and $E_{\text {YSR}}$. In particular, we notice, on the positive side $a_{\Uparrow }>0$, if $E_{a}$, $\text {Re}(E_{r})$, $E_{\text {YSR}}^{(-)}$ and $E_{\text {YSR}}^{(+)}$ can all be measured accurately, we have $2\Delta =E_{a}+\text {Re}(E_{r})-E_{\text {YSR}}^{(-)}-E_{\text {YSR}}^{(+)}$ that does not depend on $E_{\text {YSR}}$. Since this formula only relies on the existence of the gap and a mid-gap state, we anticipate it can be used to measure $\Delta$ accurately for a Fermi superfluid that can not be quantitatively described by the BCS theory.

4 Multidimension spectroscopy

In this section, we present another new extension of the FDA in the calculation of multidimensional (MD) Ramsey spectroscopy [70]. Conventional Ramsey spectroscopy, such as the ones studied in previous sections, is called 1D since it shows the signal as a function of only one variable: the frequency of the single applied RF pulse or the time between the RF pulse and measurement. Here, we investigate a scenario where multiple RF pulses manipulate the impurity at several different times. The observed signal’s dependency on the time intervals between pulses or the corresponding Fourier transformation is called MD Ramsey spectroscopy.

Pushing 1D Ramsey spectroscopy to MD shares the same spirit as the widely successful MD nuclear magnetic resonance (NMR) and optical MD coherent spectroscopy (MDCS). MD spectroscopy not only improves the resolution and overcomes spectral congestion but also carries rich information on the correlations between resonance peaks and provides insights into physics that 1D spectroscopy cannot access. For example, in a 2D NMR spectroscopy, the peaks on the diagonal map the resonances in 1D spectroscopy; however, only coupled spins give rise to off-diagonal cross-peaks between corresponding resonances. The cross peaks are thus the signature of correlations between resonances, which the 1D spectrum cannot distinguish. In our system, the correlations in MD Ramsey spectroscopy are induced by the coupling between the spin and the background Fermi gas, a genuine many-body environment, and hence called many-body correlations.

We consider the same system described in Section 2.2, a localized impurity immersed in a noninteracting Fermi gas but manipulated by multiple RF pulses. One example of a three-pulse scheme is shown in Fig. 5a, which is similar to one of the most common 2D NMR pulse sequences, namely EXSY (EXchange SpectroscopY). EXSY essentially measures the four-wave mixing response of our system. The time evolution is thus given by the unitary transformation

$$\begin{aligned} \mathcal {U}(t,T,\tau )=U(t)\mathcal {R}U(T)\mathcal {R}U(\tau )\mathcal {R}. \end{aligned}$$

(32)

Fig. 5

A sketch of EXSY (EXchange SpectroscopY) pulses scheme

We define the MD responses as

$$\begin{aligned} S(\tau ,T,t)=-\text {Tr}(\sigma _{+}\rho _{f}), \end{aligned}$$

(33)

where the choice of $\sigma _{+}$ and additional −1 prefactor are for conventions so that $S(\tau ,T=0,t=0)$ is equivalent to the 1D overlap function $S(\tau )$. Notice that we have the relation $\mathcal {R}^{-1}\mathcal {R}^{-1}\mathcal {\mathcal {\sigma _{-}\mathcal {R\mathcal {R}}=-\sigma _{+}}}$.

The multidimensional response $S(\tau ,T,t)$ can be written as a summation of sixteen contributions

$$\begin{aligned} S(\tau ,T,t)=\sum _{i=1}^{16}S_{i}(\tau ,T,t)\equiv \frac{1}{4}\sum _{i=1}^{16}\textrm{Tr}[I_{i}(\tau ,T,t)\rho _{\text {FS}}], \end{aligned}$$

(34)

where $I_{i}(\tau ,T,t)$ are named pathways. These pathways are written as a direct product of six free-evolution operators $e^{-i\hat{\mathcal {H}}^{\prime }t^{\prime }}$ or their complex conjugates, such as Eqs. (36) and (37). Here, $\hat{\mathcal {H}}^{\prime }$ can be $\hat{\mathcal {H}}_{\uparrow }$ or $\hat{\mathcal {H}}_{\downarrow }$ and $t^{\prime }$ can be $\tau$, T, or t. The expressions of pathways are recognized to be similar to the optical paths in an interferometer as sketched in Fig. 5, where the free evolution-operator is illustrated by the solid black lines, the dashed lines in the grey beam splitter correspond to the matrix elements $R_{\sigma \sigma ^{\prime }}^{(\pi /2)}$ of the rotating operator in the spin basis. The measurement operator $\sigma _{+}$ fixes the middle two terms that depend on t as $...e^{i\hat{\mathcal {H}}_{\uparrow }t}e^{-i\hat{\mathcal {H}}_{\downarrow }t}...$, and the remaining operators each have two possibilities, leading to $2\times 4=16$ possible combinations.

A summation of the contributions of all sixteen pathways gives the total response $S(t,T,\tau )$, and the spectrum in the frequency domain can be obtained via a double Fourier transformation

$$\begin{aligned} A(\omega _{\tau },T,\omega _{t})=\frac{1}{\pi ^{2}}\int _{0}^{\infty }\int _{0}^{\infty }dtd\tau e^{i\omega _{\tau }\tau }S(\tau ,T,t)e^{-i\omega _{t}t}, \end{aligned}$$

(35)

where $\omega _{t}$ and $\omega _{\tau }$ are interpreted as an absorption and emission frequency, respectively. On the other hand, the dependence of $A(\omega _{\tau },T,\omega _{t})$ on the mixing time T can reveal the many-body coherent and incoherent dynamics [71]. The physical process underlying $A(\omega _{\tau },T,\omega _{t})$ can be interpreted as an inequilibrium dynamical evolution: the system first gets excited by absorbing a photon with frequency $\omega _{\tau }$, after a period of mixing time T, and then emits a photon with frequency $\omega _{t}$. We notice that $A(\omega _{\tau },T,\omega _{t})=\sum _{i=1}^{16}A_{i}(\omega _{\tau },T,\omega _{t})$ can also be expressed as a summation of sixteen pathways, where the expression of each pathway is given by Eq. (35), with A and S replaced by $A_{i}$ and $S_{i}$, respectively.

We can take the rotating wave approximation and consider only two dominant pathways (with details given by [70])

$$\begin{aligned} I_{1}(\tau ,T,t)=e^{i\hat{\mathcal {H}}_{\downarrow }\tau }e^{i\hat{\mathcal {H}}_{\uparrow }T}e^{i\hat{\mathcal {H}}_{\uparrow }t}e^{-i\hat{\mathcal {H}}_{\downarrow }t}e^{-i\hat{\mathcal {H}}_{\uparrow }T}e^{-i\hat{\mathcal {H}}_{\uparrow }\tau }, \end{aligned}$$

(36)

$$\begin{aligned} I_{2}(\tau ,T,t)=e^{i\hat{\mathcal {H}}_{\downarrow }\tau }e^{i\hat{\mathcal {H}}_{\downarrow }T}e^{i\hat{\mathcal {H}}_{\uparrow }t}e^{-i\hat{\mathcal {H}}_{\downarrow }t}e^{-i\hat{\mathcal {H}}_{\downarrow }T}e^{-i\hat{\mathcal {H}}_{\uparrow }\tau }. \end{aligned}$$

(37)

It should be noticed that the expression of $I_{1}(\tau ,T,t)$ and $I_{2}(\tau ,T,t)$ are similar to those that correspond to the excited state emission (ESE) and ground state breaching (GSB) in the rephasing 2D coherent spectra [72, 73].

The contribution of each pathway, $S_{i}(\tau ,T,t)$, can be calculated exactly via FDA. To proceed, we define $\mathcal {H}_{\downarrow }\equiv \Gamma (h_{\downarrow })$ and $\mathcal {H}_{\uparrow }\equiv \Gamma (h_{\uparrow })+\omega _{s}$. Here $\Gamma (h)\equiv \sum _{\textbf{k},\textbf{q}}h_{\textbf{k}\textbf{q}}c_{\textbf{k}}^{\dagger }c_{\textbf{q}}$ is a bilinear fermionic many-body Hamiltonian in the Fock space, and $h_{\textbf{k}\textbf{q}}$ represents the matrix elements of the corresponding operator in the single-particle Hilbert space. These matrix elements are explicitly given by $(h_{\downarrow })_{\textbf{k}\textbf{q}}=\epsilon _{\textbf{k}}\delta _{\textbf{k}\textbf{q}}$ and $(h_{\uparrow })_{\textbf{k}\textbf{q}}=\epsilon _{\textbf{k}}\delta _{\textbf{k}\textbf{q}}+\tilde{V}(\textbf{k}-\textbf{q})$. With these definitions, we can rewrite

$$\begin{aligned} S_{i}(\tau ,T,t)=\frac{1}{4}\tilde{S}_{i}(\tau ,T,t)e^{-i\omega _{s}f_{i}(t,T,\tau )}, \end{aligned}$$

(38)

where $e^{-i\omega _{s}f_{i}(t,T,\tau )}$ gives a simple phase and $\tilde{S}_{i}(\tau ,T,t)$ is a product of the exponentials of the bilinear fermionic operator, both of which can be calculated exactly. For example, we have $S_{1}(\tau ,T,t)=\tilde{S}_{1}(\tau ,T,t)e^{i\omega _{s}t}e^{-i\omega _{s}\tau }/4$, where

$$\begin{aligned} \tilde{S}_{1}(\tau ,T,t)&= \text {Tr}[e^{i\Gamma (h_{\downarrow })\tau }e^{i\Gamma (h_{\uparrow })T}e^{i\Gamma (h_{\uparrow })t}\\&\quad \times e^{-i\Gamma (h_{\downarrow })t}e^{-i\Gamma (h_{\uparrow })T}e^{-i\Gamma (h_{\uparrow })\tau }\rho _{\text {FS}}] \end{aligned}.$$

(39)

Applying Levitov’s formula [13, 54, 55] gives

$$\begin{aligned} \tilde{S}_{1}(\tau ,T,t)=\text {det}[(1-\hat{n})+R_{1}(\tau ,T,t)\hat{n}], \end{aligned}$$

(40)

with

$$\begin{aligned} R_{1}(\tau ,T,t)=e^{ih_{\downarrow }\tau }e^{ih_{\uparrow }T}e^{ih_{\uparrow }t}e^{-ih_{\downarrow }t}e^{-ih_{\uparrow }T}e^{-ih_{\uparrow }\tau }, \end{aligned}$$

(41)

and $\hat{n}=n_{\textbf{k}}\delta _{\textbf{k}\textbf{k}'}$, where $n_{\textbf{k}}=1/(e^{\epsilon _{\textbf{k}}/k_{B}T^{\circ }}+1)$ denotes the single-particle occupation number operator.

The 2D spectrum $A_{o}(\omega _{\tau },\omega _{t})\equiv A(\omega _{\tau },T=0,\omega _{t})$ in Fig. 6 (a2) and (a3) shows a double dispersion lineshape commonly found in 2D NMR around $(\tilde{\omega }_{\tau },\tilde{\omega }_{t})\approx (\tilde{\omega }_{A-},\tilde{\omega }_{A-})$, which is called a diagonal peak denoted as AA. For attractive interaction $k_{F}a=-0.5$, the attractive singularity appears at $\tilde{\omega }_{A-}\approx -0.28E_{F}$ in the absorption spectrum. We have numerically verified that the integration of 2D spectroscopy over emission frequency $\omega _{t}$ gives the 1D absorption spectrum $A_{a}(\omega _{\tau })$ (not shown here). Interestingly, we can observe that there is no diagonal spectral weight corresponding to the wing. Rather, the spectral weight on the off-diagonal $A_{o}(\omega _{\tau },\omega _{t}\approx \omega _{A-})$ and $A_{o}(\omega _{\tau }\approx \omega _{A-},\omega _{t})$ is significant and resembles the lineshape of the wing. This is a non-trivial manifestation of OC in the 2D spectroscopy: the inhomogeneous and homogeneous lineshape does not have the OC characteristic, i.e., a power-law singularity and a broad lineshape that resembles the wings in the 1D spectroscopy [22]. Here, the inhomogeneous and homogeneous lineshape refer to the lineshape near a singularity along the diagonal or the direction perpendicular to the diagonal. As we can observe, the widths of the singularity are much sharper along these two directions, which might help experimental identification of the singularity, especially at finite temperatures. The homogeneous and inhomogeneous broadenings in MD spectroscopy also have their own experimental significance, similar to their NMR or optical counterpart. In a realistic experiment, the ensemble average of the impurity signal can give rise to a further inhomogeneous broadening induced by the disorder of the local environment (such as spatial magnetic field fluctuation). However, these disorders are usually non-correlated and would not introduce homogeneous broadening [74,75,76].

Fig. 6

(a1) and (a4) shows the 1D absorption spectrum for attractive interaction $k_{F}a=-0.05$ and finite temperature $k_{B}T^{\circ }=0.03E_{F}$. The absorption singularity is denoted as A. (a2) and (a3) shows the contour, and 3D landscape of the 2D spin-echo spectrum $\text {Re}[A_{o}(\omega _{\tau },\omega _{t})]$, where the diagonal peak is denoted as AA. (b1)–(b4) are the same as (a1)–(a4), correspondingly, but for repulsive interaction $k_{F}a=0.5$. There are two singularities in (b1), the absorption spectrum, namely repulsive and attractive singularities, which are denoted as R and A. The corresponding diagonal peaks in (b2) and (b3) are denoted as AA and RR, while the off-diagonal cross-peaks are denoted as AR and RA. Reprinted with permission from [70]

For repulsive interaction $k_{F}a=0.5$, there are two singularities, the attractive and repulsive singularities, in the 1D absorption spectrum. These singularities appear at $\tilde{\omega }_{A+}\approx -0.98E_{F}$ and $\tilde{\omega }_{R+}\approx 0.28E_{F}$ in Fig. 6 (b1) and (b4). As shown in Fig. 6 (b2) and (b3), there are two diagonal peaks, AA and RR, in the 2D spectroscopy that mirror the attractive and repulsive singularities. In addition, there are also two significant cross-peaks denoted as AR and RA. The physical interpretations of cross peaks are similar to those observed in 2D NMR, where strong cross-peaks between the two spin resonances indicate strong coupling between the two spins. In our system, the correlation between attractive and repulsive singularities is induced by the coupling between spin and the background Fermi gas, a many-body environment, which is named a many-body quantum correlation. The strong off-diagonal peaks, therefore, indicate a strong many-body quantum correlation between the attractive and repulsive singularity induced by the many-body environment. As far as we know, this is the first prediction of many-body correlations between Fermi edge singularities in cold atom systems. If the impurity has a finite mass or the background Fermi gas is replaced by a superfluid with an excitation gap, we expect these cross-peaks would remain and represent the correlations between attractive and repulsive polarons [54, 55]. The method reviewed here can also be straightforwardly applied to calculate the coherent and relaxation dynamics of the system in terms of the mixing-time T dependence of the MD Ramsey spectroscopy [70]. We also remark here that a calculation of the MD Ramsey spectroscopy for a finite mass impurity has recently been developed using a Chevy’s ansatz approximation method [77, 78].

5 Discussion and conclusion

In summary, we present a review of recent developments in the functional determinantal approach for studying the behavior of heavy impurities in ultracold Fermi gases. While this method has previously been applied to Fermi edge singularity problems in ideal Fermi gases, we now provide detailed insights into its application to the problems of impurities in a Bardeen–Cooper–Schrieffer superfluid and the extension of multidimensional Ramsey spectroscopy.

It should be noted that although our approach is essentially exact for the problems of a heavy impurity in a Bardeen–Cooper–Schrieffer superfluid, the Bardeen–Cooper–Schrieffer treatment of the background superfluid is a well-known mean-field approximation. Therefore, while we are confident in the validity of our approach within the chosen parameter regime, its applicability to other parameter regimes may be limited by several factors.

Firstly, the assumption of a constant pairing gap, even in the presence of impurities, is reasonable due to Anderson’s theorem. However, this assumption may become invalid for strongly interacting magnetic impurities. To improve this approximation, a self-consistent approach can be employed to obtain the spatial-dependent pairing gap parameter in the presence of impurities.

Secondly, in the conventional Bardeen–Cooper–Schrieffer theory, the gapless bosonic excitation is absent from the Bogoliubov spectrum and, therefore, neglected in our theory. This approximation is only valid on the Bardeen–Cooper–Schrieffer side, rendering our approach qualitative at the Bose-Einstein-Condensate side. Including the effects of bosonic excitation is an intriguing and open research topic.

Additionally, the functional determinantal approach can currently only be applied to infinitely heavy impurities, and its direct extension to finite impurity mass is unknown. However, the influence of finite mass can be estimated by comparing the recoil energy and the superfluid gap ($\Delta$), both of which play a role in suppressing multiple particle-hole excitations. By considering momentum and energy conservation, the recoil momentum of a fermion with a Fermi momentum ($k_{F}$) on a heavy impurity with mass M is approximately $2mk_{F}/M$ when $m/M\ll 1$, where m is the fermion mass. The recoil energy is given by $E_{\text {recoil}}=(2mk_{F}/M)^{2}/2m=(4m^{2}/M^{2})E_{F}$. Therefore, the finite mass effect can be neglected if $E_{\text {recoil}}\ll 2\Delta$ or equivalently $m/M\ll \sqrt{\Delta /2E_{F}}$. For $^{6}$Li-$^{133}$Cs, where the mass ratio $m/M\approx 0.045$, our predictions are valid for $\Delta \ge 0.1E_{F}$. Alternatively, the finite mass effect can be mitigated by localizing the impurity using a strong optical lattice.

In the future, it would be intriguing to extend the functional determinantal approach to other superfluid systems, such as topological superfluids. Investigating systems with more than one impurity would also yield valuable insights, where multidimensional Ramsey spectroscopy could provide important knowledge regarding medium-induced interactions between impurities.

Appendices

Appendix A: Klich’s proof of a trace formula

One of the key equations in the functional determinant approach formalism is a trace formula

$$\begin{aligned} \text {Tr}\left[ e^{\Gamma (A_{1})}e^{\Gamma (A_{2})}...e^{\Gamma (A_{N})}\right] =\text {det}\left( \textbf{1}-\xi e^{A_{1}}e^{A_{2}}...e^{A_{N}}\right) ^{-\xi }, \end{aligned}$$

(42)

where $\textbf{1}$ is an identity matrix of the dimension of single-particle Hilbert space, $\xi =1$ for bosons and $\xi =-1$ for fermions. Here the many-body Fock space operator

$$\begin{aligned} \Gamma (A_{n})=\sum _{ij}\langle i|A_{n}|j\rangle a_{i}^{\dagger }a_{j} \end{aligned}$$

(43)

is the second quantized version of a single particle operator $A_{n}$, and $n\in \{1,2,...,N\}$ are integer subscripts. In contrast, $A_{n}$ is defined as an operator on the single particle Hilbert space, with matrix elements $\langle i|A_{n}|j\rangle$, where $|i\rangle$ are single-particle basis corresponding to the creation operator $a_{i}^{\dagger }$. Here, we included the proof for completeness, mainly following Klich’s elegant proof.

First, we prove for a single operator, $\text {Tr}\left[ e^{\Gamma (A_{1})}\right] =\text {det}\left( \textbf{1}-\xi e^{A_{1}}\right) ^{-\xi }$. We recall that any matrix $A_{1}$ can be written in a basis (corresponding to creation operator $b_{i}^{\dagger }$) which it is of the form $D+K$, where D is a diagonal matrix with elements $D_{\nu \nu }\equiv \lambda _{\nu }$ known as eigenvalues of the matrix and K is an upper triangular. Since the upper trangular K does not contribute to the trace, we have

$$\begin{aligned} \text {Tr}\left[ e^{\Gamma (A_{1})}\right] =\text {Tr}\left[ e^{\Gamma (D)}\right] =\text {Tr}\left[ \prod _{\nu =1}^{K}e^{\lambda _{\nu }b_{\nu }^{\dagger }b_{\nu }}\right] . \end{aligned}$$

(44)

Notice that the trace is taking over the Fock space basis $|\vec {\alpha }\rangle \equiv |\alpha _{1}\alpha _{2}...\alpha _{K}\rangle$ with $\alpha _{\nu }$ being the occupation number of the single-particle basis $|\nu \rangle$ corresponding to $b_{\nu }^{\dagger }$. For fermions, $\vec {\alpha }$ are vectors of zeros and ones and for bosons vectors with integer coefficients. In such occupation number representation, the trace can be expressed as

$$\begin{aligned} \text {Tr}\left[ \prod _{\nu =1}^{K}e^{\lambda _{\nu }b_{\nu }^{\dagger }b_{\nu }}\right] =\prod _{\nu =1}^{K}\sum _{\alpha _{\nu }}e^{\lambda _{\nu }\alpha _{\nu }}, \end{aligned}$$

(45)

where

$$\begin{aligned} \sum _{\alpha _{\nu }}e^{\lambda _{\nu }\alpha _{\nu }}=(1-\xi e^{\lambda _{\nu }})^{-\xi }= \left\{ \begin{array}{ll} 1+e^{\lambda _{\nu }},\ ,\xi =-1 &{} \text {Fermion},\\ 1/(1-e^{\lambda _{\nu }}),\ \xi =1 &{} \text {Boson}. \end{array}\right. \end{aligned}$$

(46)

The fact that $\lambda _{\nu }$ are eigenvalues of $A_{1}$, which implies $(1-\xi e^{\lambda _{\nu }})^{-\xi }$ are eigenvalues of $(1-\xi e^{A_{1}})^{-\xi }$, leads to the products of eigenvalues $\prod _{\nu =1}^{K}(1-\xi e^{\lambda _{\nu }})^{-\xi }=\text {det}(\textbf{1}-\xi e^{A_{1}})^{-\xi }$. Consequently, we prove

$$\begin{aligned} \text {Tr}\left[ e^{\Gamma (A_{1})}\right] =\text {det}\left( \textbf{1}-\xi e^{A_{1}}\right) ^{-\xi } \end{aligned}$$

(47)

as promised. We remark that this formula does not depend on the single-state basis, and an intuitive way of understanding this formula can be thinking of $\text {Tr}\left[ e^{\Gamma (A_{1})}\right]$ as the partition function of a system with Hamiltonian $-A_{1}$ at temperature $k_{B}T^{\circ }=1$.

We proceed to prove the formula for the product of two operators

$$\begin{aligned} \text {Tr}\left[ e^{\Gamma (A_{1})}e^{\Gamma (A_{2})}\right] =\text {det}\left( \textbf{1}-\xi e^{A_{1}}e^{A_{2}}\right) ^{-\xi }. \end{aligned}$$

(48)

One can show that, the Fock space operators $\Gamma (A_{n})$ in Eq. (43) satisfies

$$\begin{aligned}{}[\Gamma (A_{n}),\Gamma (A_{m})]=\Gamma ([A_{n},A_{m}]), \end{aligned}$$

(49)

which implies for an N dimensional single particle Hilbert space $\Gamma$ is a representation of the usual Lie algebra of matrices gl(N). As a result, the Baker-Campbell-Hausdorf formula

$$\begin{aligned} e^{A_{1}}e^{A_{2}}=e^{B} \end{aligned}$$

(50)

leads to

$$\begin{aligned} e^{\Gamma (A_{1})}e^{\Gamma (A_{2})}=e^{\Gamma (B)}. \end{aligned}$$

(51)

Therefore, we have $\text {Tr}\left[ e^{\Gamma (A_{1})}e^{\Gamma (A_{2})}\right] =\text {Tr}[e^{\Gamma (B)}]=\text {det}\left( \textbf{1}-\xi e^{B}\right) ^{-\xi }=\text {det}\left( \textbf{1}-\xi e^{A_{1}}e^{A_{2}}\right) ^{-\xi }$ as shown in Eq. (48). One can also see that this relation can immediately be generalized in the same way to products of more then two operators as our trace formula Eq. (42).

A pedagogical example is the dimension of the Fock space whose corresponding single particle Hilbert space has a dimension of N, which is given by

$$\begin{aligned} \text {Tr}\textbf{1}=\text {Tr}e^{\Gamma (0)}=\text {det}(1-\xi )^{-\xi }= \left\{ \begin{array}{ll} 2^{N} &{} \text {Fermions}\\ \infty &{} \text {Bosons} \end{array}\right. , \end{aligned}$$

(52)

as it should be.

In this review, a commonly encounter case is that the last operator $e^{\Gamma (A_{N})}$ in the trace formula is a fermion density matrix in a bilinear form

$$\begin{aligned} \rho _{F}= & {} \frac{1}{Z}\exp \left( -\sum _{\alpha }\lambda _{\alpha }\hat{a}_{\alpha }^{\dagger }\hat{a}_{\alpha }\right) ,\nonumber \\\equiv & {} \prod _{\alpha }\left[ n_{\alpha }\hat{a}_{\alpha }^{\dagger }\hat{a}_{\alpha }+\left( 1-n_{\alpha }\right) \hat{a}_{\alpha }\hat{a}_{\alpha }^{\dagger }\right] , \end{aligned}$$

(53)

where

$$\begin{aligned} e^{-\lambda _{\alpha }}=\frac{n_{\alpha }}{1-n_{\alpha }}, \end{aligned}$$

(54)

with $n_{\alpha }$ being the distribution of fermions in the single particle state corresponding to $\hat{a}_{\alpha }^{\dagger }$. The normalized constant is given by $Z=\text {Tr}\exp \left( -\sum _{\alpha }\lambda _{\alpha }\hat{a}_{\alpha }^{\dagger }\hat{a}_{\alpha }\right) =\text {det}[\left( 1-\hat{n}\right) ^{-1}]$, where $\hat{n}$ is a diagonal matrix with matrix elements $n_{\alpha }$.

One familiar example is the non-interacting Fermions at a the finite temperature, where $\hat{a}_{\alpha }^{\dagger }$ creates a fermion in the state with single-particle energy $\epsilon _{\alpha }$ and

$$\begin{aligned} n_{\alpha }=\frac{1}{e^{\left( \epsilon _{\alpha }-\mu \right) /k_{B}T^{\circ }}+1},\ \lambda _{\alpha }=\frac{\epsilon _{\alpha }-\mu }{k_{B}T^{\circ }}. \end{aligned}$$

(55)

Here, $\mu$ is the chemical potential, and $k_{B}$ is the Boltzmann constant.

In this case, we have

$$\begin{aligned} \text {Tr}\left[ e^{\Gamma (A_{1})}e^{\Gamma (A_{2})}...e^{\Gamma (A_{N-1})}\rho _{F}\right]= & {} \frac{1}{Z} \text {det}[\textbf{1}+e^{A_{1}}e^{A_{2}}...\nonumber \\{} & {} \times e^{A_{N-1}}e^{-\underline{\lambda }}] \end{aligned}$$

(56)

where in the basis of single particle states corresponding to $a_{\alpha }^{\dagger }$, $e^{-\underline{\lambda }}$ is a diagonal matrix with matrix elements $e^{-\lambda _{\alpha }}$, which leads to

$$\begin{aligned} e^{-\underline{\lambda }}=\hat{n}\left( \textbf{1}-\hat{n}\right) ^{-1}. \end{aligned}$$

(57)

Inserting the expression of $e^{-\underline{\lambda }}$ and Z in terms of distribution matrix $\hat{n}$ gives

$$\begin{aligned} \text {Tr}\left[ e^{\Gamma (A_{1})}e^{\Gamma (A_{2})}...e^{\Gamma (A_{N-1})}\rho _{F}\right] =\det [(\textbf{1}-\hat{n})+\hat{R}\hat{n}], \end{aligned}$$

(58)

where

$$\begin{aligned} \hat{R}=e^{A_{1}}e^{A_{2}}...e^{A_{N-1}}. \end{aligned}$$

(59)

Another closely related and useful trace formula is

$$\begin{aligned} \text {Tr}\left[ e^{\Gamma (A_{1})}e^{\Gamma (A_{2})}...e^{\Gamma (A_{N})}a_{i}^{\dagger }a_{j}\right]= & {} (\textbf{1}-\xi e^{-W})_{ji}^{-1}\nonumber \\{} & {} \times \text {det}\left( \textbf{1}-\xi e^{W}\right) ^{-\xi } \end{aligned}$$

(60)

where $e^{W}=e^{A_{1}}e^{A_{2}}...e^{A_{N}}$. Noticing that $\text {Tr}\left[ e^{\Gamma (A_{1})}e^{\Gamma (A_{2})}...e^{\Gamma (A_{N})}\right] =\text {Tr}[e^{\Gamma (W)}]$ leads to

$$\begin{aligned} \text {Tr}\left[ e^{\Gamma (A_{1})}e^{\Gamma (A_{2})}...e^{\Gamma (A_{N})}a_{i}^{\dagger }a_{j}\right] =\frac{\partial }{\partial W_{ij}} \text {Tr}[e^{\Gamma (W)}], \end{aligned}$$

(61)

where $W_{ij}\equiv \langle i|W|j\rangle$ are the matrix element of W. Applying Jacobi’s formula gives

$$\begin{aligned} \frac{\partial \text {det}(\textbf{1}-\xi e^{W})^{-\xi }}{\partial W_{ij}}={\text {det}}(\textbf{1}-\xi e^{W})^{-\xi } \text {Tr}[(\textbf{1}-\xi e^{-W})^{-1}\frac{\partial W}{\partial W_{ij}}], \end{aligned}$$

(62)

where taking the trace on the right-hand-side gives $\text {Tr}[(\textbf{1}-\xi e^{-W})^{-1}\partial W/\partial W_{ij}]=(\textbf{1}-\xi e^{-W})_{ji}^{-1}$, which evntually leads to Eq. (60).

Appendix B: Numerical calculations

Numerical calculations are carried out in a finite system confined in a sphere of radius R. Keeping the density constant, we increase R towards infinity until numerical results are converged. Typically, we choose $k_{F}R=250\pi$ in a calculation. We focus on the s-wave interaction channel between $\left| \uparrow \right\rangle$ and the background fermions near a broad Feshbach resonance, which can be well mimicked by a spherically symmetric and short-range van-der-Waals type potential $V(r)=-C_{6}\exp (-r_{0}^{6}/r^{6})/r^{6}$ [79,80,81]. Here, $C_{6}$ determines the van-der-Waals length $l_{\text {vdW}}=(2mC_{6})^{1/4}/2$, and we choose $l_{\text {vdW}}k_{F}=0.01\ll 1$, so the short-range details are unimportant. $r_{0}$ is the short-range parameter that tunes the scattering length a. We choose $k_{F}r_{0}\approx 7\times 10^{-3}$, which can support two bound states on the positive side. We also include about 1100 continuum states in a typical calculation. Covergence with respect to both number of bound states and continnum states have been tested.