1 Introduction

Upconverting nanoparticles (UCNP) have the ability to convert multiple absorbed photons with lower energy (usually in the NIR range) into light with higher energy (NIR, visible or UV) [1, 2]. UCNP have many advantages as luminescent reporters, among which are sharp luminescence bands at tunable wavelengths, a possibility for multicolor imaging, and luminescence lifetimes in the range of tens to hundreds of μs, which permits to detect the UCNP with no background interference and to separate from the conventional fluorophores, which usually have lifetimes in the ns range, using time-gated detection schemes. UCNP are further characterized by relatively low toxicity, absence of photoblinking, chemical inertness, large anti-Stokes shifts, and outstanding photostability, which allows them to be detected with very low optical background interference even in complex biological systems such as body fluids [3,4,5,6].

The most frequently studied UCNP, up to now, consist of hexagonal or cubic NaYF4 crystal host lattice doped with a combination of Ln3+ ions, usually Yb3+ as a sensitizer and Er3+, Tm3+, or Ho3+ as activators [7,8,9,10]. Many groups have evaluated the influence of size, shape, crystalline phase, and dopant concentrations of UCNP [11,12,13,14,15,16]. Different procedures and methods to control the size and shape of lanthanide-doped UCNP have been reported, among which is the tuning of Gd3+ concentration. Gd3+ ions replace the usually used Y3+ ions in the crystal lattice of UCNP. Doping of certain amounts of Gd3+ into the crystal lattice seems to increase the prevalence of hexagonal crystal phase of UCNP and to decrease the size of UCNP without negative effects on the upconversion efficiency [12, 17, 18]. However, the influence of the Gd3+ content has been studied mostly in Yb3+, Er3+—doped UCNP, and little information has been published for the Tm3+, Gd3+—co-doped nanoparticles [19,20,21,22,23,24], even though the most prominent Tm3+ emission band (800 nm) promises potential advantages for bioapplications by fitting into the biooptical window.

Besides the influence of the Gd3+ on the photophysical properties, it also is frequently used as a contrasting agent for magnetic resonance imaging (MRI) studies [25, 26], thus, doping the UCNP with Gd3+ ions offers a possibility for creating multimodal luminescent reporters. For such applications, but also in general for applications in biosensing, the shelf life of the potential probes becomes a critical issue. Stability of NaYF4-based UCNP in water has been studied by several research groups, and anisotropic structural disintegration of the UCNPs over time in aqueous media has been shown [27,28,29,30]. Usually, these studies observe the dissolution behavior of UCNP in aqueous buffers within several days, up to a month. To our knowledge, there has not been a published investigation of the storage and aging of UCNP in dry phase over long periods of time. Redispersing them in an organic solvent in combination with a subsequent phase transfer to water, such a storage layout could be an alternative strategy to facilitate an economically required longer shelf life of UCNP.

Taking this into account, we decided to study the effect of various doping concentrations of Gd3+ as well as dry storage over a long period of time on the photophysical properties of Na(Y,Gd)F4:Yb3+,Tm3+ UCNP. A standard one-pot thermal decomposition method with oleate as a capping agent was used to synthesize the Na(Y,Gd)F4:Yb3+(18 mol%),Tm3+(2 mol%) UCNP with the content of Gd3+ being 10, 20, 30, 40 or 50 mol%, respectively [31]. The photophysical properties of the resulting five UCNP samples were investigated to evaluate the influence of Gd3+ content on the photophysical parameters. Moreover, a comparison of structural and photophysical properties of oleate-capped Na(Y,Gd)F4:Yb3+,Tm3+ right after synthesis and after 24 months of dry storage has been performed as well.

2 Results and discussion

2.1 Properties and ageing of Na(Y,Gd)F4:Yb3+,Tm3+ UCNP

2.1.1 Basic characterization

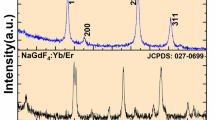
The crystalline structures of as-synthesized (AS) and 24-month (24 M) UCNP were investigated using X-Ray powder diffraction (XRD) (Fig. 1 top as well as Figures S1-S3 in SI). NaYF4 crystals can exist either in cubic (isotropic, or α-) or in hexagonal (anisotropic, or β-) phase. Despite the presence of Gd3+, the raw XRD diffractograms have shown the presence of both phases in all UCNP samples. To separately analyze the content of the two crystal phases, a Parallel Factor Analysis (PARAFAC) deconvolution algorithm was applied to the raw diffractograms [32]. Besides separating the signals coming from the two different UCNP crystal lattices, it also allowed us to further clear out the signal coming from the NaCl as a synthesis by-product. From Fig. 1 (bottom) and Figure S3, the quantitative prevalence of the cubic phase can be seen for both AS and 24 M samples. The increase in Gd3+ concentration increased the share of the hexagonal phase in the UCNP. It is widely accepted that the increase in Gd3+ content in the lattice of NaYF4 UCNP leads to the prevalence of the hexagonal crystal structure at high Gd3+ doping concentrations (up to fully replacing Y3+ ions in the lattice) [9, 12, 33, 34]. In the investigated sample set the content of the hexagonal lattice distinctly increased at a Gd3+ content of 30% for the AS samples (see Figure S3). For the 24 M samples (see Fig. 1, bottom) a steady increase of the hexagonal phase was found and at 50% Gd3+ doping only hexagonal phase was present.

Fig. 1
figure 1

X-ray powder diffractogram of the 24 M Na(Y,Gd)F4:Yb3+,Tm3+ (30 mol% Gd3+) UCNP with deconvoluted reflexes for the α- and β-phase using PARAFAC (top). Relative intensities of the cubic- and hexagonal 24 M UCNP lattices calculated from the deconvoluted XRD spectra (bottom)

Full size image

The size and shape of the UCNP (AS, 24 M) were determined by transmission electron microscopy (TEM). An example of the obtained TEM micrographs can be found in Fig. 2, and respective micrographs for all studied samples are shown in Figure S4 and S5. As can be noticed from the images, for AS as well as 24 M samples the nanoparticles could be visually divided into two distinct sub-species in all samples except for the 30 mol% Gd3+. The smaller sub-species had a round (or hexagonal) form and was more homogenous in size and shape. The larger sub-species had a shape of a 4-petal flower and was much larger and more heterogeneous in size. In the sample with 30 mol% Gd3+, only the “small” sub-species was present, and its diameter was the smallest among all samples (Table 1). The formation of such peculiar petal-like structures could be explained by the growth of a shell with a distinct composition (for example, pure NaGdF4) around a core UCNP (which could, for example, consist of cubic-phase NaYF4). The content of relative fractions calculated based on the analysis of 200–300 particles on TEM micrographs (small/large sub-species) was in the range of 50% and did not show any considerable variation in samples with different compositions.

Fig. 2
figure 2

TEM micrographs of AS (a) and 24 M (b) Na(Y,Gd)F4:Yb3+,Tm3+ (40 mol % Gd3+) UCNP. The scale bars are 50 and 20 nm, respectively (acceleration voltage 200 kV)

Full size image
Table 1 Na(Y,Gd)F4:Yb3+,Tm3+ UCNP diameters (AS and 24 M), as calculated from TEM micrographs and XRD analyses
Full size table

As complementary methods to determine the UCNP sizes, dynamic light scattering (DLS) measurements were conducted, and XRD data on the crystallite size were considered.

From the results presented in Table 1 for AS samples, one can see that, given the margin of error, the crystallite sizes determined by XRD are in good agreement with the sizes of “small” sub-species calculated from TEM micrographs. The sizes determined by DLS appear larger, but it is worth mentioning that the yielding diameters obtained by DLS are hydrodynamic, i.e. they include the solvation shell and the ligand around the particles. In addition the data processing favors the larger particles over the smaller ones, resulting into higher numbers for the particle size on average.

One could also note that the size of the “small” sub-species determined by TEM correlates well with the crystallite size measured by XRD, while the “large” sub-species are similar to the sizes determined by DLS, taking the solvation shell into consideration. This might be a consequence of the “small” sub-species consisting of single crystals, and the “large” ones being multicrystallite, and having more impact on DLS data due to the specifics of the measurement method.

As can be seen from these data, the concentration of Gd3+ ions in nanoparticles did not have a clear relationship with the sizes or crystalline phase content of Na(Y,Gd)F4: Yb3+, Tm3+ UCNP for the AS samples. The AS sample that was the most homogeneous in size and shape contained 30 mol% Gd3+ ions.

Crystalline structures and sizes of the 24 M UCNP were re-assessed using TEM. As shown in Fig. 2b and Figure S5, there seemed to be more clustering and aggregation of the UCNP compared to the AS samples. The particles still consisted of two fractions: a smaller, more homogenous sub-species and a larger, more diverse in size and shape sub-species, some of which had the four-petal shape, too. The relative content of the large/small sub-species has stayed at approximately 50% in all five samples, similarly to the AS UCNP.

The data on UCNP sizes obtained from XRD have shown no significant changes in crystallite sizes (Table 1). The sizes obtained from analyzing the XRD data were in good agreement with the diameters calculated from TEM micrographs, and the size of the “small” sub-species corresponded to the crystallite size. Unfortunately, the results of the DLS measurements could not be properly analyzed due to the interference of large UCNP clusters, which appeared over time due to aggregation processes.

2.2 Upconversion luminescence properties

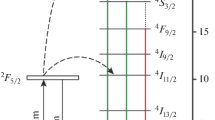
The upconversion luminescence (UCL) spectra of oleate – capped NaYF4:Yb3+,Tm3+ UCNP in cyclohexane usually show three prominent luminescence bands centered in 451 (1D2 → 3F4 transition, B1), 481 (1G4 → 3H6 transition, B2), and 800 (3H4 → 3H6 transition, NIR) nm upon excitation at 976 nm [35, 36]. Luminescence spectra of the five AS samples were recorded for the three aforementioned luminescence bands. A typical spectrum is shown for the sample with 30 mol% Gd3+ (AS and 24 M sample, Fig. 3), (all recorded spectra are shown in the SI, Figure S6).

Fig. 3
figure 3

Upconversion emission intensities of AS and 24 M Na(Y,Gd)F4:Yb3+,Tm3+ (30 mol% Gd3+) UCNP upon pulsed excitation (laser pulse energy 6.6 ± 0.2 mJ for AS and 7.1 ± 0.2 mJ for 24 M) at 976 nm. The concentration of UCNP solution was 5 mg/mL

Full size image

Comparing absolute intensities of the luminescence spectra between samples usually presents a challenge. To decouple the intensity from the particle concentration and from day-to-day fluctuations of the instrument performance (e.g., laser intensity), the ratio of integral intensities of the emission bands was calculated from the spectra. The band ratio was chosen to analyze the influence of the Gd3+ concentration. When the intensity ratios between the luminescence bands (B1/NIR and B2/NIR) of the UCNP were plotted as a function of the Gd3+ content, a maximum ratio centered at 30 mol% was found (Fig. 4). It is tempting to assume that the B1 band, corresponding to a 4-photon process (1D2 → 3F4), could be the most sensitive to changes in structure of UCNP, while the 3-photon B2 (1G4 → 3H6) and 2-photon NIR (3H4 → 3H6) bands are probably better able to withstand variations in these parameters.

Fig. 4
figure 4

Intensity ratios of B1/NIR (top) and B2/NIR (bottom) luminescence bands of Na(Y,Gd)F4:Yb3+,Tm3+ UCNP upon excitation at 976 nm

Full size image

For all 24 M UCNP samples (10–50 mol% Gd3+), upconversion luminescence spectra were recorded for the same three luminescence bands. As an example, emission spectra of the sample with 30 mol% Gd3+ are shown in Fig. 3 (all spectra are shown in the Supporting Information section, Figure S7).

Also, for the 24 M the shape of the blue band of the 30 mol% Gd3+ sample is different from the rest of the samples (Figure S7): the B1 and B2 bands, which correspond to a 4-photon and 3-photon processes, respectively, show much higher intensity than the rest of the samples (Figure S7).

The higher luminescence intensities observed in the samples doped with 30% Gd3+ could be attributed to higher size/shape homogeneity of these samples, and the presence of two sub-species in the rest of the samples could possibly negatively influence their luminescence properties.

When the intensity ratios of B1 (1D2 → 3F4), or B2 (1G4 → 3H6) bands to the NIR (3H4 → 3H6) were compared in 24-month and in as-synthesized UCNP, a drop was observed for both band ratios (Fig. 4). This could be explained by the agglomeration and also by the increase in size differences between the larger and smaller sub-species in these samples. The ratios still peaked at 30 mol%. The 10 mol% and 50 mol% samples have shown the least difference between the as-synthesized and 24-month samples.

2.3 Luminescence decay kinetics

Luminescence decay kinetics of the B1, B2 and NIR transitions were studied for all five Na(Y,Gd)F4:Yb3+,Tm3+ UCNP samples (AS as well as 24 M samples) In Fig. 5 the decay kinetics of the AS and 24 M sample containing 30 mol% Gd3+ are shown. All UCNP had their lifetimes in the range of tens to hundreds of microseconds (Table 2), which is in good agreement with the data reported in literature for UCNP with similar composition [37, 38]. The data were analyzed using a biexponential decay law (Eq. 3), and the relative fractions (see Fig. 6) \({{\varvec{f}}}_{{\varvec{i}}}\) were calculated using Eq. 4.

Fig. 5
figure 5

Normalized UC luminescence decay kinetics of the Tm3+ NIR emission band (800 nm) of AS (black) and 24 M (red) Na(Y,Gd)F4:Yb3+,Tm3+ (30 mol%, Gd3+) UCNP excited at 976 nm, initial delay Δt = 500 ns. The peaks were integrated within the full width at half maximum range. The lines represent the result of the respective data fitting using Eq. (3)

Full size image
Fig. 6
figure 6

Average luminescence decay times of AS (left) and 24 M (right) NaYF4:Yb3+,Tm3+,Gd3+ (30 mol%) UCNP

Full size image
Table 2 Luminescence decay times of AS and 24 M Yb3+,Tm3+,Gd3+-doped NaYF4 UCNP upon 976 nm excitation (as calculated from PL decay curves, e.g., in Fig. 5). τav is the average time of luminescence decay calculated according to the Eq. 5
Full size table

The complex decay kinetics (Eq. 3) is commonly explained by the presence of two different populations of Tm3+ ions in the UCNP: i) ions on (or close to) the surface of UCNP are more susceptible to quenching by solvent molecules with high-energy vibrations and due to surface defects, which results in shorter decay times; and ii) Tm3+ ions in the bulk phase of the nanoparticle that are more protected from the mentioned phenomena and subsequently tend to have longer decay times [39, 40].

On average for AS UCNP, there was also no linear relationship between luminescence lifetimes and the Gd3+ content, and AS particles with 30 mol% of Gd3+ presented relatively longer lifetimes. This is somewhat odd, since their average diameters were the smallest, thus, the higher surface/volume ratio would be expected to facilitate surface-related quenching effects. However, this could probably be counterbalanced by the regularity of the 30 mol% Gd3+—species crystallinity, and, as a result, homogeneity of their size and shape. Thus, the UCNP with 30 mol% Gd3+ were the brightest and presented longer luminescence compared to the rest of the UCNP samples.

For 24-month Na(Y,Gd)F4:Yb3+,Tm3+ UCNP, luminescence lifetimes have increased in most samples compared to the AS UCNP, especially for the samples with 10 and 20 mol% of Gd3+ (Table 2). The changes in surface-to-volume ratios due to the clustering of UCNP could be one reason for these changes. All samples, except the 30 mol% Gd3+, still displayed luminescence decay behaviors best fitted by the biexponential decay function, which could also be explained by the regularity and relatively smaller sizes of the 30 mol% samples.

Plotting the average decay times τav of the 24-month UCNP as a bar diagram over the Gd3+ content showed a decrease of average decay time with the increase of Gd3+ mol%, which was opposite to the trend observed in the AS UCNP. However, the absolute values were much higher in the 24 M samples, most likely, due to the agglomeration of the UCNP.

2.4 Low-temperature upconversion luminescence studies

We examined the effect of temperature change from 4 to 290 K on the photoluminescence of the Na(Y,Gd)F4:Yb3+,Tm3+ UCNP, in order to provide more detailed information on the luminescence and competing non-radiative deactivation processes in UCNP [12, 20]. As an example, in Fig. 7 one can find emission spectra of 50 mol% Gd3+ UCNP for the temperature range of 4 K < T < 290 K (λex = 976 nm). This pattern of temperature dependence is representative for all the studied UCNP. The intensity of the NIR emission band was usually much higher than B1 or B2 at any given temperature. Luminescence intensities of all three emission bands were lower at room temperature and showed a steady increase with cooling down from 290 to 4 K. These results differ from the data presented in literature for similar studies on Er3+-doped nanoparticles [12, 41]: for NaYF4:Yb3+,Er3+ UCNP doped with either different amounts of Gd3+ or Er3+, all samples have shown a maximum point of luminescence intensity in the range of 50–100 K (depending on the doping concentration), followed by a decrease in luminescence intensity.

Fig. 7
figure 7

Temperature-dependent UC emission of AS Na(Y,Gd)F4:Yb3+,Tm3+ (50 mol% Gd3+) UCNP (λex = 976 nm). Blue (B1) and (B2) (top) and near-infrared (NIR) (bottom) emission bands are shown. A Continuous-wave fiber coupled laser operating at 1 W was used to record the spectra

Full size image

Normalized luminescence intensities of the blue (B = B1 + B2) and NIR emission bands for all UCNP species were plotted as a function of temperature (in the range of 4–290 K) (Supporting Information, Figure S8). To further process these data, we used a Boltzmann-type equation [12, 42, 43]:

$${\varvec{R}}=\frac{{{\varvec{I}}}_{{\varvec{B}}}}{{{\varvec{I}}}_{{\varvec{N}}{\varvec{I}}{\varvec{R}}}}={\varvec{A}}\boldsymbol{ }\mathbf{e}\mathbf{x}\mathbf{p}\left(-\frac{\Delta {\varvec{E}}}{{{\varvec{k}}}_{{\varvec{B}}}{\varvec{T}}}\right)$$
(1)

where R is the ratio of integrated luminescence intensities originating from the respective UCL emission bands, ΔE is the energy gap separating the process-relevant energy levels, kB is the Boltzmann constant, T is the temperature, and A is a constant which depends on the spontaneous emission rate and the energies of the emitting states of the host material [12].

We plotted the logarithm of UCNP luminescence bands intensity ratios against reciprocal temperature (as an example, B and NIR are shown in Fig. 8), and fitted to calculate the energy gap ΔE according to Eq. 1. The resulting values of ΔE for B/NIR ratio can be found in Table S1.

Fig. 8
figure 8

Analysis of temperature dependence the integrated emission intensity ratio of B and NIR bands, shown are data for AS—Na(Y,Gd)F4:Yb3+,Tm3+ (10 and 50 mol% Gd3+)

Full size image

The resulting ΔE values were within the range of 30–40 cm−1 for all studied samples, and we did not observe any clear influence of Gd3+ content on the energy gap values. These results can be explained by the following: in Yb3+ the two lowest energy levels of the 2F5/2 multiplet are 2F5/2|0⟩ (∼10,281 cm−1) and 2F5/2|1⟩ (∼10,242 cm−1). The observed emission is determined by both population and excitation cross-section of 2F5/2|0⟩ and 2F5/2|1⟩ levels of Yb3+. The energy difference between the two Stark levels is known from literature to be just 39 cm−1 [12, 44].

The experimental values obtained from our calculations (∆E in the range of 34–42 cm−1) are an order of magnitude lower than the values of ∆E reported for the emission of Er3+ [12, 44, 45], and lower than the expected values for Tm3+ (hundreds to thousands of cm−1) [44], but very close to the values of the energy gap of Yb3+. A possible explanation for that is that, unlike in the Yb3+—Er3+-pair, energy transfer from Yb3+ to Tm3+ is not strongly influenced by the energy levels of Yb3+, as the 3H5 energy level of Tm3+ is substantially lower than either 2F5/2|0⟩ or 2F5/2|1⟩ (unlike the 4I11/2 level of Er) [12]. However, the lower level of the Yb3+ (2F5/2|1⟩) seems to be more effective in the sensitization of Tm3+ and therefore, the thermal coupling of the two states is observed. Since the content of Yb3+ in all of the studied UCNP species was kept constant, it also explains why the content of Gd3+ had no effect on the observed ΔE values. Thus, we can conclude that, most likely, the energy gap values that we obtained from the experiment could rather be assigned to the excited state of Yb3+rather than Tm3+.

Average luminescence lifetimes were recorded for all AS UCNP species at 4, 100 and 200 K and analyzed using a biexponential decay law (Eq. 3). The general trend showed a decrease of luminescence decay times with the increase of temperature (Figure S9). This could be explained by the increase of the contribution of non-radiative processes with temperature due to the increase of the population of vibrationally excited states, resulting in faster deactivation rates at higher temperatures.

3 Conclusions

We have synthesized Na(Y,Gd)F4:Yb3+,Tm3+ upconverting nanoparticles with different Gd3+-content (10–50 mol%) via thermal decomposition method and investigated the effect of Gd3+ co-doping on the physical and luminescent properties of the obtained UCNP. For the first time, we have compared these properties of the UCNP sample set shortly after synthesis (as-synthesized, AS) and after 24 months (24 M) of storing in dry phase, providing a “four-dimensional study” of their properties.

The UCNP showed good upconversion luminescence upon 976 nm pulsed Nd:YAG laser excitation and luminescence lifetimes in the range from tens to hundreds of μs both after synthesis and after the incubation period of 24 months. The analysis of XRD data has revealed an increase in the hexagonal (β-) lattice phase with the increase of Gd3+ content, although the cubic (α-) phase was prevalent in all samples except the 24 M sample with 50 mol% Gd3+. TEM images of the samples revealed the presence of small homogeneous sub-species and larger and more heterogeneous sub-species. Best size and shape regularity was observed at Gd3+ concentration of 30 mol%, and, hence, the luminescence emission intensity and luminescence decay times of UCNP with this composition were the highest. This differs from the data acquired from similar studies on Er3+-doped UCNP [12, 41], where a linear relationship between Gd3+ doping concentration and the prevalence of β-lattice UCNP was found, resulting in pure hexagonal structures at high Gd3+ concentrations, which improved the photophysical properties of the UCNP. The reason for this inconsistency may lie in another factors, such as synthesis conditions, control over temperature, and/or choice of reaction solvent.

Comparison of the properties of the same Na(Y,Gd)F4:Yb3+,Tm3+ UCNP series right after the synthesis (AS) and after 24 months of storage revealed some changes in their upconversion behavior and physical properties. Although the XRD results have shown no significant changes in the crystalline size, the data obtained from TEM have shown an increase in particle size, which could be explained by aggregation. This led to longer decay times and a change in luminescence band ratios in all samples except 10 and 50 mol% Gd3+, which have shown the least change in their luminescence band ratios over the 24-month storage time.

Thus, storing UCNP in dry phase and redispersing them in cyclohexane after a long storage period does not seem to be the most optimal way to preserve their properties, despite the conservation of upconversion luminescence in all the samples. For the applications where the size and structure of the UCNP and the exact relationship between luminescence bands are of crucial importance, it would be recommendable to turn to other methods of UCNP storage, such as freezing the UCNP in a solution.

4 Experimental

4.1 Chemicals

Yttrium (III) chloride hexahydrate (99.99%), gadolinium(III) chloride hexahydrate (99.99%), thulium (III) chloride hexahydrate (99.99%), ammonium fluoride (≥ 99.0%), and oleic acid (90%) were purchased from Sigma-Aldrich, ytterbium(III) chloride hexahydrate (99.99%) was purchased from Alfa Aesar, 1-Octadecene (≥ 91.0%) from Merck, and Sodium hydroxide (99%) and absolute ethanol were purchased from Carl Roth.

4.2 Synthesis of oleate-capped Gd3+-doped upconverting nanoparticles

Upconverting nanoparticles (UCNP) were synthesized by the thermal decomposition method, in which oleic acid (OA) was used as a capping agent and 1-Octadecene was used as a solvent [31]. In this method, lanthanide chlorides are added to a mixture of high boiling octadecene and oleic acid (volume ratio 3:2). To study the influence of different lanthanide ratios, the overall amount of lanthanide ions (Y3+, Yb3+, Tm3+ and Gd3+) was kept constant (2 mmol), while Y3+ ions were replaced by Gd3+ ions. In a typical procedure, YCl3 (30–70 mol %), GdCl3 (10–50 mol %), YbCl3 (18 mol%), TmCl3 (2 mol %), OA (15.6 ml) and 1-Octadecene (36 ml) were mixed together in a 50 ml 3-neck flask. After a clear solution was formed, the suspension is gradually heated to 145 °C under evacuation, which results in generating of Ln3+ oleates, and then cooled down to 45 °C. NaOH (0.3 g) and NH4F (0.2 g) were added to the mixture under a counter stream of argon (Ar), which induced nanocrystal growth, and the solution was stirred until the precipitate dissolved. The reaction mixture was then rapidly heated to 310 °C min under gentle Ar flow to prevent the oxidation process. At these high temperatures, the process of Ostwald ripening (90 min) leads to the formation of highly crystalline nanoparticles: smaller particles dissolve, which supports the growth of larger particles. Heating was performed using an oil bath and a magnetic stirrer with a heating plate (Heidolph MR Hei-End, Germany) and temperature was controlled using a mercury-in-glass thermometer (Labortherm-N, Germany). Subsequently, the solution was cooled down to room temperature and the resulting UCNP were precipitated in 15 ml of ethanol, centrifuged (8000 rpm for 20 min, from Sigma Laborzentrifugen 2–15, Sigma, Germany) and then washed 3 times with ethanol. Finally, the UCNP were dispersed in 15 mL of cyclohexane for further use.

4.3 Ageing of Gd3+-doped Upconverting Nanoparticles

The five Na(Y,Gd)F4:Yb3+,Tm3+ UCNP samples in cyclohexane were dried and stored at room temperature in the darkness in sealed vessels throughout 24 months. Then, the UCNP were easily redispersed in cyclohexane without any indication for a chemical alteration and their physical and luminescent properties UCNP were assessed.

4.4 X-ray diffraction

To study the crystal structure and the phase content of UCNP, X-ray powder diffraction (XRD) patterns were collected using a D5005 instrument (Siemens AG, Munich, Germany) in a range of 3–70°/2θ with divergence aperture, scattering ray aperture and graphite monochromatized CuKα radiation (λ = 0.15406 nm). The scanning step was 0.02°/2θ with a counting time of 4 s per step.

The set of XRD data was deconvoluted into different components of the spectral and concentration domain by the Parallel Factor Analysis (PARAFAC) algorithm [32] implemented in the optimization toolbox of Matlab R2019b. The non-negative constraint was applied to the XRD spectra and concentration dimension.

4.5 Transmission electron microscopy

Two transmission electron microscopes were used to estimate the size and morphology of the UCNP. The first one, JEM 1011 transmission electron microscope (Jeol Ltd, Tokyo, Japan) (TEM) using a wolfram hairpin cathode, an accelerating voltage of 80 kV and a molybdenum panel. The measurements were recorded using a side-mounted Olympus Mega View G2 (Olympus Germany GmbH, Hamburg, Germany).

The second microscope used was Tecnai G2 20, from FEI/Thermo Fisher Scientific) at an acceleration voltage of 200 kV. Samples were prepared by dropping diluted dispersions on carbon-coated copper grids (400 mesh). Particle counting was performed using ImageSP Viewer software.

4.6 Dynamic light scattering

The hydrodynamic diameters of UCNP were determined by dynamic light scattering (DLS) using a Zetasizer Nano ZS (Malvern Instruments Ltd, Herrenberg, Germany) at 25 °C with a detection angle of 173°. A He–Ne laser at 632.8 nm with P = 25mW was used as a light source.

To obtain nanocrystal sizes (D) from the X-ray diffractograms, Williamson–Hall equation was used:

$$\boldsymbol{\Delta }{\varvec{q}}\left({\varvec{q}}\right)={\varvec{k}}\bullet \frac{2{\varvec{\pi}}}{{\varvec{D}}}+{{\varvec{\varepsilon}}}^{\mathbf{^{\prime}}}\bullet {\varvec{q}};{\varvec{q}}=\frac{4{\varvec{\pi}}}{{\varvec{\lambda}}}\bullet {\varvec{s}}{\varvec{i}}{\varvec{n}}{\varvec{\theta}},$$
(2)

where D is the diameter of the nanocrystallite, k is the shape factor of particle morphology (here 0.9), λ is the wavelength of the X-ray, \({{\varvec{\varepsilon}}}^{\mathbf{^{\prime}}}\) corresponds to variations of lattice constant of an infinite number of crystallites, θ is the Bragg angle of the diffraction peak and Δq is the full width at half maximum of the diffraction peaks as a function of q. The crystallite size D was obtained from the reciprocal of the intercept: \({\varvec{D}}=2{\varvec{k}}{\varvec{\pi}}/\boldsymbol{\Delta }{{\varvec{q}}}_{0}\).

4.7 Steady-state and time-resolved upconversion luminescence measurements at room temperature

Steady state and time resolved upconversion luminescence measurements were carried out at room temperature. The UCNP were excited at 976 nm using a wavelength tunable pulsed Nd:YAG laser (Quanta Ray, Spectra-Physics, Mountain View, CA) combined with an OPO system (GWU-Lasertechnik Vertriebsges.mbH, Erftstadt, Germany) operating at 10 Hz as excitation light source. All upconversion luminescence spectra were recorded using an intensified CCD-camera (iStar DH720-18 V-73, Andor Technology, Belfast, Great Britain) coupled to a spectrograph (Shamrock SR 303i, Andor Tehcnology, Belfast, Great Britain) equipped with a 600 L/mm grating. Time resolved luminescence spectra were recorded by applying a “boxcar” technique in which the amplitude \({{\varvec{A}}}_{{\varvec{i}}}\) is converted to “true amplitude” \({\varvec{F}}{}_{{\varvec{i}}}\) because of the dependence of \({{\varvec{A}}}_{{\varvec{i}}}\) on the detection gate width \({\mathbf{t}}_{\mathbf{g}\mathbf{a}\mathbf{t}\mathbf{e}}\) [46]. Equation 2 shows this relation:

$${{\varvec{F}}}_{{\varvec{i}}}=\frac{{{\varvec{A}}}_{{\varvec{i}}}}{{{\varvec{\tau}}}_{{\varvec{i}}}\left(1-{\mathbf{e}}^{-\frac{{\mathbf{t}}_{\mathbf{g}\mathbf{a}\mathbf{t}\mathbf{e}}}{{{\varvec{\uptau}}}_{\mathbf{i}}}}\right)}$$
(3)

where \({{\varvec{F}}}_{{\varvec{i}}}\) is the coefficient by gate width \({\mathbf{t}}_{\mathbf{g}\mathbf{a}\mathbf{t}\mathbf{e}}\) correction, \({{\varvec{A}}}_{{\varvec{i}}}\) is the experimental coefficient (amplitude of the fit function), \({\mathbf{t}}_{\mathbf{g}\mathbf{a}\mathbf{t}\mathbf{e}}\) is the detection gate width (duration of the photoluminescence emission recording), and \({{\varvec{\tau}}}_{{\varvec{i}}}\) is the luminescence decay time of the i component. For fitting of recorded luminescence decay curves Eq. 3 was used:

$${\varvec{I}}\left(\mathbf{t}\right)={{\varvec{y}}}_{0}+{{\varvec{A}}}_{1}{\mathbf{e}}^{-{{\varvec{k}}}_{1}\mathbf{t}}+{{\varvec{A}}}_{2}{\mathbf{e}}^{-{{\varvec{k}}}_{2}\mathbf{t}}$$
(4)

where \({{\varvec{k}}}_{{\varvec{i}}}=\frac{1}{{{\varvec{\tau}}}_{{\varvec{i}}}}\) is the rate constant, \({\varvec{I}}\left(\mathbf{t}\right)\) is the luminescence intensity in dependence on time\(\mathbf{t}\), \({{\varvec{y}}}_{0}\) is the offset of the fitting function and accounts for background signal contribution, and \({{\varvec{\uptau}}}_{{\varvec{i}}}\) is the luminescence decay time of the i component.

The relative fractions \({{\varvec{f}}}_{{\varvec{i}}}\) were calculated using the following equation:

$${{\varvec{f}}}_{{\varvec{i}}}=\frac{{{\varvec{F}}}_{{\varvec{i}}}\boldsymbol{ }{{\varvec{\tau}}}_{{\varvec{i}}}}{{\sum }_{{\varvec{k}}}{{\varvec{F}}}_{{\varvec{k}}}{{\varvec{\tau}}}_{{\varvec{k}}}}$$
(5)

The average luminescence decay times were calculated according to this equation:

$${{\varvec{\tau}}}_{{\varvec{a}}{\varvec{v}}}={{\varvec{\tau}}}_{1}\bullet {{\varvec{f}}}_{1}{+\boldsymbol{ }{\varvec{\tau}}}_{2}\bullet {{\varvec{f}}}_{2}$$
(6)

4.8 X-ray diffraction

The temperature-dependent steady-state upconversion luminescence measurements were recorded using a continuous wave fiber coupled laser diode working at 1000 mW (SHE-SP-975–160-FS-SMA, Laser 2000 GmbH, Wessling, Germany) coupled to a shutter to avoid the heating of the sample. In order to perform low-temperature luminescence measurements in a range of 4 K < T < 293 K, the UCNP colloidal solutions or powders were sealed inside glass tubes and placed on a copper sample holder in a vacuum chamber attached to a cold plate of a closed cycle liquid helium cryostat. The cryostat system consisted of a helium compressor unit (Sumitomo Heavy Industries Ltd., Markt Indersdorf, Germany), a vacuum pump (Leybold vacuum Turbolab 80, Oerlikon, Köln, Germany) for the sample chamber, and a temperature controller (331 temperature controller, Lake Shore, Westerville, OH). The excitation light was focused directly on the samples. The upconversion luminescence emission was recorded using a lens system set in front of a fiber connected spectrograph (Shamrock SR-303i, Andor Technology, Belfast, Great Britain) equipped with an intensified CCD camera (iStar DH 720 18 V 73, Andor Technology, Belfast, Great Britain).