1 Introduction

Soil–steel composite structures (SSCSs) offer versatile and sustainable technology for various civil engineering applications. Ongoing research in this field continues to refine design practices, improve structural performance, and contribute to the development of cost-effective and environmentally friendly infrastructure solutions [1,2,3,4,5,6]. Flexible structures, most often constructed using corrugated steel plates (CSPs) and known as shell structures, find widespread application in culvert, tunnel, and bridge construction [7,8,9,10,11]. The fundamental concept underlying the SSCSs lies in the properly created interaction between the shell and the surrounding backfill. Due to this interaction, the loads from the vehicles are efficiently transferred through the backfill and the shell [12,13,14,15].

Typically, SSCS are made of uniform cross-section corrugated steel sheets. However, in situations with insufficient shell capacity, additional plates or ribs are bolted to the main profile in areas requiring additional support [16,17,18]. This reinforcement improves the overall stiffness and load capacity of the structure and helps to manage deformation during construction and operation stage [17,18,19].

The behavior of the SSCS under live load [20,21,22,23] and ultimate load has been studied by many scholars [24, 25]. Wysokowski [26] conducted full-scale tests on the shallow corrugated SSCS with a length of 3.55 m of span, a rise of 1.42 m, and 0.6 m soil height of cover. The structure is reinforced by stiffening ribs made of CSPs along the crown of the shell. From the study, it was observed that under a maximum load exerted by the hydraulic actuator, the structure showed no signs of damage. Therefore, a decision was made to reduce the soil cover from the initial 0.6 m to 0.1 m. Then, the test was repeated, and a failure occurred under a load of approximetly1990 kN. The collapse was observed around the shoulder of the shell and the corresponding displacement of 105 mm was observed. The same author [26] also conducted full-scale tests on various buried SSCSs under failure load conditions, focusing on circular PE plastic pipe with diameter of 0.80 m, circular corrugated steel pipe with diameter of 0.80 m, and pipe-arch culvert structure with a span of 2.99 m. The soil cover for the pipes was 0.6 m, while for the pipe-arch culvert, it was 0.3 m. Displacements and stresses were examined. Among the three models examined, the PE plastic pipe culvert exhibited the highest displacement. In terms of bearing capacity, the pipe-arch culvert emerged as the most reliable. Moreover, from the test, it was observed that the pipe-arch culvert retained its stability even when the stress in the steel reached its limit. It suggests that the pipe-arch formed a more favorable interaction with the surrounding backfill by redistributing the loads more effectively compared to the other considered shapes. An interesting discovery of the findings of this research is that, at a soil cover depth of 0.3 m, which falls below the minimum allowable depth of soil cover (0.5 m according to the Swedish design manual [16], 0.6 m according to AASHTO 2019 [27], and CSA 2019 [28]), the structure remained safe even under loads exceeding standard limits. For example, the maximum loads specified by the Polish bridge design [29] and NATO standards [30] are 500 kN and 600 kN, respectively. Notably, the ultimate bearing capacity of the pipe-arch culvert is nearly four times greater than the estimates provided by these standards.

Brachman et al. [31] conducted controlled experiments on an SSCS made of deep corrugated steel plates with a 10 m span and a rise of 2.4 m under ultimate load conditions. The structure was subjected to a vertical force applied to the structure with a soil cover depth of 0.45 m. The ultimate limit state (ULS) of the structure was reached with an applied force of 1100 kN, which was 1.8 times higher than the values recommended by the AASHTO bridge design specifications. Flener [19] performed a full-scale test to examine the behavior of large-span SSCSs under ultimate loading conditions. The study entails structures with span lengths of 14 m and 8 m with different depths of soil cover. The author observed that the load-bearing capacity of the structure increased linearly with increasing soil depth of cover. Furthermore, the presence of crown stiffeners doubled the ultimate load capacity of the structure. Chimauriya et al. [32], conducted an experiment and numerical simulation on an SSCS with a diameter of 1.52 m under static load. The authors proved that, by increasing soil depth of cover by 25%, crown displacement is reduced by 31%. Additionally, the authors determined that the structure failed due to local buckling in the crown section of the shell. In the study conducted by Wadi et al. [33], the impact of varying load positions on the maximum load capacity of SSCS with a span of 18.1 m was investigated. The authors simulated the effect of load positions at six specific locations: first, the tandem was at the center of the crown line, then it was placed at distances of 0.6 m, 1.6 m, 2.6 m, 3.6 m, and 4.6 m from the center of the crown. These positions are defined by the distance from the tandem center to the crown line. Maximum values of live load bending moments and normal forces were observed when the tandem load was centrally placed at the crown. However, applying asymmetric loading resulted in a reduction in the failure load.

Several methods are available to improve the bearing capacity of SSCSs, and a commonly used approach is the use of additional ribs [15, 34,35,36]. Sanaeiha et al. [35] conducted a field test on a large-span SSCS stiffened by concrete rings during backfilling. The authors compared the test results with well-known design methods and provided detailed recommendations based on their findings. The structure had a span, rise, and soil cover above the crown of 20, 8.25, and 2.1 m, respectively. The corrugated steel plate used had deep corrugations with a pitch of 400 mm, a depth of 150 mm, and a thickness of 8 mm. The test results indicated that the maximum bending moment and deflection were observed at the crown when the backfill reached the crown level. Conversely, the maximum axial force occurred at the bottom of the shell when the backfill reached its maximum level above the shell. The authors compared the test results with design methods from CSA [37] and the Swedish method as presented by Pettersson and Sundquist [38], and concluded that while the design methods are more realistic in predicting axial forces, they tend to be conservative in predicting bending moments.

Maleska and Beben [15] conducted a numerical analysis to investigate the impact of a stiffening rib on the behavior of large-span SSCS during backfilling. In their analysis, the authors observed that in the case of the shell without a stiffening rib, the allowable stresses and displacements were not exceeded during backfilling. As a result, the authors concluded that the advantages gained in terms of the higher bearing capacity of the structure may not be practically necessary when employing a stiffening rib. Moreover, the authors concluded that this method of reinforcing the shell is not economical. However, there are instances where employing this additional stiffening rib is crucial from a practical standpoint. For example, according to [39], the utilization of stiffening ribs is becoming more prevalent, particularly when the soil cover over the shell structure is limited. This is due to the prevailing conditions of the terrain where raising the road or railway embankment is neither technically nor economically feasible. In such cases, additional structural elements can be used to improve the load-bearing capacity of the structure. Nevertheless, it is important to note that the effect of this stiffening rib should be further examined under the ultimate limit state.

Reinforcing the soil cover above the crown of the shell using geotextiles or geogrids emerges as a cost-effective solution [34]. A comprehensive full-scale test has been conducted by Vaslestad et al. [34]. The authors analyzed the influence of geogrid on the mechanical behavior of box-type SSCS. The geogrid used was a biaxially oriented polypropylene geogrid LBO 220 SAMP. The tensile properties of this geogrid were tested before its application as reinforcement, revealing a tensile strength of 7 kN/m at 2% strain and 14 kN/m at 5% strain. Subsequently, one layer of geogrid was placed 0.3 m above the crown, within a soil cover of 0.6 m. The authors observed that the maximum deflection from a static traffic load of 870 kN was reduced by 29.5% with the use of the geogrid. Additionally, the deflection of the crown of the box culvert was reduced by 17.8% for the dynamic load with the use of the geogrid. The authors conclude that reinforcing the soil above the crown with a single layer of geogrid can be a practical alternative to traditional relieving concrete slabs, commonly used to redistribute traffic loads. This approach can facilitate the design of cost-effective structures while reducing the minimum required soil depth of cover. According to Wysokowski [39, 40], placing a geomembrane in the backfill 0.3 m above the crown of the shell increases the load-bearing capacity of the structure by approximately 30%. Even under loads significantly exceeding standard values [29], the stresses and displacements of the shell structure remain relatively low.

Maleska et al. [36] conducted numerical simulations to examine the influence of a single layer of geotextile on the behavior of SSCS under service loads. The structure under consideration has a soil cover of 0.6 m. The geotextile was positioned in the middle of the soil cover above the crown of the shell, redistributing the applied load and reducing the vertical displacement at the crown of the shell by 28% compared to a model without geotextile reinforcement. The results obtained from both the field test and numerical analysis, as reported by Beben et al. [41], demonstrate that the implementation of a relieving RC slab and EPS geofoam significantly reduces the stresses and displacements within the shell of the shallow-buried SSCS. The authors’ findings demonstrate that the incorporation of EPS geofoam and an RC slab significantly reduced vertical displacements within the buried SSCS, achieving reductions in the range of 40–41% and 39–41%, respectively. Moreover, the implementation of EPS geofoam led to an approximate 19% reduction in stresses within the shell of SSCS, while the RC slab contributed to a reduction of around 14%. These results underscore the effectiveness of both EPS geofoam and the RC slab in minimizing structural displacements and stresses, thus enhancing the overall stability of the shallow-buried SSCS.

In full-scale tests, quantifying the effect of geotextile on structures underloading to failure can be challenging. In such cases, a properly calibrated FE model with available experimental data can gain valuable insights into the behavior of the structure under extreme loading scenarios, offering a more comprehensive understanding of its performance. FE model allows to simulate and analyze the complex interactions within the structure and the effect of various parameters, including geotextile reinforcement, under conditions that may not be easily achievable in full-scale tests because of the reasons specified above.

As described above, there is still a need for further research on the failure mode of soil–steel composite structures under ultimate loads. Furthermore, a comprehensive exploration of the failure modes in SSCS, both with and without a stiffening rib, as well as the failure mode of the structure reinforced with geotextile, is imperative. Therefore, the primary objective of this study is to examine the influence of the stiffening rib on the bearing capacity of the SSCS and to examine how the placement of geotextile within the soil cover above the crown of the shell impacts the mechanical behavior of SSCSs subjected to ultimate loads. To achieve this objective, the effects of both: stiffening shell with additional ribs and reinforcement of backfill with geotextile are investigated through numerical simulations. Consequently, a model of box-type SSCS with a span of 3.55 m is considered for four cases of reinforcement: Model-I (with a stiffening rib), Model-II (without a stiffening rib), Model-III (with a stiffening rib and geotextile), and Model-IV (without a stiffening rib but with geotextile). For the analysis, a computational model was developed, and its parameters were validated against the data obtained from the real scale experiment.

2 Numerical model

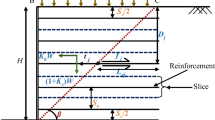
The numerical model used in this study reflects the structure considered in [26] as shown in Fig. 1a. The structure had the following dimensions: a span of 3.55 m, a longitudinal width of 13.7 m, and a rise of 1.42 m (Fig. 2). The shell was assembled using corrugated profiles with a commercial designation, specifically the MultiPlate 150 mm × 50 mm (pitch x depth), and it had a thickness of 5.0 mm, as shown in Fig. 2. To enhance its strength and stability, the structure was reinforced with the ribs made from CSP located at the top section of the perimeter, specifically at the crown, with a width of 1.54 m. The corrugated steel plates (CSP) were joined by 20 mm (in diameter) bolts, having a minimum tensile strength of 830 MPa. For the backfill material, a well-graded soil with a maximum grain size of 32 mm was utilized. The backfill was placed in layers with a maximum thickness of 25 cm, and it was compacted to achieve a degree of compaction equal to at least 97% of the Standard Proctor test.

Fig. 1
figure 1

Model of considered SSCS: a geometry, and b finite element mesh and boundary conditions adopted in the numerical model

Full size image
Fig. 2
figure 2

Corrugated steel plate model: a main shell and b main shell with stiffening rib

Full size image

The ZSoil software [42], based on finite element method (FEM), was used for the numerical analysis of the soil–steel composite structure. It was modeled as a 2D object in plane strain. The finite element mesh and kinematic boundary conditions are shown in Fig. 1b.

In terms of boundary conditions, the vertical edges of the domain were restrained against horizontal displacement and the bottom boundary was fixed in all directions. To ensure computational stability, the loading to failure is simulated in a displacement-driven manner. Selected nodes at the top boundary of the domain are restricted in the vertical direction, as illustrated in Fig. 1b. The connection between the shell and the foundation was assumed to be pinned with fixed displacement in both directions and free in rotation. To account for second-order effects, the large deformation mode is activated. Furthermore, a mesh size sensitivity analysis was performed to ensure that the results are not influenced by the element size. Finally, a fine mesh size of 5 cm was employed for both the shell and the surrounding backfill.

The shell is modeled utilizing non-linear beam elements, employing an elastic-perfectly plastic constitutive relation. It is also assumed to be continuous in the out-of-plane Z direction, following the considerations presented in the previous works [43,44,45]. The parameters of the shallow corrugation (multi-plate) profile of 150 × 50 mm with 5 mm thickness are taken from the manufacturer catalog [46] for the corrugated steel plate. Accordingly, the cross-sectional area and moment of inertia for a single CSP are A1 = 6.30 mm2/mm and I1 = 1978 mm4/mm, respectively. For the section with stiffening rib, employing Steiner’s theorem, the corresponding values are A2 = 12.6 mm2/mm and I2 = 13,485 mm4/mm. Therefore, a perfect connection between the main shell and the stiffening cover is assumed. In reality, the structure comprises a series of corrugated plates bolted together at specific locations. A study by [47] revealed that explicit modeling of the overlap between the shells or bolt connections has no significant impact on the structural response. Therefore, in the present study, the bolted connection between CSP is not explicitly included in the model. Similar assumptions are considered in recent studies [48, 49].

The CSP is characterized by Young’s modulus (E = 205 GPa), Poisson’s ratio (ν = 0.3), a unit weight (γ = 78.6 kN/m3), and by strength parameters specified in European Standard EN 10025, in particular, yield stress limit of σy = 250 MPa.

The elastic-perfectly plastic constitutive model with Coulomb–Mohr yield criterion is assumed for the backfill modeled with solid 2D elements. Initially, soil parameters, including Young’s modulus (E = 40 MPa), Poisson’s ratio (ν = 0.2), cohesion value (c = 0 kPa), and internal friction (φ = 39°), were assumed based on national standards for coarse sand/sand with gravel. However, initial simulations revealed a significant difference between the simulated and measured results. Recognizing the need for improvement, an extensive calibration process was undertaken to refine the soil parameters. Following this calibration, a good fit was observed between the simulation and measurements. This issue is addressed in the next section.

The unassociated plastic flow rule is prescribed by adopting a dilatancy angle determined based on the ZSoil user manual [42]

$$\psi = \max (0.1\varphi ,\varphi - 25^\circ ),$$
(1)

where \(\uppsi\) is the dilatancy angle and φ is the angle of internal friction.

The concrete foundation was modeled as linear elastic.

To properly reflect the interaction between the soil and shell at the interface, a one-sided contact condition was assumed. This follows that the soil medium may separate from the shell if the shell moves away from the backfill material, and subsequent contact renewal is allowed when the shell and backfill material come close together again. The behavior of the contact interface was described using the Coulomb condition. The plastic slip was governed by a non-associated plastic flow rule with the dilation angle value set to ψ = 0. The Coulomb condition governs the value of the maximum tangential stress in contact elements

$$\left| { \tau_{f} } \right| \le a + \sigma \tan \delta ,$$
(2)

where adhesion a = 0, the internal angle of friction δ = 0.6 \(\varphi\) ≈ 22°, and \(\varphi\) is the internal angle of friction of the adjacent soil. Elastic deformation moduli (normal and tangential stiffness) for interface elements were determined in accordance with ZSoil Users’ Manual [42] as

$$K_{n} \approx K_{t} = \frac{E}{h},$$
(3)

where E is the elasticity modulus of weakest adjacent material, and h represents the size of finite element (representing the backfill) adjacent to the contact interface. Based on Eq. (3), the values of normal and tangential stiffness utilized in the calculation were estimated as Kn = Kt = 1.0e6 kN/m3 for the interface between the soil and the shell, and Kn = Kt = 8.0e4 kN/m3 for the interface between the geotextile and the backfill. Similar assumption is considered in the work of [36].

The geotextile is modeled as a non-linear truss element, assuming elastic-perfectly plastic behavior with limited tensile stress and the prestressing effect is also taken into consideration. In our current model, the prestress of around 6% of the tensile strength of the geotextile material is considered. The tensile strength of geotextile in the model is 3.4 MPa with zero compressive strength and a thickness of 4.2 mm.

In this paper, initially, the response of the shell of SSCS is analyzed during backfilling and compaction. Subsequently, the structure is subjected to loading until failure. For this purpose, four different models of SSCSs are considered (see Fig. 3): Model-I (with a stiffening rib), Model-II (without a steel rib), Model-III (with a stiffening rib and geotextile), and Model-IV (without a stiffening rib but with geotextile). The ultimate load is induced using a displacement-imposing method to determine the ultimate bearing capacity of SSCS, both with and without geotextile. In this method, a controlled downward vertical displacement is applied to the nodes of the structure at the top surface, as illustrated in Fig. 1b. Moreover, due to the limitation of two-dimensional model, the effect of local buckling (incorporating out-of-plane deformation) does not fully covered.

Fig. 3
figure 3

Schematic presentation of reinforcement in the models: a Model-I, b Model-II, c Model-III, and d Model-IV (all dimensions are in millimeter)

Full size image

3 Numerical model validation

The basis for model validation was the full-scale experiment conducted at the Research Institute of Roads and Bridges in Żmigród, Poland, by Wysokowski [26] (see Fig. 4). The measurements of displacement taken on the box-type SSCS were used to adjust the parameters of the numerical model. A parametric analysis was carried out so that to fit the simulation results to the measured data. The validation process included test results from both stages: backfilling and external loading. A concise description of the test performed [25] is given below.

Fig. 4
figure 4

Model of the soil steel composite structure in laboratory test: a general view of the assembled corrugated steel structure; b after backfill model prepared for ultimate loading test [26]

Full size image

Once the backfilling process was completed, reaching a soil height of 0.6 m above the crown of the shell, the structure was subjected to steadily increasing load up to the value of 2000 kN. The overall view of the assembled shell, along with the structure after backfilling, is illustrated in Fig. 4. The test stand consists of two actuators with a maximum exciting force of 1000 kN and a maximum travel of 400 mm. Further details about the load configuration can be found in [40].

Initially, the structure showed no signs of failure under a load of 2000 kN. Consequently, the top layer of backfill was removed, leaving only a 0.10 m-thick soil cover above the shell. Subsequently, the load was directly applied to the upper surface of the structure, and the failure of the shell was observed. The results obtained for this setup, in the form of a load–displacement curve, as well as the displacement measurements taken during the backfill, are directly used to calibrate the numerical model. This process is described in detail in Sects. 3.1, 3.2.

3.1 Simulation of backfilling

To accurately estimate the failure load of the SSCS, it is essential to consider the shell stress induced by the backfilling soil [49]. The backfilling operations for flexible culverts often generate substantial bending stresses in the shell wall. Given their significance, incorporating these backfilling stresses is essential for predicting actual stresses in the shell wall, particularly upon yielding. Therefore, all models account for the effects of backfill layers and compaction to ensure comprehensive analysis.

To replicate the field measurements [26], the modeling approach incorporates eight layers of backfill, each with a maximum thickness of 0.25 m. To simulate the actual soil compaction process, a uniformly distributed surface load of 50 kPa is applied to each layer. The simulation of backfilling and compaction follows a sequential process: initially, a layer of backfill is activated, generating geostatic backfill stresses. Subsequently, a compaction load is applied, and the model is computed. This iterative process continues until the backfill reaches its final stage. Once the backfilling is completed, the structure is subjected to external loading to failure. Similar assumptions were made in [50,51,52]. Comparison of measurements and numerical modeling results for the crown displacement during backfilling is shown in Fig. 5. In the model, the crown of the shell initially exhibited upward deflection as the backfilling process progressed, and this displacement continued until the backfill reached layer five. Subsequently, as the backfilling process extended beyond layer five, the crown of the shell started moving downward. By the time the backfilling reached the final stage, which is layer eight, the maximum downward movement reached approximately −1.70 mm. In the measurement, the observed behavior showed an initial upward deflection until the backfill reached layer six. After reaching this point, the shell started moving downward slowly as subsequent backfilling layers were added. Upon the completion of the entire backfilling process, a total vertical displacement of −1.89 mm was recorded.

Fig. 5
figure 5

Comparison of measurements and numerical modeling results for the crown displacement during backfilling

Full size image

The FE model accurately determines displacements within the shell during the construction stage. However, it slightly underestimates the peak displacement (both upward and downward), deviating by approximately 11% from the field measurements. The maximum upward and downward vertical displacement of the shell during construction was less than 0.1% of the structure rise, which is in agreement with the requirements of CHBDC (CSA 2019) [28] code limit of 2%.

3.2 Simulation of ultimate load test

As mentioned, the reduction of the soil cover above the crown of the shell was intentionally carried out to facilitate the observation of shell failure. The loading-to-failure model was executed subsequent to decreasing the soil cover to a mere 0.1 m, as described in Fig. 6. After completing the backfilling phase during simulation, the nodes on the top surface were gradually moved downward, and the total loading force was calculated as the sum of nodal reactions. This allowed us to plot the curve of load versus displacement, as shown in Fig. 7. Simultaneously, the corresponding results from measurements [26] are also plotted in the same graph.

Fig. 6
figure 6

The SSCS model with reduced soil height of cover

Full size image
Fig. 7
figure 7

Load–displacement curve

Full size image

The load–displacement behavior (see Fig. 7) observed in both datasets exhibits notable congruence and reveals essential insights into the structural response. Up to 900 kN load, the structure demonstrates a nearly linear response marked by a relatively flat slope, signifying the initial, elastic phase of deformation. Beyond the aforementioned value, load increase rate drops apparently, what is reflected by a steeper slope of the plot. This is attributed to the transition from elastic to plastic deformation of soil. This phase culminates in peak value of load less than 1990 kN, signifying ultimate capacity of the entire, composite structure. The agreement in these pivotal load–displacement characteristics underscores the numerical model’s ability to replicate the result from the measurement. Especially, the convergence of simulated and measured load-bearing capacity has to be emphasized. It was achieved after robust model calibration based on the displacement results recorded during backfilling the shell. Therefore, as the validation process encompassed the entire loading history divided into two main stages—namely, the construction stage (backfilling) and operational loading—the same set of material parameters was applied. This consistency resulted in a good agreement between measurements and simulations, confirming the accuracy of the performed calibrations. In conclusion, it can be stated that the finite element model successfully described the performance of the structure and accurately determined its load-bearing capacity.

The material parameters used in the present analysis, including those which were calibrated, are given in Table 1.

Table 1 The summary of the material parameters used in the computations
Full size table

It should be emphasized that the cohesion value of the backfill soil is slightly higher than classically assumed for this type of soil. In a physical sense, the increased value of this parameter can be attributed to the so-called apparent cohesion, as described by Sobótka and Łydżba [53]. The increased cohesion value is in line with the findings of Sobótka and Łydżba [53], who explained that calibrating the parameters of the Mohr–Coulomb model, while considering the apparent cohesion in partially saturated soil, is advantageous for accurately representing the behavior of the backfill. This approach ensures better agreement with measurements.

Once the parameters are validated, the following sections present the load–displacement and internal forces extracted from four different models. Each model offers valuable insights into the structural behavior underloading to failure.

4 Effects of stiffening ribs

In this section, two models are specifically compared: Model-I (with stiffening ribs) and Model-II (without stiffening). The comparison involves the structural response, including displacement, bending moments, and axial forces for both models. While the primary focus is on the structural response of the crown section, the distribution of section forces at the shoulder is also presented and discussed.

4.1 Load–displacement curve

The deflection at the crown point was extracted and compared for both models. In Fig. 8, a load–displacement graph is presented, illustrating the behavior of the structures. Initially, the structure exhibited practically linear deformation. Next, the plot bends and its slope increases, reflecting the transition from elastic to plastic deformation. As the applied load continues to increase, it finally leads to yielding in the entire area of the shell cross-sections. Consequently, the structure is unable to carry more load. Its limit value is identified as the overall load-bearing capacity of the structure. Then, this limit value of the load, i.e., bearing capacity of the structure, was back-calculated from the reaction forces of the imposed displacement (in this case, at a controlled node).

Fig. 8
figure 8

Load displacement curve for the model with and without additional rib at the crown

Full size image

Model-I, which incorporates the stiffening rib, demonstrates a robust bearing capacity of 2533 kN. In contrast, Model-II, which does not incorporate the stiffening rib, exhibits a considerably lower bearing capacity, amounting to 1732 kN. The presence of the stiffening rib in Model-I exerts a notable positive impact on bearing capacity when compared to Model-II. Specifically, Model-I bears 801 kN more total load, equating to a substantial 47% higher bearing capacity than Model-II. This improvement is attributed to the additional role of the ribs in optimizing load distribution within the structure. It ensures more advantageous redistribution of applied load, thereby mitigating localized stress concentrations that might otherwise lead to premature structural failure.

The displacement at which the structure reaches peak load capacity provides insight into how much displacement can be expected until a failure occurs. Accordingly, at the peak load value, the crown of the shell exhibited a displacement of 115 mm and 140 mm, respectively, for Model-I and Model-II.

The failure mode of a considered soil–steel composite structure at which the structure cannot carry more load is determined by bending failure of the shell. The same is concluded in previous study [54]. Specifically, as the load surpasses the structure load-carrying capacity, the load–displacement curve changes sign of its slope indicating distinct inflection point. Beyond it, the SSCS behavior transits to post-failure mode. The structure does not break suddenly but undergoes plastic flow in a wide range of displacement. It is to be reminded here that the simulation was performed in a displacement-driven scheme. Nevertheless, such type of ductile behavior of the structure marks favorable property in terms of safety.

The failure mode of the structure is predicted under combined axial compression and bending moment, considering critical locations for this type of structure: at the shell’s crown and at its shoulder (at the end of stiffening rib). Additionally, the haunch of the shell was checked.

Employing the interaction equation, one can check whether the cross-section becomes fully plastic or not. According to CSA 2019 and AASHTO 2019, the following inequality remains true:

$$\left( {\frac{N}{{N_{p} }}} \right)^{2} + \left| {\frac{M}{{M_{p} }}} \right| \le 1.0$$
(4)

or rearranging the equation

$$M_{u} \le M_{p} \left( {1 - \left( {\frac{N}{{N_{p} }}} \right)^{2} } \right),$$
(5)

where Mp is plastic moment capacity of the shell (\({M}_{\text{p}}\) = \({\sigma }_{\text{y} }Z\)), σy is the yield strength of the steel (250 MPa), Mu is ultimate bending moment capacity of shell, Np is maximum capacity of the shell wall against normal force (\({N}_{\text{p}}\)= \({\sigma }_{\text{y} }A\)), N is normal force at maximum bending moment in the calculation, and Z is plastic section modulus of the cross-section.

At the crown section, the calculated values are as follows: \({M}_{\text{p}}\) = 88.5 kNm/m, \({N}_{\text{p}}\)= 3136 kN/m, and Z = 354 mm3/mm. The normal force N = 618.425 kN/m is extracted from the numerical model at maximum bending moment and at this point the corresponding load is 1563 kN. Using Eq. (4), the ultimate moment capacity of the shell under ultimate load at the crown section for Model-I is determined to be Mu = 85.06 kNm/m. Then, the maximum bending moment induced in the shell is extracted from the numerical model, which was found to be 75.2 kNm/m at the crown of the shell. It is worth noting that this value is less than the shell’s ultimate capacity. This means that the calculated value employing the interaction equation (Eq. 4) provided is 0.89. This shows that the shell failed before reaching the unity value of the interaction equation at the crown.

To assess whether the ultimate moment capacity of the shell is reached at other sections of the shell, we conducted further checks. Given that the first yielding occurred at the shoulder of the shell (at the end of the stiffening rib), the check was performed at this particular section. At this location, the shell is not overlaid with an additional rib, necessitating the recalculation of cross-sectional and strength parameters for the single shell. Subsequently, the plastic moment capacity of the shell was calculated as Mp = 24.18 kNm/m and the maximum capacity of the shell wall against normal force Np = 1575 kN/m. The normal force from the numerical model N = 268.88 kN/m, and plastic section modulus of the cross-section Z = 96.7 mm3/mm. Then, utilizing (Eq. 5), we determined that the ultimate moment capacity of the shell under ultimate load at the shoulder section is Mu = 23.48 kNm/m. At this specific location, the calculated maximum bending moment extracted from the simulation reaches the ultimate capacity as shown in Fig. 9a. Employing the interaction equation (Eq. 4) the calculated reached 1.0. Accordingly, the structure failed after reaching the unity value of the interaction equation at this section of the shell. Furthermore, as per Pettersson’s [55] recommendations, the design evaluation of the box-type SSCS extends beyond the crown section to include the haunch area. Consequently, an examination of the haunch section of the shell was conducted, revealing full yielding during the assessment, ultimately leading to failure at this specific section. Thus, the structure with stiffening ribs (Model-I) loses its carrying capacity due to bending at the shoulder and haunch.

Fig. 9
figure 9

Bending moment vs vertical displacement curve for a Model-I and b Model-II

Full size image

For Model-II, the cross-sectional and strength parameters are as follows: plastic moment capacity of the shell Mp = 24.18 kNm/m, maximum capacity of the shell wall against normal force Np = 1575 kN/m, normal force in the calculation N = 129.80 kN/m, and plastic section modulus of the cross-section Z = 96.7 mm3/mm. The maximum moment capacity of the shell under ultimate load at the crown of the shell is extracted from the numerical simulation and it is 24.06 kNm/m. The corresponding load to the maximum bending moment and normal force for this particular section is 1675 kN. Similarly, employing the interaction equation (Eq. 4), the calculated value is 1.0. Unlike Model-I, in Model-II, the crown section is fully plastic under peak load. Like Model-I, a check was performed on another critical section for this type of SSCS—specifically, the haunch section. The results indicated that the section underwent full plastic deformation under the ultimate load. Therefore, for Model-II, the failure mode is bending failure at the crown and haunch section of the shell, as shown in Fig. 9b.

The ultimate moment capacity’s variation between the two models is primarily attributed to the presence and absence of the additional stiffening rib. In Model-I, the capacity is reached at the shoulder due to the load redistribution facilitated by the rib. However, in Model-II, it is achieved at the crown, resulting in bending failure. These findings underline the complex interplay between geometry, materials, and structural elements in shaping the behavior and failure modes of such structures under ultimate loads, like the additional rib, on the bending failure mode of the soil–steel composite structure.

The overall circumferential bending moment distribution for model-I and model-II is depicted in Fig. 10a, b, respectively. These figures reveal notable distinctions in the locations of bending moment concentration and the positions of peak positive and negative bending moments between the two models. For instance, in Model-I, the peak positive bending moment concentrates around the shoulder of the shell. In contrast, for Model-II, this concentration shifts to the crown, which indicates the location of potential failure.

Fig. 10
figure 10

Bending moment distribution on the shell of SSCS for a Model-I and b Model-II

Full size image

In Fig. 10a, a noteworthy observation is the asymmetrical distribution of bending moments at post-failure. Initially, this distribution was nearly symmetrical until the load approached its peak. Beyond the peak load, a rapid change in both the rate and sign of displacement occurred, as illustrated in the load–displacement curve in Fig. 8. This abrupt shift signifies the onset of plastic flow within the structure, coinciding with the initiation of the asymmetrical bending moment distribution. The pronounced concentration of bending moments, particularly around the left-side shoulder, can be attributed to the presence of a stiffening rib. This is evident when comparing Model-II in Fig. 10b, where the distribution appears almost symmetrical, to the asymmetrical distribution observed in Model-I. The stiffening rib encircling the crown of the shell in Model-I plays a pivotal role in redistributing bending moments before the point of failure. Another noteworthy observation in Model-I is the first yielding occurring at the left side of the shell around the shoulder section, precisely next to the end of the stiffening rib and haunch. This localized yielding significantly influences the overall distribution of bending moments. Furthermore, in the model with the stiffener, plastic hinge development is prone at two distinct points—specifically, at both ends of the stiffening rib. In Model-I (Fig. 10a), it prominently manifests on the left side. However, it is imperative to highlight that an equivalent risk of collapse exists on the right side, as demonstrated in the case of Model-III in Fig. 15a. Moreover, the asymmetrical distribution of bending moments in the structure represents a post-failure mode. This analysis not only enhances our understanding of structural behavior but also provides valuable insights into potential failure mechanisms.

4.2 Axial force

The axial thrust of the shell in a soil–steel composite structure under ultimate load represents the maximum compressive force experienced by the wall of the shell and is a critical parameter for assessing the structural safety and integrity of the entire system. In both models, the analysis reveals that the maximum axial thrusts (compressive) reach –989 kN/m for Model-I and –674 kN/m for Model-II, as illustrated in Fig. 11a, b, respectively. In Model-I, the maximum axial thrust represents approximately 63% of the shell’s wall capacity at this specific section, which amounts to 1575 kN/m. In contrast, for Model-II, this value is around 43%. This concentration is a crucial observation, as it defines the areas of the structure subjected to the highest loading conditions. Importantly, this finding aligns with the results presented in [15].

Fig. 11
figure 11

Maximum axial thrust distribution on the shell of SSCS under ultimate load; a Model-I and b Model -II

Full size image

In both models (Fig. 11a, b), negative axial forces throughout the shell’s circumference indicate uniform compression. This behavior aligns with the norm for such structures, as concluded by Moore and Taleb [20]. The peak values of the axial forces are observed near the footing of the shell.

From the results, it can be concluded that the shell without stiffening ribs (Model-II) does not reach the axial thrust capacity of the wall. This finding suggests that, in the context of axial thrust, additional reinforcement is not necessary for such types of shells. This conclusion highlights that Model-II, despite lacking stiffening ribs, still maintains a safety margin with respect to its axial thrust capacity. Therefore, for the specific structural conditions analyzed in this study, the use of additional reinforcement ribs, as present in Model-I, may not be required to ensure that the shell can safely resist axial thrust under ultimate load conditions. This finding was also reported by [15], who conclude that the shell model without stiffening ribs does not exceed the allowable stresses and displacements in the shell.

5 Behavior of geotextile-reinforced SSCS under ultimate load

5.1 Load–displacement curve

The bearing capacity of Model-III, which incorporates a geotextile, was determined to be 3200 kN, representing a 26% increase when compared to Model-I, which does not utilize a geotextile. Similarly, Model-IV exhibited a bearing capacity of 2140 kN, reflecting a 23% increase in comparison to Model-II, which lacks geotextile reinforcement.

Under ultimate load conditions, the vertical displacement at the crown of the shell experiences a significant reduction, as illustrated in Fig. 12. This decrease in displacement and the improvement in load-bearing capacity can be attributed to the redistribution of the applied load on the shell’s top surface due to the presence of the geotextile. Geotextile reinforcement enhances the stiffness of the backfill, exerting a substantial influence on the failure mode and overall structural stability.

Fig. 12
figure 12

Load–displacement curve at crown

Full size image

As shown in Fig. 12, the reinforcement’s effect becomes more pronounced as the load increases. Consequently, a notable reduction in displacement is observed when the structure is subjected to the ultimate load. For instance, when the reinforced structure undergoes a service load (e.g., 800 kN, following the Polish Standards of bridge load [29]), the reduction in displacement is significantly less compared to when the structure is exposed to loading conditions leading to failure. This observation underscores the effectiveness of geotextile reinforcement in enhancing structural performance under critical loading conditions, providing improved stability, and minimizing displacement during ultimate load scenarios. A similar finding was observed in the full-scale test conducted by [40]. When the geotextile-reinforced structure is subjected to service load, the reduction in maximum vertical displacement at the crown of the shell was less than 20%. This further supports the effectiveness of geotextile reinforcement in reducing vertical displacement and improving the structural performance during service load conditions.

At the peak load value, the crown of the shell exhibited a displacement of 98.43 mm and 131.95 mm, respectively, for Model-III and Model-IV. Similar to the Model-I and Model-II, an interesting feature is that post-failure behavior is stable. Under peak load, the vertical displacement at the crown exceeds the permissible standard for all models except Model-III. According to the Polish standard, the maximum deflection percentage (vertical displacement to structure span ratio) should be less than 3%. Model-III complies with this requirement, with a deflection percentage of 2.8%.

5.2 Bending moment

The maximum bending moment in the shell at the crown is illustrated in Fig. 13. It can be observed that the bending moment increases when the structure is reinforced with the geotextile.

Fig. 13
figure 13

Bending moment displacement curve at the crown for Model-III

Full size image

Utilizing Eq. (5), previously applied to Model-I and Model-II in Sect. 4.1, we estimate the ultimate plastic moment capacity (Mu) for Model-III at the crown section. The geometric and strength parameters for this model are identical to those of Model-I, except the inclusion of geotextile. The axial compressive thrust at maximum bending moment for this model is extracted from the numerical model as, N (855.6 kN/m). Accordingly, using Eq. (5), the estimated Mu for the shell in this particular model is calculated as 81.9 kNm/m. Once the ultimate capacity is estimated, we extract the maximum bending moment at the crown of the shell from the numerical simulation, which amounts to 81.4 kNm/m, as shown in Fig. 13. The load corresponding to this maximum bending moment is calculated as 2382 kN. When compared to Model-I, the maximum bending moment induced in the shell is improved by 8%. This finding aligns with the results of a numerical analysis conducted by [36] on soil–steel structures subjected to service load, where the bending moment capacity of the shell is similarly improved through the reinforcement of a single layer of membrane. Despite the increase in bending moment capacity, similar to Model-I at the crown section, the ultimate capacity of the shell due to combined bending and axial forces is not reached under ultimate load. It was confirmed by employing the interaction equation given on Eq. (4) and the calculated value is 0.99. From this interaction value, it can be seen that the shell is close to reaching the full yielding at the crown section.

To find if the shell capacity due to combining axial compression and bending moment is reached at other sections of the shell, further check has been carried out. Accordingly, the maximum moment capacity of the structure is reached around the shoulder of the shell. At this specific location, the calculated interaction value based on Eq. (4) is 1.00. Unlike Model-I, the haunch section of the shell does not undergo full plastic deformation under the ultimate load. Thus, the structure with ribs and geotextile-reinforced (Model-III) loses its carrying capacity due to bending at the shoulder. The distribution of bending moment is shown in Fig. 15a for Model-III.

For the Model-IV, the ultimate plastic moment capacity of the selected profile is 21.8 kNm/m, calculated using Eq. (5). Similar to Model-II, the shell in Model-IV failed after reaching fully plastic under peak load, as shown in Fig. 14. And as shown in Fig. 15b, the maximum positive and negative bending moment induced in the shell is observed at the crown and shoulder section of the shell, respectively. Comparing this value with the ultimate capacity of the shell, it can be concluded that the shell in Model-IV failed after the cross-section at crown and haunch reached fully plastic section. Thus, potential failure modes for this structure are a local bending moment, and the development of plastic hinges.

Fig. 14
figure 14

Bending moment vs vertical displacement curve at the crown of the shell for Model-IV

Full size image
Fig. 15
figure 15

Bending moment distribution on the shell of geotextile-reinforced SSCS under ultimate load for a Model-III and b Model- IV

Full size image

The presence of geotextile enhances the bending capacity of the shell, particularly in the lower section near the foundation. For instance, in Model-II, the maximum bending moment at this section is approximately 4.06 kNm/m (as shown in Fig. 10b), whereas in Model-IV, it increased to 6.66 kNm/m (as depicted in Fig. 15b). This represents an increment of around 64%.

5.3 Axial force

The maximum calculated axial thrusts for Model-III and Model-IV are presented in Fig. 16a, b, respectively. In Model-III, the maximum calculated axial thrust (compressive) reaches 1225 kN/m, while in Model-IV, it amounts to 839 kN/m. These values are observed in the shell near the foundation. When comparing Model-I (a model without geotextile) with Model-III, there is a 16% increase, and when comparing Model-II (another model without geotextile) with Model-IV, there is a 24% increase.

Fig. 16
figure 16

Maximum axial thrust distribution on the shell of geotextile-reinforced SSCS under ultimate load; a Model-III and b Model-IV

Full size image

Furthermore, it is worth noting that the maximum thrust value for Model-III, 1225 kN/m, accounts for 78% of the theoretical crushing load, which is calculated to be 1575 kN/m. In the case of Model-IV, this value represents 53% of the theoretical crushing load. The theoretical load signifies the thrust required to induce compressive yield across the entire cross-section.

Furthermore, the introduction of geotextile contributes to structural stability. It acts as a stabilizing agent, mitigating deformations that could compromise the integrity of the composite structure. This aligns with prior research [40], which emphasizes the stabilizing role of geotextile in analogous applications.

In both models, with and without geotextile reinforcement, two critical zones were observed based on the bending moment distribution that induce maximum compressive and tensile stresses. The identified critical zones are the crown, shoulder, and haunch sections of the shell. On the research conducted by [56], on large-span structure, similar finding was observed both in field test and numerical simulation. Furthermore, the critical force due to global buckling were estimated using the methodology presented by Pettersson [55]. However, the induced normal force in the shell has kept much less than the critical value for the entire course of simulation. That fact indicates that the global buckling of the shell is not likely to occur.

6 Summary and conclusions

In this study, numerical analysis was employed to examine the failure modes of box-type soil–steel composite structures under ultimate load conditions. The numerical analysis was based on 2D non-linear finite element analysis validated with full-scale test of soil steel composite structure during both backfilling and under ultimate load. Due to the flexible nature of the structure with anticipated substantial deflection, our numerical model incorporated a large deformation mode at all simulation stages. The material and contact nonlinearity were included in the numerical simulation. The numerical models presented in this study highlight the substantial impact of stiffening ribs and geotextile reinforcement of the backfill on the bearing capacity of soil–steel composite structures. The results reveal that reinforcements substantially enhance the load-bearing capacity, with geotextile placement in the upper part of the backfill effectively reducing shell deflection due to bending. However, it is important to note that the findings of the study are limited to the assumptions and methods described in the paper. In particular, 2D model simplifies the analysis but lacks the ability to capture certain effects, such as local buckling, out-of-plane displacement, and spatial load transmission within the soil. Therefore, 3D model will be developed in the future works of the authors to account for object’s edges conditions and to provide more detailed insights into soil–steel structure behavior.

The main conclusions drawn from the numerical simulations conducted are as follows:

  • The FE model accurately predicts displacements in the shell during construction but slightly underestimates peak displacements (both upward and downward) by around 11% compared to field measurements. The maximum upward and downward vertical deflection of the shell during construction were less than 0.1% of the structure rise, which is in agreement with the requirements of CHBDC (CSA 2019) code limit of 2%.

  • The addition of a stiffening rib at the crown section enhances the structure’s load-bearing capacity by 47%, while the utilization of a single layer of geotextile reinforcement contributes to an approximate 26% increase in load-bearing capacity.

  • The structures with stiffening ribs reach their load-carrying capacity due to creation of a plastic hinge at the shell’s shoulder and haunch. On the other hand, in the structures without stiffening ribs, the crown and haunch sections of the shell become fully plastic under peak load.

  • For both structures, reinforced and unreinforced by geotextile, under peak load, the maximum axial thrust is not reached the maximum capacity of the shell due to compression. Maximum axial thrust is shown in geotextile-reinforced structure, reaching 78% of the shell maximum capacity due to compression.

  • The bending moment in structures reinforced by geotextile is increased by 8%, and the bending capacity of the shell is not reached at the haunch section, in contrast to unreinforced structures.

  • Asymmetry in bending moment distribution is evident in Model-I and Model-III, contrasting with the nearly symmetrical distribution in Model-II and Model-IV. This asymmetry results from the influence of the stiffening rib on redistributing bending moments before failure. Additionally, plastic hinge development is prone at both ends of the stiffening rib, with Model-I exhibiting it on the left side. Notably, an equivalent risk of collapse exists on the right side, as demonstrated in Model-III.

  • The potential impact of local buckling may not be comprehensively addressed due to the two-dimensional nature of the model. Nevertheless, an assessment of critical forces associated with global buckling was conducted, and the induced normal force in the shell consistently remained well below the critical value throughout the entire simulation. This observation suggests that the occurrence of global buckling in the shell is highly unlikely.