Predicting the microstructure of compacted graphite iron using a fuzzy knowledge-based system

Abstract

One of the important engineering materials is compacted graphite iron (CGI). Obtaining an expected microstructure leading to desired material properties is relatively difficult. In this paper, we present an approach to predicting the microstructure with a fuzzy knowledge-based system. On the basis of the results of statistical analysis and expert knowledge, an original taxonomy of CGI casts was formulated. The procedure of data acquisition, specimen preparation, analysis procedure and microstructures obtained are presented. Methods for expert experience-supported knowledge extraction from experimental data, as well as methods for formalizing knowledge as fuzzy rules, are introduced. The proposed rulesets, the reasoning process, and exemplary results are provided. The verification results showed that, using our approach, it is possible to effectively predict the microstructure and properties of CGI casts even in the absence of sufficient data to use data-driven knowledge acquisition. On the basis of the results obtained, examples of possible applications of the developed approach are presented.

1 Introduction

Technological advances require the use of new materials or improvement of the parameters of already known materials. One such material is compacted graphite iron (CGI). CGI has been known since the late 1940s, although the beginnings of its utilitarian use date back to the 1960s. Unfortunately, the technological problems associated with the widespread use of this material have not been solved. A key problem associated with the use of materials such as CGI is the prediction of their properties as a function of microstructure versus chemical composition in advance. This is particularly important for companies with a process called Request for Quotation (RFQ) [12]. Unfortunately, no analytical or numerical models are available to predict the microstructure as a function of the chemical composition. From the theoretical point of view, such a system could be designed, based on a combination of FEM, CALPHAD and other tools. However, the use of such complex systems might not be reasonable. To achieve sufficient prediction quality, the numerical model requires significant effort and long-lasting research. At the same time, due to inevitable uncertainties in industrial processes, the resulting prediction is never perfect.

It is widely accepted that the solution to technological problems, including the prediction of the microstructure and properties of materials, can be the use of artificial intelligence (AI) methods. However, this applies when researchers have enough industrial or experimental data to use data-driven knowledge acquisition to train inference engines. The purpose of our research was to verify the hypothesis that even incomplete experimental data can be a useful source of information for technologists, provided that expert knowledge and AI methods are used a priori.

Some attempts have been made to use Artificial Intelligence (AI) tools to formulate predictive models previously. The results of a study on the possibility of using the Sugeno-type Neuro-Adaptive Fuzzy Inference System (ANFIS) for this purpose are presented in [17]. Data from material experiments carried out by the authors of the mentioned paper were used to teach the ANFIS model. As a result of the specificity of the tool used, the tests were performed separately for each microstructure component. A model obtained ensures the maximum level of prediction error equal to 9%. At the same time, an error at the testing stage was assumed to be at the level of 5%. However, it should be noted that the cited publication used data-driven knowledge acquisition and the research was sectional (individual microstructure indicators were evaluated independently).

We acknowledged that the concept of using fuzzy inference is practically the only solution allowing modelling phenomena and processes for which it is not possible to build analytical or at least numerical models. In our research, however, we have adopted assumptions different from those in previous attempts to solve the problem [17], namely:

• the effect of alloying elements on the characteristic microstructure matrix rather than the contribution of individual phases to the structure will be investigated,

• a hybrid approach to knowledge acquisition will be used, combining direct use of expert knowledge (rote learning and/or learning by being told) with basic machine learning techniques.

The adoption of such assumptions makes it possible to solve many of the problems that AI solutions are burdened with fully or at least partially based on the concept of black-box reasoning systems. In this type of system, the process of formulating the knowledge base takes place solely on the basis of the provided results of observations without the participation of an expert (teacher). In the case where we deal with a limited number of observations that do not cover (for justified reasons) the full area of hypothetical variability of explanatory factors, we may obtain results that are not justified, in this case, technologically. In our opinion, the use of hybrid methods taking into account the participation of experts allows one to eliminate contradictions obvious from the expert's point of view and to simplify the process of knowledge acquisition.

The paper is organized as follows: Sect. 2 discusses works related to the use of AI methods in solving technological problems. Section 3 presents the subject of our research and data sources. In Sect. 4, we describe the methods used to solve the problem of predicting the microstructure of CGI. Section 5 presents the course of study. In Sect. 6, we present the results of our research in the form of a Knowledge Model of Microstructure of Compacted Graphite Iron. Finally, Sect. 7 concludes the article.

2 Related works

Our research was preceded by an analysis of the literature on CGI, the technological problems associated with obtaining the appropriate properties of this cast iron, and the use of Artificial Intelligence (AI) methods to support technological decisions.

Alloyed CGI has been the subject of many publications. These investigations have focused on an influence of an alloy’s chemical composition on its microstructure and properties, which corresponds to the subject of our research. M. König and M. Wessén [9] presented the effect of copper on the microstructure and mechanical properties of CGI. This has been evaluated through standard metallographic analysis, color etching techniques, and tensile testing of machined test bars. The effects of Cu on the morphology and growth of graphite in CGI were presented in [34]. In [11], the effect of tin on the structure and properties of CGI cast was investigated. In [10], the focus was on studying the relationship of tin on the abrasive wear behavior. In [16], the result of a study on the effect of copper content and applied machining processes on the elastic modulus of CGI is presented. In [22] the effect of alloying elements (chromium, copper, and aluminum) on the formation processes of structures is studied in cast iron with vermicular (compacted) graphite. In the paper [27] the production and characterization of alloyed compacted graphite iron in ten chemical compositions (varying silicon, copper, and tin share) are presented.

One can also find many works that focused on the possibility of obtaining the desired properties of CGI through the use of different processing. In [23], attempts to obtain Austempered Vermicular Cast Iron (AVCI) quenched with isothermal transformation were presented, as well as the results of tests on this cast iron. In the paper [7], the results of the study Influence of austempering temperature and time on microstructural and mechanical properties of CGI are presented. Similar studies were described in the paper [24]. In [32], the effect of the austempering treatment on the tribological properties of engine components manufactured from CGI was evaluated.

In recent years, the importance of AI methods in solving technological problems has been growing. The literature related to this topic is extremely extensive, and therefore we will present only selected publications. For a comprehensive overview of the applications of AI methods to engineering problems, see the publication on fracture mechanics and mechanical fault detection [20] and the publication describing the fault detection and diagnosis technique for photovoltaic systems [14]. Fault detection problems are, of course, different from the task of predicting the microstructure of metallic materials that we are considering; however, as the literature shows, the way they are solved and the methods used are remarkably similar. This can be evidenced by the similarity of the models and solutions used in the work on predicting the microstructure of CGI [17] and the estimation of the work on the parameters of photovoltaic modules [28] using adaptive neurofuzzy inference systems (ANFIS). Analogous to our approach can also be found in the work on fault detection for predicting failure of oil pipelines [1], among others.

The literature also contains many descriptions of the use of AI methods to predict the microstructure and properties of metals and alloys and, among them, CGI cast iron. Among others, the effectiveness of the use of data mining tools using AI for approximation of ausferrite content in the CGI [26] or identifying the components of the microstructure of CGI [31] has been studied in. The paper [30] presents the results of using the machine learning and the Support Vector Machine for analysis of the properties of the nodular cast iron with carbides and the austempered ductile iron. Also interesting from the point of view of the approach, we use may be the attempt to use the induction of classification and regression trees for the prediction of molding sand moisture content [25].

A special case of using AI to solve technological problems is computer vision and machine learning for microstructural characterization and analysis. An overview of these methods can be found in [8] and an example of a detailed study of bainitic subclasses in low-carbon multiphase steels can be found in the paper [18]. The essence of computer vision concept is automatic pattern recognition of microstructures based on digitized images. This is important when technological solutions are examined using machine learning methods, without the participation of experts. In the case of our research, this problem does not exist as the number of examples studied can be successfully described and evaluated by experts, without the need for error-laden automatic image recognition techniques.

It should be noted that all of the mentioned studies were based on multiple sets of observations and were implemented using appropriate data-driven knowledge acquisition techniques (machine learning). The authors did not find a description of studies seamlessly combining expert knowledge with example-based learning techniques. The advantage of our approach boils down to the possibility of using it in the absence of sufficiently numerous sets of learning observations. At the same time, as shown below, even assuming that experts can make mistakes and the number of examples is not fully representative, the level of prediction error is comparable to the results obtained with learning from observations.

3 Study area and source data

Compacted Graphite Iron, which was the subject of our study, is characterized by a specific microstructure. The shape of graphite in this cast iron is defined in EN ISO 945-1 as type III and is shown in Fig. 1.

Fig. 1

Graphite shape in CGI according to EN ISO 945-1: type III

The mechanical properties of CGI result, among others, from the shape of graphite. They are intermediate between grey and nodular cast iron, as shown in Table 1.

Table 1 The CGI grades according to EN 16079:2012

Table 1 shows that the minimum tensile strength ranges from 300 MPa for CGI with predominantly ferritic matrix to 500 MPa for cast iron with fully pearlitic matrix. Cast iron with compacted graphite, compared to high-quality gray cast iron, is characterized by, inter alia:

• higher tensile strength,

• higher elongation and resistance to dynamic loads,

• lower sensitivity to wall thickness (maintaining appropriate strength properties in thick-walled castings),

• lower oxidation and swelling tendency at elevated temperatures,

• higher resistance to thermal fatigue.

Compared to ferritic ductile cast iron, CGI has the following advantages:

• lower modulus of elasticity,

• lower coefficient of thermal expansion,

• higher thermal conductivity,

• higher resistance to thermal fatigue during very rapid changes in temperature cycles (so-called thermal shocks),

• greater ability to vibrations damping,

• better machinability,

• better castability and less tendency to create shrinkage cavities,

• less tendency to deformation at elevated temperature and better dimensional stability,

• lower tendency to hard spots,

• less environmental pollution during production.

The advantages of CGI predestine it for a wide range of applications. It is used mainly in the automotive industry for the production of cylinder heads, exhaust manifolds, brake discs, brake shoes, crankcases, diesel engine heads, and blocks.

The functional properties of different CGI variants depend on the microstructure of the casting. The right microstructure can be obtained by heat treatment or by modifying the chemical composition with suitable additives. The alloying elements in CGI include, inter alia, copper, nickel, and tin. They are used mainly to increase the tendency to form pearlite in the matrix. The need to increase the strength properties led to the development of ausferritic CGI. Ausferrite is a mixture of high-carbon austenite and lamellar ferrite. The ausferritic matrix is obtained (similarly to ADI) by heat treatment—austempering. There is also an alternative way to obtain an ausferrite, i.e. by modifying the chemical composition of cast iron. For this purpose, Mo with Ni or Cu is added to the cast iron. This thesis was confirmed, among others, in the paper [6], which indicated that ausferrite has been shown to form during casting of gray iron by carefully controlling alloying additions of Mo, Mn, Si and Cu. In the work [33], it was indicated that it is possible that, with the right composition of components, the alloy has a microstructure and mechanical properties comparable to austempered gray iron without many of the problems associated with austempering. In article [34] Cu is found to have a great influence on graphite morphology and growth mode in CGI. As mentioned above, the effect of additives on the CGI microstructure is described in many other publications.

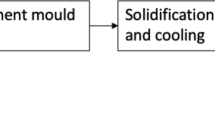
As mentioned above, we used as a data source the results presented in [17], which refer to compacted graphite in cast iron obtained using Inmold technology. It consists of placing the master alloy inside the reaction chamber located in the gating system between the sprue and the test casting. The schematic layout of elements in the mold is presented in Fig. 2.

Fig. 2

The schematic layout of elements in the mold to obtain CGI with different microstructure: 1, pouring cup; 2, main gate; 3, reaction chamber; 4, mixing chamber; 5, control chamber; 6, test casting; 7, flow-off.

The test casting was shaped as a step with a wall thickness of 3, 6, 12 and 24 mm. The cast iron for the tests was smelted in a medium-frequency electric induction furnace with a capacity of 30 kg (ELKON, Rybnik, Poland). The charge used was special pig iron (with reduced sulfur content), ferrosilicon, ferromanganese, and technically pure: Cu, Ni, and Mo. The pouring temperature was approximately 1480 °C. After solidification, the casting was knocked down, the gating system was cut off and the casting was cleaned of the used sand. Next, specimens for metallographic tests from the central parts of the step-shaped casting were cut out. Microsections were prepared with the use of abrasive papers with 100, 600 and 1200 grains, followed by polishing on 3 μm and 1 μm diamond suspensions. The microsections were etched with a 4% HNO₃ solution in C₂H₅OH. The microstructure was examined using Eclipse MA 200 (Nikon, Japan) metallographic microscope with a magnification of × 500 and NIS-Elements BR (Nikon, Japan) image analysis software. The chemical composition of the cast iron was tested on SPECTROMAXx arc spark OES metal analyzer from SPECTRO Analytical Instruments GmbH. In this way, a data set was obtained, in which the input data was the concentration of elements in the cast iron, and the output data was the share of CGI matrix components. The source database can be treated as a set of observations, containing the results of examinations and measurements of the content of individual microstructural constituents of CGI (ferrite, pearlite, carbides, martensite, ausferrite, and austenite), as well as the content of individual alloy additions within the studied range of the chemical composition, including Cu content (wt.%), Ni content (wt.%) and Mo content (wt.%). The studies whose results we used also took into account the wall thickness of the castings, a feature of the technological nature. In the aforementioned studies, the microstructures of castings with wall thicknesses of 3, 6, 12 and 24 mm were analyzed, treating them as explanatory variables together with the amount of alloying elements. We considered taking wall thickness into account when assessing the influence of alloying elements on the microstructure of a casting to be extremely important. Unfortunately, the inclusion of this premise complicates the knowledge model, which in the case of the knowledge acquisition method we adopted (learning by example with an expert) makes the formulation of rules much more difficult. At the same time, as a result of preliminary analyses, it was discovered that some regularities appear that are different for "thin" (3 and 6 mm) and "thick" (12 and 24 mm) walls. An example of CGI microstructure in thin- and thick-walled castings is shown in Figs. 3, 4, 5.

Fig. 3

a, b Microstructure of unalloyed CGI in castings with a wall thickness of: a 3 mm, b 24 mm

Fig. 4

a, b Microstructure of CGI containing about 7% Ni in castings with a wall thickness: a 3 mm, b 24 mm

Fig. 5

a, b Microstructure of CGI containing about 1.7% Mo and 2% Ni in castings with a wall thickness: a 3 mm, b 24 mm

We considered that it would be useful to build the knowledge model independently for examples concerning "thin" and "thick" walls. Finally, we used two databases that contained 67 records for thin-wall castings and 70 records for thick-wall castings for further research.

4 Research questions, hypotheses, methods, and techniques

On the basis of previous studies, it is possible to formulate the thesis that obtaining a specific CGI matrix microstructure depends on the proportion of alloying elements in the cast iron. As can be seen, the problem of microstructure prediction depending on the chemical composition is, in our case, the character of classification and not regression as it was in previous studies. Our previous work on microstructure evolution prediction [12] and forging die wear prediction [13] had shown that such a problem might be successfully solved with Fuzzy Knowledge-Based Systems.

When using a rule-based classification system for prediction, the problem can be represented by the general formula (1) [5]:

$$IF\ {X}_{1}\ is\ {A}_{1}^{1}\ AND\ {X}_{2 }\ is\ {A}_{2}^{1}, \ldots , {X}_{n}\ is\ {A}_{n}^{1}\ THEN\ Y \in {C}^{j},$$

(1)

where X_i—variables of the premises,—${A}_{i}^{j}$fuzzy sets representing a fuzzy subspace of the ith premise in jth rule, Y—conclusion of the rule and C^j—the class of the resultant value assigned for a given set of premise values. The classes of resultant values should be understood as an a priori defined patterns of microstructures.

Applying this approach requires solving two key research problems: how to identify groups (clusters) of substantially different microstructures and how to connect these groups with the chemical composition of the relevant examples using fuzzy reasoning methods and verifying the correctness of the assumptions made. The novelty of our method is that experts play an important role at each stage. The general concept of our methodology is shown in Fig. 6.

Fig. 6

The general concept of the proposed methodology

4.1 Clustering

The first stage is to formulate patterns of microstructures in such a way that each class unambiguously represents a certain "type" of material with consistent functional properties. Taking into account the fact that in our research we had a number of examples of experimental results, it was natural to try to group the microstructure components into certain patterns using cluster analysis methods. Cluster analysis is based on grouping objects according to their features (in our case, the proportion of phases in the microstructure) indicating their similarity (correspondence of feature values) and/or dissimilarity [2]. Here, the principle of intrinsic similarity and extrinsic dissimilarity is applied, expressed by means of a similarity function (metric). In our case, the measure of similarity is the proportion of individual phases in the microstructure. Clustering consists in assigning objects to groups in such a way that within each group the belonging objects are similar to each other but different groups are least similar to each other. There are many algorithms that perform cluster analysis.

Taking into account the results of our previous studies, we applied hierarchical clustering, in particular Agglomerative Clustering [19], to group the microstructure patterns. The Agglomerative Clustering performs a hierarchical clustering using the bottom-up approach: each observation starts in its own cluster, and clusters are successively merged together.

In our case, a microstructure data source for the clustering was the results of material tests. These tests were not designed to cover the full area of variation in the microstructure patterns, and therefore we decided that it would be necessary to verify the results obtained by an expert. It should be emphasized that the clustering of microstructures, both by cluster analysis methods and by the expert, was carried out independently of the relationship of microstructures to the chemical composition of the cast iron. The only criterion for clustering was, in the case of the statistical method, the similarity of the structures and, in the case of the expert evaluation, the influence of the proportion of individual phases on the useful properties of cast iron.

4.2 Fuzzy knowledge acquisition

Another research problem is related to the formulation of a knowledge model in the form of a set of rules linking linguistic variables representing the content of particular elements to an input with the expected microstructure pattern. Due to the fact that our problem is of a classification rather than regression nature, it was assumed that Mamdani's scheme [15] would be an adequate method of fuzzy reasoning. Formulating a predictive model requires establishing the parameters of the membership functions of fuzzy sets for input variables and defining If–Then rules. Both of these tasks are closely related, and according to our assumptions, expert knowledge will play an important role in their implementation. Therefore, we adopted the simplest way to represent linguistic variables (triangular numbers) and the human-understandable fuzzy ID3 algorithm. The difference between the ordinary ID3 algorithm and the fuzzy version of the ID3 algorithm is that the object attributes have degrees of membership and it is possible that an attribute belongs to several nodes. To construct a fuzzy decision tree, the following procedure is proposed [3]:

• 1. defining a fuzzy database, i.e. fuzzy granulation for continuous feature domains,

• 2. replacing the continuous features of the training set with the linguistic labels of the fuzzy sets with the highest correspondence to the input values [4],

• 3. computing the entropy and information gain of each feature, then splitting the training set, and defining successive tree nodes until all features are used or all training examples are classified.

Information gain ${G}_{j}$ tells how much uncertainty in dataset was reduced after splitting it on jth premise (2).

$${G}_{j} = I - {E}_{j}.$$

(2)

The entropy of a dataset without any information is given by Eq. (3).

$$I = - \sum_{c=1}^{m}\frac{{n}_{i}}{n} {\mathrm{log}}_{2}\frac{{n}_{i}}{n},$$

(3)

where m—the number of conclusions classes, n—the number of examples and n_c—the number of examples indicating cth conclusion. The entropy of the jth premise is given by Eq. (4).

$${E}_{j} = \sum_{k}\frac{(\sum_{i=1}^{n}{\mu }_{j,k}^{i}(x)){S}_{j,k}}{\sum_{k}\sum_{i=1}^{n}{\mu }_{j,k}^{i}(x)}$$

(4a)

and

$${S}_{j,k} = \sum_{c=1}^{m}\frac{\sum_{l}{\mu }_{j,k}^{l}\left(x\right),{conclusion}^{l}=c}{\sum_{i=1}^{n}{\mu }_{j,k}^{i}\left(x\right)},$$

(4b)

where ${\mu }_{j,k}^{l(i)}\left(x\right)$—the membership function value of kth value of jth premise in lth or ith example, conclusion^l—conclusion index in lth example.

The idea of the fuzzy ID3 algorithm can be represented as in Fig. 7. Details may be found in the paper [29]

Fig. 7

A graphical description of the algorithm used

4.3 Fuzzy knowledge formulation (hypothesis)

One of the goals of our research was to verify the hypothesis that a knowledge model created with the participation of experts rather than automatically can be used effectively in conditions where an adequate number of observations are not available.

The knowledge formulation process is carried out iteratively. Initially, the ranges of variables defining the content of individual alloy additives have been divided into three fuzzy sets with the names {Small, Medium, Large} and the crisp value “null”, while the parameters a, b and c for each fuzzy number are set so as to cover the area of variation evenly. The modelling of the wall thickness of castings will be different. They will also be treated as triangular fuzzy numbers, but the number of subsets will be different. Then, on the available examples, the rules are formulated using the fuzzy ID3 algorithm. As this algorithm does not guarantee the logical correctness of knowledge, contradictions may arise (the same in a fuzzy sense, premises lead to different conclusions). To remove these contradictions, the expert corrects the parameters of fuzzy numbers, and if this does not solve the problem, the number of fuzzy sets for selected premises increases. The process ends when all contradictions are removed.

5 Course of study

Our research was carried out in three main stages: formulation of microstructure groups using the clustering method, induction of fuzzy inference rules, and evaluation of inference sensitivity. Research was carried out according to the scheme shown in Fig. 7.

5.1 Source examples of microstructure clustering

In the first step, we clustered examples of microstructures obtained from material tests independently for both thin- and thick-walled castings. In both cases, we used the Agglomerative Clustering method mentioned above. For the calculations, we used the Scikit-learn package [21]. As a metric to compute the linkage, we used the Euclidean distance and as a linkage criterion the “ward” method, which minimizes the variance of the clusters being merged. We did not assume the number of clusters in advance, but using the method of successive approximations, we determined the linkage distance threshold above which clusters will not be merged. This resulted in 14 clusters for thin-wall castings and 11 for thick-wall groups. The results of the statistical clustering in both cases (thin and thick walls) gave similar, quite characteristic results. This can be clearly seen in Fig. 8.

Fig. 8

Clusters identified for thin (a) and thick (b) walls, projection on a 2D plane. Clusters are represented with the shapes of the marks

The clusters are very far apart from each other. This is because individual clusters were formed around dominant fractions. Analyzing the numerical results, it is clear that we are dealing with four basic groups of microstructure patterns (the figures are somewhat misleading, but it should be remembered that they have arisen as a result of projecting the results onto a plane). Of the six constituents, four can play this role, namely pearlite, martensite, ausferrite, and austenite. Statistical clustering clearly confirmed this thesis. The greater than four final number of clusters is due to the fact that the remaining nondominant constituents are significantly differentiated within the main groups.

The next step consisted of an expert analysis to assess whether the statistically generated clusters correspond to patterns of microstructures that determine significantly different properties of cast iron. In the case of thin-wall castings, minor corrections had to be made, which resulted in the creation of 13 groups. This division is presented in Table 2, together with the relevant commentary. In the case of castings with thick walls, no corrections were necessary. The results of the annotated division are presented in Table 3. The tables show the linguistic values assigned by the experts to each subgroup in the major casting groups (e.g., small share of martensite) and measurements of the content of individual microstructural constituents from the source data. It should be noted that the numerical (crisp) values are partly random and auxiliary to experts. The properties of cast iron are determined by linguistic variables.

Table 2 Subdivision proposal for castings with wall thicknesses of 3–9 mm

Table 3 Subdivision proposal for castings with wall thickness 9–24 mm

5.2 Induction of reasoning rules

The main objective of our study is to relate the microstructure of the CGI matrix extracted above to its chemical composition. According to our concept, this stage was also carried out by experts assisted in this case by fuzzy data analysis and classification methods. Preliminary expert analysis of the data linking the chemical composition with the matrix microstructure determined in the previous stage has shown that both in the case of thin and thick wall castings, the known facts have been confirmed that microstructures with a dominant share of austenite and martensite can be obtained at high nickel percentages. No other additives are used in this case.

A separate knowledge base is justified for these two types of microstructure. In this knowledge base only one premise is considered, that is, the nickel content, which is described by four triangular fuzzy numbers for castings with "thin" walls “about 7%", "about 14.5%", "about 16.5%" and "about 21%" and five numbers for castings with “thick” walls “about 5.5%”, “about 9%”, “about 14.5%”, “about 16.5%”, “about 21%” (Fig. 9).

Fig. 9

Membership functions for nickel content, cases with a dominant share of austenite and martensite; thin (a) and thick walls (b)

The formulation of the rules was straightforward and did not require any procedures. The complete knowledge base for austenite and martensite is presented in Sect. 5.

After removing the results for the cases with dominant austenite and martensite from the database, 54 examples with thin walls and 58 with thick walls remained for further analysis. For these examples, the dependence of the microstructure on the chemical composition is not obvious and requires the methodology described in the previous section. The study was carried out independently for both groups of castings. After the initial formulation of the model that describes the fuzzy form of the premises (content of particular elements), an attempt was made to formulate rules using the fuzzy ID3 method under the assumptions described in Sect. 3. Then, the inconsistency of the knowledge base formulated in this way was verified on the same group of examples using Mamdani's approach.

For thin-wall castings, it turned out that in the case of copper and molybdenum, the division into three subsets was insufficient to describe the influence of variations in the content of these elements on the microstructure. For all elements, the uniform subdivision into subsets proved ineffective. Based on data analysis, but also taking into account knowledge and technological experience, the experts made successive corrections in the number and form of subsets and then repeated the procedure of generating rules and verifying them until the examples were fully consistent with the deduced outputs of the reasoning system. This effect was obtained for the division of the premises describing the copper and molybdenum contents into five subsets (S2—very small, S1—small, CE—central, B1—big, B2—very big) and the appropriate modification of the characteristics of the fuzzy numbers describing the share of all elements, as presented in Fig. 10.

Fig. 10

Membership functions for copper, nickel, molybdenum contents and wall thickness, cases without a dominant share of austenite and martensite, thin walls

A fragment of the knowledge model generated by the ID3 fuzzy method for thin-walled castings can be represented graphically (Fig. 11).

Fig. 11

A fragment of the knowledge model generated by the ID3 fuzzy method for thin-walled castings

In the case of castings with thick walls, it was possible to formulate a simpler knowledge model. An uncontradictory model was obtained to divide the premise description for the molybdenum content into five subsets and that for copper and nickel into three subsets (Fig. 12). It was also necessary to modify the parameters of all fuzzy numbers that describe the premises.

Fig. 12

Membership functions for copper, nickel, molybdenum contents and wall thickness, cases without a dominant share of austenite and martensite, thick walls

Complete knowledge models for both groups of castings are presented in Sect. 5.

5.3 Assessing the sensitivity of the method

The peculiarity of our knowledge extraction method is the use of expert knowledge to formulate linguistic variables (triangular numbers) and the method of learning by example to formulate the final form of the knowledge base. This approach makes it unreasonable to perform tests that are implemented in machine learning methods based on observations. Thanks to the application of this novel method of knowledge acquisition, it was possible to build such a knowledge base, which 100% represents the investigated relations. Nevertheless, we carried out an assessment of the sensitivity of our method to possible errors in expert judgment and a nonrepresentative set of learning examples. To this end, we conducted a kind of cross-validation, a technique that is often used for machine learning from observations. We conducted a series of experiments in which the number of learning examples was randomly limited and also the test set was randomly selected. The test set was assumed to be about 30% of the number of available examples. Thirty experiments were conducted to test the effectiveness of inference for microstructures with dominant ausferrite and pearlite phases and thin-wall castings, which are the most error-prone. The accuracy of the microstructure prediction was 91% and the standard deviation was 6.9%. The relatively low standard deviation indicates a low probability of making a coarse error in microstructure prediction. In previous studies [17], the efficiency of inference in a test sample was estimated at 91% and in a learning sample at 95%, but this was for predicting the contribution of individual phases rather than patterns of the microstructure of castings. Analogous results are obtained when AI methods are used to solve similar problems. Due to the original nature of our approach, it is difficult to compare them directly. Nevertheless, the error rate when using learning-from-observation methods is similar to that which may occur in our methodology, assuming that expert errors and/or an incomplete/inconsistent set of examples are possible. An assessment of the accuracy of different AI methods can be found in a review article describing, among other things, the accuracy in fracture mechanics and mechanical fault detection [20].

6 Knowledge model of microstructure of compacted graphite iron

As mentioned above, the knowledge base is divided into four separate rulesets. The first two concern microstructures with dominant austenite and martensite phases. For thin-wall castings, the knowledge base can be represented as the decision table shown in Table 4, while for thick-wall casting, as the decision table shown in Table 5.

Table 4 Decision table for microstructures with dominant austenite and martensite phases and thin-wall castings

Table 5 Decision table for microstructures with dominant austenite and martensite phases and thick-wall castings

More complex is the knowledge models describing the possibility of obtaining structures with dominant ausferrite and pearlite. The corresponding rulesets are presented in the decision tables shown in Tables 6 and 7.

Table 6 Decision table for microstructures with dominant ausferrite and pearlite phases and thin-wall castings

Table 7 Decision table for microstructures with dominant ausferrite and pearlite phases and thick-wall castings

Each row in the decision table can be interpreted as a rule. Thus, the first row in Table 6 corresponds to a rule:

IF (Cu IS S1) AND (Thickness IS 3) THEN (Cluster name IS ausferrite3)

The data presented reflect the real changes in the microstructure of CGI castings resulting from the change in the chemical composition and wall thickness. A particularly important aspect of the presented knowledge model is the ability to predict the microstructure of CGI vs. the wall thickness of the casting. This is very important in the case of material that is characterized by a certain "sensitivity" to a change in microstructure versus the cooling rate (i.e. the thickness of the casting wall). Thus, it is possible to predict the properties of the real casting, which is usually characterized by a complex geometry and varying wall thickness.

The knowledge model presented above can be used in a variety of ways. First, the inference engine allows us to evaluate what the effects will be of the chemical composition proposed by the technologist. This may be illustrated by the following example. Let us assume that the technologist wants to check whether for castings with a wall thickness equal to 5.0 mm the addition of 2.3% nickel and 1.7% molybdenum will allow the microstructure described as ausferrite3 to be obtained, that is, cast iron with improved resistance to abrasive and adhesive wear, high strength properties and resistance to thermal fatigue. Machineability is not of significant importance to the technologist. The application system will consider three rules:

IF (Cu IS Null) AND (Ni IS B1) AND (Mo IS CE) AND (Thickness IS 6) THEN (Cluster IS ausferrite3)

IF (Cu IS Null) AND (Ni IS B1) AND (Mo IS CE) AND (Thickness IS 3) THEN (Cluster IS ausferrite5)

IF (Cu IS Null) AND (Ni IS CE) AND (Mo IS CE) THEN (Cluster IS ausferrite1)

and taking into account the measure of the membership of the value of the shares of individual components for presented example to fuzzy sets describing the premises in the rules (0.5, 0.33 and 0.33 respectively), it will be confirmed that for a given chemical composition, obtaining the microstructure described as ausferrite3 is the most probable. It is worth noting that for an identical chemical composition but a wall thickness of 4.0 mm, the same rules will be fired, but the membership measures will be different (0.33, 0.5, 0.33), indicating the conclusion of ausferrite5. Obtaining an ausferrite3 microstructure for a wall thickness of 4.0 mm would require replacing nickel with copper. The molybdenum content can be reduced. For a copper content of 2.2% and a molybdenum content of 1.5%, the following rules would be fired:

IF (Cu IS CE) AND (Ni IS Null) AND (Mo IS S1) AND (Thickness IS 6) THEN (Cluster IS ausferrite2)

IF (Cu IS CE) AND (Ni IS Null) AND (Mo IS S1) AND (Thickness IS 3) THEN (Cluster IS ausferrite3)

and the distribution of the membership function (0.65, 0.76) will point to the ausferrite3 conclusion.

The inference mechanism used in our study is the classical forward inference one for solving the problems presented above. A relatively simple modification of the backward inference mechanism will allow the formulation of a tool that will allow all possible combinations of chemical composition to obtain the desired microstructure. Due to this mechanism, it will be possible to determine what may be the most advantageous (e.g. from an economic point of view) chemical composition of CGI allowing one to obtain the desired microstructure and, consequently, the properties of the casting. This can be illustrated by an example. Let us assume that the technologist is interested in obtaining a casting with a wall thickness of 4 mm with very high resistance to abrasive and adhesive wear, which is guaranteed by the structure described as ausferrite5. The inference mechanism will indicate that obtaining such a structure is possible at high nickel content (B1) and medium molybdenum content (CE), as well as low copper content (S1) and high molybdenum content (B1). Taking into account the current prices of these elements, the technologist can find an economically optimal solution. Note that nickel is on average twice as expensive as copper and molybdenum is 2.5 times more expensive than nickel.

The knowledge base we have formulated will allow users to avoid obvious errors in the chemical composition. Obtaining cast iron with very good resistance to abrasive and adhesive wear, high strength properties, and resistance to thermal fatigue described in our model as ausferrite1 for castings with thin walls is possible with a very high proportion of molybdenum (B2) and a very low proportion of copper (S2) and with a low proportion of molybdenum (S1) and a very high proportion of copper. Due to the price differences of these two elements, the first solution should not be considered.

7 Conclusions

The conclusions of our research address two issues. The first relates directly to technological issues and, more specifically, to the possibility of building a knowledge base on the effect of chemical composition on the microstructure of finished CGI castings. The second side issue is related to evaluating the usefulness of a novel hybrid method for the acquisition and modeling of the knowledge necessary to solve such technological problems.

With respect to the first issue, we were able to show that the relationships exist between the chemical composition and the microstructure of the CGI castings. The knowledge base that we developed can be a key component of applications used in industrial practice.

The data presented show that the proposed tool can be very useful for supporting the production of high-quality CGI castings with various chemical compositions and a given microstructure. The system accurately predicts the microstructure of CGI versus the concentration of alloying elements and the related changes in mechanical properties. The proposed tool can be very useful in the development of both new types of CGI, as well as in predicting the microstructure of unalloyed CGI, as defined in the EN 16079 standard. The economic aspect seems to be important here because the systems supporting the development of new types of cast iron make it possible to reduce very costly (and time-consuming) experimental research.

Our proposed knowledge acquisition method, which combines simple machine learning methods (fuzzy ID3 algorithm) with direct knowledge modification by an expert, has proven to be extremely effective. First, it allows knowledge formulation in the absence of statistically significant learning datasets. It also allows for the elimination of obvious semantic errors that occur when using black-box systems. Such learning systems will generate rules that are absurd from a factual point of view (e.g., very high proportion of copper, nickel, and molybdenum). Our inference system, in the case of attempting to obtain an answer to a query formulated in such a way, will provide information that such a set of premise values is not acceptable according to the current state of knowledge.

Our research has addressed only one of the many types of technological problems. It is necessary to verify the methodology of this research in other areas as well. Improving the rules for formulating descriptions of linguistic variables is also an important problem that requires further study. In our case, we relied heavily on expert knowledge. However, it seems necessary in the future to develop techniques that could help domain experts in describing their own knowledge using sets and fuzzy numbers.

Our research involved a selected group of castings. It is necessary to conduct similar studies for other groups of materials (not only castings). The application of the approach we presented will allow us to formulate recommendations for technologists reducing the number of conducting expensive physical experiments.