Aggregate interlock in fractured concrete mesoscale models: a novel finite element modelling approach

Abstract

Aggregate interlock is a stress transfer mechanism in cracked concrete. After concrete cracks under tensile loading, crack interfaces can experience significant slip deformation due to the applied crack kinematics. Upon rising slip along crack interfaces, aggregate interlock stresses are generated which transfer shear stress and normal stress. Many experimental programmes and analytical expressions have been developed for several decades. However, a finite element model considering realistic crack surfaces was still not developed. The complexity of developing a FE model lies due to the mesoscopic nature of the problem. In this study, concrete mesoscale models were employed to generate realistic cracked concrete surfaces. Uniaxial tensile fracture propagation in concrete mesoscale models were achieved using Zero-thickness cohesive elements approach. Once cracked concrete FE models are developed, validation of the proposed FE models was conducted against two experimental campaigns. The study comprises the evaluation of the surface roughness index of the cracked concrete surfaces. The FE model predicts secondary cracking under low initial crack widths and mixed mode angles. FE predictions were further compared with Walraven’s simplified formulae, Bažant’s rough crack model, Cavagnis’s aggregate interlock formulae and contact density model and consistence agreement was observed. Finally, strengths and weaknesses of the proposed FE modelling approach for aggregate interlock was discussed and further implementations were also highlighted.

1 Introduction

Concrete is a rather brittle material that can crack under service loads creating brittle failure modes. Thus, effective utilisation of this material requires extensive understanding of fracture mechanics, strain localisation and stress transfer after cracking. In fact, the complexity of the problem is greater compared to other brittle materials as concrete shows more of quasi-brittle material properties. Concrete develops a large zone of distributed cracking which grows and dissipates energy before a localised crack forms. Hence, the complexity of the evolving fracture mechanics of the concrete, sparse of analytical and numerical models were developed over past decades.

In most Reinforced Concrete (RC) designs, concrete can be subjected to cracking in serviceability limit state and ultimate limit state resulting substantial crack openings [1]. Subsequently, the failure of an RC element occurs due to the disengagement of the crack surfaces and the yielding of the reinforcement crossing the crack [2]. Shear failures of beams [3] and punching shear failures of slabs [4] are prefect examples of this failure process. Aside from fracture propagation, kinematics of the crack is very important as it defines the applied displacements on the crack surfaces [5]. There are three fracture propagation modes in solids i.e. Mode-I failure is related to pure crack opening, Mode-II is the pure shear failure mode and Mode-III failure can be considered as out of plane shearing failure mode [6]. In general, a concrete crack opens first in Mode-I, but later progresses in mixed modes (Mode-I + Mode-II) [5]. In fact, due to the Mode-II component and accounting for the roughness of concrete (due to protruding aggregate from the crack surface and uneven fracture surface of the cement mortar), one crack surface can engage contact with its counterpart. As a result, the contact enforcement allows the transfer of forces between the crack surfaces and this phenomenon is called as “Aggregate Interlock” [7]. Aggregate interlock plays a crucial role in transferring shear force from point of application of a load to the supports in RC elements. Aggregate interlock governs the failure of elements in all scenarios such as, shear in beams [2], punching shear in slabs or footings [8] and force transfer between concrete elements cast at two different times (e.g. construction joints) [9]. However, there were no evidence in the literature of finite element modelling of the push-off test which can actually simulate the surface asperities and the strass transfer in the cracked concrete.

To develop FE modelling approach for aggregate interlock, more realistic crack surfaces of the concrete must be developed. Thus, considering concrete as a homogeneous continuum does not actually represent the asperities of the crack surface such protruding aggregate from the crack surface. Therefore, in this study, concrete was modelled in mesoscale level in which concrete has three constitutes i.e., aggregates, mortar and interfacial transition zone. Fracture propagation in concrete mesoscale models were achieved using zero-thickness cohesive elements where cohesive elements were pre-inserted along element boundaries. Zero-thickness cohesive interface elements are widely used to develop discrete fracture in the concrete mesoscale models [10]. Furthermore, fracture propagation using cohesive interface elements has been employed in various cracking phenomenon such as fracture propagation due to sulphate attack [11], corrosive reinforcements [12], shrinkage [13], thermal expansions [14] and alkali-silica reaction expansion [15]. Moreover, cohesive elements were used to investigate hydraulic fracture propagations in rocks [16].

With this background, this study aims to develop a novel finite element modelling approach to investigate the stress transfer due to aggregate interlock by using concrete mesoscale models. Roughness of the fractured mesoscale models were evaluated based on the surface roughness index. Validation was conducted using two small-scale experimental campaigns. Further, predictions of Walraven’s simplified formulae, Bažant’s rough crack model, Cavagnis’s aggregate interlock formulae and Contact Density Model (CDM) were compared with the finite element model (FEM) results. Finally, the strengths and weaknesses of the proposed FEM were discussed recommending further research directions to investigate aggregate interlock in cracked concrete.

1.1 Research significance and scope of the study

This study provides guidance to develop a novel mesoscopic FE modelling method to investigate the aggregate interlock stresses when crack surfaces are subjected to mixed-mode crack kinematics. The mesoscopic nature of the FE model yields most realistic crack surfaces with less effort compared to the mathematically develop crack surfaces [17]. This study helps to understand the aggregate interlock mechanism and its influence on the amount of stress transfer between two crack surfaces under different crack kinematics. The scope of this study can be summarized as follows,

• 1. Development of concrete mesoscale models.

• 2. Generating a uniaxial fracture in the mesoscale models using zero-thickness cohesive elements.

• 3. Developing FE model for aggregate interlock from the fractured concrete mesoscale models.

1.2 Overview of aggregate interlock in cracked concrete

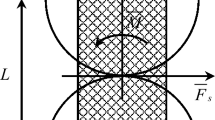
Concrete cracking occurs in Mode I due to tensile loading. With increasing tensile load beyond the linear elastic region, the tension softening takes place resulting in the micro cracks coalescing into macro cracks which defines the Mode I cracking of concrete [10]. Subsequently, cracked surfaces are subjected to mixed-mode crack kinematics due to the applied stress [18]. In general, the Mode I crack reaches an initial crack opening followed by mixed-mode crack opening with constant crack dilation, as depicted in Fig. 1.

Fig. 1

Mixed mode crack kinematics

Aggregate interlock can occur due to the Mode II component of the crack dilatancy. Under Mode II crack displacement (shear slip), both the rough cracked surfaces come to contact with each other. Aggregate interlock between concrete cracks is a complex phenomenon as it involves complex force resisting mechanisms under given crack kinematics. As the crack slides, it tends to open due to overriding of the aggregate particles against each other [7]. Due to overriding and applied Mode II kinematics, normal stress is introduced at the crack surface [19], if the widening of the crack is constrained by embedded or external reinforcement. The normal stress must be balanced by the reinforcement bars crossing the crack in addition to the tensile force which satisfies the equilibrium [19]. Furthermore, the shear stiffness decreases as the crack gets wider due to contact loss between crack faces [7].

The aggregate interlock forces are considered to play a major role in the overall transfer of shear force thus, accurate estimation of aggregate interlock is paramount for predicting the shear resistance of RC elements [8]. For RC beams without shear reinforcement, aggregate interlock plays an important role as 70% of the ultimate shear capacity of the beams is due to Aggregate interlock [20]. Moreover, Vecchio and Collins [21] considered aggregate interlock as the governing shear transfer mechanism between cracked RC panels for their Modified Compression Field Theory.

A well-known theoretical work, the so-called “Two-phase model for aggregate interlock mechanism” introduced by Walraven has been the basis for most of the aggregate interlock formulations [22]. Two simplified formulae (Eqs. (1) and (2)) based on Walraven’s work were included in the Fib Model code 2010 [23]. “Contact density model” [24] and “rough crack model” [19] are other approaches to estimate aggregate interlock between rough interfaces. Both approaches consider the crack plane as one material with stiff uneven surface variation defined by model parameters.

$$\sigma_{{{\text{ag}}}} = C_{{\text{f}}} \left\{ { - 0.06f_{{\text{c}}} + \left[ {\left. {1.35w^{ - 0.63} + 0.242w^{ - 0.55} - 0.19} \right)f_{{\text{c}}} } \right]s} \right\}$$

(1)

$$\tau_{{{\text{ag}}}} = C_{{\text{f}}} \left\{ { - 0.04f_{{\text{c}}} + \left[ {\left. {1.8w^{ - 0.8} + 0.292w^{ - 0.7} - 0.25} \right)f_{{\text{c}}} } \right]s} \right\}.$$

(2)

Equations (1) and (2) give shear stress and normal stresses due to aggregate interlock as a function of the crack kinematics (sliding and crack width) and concrete strength. The aggregate effectivity factor, ${C}_{\mathrm{f}}$, was originally introduced by Walraven and Stroband [25], representing the aggregate fracturing. The ${C}_{\mathrm{f}}$ can vary between 1 and 0.35 where 1 represents no aggregate fracturing, while 0.35 represents complete aggregate fracturing. As shown in Fig. 2, high strength concrete under compression can be subjected to aggregate fracturing reducing the surface roughness and eventually, reducing the capacity of aggregate interlock [26]. Therefore, aggregate fracturing in RC elements has been a cause for concern for many researchers [7].

Fig. 2

Fractured concrete surface in a normal strength concrete b high strength concrete observed from a laser light confocal microscope [26]

However, a more refined understanding of the problem is still far from satisfactory. Hamadi and Regan [27] experienced aggregate fracturing in high strength concrete and lightweight aggregate concrete using push-off test results. Furthermore, Collins et al. [28] and Perera and Mutsuyoshi [26] experienced occurrence of aggregate fracturing in RC elements with high strength concrete under compression. Subsequently, aggregate interlock was deteriorated developing abrupt failure modes as aggregate fracturing produces smooth crack surfaces. However, Walraven and Al-Zubi [29] and Sagaseta and Vollum [30] highlighted that, at mesoscale level, significant shear stresses can be transferred due to the macro-roughness despite aggregate fracturing. Roughness of the cracked surface can be divided into three groups depending on the scale in which the aggregate interlock stress can be transferred [18].

• (1) Macro-roughness The macroscale roughness can be defined by the global crack geometry. Concrete cracks are usually not straight, and their path is governed by stress–strain distribution of the structure. Due to irregularity the crack shape, contact forces can be generated upon opening and sliding of the cracked interfaces.

• (2) Meso-roughness Meso-roughness is related to the roughness due to material constituents. Meso-roughness is comparable to maximum aggregate size. Aggregate interlock due to meso-roughness is more pronounced when aggregates are protruding from the crack surface [22].

• (3) Micro-roughness Micro-roughness is associated with the roughness of the mortar matrix. It can influence the overall stress transfer between crack surfaces where the associated fractal dimensions are typically between 1/10 and 1/100 of maximum aggregate size [31].

The capacity of aggregate interlock due to these three levels of roughness exclusively depends on the concrete mixture. Strength of concrete which determines the strength of mortar and Interfacial Transition Zone (ITZ) is governing the aggregate fracturing as mentioned earlier. Furthermore, the percentage volume of course aggregates and the maximum aggregate size in the concrete mixture are paramount to the capacity of aggregate interlock [32]. Therefore, Huber et al. [32] and Kim et al. [33] highlighted that the use of self-compacting concrete can lead to reduced shear capacity due to lower coarse aggregate percentage which can incapacitate the aggregate interlock. Safeguarding aggregate interlock mechanism in cracked RC elements is very important to maintain smeared cracking conditions [34]. In fact, loss of aggregate interlock between two crack surfaces activates localised cracking which may cause catastrophic failures in RC elements.

2 Analytical formulations for aggregate interlock in cracked concrete

2.1 Walraven’s simplified formulae

Walraven developed an empirical equation for aggregate interlock using push-off specimens with externally restrained reinforcements [22]. His approach considered linear relations between the four variables i.e., shear stress, shear displacement, normal stress and crack width. Equations (3) and (4) calculate shear stress due to aggregate interlock ($\tau$) and normal stress induced on crack surface due to aggregate interlock ($\sigma$), respectively.

$$\tau = - \frac{{f_{{{\text{cc}}}}^{^{\prime}} }}{30} + \left[ {1.8w^{ - 0.8} + \left( {0.234w^{ - 0.707} - 0.2} \right).f_{{{\text{cc}}}}^{^{\prime}} } \right]\Delta > 0$$

(3)

$$\sigma = \frac{{f_{{{\text{cc}}}}^{^{\prime}} }}{20} + \left[ {1.35w^{ - 0.63} + \left( {0.234w^{ - 0.552} - 0.15} \right).f_{{{\text{cc}}}}^{^{\prime}} } \right]\Delta > 0,$$

(4)

where, ${f}_{\mathrm{cc}}^{^{\prime}}$ is the cube compressive strength of concrete, $w$ is the crack width and $\Delta$ is the shear displacement. These equations were obtained from push-off tests where the maximum aggregate sizes were between 16 and 32 mm.

2.2 Bažant’s rough crack model [19]

Bažant developed an empirical formulation by fitting the Paulay and Loeber’s [35] push-off test data [19]. Based on Bažant’s formulation, shear stress due to aggregate interlock depends primarily upon the ratio, $r=\frac{{\delta }_{\mathrm{t}}}{{\delta }_{\mathrm{n}}}$, where ${\delta }_{\mathrm{t}}$ and ${\delta }_{\mathrm{n}}$ are shear deformation and normal deformation, respectively. It was further suggested that ${\sigma }_{\mathrm{nn}}^{\mathrm{c}}$ should vary approximately in proportion to ${\sigma }_{\mathrm{nt}}^{\mathrm{c}}$ and inversely proportional to ${\delta }_{\mathrm{n}}$, where ${\sigma }_{\mathrm{nn}}^{\mathrm{c}}$ and ${\sigma }_{\mathrm{nt}}^{\mathrm{c}}$ are normal stress and shear stress due to aggregate interlock, respectively.

$$\sigma_{{{\text{nt}}}}^{{\text{c}}} = \tau_{{\text{u}}} {.}r.\frac{{a_{3} + a_{4} .\left| r \right|^{3} }}{{1 + a_{4} r^{4} }}$$

(5)

$$\sigma_{{{\text{nn}}}}^{{\text{c}}} = - \frac{{a_{1} }}{{\delta_{{\text{n}}} }}.\left( {a_{2} .\left| {\sigma_{{{\text{nn}}}}^{{\text{c}}} } \right|} \right)^{p} ,$$

(6)

where,

$$r = \frac{{\delta_{{\text{t}}} }}{{\delta_{{\text{n}}} }}$$

(7)

$$\tau_{{\text{u}}} = \tau_{0} \frac{{a_{0} }}{{a_{0} + \delta_{{\text{n}}}^{2} }}$$

(8)

$$p = 1.30\left( {1 - \frac{0.231}{{1 + 0.185\delta_{{\text{n}}} + 5.63\delta_{{\text{n}}}^{2} }}} \right)$$

(9)

$$\begin{aligned} a_{0} & = 0.01D_{{\text{a}}}^{2} ;\;a_{1} = 0.000534 {\text{N}}/{\text{mm;}}\;a_{2} = 145 \;{\text{mm}}^{2} /{\text{N;}}\;a_{3} = \frac{1}{{\tau_{0} }}0.2.45{\text{ N}}/{\text{mm}}^{2} ;\;a_{4} = 2.44\left( {1 - \frac{4}{{\tau_{0} }}} \right) \\ \tau_{0} & = 0.245f_{{\text{c}}}^{^{\prime}} , \\ \end{aligned}$$

(10)

$f_{{\text{c}}}^{^{\prime}}$ is the 28-day standard cylindrical compressive strength of concrete, $D_{{\text{a}}}$ is the maximum aggregate size of the concrete mix.

2.3 Contact density model

This model is capable of predicting the deformation characteristics of a crack interface under various stress paths of both monotonic loadings and cyclic loadings [36]. The model assumes the crack surface as a set of contact units with various inclinations, and distribution of the inclinations of the contact unit is called the contact density function which is central to the model proposed by Li et al. [37]. The geometry of the crack surface is assumed to be characterized by infinitely small contact units. The model proposed the contact density function representing all possible contact units with possible contact areas and directions as shown in Fig. 3.

Fig. 3

Two-dimensional projection of crack surface of concrete [37]

As far as monotonic loading paths are concerned, the contact force acting on the crack interface increases monotonically. The total of stresses transferred across the crack interface is equal to the integration of the constitutive equations with respect to contact direction, and the following expression were obtained,

$$\tau = g\left\{ {\frac{{\delta \sin^{3} \beta + \omega \cos^{3} \beta }}{3} - \frac{\delta \omega }{{3\sqrt {\delta^{2} + \omega^{2} } }} + 0.5\omega_{\lim }^{^{\prime}} \cos^{2} \beta } \right\}$$

(11)

$$\sigma^{\prime} = g\left\{ {\frac{{ - \delta \cos^{3} \beta + \omega \sin^{3} \beta }}{3} - \omega \sin \beta + \frac{{\delta^{2} + 2\omega^{2} }}{{3\sqrt {\delta^{2} + \omega^{2} } }} + \omega_{\lim }^{^{\prime}} \left[ {\frac{\pi }{4} - \frac{\beta }{2} - \frac{\sin 2\beta }{4}} \right]} \right\}$$

(12)

where

$$g = 0.5A_{{\text{l}}} R_{^{\prime}} K\left( \omega \right)$$

(13)

$$K\left( \omega \right) = 1 - \exp \left( {1 - \frac{{0.5G_{\max } }}{\omega }} \right) \ge 0$$

(14)

$$\beta = \arcsin \left( {\frac{{\omega_{\lim }^{^{\prime}} \delta + \omega \sqrt {\omega^{2} + \delta^{2} - \omega_{\lim }^{^{\prime}2} } }}{{\omega^{2} + \delta^{2} }}} \right)\;{\text{if}}\;\delta \ge \omega_{\lim }^{^{\prime}}$$

(15)

$$\beta = \frac{\pi }{2}\;{\text{if}}\;\delta < \omega_{\lim }^{^{\prime}}$$

(16)

$$R = 436f_{{\text{c}}}^{{^{\prime}\frac{1}{3}}} , A_{l} = \frac{4}{\pi } = 1.27, \omega_{\lim }^{^{\prime}} = 0.04$$

2.4 Cavagnis’s aggregate interlock formulae

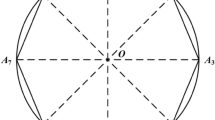
Cavagnis et al. [2] developed an analytical formula based on the Walraven’s two phase model considering the kinematic paths of Guidotti [38], which is more representative of the actual case. Therefore, the following equations are only applicable for the kinematic paths as shown in Fig. 4. Also note that, Cavagnis’s equation considered the effect of residual tensile strength of concrete on the normal stress due to aggregate interlock [2]. However, this study only focusses on the generated shear stress due to aggregate interlock.

$$\tau_{{{\text{agg}}}} = \sqrt {f_{{\text{c}}} } . \frac{{c_{4} .\overline{\delta }^{4/3} }}{{\left( {c_{2} \overline{w}} \right)^{{1.8 + c_{2} .\overline{\delta }}} }}$$

(17)

$$\sigma_{{{\text{agg}}}} = \sigma_{{{\text{res}}}} - \sqrt {f_{{\text{c}}} } . \frac{{c_{4} .\overline{\delta }^{\frac{7}{3}} }}{{\left( {c_{2} \overline{w}} \right)^{{3 + c_{2} .\overline{\delta }}} }},$$

(18)

where

$$\begin{aligned} c_{2} & = 40,\;c_{3} = 35,\;c_{4} = 400 \\ \overline{\delta } & = \frac{\delta }{{d_{{{\text{dg}}}} }},\;\overline{w} = \frac{w}{{d_{{{\text{dg}}}} }}. \\ \end{aligned}$$

Fig. 4

Crack kinematics proposed by Guidotti [38]

The parameter $d_{dg}$ is the average diameter of the aggregates used for the construction of beams and the following equations provide recommended values for $d_{{{\text{dg}}}}$ depending on the compressive strength of concrete.

$$d_{{{\text{dg}}}} = \min \left( { 40\;{\text{mm}},16 + d_{{\text{g}}} } \right)\;{\text{for}}\;f_{{\text{c}}} \le 60\, {\text{MPa}}$$

(19)

$$d_{{{\text{dg}}}} = \min \left( { 40\;{\text{mm,}}16 + d_{{\text{g}}} .\left( {\frac{60}{{f_{{\text{c}}} }}} \right)^{2} } \right)\;{\text{for}}\;f_{{\text{c}}} > 60\, {\text{MPa}}{.}$$

(20)

3 Experimental investigations on aggregate interlock

3.1 Push-off test

Aggregate interlock is a complex shear resisting mechanism which can be found in cracked RC elements. Aggregate interlocking activates when the two interfaces of a cracked concrete element slide relative to each other. Furthermore, due to the irregular nature of crack patterns and heterogeneity of concrete, these interfaces are characterised by rough surfaces with protruding materials. Once the crack begins sliding, the crack width further widens due to the overriding of aggregate particles against each other. This phenomenon is known as crack dilatancy [7]. To experimentally investigate stress transfer due to aggregate interlock, a common approach is to create an isolated crack and applying sliding and normal displacements to observe stress transfer due to aggregate interlock. The push-off test is a widely recognised testing procedure to assess normal stress and shear stress on concrete cracks subjected to crack kinematics [7]. In general, the push-off test is a two-step approach; first, the specimen is pre-cracked and secondly, a shearing load is applied vertically. Pre-cracking can be achieved by transverse splitting along a pre-inserted groove on the specimen. According to this test, the entire force applied is transmitted along the crack plane, as shown in Fig. 5.

Fig. 5

Push-off specimen [7]

3.2 Mixed mode tests

More recently, due to the introduction of advanced testing machines, mixed-mode test setups were developed with hydraulic jacks acting in two perpendicular directions [39]. This test is a small-scale test compared to the push-off test and no reinforcement bars were used. Thus, results are purely due to the aggregate interlock. Furthermore, this test promotes the propagation of uniaxial tensile cracks rather than splitting tensile cracks as obtained from push-off tests. Once the crack is initiated in Mode I (uniaxial tension), crack propagation is associated with mixed-mode conditions. For instance, in beams without shear reinforcement failing in shear, crack kinematic of shear cracks have shown that the critical shear crack typically propagates in Mode I and then opens further under mixed-mode conditions [5].

Nooru-Mohamed [40] and Hassanzadeh [41] initially conducted an experimental program on small-scale mixed-mode tests. Both researchers found that the secondary cracks propagated from initial Mode1 crack. Cavagnis et al. [2] also had observed similar observations in beams as the secondary cracks were developed along the critical shear crack in RC beams without shear reinforcement. Jacobsen [39] conducted a similar experimental programme with 20 small-scale specimens subjected to mixed-mode kinematics. Recently, Tirassa et al. [5] conducted an experimental programme on specimens similar to Jacobsen’s specimens, and the dimensions of these specimens are shown in Fig. 6. Tirassa et al. [5] noticed three types of cracking: Primary cracking (PC), non-dominant secondary cracking (NDSC) and dominant secondary cracking (DSC). These observations were dependent on the initial crack width (${w}_{0})$ and the mixed mode angle ($\alpha )$. Furthermore, Tirassa et al. investigated the role of surface roughness on the transfer of forces via aggregate interlock, contribution of residual tensile strength in the fracture process zone to the stress transfer and reasons for the three different failure modes (PC, NDSC and DSC). Observations of Tirassa et al. and Jacobsen are reasonably comparable although the size of the specimens were different. For the study presented in this paper, seven and nine specimens were selected from Jacobsen and Tirassa et al., respectively. Development of FE models are discussed later in this paper.

Fig. 6

Max Tirassa’s specimen [18]

4 Development of concrete mesoscale FE models

4.1 Mesoscale model for concrete

The following section of this paper discusses the generation of aggregate geometry and size according to the particle size distribution curve and overlap checking algorithms as carried out in this study.

4.1.1 Particle size distribution of aggregate

In general, aggregates can occupy 50–70% of the total volume of the concrete. Aggregates can be classified into two categories, i.e. coarse aggregates and fine aggregates. Aggregates with diameter less than 2.36 mm is considered as fine aggregates and for mesoscale modes, it is assumed that these particles are embedded in the mortar phase. A typical example of aggregate size distribution for mesoscale modelling is shown in Table 1 [42].

Table 1 Aggregate size distribution with four segment gradations

The aggregate size distribution of concrete is determined by the Fuller curve which results in optimum compaction and widely accepted for mesoscale modelling of concrete [43]. The Fuller curve can be defined as,

$$P\left( d \right) = 100\left( {\frac{d}{{d_{\max } }}} \right)^{n} ,$$

(21)

where $P\left( d \right)$ is the cumulative percentage of aggregates passing a sieve with diameter d, $d_{\max }$ is the maximum aggregate size and n can be any value between 0.45 and 0.7.

For the simplicity of numerical implementation, the gradation curve can be divided into segments. The volume fraction of each segment can be determined as,

$$V_{{\text{p}}} \left[ {d_{{\text{s}}} - d_{{{\text{s}} + 1}} } \right] = \frac{{P\left( {d_{{\text{s}}} } \right) - P\left( {d_{{{\text{s}} + 1}} } \right)}}{{P\left( {d_{\max } } \right) - P\left( {d_{\min } } \right)}} \times P_{{{\text{agg}}}} \times V,$$

(22)

where $d_{\max }$ and $d_{\min }$ are the maximum and minimum sizes of aggregates, respectively, $P_{agg}$ is the volume fraction of aggregate and V is the total volume of the concrete specimen.

4.1.2 Generation of aggregate geometry and overlap checking algorithms

The next step of the numerical implementation is placing the aggregates within the boundaries of the concrete volume. The position of the aggregates must be numerically determined considering the following three conditions:

• (I) aggregates must be within the concrete volume,

• (II) aggregates must not overlap with previously generated aggregates and

• (III) Minimum distance should be maintained between two adjacent aggregates particles.

As far as spherical aggregates are concerned, their coordinates within the concrete volume and diameters are sufficient to generate spherical aggregates. To avoid overlapping, intersections can be checked by satisfying the following expression,

$$\sqrt {\left( {x_{i} - x_{o} } \right)^{2} + \left( {y_{i} - y_{o} } \right)^{2} + \left( {z_{i} - z_{o} } \right)^{2} } \le 1.1x\left[ {R + R^{\prime}} \right],$$

(23)

where ${x}_{i}$, ${y}_{i}$, ${z}_{i}$ and ${x}_{o}$, ${y}_{o}$, ${z}_{o}$ are the coordinates of centres of two spheres; $R$ and ${R}^{^{\prime}}$ are the radii of the previous generated and new spheres, respectively [43]. Figure 7 shows the spherical aggregates developed in this study. Even though this study only employed spherical aggregates, the method proposed in this study can be used with any aggregate shape. For example, generated spherical aggregates according to the fuller curve and generate-and-place method, can be converted to convex polyhedral aggregates. As described in Thilakarathna et al. [43], the vertices of convex polyhedral aggregates can be generated from the randomly selected points on the spheres. Then intersection check can be done for any possible overlapping before importing it to Abaqus.

Fig. 7

Generated spherical aggregates in MATLAB for small-scale test for aggregate interlock according to Tirassa et al. [5]. (Maximum aggregate size: 16 mm and aggregate content: 50%)

4.2 Fracture propagation in concrete mesoscale models

4.2.1 Insertion of zero-thickness cohesive elements

Zero-thickness cohesive elements can be inserted to the finite element mesh in two different ways i.e.

• (I) Pre-insertion also known as intrinsic cohesive method [44], and

• (II) Dynamic insertion during the analysis also known as extrinsic cohesive method [45].

In this study, the pre-insertion procedure was adapted. To the best of authors’ knowledge, most finite element software packages cannot insert cohesive elements along element boundaries of each element. In fact, Abaqus [46] can insert cohesive elements on instance boundaries using mesh editing tools. Thilakarathne et al. [43] used this technique to model ITZ using cohesive elements. Developing a program to generate zero-thickness elements at all element boundaries, at material interfaces and at grain boundaries of polycrystalline material, was a challenge in the past 2 decades. Some of the earliest algorithms were developed to insert cohesive elements during fragmentation processes following the extrinsic cohesive modelling approach [44]. However, Hillerborg et al. [47] introduced CIEs for concrete to study crack formation and crack growth. Later, Lopez et al. [44] utilised zero-thickness cohesive elements in concrete 2D mesoscale models to investigate the tensile behaviour of concrete under uniaxial tensile loading. Lopez et al. [44] inserted CIEs only along selected inter-element boundaries representing potential crack paths. Furthermore, continuum elements were assumed to remain in the linear elastic region while whole nonlinear characteristics concentrated on the behaviour of CIEs [45]. Zero-thickness CIEs are more advantageous in propagating discontinuous fractures as remeshing is not required along with the crack propagation [12, 45, 48,49,50,51,52,53,54,55]. The crack initiation location is completely arbitrary, and the crack path is fully dependent on fracture energy which resembles the reality of fracture propagation in a polycrystalline material like concrete. However, the crack path is mesh dependent. Therefore, a sensitivity analysis is recommended to neutralise the mesh dependency [10]. In 2D mesoscale studies, 2D 4-node or 3-node zero-thickness CIEs were employed, whereas in 3D mesoscale studies, 6-node or 8-node zero-thickness CIEs were used. Ren et al. [56] used 4-node cohesive interfaces to study fracture initiation and propagation in a 2D mesoscale model under uniaxial tension. Wang et al. [10] utilised pre-inserted zero-thickness CIEs in 3D concrete mesoscale models to investigate the fracture propagation in concrete blocks subjected to uniaxial tension. Trawiński et al. [57] used zero-thickness CIEs to investigate the concrete fracture at mesoscale level in a notched concrete beam under three-point bending, although the concrete meso-structure was generated using X-ray µCT images. Both Trawiński et al. [57] and Ren et al. [56] discussed the mesh dependency of the results and material properties of the zero-thickness CIEs (traction separation law, discussed in detail later in the paper). Furthermore, Wu et al. [58] used zero-thickness CIEs in a 2D mesoscale model of concrete to investigate the dynamic fracture behaviour of NSC. Chen et al. [59] investigated the two-dimensional crack propagation of Cement Treated Base utilizing zero-thickness cohesive elements to simulate micro-crack propagation in cement mortar and aggregate–mortar interface. Zhou et al. [49] developed a mesoscale framework using zero-thickness cohesive elements to investigate the dynamic behaviour of concrete under high strain rate tension.

Nguyen [60] developed an open source program, written in C +  + language, to generate 1D and 2D zero-thickness CIEs in polycrystalline materials. Polycrystalline structures can experience cracking at granular interfaces, thus, Nguyen inserted zero-thickness CIEs along the grain boundaries where the crack path was known in advance. Figure 8 shows how cohesive elements were inserted in mortar (CIE_MOR), in aggregate (CIE_AGG) and interface between mortar and aggregate (CIE_INT) in a 3D concrete mesoscale model meshed using tetrahedral elements.

Fig. 8

Cohesive elements insertion to 3D concrete mesoscale model [45]

In this study, a programme developed in Matlab was used to generate zero-thickness CIEs at any interface or intraface, similar steps can be found elsewhere [60]. Figure 9 shows generated cohesive elements in mortar, ITZ and aggregates. The basic steps in the Matlab programme are as follows, (a similar procedure can be found in Nguyen [60]),

• 1. Create an input file in the ABAQUS containing node coordinates, element information, material properties, section assignments, step definition and boundary conditions.

• 2. Run through each node in FE mesh and store the element information attached to each node.

• 3. Run through each element in the FE mesh and determine faces that are not connected with any other face (faces on boundary elements), faces on material interfaces (if user requested to insert CIEs) and faces on elements with same material properties.

• 4. Replicate the nodes on interfaces between aggregate and mortar.

  • a. Find the node coordinates which requires node replication

  • b. Replication the nodal coordinate.

  • c. Update the nodal connectivity.

• 5. Replicate the nodes on interfaces in aggregate and mortar. (follow the same as 4(a), (b) and (c))

• 6. Apply relevant traction separation law for CIEs on interfaces.

• 7. Update the.inp file according to the new node coordinates, element information and add constitutive relations for cohesive elements.

• 8. Import the.inp file to Abaqus as a new model.

Fig. 9

Cohesive elements in the concrete 3D mesoscale model developed in this study. a Cohesive element in mortar, b cohesive elements in ITZ and c cohesive elements in aggregates

4.3 Development of the FE model for aggregate interlock

After completing Mode-I crack propagation, the result file (.obd file) containing fractured mesoscale model of the concrete specimen was imported back to the Abaqus as a new model. The imported cracked part did not have a geometry, it was only an orphan mesh. The orphan mesh still had cohesive elements inserted from the previous analysis. Newly imported cracked mesoscale model included the deformed cohesive elements between two crack halves. These deformed cohesive elements between crack halves must be removed before the next step. Figure 10a shows the cracked mesoscale model after importing the.obd file back to the Abaqus and Fig. 10b shows the crack FE model after removing the deformed cohesive elements.

Fig. 10

a Imported.obd file back to Abaqus and b after removing deformed cohesive elements between two crack surfaces

The new FE model do not need cohesive elements since in this step, a discrete fracture propagation is not required. Hence, to remove cohesive elements inside the cracked mesoscale model and to convert the orphan mesh to a geometry, the cracked halves were exported as a “. stl” file and then, imported to a 3D modelling software. In this study, BLENDER [61], a freely available software was used. Using the “weld” function in BLENDER, all vertices in the cracked parts were removed. Then, the “. stl” file was exported and that was imported back to the Abaqus model. The imported “. stl” file only had boundary shell elements. Using the freely available plugin “Create geometry from mesh”, the geometry was created from the orphan mesh. After that, a virtual topology was applied for removing all meshing details on the surfaces of the geometry. Figure 12 summaries the flowchart of the proposed FE approach for aggregate interlock using fractured mesoscale models. This procedure was followed for aggregates as well. Finally, in the new model, two cracked mortar geometries and aggregates were transferred to the assembly module where the complete meso-structure of the complete cracked model was assembled. Figures 15 and 16 show the final FE models for aggregate interlock with embedded aggregate and combined aggregate, respectively [Figs. 11, 12].

Fig. 11

FE model with separate aggregates and surface partitions on the aggregates crossing the crack

Fig. 12

Flowchart of the proposed FE approach for aggregate interlock using fractured mesoscale models

The Concrete Damage Plasticity Model (CDPM) was used as the constitutive law for the cracked mortar and aggregates. Interfacial Transition Zone (ITZ) was modelled as a cohesive contact. CDPM model is usually employed for modelling the inelastic behaviour of the constitutive phases of the concrete mesoscale models. In fact, ITZ can be modelled using several methods: (i) ITZ using solid finite elements, (ii) ITZ using cohesive contact and (iii) ITZ using cohesive elements [43, 62]. A solid finite element layer between aggregates and mortar can be generated by shrinking the aggregate particles and then, the corresponding material model can be applied to solid elements. However, in realty, ITZ has a thickness in the micro scale and it is quite challenging to mesh such thin solid layers. Cohesive contact approach is a very effective and realistic method to model ITZ in concrete mesoscale models. The cohesive contact can be defined as a surface interaction property. Moreover, cohesive element approach is also an effective method of representing the behaviour of ITZ in concrete mesoscale models. The constitutive relationship for both cohesive contacts and cohesive elements is called the “traction separation law”. In fact, for cohesive elements, the traction separation law must be defined in property definition, whereas for cohesive contact, it can be defined in the surface interaction definition. In fact, the cohesive contact approach is numerally less intensive than the cohesive element approach, thus the cohesive contact approach was used for the FE model for the aggregate interlock. However, in the first FE model of this study, ITZ was modelled using cohesive elements, and the material properties of the cohesive elements used in this model is presented in Table 2.

Table 2 Material properties of solid elements and CIEs

Protruding aggregates from the crack surface should have two contact definitions, namely, cohesive contact and penalty contact. The area of these aggregates which is still embedded in the mortar was applied as cohesive contact to connect to the mortar (ITZ). The exposed area of the aggregates, which develops aggregate interlock forces due to contact with the opposite crack surface, was applied as penalty contact to impose friction. To apply two different contact definitions, aggregates which came out of the crack surface should be partitioned. Such partitioned aggregates in this FE model are shown in Fig. 11. Furthermore, the same penalty contact was applied for the crack surface of the mortar. A friction coefficient of 0.85 was used for the mortar surface and exposed surface of the aggregate. However, for combined aggregate models, modelling of the ITZ was not required. Only a penalty contact was needed to activate friction between crack surfaces. Also note that, FE models discussed in this paper did not consider the residual tensile strength of concrete. Implementation of the FE model to incorporate residual tensile strength concrete is outside the scope of this study and will be carried out in a separate detailed study.

4.4 Constitutive relations and material properties

4.4.1 Constitutive relations and material properties for fracture modelling in concrete mesoscale model

Continuum elements The continuum elements in the FE model, i.e., solid elements in mortar and aggregates, were assumed to behave as a linear elastic material. Most of the deformations between two solid elements are acquired by the cohesive elements [45]. Continuum elements can only deform when cohesive elements are in the linear elastic range. Due to very high initial stiffness of the cohesive elements, they experience negligible deformation in the linear elastic range. Therefore, deformation in continuum elements is negligible. Young’s modulus, E, Poisson’s ratio, v, and mass density, if Abaqus explicit solver is employed, are the only required input parameters for mesoscale models [46]. The material properties of continuum elements can be found in Table 2.

Zero-thickness cohesive interface elements The constitutive relationship for cohesive elements can be defined using the traction separation law (TSL). In 2D cohesive elements, one normal traction and one tangential traction across the element must be defined [56]. In 3D, one normal traction and two tangential tractions need to be defined, and these can represent mechanisms such as material debonding, aggregate interlock and surface friction in fracture process zone [45]. The TSL can be divided into two distinct phases as below;

• (i) From zero deformation to damage initiation point in which the surface can maintain full integrity with continuum elements (Initial stiffness), and

• (ii) From damage initiation to complete loss of cohesiveness.

For quasi-brittle materials like concrete, the initial stiffness can be assumed to be constant up to the damage initiation point [45]. Yang and Xu [63] and Trawiński et al. [57] highlighted that the initial stiffness of the zero-thickness CIEs is a penalty parameter, and unless chosen carefully, traction oscillations can occur in the elastic region. Therefore, the initial stiffnesses ${k}_{\mathrm{no}}$, ${k}_{\mathrm{so}}$ and ${k}_{\mathrm{to}}$ must be high enough to suppress the overly flexible response of the cohesive elements compared to the continuum elements. A sensitivity analysis maybe required to determine the correct value for the initial stiffnesses as excessively higher values can cause ill-conditioning of the system equations. Yang and Xu [63] and Qiang et al. [64] investigated the influence of initial stiffness and Qiang et al. developed the following equation to determine initial stiffness,

$$k_{{\text{n}}} = \frac{{c\left( {1 - v} \right)}}{{b\left( {1 + v} \right)\left( {1 - 2v} \right)}}E,$$

(24)

where E and v are young’s modulus and Poisson’s ratio, respectively, b is a size-dependent parameter and c was taken as any value between 10 and 100.

Due to the lack of evidence of the behaviour in the other two direction, the same stiffness is used in the other two directions as well. However, most of the concrete mesoscale modelling in 2D and 3D an initial stiffness of 1.0 × 10⁶ MPa/mm was chosen and it has shown adequate alignment with experimental results [44]. Therefore, in this study, the same value was used for cohesive elements subjected to uniaxial tension.

The process of damage begins when the stresses and/or strain in each direction of the cohesive elements reach the pre-defined critical point, the so-called damage initiation point. A cohesive element with low damage initiation point starts decohesion before other cohesive elements. Therefore, mis-chosen values can create localised damage patterns in a mesoscale model. Cohesive elements initiate damage when the following condition is reached [46],

$$\left\{ {\frac{{t_{{\text{n}}} }}{{t_{{{\text{n}}0}} }}} \right\}^{2} + \left\{ {\frac{{t_{{\text{s}}} }}{{t_{{{\text{s}}0}} }}} \right\}^{2} + \left\{ {\frac{{t_{{\text{t}}} }}{{t_{{{\text{t}}0}} }}} \right\}^{2} = 1,$$

(25)

where ${t}_{\mathrm{n}0}$, ${t}_{\mathrm{s}0}$ and ${t}_{\mathrm{t}0}$ represent the damage initiation stress in the normal direction to the cohesive element and two tangential directions to the cohesive elements, respectively. The Macaulay bracket is used to signify that a pure compressive deformation or stress does not initiate damage. Note that, as previously discussed, due to the lack of experimental data to determine damage initiation along tangential directions, ${t}_{\mathrm{s}0}$ and ${t}_{\mathrm{t}0}$ were assumed to be same as the ${t}_{\mathrm{n}0}$ (see Table 2).

After stresses and/or strains exceed the damage initiation point, “damage evolution law” must be defined to describe the rate at which the material stiffness degrades [46]. In general, there are two criteria to define damage evolution, namely

• (i) Defining the effective displacement at complete failure, ${\delta }_{\mathrm{m}}^{\mathrm{f}}$ (decohesion), and

• (ii) Energy dissipation during fracture propagation, ${G}^{\mathrm{C}}$, see Table 2.

Furthermore, the softening region of the damage evolution can be defined in three different ways i.e. linear, exponential and tabular. Mode dependency is another phenomenon which governs the damage evolution. In fact, when cohesive elements are subjected to mixed-mode loading, depending on the loading path as depicted in Fig. 13, the damage evolution differs. ABAQUS provides a modified TSL for mixed-mode loading, and several TSL models for mixed-mode loading can found elsewhere [10]. Note that, in this research, elements were only subjected Mode I loading i.e. uniaxial tensile deformation at macro level. Thus, TSL explicitly becomes mode-independent in this regard [64]. The calibration of the material properties of solid elements and cohesive elements was done by validating the experimental uniaxial tensile test result for normal strength concrete presented in Li and Ansari [65]. The validation was performed on the small specimens presented in Tirassa et al. [5]. Figure 14 depicts the validation of experimental result and uniaxial tensile curve obtained from FE model incorporating material properties presented in Table 2. As can be seen, the numerically determined curved demonstrated appreciable accuracy thus, mesoscopic parameters presented in Table 2 are used for the FE modelling approach presented in this study.

Fig. 13

Two possible paths in mixed-mode loading

Fig. 14

Calibration of mesoscopic properties using Li and Ansari [65] uniaxial test results

4.4.2 Constitutive relations and material properties for aggregate interlock model

Concrete damage plasticity model (CDPM) was used as the material model for cracked concrete. For FE models with separate aggregates inside the cracked models, mortar and aggregates were separately modelled using CDPM. For cracked FE models with integrated aggregates, only one material was defined according to the ultimate strengths of concrete. Tables 3 and 4 show the strength of materials that can be used to generate CDPM parameters for 30 MPa concrete for the separate aggregate model and integrated aggregate model, respectively.

Table 3 Strength of materials for the FE models with separate aggregates

Table 4 Strength of materials for the FE models with combined aggregates

5 Results and discussion

5.1 Surface roughness index

The crack surface obtained using CIEs can be used to determine the surface roughness index which is an important parameter in determining the aggregate interlock and shear friction. The fractured surface area was measured using a 3D modelling software “BLENDER”. One of the fractured halves was exported from Abaqus as a.stl file and then, it was imported to the BLENDER [61]. Then, the roughness parameter defined by Perera and Mutsuyosi [26] and Tirassa et al. [5] was used to determine the roughness of the crack surfaces. The equation of surface roughness index is given in Eq. (16) and its schematic representation is shown in Fig. 15. The corresponding surface roughness index values for FE models developed in this study can be found in Table 6.

$$R_{{\text{s}}} = \sum \frac{{A_{i} }}{{\underline {A} }},$$

(26)

where, $A_{i}$ is the fractured surface area, $\underline {A}$ is the projected surface area on a horizontal plane.

Fig. 15

Schematic representation of the surface roughness index [26]

5.2 Comparison between FE model with separate aggregates and combined aggregates

Section 4.3 of this paper described the procedure for the development of the proposed FE model with separate aggregates. This procedure is very time consuming as each aggregate on the crack surface needs to be partitioned to apply cohesive contact and penalty contacts as described in Sect. 4.3. Figures 16 and 17 depict FE models with separate aggregate and combined aggregates, respectively. Thus, authors propose a simplified method which does not require separate aggregates in the model. According to the simplified method, two crack halves can be directly exported as.stl files where in separate aggregate FE model, aggregates and mortar in each cracked specimen need to be exported as.stl files and performed the steps described in Sect. 4.3 The simplified method is straightforward as only one material is in the model. Material properties of the concrete was used for the combined aggregate model. The simplified method yielded comparable results with the separate aggregate model as shown in Fig. 16. Thus, the rest of the FE models described in this paper are based on this simplified FE model. As can be seen in Fig. 18, the simplified method with combined aggregate yielded similar results in shear stress vs shear slip response compared to the separate aggregates.

Fig. 16

FE model with separate aggregates

Fig. 17

FE model with combined aggregates

Fig. 18

Comparison of shear stress vs shear slip curves of seperate aggregate and combined aggregate models

5.3 Validation of FE models of aggregate interlock using experimental results under mixed mode crack kinematics

To validate the FE results, two experimental campaigns were considered i.e. Jacobsen experiments and Max Tirassa experiments [18, 39]. Also, note that comparison of results for validation will only be conducted based on the shear stress-shear slip curve due to presence of aggregate interlock.

5.3.1 Validation of FE Results against Jacobsen’s mixed-mode experiment

Experiment Jacobsen’s [39] experimental investigation was a two-step approach. The first step was the crack initiation under pure Mode-I opening followed by the second step of mixed-mode opening. The loading set-up has consisted of two independent actuators which could apply vertical and horizontal loads simultaneously. As shown in Fig. 19b, the specimen consisted of two deep notches. The specimen’s dimensions were 150 × 80 × 75 mm³ and the depth of the notch was 55 mm. Introduction of deep notches has ensured that a single plane crack developed between these notches, as shown in Fig. 19a. The specimens have been cut from a beam with a cross section of 150 × 150 mm² ensuring minimum affect due to segregation. The concrete had a maximum aggregate size of 8 mm, and the compressive strength was measured using standard cylinder test to be 42 MPa.

Fig. 19

a Cracked Jacobsen’s specimens. b Jacobsen’s specimen dimensions

Validation Jacobsen [39] presented results under two categories as listed below; and the same procedure will be used for the comparison with FE results.

• (I) Varying the mixed-mode angle (MMA) under constant initial crack width (iCW) and

• (II) Varying iCW under constant MMA.

The graphs shown in Figs. 21 and 23 were named corresponding to these two mixed mode paths. For example, constant iCW of 0.025 mm and varying MMA of 40⁰ was named as iCW_0.025mm_MMA_40. The same naming procedure was used for Fig. 28. As can be seen in Fig. 20, only a small portion of the concrete specimen was taken for the mesoscale modelling approach. However, shearing area of the specimens were kept identical. Table 5 illustrates the more details of the validation with the Jacobsen’s experiments according to iCWs and MMAs.

Fig. 20

Extraction of the FE model specimen from the experimented specimen

Table 5 Validation programme, initial crack opening (iCW) and mixed mode angle (MMA)

Varying mixed-mode angle (MMA) under constant initial crack width (iCW) Fig. 21 shows the mixed-mode behaviour for four specimens with an initial crack opening of 0.025 mm followed by four different MMAs; 40°, 45°, 50° and 60°.

Fig. 21

Comparison of FE results against Jacobsen’s experiment under varying MMA (mixed-mode angle) and constant iCW (initial crack width)

A lower MMA results in a higher level of sliding compared to crack opening displacement, which thereby intensifies the aggregate interlock stress. As highlighted in Fig. 21, MMA of 40° transferred the higher shear stress compared to the rest of MMAs. According to experimental observations using Distributed Image Correlation (DIC) techniques, secondary cracks, which initiated with an inclination to the primary crack (crack between two notches), were overserved except for MMA of 45°. Moreover, Jacobsen highlighted that the secondary cracking is more pronounced for low MMAs.

According to FE results presented in Fig. 21, the FE model achieved comparable accuracy despite the complexity of the problem. In fact, the initial segment of the shear stress vs shear slip relationship was well captured by the FE model except slight underestimation of the ultimate shear stress due to aggregate interlock which can be explained by the difference in actual meso-structure in specimens and FE models. However, large deviations were observed with the FE model for MMA of 60°. Furthermore, FE models overestimated the shear stresses in the softening region. In fact, this deterioration of shear stress in the softening region is due to secondary cracking. As FE models do not capture any secondary cracking, they exhibit higher shear stresses in the softening region compared to the experimental results. Figure 22 shows the variation of maximum principal plastic strain in cracked mesoscale models.

Fig. 22

Maximum principal plastic strain in crack mesoscale models subjected mixed mode crack kinematics

Varying iCW under constant MMA Varying iCW under constant MMA, as shown in Fig. 23, also indicated that the FE results yielded appreciable accuracy in the initial region before reaching the maximum shear stress compared to the experimental curve. However, when reaching the maximum shear stress transferred due to aggregate interlock, FE results turned away from the experimental curve underestimating the maximum shear stress. It can also be seen that softening is overestimated by the FE models as FE models did not capture secondary cracking. It must also be highlighted that the shear stress transfer due to aggregate interlock in the small-scale test is a highly randomised case, as the aggregate distribution in the specimen affects the results.

Fig. 23

Comparison of FE results against Jacobsen’s experiment under varying iCW (initial crack width) and constant MMA (mixed-mode angle)

Figures 22 and 24 illustrate maximum principal plastic strain in cracked mesoscale models. As can be seen in Fig. 21, increasing mixed mode angle reduces the contact engagements between crack surfaces. Therefore, overall shear stress transfer between crack surfaces reduces as can be seen in Fig. 21. Furthermore, comparing Figs. 22 and 24 revealed that increasing MMA and while keeping constant iCW has significant impact on shear transfer due aggregate interlock compared to varying iCW keeping constant MMA.

Fig. 24

Maximum principal plastic strain in crack mesoscale models subjected mixed mode crack kinematics

5.3.2 Validation of FE results against Tirassa’s mixed-mode experiment

Experiment Tirassa [5, 18] also followed the two-step approach as in Jacobson’s [39] experiment and the test set-up was very similar. In fact, the dimensions of the specimen and the concrete properties were only slightly different. Tirassa has used double notched specimens produced from a concrete bar to minimise the accumulation of water under aggregates from bleeding and to minimise segregation in concrete. The specimen sizes were slightly deferent to each specimen and the gap between two notches were also different creating a different shearing area (i.e., area subjected to aggregate interlock). Figure 6 shows the dimensions of Tirassa’s specimens. Various concrete mixes and different maximum aggregate sizes were used potentially affecting the aggregate interlock behaviour.

Validation Tirassa et al. [5] tested 26 small-scale tests with different dimensions, shearing area, initial crack width and compressive strength of concrete. Among them, nine tests were selected for validation with the FE models proposed in this study. Tirassa et al. [5] observed three different crack developments during the experimental programme, namely, Primary cracking (PC), Non-Dominant Secondary Cracking (NDSC) and Dominant Secondary Cracking (DSC). The selected tests include all possible failure modes observed in Tirassa’s experiment campaign. Table 6 shows the details of these selected specimens and surface roughness index values. According to surface roughness index values obtained from the FE, a correlation can be seen between aggregate size and the roughness index. Furthermore, it further depends on the aggregate content, because number of protruding aggregates from crack surface increases with aggregate content. Concrete strength also plays an important role as higher concrete strengths have higher ITZ strengths thus, trans-granular fracturing can be expected [66].

Table 6 Details of the selected specimens from Tirassa et al. [5] for the validation of the FE model and their surface roughness indices

As observed through the validation process, the proposed FE modelling approach yields reasonable accuracy compared to the experimental results. However, for specimens which experienced DSC, FE models considerably underpredict the ultimate shear stress due to aggregate interlock. As observed in Fig. 25, FE results against specimens 050101, 050802, showed large deviation from the experimental results. As observed in Fig. 26, these specimens did not develop secondary carking, whereas experimental results showed failure due to DSC. The significant difference can be explained by the difference in the mesoscopic nature of the experimental specimens and FE models. Although, the same specimen sizes, max aggregate size and aggregate content were used, the orientation of aggregates can affect the result considerably. Also, due to the area of the crack surface is small and the number of aggregates crossed by the Mode I crack clearly affecting the surface roughness index, and hence, the stress transfer due to aggregate interlock is inconsistent in the experimental results. Specimens such as 030802, 050301, 050801 that had no secondary cracking reasonably agreed with experimental results. Tirassa recorded non-dominant secondary cracking (NDSC) in specimens 050801, 050102 and 050902. However, FE models of these specimens did not capture NDSC, yet reasonable agreement was observed when comparing shear stress vs shear slip curves. Furthermore, comparing surface roughness index of 05802, a considerable difference can be seen compared to other specimens. Thus, large deviation between the experimental curve and FE curve can be expected as the surface roughness governs the stress transfer between crack surfaces. Specimens with least difference between surface roughness index values such as 030802 and 050801 have the best validations against experimental curves.

Fig. 25

Comparison of FE results with Tirassa experiment results

Fig. 26

Comparison of crack pattern obtained from DIC (left hand side) and FE results (right hand side)

Figure 26 shows the DIC pictures of the Tirassa’s experimental programme for the specimens mentioned in Table 6 and corresponding FE figures that show maximum principal strain at the end of the shear stress vs shear slip curve. Formation of cracks are defined by red colour in DIC figures. Mode I crack is already formed in FE models; thus, FE models do not show plastic deformation between two notches. However, they show plastic deformations on the crack surface and the development of secondary cracking can be seen in Fig. 26a, e, respectively. In fact, the FE models predicted secondary cracking in 050102, 050202, 050802 in which experiment also experienced secondary cracking. However, FE model did not show any secondary cracking in 050101, 050301 and 050801 specimens while DIC results show secondary cracking. This difference can be due to the differences in the mesoscopic nature of concrete as identified and noted by Tirassa et al. [5]. Moreover, 030802, 050902 and 070101 specimens did not experience secondary cracking in both FE models and DIC figures. PC occurs by sliding of the Mode I crack, and no secondary cracks are developed. The FE model demonstrated PC in 030802, 050101, 050301, 050801, 050902 and 070101 specimens. NDSC was identified as a secondary cracking, however, NDSCs were stable and had limited influence on the overall behaviour of FE models. In fact, NDSC was not directly identifiable in FE models. However, since NDSC and DSC are very similar expect for a large spike in shear stress vs shear slip curve as described in Tirassa, NDSC could be identified. DSC is a very unstable secondary crack which starts from a Mode I crack. FE models predicted DSC in 050102, 050202 and 050802.

The reasons for secondary cracking as demonstrated by FE models are low initial crack widths (iCW) and low mixed mode angles (MMA). Furthermore, this can also be affected by maximum aggregate size, aggregate content, and the strength of concrete. In Fig. 26e, h, DIC figures show few secondary cracks slightly inclined to the notch line, and these cannot be seen in the corresponding images of the FE models. However, it is suspected that this could be due to the residual tensile effect of concrete which is not considered in the FE models. Thus, further studies with modifications to the FE models are required to consider residual tensile effect of concrete.

5.4 Comparison with analytical expressions under mixed mode crack kinematics

Due to rising sliding along the crack surfaces, the rough surfaces of concrete can transfer stress when two opposite crack surfaces contact each other. In fact, the so-called “aggregate interlock stress transfer” can transfer considerable amounts of shear stress between crack surfaces. Apart from that, crack dilatancy induces normal stresses perpendicular to crack surfaces and these have to be transferred by shear reinforcement crossing the crack. However, this phenomenon is influenced by several mesoscale level parameters such as the size, shape, grading, and strength of aggregates and strength of cement paste. Several analytical models have been developed over the last 4 decades to predict the constitutive behaviour of aggregate interlock. Among them were some empirical approaches based on the push-off test results and mechanical approaches with physical background. From these, this study investigated the performance of the proposed FE modelling approach for aggregate interlock against the analytical expressions of Walraven’s simplified formulae [22], Bažant’s rough crack model [19], contact density model [37] and Cavagnis’s aggregate interlock formulae [67] as detailed in Sect. 2 of this paper. Furthermore, the FE results were evaluated against these expressions under two kinematics i.e.

• (I) Shear slip under constant crack width, and

• (II) Initial crack width followed by mixed mode crack kinematics.

5.4.1 Comparison with constant crack width condition

Upon undergoing tensile cracking under Mode-I displacement, the constant crack width condition only experiences shear slip (Mode-II). In reality, it is impossible to maintain a constant crack width under shear slip deformation along the crack surface. However, if reinforcement was provided across the crack, the crack width could be maintained in a controlled manner. In RC beams, shear reinforcement does this job. However, no experimental work which maintained a constant crack width throughout the slip deformation was found. Therefore, constant crack width condition can only be considered in analytical expressions and finite element modelling as in this study. As mentioned before, Cavagnis’s equation was developed based on Guidotti mixed mode crack kinematic path. Hence, Cavagnis’s equation is not applicable for the constant crack width condition. Contact density model was also developed for monotonic and realistic crack kinematic paths that can be experienced in reinforced concrete elements. Therefore, only Walraven’s equations and Bažant’s equations were consider for the constant crack width condition. Figure 27a, b show the performance of Walraven and Bažant equations, respectively, under constant crack width condition against Jacobsen’s specimens.

Fig. 27

Comparison of FEM model results against a Walraven and b Bažant formulation under constant crack widths of 0.1 mm, 0.2 mm, 0.3 mm, 0.4 mm and 0.5 mm

As shown in Fig. 27a, Walraven’s expression gives linear relations between shear stress and shear slip under constant crack width. Further to their linearity, the curves start with positive shear slip at zero shear stress and it appears that wider the crack width larger the shear slip. This in fact is reasonably accurate, because the shear slip required for initial contact enforcement increases as the crack gets wider. FE curves also show very low shear stress at the beginning of the shear slip. Furthermore, Walraven’s expression does not specify the maximum shear stress that can be attained under shear slip. Thus, if Walraven’s equation was employed for constant crack width condition, the maximum shear stress between two crack surfaces need to be defined. For example, Modified Compression Field Theory (MCFT) defines the following equation for the maximum shear stress between two crack surfaces under constant crack width.

$$v_{{{\text{cimax}}}} = \frac{{0.18\sqrt {f_{{\text{c}}}^{^{\prime}} } }}{{0.31 + \frac{24w}{{a_{{\text{g}}} + 16}}}}.$$

(23)

Bažant’s expression for aggregate interlock was developed by optimizing the fits of Paulay and Loeber’s [35] push-off test results. As shown in Fig. 26b, Bažant expression does not result in linear curves under constant crack width, and they start from zero shear slip. Furthermore, at the beginning of shear slip, FE curves and Bažant curves are in reasonable agreement compared to the Walraven’s curves. The shape of the FE curve and Bažant’s curve are comparable in the linear range (from end of the initial curve to maximum shear stress point). However, Bažant’s equation overestimated the maximum shear stress due to aggregate interlock compared to the FE curve.

5.4.2 Comparison under mixed mode crack kinematics

The same FE models that were developed to compare with the Jacobsen’s experimental results were used to compare against analytical predictions under mixed-mode crack kinematics. Figure 28 shows the FE prediction validation of Jacobsen’s specimens against Walraven’s equation, Bažant’s equation, Cavagnis’s equation and contact density model (CDM). Note that, Figs. 28a–d show comparison of the varying mixed-mode angle (MMA) under constant initial crack width (iCW) and Figs. 28 e–h show the varying iCW width under constant MMA.

Fig. 28

Comparison of FE results against analytical expressions of mixed-mode crack kinematics

As observed in Fig. 28, the proposed finite element approach in this study yielded reasonable agreement with the all the analytical expressions in the linear region of the shear stress-shear slip curve. The pre-peak response, the maximum shear stress and the shear slip at maximum shear stress were matching well with the Walraven’s expression. However, CDM and Cavagnis’s equation underestimated the shear slip at the maximum shear stress compared to the FE results. Bažant’s equation overestimated the maximum shear stress compared to other analytical expressions and FE models except the ones in Fig. 28g, h. Moreover, CDM underestimated the maximum shear stress due to aggregate interlock compared to the other models and the FE model except for the ones in Fig. 28c, d. It can also be seen that Fig. 28d shows a significant difference between the curve from FE result and the curves from analytical expressions. Furthermore, CDM and Cavagnis’s equation demonstrated high softening of shear stress against the shear slip compared to other analytical expression while FE model exhibited lower softening of the shear stress against the shear slip. In the whole, increasing both MMA and iCW reduced the maximum shear stress transfer due to aggregate interlock. However, as shown in Fig. 28, increasing MMA under constant crack width had pronounced impact on the shear stress transfer compared to the iCW under constant MMA. As it can be seen, FE models demonstrated some noise in shear stress vs shear slip curves. The nature of the crack surface can create these sudden variations in shear stress. The formation of contact surfaces is not a gradual process, when some contact areas are forming some already formed contact areas could be deforming plastically. Thus, the noise associated with the curves resulting from the FE models is acceptable and similar observations were recorded in the Jacobsen’s experiments as well.

6 Conclusions

This study proposed a novel FE modelling approach for investigating force transfer due to aggregate interlock in cracked concrete. Results from the proposed FE method was compared against cracked specimens from the experimental studies of Jacobsen and Tirassa. They were also compared against results from analytical expressions in the form of Walraven’s simplified formulae, Bažant’s rough crack model, contact density model and the Cavagnis’s aggregate interlock formulae. Furthermore, the DIC figures obtained by Tirassa was compared with plastic deformations in the FE models. It was observed that the proposed FE modelling approach yielded appreciable agreement with the two experimental campaigns and the four analytical expressions. However, further studies are encouraged to extend its applications into areas such as combined effect of dowelling action and aggregate interlock, aggregate interlock in steel fibre-reinforced concrete, effect of fractured aggregate, and cyclic response. The conclusions from this study and further improvements for the proposed FE method are listed below:

• 1. Zero-thickness cohesive element approach is very effective in accurately simulating fracture propagation in concrete mesoscale models.

• 2. Surface roughness indices determined from cracked FE models are comparable with the referred experimental results. Surface roughness index determines the development of contact forces between cracked surfaces.

• 3. Surface roughness indices are related to the aggregate size, aggregate content, and concrete strength.

• 4. The proposed aggregate interlock FE models with separate aggregates and combined aggregates yielded comparable results, thus, the FE model with combined aggregate is the most effective modelling approach in terms of the complexity of the model.

• 5. Comparison of FE models with two experimental campaigns demonstrated reasonably agreement except for softening branches of the shear stress vs shear slip curves from FE models which did not exhibit secondary cracking.

• 6. Capacity of shear transfer and development of secondary cracks are also dependent on the initial cracking width and mixed mode angle.

• 7. Normal stress induced by aggregate interlock which is acting perpendiculars to the crack surface was not investigated in this study, as residual tensile stress of concrete explicitly affects the normal stress which is currently not included in the proposed FE method.

• 8. Proposed FE method provides more economical approach to investigate stress transfer due to aggregate interlock and this work could be further extended to investigate the effect of aggregate fracturing on aggregate interlock, aggregate interlock in steel-fiber reinforced concrete and the effect of doweling action on the aggregate interlock.