Theoretical, numerical, and experimental study on the synchronization in a vibrator–pendulum coupling system

Abstract

For a vibrating system where the pendulum and vibrators are coupled together, the relevant dynamic model and the corresponding synchronization problem are rarely studied, due to its complex dynamic coupling relationships. In this paper, a vibrator–pendulum coupling system is proposed to study its synchronization principle; here, the pendulum is driven by the synchronous motion of the two vibrators directly. By exploiting the system motion differential equations and their vibration responses, the synchronization criterion of the two vibrators is deduced via the average method. After that, the stability criterion for the synchronous states is presented according to the convergence and divergence characteristics of the perturbed differential equation in the balanced state. Based on the theoretical results, the synchronous stable states and motion characteristics of the system under different parameter conditions are discussed by numerical qualitative analyses, and the reasonable parameters matching principles in designing the real vibrating machine are provided. A series of numerical simulations and experiments are further given to examine the validity of the theoretical methods and the obtained results. The dynamic model and research results presented in this paper can be applied to design a new kind of vibrating jaw crusher; in this case, the pendulum is served as the moving jaw and can work with its swing motion trajectory under the premise of the stable zero-phase difference between the two vibrators.

Appendices

Appendix A: Details for the deducing process of the motion differential equations in Eq. (1)

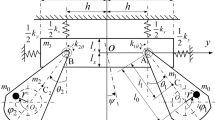
The coordinates of the two vibrators and the pendulum in the fixed frame $oxy$ are denoted by ${\mathbf{X}}_{1}$, ${\mathbf{X}}_{2}$, and ${\mathbf{X}}_{3}$, respectively, and they are presented as

$${\mathbf{X}}_{1} = \left[ {\begin{array}{*{20}c} {l_{1} \sin \theta + r_{1} \sin \varphi_{1} } \\ { - l_{1} \cos \theta - r_{1} \cos \varphi_{1} } \\ \end{array} } \right],\;{\mathbf{X}}_{2} = \left[ {\begin{array}{*{20}c} {l_{2} \sin \theta + r_{2} \sin \varphi_{2} } \\ { - l_{2} \cos \theta + r_{2} \cos \varphi_{2} } \\ \end{array} } \right],\;{\mathbf{X}}_{3} = \left[ {\begin{array}{*{20}c} {l_{3} \sin \theta } \\ { - l_{3} \cos \theta } \\ \end{array} } \right],$$

(22)

where $l_{i}$ ($i = 1,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2$) is the mounting dimension of the vibrator $i$; $l_{3}$ is the distance from the mounting point of the pendulum to its mass center; $r_{1}$ and $r_{2}$ are the eccentric radii of the two vibrators, and $r_{1} = r_{2} = r$.

In the moving frame $o^{\prime}x^{\prime\prime}y^{\prime\prime}$, the final coordinates of the two vibrators and the pendulum, denoted by ${\mathbf{X^{\prime\prime}}}_{1}$, ${\mathbf{X^{\prime\prime}}}_{2}$, and ${\mathbf{X^{\prime\prime}}}_{3}$, are expressed as

$${\mathbf{X^{\prime\prime}}}_{1} = {\mathbf{X}}_{{\mathbf{m}}} + {\mathbf{L}} \cdot {\mathbf{X}}_{1} ,\;\;{\mathbf{X^{\prime\prime}}}_{2} = {\mathbf{X}}_{{\mathbf{m}}} + {\mathbf{L}} \cdot {\mathbf{X}}_{2} ,\,{\mathbf{X^{\prime\prime}}}_{3} = {\mathbf{X}}_{{\mathbf{m}}} + {\mathbf{L}} \cdot {\mathbf{X}}_{3}$$

(23)

with

$${\mathbf{X}}_{{\mathbf{m}}} = \left[ {\begin{array}{*{20}c} x \\ y \\ \end{array} } \right],\;{\mathbf{L}}{ = }\left[ {\begin{array}{*{20}c} {\cos \psi } & { - \sin \psi } \\ {\sin \psi } & {\cos \psi } \\ \end{array} } \right],$$

where ${\mathbf{X}}_{{\mathbf{m}}}$ is the displacement vector of the rigid frame and ${\mathbf{L}}$ denotes the rotation matrix.

According to the above treatments of coordinate transformations, the kinetic energy of the system, denoted by $T$, is deduced as

$$T = \frac{1}{2}m\left( {\dot{x}^{2} + \dot{y}^{2} } \right) + \frac{1}{2}J_{{\text{m}}} \dot{\psi }^{2} + \frac{1}{2}\sum\limits_{{i = 1}}^{3} {m_{i} {\mathbf{\dot{X}}}^{{\prime \prime {\text{T}}}} _{i}} {\mathbf{\dot{X}^{\prime\prime}}}_{i} + \frac{1}{2}J_{t} \dot{\theta }^{2} ,$$

(24)

where $J_{{\text{m}}}$ and $J_{{\text{t}}}$ are the moments of inertia of the rigid frame and that of the pendulum, respectively, $J_{{\text{t}}} = m_{3} l_{{\text{e}}}^{{2}}$; $m_{3}$ and $l_{{\text{e}}}$ denote the mass and the equivalent radius of the pendulum, respectively.

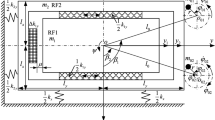
After the system is powered, the rigid frame generates displacements in x-, y-, and $\psi$-directions, leading to the deformations of the isolative springs. The deformations of the springs at the points A–D in Fig. 2 are denoted by $\Delta {\mathbf{x}}_{{\text{A}}}$, $\Delta {\mathbf{x}}_{{\text{B}}}$, $\Delta {\mathbf{x}}_{{\text{C}}}$, and $\Delta {\mathbf{x}}_{{\text{D}}}$, presented as

$$\begin{gathered} \Delta {\mathbf{x}}_{{\text{A}}} = \left[ {\begin{array}{*{20}c} {x - l_{x1} \cos \psi + l_{x1} } \\ {y - l_{x1} \sin \psi } \\ \end{array} } \right],\;\Delta {\mathbf{x}}_{{\text{B}}} = \left[ {\begin{array}{*{20}c} {x - l_{x2} \cos \psi + l_{y} \sin \psi + l_{x2} } \\ {y - l_{x2} \sin \psi - l_{y} \cos \psi + l_{y} } \\ \end{array} } \right], \hfill \\ \Delta {\mathbf{x}}_{{\text{C}}} = \left[ {\begin{array}{*{20}c} {x + l_{x2} \cos \psi + l_{y} \sin \psi - l_{x2} } \\ {y + l_{x2} \sin \psi - l_{y} \cos \psi + l_{y} } \\ \end{array} } \right],\;\Delta {\mathbf{x}}_{{\text{D}}} = \left[ {\begin{array}{*{20}c} {x + l_{x1} \cos \psi - l_{x1} } \\ {y + l_{x1} \sin \psi } \\ \end{array} } \right], \hfill \\ \end{gathered}$$

(25)

where $l_{x1}$ and $l_{x2}$ are the mounting dimensions of the isolative springs in the horizontal direction, and $l_{y}$ denotes that in the vertical direction.

Based on Eq. (25), the potential energy ($V$) and the energy dissipation ($D$) of the system are deduced as

$$\left\{ \begin{gathered} V = \frac{1}{2}\Delta {\mathbf{x}}_{{\text{A}}}^{{\text{T}}} {\mathbf{k}}_{{\text{A}}} \Delta {\mathbf{x}}_{{\text{A}}} + \frac{1}{2}\Delta {\mathbf{x}}_{{\text{B}}}^{{\text{T}}} {\mathbf{k}}_{{\text{B}}} \Delta {\mathbf{x}}_{{\text{B}}} + \frac{1}{2}\Delta {\mathbf{x}}_{{\text{C}}}^{{\text{T}}} {\mathbf{k}}_{{\text{C}}} \Delta {\mathbf{x}}_{{\text{C}}} + \frac{1}{2}\Delta {\mathbf{x}}_{{\text{D}}}^{{\text{T}}} {\mathbf{k}}_{{\text{D}}} \Delta {\mathbf{x}}_{{\text{D}}} + \frac{1}{2}k_{\theta } \theta^{2} \hfill \\ D = \frac{1}{2}\Delta {\dot{\mathbf{x}}}_{{\text{A}}}^{{\text{T}}} {\mathbf{f}}_{{\text{A}}} \Delta {\dot{\mathbf{x}}}_{{\text{A}}} + \frac{1}{2}\Delta {\dot{\mathbf{x}}}_{{\text{B}}}^{{\text{T}}} {\mathbf{f}}_{{\text{B}}} \Delta {\dot{\mathbf{x}}}_{{\text{B}}} + \frac{1}{2}\Delta {\dot{\mathbf{x}}}_{{\text{C}}}^{{\text{T}}} {\mathbf{f}}_{{\text{C}}} \Delta {\dot{\mathbf{x}}}_{{\text{C}}} + \frac{1}{2}\Delta {\dot{\mathbf{x}}}_{{\text{D}}}^{{\text{T}}} {\mathbf{f}}_{{\text{D}}} \Delta {\dot{\mathbf{x}}}_{{\text{D}}} + \frac{1}{2}f_{\theta } \dot{\theta }^{2} \hfill \\ \end{gathered} \right.$$

(26)

with

${\mathbf{k}}_{{\text{A}}} = {\mathbf{k}}_{{\text{B}}} = {\mathbf{k}}_{{\text{C}}} = {\mathbf{k}}_{{\text{D}}} = {\text{diag}}\left( {\frac{{k_{x} }}{2},\frac{{k_{y} }}{2}} \right)$, ${\mathbf{f}}_{{\text{A}}} = {\mathbf{f}}_{{\text{B}}} = {\mathbf{f}}_{{\text{C}}} = {\mathbf{f}}_{{\text{D}}} = {\text{diag}}\left( {\frac{{f_{x} }}{2},\frac{{f_{y} }}{2}} \right),$ where ${\mathbf{k}}_{{\text{A}}}$, ${\mathbf{k}}_{{\text{B}}}$, ${\mathbf{k}}_{{\text{C}}}$, and ${\mathbf{k}}_{{\text{D}}}$ are the stiffness matrixes of the isolative springs at the points A–D, while ${\mathbf{f}}_{{\text{A}}}$, ${\mathbf{f}}_{{\text{B}}}$, ${\mathbf{f}}_{{\text{C}}}$, and ${\mathbf{f}}_{{\text{D}}}$ correspond to the damping matrixes; $k_{\theta }$ and $f_{\theta }$ are the stiffness of the torsion spring and the damping constant of the pendulum, respectively.

Based on Lagrange’s equation [12], the energy relationship of the system satisfies the fact of

$$\frac{{\text{d}}}{{{\text{d}}t}}\frac{(T - V)}{{\partial {\dot{\mathbf{q}}}_{i} }} - \frac{\partial (T - V)}{{\partial {\mathbf{q}}_{i} }} + \frac{\partial D}{{\partial {\dot{\mathbf{q}}}_{i} }} = {\mathbf{Q}}_{{\mathbf{i}}} ,$$

(27)

where ${\mathbf{q}}_{i}$ and ${\mathbf{Q}}_{{\mathbf{i}}}$ are the matrixes of generalized coordinate and generalized force (or torque), respectively. In this paper, ${\mathbf{q}} = [x,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} y,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \psi ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \theta ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi_{1} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi_{2} ]^{{\text{T}}}$ is set as the generalized coordinates, $Q_{x} = Q_{y} = Q_{\psi } = Q_{\theta } = 0$, $Q_{\varphi 1} = T_{{{\text{e1}}}}$, and $Q_{\varphi 2} = T_{{{\text{e2}}}}$.

Appendix B: Details for Eqs. (2)–(5)

$$F_{y} = - \frac{{m_{0} r}}{{M\mu_{y} }},\;\gamma_{y} = \arctan \left( {\frac{{2\xi_{ny} z_{ny} }}{{1 - z_{ny}^{2} }}} \right),\;\mu_{y} = \frac{{\omega_{{{\text{m0}}}}^{{2}} - \omega_{ny}^{2} }}{{\omega_{{{\text{m0}}}}^{{2}} }},\;z_{ny} = \frac{{\omega_{ny} }}{{\omega_{{{\text{m}}0}} }},$$

$$\omega_{ny} = \sqrt {\frac{{k_{y} }}{M}} ,\;\xi_{ny} = \frac{{f_{y} }}{{2\sqrt {k_{2y} M} }},\;F_{xj} = m_{0} r\omega_{{{\text{m0}}}}^{2} \sqrt {\frac{{r_{xj}^{2} + i_{xj}^{2} }}{{d_{xr}^{2} + d_{xi}^{2} }}} ,\;j = x,\psi ,\theta ,r_{x1} = \left( {MJ_{{\text{M}}} J_{\theta } - M\tau^{2} } \right)\omega_{{{\text{m0}}}}^{6} - k_{\psi } k_{\theta } k_{x} ,$$

$$r_{x2} = - \;\left( {MJ_{{\text{M}}} k_{\theta } + MJ_{\theta } k_{\psi } + Mf_{\psi } f_{\theta } - \tau^{2} k_{x} + J_{{\text{M}}} J_{\theta } k_{x} + J_{{\text{M}}} f_{\theta } f_{x} + J_{\theta } f_{\psi } f_{x} } \right)\omega_{{{\text{m0}}}}^{4} ,$$

$$r_{x3} = \left( {Mk_{\psi } k_{\theta } + J_{{\text{M}}} k_{\theta } k_{x} + J_{\theta } k_{\psi } k_{x} + f_{\psi } f_{\theta } k_{x} + f_{\psi } f_{x} k_{\theta } + f_{\theta } f_{x} k_{\psi } } \right)\omega_{{{\text{m0}}}}^{2} ,$$

$$\begin{gathered} r_{xx} = r_{x1} + r_{x2} + r_{x3} ,\;i_{x1} = - \;\left( {MJ_{{\text{M}}} f_{\theta } + MJ_{\theta } f_{\psi } - \tau^{2} f_{x} + J_{{\text{M}}} J_{\theta } f_{x} } \right)\omega_{{{\text{m0}}}}^{5} , \hfill \\ i_{x2} = \left( {Mf_{\psi } k_{\theta } + Mf_{\theta } k_{\psi } + J_{{\text{M}}} f_{\theta } k_{x} + J_{{\text{M}}} f_{x} k_{\theta } + J_{\theta } f_{\psi } k_{x} + J_{\theta } f_{x} k_{\psi } + f_{\psi } f_{\theta } f_{x} } \right)\omega_{{{\text{m0}}}}^{3} , \hfill \\ \end{gathered}$$

$$\begin{gathered} i_{x3} = - \left( {f_{\psi } k_{\theta } k_{x} + f_{\theta } k_{\psi } k_{x} + f_{x} k_{\psi } k_{\theta } } \right)\omega_{{{\text{m0}}}} ,\;i_{xx} = i_{x1} + i_{x2} + i_{x3} , \hfill \\ r_{x\psi } = \sigma \tau M\omega_{{{\text{m0}}}}^{6} - \sigma \tau k_{x} \omega_{{{\text{m0}}}}^{4} ,i_{x\psi } = - \sigma \tau f_{x} \omega_{{{\text{m0}}}}^{5} , \hfill \\ \end{gathered}$$

$$r_{x\theta } = - \sigma MJ_{M} \omega_{{{\text{m0}}}}^{6} + \sigma \left( {Mk_{\psi } + J_{M} k_{x} + f_{\psi } f_{x} } \right)\omega_{{{\text{m0}}}}^{4} - \sigma k_{\psi } k_{x} \omega_{{{\text{m0}}}}^{2} ,$$

$$i_{x\theta } = \sigma \left( {Mf_{\psi } + J_{{\text{M}}} f_{x} } \right)\omega_{{{\text{m0}}}}^{5} - \sigma \left( {f_{\psi } k_{x} + f_{x} k_{\psi } } \right)\omega_{{{\text{m0}}}}^{3} ,\;d_{xr} = d_{x1} + d_{x2} + d_{x3} + d_{x4} ,$$

$$d_{xi} = d_{x5} + d_{x6} + d_{x7} ,\;\;d_{x1} = \left( {\sigma^{2} MJ_{{\text{M}}} + \tau^{2} M^{2} - J_{{\text{M}}} J_{\theta } M^{2} } \right)\omega_{{{\text{m0}}}}^{8} - k_{\psi } k_{\theta } k_{x}^{2} ,$$

$$\begin{aligned} d_{x2} & = \left( { - \sigma^{2} } \right.Mk_{\psi } - \sigma^{2} J_{{\text{M}}} k_{x} - \sigma^{2} f_{\psi } f_{x} - 2\tau^{2} Mk_{x} - \tau^{2} f_{x}^{2} + M^{2} J_{{\text{M}}} k_{\theta } \\ & \;\;{\kern 1pt} + M^{2} J_{\theta } k_{\psi } + M^{2} f_{\psi } f_{\theta } + 2MJ_{{\text{M}}} J_{\theta } k_{x} + 2MJ_{{\text{M}}} f_{\theta } f_{x} + 2MJ_{\theta } f_{\psi } f_{x} + J_{{\text{M}}} \left. {J_{\theta } f_{x}^{2} } \right)\omega_{{{\text{m0}}}}^{6} , \\ \end{aligned}$$

$$\begin{aligned} d_{x3} & = \left( {\sigma^{2} k_{\psi } k} \right._{x} + \tau^{2} k_{x}^{2} - M^{2} k_{\psi } k_{\theta } - 2MJ_{{\text{M}}} k_{\theta } k_{x} - 2MJ_{\theta } k_{\psi } k_{x} \\ & \;\;\;{\kern 1pt} {\kern 1pt} - 2Mf_{\psi } f_{\theta } k_{x} - 2Mf_{\psi } f_{x} k_{\theta } - 2Mf_{\theta } k_{\psi } f_{x} - J_{{\text{M}}} J_{\theta } k_{x}^{2} - 2J_{{\text{M}}} f_{\theta } f_{x} k_{x} \\ & \;\;\;{\kern 1pt} {\kern 1pt} - J_{{\text{M}}} f_{x}^{2} k_{\theta } - 2J_{\theta } f_{\psi } f_{x} k_{x} - J_{\theta } f_{x}^{2} k_{\psi } - f_{\psi } \left. {f_{\theta } f_{x}^{2} } \right)\omega_{{{\text{m0}}}}^{4} , \\ \end{aligned}$$

$$d_{x4} = \left( {2Mk_{\psi } k_{\theta } k_{x} + J_{M} k_{\theta } k_{x}^{2} + J_{\theta } k_{\psi } k_{x}^{2} + f_{\psi } f_{\theta } k_{x}^{2} + 2f_{\psi } f_{x} k_{\theta } k_{x} + 2f_{\theta } f_{x} k_{\psi } k_{x} + f_{x}^{2} k_{\psi } k_{\theta } } \right)\omega_{{{\text{m0}}}}^{2} ,$$

$$\begin{aligned} d_{x5} & = \left( { - \sigma^{2} Mf_{\psi } - \sigma^{2} J_{{\text{M}}} f_{x} - 2\tau^{2} Mf_{x} + M^{2} J_{{\text{M}}} f_{\theta } + M^{2} J_{\theta } f_{\psi } + 2MJ_{{\text{M}}} J_{\theta } f_{x} } \right)\omega_{{{\text{m0}}}}^{7} \\ & \;\; - \left( {f_{\psi } k_{\theta } k_{x}^{2} + f_{\theta } k_{\psi } k_{x}^{2} + 2f_{x} k_{\psi } k_{\theta } k_{x} } \right)\omega_{{{\text{m0}}}} , \\ \end{aligned}$$

$$\begin{aligned} d_{x6} & = (\sigma^{2} f_{\psi } k_{x} + \sigma^{2} f_{x} k_{\psi } + 2\tau^{2} f_{x} k_{x} - M^{2} f_{\psi } k_{\theta } - M^{2} f_{\theta } k_{\psi } - 2MJ_{{\text{M}}} f_{\theta } k_{x} - 2MJ_{M} f_{x} k_{\theta } \\ & \;\;{\kern 1pt} {\kern 1pt} - 2MJ_{\theta } f_{\psi } k_{x} - 2MJ_{\theta } f_{x} k_{\psi } - 2Mf_{\psi } f_{\theta } f_{x} - 2J_{{\text{M}}} J_{\theta } f_{x} k_{x} - J_{M} f_{\theta } f_{x}^{2} - J_{\theta } f_{\psi } f_{x}^{2} )\omega_{{{\text{m0}}}}^{5} , \\ \end{aligned}$$

$$\begin{aligned} d_{x7} & = (2Mf_{\psi } k_{\theta } k_{x} + 2Mf_{\theta } k_{\psi } k_{x} + 2Mf_{x} k_{\psi } k_{\theta } + J_{{\text{M}}} f_{\theta } k_{x}^{2} + 2J_{{\text{M}}} f_{x} k_{\theta } k_{x} \\ & \;\;\;\;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + J_{\theta } f_{\psi } k_{x}^{2} + 2J_{\theta } f_{x} k_{\psi } k_{x} + 2f_{\psi } f_{\theta } f_{x} k_{x} + f_{\psi } f_{x}^{2} k_{\theta } + f_{\theta } f_{x}^{2} k_{\psi } )\omega_{{{\text{m0}}}}^{3} , \\ \end{aligned}$$

$$\gamma _{{xj}} = \left\{ {\begin{array}{*{20}l} {\arctan \frac{{r_{{xj}} d_{{xi}} - i_{{xj}} d_{{xr}} }}{{r_{{xj}} d_{{xr}} + i_{{xj}} d_{{xi}} }},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} r_{{xj}} d_{{xr}} + i_{{xj}} d_{{xi}} > 0} \\ {\pi {\text{ + }}\arctan \frac{{r_{{xj}} d_{{xi}} - i_{{xj}} d_{{xr}} }}{{r_{{xj}} d_{{xr}} + i_{{xj}} d_{{xi}} }},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} r_{{xj}} d_{{xr}} + i_{{xj}} d_{{xi}} < 0} \\ \end{array} } \right.,j = x,\psi ,\theta ,$$

$$F_{\psi j} = m_{0} r\omega_{{{\text{m0}}}}^{2} \sqrt {\frac{{r_{\psi j}^{2} + i_{\psi j}^{2} }}{{d_{\psi r}^{2} + d_{\psi i}^{2} }}} ,\;j = x,\psi ,\theta ,\;r_{\psi x} = \sigma \tau J_{{\text{M}}} \omega_{{{\text{m0}}}}^{6} - \sigma \tau k_{\psi } \omega_{{{\text{m0}}}}^{4} ,$$

$$i_{\psi x} = - \sigma \tau f_{\psi } \omega_{{{\text{m0}}}}^{5} ,\;r_{\psi \psi } = r_{\psi 1} + r_{\psi 2} + r_{\psi 3} ,\;r_{\psi 1} = \left( {MJ_{{\text{M}}} J_{\theta } - \sigma^{2} J_{{\text{M}}} } \right)\omega_{{{\text{m0}}}}^{6} - k_{\psi } k_{\theta } k_{x} ,$$

$$r_{\psi 2} = - \left( {MJ_{{\text{M}}} k_{\theta } + MJ_{\theta } k_{\psi } + Mf_{\psi } f_{\theta } - \sigma^{2} k_{\psi } + J_{{\text{M}}} J_{\theta } k_{x} + J_{{\text{M}}} f_{\theta } f_{x} + J_{\theta } f_{\psi } f_{x} } \right)\omega_{{{\text{m0}}}}^{4} ,$$

$$r_{\psi 3} = \left( {Mk_{\psi } k_{\theta } + J_{M} k_{\theta } k_{x} + J_{\theta } k_{\psi } k_{x} + f_{\psi } f_{\theta } k_{x} + f_{\psi } f_{x} k_{\theta } + f_{\theta } f_{x} k_{\psi } } \right)\omega_{{{\text{m0}}}}^{2} ,\;i_{\psi \psi } = i_{\psi 1} + i_{\psi 2} + i_{\psi 3} ,$$

$$i_{\psi 1} = - (MJ_{{\text{M}}} f_{\theta } + MJ_{\theta } f_{\psi } - \sigma^{2} f_{\psi } + J_{{\text{M}}} J_{\theta } f_{x} )\omega_{{{\text{m0}}}}^{5} ,i_{\psi 2} = - (f_{\psi } k_{\theta } k_{x} + f_{\theta } k_{\psi } k_{x} + f_{x} k_{\psi } k_{\theta } )\omega_{{{\text{m0}}}} ,$$

$$i_{\psi 3} = (Mf_{\psi } k_{\theta } + Mf_{\theta } k_{\psi } + J_{{\text{M}}} f_{\theta } k_{x} + J_{{\text{M}}} f_{x} k_{\theta } + J_{\theta } f_{\psi } k_{x} + J_{\theta } f_{x} k_{\psi } + f_{\psi } f_{\theta } f_{x} )\omega_{{{\text{m0}}}}^{3} ,$$

$$r_{\psi \theta } = - \tau MJ_{{\text{M}}} \omega_{{{\text{m0}}}}^{6} + \tau (Mk_{\psi } + J_{{\text{M}}} k_{x} + f_{\psi } f_{x} )\omega_{{{\text{m0}}}}^{4} - \tau k_{\psi } k_{x} \omega_{{{\text{m0}}}}^{2} ,$$

$$i_{\psi \theta } = \tau \left( {Mf_{\psi } + J_{{\text{M}}} f_{x} } \right)\omega_{{{\text{m0}}}}^{5} - \tau \left( {f_{\psi } k_{x} + f_{x} k_{\psi } } \right)\omega_{{{\text{m0}}}}^{3} ,d_{\psi r} = d_{\psi 1} + d_{\psi 2} + d_{\psi 3} + d_{\psi 4} ,$$

$$d_{\psi i} = d_{\psi 5} + d_{\psi 6} + d_{\psi 7},$$

$$d_{\psi 1} = (\sigma^{2} J_{M}^{2} + \tau^{2} MJ_{M} - MJ_{M}^{2} J_{\theta } )\omega_{{{\text{m0}}}}^{8} - k_{\psi }^{2} k_{\theta } k_{x},$$

$$\begin{aligned} d_{\psi 2} & = ( - 2\sigma^{2} J_{{\text{M}}} k_{\psi } - \sigma^{2} f_{\psi }^{2} - \tau^{2} Mk_{\psi } - \tau^{2} J_{{\text{M}}} k_{x} - \tau^{2} f_{\psi } f_{x} + MJ_{{\text{M}}}^{{2}} k_{\theta } + 2MJ_{{\text{M}}} J_{\theta } k_{\psi } \\ & \;\;{\kern 1pt} {\kern 1pt} {\kern 1pt} + 2MJ_{{\text{M}}} f_{\psi } f_{\theta } + MJ_{\theta } f_{\psi }^{2} + J_{{\text{M}}}^{2} J_{\theta } k_{x} + J_{{\text{M}}}^{{2}} f_{\theta } f_{x} + 2J_{{\text{M}}} J_{\theta } f_{\psi } f_{x} )\omega_{{{\text{m0}}}}^{6} , \\ \end{aligned}$$

$$\begin{aligned} d_{\psi 3} & = (\sigma^{2} k_{\psi }^{2} + \tau^{2} k_{\psi } k_{x} - 2MJ_{M} k_{\psi } k_{\theta } - MJ_{\theta } k_{\psi }^{2} - Mf_{\psi }^{2} k_{\theta } \\ & \;\;\;\;{\kern 1pt} {\kern 1pt} {\kern 1pt} - 2Mf_{\psi } f_{\theta } k_{\psi } - J_{{\text{M}}}^{{2}} k_{\theta } k_{x} - 2J_{{\text{M}}} J_{\theta } k_{\psi } k_{x} - 2J_{{\text{M}}} f_{\psi } f_{\theta } k_{x} - 2J_{{\text{M}}} f_{\psi } f_{x} k_{\theta } \\ & \;\;\;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - 2J_{{\text{M}}} f_{\theta } f_{x} k_{\psi } - J_{\theta } f_{\psi }^{2} k_{x} - 2J_{\theta } f_{\psi } f_{x} k_{\psi } - f_{\psi }^{2} f_{\theta } f_{x} )\omega_{{{\text{m0}}}}^{4} , \\ \end{aligned}$$

$$d_{\psi 4} = \left( {Mk_{\psi }^{2} k_{\theta } + 2J_{{\text{M}}} k_{\psi } k_{\theta } k_{x} + J_{\theta } k_{\psi }^{2} k_{x} + f_{\psi }^{2} k_{\theta } k_{x} + 2f_{\psi } f_{\theta } k_{\psi } k_{x} + 2f_{\psi } f_{x} k_{\psi } k_{\theta } + f_{\theta } f_{x} k_{\psi }^{2} } \right)\omega_{{{\text{m0}}}}^{2} ,$$

$$\begin{aligned} d_{\psi 5} & = ( - 2\sigma^{2} J_{{\text{M}}} f_{\psi } - \tau^{2} Mf_{\psi } - \tau^{2} J_{{\text{M}}} f_{x} + MJ_{{\text{M}}}^{{2}} f_{\theta } + 2MJ_{{\text{M}}} J_{\theta } f_{\psi } + J_{{\text{M}}}^{{2}} J_{\theta } f_{x} )\omega_{{{\text{m0}}}}^{7} \\ & \;\;\;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - (2f_{\psi } k_{\psi } k_{\theta } k_{x} + f_{\theta } k_{\psi }^{2} k_{x} + f_{x} k_{\psi }^{2} k_{\theta } )\omega_{{{\text{m0}}}} , \\ \end{aligned}$$

$$\begin{aligned} d_{\psi 6} & = (2\sigma^{2} f_{\psi } k_{\psi } + \tau^{2} f_{\psi } k_{x} + \tau^{2} f_{x} k_{\psi } - 2MJ_{{\text{M}}} f_{\psi } k_{\theta } - 2MJ_{{\text{M}}} f_{\theta } k_{\psi } - 2MJ_{\theta } f_{\psi } k_{\psi } - Mf_{\psi }^{2} f_{\theta } \\ {\kern 1pt} & \;\;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - J_{{\text{M}}}^{{2}} f_{\theta } k_{x} - J_{{\text{M}}}^{{2}} f_{x} k_{\theta } - 2J_{{\text{M}}} J_{\theta } f_{\psi } k_{x} - 2J_{{\text{M}}} J_{\theta } f_{x} k_{\psi } - 2J_{{\text{M}}} f_{\psi } f_{\theta } f_{x} - J_{\theta } f_{\psi }^{2} f_{x} )\omega_{{{\text{m0}}}}^{5} , \\ \end{aligned}$$

$$\begin{aligned} d_{\psi 7} & = (2Mf_{\psi } k_{\psi } k_{\theta } + Mf_{\theta } k_{\psi }^{2} + 2J_{{\text{M}}} f_{\psi } k_{\theta } k_{x} + 2J_{{\text{M}}} f_{\theta } k_{\psi } k_{x} + 2J_{{\text{M}}} f_{x} k_{\psi } k_{\theta } + 2J_{\theta } f_{\psi } k_{\psi } k_{x} \\ & \;\;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + J_{\theta } f_{x} k_{\psi }^{2} + f_{\psi }^{2} f_{\theta } k_{x} + f_{\psi }^{2} f_{x} k_{\theta } + 2f_{\psi } f_{\theta } f_{x} k_{\psi } )\omega_{{{\text{m0}}}}^{3} , \\ \end{aligned}$$

$$\gamma _{{\psi j}} = \left\{ {\begin{array}{*{20}l} {\arctan \frac{{r_{{\psi j}} d_{{\psi i}} - i_{{\psi j}} d_{{\psi r}} }}{{r_{{\psi j}} d_{{\psi r}} + i_{{\psi j}} d_{{\psi i}} }},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} r_{{\psi j}} d_{{\psi r}} + i_{{\psi j}} d_{{\psi i}} > 0} \\ {\pi {\text{ + }}\arctan \frac{{r_{{\psi j}} d_{{\psi i}} - i_{{\psi j}} d_{{\psi r}} }}{{r_{{\psi j}} d_{{\psi r}} + i_{{\psi j}} d_{{\psi i}} }},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} r_{{\psi j}} d_{{\psi r}} + i_{{\psi j}} d_{{\psi i}} < 0} \\ \end{array} } \right.,j = x,\psi ,\theta ,$$

$$F_{\theta j} = m_{0} r\omega_{{{\text{m0}}}}^{2} \sqrt {\frac{{r_{\theta j}^{2} + i_{\theta j}^{2} }}{{d_{\theta r}^{2} + d_{\theta i}^{2} }}} ,\;j = x,\psi ,\theta ,\;r_{\theta x} = \sigma J_{M} \omega_{{{\text{m0}}}}^{4} - \sigma k_{\psi } \omega_{{{\text{m0}}}}^{2} ,\;i_{\theta x} = - \sigma f_{\psi } \omega_{{{\text{m0}}}}^{3} ,$$

$$\begin{gathered} r_{\theta \psi } = \tau M\omega_{{{\text{m0}}}}^{4} - \tau k_{x} \omega_{{{\text{m0}}}}^{2} ,\;i_{\theta \psi } = - \tau f_{x} \omega_{{{\text{m0}}}}^{3} , \hfill \\ r_{\theta \theta } = - J_{M} M\omega_{{{\text{m0}}}}^{4} + (Mk_{\psi } + J_{M} k_{x} + f_{\psi } f_{x} )\omega_{{{\text{m0}}}}^{2} - k_{\psi } k_{x} , \hfill \\ \end{gathered}$$

$$i_{\theta \theta } = \left( {Mf_{\psi } + J_{{\text{M}}} f_{x} } \right)\omega_{{{\text{m0}}}}^{3} - (f_{\psi } k_{x} + f_{x} k_{\psi } )\omega_{{{\text{m0}}}} ,\;d_{\theta r} = d_{\theta 1} + d_{\theta 2} + d_{\theta 3} ,$$

$$d_{\theta i} = d_{\theta 4} + d_{\theta 5} + d_{\theta 6} ,\;\;d_{\theta 1} = \left( {MJ_{{\text{M}}} J_{\theta } - \sigma^{2} J_{{\text{M}}} - \tau^{2} M} \right)\omega_{{{\text{m0}}}}^{6} - k_{\psi } k_{\theta } k_{x} ,$$

$$d_{\theta 2} = \left( {\sigma^{2} k_{\psi } + \tau^{2} k_{x} - MJ_{{\text{M}}} k_{\theta } - MJ_{\theta } k_{\psi } - Mf_{\psi } f_{\theta } - J_{{\text{M}}} J_{\theta } k_{x} - J_{{\text{M}}} f_{\theta } f_{x} - J_{\theta } f_{\psi } f_{x} } \right)\omega_{{{\text{m0}}}}^{4} ,$$

$$d_{\theta 3} = \left( {Mk_{\psi } k_{\theta } + J_{M} k_{\theta } k_{x} + J_{\theta } k_{\psi } k_{x} + f_{\psi } f_{\theta } k_{x} + f_{\psi } f_{x} k_{\theta } + f_{\theta } f_{x} k_{\psi } } \right)\omega_{{{\text{m0}}}}^{2} ,$$

$$d_{\theta 4} = \left( {\sigma^{2} f_{\psi } + \tau^{2} f_{x} - MJ_{{\text{M}}} f_{\theta } - MJ_{\theta } f_{\psi } - J_{{\text{M}}} J_{\theta } f_{x} } \right)\omega_{{{\text{m0}}}}^{5} ,$$

$$d_{\theta 5} = \left( {Mf_{\psi } k_{\theta } + Mf_{\theta } k_{\psi } + J_{{\text{M}}} f_{\theta } k_{x} + J_{{\text{M}}} f_{x} k_{\theta } + J_{\theta } f_{\psi } k_{x} + J_{\theta } f_{x} k_{\psi } + f_{\psi } f_{\theta } f_{x} } \right)\omega_{{{\text{m0}}}}^{3} ,$$

$$d_{\theta 6} = - \;\;\left( {f_{\psi } k_{\theta } k_{x} + f_{\theta } k_{\psi } k_{x} + f_{x} k_{\psi } k_{\theta } } \right)\omega_{{{\text{m0}}}}^{{}} ,$$

$$\ \gamma _{{\theta j}} = \left\{ {\begin{array}{*{20}l} {\arctan \frac{{r_{{\theta j}} d_{{\theta i}} - i_{{\theta j}} d_{{\theta r}} }}{{r_{{\theta j}} d_{{\theta r}} + i_{{\theta j}} d_{{\theta i}} }},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} r_{{\theta j}} d_{{\theta r}} + i_{{\theta j}} d_{{\theta i}} > 0} \\ {\pi {\text{ + }}\arctan \frac{{r_{{\theta j}} d_{{\theta i}} - i_{{\theta j}} d_{{\theta r}} }}{{r_{{\theta j}} d_{{\theta r}} + i_{{\theta j}} d_{{\theta i}} }},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} r_{{\theta j}} d_{{\theta r}} + i_{{\theta j}} d_{{\theta i}} < 0} \\ \end{array} } \right.,\;j = x,\psi ,\theta ,$$

$$\sigma = m_{1} l_{1} + m_{2} l_{2} + m_{3} l_{3} ,\;\tau = m_{1} l_{1}^{2} + m_{2} l_{2}^{2} + m_{3} l_{3}^{2} .$$

Appendix C: Details for the derivation process of Eqs. (3)-(6)

The transfer function method [25] is briefly introduced for understanding the detailed derivation process of Eqs. (3)–(6).

First, the Laplace transforms of the motion differential equations with respect to $x$, $\psi$, and $\theta$ are carried out. Therefore, the problem of differential equations is converted to that of algebraic equations. Assuming the Laplace transform of a function $h(t)$ is denoted by $L[h(t)] = h(z)$, then the Laplace transforms of $\dot{h}(t)$ and $\ddot{h}(t)$ are presented as

$$\left\{ \begin{gathered} {\kern 1pt} L[\dot{h}(t)] = - h(0) + zh(z) \hfill \\ L[\ddot{h}(t)] = - \dot{h}(0) - zh(0) + z^{2} h(z) \hfill \\ \end{gathered} \right.,$$

(28)

where $z = \rho \omega_{{{\text{m0}}}}$ and $\rho$ is the imaginary unit; $h(0)$ and $\dot{h}(0)$ are the initial displacement and initial velocity, respectively.

Since the response under the initial conditions corresponding to the free vibration is an attenuated vibration, we only consider the response in the steady state. Hence, Eq. (28) can be simplified as

$$L[\dot{h}(t)] = zh(z),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} L[\ddot{h}(t)] = z^{2} h(z).$$

(29)

Assuming $P_{x} (z)$, $P_{\psi } (z)$, and $P_{\theta } (z)$ are the transfer functions in the right-hand side of the formulae with respect to $x$, $\psi$, and $\theta$, and considering Eqs. (28) and (29), we yield

$$\left\{ \begin{gathered} (Mz^{2} + f_{x} z + k_{x} )X(z) + \sigma z^{2} {\kern 1pt} {\kern 1pt} {{\varvec{\Theta}}}(z) = P_{x} (z) \hfill \\ (J_{{\text{M}}} z^{2} + f_{\psi } z + k_{\psi } ){{\varvec{\Psi}}}(z) + \tau z^{2} {{\varvec{\Theta}}}(z) = P_{\psi } (z) \hfill \\ (J_{\theta } z^{2} + f_{\theta } z + k_{\theta } ){{\varvec{\Theta}}}(z) + \sigma z^{2} X(z) + \tau z^{2} {{\varvec{\Psi}}}(z){\kern 1pt} = P_{\theta } (z) \hfill \\ \end{gathered} \right..$$

(30)

After the excitation on the right side of Eq. (1) is expressed in the complex form, the motion differential equations about $x$, $\psi$, and $\theta$, are rewritten as

$$\left\{ \begin{gathered} M\ddot{x} + f_{x} \dot{x} + k_{x} x + \sigma \ddot{\theta } = R_{{\text{A}}} m_{0} r\omega_{{{\text{m0}}}}^{{2}} \hfill \\ J_{{\text{M}}} \ddot{\psi } + f_{\psi } \dot{\psi } + k_{\psi } \psi + \tau \ddot{\theta } = R_{{\text{B}}} m_{0} r\omega_{{{\text{m0}}}}^{{2}} \hfill \\ J_{\theta } \ddot{\theta } + f_{\theta } \dot{\theta } + k_{\theta } \theta + \sigma \ddot{x} + \tau \ddot{\psi } = R_{{\text{B}}} m_{0} r\omega_{{{\text{m0}}}}^{{2}} \hfill \\ \end{gathered} \right.$$

(31)

with $\sigma = m_{1} l_{1} + m_{2} l_{2} + m_{3} l_{3}$, $\tau = m_{1} l_{1}^{2} + m_{2} l_{2}^{2} + m_{3} l_{3}^{2}$, $R_{{\text{A}}} = e^{{z\varphi_{1} }} + e^{{z\varphi_{2} }}$, $R_{{\text{B}}} = l_{1} e^{{z\varphi_{1} }} + l_{2} e^{{z\varphi_{2} }}$.

Based on Eqs. (30) and (31), the responses of $x$, $\psi$, and $\theta$ in the complex frequency domain are deduced as

$$\left\{ \begin{gathered} X(z) = F_{xx} (z)R_{{\text{A}}} + F_{x\psi } (z)R_{{\text{B}}} + F_{x\theta } (z)R_{{\text{B}}} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = m_{0} r\omega_{{{\text{m0}}}}^{2} \left( {\frac{{1 - \sigma z^{2} \mu_{x} }}{{\varepsilon_{x} }}R_{{\text{A}}} - \frac{{\sigma z^{2} \mu_{\psi } }}{{\varepsilon_{x} }}R_{{\text{B}}} - \frac{{\sigma z^{2} \mu_{\theta } }}{{\varepsilon_{x} }}R_{{\text{B}}} } \right) \hfill \\ {{\varvec{\Psi}}}(z) = F_{\psi x} (z)R_{{\text{A}}} + F_{\psi \psi } (z)P_{\psi } + F_{\psi \theta } (z)P_{\theta } \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = m_{0} r\omega_{{{\text{m0}}}}^{2} \left( { - \frac{{\tau z^{2} \mu_{x} }}{{\varepsilon_{\psi } }}R_{{\text{A}}} + \frac{{1 - \tau z^{2} \mu_{\psi } }}{{\varepsilon_{\psi } }}R_{{\text{B}}} - \frac{{\tau z^{2} \mu_{\theta } }}{{\varepsilon_{\psi } }}R_{{\text{B}}} } \right) \hfill \\ {{\varvec{\Theta}}}(z) = F_{\theta x} (z)R_{{\text{A}}} + F_{\theta \psi } (z)R_{{\text{B}}} + F_{\theta \theta } (z)R_{{\text{B}}} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = m_{0} r\omega_{{{\text{m0}}}}^{2} \left( {\mu_{x} R_{{\text{A}}} + \mu_{\psi } R_{{\text{B}}} + \mu_{\theta } R_{{\text{B}}} } \right) \hfill \\ \end{gathered} \right.$$

(32)

with

$$\mu_{x} { = } - \frac{{\sigma z^{2} \varepsilon_{\psi } }}{{\varepsilon_{d} }},\mu_{\psi } { = } - \frac{{\tau z^{2} \varepsilon_{x} }}{{\varepsilon_{d} }},\mu_{\theta } { = }\frac{{\varepsilon_{x} \varepsilon_{\psi } }}{{\varepsilon_{d} }},\varepsilon_{d} = \varepsilon_{\psi } \varepsilon_{x} \varepsilon_{\theta } - \sigma^{2} z^{4} \varepsilon_{\psi } - \tau^{2} z^{4} \varepsilon_{x} ,$$

$$\varepsilon_{x} = Mz^{2} + f_{x} z + k_{x} ,\varepsilon_{\psi } = J_{M} z^{2} + f_{\psi } z + k_{\psi } ,\varepsilon_{\theta } = J_{\theta } z^{2} + f_{\theta } z + k_{\theta } .$$

From Eq. (32), the responses in the real frequency domain can be further deduced. Taking $F_{xx} (z)R_{{\text{A}}}$ in the expression of $X(z)$ for example, after considering $z = \rho \omega_{{{\text{m0}}}}$ ($\rho$ is the imaginary unit), we obtain

$$\begin{aligned} F_{xx} (z)R_{{\text{A}}} & = F_{xx} (z)(e^{{z\varphi_{1} }} + e^{{z\varphi_{2} }} ) \\ & {\kern 1pt} {\kern 1pt} {\kern 1pt} = m_{0} r\omega_{{{\text{m0}}}}^{2} \frac{{r_{xx} + \rho i_{xx} }}{{d_{xr} + \rho d_{xi} }}e^{{ - z\gamma_{xx} }} \left( {e^{{z\varphi_{1} }} + e^{{z\varphi_{2} }} } \right) \\ & {\kern 1pt} {\kern 1pt} {\kern 1pt} = m_{0} r\omega_{{{\text{m0}}}}^{2} \sqrt {\frac{{r_{xx}^{2} + i_{xx}^{2} }}{{d_{xr}^{2} + d_{xi}^{2} }}} \left( {e^{{z\varphi_{1} - z\gamma_{xx} }} + e^{{z\varphi_{2} - z\gamma_{xx} }} } \right) \\ & {\kern 1pt} {\kern 1pt} {\kern 1pt} = {\kern 1pt} m_{0} r\omega_{{{\text{m0}}}}^{2} \sqrt {\frac{{r_{xx}^{2} + i_{xx}^{2} }}{{d_{xr}^{2} + d_{xi}^{2} }}} \left[ {\sin (\varphi_{1} - \gamma_{xx} ) + \sin (\varphi_{2} - \gamma_{xx} )} \right] \\ & {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {\kern 1pt} F_{xx} [\sin (\varphi_{1} - \gamma_{xx} ) + \sin (\varphi_{2} - \gamma_{xx} )], \\ \end{aligned}$$

(33)

where the detailed expressions and definitions of the symbols in Eq. (33) can be found in Appendix B.

Based on the derivative process presented in Eqs. (28)–(33), the responses in Eqs. (3)–(5) and the relationships in Eq. (6) are deduced.

Appendix D: Details for Eq. (7)

$$\lambda_{{\,x{\text{A}}}} = (c_{x1} + c_{x3} )\cos \alpha + (c_{x4} - c_{x2} )\sin \alpha ,\;\lambda_{{\,x{\text{B}}}} = (c_{x1} - c_{x3} )\sin \alpha + (c_{x2} + c_{x4} )\cos \alpha ,$$

$$\lambda_{{\,\psi {\text{A}}}} = (c_{\psi 1} + c_{\psi 3} )\cos \alpha + (c_{\psi 4} - c_{\psi 2} )\sin \alpha ,\;\lambda_{{\,\psi {\text{B}}}} = (c_{\psi 1} - c_{\psi 3} )\sin \alpha + (c_{\psi 2} + c_{\psi 4} )\cos \alpha ,$$

$$\begin{gathered} c_{\,x1} = F_{xx} \cos \gamma_{xx} + l_{1} F_{x\psi } \cos \gamma_{x\psi } + l_{1} F_{x\theta } \cos \gamma_{x\theta } , \hfill \\ c_{\,x2} = - F_{xx} \sin \gamma_{xx} - l_{1} F_{x\psi } \sin \gamma_{x\psi } - l_{1} F_{x\theta } \sin \gamma_{x\theta } , \hfill \\ \end{gathered}$$

$$\begin{gathered} c_{\,x3} = F_{xx} \cos \gamma_{xx} + l_{2} F_{x\psi } \cos \gamma_{x\psi } + l_{2} F_{x\theta } \cos \gamma_{x\theta } , \hfill \\ c_{\,x4} = - F_{xx} \sin \gamma_{xx} - l_{2} F_{x\psi } \sin \gamma_{x\psi } - l_{2} F_{x\theta } \sin \gamma_{x\theta } , \hfill \\ \end{gathered}$$

$$\lambda_{{\,y{\text{A}}}} = 2F_{y} \cos \gamma_{y} \sin \alpha ,\lambda_{{\,y{\text{B}}}} = 2F_{y} \sin \gamma_{y} \sin \alpha ,F_{y} = - m_{0} r/(M\mu_{y} ),$$

$$\begin{gathered} c_{\psi 1} = F_{\psi x} \cos \gamma_{\psi x} + l_{1} F_{\psi \psi } \cos \gamma_{\psi \psi } + l_{1} F_{\psi \theta } \cos \gamma_{\psi \theta } , \hfill \\ c_{\psi 2} = - F_{\psi x} \sin \gamma_{\psi x} - l_{1} F_{\psi \psi } \sin \gamma_{\psi \psi } - l_{1} F_{\psi \theta } \sin \gamma_{\psi \theta } , \hfill \\ \end{gathered}$$

$$\begin{gathered} c_{\psi 3} = F_{\psi x} \cos \gamma_{\psi x} + l_{2} F_{\psi \psi } \cos \gamma_{\psi \psi } + l_{2} F_{\psi \theta } \cos \gamma_{\psi \theta } , \hfill \\ c_{\psi 4} = - F_{\psi x} \sin \gamma_{\psi x} - l_{2} F_{\psi \psi } \sin \gamma_{\psi \psi } - l_{2} F_{\psi \theta } \sin \gamma_{\psi \theta } , \hfill \\ \end{gathered}$$

$$\begin{gathered} \lambda_{{\,\theta {\text{A}}}} = 2F_{\theta x} \cos \alpha \cos \gamma_{\theta x} + [(l_{1} + l_{2} )\cos \alpha (F_{\theta \psi } \cos \gamma_{\theta \psi } + F_{\theta \theta } \cos \gamma_{\theta \theta } ) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + (l_{1} - l_{2} )\sin \alpha (F_{\theta \psi } \sin \gamma_{\theta \psi } + F_{\theta \theta } \sin \gamma_{\theta \theta } )], \hfill \\ \end{gathered}$$

$$\begin{gathered} \lambda_{{\,\theta {\kern 1pt} {\text{B}}}} = - 2F_{\theta x} \cos \alpha \sin \gamma_{\theta x} + [ - (l_{1} + l_{2} )\cos \alpha (F_{\theta \psi } \sin \gamma_{\theta \psi } + F_{\theta \theta } \sin \gamma_{\theta \theta } ) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + (l_{1} - l_{2} )\sin \alpha (F_{\theta \psi } \cos \gamma_{\theta \psi } + F_{\theta \theta } \cos \gamma_{\theta \theta } )]. \hfill \\ \end{gathered}$$