1 Introduction

With economic development, the output of automobiles has increased, which has resulted in the accumulation of waste tires. The China Rubber Industry Association pointed out that in 2019, waste rubber exceeded 20 million tons in China, of which, 14.8 million tons were produced from waste tires [1]. Hence, there is an urgent need to promote its recycling and application. Rubber has characteristics of great elasticity and toughness, making it a flexible material. Currently, mixing crumb rubber with fresh concrete as a part of the aggregate, namely, rubberised concrete (RC), is recognised as a feasible way of using it. By adding rubber, the damping performance [2], fatigue resistance [3], durability [4], and fire resistance [5] of concrete can be improved.

However, several concrete structures may get affected by explosion and impact loading during their service life. Owing to the propagation and reflection of stress waves, the stress state of concrete is significantly complex under high-speed loading. Therefore, it is important to understand the dynamic characteristics of concrete materials under this complex stress state [6]. Thus far, numerous studies related to concrete materials have found that ordinary concrete with no rubber particles (NC) has an evident strain-rate effect, i.e., the strength of concrete increases with the strain rate [7]. In addition, there is a significant and non-negligible strain-rate effect on the strength of concrete in the range of high strain rates. Song [8] indicated that the internal microcracks of concrete cannot be fully expanded under high-speed loading, which leads to the failure of coarse aggregates. When the strain rate is high, the aggregate is destroyed more coarsely and the strength of the concrete increases. Besides, a hysteresis effect of deformation induced strength development of concrete materials with the strain rate, according to Zhang et al. [9]. As a result, the shift from stress to strain has a time interval, implying that deformation is time-dependent [10]. Liu et al. [11] reported that the strain-rate effect on the compressive strength of RC is more sensitive than that of NC, as determined by the split Hopkinson pressure bar (SHPB). Further findings tested by the SHPB can be obtained in the study by Feng et al. [12]. The experimental results [12] showed that the fragment size of post-tested specimens of RC is larger than that of NC at a close strain rate, which confirms that crumb rubber can inhibit the crack development and boost the energy-dissipation capacity of concrete under impact loading. Meanwhile, the fracture toughness of RC is also larger than that of NC under impact loads [13]. This is one of the reasons why RC has a more sensitive strain-rate effect than NC.

However, the experimental results measured by the SHPB on concrete materials include various structural factors, such as interface friction, specimen size, and lateral inertia. Li et al. [14] indicated that the inertia effect mainly controls the dynamic strength of concrete under the strain rate; consequently, the strain-rate effect of concrete materials has been overestimated in many experimental studies tested by the SHPB. Therefore, the experimental strain-rate effects cannot be considered as the real strain-rate effect of the concrete material. If this strain-rate effect is used in numerical models to analyse the dynamic response of concrete structures, the inertia effect is overestimated. This is because the inertia effect includes both the structural effect of the SHPB test and the impact test on concrete structures that needs to be studied [15]. Some scholars [16, 17] have pointed out that the inertia effect of concrete materials is more obvious than that of metallic materials. It has been explained that the compressive strength of concrete material is sensitive to hydrostatic pressure, and lateral confinement during the SHPB test can effectively enhance its axial compressive strength. Recent studies [18] on the dynamic response of RC structures did not eliminate the influence of the inertia effect. Nevertheless, it is complicated to measure the structural effects of concrete materials during the impact test directly. To further investigate the dynamic mechanics and the actual strain-rate effect of RC, the experimental results obtained by the SHPB should be modified using finite element analysis (FEA).

A proper material model is crucial for rendering precise results in SHPB simulations. The Karagozian and Case (K&C) concrete model was established in LS-DYNA to analyse the mechanical response of concrete structures under impact loading [19]. Compared with other material models for concrete, such as the Holmquist–Johnson–Cook (HJC) model [20], Taylor–Chen–Kuszmaul (TCK) model [21], and elastic–plastic–hydrodynamic (EPH) model [22, 23], the K&C model is a more comprehensive model because it is suitable for more stress status. For example, HJC model cannot accurately describe the tensile damage because the third invariant of the deviating stress tensor is not taken into account [24], TCK model cannot reliably forecast compressive damage [25], and EPH model cannot render the strain-rate effect of material [26]. Comparing the above models, K&C model can reflect the damage caused by compressive and tensile stress, and it is suitable for relatively soft materials, such as asphalt concrete [27]. It considers the strain-rate effect, implying that researchers are required to determine a proper dynamic-increase-factor (DIF) curve of the target materials. Moreover, the K&C model has been proven to reflect the damage process of RC in a previous study [28].

In this study, FEA was performed using the LS-DYNA software to study the inertia effect in the SHPB test of RC and compare it with that of ordinary concrete. The remainder of this paper is organised as follows. Section 2 presents the quasi-static and dynamic experimental arrangements of RC with various rubber contents (10%, 20%, and 30%) and discusses the experimental strain-rate effects of RC. Section 3 describes the modifications of the K&C model based on experimental data. Section 4 presents the modelling of the SHPB test. Section 5 presents the real strain-rate effects of RC and the analysis of its mechanism. Section 6 presents the main conclusions of this study. The purpose of this investigation is to explore the real strain-rate effects of RC and explain the differences in the dynamic mechanical properties between RC and NC.

2 Quasi-static and dynamic experiments

2.1 Raw materials and specimen preparations

RC and NC specimens were constructed using cement, coarse aggregate, fine aggregate, and crumb rubber. The selected cement was P.O. 42.5R; the fine aggregate was medium sand with a fineness modulus, apparent density, and bulk density of 2.25, 2722 kg/m3, and 1221 kg/m3, respectively; the coarse aggregate was granite gravel with a maximum particle size, apparent density, and bulk density of 10 mm, 2589 kg/m3, and 1452 kg/m3, respectively; the crumb rubber were made from waste tires with a fineness modulus, apparent density and bulk density were 2.21, 1020 and 539 kg/m3, respectively. Based on the demands in the Chinese code GB/T 14,864 [29], the sand and rubber crumb were classified into Grade III. The grading curves of sand and rubber crumb are illustrated in Fig. 1. The rubber particles were added to the fresh concrete, replacing the same volume of sand. The mix proportions of the aforementioned raw materials are listed in Table 1. The apparent densities of NC and RC were determined based on the Chinese standard JTG 3420 [30]. After 28 days of curing under standard conditions, RC and NC were prepared. Ordinary concrete without rubber and RC with volume replacement ratio of 10%, 20%, and 30% of rubber particles are denoted NC, RC10, RC20, and RC30, respectively.

Fig. 1
figure 1

Grading curves of sand and rubber crumb

Full size image
Table 1 Mix proportions of raw materials and the densities of NC and RC
Full size table

2.2 Testing methods

2.2.1 Quasi-static compression test

According to Chinese standard GB/T 50081 [31], a quasi-static uniaxial compression test was used to measure the quasi-static compression strength and the relationship between stress and strain. The standard requires the specimen to be cast in a cylinder and the standard height and diameter should be 300 mm and 150 mm, respectively. Hence, the cylinders with the dimensions of Ф 300 × 150 mm were prepared. A universal testing machine (Matest C088-01, Italy) with a maximum load of 4000 kN was employed. An upfront operation was performed to ensure that the upper and lower surfaces of each cylinder were flat, and each surface was blanketed with high-strength gypsum layers to satisfy the demand in GB/T 50081 [31].

Four strain gauges were attached to the circumference of the specimen, which was made by Zhejiang Huangyan Testing Instrument, China, with an electric resistance and sensitivity coefficient of 120 \(\pm\) 0.1 \(\Omega\) and 2.08 \(\pm\) 1%, respectively. The vertical and horizontal lengths of the strain gauges were 100 and 80 mm, respectively; two horizontal strain gauges were used to measure the strain history during the elastic stage, and the other two (vertical) strain gauges were used to offset the unparallel condition of the specimen surface and the loading plate of the machine before the specimen was uniformly compressed. The strain gauges measured the strain information until the specimens reached their plastic stress stage. To avoid the influence of hoop effect near the end of the specimen during the compression test as much as possible, two 120 mm-length linear variable differential transformers (LVDTs) were used to measure the middle height of vertical deformation. Besides, to reduce the testing errors caused by the end friction, lubricating oil was used to reduce the friction coefficient between two ends of the sample and the loading platform. The data obtained from the four strain gauges and two LVDTs were recorded using a multichannel data acquisition system (TDS530, Tokyo Sokki Kenkyujo Co., Ltd., Japan).

The photo and diagram of the uniaxial compression test are shown in Fig. 2. In the experiment, displacement control, which limits the loading rate at 0.18 mm/min (around a strain rate of 1 × 105 s−1), was adopted as the loading mode. Three cylinders were tested to reduce the discreteness of each mix proportion. In accordance with GB/T 50,081 [31], the elastic modulus and Poisson’s ratio can be obtained using Eq. (1) as follows:

$$E = \frac{{\sigma_{2} - \sigma_{1} }}{{\varepsilon_{2} - 0.00005}};\,\nu = \frac{{\varepsilon_{c2} - \varepsilon_{c1} }}{{\varepsilon_{2} - 0.00005}}$$
(1)

where σ1 is the stress value related to the vertical strain of 5 × 10−5, ε2 is the strain corresponding to σ1, and εc1 and εc2 denote the circumferential strains corresponding to the longitudinal strain of 5 × 10−5 and ε1, respectively. Meanwhile, σ1 = 40%σcm, where σcm is the peak stress during the test.

Fig. 2
figure 2

Photo and diagram of uniaxial compression test

Full size image

2.2.2 Dynamic compression test

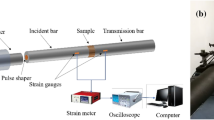
The SHPB system in this investigation consisted of four main parts, namely a striker, incident bar, transmitter bar, and cushion bar, with a length of 1000, 5500, and 3500 mm, respectively, as shown in Fig. 3. Four strain gauges were used in this system, which were produced by Zhonghang Electronic Measuring Instrument Co., Ltd., China. Each strain gauge had an electricity resistance and sensitivity coefficient of 120.2 ± 0.1 Ω and 2.22 ± 1%, respectively. Compressive impulses captured by the strain gauges were collected using a dynamic multichannel strain acquisition device with a sampling rate of 1 MHz. Before making a formal impact on a specimen, the two interfaces between the specimen and incidental bar as well as the specimen and transmitter bar should coincide to rule out the influence of eccentric compression during the tests. Therefore, the ends of the incident and transmitter bars should be polished and parallelized horizontally and vertically. The parallelism error of the two end surfaces of all specimens was controlled within 0.02 mm by using a high-precision grinder (MY250, China). Moreover, the surface friction can result in the lateral restriction of specimens, which causes an undesirable enhancement in the compressive strength; to eliminate this irrelevant factor, molybdenum disulphide grease, which can effectively adhere to the specimen and bar ends, was used to significantly reduce the influence of friction [32].

Fig. 3
figure 3

SHPB setup of compression dynamic tests: a photo, b diagram

Full size image

In addition, in the impact process, red copper pulse shapers were used to eliminate the high frequency of stress waves and extend the rising phase of incident waves; the thickness and radius of the shaper were 2 and 5 mm, respectively. In this process, two basic assumptions (i.e., one-dimensional stress wave propagation and stress equilibrium of the specimen) should be acknowledged [6]. Meanwhile, these assumptions are reasonable only when the dimensions of specimens meet a specific diameter-to-length ratio. In this regard, 2:1 is the widely accepted ratio in the SHPB compression tests; therefore, the diameter and length of the specimen, in this case, are 100 and 50 mm, respectively. Based on these two assumptions, we can calculate the strain rate \(\dot{\varepsilon }(t)\), strain ε(t), and stress σ(t) histories using Eqs. (2)–(4) [6].

$$\dot{\varepsilon }(t) = \frac{{2C_{0} }}{L}\varepsilon_{r} (t)$$
(2)
$$\varepsilon (t) = - \frac{{2C_{0} }}{L}\int_{0}^{t} {\varepsilon_{r} (t)} dt$$
(3)
$$\sigma (t) = \frac{A}{{A_{s} }}E\varepsilon_{t} (t)$$
(4)

where C0 denotes the wave velocity of the bar; L is the length of the specimen; A and As are the cross-sections of the bar and specimen, respectively; E denotes the Young’s modulus of the bar; εt and εr are the transmitted and reflected strain signals, respectively. These were recorded by the strain sensors attached to the incident and transmitter bars. After obtaining the original data, as shown in Fig. 4a, it is necessary to verify the experimental reliability. Because the justification of Eqs. (2)–(4) lies on one-dimensional stress wave propagation, the phase difference of the incident signal, transmitter signal, and reflected signal must be offset to ensure that the sum of the incident and reflected waves is equal to the transmitted wave. Figure 4b shows the result of this procedure taking NC-1 as an example. To validate the stress uniformity of the specimen during the test, a parameter η is adopted, which is shown as Eq. (5) [7]. Hence, Fig. 4c illustrates the variation of η with time. The initially large value of η decreases rapidly with time. When the transmitted strain reaches about 40% of its peak value, the value of η maintains less than 0.05. The final value of η exceeds 0.05 again resulting from the fracture of the specimen, which leads to highly uneven deformation and stress.

$$\eta = \left| {\frac{{\varepsilon_{i} + \varepsilon_{r} - \varepsilon_{t} }}{{\left( {\varepsilon_{i} + \varepsilon_{r} + \varepsilon_{t} } \right)/2}}} \right|$$
(5)
Fig. 4
figure 4

Experimental strain waves: a original incidence, reflected and transmitted waves, b–c verification of stress uniformity

Full size image

To reduce the discreteness, three specimens of each mix proportion were taken as a group and tested at a similar strain rate (same gas pressure applied on the striker from the gas vessel in Fig. 3). After the experimental data of some groups (more than five strain rates) were obtained, the relationship between the dynamic compressive strength and strain rate was comprehensively observed.

2.3 Experimental results

2.3.1 Quasi-static compression tests

The elastic modulus E, Poisson’s ratio υ, and uniaxial compressive strength fco can be obtained from the experimental data. The experimental results for NC and RC are summarised in Table 2, and the stress–strain curves of NC and RC are shown in Fig. 5. Both the NC and RC have elastic and plastic stages when the stress increases; after the elastic stages, the curves of NC and RC increase nonlinearly. Compared with NC, the peak stress values of RC specimens are smaller, and they decrease as the rubber mix ratio increases; however, in the softening phase, the curves of RC decrease smoothly.

Table 2 Quasi-static mechanical properties of NC and RC
Full size table
Fig. 5
figure 5

Stress–strain curves of NC and RC

Full size image

2.3.2 Dynamic compression tests

Li et al. [33] noted that the strain rate corresponding to the peak stress represents the total axial strain rate because there is no elastic strain increment after reaching the peak stress, and the remaining plastic strain rate is the total strain rate. Based on this method, we averaged the strain rates in a certain period around the peak stress as the representative strain rate. The effective points of the four different materials are summarised in Table 3, where each group includes three repeated tests at a similar strain rate; the thickness was averaged by three directions and DIF represents the ratio of the dynamic compressive strength and quasi-static compressive strength at a specific strain rate.

Table 3 Experimental results of SHPB tests
Full size table

2.4 Experimental strain-rate discussion

Several researchers [1, 12, 34, 35] have proved that concrete materials, especially RC, are sensitive to the strain rate, implying that the uniaxial strength of concrete materials increases sharply at high strain rates. DIF plays a significant role in the mechanical study of concrete materials, especially in high-strain-rate situations. For comparison, we have summarised the results of the SHPB investigation in NC [15, 36,37,38,39,40,41], and RC (rubberised ordinary concrete [11], rubberised recycled aggregate concrete [42], and rubberised self-compacted concrete [43]) in Fig. 6a and b, respectively.

Fig. 6
figure 6

Experimental DIF comparisons of (a) NC and b RC with existing studies

Full size image

As shown in Fig. 6a, it can be observed that the experimental data of NC has satisfied with the data from the similar specimen size. Due to the structural effects during the SHPB test, slightly different experimental DIF produced by the various specimen size. Gao [44] pointed out that the influence of the quasi-static strength on DIF at similar strain rate can be neglected. Besides, to meet the assumption of one-dimensional bar, the smaller the size of the specimen is, the smaller the test error is. Hence, it can be found that there are experimental data of specimens with a diameter of less than 50 mm. However, there are coarse aggregates in concrete, and if the size of specimen is very small, which seriously reduces the uniformity of the specimen. As depicted in Fig. 6b, the results of RC in this study are also consistent with other results. Obviously, the strain-rate effect of RC was significantly larger than that of NC. Therefore, it is not appropriate to use the classical model (such as the CEB model [45]) in a simulation study directly for RC.

The experimental data points and their fitting curves of NC and RC are shown in Fig. 7, which demonstrate that the experimental DIF (DIFe) of RC increases when the rubber content increases at a similar strain rate. Then, we used the least squares method and linear fitting to determine the relationship between the DIFe and strain rates; the fitting results (Eq. (6)) were significantly consistent with the experimental data, which are also shown in Fig. 7. Thus, it is evident that the slopes of the fitting curves positively correspond to the rubber content, and this conclusion confirms that a higher rubber content results in a higher strain-rate sensitivity in concrete materials.

$${\text{DIF}}_{{\text{e}}} = \left\{ {\begin{array}{*{20}c} {1.98 \cdot \lg (\dot{\varepsilon })^{2} - 6.28 \cdot \lg (\dot{\varepsilon }) + 6.00{ (}\dot{\varepsilon } \ge 30s^{ - 1} {)}} & {\text{(NC)}} \\ {1.99 \cdot \lg (\dot{\varepsilon })^{2} - 5.59 \cdot \lg (\dot{\varepsilon }){ + 5}{\text{.20 (}}\dot{\varepsilon } \ge 30s^{ - 1} {)}} & {\text{(RC10)}} \\ {2.32 \cdot \lg (\dot{\varepsilon })^{2} - 6.55 \cdot \lg (\dot{\varepsilon }) + 5.86{ (}\dot{\varepsilon } \ge 30s^{ - 1} {)}} & {\text{(RC20)}} \\ {2.63 \cdot \lg (\dot{\varepsilon })^{2} - 8.09 \cdot \lg (\dot{\varepsilon }) + 7.87{ (}\dot{\varepsilon } \ge 30s^{ - 1} {)}} & {\text{(RC30)}} \\ \end{array} } \right.$$
(6)
Fig. 7
figure 7

Experimental DIF and fitting curves of NC and RC

Full size image

3 Constitutive models of RC

The K&C model was used as the constitutive model for the NC and RC. Because the K&C model was originally supposed to describe NC [27, 46, 47], for RC, it should be modified before being applied to RC materials. In this numerical simulation, we selected the unit group of centimetres (cm) in length, grams (g) in mass, microseconds (μs) in time, and megabar (1 Mbar = 105 MPa) in stress. In addition, the parameters not mentioned in this section are the default values.

3.1 Modified K&C model for RC

The entire modification for RC can be reduced to four main perspectives, namely, the strength surface, damage factor, equation of state, and strain-rate effect.

3.1.1 Strength surface

The K&C model was designed for concrete materials under high-strain-rate loading. Owing to lateral confinement, the interior of the material demonstrates a triaxial stress status; thus, it is essential to determine a triaxial strength model of RC, which is described in the K&C model through Eqs. (7)–(9).

$$\Delta \sigma_{y} \, = \, a_{0y} + \frac{p}{{a_{1y} + a_{2y} p}}$$
(7)
$$\Delta \sigma_{m} \, = \, a_{0m} + \frac{p}{{a_{1m} + a_{2m} p}}$$
(8)
$$\Delta \sigma_{r} \, = \, \frac{p}{{a_{1f} + a_{2f} p}}$$
(9)

where \(\Delta {\sigma }_{m}\), \(\Delta {\sigma }_{y}\), and \(\Delta {\sigma }_{r}\) are the maximum, yield, and residual deviatoric stresses of the surfaces, respectively, a0m and a0y represent the maximum cohesion and yield cohesion, respectively, and aiy and aif (i = 1, 2) are the hardening parameters used on the yield limit and failure, respectively. In addition, Gholampour et al. [48] determined empirical formulae to define the relationship between peak stress vs. lateral stress and residual stress vs. lateral stress. The empirical formulae are given by Eqs. (10) and (11), as follows:

$$f_{{cc}}^{{}} {\mkern 1mu} = {\mkern 1mu} f_{{co}}^{{}} + 5.2f_{{co}}^{{0.91}} \left( {\frac{{f_{l}^{{}} }}{{f_{{co}}^{{}} }}} \right)^{a} {\text{, where }}a{\mkern 1mu} = {\mkern 1mu} f_{{co}}^{{ - 0.06}}$$
(10)
$$f_{{c,res}} {\mkern 1mu} = {\mkern 1mu} 1.6f_{{cc}}^{{}} \left( {\frac{{f_{l}^{{0.24}} }}{{f_{{co}}^{{0.32}} }}} \right){\text{, and }}f_{{c,res}} {\mkern 1mu} \le f_{{cc}}^{{}} - 0.15f_{{co}}^{{}} ,$$
(11)

where fco represents the uniaxial compression strength, which can be obtained from Table 2; and fl, fcc, and fc,res represent the lateral stress, peak compression stress, and residual stress of the specimens under confinement, respectively. By employing Eqs. (10) and (11), we can obtain a series of damage strength and residual stress corresponding to different lateral stress; the yield strength surface of concrete material can be estimated by the locus of points at ∆σ = 0.45∆σm on the triaxial compression paths [19]. Therefore, aim, aiy (i = 0, 1, 2), and aif (i = 1, 2) can be obtained via nonlinear fitting, and the results are summarised in .

Table 4. The triaxial strength surfaces of the NC and RC samples are shown in Fig. 8.

Table 4 Triaxial strength surface parameters of RC and NC
Full size table
Fig. 8
figure 8

Triaxial strength surface: a NC, b RC10, c RC20, and d RC30

Full size image

3.1.2 Damage factor

The K&C model used λ and η to determine the damage incurred during the loading process. The plastic damage begins after reaching the yield stress surface, and as shown by Eqs. (12) and (13), η defines the current strength surface and λ defines the accumulated plastic damage. The value of η generally starts at 0, increases to 1 when λ equals λm, and decreases to 0 when the current surface reaches the residual surface; λm denotes the plastic strain at the maximum strength surface.

$$\Delta \sigma { = }\eta \left( {\Delta \sigma_{m} - \Delta \sigma_{y} } \right) + \Delta \sigma_{y}$$
(12)
$$\lambda = {\mkern 1mu} \left\{ {\begin{array}{*{20}c} {\int_{0}^{{\bar{\varepsilon }^{p} }} {\frac{{d\bar{\varepsilon }^{p} }}{{r_{f} \left[ {1 + p/(r_{f} f_{t} )} \right]^{{b_{1} }} }}} {\text{, for }}p{\mkern 1mu} \ge 0} \\ {\int_{0}^{{\bar{\varepsilon }^{p} }} {\frac{{d\bar{\varepsilon }^{p} }}{{r_{f} \left[ {1 + p/(r_{f} f_{t} )} \right]^{{b_{2} }} }}} {\text{ for }}p{\mkern 1mu} < 0} \\ \end{array} } \right.,$$
(13)

where \({r}_{f}\) is the DIF. To determine η and λ, Kong et al. [49] developed a formula to bridge these two damage factors. The relationship between η and λ can be obtained using Eq. (14) [49]:

$$\eta (\lambda ) \, = \, \left\{ {\begin{array}{*{20}l} {\alpha \lambda /\lambda_{m} + (3 - 2\alpha )(\lambda /\lambda_{m} )^{2} + (\alpha - 2)(\lambda /\lambda_{m} )^{3} } \hfill & {\lambda \, \le \, \lambda_{m} } \hfill \\ {\frac{{\lambda /\lambda_{m} }}{{\alpha_{c} (\lambda /\lambda_{m} - 1)^{{\alpha_{d} }} + \lambda /\lambda_{m} }}} \hfill & {\lambda { > }\lambda_{m} } \hfill \\ \end{array} } \right.,$$
(14)

where α, αc, and αd are undetermined constants. Based on the experimental results of uniaxial compression curves for NC, RC10, RC20, and RC30, RC has an extensive softening phase compared to NC; moreover, αc, αd, and λm should be modified according to the compression characteristics presented in Sect. 2. Because the advantages of RC are mainly reflected in the descending phase and α = 3, as proved by Kong et al. [49], only the softening phase is determined again, and the relevant parameters are listed in .

Table 5. After that, the compressive softening parameter b1 also plays a crucial role in the stress–strain curve, which is related to the compression energy Gc (area under the stress–strain curve) [27]. The value of b1 equals to (Gc/h), where h represents the mesh size in the numerical model. After calculating based on the experimental results mentioned in Sect. 2 and validating from the single-element test process (detailed in Subsection 3.2), the compressive softening parameters of NC, RC10, RC20, and RC30 were determined. Besides, the tensile softening parameter b2 is correlated with the fracture toughness and the aggregate size. Based on the results of Ref. [28], b2 was set to 3.0 for NC and RC due to the lack of test data in this investigation. The values of b1 and b2 are demonstrated in Table 6.

Table 5 Fitting results of damage model parameters
Full size table
Table 6 Values of b1 and b2 for NC, RC10, RC20, and RC30
Full size table

3.1.3 Equation of state

The K&C model requires an equation of state (EOS) to describe the relationship between the hydrostatic pressure and the specific volume. In general, *EOS_TABULATED_COMPACTION (EOS#8 in LS-DYNA) was utilized together with the K&C model. The EOS parameters of NC can be obtained using the volumetric scaling method [19]. Thus, the new EOS parameters of NC and RC can be estimated using the existing experimental data at the same volume strain. The new pressure Pnew and new unloading bulk modulus Knew are defined by Eqs. (15) and (16) [19], respectively, as follows:

$$P_{{{\text{new}}}} \, = \, P_{{{\text{old}}}} \sqrt r$$
(15)
$$K_{{{\text{new}}}} \, = \, K_{{{\text{old}}}} \sqrt r$$
(16)

Owing to better toughness, RC should possess greater volumetric strains under the same pressure. This method used on RC is a compromise because there are no existing data for accurate EOS parameters of RC. The auto-generated EOS parameters in the original K&C model for NC and RC are presented in Table 7. In addition, the bulk modulus K at the first inflection point of the pressure–volume strain curve in the EOS was corrected to satisfy the experimental elastic modulus in Table 2, based on the method in Ref. [46].

Table 7 EOS parameters of RC and NC
Full size table

3.2 Single-element test for parameter verification

To validate the K&C model, the single-element test (SET) was used, as shown in Fig. 9, which is a common method for identifying the precision of material parameters, especially for the elastic modulus and damage factors [28]. The SET model is only one element with the dimension of 1 × 1 × 1 cm. The displacement load of 1 × 10−5 cm/s was applied on the surface nodes, and the loading rate was consistent with the quasi-static test. Figure 10 shows that the simulated stress–strain curves of NC and RC are in good agreement with the experimental curves, implying that the modified parameters in the K&C model are reasonable.

Fig. 9
figure 9

Schematic of single-element model simulation

Full size image
Fig. 10
figure 10

Verification of quasi-static stress–strain curves by SET: a NC, b RC10, c RC20, and d RC30

Full size image

4 Development of numerical model and correction methodology

4.1 Modelling

This numerical study is based on the experimental data presented in Sect. 2. Accordingly, the length of the incident and transmitter bars is 550 and 350 cm, respectively. The diameter, Young’s modulus, and density of both the incident and transmitter bars are 10 cm, 0.206 Mbar, and 7.710 g/cm3, respectively, which were given as input to the first material card in LS-DYNA (*MAT_ELASTIC). In addition, using the keyword *LOAD_SEGMENT_SET in LS_DYNA, the loading curves from the experiment were directly applied to the left end of the incident bar. Furthermore, two interfaces must be determined for the boundary condition, i.e., the interface between the incident bar and specimen and that between the specimen and transmitter bar. The keyword *CONTACT_AUTOMATIC_NODES_TO_SURFACE was used to define the contact conditions. In the SHPB test, two contact surfaces of the specimen and bars were lubricated, which can effectively alleviate the radial strain restriction caused by surface friction; hence, it can be neglected based on the experimental process. The numerical model is illustrated in Fig. 11. The K&C model (#MAT72 REL3) was used to define the concrete material; the parameters of material properties, such as density and elastic modulus, are based on Table 1 and Table 2 respectively.

Fig. 11
figure 11

Schematic setup of SHPB simulation

Full size image

4.2 Mesh size convergence

In addition, elements meshed in different sizes resulted in considerable differences in the simulation results. To eliminate this irrelevant factor, we conducted an element-sensitive simulation to determine the most suitable element size in this study. Based on the method of Alañón et al. [50], as shown in Fig. 12, we meshed the specimen in 1.0, 0.5, 0.2, and 0.1 cm; we observed that when smaller sizes were meshed, less energy was lost from the system. Therefore, considering the efficiency and reliability, all specimens were meshed in an element size of 0.2 cm.

Fig. 12
figure 12

Results of mesh size convergence

Full size image

4.3 Correction methodology for real DIF

The inertial effect can be eliminated in two ways to obtain the real DIF without structural effects. Here, indirect and iterative means were employed to address this issue [33]. Initially, all concrete materials were considered strain-rate insensitive, i.e., the initial DIFi was set to 1. Compared with the quasi-static compressive strength, enhancements were observed in the simulation results, which can be attributed to the inertial effect. Thus, we can ensure enhancement due to factors other than material properties. Moreover, the numerical results were naturally smaller than the experimental results; then, the DIFi of the next iteration can be calculated using Eq. (17), as follows:

$$DIF_{i} = DIF_{i - 1} \times \frac{{f_{{{\text{experimental}}}} }}{{f_{{{\text{numerical}}_{i - 1} }} }},$$
(17)

where DIFi represents the current input DIF, DIFi−1 represents the DIF of the last iteration, and fexperiment and fnumerical(i−1) represent the experimental strength and numerical strength of the last iteration, respectively. Now, a curve should be given as input to define the relationship between the DIF and strain rates; therefore, before inputting the curve, we used the data from limited experimental and numerical SHPB tests to fit a DIF-strain rate curve for each iteration. This iteration ends when the relative difference between the experimental and numerical strength is smaller than δ, which is set to 10% in this case. The entire iterative procedure is shown in Fig. 13, where the last iteration DIF is the real DIF (DIFg).

Fig. 13
figure 13

Flowchart of iteration for generating the real DIF

Full size image

5 Numerical results and further discussions

To reduce the computing cost, only the first specimen of each group, as a representative of the neighbourhood of each specific strain rate, in Table 3 was simulated.

5.1 Real DIF of RC

5.1.1 Correction process of real DIF

The real DIF is a function that only corresponds to the strain rate. First, we settled the strain rates and calculated the strain rate of each effective point by averaging the strain rates when they were about to reach the peak strength. Next, we verified whether the stress of both interfaces between the bars and specimen was in equilibrium because it is a fundamental premise to acquire an eligible result. Figure 14 (taking NC-1 as an example) shows a fair stress consistency: 10% difference in the end surfaces. When the stress state of the end reaches around 40% of the peak stress, the stress equilibrium can be regarded as achieved. It is well-known that concrete-like material collapses due to tensile strain; therefore, for four different concrete materials (i.e., NC, RC10, RC20, and RC30), the maximum principal tensile strains at failure were set to 20 times λm. Subsequently, based on the experimental data listed in Sect. 2, we used the aforementioned correction method to obtain the relationship between the strain and DIFg curves of the four concrete materials. The data points of the experiments and every iteration of the concrete materials are shown in Fig. 15, and the results are summarised in Table 8, where the numerical specimen ID is the same as the experimental specimen ID. All relative errors between the simulation and experimental strength were less than 10%, which indicates that the reliability of the numerical model was high.

Fig. 14
figure 14

Stress history of two ends of the specimen

Full size image
Fig. 15
figure 15

Iteration process for DIF correction: a NC, b RC10, c RC20, and d RC30

Full size image
Table 8 Correction results of NC and RC
Full size table

5.1.2 Correction results of the real DIF

For NC, two iterations are required to obtain a fair agreement with the experimental data; for RC10, five iterations are required to yield a reasonable result, whereas RC20 and RC30 require three and four iterations, respectively, to achieve an acceptable agreement with the experimental data. During the iteration procedure, if the data are highly scattered, more iterations are required. Four functions that describe the relations between the real DIF (DIFg) of the NC and RC and the strain rates are given in Eq. (18). As shown in Fig. 16, the input DIF was obtained from the fitted results of DIFg. If some parts in the fitted results of real DIFg were lower than 1.0, the input DIF was set to 1.0.

$$DIF_{i} = \left\{ {\begin{array}{*{20}c} {0.33 \cdot \lg (\dot{\varepsilon })^{2} - 0.75 \cdot \lg (\dot{\varepsilon }) + 1.22} & {\text{(NC)}} \\ {0.35 \cdot \lg (\dot{\varepsilon })^{2} - 0.63 \cdot \lg (\dot{\varepsilon }){ + 0}{\text{.97}}} & {\text{(RC10)}} \\ {0.36 \cdot \lg (\dot{\varepsilon })^{2} - 0.53 \cdot \lg (\dot{\varepsilon }) + 1.17} & {\text{(RC20)}} \\ {0.39 \cdot \lg (\dot{\varepsilon })^{2} - 0.64 \cdot \lg (\dot{\varepsilon }) + 1.{09 }} & {\text{(RC30)}} \\ \end{array} } \right.$$
(18)
Fig. 16
figure 16

Real and input DIFs of the NC and RC

Full size image

In Fig. 16, several regulations should be noted. First, the real DIF curve of NC has the smallest gradient and that of RC increases as the rubber mixture increases. Second, the transition strain rate (a starting point of steep growth for DIF) increases as the rubber content decreases (approximately 50 s−1 for RC20 and RC30 and 100 s−1 for RC10 and NC). Third, when the strain rate continues to increase, the difference in the real DIF between RC10, RC20, and RC30 becomes identical. These phenomena can be elucidated by the following two explanations: (1) based on Eq. (19) [51], where υ represents the Poisson’s ratio; \(\dot{{\varepsilon }_{z}}\) and \(\ddot{{\varepsilon }_{z}}\) represent the rate and acceleration of axial strain, respectively; and \(\tilde{\sigma }\) represents the average radial stress, the density of material (ρ0) is positively related to the average radial stress. In other words, a higher density with the same volume results in a higher inertial effect in the SHPB test. It is evident from the experiment in Sect. 2 that a higher rubber content renders a greater experimental (or apparent) DIF, and the experimental DIF includes a part of the real DIF and another part that can be attributed to the inertial effect. Therefore, the real DIF also positively corresponds to the rubber content owing to the low densities of RC. (2) From a microscopic perspective, in comparison to the quasi-static experiment, where the interior weaknesses, such as gaps between the aggregates and micro holes, play a significant role in material failure, the influence of interior inconsistency of the specimens can be undermined in SHPB tests because the gaps and micro holes are eliminated before the material reaches the stress equilibrium status at high strain rates [15]. Because rubber particles enhance the crack resistance of concrete under impact loads [12], the deformation capacity of RC is higher than that of NC. Hence, the rate and acceleration of axial strain for RC can reach a higher limit; consequently, rubber particles can enhance the apparent strain-rate effect and the real strain-rate effect of concrete.

$$\overline{\sigma } = \frac{{v\rho_{0} R_{0}^{2} }}{{4L_{0} (1 - \varepsilon_{z} )^{2} }}\left[ {\frac{v + 1}{{L_{0} (1 - \varepsilon_{z} )}}\dot{\varepsilon }_{z} + \ddot{\varepsilon }_{z} } \right]$$
(19)

5.2 Waveform data validation

The simulation strain curves were compared with the strain waves obtained from the experiments to validate the accuracy of the parameters in the constitutive model; and the validation results can help us in making further modifications.

In Fig. 17, we present the strain impulses of NC-5 and RC20-5 as examples from both the experiment and simulation. The transmitted curves indicate the stress–strain curves of the specimens; the peaks of the curve reflect the strength in the dynamic tests, and the relative difference between the two peak values of the transmitted wave was found to be 5.4% and 0.8% for NC and RC20, respectively, which is acceptable. However, the unloading phase of the transmitted curves of the simulated result differed from that of the experimental result. Specifically, a cliff was observed after reaching the peak value in the simulation data, whereas the unloading phase in the simulation curve was found to be relatively smooth. This can be attributed to the erosions on the specimen, owing to which, elements get deleted when the strain overpasses the limited value, i.e., 20 times λm. Figure 18, which presents the contour plot when the specimen is compressed, demonstrates that the greatest strain occurs in the middle of the specimen from the longitudinal side. Therefore, this area collapses first; consequently, the stress wave propagation is cut-off in the numerical model. Meanwhile, the loading phase of the reflected strain wave of the simulation coincides perfectly with that of the experiments. In contrast to the loading phase, a brief plateau can be observed in the unloading phase of the simulation, and the simulation curve decreases more slowly than the experimental curve. Therefore, as shown in Fig. 17, even though the area under the simulated transmitted wave, also known as transmitted energy, is smaller than that in the experiment, the complement in the unloading phase counteracts this error in the transmitted wave. Therefore, the energy validation, i.e., comparison of the sum of incident and reflected waves and the transmitted wave, reaches a good agreement; hence, the validation of energy consistency over the simulation SHPB test is satisfied.

Fig. 17
figure 17

Comparison of strain waves between the experiment and simulation: a NC-5 and b RC20-4

Full size image
Fig. 18
figure 18

Contour plot of lateral stress and effective plastic strain of NC-5 and RC20-5

Full size image

5.3 Stress–strain curve validation

To further validate the numerical model, we proposed a stress–strain curve comparison between the experiment and simulation. The transmitted curve reflects the strength of the material, and according to the reflected curve, we can retrieve the original strain curve during the SHPB test. Similarly, the strain of the specimen can be calculated by using Eqs. (2) and (3), offset the phase difference resulting from the distance between two sensor elements (simulating the collected signals from strain gauges glued on bars in experiment), and obtain the simulation stress–strain curves. As shown in Fig. 19, the stress–strain curves obtained from the simulation SHPB tests correspond well with those of the experiments. The comparison outcomes of all test cases in NC, RC10, RC20, and RC30 are summarised in Table 9, where the greatest error is 7.61%; this discrepancy can be attributed to numerous factors, such as the inconsistency in specimen in the experimental setup, micro gap between the bar ends and specimen, and surface friction.

Fig. 19
figure 19

Stress–strain curves of NC and RC: a NC-5, b RC10-6, c RC20-5, and d RC30-6

Full size image
Table 9 Comparison outcomes of experiment and simulation of NC and RC
Full size table

5.4 Further discussions

5.4.1 Lateral stress distribution

As shown in Fig. 20, taking NC and RC20 as examples, the structural effects of these two materials significantly enhanced the compressive strength of concrete in the SHPB test, which cannot be ignored in the analysis of impact mechanics. To determine the influence of the structural effect on the dynamic compressive strength (because the specimens are in the shape of a cylinder, which is a centrosymmetric structure), we set a series of elements along the radial side of the specimen, as shown in Fig. 21. The first selected element is located at the centre and every other element is located by increasing the radius by 10%. Accordingly, the lateral stress response of specimens subjected to dynamic loads can be obtained. Therefore, we can observe how the structural effect contributes to strength enhancement. To compare the structural effects in different materials, the DIF was set as a constant with a value of 1, i.e., strain-rate insensitive. This setting ensures that strength enhancement does not result from the rate-sensitivity of the material, but can only be attributed to the structural effect. In other words, by comparing the numerical stress outcomes of different groups of elements in NC and RC, the contribution of the structural effect to strength enhancement can be determined. Meanwhile, because each material containing every element is subjected to a triaxial stress condition in the SHPB test, strength enhancement can be attributed to lateral confinement. Therefore, the improvement relative to the structure effect can be legitimately explored by comparing the normalised lateral (axial) strength, i.e., the ratio between the simulation lateral (axial) strength and experimental compressive strength.

Fig. 20
figure 20

Structural effects of (a) NC and b RC20

Full size image
Fig. 21
figure 21

Schema of selected elements for lateral confinement analysis

Full size image

Based on Fig. 21, four specimens from Table 9 were selected as the examples, whose relative outcomes are shown in Fig. 22. In these four groups, NC is the most sensitive to lateral confinement, while higher rubber content was found to result in lower sensitivity in the structural effect. This regulation is consistent with that obtained from Eq. (19), i.e., the lower the density, the smaller the radial stress. Besides, it is found that the stresses captured from the peripheral area of NC and RC are smaller than quasi-static strength. This is because the specimen dilates when it is compressed, which results in the peripheral area exceeding the loading area of the bar. This short loading interval cannot allow the peripheral elements to achieve quasi-static strength.

Fig. 22
figure 22

Nominal stress distribution with specimen radius: a lateral stress and b axial stress

Full size image

5.4.2 Friction sensitivity analysis

Because a high-performance lubricant (molybdenum disulphide grease) was used to eliminate the effect of interface friction in the SHPB experiment and it was difficult to determine the friction coefficient of the specimen, the friction coefficient was assumed to be 0 in previous subsections. It should be noted that interfacial friction between two materials must exist. In other words, the structural effects include the lateral inertia and interface friction. Hence, to understand the contribution of interface friction to strength enhancement in the SHPB test, RC20-5 was selected as an example of RC. In addition, the friction sensitivity of RC was discussed and compared with that of NC (NC-5).

For both materials, we listed a group of variants of friction coefficient (f), i.e., 0.05, 0.1 0.15, and 0.2, to investigate the influence of friction. Similarly, we employed the strain-rate insensitive model in the simulation because it more directly reflects the outcomes of friction-relative enhancement. From Fig. 23, it is evident that the entire setup of the SHPB test is sensitive to interface friction. This indicates that an increment of 0.05 in the friction coefficient significantly enhances the dynamic axial strength. In addition, as the strain rate increased, the influence on the axial strength of friction generally decreased. For comparison, as shown in Fig. 24, when NC and RC are under a similar strain rate (approximately 90 s−1), strength enhancement caused by the surface friction of NC is similar to that of RC, and the enhancement of axial stress near the centre of the specimen is significant. In other words, the enhancement effect of interface friction is mainly related to the smoothness of the contact surfaces, which is consistent with the results from Flores-Johnson and Li [16]. Therefore, lateral confinement can be enhanced by increasing the friction coefficient.

Fig. 23
figure 23

Friction sensitivity analysis of RC20

Full size image
Fig. 24
figure 24

Stress distributions of NC and RC20 under the same friction coefficients

Full size image

5.4.3 Strain-rate effect mechanisms of RC

Based on the above analysis of the simulation results, a flowchart (Fig. 25) was designed to summarise the constitutive factors and their relationship with each other. The external source of the structural effect consists of two parts: (1) radial inertia; owing to the high loading rates on the specimen during the SHPB test, axial acceleration occurs in the impacting process, which causes radial inertia. Based on Newton’s second law, the radial acceleration and density of material cause the lateral stress; and (2) the interface friction between the specimen and bars, which significantly contributes to lateral confinement.

Fig. 25
figure 25

Flowchart of parameters affecting the enhancement of compressive strength under impact loads

Full size image

The simulation results of this study indicate that the experimental DIFs attached to the K&C model overestimate the strain-rate sensitivity of concrete-like materials because the DIFs obtained by the SHPB experiment include the structural effects observed during the test. To acquire precise simulation results, the input DIF should eliminate the structural effects. In other words, different materials with the same geometric appearance have a distinct real DIF curve, and vice versa. Therefore, the real strain-rate effects of NC and RC are smaller than the experimental strain rate effects. However, by adding crumb rubber to the concrete, the structural effect can be effectively reduced; thus, the real DIF was significantly closer to the experimental DIF.

6 Conclusion

In this study, we aimed to investigate and analyse the contribution of the structural effect to compressive strength enhancement in SHPB tests. The presented eligible data were obtained from the SHPB tests of one group of NC material and three groups of RC. Based on the experimental results of the quasi-static and dynamic tests, the parameters of the K&C model were modified, and the results were found to be significantly consistent with the experimental data. Then, the modified K&C model was employed to separate the real DIF from experimental DIF using an iterative method. Based on the outcomes, several conclusions can be summarised, as follows:

  1. 1.

    The experimental DIF mainly consists of two parts, i.e., inertial enhancement and real DIF. The enhancement of compressive strength due to lateral confinement has a non-negligible effect; hence, to improve the SHPB simulation accuracy, the input DIF should be independent of the structural effects.

  2. 2.

    The parameters of the K&C model were modified according to the mechanical properties of RC. The triaxial strength curves were determined based on the existing results, and the softening phase and damage factors were determined by the unloading period of the quasi-static stress–strain curve. The modified constitutive model was validated by the SET.

  3. 3.

    The radial stress distribution denotes that the stress at the core of NC specimen is the greatest among the tested materials, and all NC and RC specimens decrease sharply from 40% radius; moreover, the strength of the peripheral area of the specimen is less than the quasi-static strength owing to the lateral tensile stress. This phenomenon proves that the inertial effects are more prominent in NC than those in RC because the density of RC is less than that of NC.

  4. 4.

    SHPB tests are highly sensitive to interface friction. For the specimen with a thickness of 50 mm, an increment of 0.05 in the friction coefficient results in a considerable lateral confinement and causes extra strength improvement in the tests. By comparing the strength enhancement due to friction, it was found that strength enhancement due to surface friction in NC is similar to that in RC; however, the enhanced effect of friction generally decreases as the strain rate increases.

  5. 5.

    The structural effect includes the radial inertia and interface friction. The real strain-rate effects of NC and RC are less than the experimental strain-rate effects. However, by adding crumb rubber in concrete, the structural effect can be effectively reduced and the real DIF becomes closer to the experimental DIF.

RC exhibits greater strain-rate sensitivity than NC regardless of the experimental or real strain-rate effect, which is a remarkable mechanical property under impact load. In future work, we will analyse the real strain-rate effect of RC under dynamic tensile load.