A dislocation density-based model for the work hardening and softening behaviors upon stress reversal

Abstract

The mechanical behaviours of microalloyed and low-carbon steels under strain reversal were modelled based on the average dislocation density taking into account its allocation between the cell walls and cell interiors. The proposed model reflects the effects of the dislocations displacement, generation of new dislocations and their annihilation during the metal-forming processes. The back stress is assumed as one of the internal variables. The value of the initial dislocation density was calculated using two different computational methods, i.e. the first one based on the dislocation density tensor and the second one based on the strain gradient model. The proposed methods of calculating the dislocation density were subjected to a comparative analysis. For the microstructural analysis, the high-resolution electron backscatter diffraction (EBSD) microscopy was utilized. The calculation results were compared with the results of forward/reverse torsion tests. As a result, good effectiveness of the applied computational methodology was demonstrated. Finally, the analysis of dislocation distributions as an effect of the strain path change was performed.

1 Introduction

During metal forming, plastic flow is the result of both generating new dislocations and their movement. The change of the dislocation density allows to determine not only the loading parameters but also evaluate the microstructure development that controls many physical and mechanical properties of the deformed metal. As shown in the studies by Bartolome et al. [1], rheological properties may significantly change as a result of changing the strain path, especially in microalloyed steels. To understand the evolution of the dislocation substructure during plastic deformation, it is necessary to develop its qualitative and quantitative relationships with the mechanical response of the analyzed system. Thus, important information can be obtained that may be helpful in understanding the work hardening phenomena and in general predicting stress–strain characteristics, as shown in the publication of Muszka et al. [2]. Such knowledge cannot be overestimated in the design processes of metal forming as well as forecasting the range of load strength and safety of structures, subassemblies of machines and devices. This goal can be achieved by developing physically based models where the dislocation density is used as the internal variable. The physical-based models are more universal and can be flexibly applied to different and can be applied in various areas of research issues, comparing to the empirical models [3]. For this reason, such models are still being developed and successfully used in solving theoretical and practical problems, for example in the metal industry for optimization of the metal forming processes to control and improve the mechanical properties of the final products. A correctly constructed model will enable the analysis of the strengthening processes and the impact of the complex strain path in traditional and advanced, constantly improved processes of producing various metal products, as well as during their loading under operating conditions.

Strain-induced precipitation effect is well known in Nb-microalloyed low-carbon steels that are widely used in various applications (shipbuilding, pipelines, automotive). Addition of microalloying elements such as Nb and Ti promotes the formation of disperse second phase particles, among others Nb(C,N). During thermomechanical processing of Nb-microalloyed steels, they are first reheated to the temperature that is high enough to dissolve those particles and cause the Nb goes into solid solution. Then during rolling, the process is thermomechanically controlled in such a way that high deformation is applied in the austenite regime below recrystallization stop temperature. These conditions favour precipitation process of Nb(C,N) that is hence called strain-induced precipitation process. Produced in such a way fine disperse second-phase Nb carbonitrides (in the size ranging from a few to several dozen of nanometers) are very effective in strengthening the material as they act as obstacles for moving dislocations (Mott–Nabarro effect [4]). The effect of strain path on the interactions between strain-induced particles has not been studied well.

The use of microalloyed steel as a research material in the present studies results from the presence in this steel grade of all possible strengthening mechanisms that may occur in metals and alloys. At the same time, assuming that the strengthening is described by the effects of the interaction between dislocations and various kinds of obstacles, the development of the dislocation strengthening and softening models seems to be fully justified. In the literature, the physical dislocation-based models which describe the strain hardening processes and the impact of recovery in the microstructure are divided into three main groups. The first one is based on the evolution of the average dislocation density, as proposed for example by Kocks and Mecking [5]. The second one is focused on the distribution of the average dislocation density in the cell walls and interiors. This idea was presented in the work of Estrin and co-workers [6, 7] as well as Nes [8]. In the last group, three types of average dislocation density are applied by Roters and co-workers [9], i.e. mobile, immobile in the cell interiors and immobile in the cell walls.

In the present study, a work hardening model for the cyclic deformation, based on the second group of the mentioned above models is discussed. The global dislocation density was divided into dislocation density in the cell walls and cell interiors, as was suggested by Muszka et al. [10]. Additionally, the model includes the total dislocation density calculated based on the Bergström model, which was presented in the works [11, 12]. In the present study, Hu et al.’s [13] suggestion was used to apply the back stress as a variable X to describe the rapid changes under reverse loading.

2 Experimental part

2.1 Material processing

The mechanical behavior under strain path change has been studied for two different steel grades with particular attention to the reduction of yield stress after changing the deformation direction (Bauschinger effect). In the present study, two grades of steel were investigated. Both steels are characterized by bcc structure. The chemical compositions are presented in Table 1. To examine the strain-induced precipitation effect on work hardening, microalloyed steel was compared with low-carbon steel (LC). The cyclic torsion test was carried out using the Arbitrary Strain Path (ASP) test machine from the University of Sheffield. This machine is capable of applying torsion and axisymmetric deformation under well-controlled thermo-mechanical conditions either sequentially or concurrently at strain rates and temperatures observed in industrial operations. The max rotary speed in a fully controlled multi-stroke manner is 150 rpm and for a single stroke, this speed can reach 500 rpm. The maximum load capacity of the actuator is 100 kN and the maximum torque is 500 Nm.

Table 1 Basic chemical composition of the investigated materials, %wt

Cyclic torsion test was performed at ambient (room) temperature. Solid bar specimens (gauge length 20 mm; diameter 10 mm) were used. Both steels were deformed according to similar strain paths: 4 cycles of forward/reverse deformation with 0.25 equivalent strain per pass at strain rate of 0.1 s⁻¹. This deformation route led to the total equivalent strain of 2 (as measured at the point of 72.4% of the specimen’s radius). The initial microstructures of both tested materials are presented in Fig. 1.

Fig. 1

Initial microstructure of microalloyed (a) and low-carbon (b) steel (for low-angle grain boundary, the misorientation angle between neighbouring grains is lower or equal to 15°—red colour; for high-angle grain boundary, the misorientation angle between neighbouring grains is higher than 15°—black colour)

A characteristic feature of the torsion test is the strain gradient along the specimen’s radius. In the centre of the cross section, the strain is zero while at the surface the calculated strain achieves the maximum value. In torsion test, the strain can be calculated as a shear strain determined by the cross section (r—distance from the sample axis; l—gauge length) and rotation angle ($\theta$). The shear strain was calculated using the following relationship:

$$\gamma =\mathrm{tan}\,\alpha =\frac{r\mathrm{sin}\,\theta }{l}=\frac{r\theta }{l}.$$

(1)

2.2 Electron backscatter diffraction (EBSD) analysis

According to Eq. (1), the shear strain was calculated along specimen radius as shown in Fig. 2. In the current work, the microstructure evolution in this area was characterised using EBSD analysis. The selected areas for the analysis were separated by 0 mm, 2 mm and 4 mm distance from the centre of the specimen. The marked microstructure regions were characterized by the shear strain equal 0, 0.14, 0.28, respectively.

Fig. 2

The torsion test specimen (a); cross section with indicated EBSD analysis places and shear strain values (b)

The EBSD analysis was performed using scanning electron microscope SEM (FEI Nova NanoSEM 450). Before the microscope analysis, the specimens were ground and polished. To get information about small orientation deviations in the area described by the high dislocation density, using small beam diameter and high brightness is necessary. The obtained results were analyzed using two types of software (TSL OMI and Channel 5). The step size used in the EBSD data collecting was 0.05 μm.

2.3 GND density calculation

The EBSD data were used to calculate the Geometrically Necessary Dislocation (GND) density. In the literature, several approaches can be found to calculate GND density. Calcagnotto et al. studied the geometrically necessary dislocations in ultrafine-grained dual-phase steels by 2D and 3D EBSD [14] similar to Ruggles and Fullwood [15]. In this work, we were focused on two different methods.

The first method used in the current work was described by Field et al. [16] and is based on Nye’s dislocation density tensor. The detailed description of the Ney dislocation tensor calculation method is given by Pantleon [17]. In this approach, the dislocation density tensor is represented by the relationship with the dislocations that are present in the neighbourhood, by the formula (where ${\rho }^{i}$ is the dislocation density of the i type of the dislocation defined by a Burgers vector ${b}^{i}$ of and a slip plane normal direction ${z}^{i}$):

$$\alpha =\sum_{i=1}^{K}{\rho }^{i}\left({b}^{i} {z}^{i}\right).$$

(2)

In the presented methods, only edge and screw dislocation types are considered in the dislocation density tensor. Other structures likedislocation dipole are not directly taken into account in the calculation of dislocation density tensor [16, 17]. In this calculation method, it is necessary to enter the threshold value of the maximum misorientation between neighbouring points. In the present work, this value was 5°. The larger value of the misorientation was not considered in the dislocation density calculation. The Field et al. [16] approach was used as an automatic method in TSL OMI software.

The second analysed approach was based on the strain gradient model presented in the works of Gao et al. [18] and Kubin and Mortensen [19]. The authors presented the main correlations between the misorientation angles with GND density. To achieve this goal, they performed the simple torsion tests.

$${\rho }_{\mathrm{gnd}}=\frac{a\theta}{bx},$$

(3)

where ${\theta}$ is the misorientation angle, x is the unit length between measurement points, and $a$ is the constant dependent on the boundary type.

Presented methods use information about kernel average misorientation (KAM) directly received from the EBSD data. Based on the KAM data, the local misorientation angle was indicated. KAM parameters give information about the local deformation value. Increasing the kernel average misorientation represents an increase in the GND density. Similarly, like in the previous method, in the KAM parameter distribution analysis, it is necessary to identify the maximum threshold value for the misorientation angle between analysed kernel point. In the present study, this value is equal to 2°.

3 Modelling of the strain reversal tests

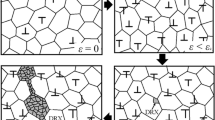
The basic concept of the present model is the assumption that changes in dislocation density are a direct effect of the relationship between the rates of dislocation generation and annihilation rates. The concept was based on the modification of the RGB model (Rauch–Gracio–Barlat model) [20] and can be presented in two steps. The first relies on changes in the average dislocation density description. Generally, the dislocations in the deformed material form cellular dislocation structure as well as can be present in the cell interiors. The changing dislocation density of the latter ones can be presented as it was suggested by Mecking and Kocks [21]:

$${\dot{\rho }}_{c}={\alpha }^{*}\frac{1}{\sqrt{3}}\frac{\sqrt{{\rho }_{w}}}{b}{\dot{\gamma }}_{w}-{\beta }^{*}\frac{6{\dot{\gamma }}_{c}}{bd{\left(1-f\right)}^\frac{1}{3}}-{k}_{0}{\left(\frac{{\dot{\gamma }}_{c}}{{\dot{\gamma }}_{0}}\right)}^{-\frac{1}{n}}{\dot{\gamma }}_{c}{\rho }_{c}.$$

(4)

Equation 4 describes three mechanisms that contribute to the change of dislocation density in the cell interiors. The first one represents a decrease in dislocation density in the cell interiors as a result of moving of some dislocations from the cell interior to the wall structure. Relation that describes the rate of decreasing of the dislocation density in the cells interiors can be written as

$${\left({\dot{\rho }}_{c}\right)}_{\mathrm{walls}}^{-}={-\beta }^{*}\frac{6{\dot{\gamma }}_{c}}{bd{(1-f)}^{1/3}}.$$

(5)

The second part describes the dislocations density change called by the Frank–Read sources activated by dislocation moving from the walls. By this process, the dislocation density in the cell interiors increases by

$${\left({\dot{\rho }}_{c}\right)}^{+}=\frac{3{\alpha }^{*}{n}_{d}{\upsilon }_{w}}{{\left(d-w\right)}^{2}l}.$$

(6)

The third part contributes to the annihilation process connected with cross-slip. This recovery process can be described as follows:

$${\left({\dot{\rho }}_{c}\right)}_{cs}^{-}=-{k}_{0}{\left(\frac{{\dot{\gamma }}_{c}}{{\dot{\gamma }}_{0}}\right)}^{-\frac{1}{n}}{\dot{\gamma }}_{c}{\rho }_{c}.$$

(7)

The second type of dislocation is that which is in the cellular structure. The change of the dislocation density in cell walls can be described similar to Toth et al. [22]:

$${\dot{\rho }}_{w}=\frac{6{\beta }^{*}{\dot{\gamma }}_{c}{(1-f)}^{2/3}}{bdf}+\frac{\sqrt{3}{\beta }^{*}{\dot{\gamma }}_{c}(1-f)\sqrt{{\rho }_{w}}}{fb}-{k}_{0}{\left(\frac{{\dot{\gamma }}_{w}}{{\dot{\gamma }}_{0}}\right)}^{-1/n}{\dot{\gamma }}_{c}{\rho }_{w}.$$

(8)

Dislocations are leaving the cell interiors and moving to the cell walls and have to be integrated into the wall structure. The increased dislocation density in the walls is

$${\left({\dot{\rho }}_{w}\right)}^{+}=\frac{6{\beta }^{*}{\dot{\gamma }}_{c}{(1-f)}^{2/3}}{bdf}.$$

(9)

The second process that increases the dislocation density in the walls is the generation process of new dislocations due to the Frank–Read source, i.e. by the dislocations coming from the cell interiors. This process is similar to the case of the change dislocation density in the cell interiors (Eq. 6), but works in the opposite direction:

$${\left({\dot{\rho }}_{w}\right)}^{+}=\frac{\sqrt{3}{\beta }^{*}{\dot{\gamma }}_{c}(1-f)\sqrt{{\rho }_{w}}}{fb}.$$

(10)

The last mechanism provides information about the annihilation of the dislocations as the effect of the cross-slip process:

$${\left({\dot{\rho }}_{w}\right)}_{cs}^{-}=-{k}_{0}{\left(\frac{{\dot{\gamma }}_{w}}{{\dot{\gamma }}_{0}}\right)}^{-\frac{1}{n}}{\dot{\gamma }}_{w}{\rho }_{w}.$$

(11)

The description of the variable used in Eqs. (4–11) is as follows: ${\alpha }^{*}, {\beta }^{*}$ factors characterize the Frank–Read source and dislocation friction glide, respectively, b the Burgers vector, n the parameters described of the strain rate sensitivity of annihilation process, n_d total number of dislocation sources, d cell size, w—wall thickness, f volume fraction of the cell wall, ${k}_{0}$ constant, and ${\upsilon }_{w}$ the dislocation glide velocity in a wall.

The kinetics of the dislocation density evolution is represented in Eqs. (4, 8) and can be complemented with the relation between the average cell size and total dislocation density by

$$d=\frac{K}{\sqrt{{\rho }_{t}}}.$$

(12)

In the presented model, the total dislocation density was calculated as an average, weighted sum of the dislocation densities in the cell walls and the cell interiors:

$${\rho }_{t}=f{\rho }_{w}+\left(1-f\right){\rho }_{c}.$$

(13)

The volume fracture of the cell walls can be represented as an empirical formula:

$$f={f}_{\infty }+\left({f}_{0}-{f}_{\infty }\right)\mathrm{exp}\left(\frac{-\gamma }{\mathop \gamma \limits^{{ \sim r}} }\right),$$

(14)

where ${f}_{0}$ is the initial value of $f$, ${f}_{\infty }$ is saturation value at large strains of volume fracture in the cell walls, $\mathop \gamma \limits^{{ \sim r}}$ the rate of decrease of $f$.

In the case of the microalloyed steels, where the precipitation process of second phase particles occurs, the mechanism of precipitation strengthening plays a special role. Therefore, in the overall stress formula the precipitation hardening formula based on the Orowan–Ashby equation is added [23], which constituted the second stage of the RGB model modification.

$$\sigma =\left({\sigma }_{0}+M[X+\left(1-\alpha \right)\left(\tau -{\tau }_{0}\right)]\right)+ \left[\beta \frac{{f}^{1/2}}{\kappa }ln\left(\frac{\kappa }{\mathrm{6125}\cdot {10}^{-4}}\right)\right].$$

(15)

In Eq. (15) the σ₀ describes the initial stress value, τ₀ is the stress related to the lattice fiction and solute content, M is Taylor factor, f is the precipitate volume fraction and $\kappa$ is their mean diameter.

The change in the stress level under various strain paths is included here as an internal variable X. The objective that appears here, i.e. to keep the model as simple as possible, is the reason that the expression of the back-stress variable is purely empirical. The internal variable is bounded by

$${{\mathrm{X}}_{\mathrm{s}}=\mathrm{a}(\uptau -\uptau }_{0}),$$

(16)

and its delay is controlled by a dedicated evolutionary law:

$$\dot{X}={C}_{x}\left({X}_{s}\dot{\gamma }-X\left|\dot{\gamma }\right|\right),$$

(17)

where C_x is constant characterizing the dynamic of the back stresses change, (α fraction of the stress that experience some delay in the development of the backstress). The shear stress can be described as follows:

$$\tau ={\tau }_{0}+\alpha Gb\sqrt{{\rho }_{t}},$$

(18)

where the total dislocation density is represented by Eq. (13), the ${\tau }_{0}$ is the stress related to lattice friction and solute contents, $G$ is the shear modulus and $\alpha$ is a factor that weights the dislocation interaction.

The basic idea of the present approach is coupling existing models [20,21,22] and discussed by Ashby [23] for a better prediction of the material behaviour subjected to complex history of deformation. This calculation method allows for more universal application. The coefficients of the most important equations in the adopted model are presented in Table 2. All model parameters were identify based on the experimental data and from the literature [18,19,20]. Parameters C_x and n have been identified based on the stress–strain curve from the experiment using the inverse method. The precipitate volume fraction and their mean diameter were identified based on the transmission electron microscopy (TEM) analysis presented in the previous work [24].

Table 2 Selected values for the model parameters

The above modified model has been implemented to Abaqus CAE as a subroutine. Due to the recurrent nature of the numerical solution typical approach based on user-defined material definition implemented in UHARD method was not sufficient for the case discussed in the present study. Therefore, the authors decided to implement a model in URDFIL subroutine which is called at the end of each time increment and allows to calculate ${\dot{\rho }}_{w}$, ${\dot{\rho }}_{c}$, ${\rho }_{t}$ and X outside of the main FEM loop. For each finite element the parameters of the precipitation effects are calculated and stored globally. Calculated parameters can be accessed in UHARD subroutine using SMAFloatArrayCreate/SMAFloatArrayAccess methods from Abaqus API. Stress according to Eq. 12 as well as first derivative with respect to the equivalent plastic strain are calculated directly in UHARD. Derivatives were calculated using the centered differencing formula.

4 Discussion

4.1 Microstructural analysis

The materials analysed in the present study are characterized by the bcc structure. Additionally, in the case of microalloyed steel, the disperse Nb(C, N) are found. Due to the presence of the fine precipitates in the investigated material, the process of free motion of dislocation during deformation can be effectively blocked. The differences between both the analysed steel structures are presented in Figs. 3 and 4. The inverse pole figure (IPF) maps (Figs. 3a, c, e, 4a, c, e) and corresponding kernel average misorientation (KAM) parameter maps (Figs. 3b, d, f; 4b, d, f) after cyclic torsion test of the microalloyed and low-carbon steels shows the accumulation of dislocation in the grain boundary regions. The KAM parameters distribution presented in Figs. 3 and 4 show the accumulation of dislocation in the grain boundary regions. Additionally, the dislocation pill-up effect on the cell substructures can be observed. These phenomena can be observed already in the beginning stage of the deformation, where the shear strain achieves low values. Along with increasing shear strain, the high volume areas of the dislocation accumulation increase as well. Comparing the distribution maps in low-carbon (Fig. 3) and microalloyed steel (Fig. 4) it can be observed that a significant difference in the structure of both steels appears, especially for the highest values of shear strain microstructures (equal 0.27). The produced substructure in the microalloyed steel is much stronger developed than in LC steel, as a result of the additional strengthening mechanism that occurred in the microalloyed steel. Because of the presence of fine precipitates and solid solution effect, moving dislocations encounter more obstacles, which forces the generation of new dislocations, increasing their density.

Fig. 3

The IPF maps with grain boundary (high-angle boundary—black line; low-angle boundary—red line) for the shear strain values presented in Fig. 2—a, c, e) and corresponding them KAM parameter maps—b, d, f) for low-carbon steel (LC)

Fig. 4

The IPF maps with grain boundary (high-angle boundary—black line; low-angle boundary—red line) for the shear strain values presented on Fig. 2—a, c, e) and corresponding them KAM parameters maps—b, d, f) for microalloyed steel

Additionally, cyclic torsion deformation affects in different ways both types of grain boundaries (geometrically necessary and incidental) present in the material structure, leading to annihilation of geometrically necessary dislocation boundaries from one side and accumulating incidental dislocations on the other hand. As it can be seen, the IPF maps with grain boundary (Fig. 4) the presence of hard second-phase particles delays the formation of dislocation patterns mentioned above, which makes them less difficult to disintegrate.

Similar behaviour can be observed in the second GDN calculation method. The presented results in Fig. 5 clearly indicate that despite the initial dislocation density was lower when the density growth rate was higher in the case of the microalloyed steel compared to low-carbon steel. These phenomena directly result from precipitation strengthening mechanism due to the presence of dispersed second-phase particles that act as obstacles to moving dislocations and form more visible substructure in the microalloyed steel. The curve (Fig. 5) obtained for both GND density calculated methods shows convergent results.

Fig. 5

Comparison of the calculation of the average GDN density changes based on the analysed methods

It is also noticed that the majority of the rotation axes (Fig. 6), corresponding to the inverse pole figure maps from Figs. 3 and 4, are closely aligned with the r direction in the deformation geometry, which is the invariant direction during torsion deformation. Additionally, the rotation axis for every shear strain calculation has higher max value for LC steel compared to microalloyed steel. The differences between LC and microalloyed steel result from additional precipitation strengthening mechanism in the latter steel, where disperse particles act as obstacles for moving dislocations. The greater spread of rotation axes in LC steel is due to initially stronger texture in this material.

Fig. 6

Rotation axes of the crystal with respect to macroscopic coordinates for LC (a) and microalloyed (b) steel

4.2 Numerical simulation

The phenomena presented in the microstructural part of the analysis have a significant impact on the final properties of the tested materials. The stress–strain curve corresponding to the effective radius of the torsion specimen (0.724R), as it was suggested by Barraclough et al. [25], for both steel grades are presented in Fig. 7c, d. As it can be seen, in both specimens, the stress level upon strain reversal is lower compared to prestrain, which confirms the presence of Bauschinger effect. This flow behaviour is attributed to the rearrangement of the dislocation substructure upon reversal—annihilation of dislocations causes a decrease in the local dislocation density. During prestraining, dislocations arrange themselves into planar polarized dense dislocation boundaries called dislocation walls [26]. Based on the presented (Fig. 7) flow curve it can be observed that the Bauschinger effect is more pronounced in the microalloyed steel.

Fig. 7

Compression of the error calculated and measured for LC steel (a) and microalloyed steel (b). The flow stress–strain curve measured and calculated of the RGB and modified model for LC steel (c) and microalloyed steel (d)

Based on the experimental results, computer simulation of forward/reverse torsion test was performed using a commercial Abaqus Standard package. To take into account the phenomena related to microstructure evolution and strain path change during cyclic torsion test, the modified model presented in the previous section was used. For comparison, the original RGB model is also presented in Fig. 7. The initial dislocation density which is necessary to calculate the modified model was taken directly from the EBSD data.

Furthermore, Fig. 7a, b shows the comparison of errors between calculations and measurements of flow stress for RGB and modified models. The results obtained from the modified overall stress formula present a very well agreement in predictions for both materials. It was observed that for both analysed steels more consistent results were obtained for the second pass of the deformation process. Consideration of the precipitation strengthening mechanism made it possible to improve the proposed model description in case of microalloyed steel, especially in the torsion test calculations. The presented results show how difficult and complex the problem is to include the Bauschinger effect in predicting the mechanical behavior of deformed materials. It has also been shown that in the case of microalloyed steels, the proposed approach allows for qualitative and quantitative representation of the influence of precipitation and solution strengthening mechanisms.

5 Summary

The presented experimental studies and theoretical analysis show the effectiveness of the proposed model of changes in the dislocation density as a criterion controlling both microstructural changes and rheological properties observed during the deformation path change. The main aim of the study was to show the possibility of reflecting microstructural phenomena and their influence on the mechanical behavior of the tested steels in the presence of complex strengthening mechanisms and the strain path. The results of numerical simulations compared with the observations obtained by the EBSD method show the correctness of the assumptions made and theoretical relationships. It has also been shown that the most important effects controlling the development of the dislocation substructure in the presence of fine particle strengthening and solid solution mechanisms, typical in steel with microalloying elements, can be successfully predicted in the states of changing the direction of the load and strain paths, so characteristic for many of metal forming processes. The models used define the dislocation density as a complex effect of the dislocations that make up the walls of the cells, as well as those inside them. Again, the EBSD analysis has been shown to be very helpful in identifying the model parameters. The initial dislocation density for the calculations has been taken from the microstructural analysis of the initial material. In the presented model two different methods for the GND density calculations were used. The results obtained for both models were quite similar. The obtained results indicate that the GND density can be successfully calculated with the aid of the EBSD data. Both methods (based on the KAM parameters and dislocation tensor) can be used in the proposed approach.

As it can be expected, the results from the EBSD analysis showed that with increasing the shear strain, the GND density value also increases.

During the cyclic torsion test in the reverse direction, the flow stress level was lower than in the forward direction. The microstructure analysis confirms the supposition that this effect is directly connected to the reorganization of dislocation substructures after the direction change of the deformation. Using proposed, modified model in numerical modelling, the stress level after changing the loading direction was similar to the measured data. It is very promising that the observed compliance of the computer simulation results with the experiment was particularly visible in the case of microalloyed steel, even though in this case due to the more complex interaction of dislocations with various obstacles the rate of generating new dislocations and the slowing down of their annihilation are greater than in the reference material, which was low-carbon steel.