1 Introduction

Soil erosion is a natural process in which topsoil is removed as a result of various erosive factors including topographical settings, land use and land cover change, intensity of rainfall, soil properties, and wind can also be accelerated by human activities of intensive agriculture, deforestation, and tillage on steep slopes (Aga et al., 2018; Bekele, 2021; Borrelli et al., 2020; Rosas & Gutierrez, 2020; Sewnet & Sewnet, 2016; Teng et al., 2019; Yan et al, 2018). This is a serious issue in a country, where land management is inadequate (Thapa, 2020). Reduced soil quality and productivity decreased agricultural productivity (Girmay et al., 2020), infrastructure destruction, sedimentation of various water bodies, ecosystem disturbances, and contamination of downstream and groundwater resources are some of the major negative impacts of soil erosion that occur globally (Aga et al., 2018; Asmamaw & Mohammed, 2019; Borrelli et al., 2020; Getachew et al., 2021). Soil erosion rates must be assessed spatially, quantitatively, and qualitatively using various scientific models to prevent environmental degradation, restore eroded soil, and decrease the likelihood of eroded materials entering the ecosystem (Cerdà et al., 2020; Keesstra et al., 2018; Tóth et al., 2018).

The RUSLE combined with the GIS is the most popular empirical model for quantifying soil loss, as it is relatively easy to use, flexible, and time-effective and its spatial distribution is feasible with reasonable cost and higher accuracy over a wide area (Reusing et al., 2000). When using the RUSLE to analyze the average annual soil loss per unit area, five-component factors are used and multiplied together, including rainfall erosivity factor (R), soil erodibility factor (K), topographic factors (LS), land cover factors (C), and management practices factor (P).

Several studies have been conducted in Ethiopia's highlands to assess soil erosion at various spatial and temporal scales (Amsalu & Mengaw, 2014; Asmamaw et al., 2019; Bewket & Teferi, 2009; Elnashar et al., 2021; Gashaw et al., 2018; Haregeweyn et al., 2017; Negese et al., 2021; Sewnet & Sewnet, 2016; Woldemariam et al, 2018; Zerihun et al., 2018). These scholars highlighted that erosion was the root cause of the major issues that affected the soil fertility, water holding capacity, and biodiversity of the environment. However, the extent and magnitude vary by region due to differences in agricultural practices, population pressures, soil type and susceptibility to erosion, local climate, general topographic formations, and agro-ecological conditions. All of this suggests that site-specific soil erosion studies are still necessary to address soil loss in Ethiopia.

There has been no previous research in the Tashat watershed, which is one of the most prone to soil erosion in the Upper Blue Nile Basin. The study goal was to estimate and map the spatial distribution of soil erosion rates in the Tashat watershed using the RUSLE, as well as to identify areas of high and low soil erosion. Spatial soil erosion maps created using the RUSLE model and GIS tools can be used to design land management and planning strategies, as well as decision-making plans for soil erosion prevention and control.

2 Study area

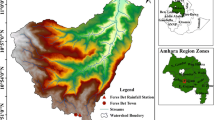
The Tashat watershed was selected for this study, geographically lies between latitudes of 10° 3′ 0″ N to 10° 21′ 50″ N and longitudes of 37° 19′ 45″ E to 37° 36′ 40″ E in East Gojam Zones, Amhara Region. The watershed is a tributary of the Abay River basin, and it encompasses two districts, Debre Elias and Guzamn woredas. The watershed covers a total drainage area of 48,348.4 ha, with elevations ranging from 860 to 2315 m above sea level (Fig. 1). The mean annual rainfall of the area from three meteorological stations for the period from 1986 to 2018, varies between 1329.3 mm in Debre Markos and 1884.7 mm in Debre Elias.

Fig. 1
figure 1

Location map of the study area

Full size image

3 Materials and methods

3.1 Data and processes

The parameters of the RUSLE model were estimated using different data sources by ArcGIS 10.3.1. The rainfall erosivity factor (R value) was estimated from the annual rainfall data of three meteorological stations located throughout the study watershed from 1986 to 2018. The soil erodibility factor (K value) was derived from a soil map provided by the Ethiopian Ministry of Water, Irrigation, and Energy (MoWIE) for the study area. The topographic factor (LS-value) was calculated by analyzing a digital elevation model (DEM) with a spatial resolution of 12.5 m from Alaska (https://search.asf.alaska.edu/#). The crop factor (C) and conservation practice factor (P) were derived from Landsat satellite images and DEM (Table 1). The land cover map of this study area was collected from Ethiopian mapping agency which was developed from Landsat 8 OLI/TIRS C1 Level-1 Images for 27-12-2020 with a cloud cover of 0.01%. Since the spatial resolution of the used factor maps is different it requires resampling the factor maps. So, in this study, the nearest neighbor re-sample sub-tool of the data management toolbox in the ArcGIS platform was used.

Table 1 Sources and a spatial database
Full size table

3.2 RUSLE parameter estimation

The present study began with delineating the Tashat watershed using ArcGIS software version 10.3.1. RUSLE is the simplest and most extensively used model in the world for estimating the rates of inter-rill and rill erosion from field-sized units to regional scales under various management strategies (Fig. 2). RUSLE considers that the sediment composition of the flow regulates soil detachment and deposition. Even if the eroded material did not come from a finite source, soil erosion is limited by the carrying capacity of the flow. Erodibility does not occur when the sediment load exceeds the carrying capacity of the flow (Kim & Julien, 2006). The RUSLE model is the best erosion prediction model that can be simply deployed at the local or regional level. RUSLE (Wischmeier & Smith, 1978) calculates the average yearly erosion anticipated on field slopes (Eq. 1):

$$A=R\times K\times \mathrm{LS}\times C\times P,$$
(1)

where A is the annual soil loss (ton ha−1 year−1); R is the rainfall erosivity factor (MJ mm h−1 ha−1 year−1); K is the soil erodibility factor (Mg ha−1 MJ−1 mm−1); LS is the slope length–steepness factor (dimensionless); C is the cover and management factor (dimensionless), and P is the erosion support practice or land management factor. Helldén (1987) and Hurni (1985a) adapted the RUSLE model input components to Ethiopian settings.

Fig. 2
figure 2

Overall workflow for estimating soil loss using RUSLE

Full size image

3.3 Rainfall erosivity factor (R)

In RUSLE, there is only one climatic parameter called rainfall erosivity factor (R), which measures the impact of rainfall on sheet and rill erosion and gives the result in MJ mm ha−1 h−1 year−1. R-factor denotes the amount of erosive force exerted by a rainfall event (Alexakis et al., 2013; Wischmeier & Smith, 1978). R-factor computed using the ArcGIS raster calculator by employing Eq. 2 suggested by Hurni (1985b) for Ethiopian highlands (Asmamaw & Mohammed, 2019; Bekele, 2021; Belayneh et al, 2019; Gashaw et al., 2018; Girma & Gebre, 2020; Girmay et al., 2020; Hagos, 2020; Tessema et al., 2020; Zerihun et al., 2018). The inverse distance weighted (IDW) interpolation techniques have been most well-liked as geostatistical spatial interpolation methods to get comparatively correct rainfall erosivity information from sample points to the points of unknown values. IDW also allows a fast interpolation of the desired information from a grid-primarily based on irregular basis spaced samples (Li & Heap, 2008):

$$R=-8.12+(0.562\times P)$$
(2)

where R is the rainfall erosivity factor and P is the mean annual rainfall in mm from three gauging stations estimated from 33 years (1986–2018) of rainfall data collected from Ethiopian National Meteorological Agency (Table 2).

Table 2 Mean annual rainfall and R-factors of the three meteorological stations around the Tashat watershed
Full size table

The point level R-factor value were interpolated using IDW for producing the spatial R-factor map with a resolution of 20 m (Fig. 3).

Fig. 3
figure 3

Mean annual rainfall and R-factor value

Full size image

3.4 Soil erodibility (K) factor

Dystric Cambisols (6752.15 ha), Eutric Nitisols (20,354.81 ha), and Cambic Arenosols (21,241.49 ha) were the dominant soil class in the Tashat watershed (Fig. 4; Table 3). The K-factor values were computed for the three soil types in this study watershed. The erodibility of soils is the indicator of the properties of soil particles for the detachment and transport by precipitation (McCool et al., 1995; Wischmeier & Smith, 1978). The cohesiveness of a soil type is determined by this factor, which quantifies its resistance to dislodging and transport caused by raindrop impact and overland flow. The K-factor, which represents the soil physical and chemical properties that contribute to its erodibility, is empirically determined for a particular soil type (Tirkey et al., 2013). The value of K factor value was determined using the equation proposed by Williams (1995):

$${K}_{\mathrm{RUSLE}}={f}_{\mathrm{csand}}\times {f}_{\mathrm{cl}-\mathrm{si}}\times {f}_{\mathrm{orgC}}\times {f}_{\mathrm{hisand}},$$
(3)

where \({f}_{\mathrm{csand}}\) is a factor that gives low soil erodibility factors for soils with high coarse-sand contents and high values for soils with little sand, \({f}_{\mathrm{cl}-\mathrm{si}}\) is a factor that gives low soil erodibility factors for soils with high clay to silt ratios, \({f}_{orgC}\) is a factor that reduces soil erodibility for soils with high organic carbon content, and \({f}_{\mathrm{hisand}}\) is a factor that reduces soil erodibility for soils with extremely high sand contents. The factors are calculated as follows (Eqs. 4–7), adapted from Neitsch et al. (2002):

$${f}_{\mathrm{csand}}=\left(0.2+0.3\times \mathrm{Exp}\left[-0.256\times \mathrm{ms}\times \left(1+\frac{{m}_{\mathrm{silt}}}{100}\right)\right]\right),$$
(4)
$${f}_{\mathrm{cl}-\mathrm{si}}={\left(\frac{{m}_{\mathrm{silt}}}{{m}_{\mathrm{c}}+{\mathrm{m}}_{\mathrm{silt}}}\right)}^{0.3}$$
(5)
$${f}_{\mathrm{orgC}}=\left(1-\frac{0.256\times 0\mathrm{rgC}}{\mathrm{orgC}+\mathrm{Exp}\left[3.72-2.95\times \mathrm{orgC}\right]}\right)$$
(6)
$${f}_{\mathrm{hisand}}=\left(1-\frac{0.7\times \left(1-\frac{\mathrm{ms}}{100}\right)}{\left(1-\frac{\mathrm{ms}}{100}\right) +\mathrm{Exp}\left[-5.51+22.9\left(1-\frac{\mathrm{ms}}{100}\right)\right]}\right)$$
(7)

where ms is the percent sand content (0.05–2.00 mm diameter particles), msilt is the percent silt content (0.002–0.05 mm diameter particles), mc is the percent clay content (< 0.002 mm diameter particles), and orgC is the percent organic carbon content of the layer (%).

Fig. 4
figure 4

Major soil type (left) and K-factor (right) maps

Full size image
Table 3 Soil types, area coverage and estimated K value
Full size table

3.5 Topographic LS factor

In RUSLE, the LS-factor is made up of slope length (L) and slope steepness (S) elements (Alexakis et al., 2013; McCool et al., 1995; Moore & Wilson, 1992; Wischmeier & Smith, 1978). The topographic factor (LS) depicts the impacts of topography on erosion and includes the length and steepness of the slope, which determine surface runoff speed (Beskow et al., 2009). The LS-factor is taken into account in the soil loss equation model, because the length and steepness of the slope have a significant impact on the rate of soil erosion by water. The steeper and longer the slope, the greater the rate of erosion by water due to the greater buildup of runoff (Alexakis et al., 2013; Shiferaw, 2011; Tadesse & Abebe, 2014; Wischmeier & Smith, 1978). The flow accumulation, slope steepness, and slope gradient were calculated in this work using an ArcGIS environment and a DEM with a resolution of 12.5 m, and the slope length was obtained using the map algebra expressions' aster calculator. As in other studies, the slope length (Eq. 8) and slope steepness (Eq. 9) parameters were used in this work to calculate and map the LS-factor (Fig. 5d) (Bewket & Teferi, 2009; Kamaludin et al, 2013; Tessema et al., 2020):

$$L={\left(\frac{\text{Flow accumulation }\times \text{ cell size}}{22.1}\right)}^{\mathrm{m}}$$
(8)
$$S=\left(0.065+0.045\mathrm{S}+0.0065{\mathrm{S}}^{2}\right)$$
(9)
$$\mathrm{LS}={\left(\frac{\text{Flow accumulation }\times \text{ cell size}}{22.1}\right)}^{\mathrm{m}}\times \left(0.065+0.045S+0.0065{S}^{2}\right)$$
(10)

where LS is slope length–steepness factor, m is an exponent that depends on slope steepness and S is slope gradient in percent. By classifying the slope of the watershed according to m values shown in (Fig. 5b, Table 4) that vary from 0.2 in the upper part of the watershed to 0.5 in the downstream and middle of the watershed was generated to run the equation (Eq. 10). The resulting slope length (L) map (Fig. 5a) shows that the slope length varied from 0 to 313.12. The slope steepness (S) map (Fig. 5c) indicates that the slope gradient ranged from 0.065 in the lower and upstream part of the watershed to 1371.8 in the middle part of the watershed. The combination of these two sub-factors, the slope length (L) and the slope gradient (S) give a single factor known as a topographic factor (LS) varied between 0 and 3970.6 ton ha−1 year−1.

Fig. 5
figure 5

m value (a), slope length (b), slope steepness (c) and LS-factor (d) map

Full size image
Table 4 m Values for a range of slope classes (Wischmeier & Smith, 1978)
Full size table

3.6 Cover and management (C) factor

The land use maps were used to establish the crop management factor for the area (Morgan, 2005; Wischmeier & Smith, 1978). The land use categories in Tashat watershed are cropland, forest land, shrubland, grassland, water body, bare land, and settlement areas (Fig. 6). C values were allocated to each land cover type based on the values recommended and used in various studies (Table 5).

Fig. 6
figure 6

Land use/cover (left), and C-factor (right) map

Full size image
Table 5 Land cover classes and their distribution and C-values for the Tashat watershed
Full size table

3.7 Conservation practice (P) factor

The conservation practice (P) factor is the ratio of soil loss caused by a certain conservation practice, such as contouring, strip-cropping, or terracing, to the corresponding loss caused by up and downslope cultivation (Borrelli et al., 2020; Pandey et al., 2007; Wischmeier & Smith, 1978). According to agricultural land management, the P-factor numerical value is always between 0 (good conservation practice) and 1 (bad conservation practice) (Bagherzadeh, 2014; Issa et al., 2016). For this analysis, the slope of the area was correlated with the land use categories using the P value from Wischmeier and Smith (1978), because management activities are heavily dependent on the slope of the region (Table 6). The LULC was grouped into agricultural land use (cropland) and non-agricultural land use. The category under non-agricultural land use was given the P-value of 1 regardless of their slope class, whereas the agricultural land use (cropland) was classified into six slope classes.

Table 6 Conservation practices factor value (Wischmeier & Smith, 1978)
Full size table

4 Results and discussion

4.1 Spatial distribution of soil erosion factors in the Tashat Watershed

The study used the GIS–RUSLE interface model for analyzing the spatial distribution of soil erosion in the study area. The mean annual soil loss rate (t ha−1 year−1) was determined by conducting cell by cell calculation.

4.1.1 Rainfall erosivity (R) factor

The point rainfall data obtained from three rain gauge stations (Debre Elias, Debre Markos and Yejubie) used for computing the rainfall erosivity (R) value across the watershed employing Inverse Distance weighted (IDW) method on ArcGIS 10.3.1 environment. The results of the R-factor analysis vary from 877.5 to 1051.1 MJ mm ha−1 h−1 year−1 in the western and southwest, and eastern parts of the study watershed, respectively. This showed that there is a variation of rainfall erosivity throughout the watershed (Fig. 3).

4.1.2 Soil erodibility (K value)

The soil erodibility (K) factor map was estimated from the soil property data like percent of sand, silt, clay, and organic carbon content data are taken from the digital soil map of the world of Version 3.6, completed in January 2003 and prepared by the Food and Agriculture Organization of the United Nations. The values of the K factor for our watershed area are found to be ranging between 0.124 and 0.139 t ha MJ−1 mm−1 (Fig. 4). Most of the central part which is 43.9% of the watershed was dominated by Cambic Arenosols and characterized by a maximum K value of 0.139 t ha MJ−1 mm−1. On the other hand, the upper part (42.1% of the watershed) consists of Eutric Nitosols with a K value of 0.135 t ha MJ−1 mm−1 and 14.0% is characterized by the presence of Dystric cambisols with a K value of 0.117 t ha MJ−1 mm−1. From these values, the dystric cambisols having lower k values indicates that it has high infiltration rates and greater resistance or lower susceptibility to soil erosion in this study watershed area.

4.1.3 Topography factor (LS)

The LS topographic factor signifies the combined influence of slope length and slope steepness on the soil erosion process. The mapping of m value was undertaken by ranking the slope of the watershed in step with the values m presented in Table 4. The m value map produced varies from 0.2 in the upper parts of the watershed to 0.5 in the downstream and middle parts of the watershed (Fig. 5a). The resulting slope length (L) map (Fig. 5b) illustrates that the slope length fluctuates from 0 to 313.1. The slope steepness (S) map indicates that the gradient ranged from 0.065 to 1371.8 in the middle and around the outlet of the watershed (Fig. 5c). The combination of these two sub-factors results in a single factor known as the topographic factor (LS) which ranges between 0 and 202.1 (Fig. 5d).

4.1.4 Cover and management (C value)

Based on the 2020 Landsat image analysis using ArcGIS 10.3.1 software, seven different LULC classes (Table 5), such as cropland (22,409.7 ha), grassland (526.4 ha), forest (2320.5 ha), shrubland (16,576.9 ha), settlement areas (6494.0 ha), water body (5.4 ha) and bare land (15.7 ha) were identified. For each LULC class, the corresponding C-values were assigned from 0.001 for forest land to 1 for bare land. The bare land had a maximum cover factor which indicated higher erosion.

4.1.5 Conservation practice factor (P)

The LULC and slope map of the study area were reclassified based on the desired range and given in Fig. 7 and Table 6. The LULC was grouped into agricultural land use and non-agricultural land use. The lands containing grassland (526.4 ha), forest (2320.5 ha), shrubland (16,576.9 ha), bare land (15.7 ha), water body (5.4 ha), and settlement areas (6494.0 ha) were assigned as non-agricultural land use and given the P value of 1 regardless of their slope class, whereas the agricultural land use was classified into six slope classes and assigned their respective P-values (Table 6). As shown in Fig. 7, the cropland especially having a slope of less than 30% having a P-value of 0.1–0.19 is observed in the major parts of the watershed. On the other hand, higher P-value 1 representing non-agricultural areas (other than croplands) are distributed on a different part of the watershed and covers large area.

Fig. 7
figure 7

Slope class (left) and P-factor (right)

Full size image

4.2 Annual soil erosion estimation and prioritization for soil conservation planning

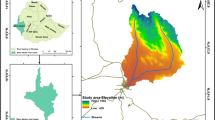
The erosion risk assessment in the Tashat watershed was performed by overlaying the five RUSLE parameters using a raster calculator in ArcGIS spatial analyst tool. The annual soil loss values found from 0 (in the flat landscape) to 3970.6 t ha−1 year−1 in the middle part of the watershed and extended to some lower parts of the watershed due to the presence of high LS-factor values and an unforeseen change in slope from < 11 to > 50% (Figs. 8 and 9). Because of the limited number of resources, soil conservation measures can't be implemented at once throughout the entire watershed. Therefore, it is imperative to prioritize intervention areas according to the severity and risks of soil erosion. The estimated soil loss rate was divided into five erosion risk classes (Gashaw et al., 2018; Girmay et al., 2020; Hagos, 2020), as shown in Fig. 9 and Table 7, with their coverage area and amount of soil loss. The mean annual soil loss was found to be 64.2 t ha−1 year−1 and the total annual soil loss from the entire watershed area of 48,348.4 ha was about 61,885,742.9 tons. Concerning the coverage of the risk of erosion from total loss, approximately 53.2% of the watershed is classified as having a low soil erosion rate, which is regarded a very minor risk area. As shown in Table 7, the remaining areas are classified as low (7.7%), moderate (6.5%), high (7.1%), and extremely high (25.5%).

Fig. 8
figure 8

Annual soil loss map

Full size image
Fig. 9
figure 9

Soil loss rate (left) and severity class (right) map

Full size image
Table 7 Annual soil loss range, severity class, and area coverage
Full size table

The total area experiencing soil erosion at a rate less than the maximum tolerable erosion limit of 11 t ha−1 year−1 (Renard et al., 1996) covers 53.2% of the entire watershed. Based on soil erosion area estimates, about 25.5% had high soil erosion risk. In this study, it was observed that RUSLE analysis provided significant, synthesized, and systematic information about the spatial distribution of soil erosion problems, that enables the identification of the most affected areas and the types of dominant erosion over time.

The numerical data outputs of similar research work in the Ethiopian highlands were used to validate the model output, because there are no case studies in the study area. The average annual soil loss rate estimated for the entire watershed was 64.2 t ha−1 year−1. This value is higher as compared to other reports by: Negese et al., (2021); for Chereti Watershed, Northeastern Ethiopia (38.7 t ha−1 year−1); Elnashar et al. (2021); for the Blue Nile Basin (39.7 t ha−1 year−1); Bekele (2021) for Anka-Shashara watershed (15.22 t ha−1 year−1); Tsegaye and Bharti (2021) for Anjeb watershed, Northwest Ethiopia (17.3 t ha−1 year−1) and; Hurni (1985a) for the highland of Ethiopia (20 t ha−1 year−1). Because of the lesser amount of soil and water conservation efforts made in the country in recent decades, the new findings differ considerably from those observed earlier in Ethiopian Northwestern highlands. This study discovered that the watershed is impacted by moderate to severe erosion rates, implying that it requires immediate intervention.

5 Conclusions

Among the several fundamental approaches for calculating soil erosion rate, the RUSLE is a critical tool for improved conservation planning based on evidence (priority) to be more effective with the limited resources available. As a result, the focus of this work is on the application of RUSLE in conjunction with GIS techniques to analyze soil loss rate and identify hotspot areas in the Tashat watershed. Based on the analysis, the spatial distribution map of soil loss in the watershed was generated and concluded that the soil loss varies from 0 to 3970.6 t ha−1 year−1 with an average soil erosion rate of 64.2 t ha−1 year−1 from the total watershed area of 48,348.4 ha in the Tashat watershed. More than half of the area has very minor to moderate soil loss, with 32.6 percent experiencing severe or very severe erosion. The permitted soil erosion rate was surpassed in the watershed steep slope midsection. This could be due to the steepness of the slope, the dominance of the essentially less resistant soil type (Cambic Arenosols) to eroding rainfall strength, and a lack of supportive practice. On the other hand, in most of the upper areas of the watershed, a tolerable soil loss rate was projected. This is due to the abundance of soil types that are resistant to erosion (Eutric Nitosols). According to the information on the soil erosion risk map, the risk of soil erosion was greater in the middle and downstream portions of the watershed than in the upstream area. As a result, effective soil conservation methods must be undertaken in such areas. Analyzing the influence of increased agricultural area on soil erosion leads to the conclusion that as agricultural area increases, so does the threat of erosion due to agricultural activities. The study would serve as a baseline for future research to determine the unique driving causes of erosion in the area and give appropriate remedial measures for specific parts of the watershed by visiting the site and consulting the local community for better results. Further research is required to identify the many driving forces of erosion in the specific watershed to build and seek alternate solutions for future development plans and strategies.