Abstract
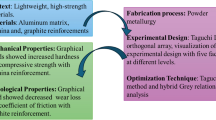
In this research, Taguchi–grey relational analysis has been applied to mitigate the insufficient assumptions made on the optimization of mechanical and structural (mechanostructural) properties of synthesized hydroxyapatite (HAp)–alumina–titanium nanocomposite. This nanocomposite has already been developed and studied in the previous study. This paper employs the L9 (3**3) orthogonal array, including displaying factors and levels of 3, 5, 7 wt % for alumina, 5, 10, 15 wt % for titanium, and 1100, 1150, 1200 °C sintering temperature. The computational analysis presents the predicted mechanostructural grey relational response as 0.7271, higher than the highest response shown in the ninth experimental run. The optimal control factors are analyzed to be 7 wt % alumina, 15 wt % titanium, and 1200 °C sintering temperature. The obtained result elucidates the hypothesis that a singular response optimization is not enough in the fabrication of biomedical material, disproving the assumption made in the previous literature. Importantly, to fabricate a high clinical grade HAp–alumina–titanium nanocomposite, titanium is the most invaluable contributor with a contribution of 49.11%, followed by alumina (45.52%), and then sintering temperature (3.2%). Although the confidence level and probability distribution analysis show that all the experimental mechanostructural responses were within the 95% confidence level, the employment of the predicted optimal factors is strongly recommended for experimentation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Hydroxyapatite of biogenic or synthetic origin has extensive applications in biomedical repairs, substitutions, and augmentations and as scaffolds in tissue engineering for bone regeneration [1,2,3]. HAp can be applied as abrasives to roughen metal implant surfaces and as a bioactive coating on orthopedic and dental implants [4,5,6,7,8]. This material has also been used as transfection agents, drug carriers, and percutaneous devices. In the same vein, HAp is disadvantaged as it relates to its fracture toughness which somewhat restricts its use for load-bearing clinical applications. Therefore, extensive studies are geared toward methods that have the potential of enhancing the mechanical properties of HAp without overly compromising its biocompatibility. These methods stem from tailoring the processing of the HAp powders, carefully optimizing the sintering temperature, pressure, and reinforcements for better biomedical performance of HAp [9,10,11].
Alumina has received great attention as a promising material in improving the osteoconductivity of hydroxyapatite. Because of the bioinert nature of the material, it allows the bone and tissues surrounding it to re-grow and integrate without causing any negative immune response. In dentistry, bioinert materials are an essential component of implants, bone grafts, prostheses, and fillings. In addition to not harming the body, a bioinert substance in dentistry will also be osteoconductive and promote osteogenesis. These attributes show the fact that the material possesses unique properties like nontoxicity, excellent biocompatibility, and in-vivo biodegradability [12, 13]. Alumina-based materials find applications most often as bone substitute material, implant coats, and drug delivery systems [14,15,16,17]. One of the major benefits offered by alumina-based biomaterials is their ability to produce the apatite layer when immersed in a simulated body fluid. This action plays a crucial part in inducing bonding between the implant and human bone [17]. Many biological studies involving alumina-based materials have demonstrated that these materials have superior mechanical properties, and can enhance the rate and quality of bone tissue repair compared with pure HAp [18]. Titanium and titanium alloys have been shown in several studies to have a distinctive combination of strength and biocompatibility, which makes them useful in medical applications. They have gained ground in biomedical engineering because of their exceptional properties, namely, fluid effects resistance, high tensile strength, high toughness, higher bending strength, high corrosion resistance, and high flexibility [19,20,21,22,23]. Hence, a mixture of alumina and titanium with an effective sintering technique tends to improve the mechanical and biological properties of HAp. Importantly, careful optimization of reinforcements and sintering temperature will give an excellent mechanically and biologically enhanced HAp suitable for tissue engineering.
Taguchi experimental design technique is an efficient technique that ensures excellent performance in the design of processes or products. The technique can reduce the number of experiments for better products or process performance, thereby reducing cost and mitigating errors [24]. Despite the advantage of Taguchi experimental design, it can only optimize singular performance characteristic, which limits it for optimizing multiple performance characteristics [25]. However, grey computational analysis can convert non-additive multiple performance characteristics into a singular characteristic, thereby assisting Taguchi experimental design to optimize multiple responses of products or processes [26, 27]. In this recent time, researchers have started exploring the assistance of grey computational analysis with Taguchi design experimental design technique to optimize multiple response of a product or process [23, 28, 29].
Hence, in this study, Taguchi experimental design technique assisted by grey computational analysis was employed to optimize and to investigate the effect of alumina, titanium, and sintering temperature on mechanostructural properties of hydroxyapatite.
2 Experimental data curation and orthogonal array experiment
The synthesis, characterization, and mechanostructural properties evaluation of hydroxyapatite–alumina–titanium nanocomposite have been conducted in the study of Ebrahimi et al. [30]. The L9 (3**3) Taguchi orthogonal array employed in this study agrees with the previous study, having the control factors and levels, shown in Table 1. This design resulted to only nine experimental runs, shown in Table 2. The mechanostructural experimental data employed for the Taguchi–grey computational analysis was obtained from the previous report, and it is displayed in Table 3.
3 Mechanostructural grey computational analysis
As established in the grey computational analysis technique, the five experimental mechanostructural data were first preprocessed to range within zero and one. The preprocessing data technique used for phase decomposition, open porosity, toughness, and bending strength was the higher-the-better (Eq. 1), while for the grain size was the smaller-the-better (Eq. 2). The reason for the choice is that a higher porosity, higher phase decomposition rate, and smaller grain size enhance cell proliferation and surface growth [2, 31,32,33,34], while a higher mechanical strength is desired for load-bearing biomedical application. The preprocessed data are displayed in Table 4, and it is usually called grey relational generation. A comparison was done with an ideal sequence, x0(k) (k = 1, 2,…,9) for the five mechanostructural data.
where xi (k) is the preprocessed data for the ith experiment, and yi (k) is the initial sequence of the mean of the responses.
The deviation sequence (Eq. 3) was then computed to process the grey relational coefficient. The deviation sequence of the five experimental data is displayed in Table 5.
where \({\Delta }_{oi}\left(k\right)\), xo (k), and xi (k) are the deviation, reference, and comparability sequences, respectively.
Then the grey relational coefficient (GRC) was computed using Eq. 4. The grey relational coefficient shows the relationship between the expected and obtained experimental data. It also gives the possibility to relate and carry out statistical mean of the non-additive multiple experimental data.
where \({\xi }_{i}\left(k\right)\) reflects the GRC value of the individual mechanostructural responses computed as a function of Δmin and Δmax, the minimum and the maximum deviations of each response variable. \(\zeta\) is the distinguishing coefficient (0–1), but a different weight of 0.5 is usually assigned to each parameter.
Next, the grey relational grade, i.e., GRG in Eq. 5 was computed by averaging the five grey relational coefficients. The GRC and GRG values are displayed in Table 6. The grey relational grade gives the overall response of the five experimental mechanostructural data. In other words, the unfeasible optimization of the five complicated data becomes feasible by the singular response (GRG) generated by the grey computational analysis. Optimization of the materials design parameters is the level showing the highest GRG.
where \({\gamma }_{i}\)= the value of GRG determined for the ith experiment, n is the aggregate count of the performance characteristics.
4 Taguchi design of experiment (DOE)
The obtained GRG values were subjected to the Minitab software and analyzed according to the considered orthogonal array design. Then the signal-to-noise ratio corresponding to the respective GRG values is displayed in Fig. 1. Table 7 displays the response table for GRG. The respective delta value shown in Table 7 is the difference between the maximum and the minimum value of GRG of each factor, and it is ranked. The ranking shows the order of significance on the resultant GRG values.
Figure 2 displays the effect of control factors on the mechanostructural response (GRG) of the composite. It is seen that the increase in factor level increased the mechanostructural response. This shows that the optimal mehanostructural response is derived with factors at level 3, i.e., 7 wt % alumina, 15 wt % titanium, and 1200 °C sintering temperature are the optimal control factors for better mechanostructural properties of the composite. These findings disagree with the conclusive optimal control factors in the study of Ebrahimi et al. [30]. The reason for the disagreement is that Ebrahimi et al. [30] assumed only one response (structural property) to be the most desired property, and then singularly optimizing it for composite production. Whereas all the properties are essential for a functional biomedical material (See Sect. 3.0 for the importance of each factor). The grey computational analysis has been able to optimize all the five complicated mechanostructural data for better biomedical performance.
5 Analysis of variance
Analysis of variance (ANOVA) helps to investigate the level of significance of each control factor on the mechanostructural response of the composite. Table 8 displays the ANOVA of GRG. The table was generated by Minitab 16 software considering the resultant GRG values, but the percentage of contribution was calculated to quantitatively know the level of significance of each control factor. A higher F value and a lower P show a greater level of significance. The result shows titanium has the highest percentage of contribution of 49.11%, followed by alumina and then a very little contribution from sintering temperature. It is important to note that residual error is insignificant, having a contribution of 3.2%.
6 Validation analysis
Having known the optimal and the significance of the composite fabrication parameters, it is expedient to investigate the predicted response from the design analysis. This is shown in Eq. 6: [23, 35].
\({\gamma }_{0}\) is the highest average value of GRG at the optimal fabrication parameter levels and \({\gamma }_{m}\) is the average of GRG. q is the number of the fabrication parameters.
In Eq. 5 and Table 6, the value of GRG was predicted using the optimal fabrication parameter levels. The predicted GRG was gotten to be 0.7271.
Confidence interval (CI) was then computed using Eq. 7. This was done to determine the correlation between the experimental GRG value and the predicted GRG value [23, 36]:
\({F}_{\propto }(1,{f}_{e})\)= F ratio required for \(\alpha\); \(\alpha\)= risk; \({f}_{e}\)= DOF of error; Ve = variance of error; \({\eta }_{eff}\)= effective number of replications, which is Eq. 8 given below:
R = number of replications when the experiment is carried out for confirmation; N = total number of experiments.
Therefore,
Ve = 0.000829; fe = 2.
Total DOF of control factors = 6.
R = 1, N = 9.
\(\alpha\)= 0.5 (95% confidence interval).
\({F}_{0.5}(\mathrm{1,2})\)= 18.51 (tabulated values from the F-Tables)
95% confidence interval of the predicted optimal grey relational grade is given in Eq. 9, as posited by Abifarin (2021):
The optimal fabrication parameters predicted in this study happened to be outside the experimental run in the study. There is a need to fabricate a composite based on the optimal fabrication parameters and then conduct its mechanostructural properties, thereafter benchmarking it with the generated confidence interval having the minimum and maximum mechanostructural response boundaries of 0.5619 and 0.8923. Putting all the fabrication conditions, it is expected that the mechanostructural grey relational response should correlate with the predicted response.
Having recommended a need to conduct experiment based on the predicted optimal conditions, probability distribution is another way of validating the predicted result. This is shown in Fig. 3. The experimental mechanostructural grey relational responses displayed in Fig. 3 are within the 95% confidence level. In other words, the optimal mechanostructural grey relational response is expected to correlate with the predicted mechanostructural response under 95% confidence level.
7 Multi-mechanostructural modeling and interaction plot of the composite
The experimental and modeled mechanostructural response of the composite is shown in Fig. 4a. The graph shows a very similar and close pattern between the experimental and the modeled mechanostructural response as generated by regression analysis on the GRG values obtained. Also, the mathematical model of the mechanostructural response of the composite is shown in Eq. (10). Figure 4b–d displays the reactions between the considered factors relative to their corresponding mechanostructural response. It is shown from the plot, the combination of factors settings resulting to as high as possible the mechanostructural response of the composite.
where A, B, and C denote the responses generated by alumina, titanium, and sintering temperature, respectively.
8 Conclusion
Taguchi–grey relational analysis for the optimization of control factors of hydroxyapatite–alumina–titanium composite synthesis for complicated multiple mechanostructural properties has been reported in this paper. The highest GRG value, which was 0.7010 for the nine experimental run, was obtained at the ninth experimental run (7 wt % alumina, 15 wt% titanium, and 1150 °C sintering temperature), but was proven not to be the actual optimal conditions. The best optimal control factors are validated to be 7 wt % alumina, 15 wt % titanium, and 1200 °C sintering temperature. These findings validated the research hypothesis that a singular response optimization is not enough for a biomedical material, disproving the assumption of Ebrahimi et al. [30]. Quantitatively, titanium displayed the highest significance of 49.11%, followed by alumina (45.52%), and then sintering temperature (3.2%). From the study, the mathematical and graphical model displaying similar pattern of the experimental mechanostructural response shows the efficacy of the design analysis.
Data availability
Not applicable.
Code availability
Not applicable.
References
J. Abifarin et al., Experimental data on the characterization of hydroxyapatite synthesized from biowastes. Data Brief 26, 104485 (2019)
D. Obada et al., Mechanical properties of natural hydroxyapatite using low cold compaction pressure: Effect of sintering temperature. Mater. Chem. Phys. 239, 122099 (2020)
J.K. Abifarin, O.A. Owolabi, New insight to the mechanical reliability of porous and nonporous hydroxyapatite. J. Aust. Ceram. Soc. 59(1), 43–55 (2023)
B.I. Oladapo et al., Three-dimensional finite element analysis of a porcelain crowned tooth. Beni-Suef Univ. J. Basic Appl. Sci. 7(4), 461–464 (2018)
B.I. Oladapo, S. Zahedi, A. Adeoye, 3D printing of bone scaffolds with hybrid biomaterials. Compos. B Eng. 158, 428–436 (2019)
Abifarin, F.B., Z. Musa, and J.K. Abifarin, Mechanical processing of hydroxyapatite through sintering and multi-objective optimization technique for biomedical application. MRS Advances, 2023: p. 1–6.
B.I. Oladapo, S.A. Zahedi, S.O. Ismail, Mechanical performances of hip implant design and fabrication with PEEK composite. Polymer 227, 123865 (2021)
B.I. Oladapo et al., 3D printing of PEEK–cHAp scaffold for medical bone implant. Bio-Design Manuf. 4, 44–59 (2021)
D. Obada et al., Mechanical measurements of pure and kaolin reinforced hydroxyapatite-derived scaffolds: a comparative study. Mater. Today 38, 2295–2300 (2021)
Abifarin, J.K., et al., Fabrication of mechanically enhanced hydroxyapatite scaffold with the assistance of numerical analysis. Int. J. Adv. Manuf. Technol., 2021: p. 1–14.
Obada, D.O., et al., Hydroxyapatite materials-synthesis routes, mechanical behavior, theoretical insights, and artificial intelligence models: a review. J. Aust. Ceramic Soc., 2023: p. 1–32.
M. Colilla, M. Manzano, M. Vallet-Regí, Recent advances in ceramic implants as drug delivery systems for biomedical applications. Int. J. Nanomed. 3(4), 403–414 (2008)
M. Tadic et al., Magnetic properties of mesoporous hematite/alumina nanocomposite and evaluation for biomedical applications. Ceram. Int. 48(7), 10004–10014 (2022)
D.S. Nakonieczny et al., Alkali-treated alumina and zirconia powders decorated with hydroxyapatite for prospective biomedical applications. Materials 15(4), 1390 (2022)
Pourmadadi, M., et al., Porous alumina as potential nanostructures for drug delivery applications, synthesis and characteristics. J. Drug Delivery Sci. Technol., 2022: p. 103877.
D.O. Obada et al., Fabrication of novel kaolin-reinforced hydroxyapatite scaffolds with robust compressive strengths for bone regeneration. Appl. Clay Sci. 215, 106298 (2021)
P.N. Silva-Holguín, S.Y. Reyes-López, Alumina-hydroxyapatite-silver spheres with antibacterial activity. Dose-Response 19(2), 15593258211011336 (2021)
Q. Hu et al., Facile synthesis and in vitro bioactivity of monodispersed mesoporous bioactive glass sub-micron spheres. Mater. Lett. 106, 452–455 (2013)
H. Li, K. Khor, P. Cheang, Titanium dioxide reinforced hydroxyapatite coatings deposited by high velocity oxy-fuel (HVOF) spray. Biomaterials 23(1), 85–91 (2002)
S.H. Li et al., Synthesis of macroporous hydroxyapatite scaffolds for bone tissue engineering. J. Biomed. Mater. Res. 61(1), 109–120 (2002)
M. Kulkarni et al., Titanium nanostructures for biomedical applications. Nanotechnology 26(6), 062002 (2015)
M. Topuz, B. Dikici, M. Gavgali, Titanium-based composite scaffolds reinforced with hydroxyapatite-zirconia: production, mechanical and in-vitro characterization. J. Mech. Behav. Biomed. Mater. 118, 104480 (2021)
J.K. Abifarin, Taguchi grey relational analysis on the mechanical properties of natural hydroxyapatite: effect of sintering parameters. Int. J. Adv. Manuf. Technol. 117(1–2), 49–57 (2021)
J. Abifarin, J. Ofodu, Modeling and grey relational multi-response optimization of chemical additives and engine parameters on performance efficiency of diesel engine. Int. J. Grey Syst. 2(1), 16–26 (2022)
M.O. Esangbedo, J.K. Abifarin, Cost and quality optimization taguchi design with grey relational analysis of halloysite nanotube hybrid composite: CNC machine manufacturing. Materials 15(22), 8154 (2022)
A.J. Kehinde, O.J. Chukwuka, Determination of an efficient power equipment oil through a multi-criteria decision making analysis. Vojnotehnički glasnik 70(2), 433–446 (2022)
O.J. Chukwuka, A.J. Kehinde, Employment of probabilitybased multi-response optimization in high voltage thermofluids. Vojnotehnički glasnik 70(2), 393–408 (2022)
R.S. Pawade, S.S. Joshi, Multi-objective optimization of surface roughness and cutting forces in high-speed turning of Inconel 718 using Taguchi grey relational analysis (TGRA). Int. J. Adv. Manuf. Technol. 56(1), 47 (2011)
Rajyalakshmi, G. and P. Venkata Ramaiah, Multiple process parameter optimization of wire electrical discharge machining on Inconel 825 using Taguchi grey relational analysis. The International Journal of Advanced Manufacturing Technology, 2013. 69: p. 1249–1262.
M. Ebrahimi et al., Taguchi design for optimization of structural and mechanical properties of hydroxyapatite-alumina-titanium nanocomposite. Ceram. Int. 45(8), 10097–10105 (2019)
S. Dasgupta et al., Effect of grain size on mechanical, surface and biological properties of microwave sintered hydroxyapatite. Mater. Sci. Eng., C 33(5), 2846–2854 (2013)
S. Sahmani et al., Effect of magnetite nanoparticles on the biological and mechanical properties of hydroxyapatite porous scaffolds coated with ibuprofen drug. Mater. Sci. Eng., C 111, 110835 (2020)
A.J. Ryan et al., Effect of different hydroxyapatite incorporation methods on the structural and biological properties of porous collagen scaffolds for bone repair. J. Anat. 227(6), 732–745 (2015)
M. Abd El-Kader et al., Morphological, ultrasonic mechanical and biological properties of hydroxyapatite layers deposited by pulsed laser deposition on alumina substrates. Surf. Coat. Technol. 409, 126861 (2021)
J.K. Abifarin, C. Prakash, S. Singh, Optimization and significance of fabrication parameters on the mechanical properties of 3D printed chitosan/PLA scaffold. Mater. Today 50, 2018–2025 (2022)
Taguchi, G. and M.S. Phadke, Quality engineering through design optimization. Quality control, robust design, and the Taguchi method, 1989: p. 77–96.
Acknowledgements
Johnson Kehinde Abifarin would like to acknowledge the financial support received from an ANU PhD. Student Scholarship.
Funding
Open Access funding enabled and organized by CAUL and its Member Institutions. This research did not receive any funding.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of the other authors, the author declares no conflict of interest.
Ethics approval
Not applicable.
Consent to participate
Not applicable.
Consent for publication
Not applicable.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Abifarin, J.K., Abifarin, F.B., Oyedeji, E.O. et al. Computational analysis on mechanostructural properties of hydroxyapatite–alumina–titanium nanocomposite. J. Korean Ceram. Soc. 60, 950–958 (2023). https://doi.org/10.1007/s43207-023-00320-6
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s43207-023-00320-6