Abstract
Let E and F be complex Banach spaces, U be an open subset of E and \(1\le p\le \infty .\) We introduce and study the notion of a Cohen strongly p-summing holomorphic mapping from U to F, a holomorphic version of a strongly p-summing linear operator. For such mappings, we establish both Pietsch Domination/Factorization Theorems and analyse their linearizations from  (the canonical predual of
(the canonical predual of  ) and their transpositions on
) and their transpositions on  Concerning the space
Concerning the space  formed by such mappings and endowed with a natural norm
formed by such mappings and endowed with a natural norm  we show that it is a regular Banach ideal of bounded holomorphic mappings generated by composition with the ideal of strongly p-summing linear operators. Moreover, we identify the space
we show that it is a regular Banach ideal of bounded holomorphic mappings generated by composition with the ideal of strongly p-summing linear operators. Moreover, we identify the space  with the dual of the completion of tensor product space
with the dual of the completion of tensor product space  endowed with the Chevet–Saphar norm \(g_p.\)
endowed with the Chevet–Saphar norm \(g_p.\)
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The linear theory of absolutely summing operators between Banach spaces was initiated by Grothendieck [11] in 1950 with the introduction of the concept of 1-summing operator. In 1967, Pietsch [22] defined the class of absolutely p-summing operators for any \(p>0\) and established many of their fundamental properties.
The nonlinear theory for such operators started with Pietsch [23] in 1983. Since then, the idea of extending the theory of absolutely p-summing operators to other settings has been developed by various authors, namely, the polynomial, multilinear, Lipschitz and holomorphic settings (see, for example, [1, 2, 7, 8, 19, 27, 28]).
Summability for holomorphic mappings was first considered by Matos in a series of papers (see e.g. [13, 14]). Our approach in this paper is different from that of Matos. Moreover, strong p-summability in the sense of Dimant [7] was also addressed for subspaces of holomorphic mappings as polynomials and multilinear mappings under the name of factorable strongly p-summing (see [20, 24, 25]). In these papers, it was proved that the ideal of factorable strongly p-summing polynomials (multilinear mappings) coincides with the ideal formed by composition with p-summing linear operators. Ideals of polynomial mappings were also studied by Floret and García [9, 10].
In 1973, Cohen [5] introduced the concept of a strongly p-summing linear operator to characterize those operators whose adjoints are absolutely \(p^*\)-summing operators, where \(p^*\) denotes the conjugate index of \(p\in (1,\infty ].\) Influenced by this class of operators, we introduce and study a new concept of summability in the category of bounded holomorphic mappings, which yields the called Cohen strongly p-summing holomorphic mappings.
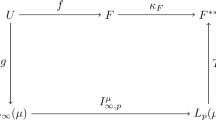
We now describe the contents of the paper. Let E and F be complex Banach spaces, U be an open subset of E and \(1\le p\le \infty .\) We denote by  the Banach space of all bounded holomorphic mappings from U to F, equipped with the supremum norm. In particular,
the Banach space of all bounded holomorphic mappings from U to F, equipped with the supremum norm. In particular,  stands for the space
stands for the space  It is known that
It is known that  is a dual Banach space whose canonical predual, denoted
is a dual Banach space whose canonical predual, denoted  is the norm-closed linear subspace of
is the norm-closed linear subspace of  generated by the evaluation functionals at the points of U.
generated by the evaluation functionals at the points of U.
In Sect. 1, we fix the notation and recall some results on the space  essentially, a remarkable linearization theorem due to Mujica [16] which is a key tool to establish our results.
essentially, a remarkable linearization theorem due to Mujica [16] which is a key tool to establish our results.
In Sect. 2, we show that the space of all Cohen strongly p-summing holomorphic mappings denoted  and equipped with a natural norm
and equipped with a natural norm  is a regular Banach ideal of bounded holomorphic mappings. Furthermore,
is a regular Banach ideal of bounded holomorphic mappings. Furthermore,  with
with 
The elements of the tensor product of two linear spaces can be viewed as linear mappings or bilinear forms (see [26, Section 1.3]). Following this idea, in Sect. 3 we introduce the tensor product \(\Delta (U)\otimes F\) as a space of linear functionals on the space  and equip this space with the known Chevet–Saphar norms \(g_p\) and \(d_p.\)
and equip this space with the known Chevet–Saphar norms \(g_p\) and \(d_p.\)
Section 4 addresses the duality theory: the space  is canonically isometrically isomorphic to the dual of the completion of the tensor product space
is canonically isometrically isomorphic to the dual of the completion of the tensor product space  In particular, we deduce that
In particular, we deduce that  is a dual space.
is a dual space.
Pietsch [22] established a Domination/Factorization Theorem for p-summing linear operators between Banach spaces. Characterizing previously the elements of the dual space of \(\Delta (U)\otimes _{g_p} F,\) we present for Cohen strongly p-summing holomorphic mappings both versions of Pietsch Domination Theorem and Pietsch Factorization Theorem in Sects. 5 and 6, respectively.
Moreover, in Sect. 5, we prove that a mapping \(f:U\rightarrow F\) is Cohen strongly p-summing holomorphic if and only if Mujica’s linearization  is a strongly p-summing operator. Several interesting applications of this fact are obtained.
is a strongly p-summing operator. Several interesting applications of this fact are obtained.
In addition, we show that the ideal  is generated by composition with the ideal
is generated by composition with the ideal  of strongly p-summing linear operators, that is, every mapping
of strongly p-summing linear operators, that is, every mapping  admits a factorization in the form \(f=T\circ g,\) for some complex Banach space G,
admits a factorization in the form \(f=T\circ g,\) for some complex Banach space G,  and
and  Moreover,
Moreover,  coincides with \(\inf \{d_p(T)\left\| g\right\| _{\infty }\},\) where the infimum is extended over all such factorizations of f, and, curiously, this infimum is attained at Mujica’s factorization of f. We also show that every
coincides with \(\inf \{d_p(T)\left\| g\right\| _{\infty }\},\) where the infimum is extended over all such factorizations of f, and, curiously, this infimum is attained at Mujica’s factorization of f. We also show that every  factors through a Hilbert space whenever F is reflexive, and establish some inclusion and coincidence properties of spaces
factors through a Hilbert space whenever F is reflexive, and establish some inclusion and coincidence properties of spaces 
These results represent advances in the research program initiated by Aron et al. [4] on the factorization of bounded holomorphic mappings in terms of an element of an operator ideal and a bounded holomorphic mapping.
Finally, we analyse holomorphic transposition of their elements and prove that every member of  has relatively weakly compact range that becomes relatively compact whenever F is reflexive. We thus contribute to the study of holomorphic mappings with relatively (weakly) compact range, begun by Mujica [16] and continued in [12].
has relatively weakly compact range that becomes relatively compact whenever F is reflexive. We thus contribute to the study of holomorphic mappings with relatively (weakly) compact range, begun by Mujica [16] and continued in [12].
2 Notation and preliminaries
Throughout this paper, unless otherwise stated, E and F will denote complex Banach spaces and U an open subset of E.
We first introduce some notation. As usual, \(B_E\) denotes the closed unit ball of E. For two vector spaces E and F, L(E, F) stands for the vector space of all linear operators from E into F. In the case that E and F are normed spaces,  represents the normed space of all bounded linear operators from E to F endowed with the canonical norm of operators. In particular, the algebraic dual \(L(E,{\mathbb {K}})\) and the topological dual
represents the normed space of all bounded linear operators from E to F endowed with the canonical norm of operators. In particular, the algebraic dual \(L(E,{\mathbb {K}})\) and the topological dual  are denoted by \(E^{\prime }\) and \(E^*,\) respectively. For each \(e\in E\) and \(e^*\in E^{\prime },\) we frequently will write \(\langle e^*,e\rangle \) instead of \(e^*(e).\) We denote by \(\kappa _E\) the canonical isometric embedding of E into \(E^{**}\) defined by \(\left\langle \kappa _E(e),e^*\right\rangle =\left\langle e^*,e\right\rangle \) for \(e\in E\) and \(e^*\in E^*.\) For a set \(A\subseteq E,\) \({\textrm{co}}(A)\) denotes the convex hull of A.
are denoted by \(E^{\prime }\) and \(E^*,\) respectively. For each \(e\in E\) and \(e^*\in E^{\prime },\) we frequently will write \(\langle e^*,e\rangle \) instead of \(e^*(e).\) We denote by \(\kappa _E\) the canonical isometric embedding of E into \(E^{**}\) defined by \(\left\langle \kappa _E(e),e^*\right\rangle =\left\langle e^*,e\right\rangle \) for \(e\in E\) and \(e^*\in E^*.\) For a set \(A\subseteq E,\) \({\textrm{co}}(A)\) denotes the convex hull of A.
We now recall some concepts and results of the theory of holomorphic mappings on Banach spaces.
Theorem 1.1
(See [18, 7 Theorem] and [15, Theorem 8.7]) Let E and F be complex Banach spaces and let U be an open set in E. For a mapping \(f:U\rightarrow F,\) the following conditions are equivalent :
-
(i)
For each \(a\in U,\) there is an operator
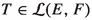 such that $$\begin{aligned} \lim _{x\rightarrow a}\frac{f(x)-f(a)-T(x-a)}{\left\| x-a\right\| }=0. \end{aligned}$$
such that $$\begin{aligned} \lim _{x\rightarrow a}\frac{f(x)-f(a)-T(x-a)}{\left\| x-a\right\| }=0. \end{aligned}$$ -
(ii)
For each \(a\in U,\) there exist an open ball \(B(a,r)\subseteq U\) and a sequence of continuous m-homogeneous polynomials \((P_{m,a})_{m\in {\mathbb {N}}_0}\) from E into F such that
$$\begin{aligned} f(x)=\sum _{m=0}^\infty P_{m,a}(x-a), \end{aligned}$$where the series converges uniformly for \(x\in B(a,r).\)
-
(iii)
f is G-holomorphic (that is, for all \(a\in U\) and \(b\in E,\) the map \(\lambda \mapsto f(a+\lambda b)\) is holomorphic on the open set \(\{\lambda \in {\mathbb {C}}:a+\lambda b\in U\})\) and continuous. \(\square \)
A mapping \(f:U\rightarrow F\) is said to be holomorphic if it verifies the equivalent conditions in Theorem 1.1. The mapping T in condition (i) is uniquely determined by f and a, and is called the differential of f at a and denoted by Df(a).
A mapping \(f:U\rightarrow F\) is locally bounded if f is bounded on a suitable neighborhood of each point of U. Given a Banach space E, a subset \(N\subseteq B_{E^*}\) is said to be norming for E if the function
defines the norm on E.
If \(U\subseteq E\) and \(V\subseteq F\) are open sets,  will represent the set of all holomorphic mappings from U to V. We will denote by
will represent the set of all holomorphic mappings from U to V. We will denote by  the linear space of all holomorphic mappings from U into F and by
the linear space of all holomorphic mappings from U into F and by  the subspace of all
the subspace of all  such that f(U) is bounded in F. When \(F={\mathbb {C}},\) then we will write
such that f(U) is bounded in F. When \(F={\mathbb {C}},\) then we will write 
It is easy to prove that the linear space  equipped with the supremum norm:
equipped with the supremum norm:

is a Banach space. Let  denote the norm-closed linear hull in
denote the norm-closed linear hull in  of the set \(\left\{ \delta (x):x\in U\right\} \) of evaluation functionals defined by
of the set \(\left\{ \delta (x):x\in U\right\} \) of evaluation functionals defined by

In [16, 17], Mujica established the following properties of 
Theorem 1.2
[16, Theorem 2.1] Let E be a complex Banach space and let U be an open set in E.
-
(i)
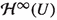 is isometrically isomorphic to
is isometrically isomorphic to 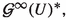 via the evaluation mapping
via the evaluation mapping 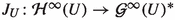 given by
given by 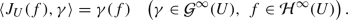
-
(ii)
The mapping
 defined by \(g_U(x)=\delta (x)\) is holomorphic with \(\left\| g_U(x)\right\| =1\) for all \(x\in U.\)
defined by \(g_U(x)=\delta (x)\) is holomorphic with \(\left\| g_U(x)\right\| =1\) for all \(x\in U.\) -
(iii)
For each complex Banach space F and each mapping
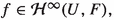 there exists a unique operator
there exists a unique operator 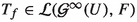 such that \(T_f\circ g_U=f.\) Furthermore, \(\left\| T_f\right\| =\left\| f\right\| _{\infty }.\)
such that \(T_f\circ g_U=f.\) Furthermore, \(\left\| T_f\right\| =\left\| f\right\| _{\infty }.\) -
(iv)
The mapping \(f\mapsto T_f\) is an isometric isomorphism from
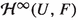 onto
onto 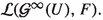
-
(v)
[16, Corollary 4.12] (see also [17, Theorem 5.1]).
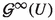 consists of all functionals
consists of all functionals 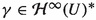 of the form \(\gamma =\sum _{i=1}^{\infty }\lambda _i\delta (x_i)\) with \((\lambda _i)_{i\ge 1}\in \ell _1\) and \((x_i)_{i\ge 1}\in U^\mathbb {N}.\) Moreover, \(\left\| \gamma \right\| =\inf \left\{ \sum _{i=1}^{\infty }\left| \lambda _i\right| \right\} \) where the infimum is taken over all such representations of \(\gamma .\) \(\square \)
of the form \(\gamma =\sum _{i=1}^{\infty }\lambda _i\delta (x_i)\) with \((\lambda _i)_{i\ge 1}\in \ell _1\) and \((x_i)_{i\ge 1}\in U^\mathbb {N}.\) Moreover, \(\left\| \gamma \right\| =\inf \left\{ \sum _{i=1}^{\infty }\left| \lambda _i\right| \right\} \) where the infimum is taken over all such representations of \(\gamma .\) \(\square \)
3 Cohen strongly p-summing holomorphic mappings
Let E and F be Banach spaces and \(1\le p\le \infty .\) Let us recall [6] that an operator  is p-summing if there exists a constant \(C\ge 0\) such that, regardless of the natural number n and regardless of the choice of vectors \(x_1,\ldots ,x_n\) in E, we have the inequalities:
is p-summing if there exists a constant \(C\ge 0\) such that, regardless of the natural number n and regardless of the choice of vectors \(x_1,\ldots ,x_n\) in E, we have the inequalities:
The infimum of such constants C is denoted by \(\pi _p(T)\) and the linear space of all p-summing operators from E into F by \(\Pi _p(E,F).\)
The analogous notion for holomorphic mappings could be introduced as follows.
Definition 2.1
Let E and F be complex Banach spaces, let U be an open subset of E, and let \(1\le p\le \infty .\) A holomorphic mapping \(f:U\rightarrow F\) is said to be p-summing if there exists a constant \(C\ge 0\) such that for all \(n\in {\mathbb {N}}\) and \(x_1,\ldots ,x_n\in U,\) we have

We denote by  the infimum of such constants C, and by
the infimum of such constants C, and by  the set of all p-summing holomorphic mappings from U into F.
the set of all p-summing holomorphic mappings from U into F.
p-Summing holomorphic mappings are of little interest to us as  with
with  for all
for all  and furthermore the subclass of p-summing holomorphic mappings that we will study in this paper includes this case.
and furthermore the subclass of p-summing holomorphic mappings that we will study in this paper includes this case.
Let \(1\le p\le \infty \) and let \(p^*\) denote the conjugate index of p given by
In [5], Cohen introduced the following subclass of p-summing operators between Banach spaces: an operator  is strongly p-summing if there exists a constant \(C\ge 0\) such that for all \(n\in {\mathbb {N}},\) \(x_1,\ldots ,x_n\in E\) and \(y^*_1,\ldots ,y^*_n\in F^*,\) we have
is strongly p-summing if there exists a constant \(C\ge 0\) such that for all \(n\in {\mathbb {N}},\) \(x_1,\ldots ,x_n\in E\) and \(y^*_1,\ldots ,y^*_n\in F^*,\) we have
The infimum of such constants C is denoted by \(d_p(T),\) and the space of all strongly p-summing operators from E into F by  If \(p=1,\) we have
If \(p=1,\) we have 
We now introduce a version of this concept in the setting of holomorphic mappings.
Definition 2.2
Let E and F be complex Banach spaces, let U be an open subset of E, and let \(1\le p\le \infty .\) A holomorphic mapping \(f:U\rightarrow F\) is said to be Cohen strongly p-summing if there exists a constant \(C\ge 0\) such that for all \(n\in {\mathbb {N}},\) \(\lambda _1,\ldots ,\lambda _n\in {\mathbb {C}},\) \(x_1,\ldots ,x_n\in U\) and \(y^*_1,\ldots ,y^*_n\in F^*,\) we have
We denote by  the infimum of such constants C, and by
the infimum of such constants C, and by  the set of all Cohen strongly p-summing holomorphic mappings from U into F.
the set of all Cohen strongly p-summing holomorphic mappings from U into F.
The introduction of the scalars \(\lambda _i\) in the previous definition is justified by the assertion (v) of Theorem 1.2. Proposition 2.5 shows that 
The concept of an ideal of bounded holomorphic mappings is inspired by the analogous one for bounded linear operators between Banach spaces [26, Section 8.2].
Definition 2.3
An ideal of bounded holomorphic mappings (or simply, a bounded-holomorphic ideal) is a subclass  of the class
of the class  of all bounded holomorphic mappings such that for each complex Banach space E, each open subset U of E and each complex Banach space F, the components
of all bounded holomorphic mappings such that for each complex Banach space E, each open subset U of E and each complex Banach space F, the components

satisfy the following properties:
-
(I1)
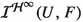 is a linear subspace of
is a linear subspace of 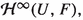
-
(I2)
For any
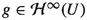 and \(y\in F,\) the mapping \(g\cdot y:x\mapsto g(x)y\) from U to F is in
and \(y\in F,\) the mapping \(g\cdot y:x\mapsto g(x)y\) from U to F is in 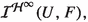
-
(I3)
The ideal property: If H, G are complex Banach spaces, V is an open subset of H,
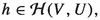
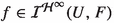 and
and 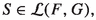 then \(S\circ f\circ h\) is in
then \(S\circ f\circ h\) is in 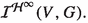
A bounded-holomorphic ideal  is said to be normed (Banach) if there exists a function
is said to be normed (Banach) if there exists a function  such that for every complex Banach space E, every open subset U of E and every complex Banach space F, the following conditions are satisfied:
such that for every complex Banach space E, every open subset U of E and every complex Banach space F, the following conditions are satisfied:
-
(N1)
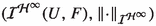 is a normed (Banach) space with
is a normed (Banach) space with 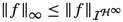 for all
for all 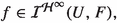
-
(N2)
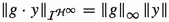 for every
for every 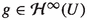 and \(y\in F,\)
and \(y\in F,\) -
(N3)
If H, G are complex Banach spaces, V is an open subset of H,
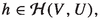
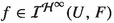 and
and 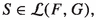 then
then 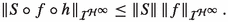
A normed bounded-holomorphic ideal  is said to be regular if for any
is said to be regular if for any  we have that
we have that  with
with  whenever
whenever 
The following class of bounded holomorphic mappings appears involved in Definition 2.3.
Lemma 2.4
Let  and \(y\in F.\) The mapping \(g\cdot y:U\rightarrow F,\) given by \((g\cdot y)(x)=g(x)y,\) belongs to
and \(y\in F.\) The mapping \(g\cdot y:U\rightarrow F,\) given by \((g\cdot y)(x)=g(x)y,\) belongs to  with \(\left\| g\cdot y\right\| _{\infty }=\left\| g\right\| _{\infty }\left\| y\right\| .\) \(\square \)
with \(\left\| g\cdot y\right\| _{\infty }=\left\| g\right\| _{\infty }\left\| y\right\| .\) \(\square \)
We are now ready to establish the main result of this section.
Proposition 2.5
 is a regular Banach ideal of bounded holomorphic mappings. Furthermore,
is a regular Banach ideal of bounded holomorphic mappings. Furthermore,  with
with 
Proof
We will only prove the case \(1<p<\infty .\) The cases \(p=1\) and \(p=\infty \) follow similarly.
(N1) We first show that  with
with  for all
for all  Indeed, given
Indeed, given  we have
we have

for all \(x\in U\) and \(y^*\in F^*.\) By Hahn–Banach Theorem, we obtain that  for all \(x\in U.\) Hence
for all \(x\in U.\) Hence  with
with 
Let  Given \(n\in {\mathbb {N}},\) \(\lambda _1,\ldots ,\lambda _n\in {\mathbb {C}},\) \(x_1,\ldots ,x_n\in U\) and \(y^*_1,\ldots ,y^*_n\in F^*,\) we have
Given \(n\in {\mathbb {N}},\) \(\lambda _1,\ldots ,\lambda _n\in {\mathbb {C}},\) \(x_1,\ldots ,x_n\in U\) and \(y^*_1,\ldots ,y^*_n\in F^*,\) we have

Using the two inequalities above, we obtain

This tells us that  with
with 
Let \(\lambda \in {\mathbb {C}}\) and  Given \(n\in {\mathbb {N}},\) \(\lambda _i\in {\mathbb {C}},\) \(x_i\in U\) and \(y^*_i\in F^*\) for \(i=1,\ldots ,n,\) we have
Given \(n\in {\mathbb {N}},\) \(\lambda _i\in {\mathbb {C}},\) \(x_i\in U\) and \(y^*_i\in F^*\) for \(i=1,\ldots ,n,\) we have

and thus  with
with  This implies that
This implies that  if \(\lambda =0.\) For \(\lambda \ne 0,\) we have
if \(\lambda =0.\) For \(\lambda \ne 0,\) we have  hence
hence  and so
and so 
Moreover, if  and
and  then \(\left\| f\right\| _{\infty }=0\) by (N1), and so \(f=0.\) Thus,
then \(\left\| f\right\| _{\infty }=0\) by (N1), and so \(f=0.\) Thus,  is a normed space.
is a normed space.
To prove that  is complete, it suffices to prove that every absolutely convergent series is convergent. So let \((f_n)_{n\in {\mathbb {N}}}\) be a sequence in
is complete, it suffices to prove that every absolutely convergent series is convergent. So let \((f_n)_{n\in {\mathbb {N}}}\) be a sequence in  such that
such that  is convergent. Since
is convergent. Since  for all \(n\in {\mathbb {N}}\) and
for all \(n\in {\mathbb {N}}\) and  is a Banach space, then \(\sum _{n\in {\mathbb {N}}}f_n\) converges in
is a Banach space, then \(\sum _{n\in {\mathbb {N}}}f_n\) converges in  to a function
to a function  Given \(m\in {\mathbb {N}},\) \(x_1,\ldots ,x_m\in U,\) \(y^*_1,\ldots ,y^*_m\in F^*\) and \(\lambda _1,\ldots ,\lambda _m\in {\mathbb {C}},\) we have
Given \(m\in {\mathbb {N}},\) \(x_1,\ldots ,x_m\in U,\) \(y^*_1,\ldots ,y^*_m\in F^*\) and \(\lambda _1,\ldots ,\lambda _m\in {\mathbb {C}},\) we have

for all \(n\in {\mathbb {N}},\) and by taking limits with \(n\rightarrow \infty \) yields

Hence  with
with  Moreover, we have
Moreover, we have

for all \(n\in {\mathbb {N}},\) and thus f is the  -limit of the series \(\sum _{n\in {\mathbb {N}}}f_n.\)
-limit of the series \(\sum _{n\in {\mathbb {N}}}f_n.\)
(N2) Let  and \(y\in F.\) If \(y=0,\) there is nothing to prove. Assume \(y\ne 0.\) By Lemma 2.4,
and \(y\in F.\) If \(y=0,\) there is nothing to prove. Assume \(y\ne 0.\) By Lemma 2.4,  Given \(n\in {\mathbb {N}},\) \(x_1,\ldots ,x_n\in U,\) \(y^*_1,\ldots ,y^*_n\in F^*\) and \(\lambda _1,\ldots ,\lambda _n\in {\mathbb {C}},\) we have
Given \(n\in {\mathbb {N}},\) \(x_1,\ldots ,x_n\in U,\) \(y^*_1,\ldots ,y^*_n\in F^*\) and \(\lambda _1,\ldots ,\lambda _n\in {\mathbb {C}},\) we have
by applying the Hölder inequality, and therefore  with
with  Conversely, by applying what was proved in (N1), we have
Conversely, by applying what was proved in (N1), we have 
(N3) Let H, G be complex Banach spaces, V be an open subset of H, 
 and
and  We can suppose \(S\ne 0.\) Given \(n\in {\mathbb {N}},\) \(x_1,\ldots ,x_n\in U,\) \(y^*_1,\ldots ,y^*_n\in G^*\) and \(\lambda _1,\ldots ,\lambda _n\in {\mathbb {C}},\) we have
We can suppose \(S\ne 0.\) Given \(n\in {\mathbb {N}},\) \(x_1,\ldots ,x_n\in U,\) \(y^*_1,\ldots ,y^*_n\in G^*\) and \(\lambda _1,\ldots ,\lambda _n\in {\mathbb {C}},\) we have

and therefore  with
with 
We now prove that the ideal  is regular. Let
is regular. Let  and assume that
and assume that  Given \(n\in {\mathbb {N}},\) \(x_1,\ldots ,x_n\in U,\) \(y^*_1,\ldots ,y^*_n\in F^*\) and \(\lambda _1,\ldots ,\lambda _n\in {\mathbb {C}},\) we have
Given \(n\in {\mathbb {N}},\) \(x_1,\ldots ,x_n\in U,\) \(y^*_1,\ldots ,y^*_n\in F^*\) and \(\lambda _1,\ldots ,\lambda _n\in {\mathbb {C}},\) we have

and thus  with
with  The reverse inequality follows from (N3).
The reverse inequality follows from (N3).
Finally, we have seen in (N1) that  with
with  for all
for all  For the converse, let
For the converse, let  If \(f=0,\) there is nothing to prove. Assume \(f\ne 0.\) Given \(n\in {\mathbb {N}},\) \(x_1,\ldots ,x_n\in U,\) \(y^*_1,\ldots ,y^*_n\in F^*\) and \(\lambda _1,\ldots ,\lambda _n\in {\mathbb {C}},\) we have
If \(f=0,\) there is nothing to prove. Assume \(f\ne 0.\) Given \(n\in {\mathbb {N}},\) \(x_1,\ldots ,x_n\in U,\) \(y^*_1,\ldots ,y^*_n\in F^*\) and \(\lambda _1,\ldots ,\lambda _n\in {\mathbb {C}},\) we have
and therefore  with
with  \(\square \)
\(\square \)
4 The tensor product \(\Delta (U)\otimes F\)
We introduce \(\Delta (U)\otimes F\) as a space of linear functionals on 
Definition 3.1
Let E and F be complex Banach spaces and let U be an open subset of E. For each \(x\in U,\) let  be the linear functional defined by
be the linear functional defined by

Let \(\Delta (U)\) be the linear subspace of  spanned by the set \(\left\{ \delta (x):x\in U\right\} .\)
spanned by the set \(\left\{ \delta (x):x\in U\right\} .\)
For any \(x\in U\) and \(y\in F,\) let  be the linear functional given by
be the linear functional given by

We define the tensor product \(\Delta (U)\otimes F\) as the linear subspace of  spanned by the set
spanned by the set
We say that \(\delta (x)\otimes y\) is an elementary tensor of \(\Delta (U)\otimes F.\) Note that each element u in \(\Delta (U)\otimes F\) is of the form \(u=\sum _{i=1}^n\lambda _i(\delta (x_i)\otimes y_i),\) where \(n\in {\mathbb {N}},\) \(\lambda _i\in {\mathbb {C}},\) \(x_i\in U\) and \(y_i\in F\) for \(i=1,\ldots ,n.\) This representation of u is not unique. It is worth noting that each element u of \(\Delta (U)\otimes F\) can be represented as \(u=\sum _{i=1}^n \delta (x_i)\otimes y_i\) since \(\lambda (\delta (x)\otimes y)=\delta (x)\otimes (\lambda y).\)
As a straightforward consequence from Definition 3.1, we describe the action of a tensor u in \(\Delta (U)\otimes F\) on a function f in  :
:
Lemma 3.2
Let \(u=\sum _{i=1}^n \lambda _i\delta (x_i)\otimes y_i\in \Delta (U)\otimes F\) and  Then
Then
\(\Box \)
The following characterization of the zero tensor of \(\Delta (U)\otimes F\) follows immediately from [26, Proposition 1.2].
Proposition 3.3
If \(u=\sum _{i=1}^n\delta (x_i)\otimes y_i\in \Delta (U)\otimes F,\) the following are equivalent :
-
(i)
\(u=0.\)
-
(ii)
\(\sum _{i=1}^ng(x_i)\phi (y_i)=0\) for every
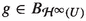 and \(\phi \in B_{F^*}.\) \(\Box \)
and \(\phi \in B_{F^*}.\) \(\Box \)
By Definition 3.1, \(\Delta (U)\otimes F\) is a linear subspace of  In fact, we have:
In fact, we have:
Proposition 3.4
 forms a dual pair, where the bilinear form \(\left\langle \cdot ,\cdot \right\rangle \) associated to the dual pair is given by
forms a dual pair, where the bilinear form \(\left\langle \cdot ,\cdot \right\rangle \) associated to the dual pair is given by
for \(u=\sum _{i=1}^n\lambda _i \delta (x_i)\otimes y_i\in \Delta (U)\otimes F\) and 
Proof
Since \(\langle u,f\rangle =u(f)\) by Lemma 3.2, it is immediate that \(\langle \cdot ,\cdot \rangle \) is a well-defined bilinear map from  to \({\mathbb {C}.}\) On the one hand, if \(u\in \Delta (U)\otimes F\) and \(\langle u,f\rangle =0\) for all
to \({\mathbb {C}.}\) On the one hand, if \(u\in \Delta (U)\otimes F\) and \(\langle u,f\rangle =0\) for all  then \(u=0\) follows easily from Proposition 3.3, and thus
then \(u=0\) follows easily from Proposition 3.3, and thus  separates points of \(\Delta (U)\otimes F.\) On the other hand, if
separates points of \(\Delta (U)\otimes F.\) On the other hand, if  and \(\langle u,f\rangle =0\) for all \(u\in \Delta (U)\otimes F,\) then \(\left\langle f(x),y\right\rangle =\left\langle \delta (x)\otimes y,f\right\rangle =0\) for all \(x\in U\) and \(y\in F,\) this means that \(f=0\) and thus \(\Delta (U)\otimes F\) separates points of
and \(\langle u,f\rangle =0\) for all \(u\in \Delta (U)\otimes F,\) then \(\left\langle f(x),y\right\rangle =\left\langle \delta (x)\otimes y,f\right\rangle =0\) for all \(x\in U\) and \(y\in F,\) this means that \(f=0\) and thus \(\Delta (U)\otimes F\) separates points of  \(\square \)
\(\square \)
Since  is a dual pair, we can identify
is a dual pair, we can identify  with a linear subspace of \((\Delta (U)\otimes F)^{\prime }\) as follows.
with a linear subspace of \((\Delta (U)\otimes F)^{\prime }\) as follows.
Corollary 3.5
For each  the functional \(\Lambda _0(f):\Delta (U)\otimes F\rightarrow {\mathbb {C}},\) given by
the functional \(\Lambda _0(f):\Delta (U)\otimes F\rightarrow {\mathbb {C}},\) given by
for \(u=\sum _{i=1}^n \lambda _i\delta (x_i)\otimes y_i\in \Delta (U)\otimes F,\) is linear. We will say that \(\Lambda _0(f)\) is the linear functional on \(\Delta (U)\otimes F\) associated to f. Furthermore, the map \(f\mapsto \Lambda _0(f)\) is a linear monomorphism from  into \((\Delta (U)\otimes F)^{\prime }.\)
into \((\Delta (U)\otimes F)^{\prime }.\)
Proof
Let  Note that \(\Lambda _0(f)(u)=\left\langle u,f\right\rangle \) for all \(u\in \Delta (U)\otimes F.\) It is immediate that \(\Lambda _0(f)\) is a well-defined linear functional on \(\Delta (U)\otimes F\) and that \(f\mapsto \Lambda _0(f)\) from
Note that \(\Lambda _0(f)(u)=\left\langle u,f\right\rangle \) for all \(u\in \Delta (U)\otimes F.\) It is immediate that \(\Lambda _0(f)\) is a well-defined linear functional on \(\Delta (U)\otimes F\) and that \(f\mapsto \Lambda _0(f)\) from  into \((\Delta (U)\otimes F)^{\prime }\) is a well-defined linear map. Finally, let
into \((\Delta (U)\otimes F)^{\prime }\) is a well-defined linear map. Finally, let  and assume that \(\Lambda _0(f)=0.\) Then \(\left\langle u,f\right\rangle =0\) for all \(u\in \Delta (U)\otimes F.\) Since \(\Delta (U)\otimes F\) separates points of
and assume that \(\Lambda _0(f)=0.\) Then \(\left\langle u,f\right\rangle =0\) for all \(u\in \Delta (U)\otimes F.\) Since \(\Delta (U)\otimes F\) separates points of  by Proposition 3.4, it follows that \(f=0\) and this proves that \(\Lambda _0\) is one-to-one. \(\square \)
by Proposition 3.4, it follows that \(f=0\) and this proves that \(\Lambda _0\) is one-to-one. \(\square \)
Given two linear spaces E and F, the tensor product space \(E\otimes F\) equipped with a norm \(\alpha \) will be denoted by \(E\otimes _{\alpha } F,\) and the completion of \(E\otimes _{\alpha } F\) by \(E{\widehat{\otimes }}_{\alpha } F.\) If E and F are normed spaces, a cross-norm on \(E\otimes F\) is a norm \(\alpha \) such that \(\alpha (x\otimes y)=\left\| x\right\| \left\| y\right\| \) for all \(x\in E\) and \(y\in F.\)
Given two normed spaces E and F, the projective norm \(\pi \) on \(E\otimes F\) (see [26, Chapter 2]) takes the following form on \(\Delta (U)\otimes F\):
where the infimum is taken over all the representations of u as above.
We next see that, on the space \(\Delta (U)\otimes F,\) the projective norm and the norm induced by the dual norm of the supremum norm of  coincide.
coincide.
Theorem 3.6
The linear space \(\Delta (U)\otimes F\) is contained in  Moreover, \(\pi (u)=H(u)\) for all \(u\in \Delta (U)\otimes F,\) where H is the norm on \(\Delta (U)\otimes F\) defined by
Moreover, \(\pi (u)=H(u)\) for all \(u\in \Delta (U)\otimes F,\) where H is the norm on \(\Delta (U)\otimes F\) defined by

Proof
Let \(\lambda \in {\mathbb {C}},\) \(x\in U\) and \(y\in F.\) Since \(\lambda \delta (x)\otimes y\) is a linear map on  and
and
for all  then
then  with \(\left\| \lambda \delta (x)\otimes y\right\| \le \left| \lambda \right| \left\| y\right\| ,\) and thus
with \(\left\| \lambda \delta (x)\otimes y\right\| \le \left| \lambda \right| \left\| y\right\| ,\) and thus 
Let \(u\in \Delta (U)\otimes F\) and let \(\sum _{i=1}^n\lambda _i\delta (x_i)\otimes y_i\) be a representation of u. Since u is linear and
for all  we deduce that \(H(u)\le \sum _{i=1}^n\left| \lambda _i\right| \left\| y_i\right\| .\) Since this holds for each representation of u, it follows that \(H(u)\le \pi (u).\) Hence, \(H\le \pi .\) To prove that the reverse inequality, suppose by contradiction that \(H(u_0)<1<\pi (u_0)\) for some \(u_0\in \Delta (U)\otimes F.\) Denote \(B=\{u\in \Delta (U)\otimes F:\pi (u)\le 1\}.\) Clearly, B is a closed and convex set in \(\Delta (U)\otimes _\pi F.\) Applying the Hahn–Banach Separation Theorem to B and \(\{u_0\},\) we obtain a functional \(\eta \in (\Delta (U)\otimes _\pi F)^*\) such that
we deduce that \(H(u)\le \sum _{i=1}^n\left| \lambda _i\right| \left\| y_i\right\| .\) Since this holds for each representation of u, it follows that \(H(u)\le \pi (u).\) Hence, \(H\le \pi .\) To prove that the reverse inequality, suppose by contradiction that \(H(u_0)<1<\pi (u_0)\) for some \(u_0\in \Delta (U)\otimes F.\) Denote \(B=\{u\in \Delta (U)\otimes F:\pi (u)\le 1\}.\) Clearly, B is a closed and convex set in \(\Delta (U)\otimes _\pi F.\) Applying the Hahn–Banach Separation Theorem to B and \(\{u_0\},\) we obtain a functional \(\eta \in (\Delta (U)\otimes _\pi F)^*\) such that
Define \(f:U\rightarrow F^*\) by \(\langle f(x),y\rangle =\eta \left( \delta (x)\otimes y\right) \) for all \(y\in F\) and \(x\in U.\) It is easy to prove that f is well defined and  with \(\left\| f\right\| _{\infty }\le 1.\) Moreover, \(u(f)=\eta (u)\) for all \(u\in \Delta (U)\otimes F.\) Therefore \(H(u_0)\ge |u_0(f)|\ge {\textrm{Re}}\,u_0(f)={\textrm{Re}}\,\eta (u_0),\) so \(H(u_0)>1\) and this is a contradiction. \(\square \)
with \(\left\| f\right\| _{\infty }\le 1.\) Moreover, \(u(f)=\eta (u)\) for all \(u\in \Delta (U)\otimes F.\) Therefore \(H(u_0)\ge |u_0(f)|\ge {\textrm{Re}}\,u_0(f)={\textrm{Re}}\,\eta (u_0),\) so \(H(u_0)>1\) and this is a contradiction. \(\square \)
We now will define the Chevet–Saphar norms on the tensor product \(E\otimes F.\) Let E and F be normed spaces and let \(1\le p\le \infty .\) Given \(u=\sum _{i=1}^n x_i\otimes y_i\in E\otimes F,\) denote
and
If \(E=F={\mathbb {C}},\) we write \(\ell ^n_p(E)=\ell ^n_p\) and \(\ell ^{n,w}_{p^*}(F)=\ell ^{n,w}_{p^*}.\) According to [26, Section 6.2], the Chevet–Saphar norms are defined on \(E\otimes F\) by
the infimum being taken over all representations of u as \(u=\sum _{i=1}^nx_i\otimes y_i\in E\otimes F.\)
Since \(\left\| \delta (x)\right\| =1\) for all \(x\in U,\) the norm \(g_p\) on \(\Delta (U)\otimes F\) takes the form:
Notice that \(g_p\) is a cross-norm on \(\Delta (U)\otimes F.\)
We next show that \(g_1\) on \(\Delta (U)\otimes F\) is just the projective tensor norm \(\pi .\)
Proposition 3.7
\(g_1(u)=\pi (u)\) for all \(u\in \Delta (U)\otimes F.\)
Proof
Let \(u\in \Delta (U)\otimes F\) and let \(\sum _{i=1}^n\lambda _i\delta (x_i)\otimes y_i\) be a representation of u. We have
and taking the infimum over all representations of u gives \(\pi (u)\le g_1(u).\) For the reverse inequality, notice that \(g_1(\lambda \delta (x)\otimes y)\le |\lambda |\left\| y\right\| \) for all \(\lambda \in {\mathbb {C}},\) \(x\in U\) and \(y\in F.\) Since \(g_1\) is a norm on \(\Delta (U)\otimes F,\) it follows that
and taking the infimum over all representations of u yields \(g_1(u)\le \pi (u).\) \(\square \)
5 Duality for Cohen strongly p-summing holomorphic mappings
We now show that the duals of the tensor product  can be canonically identified as spaces of Cohen strongly p-summing holomorphic mappings.
can be canonically identified as spaces of Cohen strongly p-summing holomorphic mappings.
Theorem 4.1
Let \(1\le p\le \infty .\) Then  is isometrically isomorphic to
is isometrically isomorphic to  via the mapping
via the mapping  defined by
defined by
for  and \(u=\sum _{i=1}^n\lambda _i\delta (x_i)\otimes y_i\in \Delta (U)\otimes F.\) Furthermore, its inverse is given by
and \(u=\sum _{i=1}^n\lambda _i\delta (x_i)\otimes y_i\in \Delta (U)\otimes F.\) Furthermore, its inverse is given by
for  \(x\in U\) and \(y\in F.\)
\(x\in U\) and \(y\in F.\)
Proof
We prove it for \(1<p\le \infty .\) The case \(p=1\) is similarly proved.
Let  and let \(\Lambda _0(f):\Delta (U)\otimes F\rightarrow {\mathbb {C}}\) be its associate linear functional. We claim that \(\Lambda _0(f)\in (\Delta (U)\otimes _{g_p} F)^*\) with
and let \(\Lambda _0(f):\Delta (U)\otimes F\rightarrow {\mathbb {C}}\) be its associate linear functional. We claim that \(\Lambda _0(f)\in (\Delta (U)\otimes _{g_p} F)^*\) with  Indeed, given \(u=\sum _{i=1}^n\lambda _i\delta (x_i)\otimes y_i\in \Delta (U)\otimes F,\) we have
Indeed, given \(u=\sum _{i=1}^n\lambda _i\delta (x_i)\otimes y_i\in \Delta (U)\otimes F,\) we have

and taking infimum over all the representations of u, we deduce that  Since u was arbitrary, then \(\Lambda _0(f)\) is continuous on \(\Delta (U) \otimes _{g_p} F\) with
Since u was arbitrary, then \(\Lambda _0(f)\) is continuous on \(\Delta (U) \otimes _{g_p} F\) with  as claimed.
as claimed.
Since \(\Delta (U)\) is a norm-dense linear subspace of  and \(g_p\) is a cross-norm on
and \(g_p\) is a cross-norm on  then \(\Delta (U)\otimes F\) is a dense linear subspace of
then \(\Delta (U)\otimes F\) is a dense linear subspace of  and therefore also of its completion
and therefore also of its completion  Hence there is a unique continuous mapping \(\Lambda (f)\) from
Hence there is a unique continuous mapping \(\Lambda (f)\) from  to \( {\mathbb {C}}\) that extends \(\Lambda _0(f).\) Further, \(\Lambda (f)\) is linear and \(\left\| \Lambda (f)\right\| =\left\| \Lambda _0(f)\right\| .\)
to \( {\mathbb {C}}\) that extends \(\Lambda _0(f).\) Further, \(\Lambda (f)\) is linear and \(\left\| \Lambda (f)\right\| =\left\| \Lambda _0(f)\right\| .\)
Let  be the mapping so defined. Since the mapping
be the mapping so defined. Since the mapping  is a linear monomorphism by Corollary 3.5, it follows easily that \(\Lambda \) is so. To prove that \(\Lambda \) is a surjective isometry, let
is a linear monomorphism by Corollary 3.5, it follows easily that \(\Lambda \) is so. To prove that \(\Lambda \) is a surjective isometry, let  and define \(f_{\varphi }:U\rightarrow F^*\) by
and define \(f_{\varphi }:U\rightarrow F^*\) by
Given \(x\in U,\) the linearity of both \(\varphi \) and the product tensor in the second variable yields that the functional \(f_{\varphi }(x):F\rightarrow {\mathbb {C}}\) is linear, and since
for all \(y\in F,\) we deduce that \(f_{\varphi }(x)\in F^*\) with \(\Vert f_{\varphi }(x)\Vert \le \left\| \varphi \right\| .\) Since x was arbitrary, we have that \(f_{\varphi }\) is bounded with \(\left\| f_{\varphi }\right\| _{\infty }\le \left\| \varphi \right\| .\)
We now prove that \(f_{\varphi }:U\rightarrow F^*\) is holomorphic. To this end, we first claim that, for every \(y\in F,\) the function \(f_y:U\rightarrow {\mathbb {C}}\) defined by
is holomorphic. Let \(a\in U.\) Since  is holomorphic by Theorem 1.2, there exists
is holomorphic by Theorem 1.2, there exists  such that
such that
Consider the function \(T(a):E\rightarrow {\mathbb {C}}\) given by
Clearly, \(T(a)\in E^*\) and since
it follows that
Hence, \(f_y\) is holomorphic at a with \(Df_y(a)=T(a),\) and this proves our claim. Now, notice that the set \(\left\{ \kappa _F(y):y\in B_F\right\} \subseteq B_{F^{**}}\) is norming for \(F^*\) since
for every \(y^*\in F^*,\) and that \(\kappa _F(y)\circ f_{\varphi }=f_y\) for every \(y\in F\) since
for all \(x\in U.\)
We are now ready to show that \(f_{\varphi }:U\rightarrow F^*\) is holomorphic. Indeed, let \(a\in U\) and \(b\in E.\) Denote \(V=\left\{ \lambda \in {\mathbb {C}} :a+\lambda b\in U\right\} .\) Clearly, the mapping \(h:V\rightarrow U\) given by \(h(\lambda )=a+\lambda b\) is holomorphic. Since \(f_{\varphi }\circ h\) is locally bounded and \(\kappa _F(y)\circ (f_{\varphi }\circ h)=f_y\circ h\) is holomorphic on the open set \(V\subseteq {\mathbb {C}}\) for all \(y\in F,\) Proposition A.3 in [3] assures that \(f_{\varphi }\circ h\) is holomorphic. This means that \(f_{\varphi }\) is G-holomorphic but since it is also locally bounded, we deduce that \(f_{\varphi }\) is continuous by [15, Proposition 8.6]. Now, we conclude that \(f_{\varphi }\) is holomorphic by Theorem 1.1.
We now prove that  To see this, take \(n\in {\mathbb {N}},\) \(\lambda _i\in {\mathbb {C}},\) \(x_i\in U\) and \(y^{**}_i\in F^{**}\) for \(i=1,\ldots ,n.\) Let \(\varepsilon >0\) and consider the finite-dimensional subspaces \(V={\textrm{lin}}\{y^{**}_1,\ldots ,y^{**}_n\} \subseteq F^{**}\) and \(W={\textrm{lin}}\{f_{\varphi }(x_1),\ldots ,f_{\varphi }(x_n) \}\subseteq F^{*}.\) The principle of local reflexivity [6, Theorem 8.16] gives us a bounded linear operator \(T_{(\varepsilon , V,W)}:V\rightarrow F\) such that
To see this, take \(n\in {\mathbb {N}},\) \(\lambda _i\in {\mathbb {C}},\) \(x_i\in U\) and \(y^{**}_i\in F^{**}\) for \(i=1,\ldots ,n.\) Let \(\varepsilon >0\) and consider the finite-dimensional subspaces \(V={\textrm{lin}}\{y^{**}_1,\ldots ,y^{**}_n\} \subseteq F^{**}\) and \(W={\textrm{lin}}\{f_{\varphi }(x_1),\ldots ,f_{\varphi }(x_n) \}\subseteq F^{*}.\) The principle of local reflexivity [6, Theorem 8.16] gives us a bounded linear operator \(T_{(\varepsilon , V,W)}:V\rightarrow F\) such that
-
(i)
\(T_{(\varepsilon , V,W)}(y^{**})=y^{**}\) for every \(y^{**}\in V\cap \kappa _F(F),\)
-
(ii)
\((1-\varepsilon )\left\| y^{**}\right\| \le \left\| T_{(\varepsilon ,V,W)}(y^{**})\right\| \le (1+\varepsilon )\left\| y^{**}\right\| \) for every \(y^{**}\in V,\)
-
(iii)
\(\left\langle y^*,T_{(\varepsilon , V,W)}(y^{**})\right\rangle =\left\langle y^{**},y^* \right\rangle \) for every \(y^{**}\in V\) and \(y^*\in W.\)
Using (iii) and taking \(y_i=T_{(\varepsilon , V,W)}(y_i^{**}),\) we first have
Since
it follows that
By the arbitrariness of \(\varepsilon ,\) we deduce that
and this implies that  with
with 
For any \(u=\sum _{i=1}^n \lambda _i\delta (x_i)\otimes y_i\in \Delta (U)\otimes F,\) we get
Hence \(\Lambda (f_{\varphi })=\varphi \) on a dense subspace of  and, consequently, \(\Lambda (f_{\varphi })=\varphi ,\) which shows the last statement of the theorem. Moreover,
and, consequently, \(\Lambda (f_{\varphi })=\varphi ,\) which shows the last statement of the theorem. Moreover,  and the theorem holds. \(\square \)
and the theorem holds. \(\square \)
In particular, in view of Theorem 4.1 and taking into account Propositions 2.5, 3.6 and 3.7, we can identify the space  with the dual space of
with the dual space of 
Corollary 4.2
 is isometrically isomorphic to
is isometrically isomorphic to  via the mapping
via the mapping  given by
given by
for  and \(u=\sum _{i=1}^n\lambda _i\delta (x_i)\otimes y_i\in \Delta (U)\otimes F.\) Furthermore, its inverse is given by
and \(u=\sum _{i=1}^n\lambda _i\delta (x_i)\otimes y_i\in \Delta (U)\otimes F.\) Furthermore, its inverse is given by
for  \(x\in U\) and \(y\in F.\) \(\square \)
\(x\in U\) and \(y\in F.\) \(\square \)
Remark 4.3
It is known (see [26, p. 24]) that if E and F are Banach spaces, then  is isometrically isomorphic to \((E{\widehat{\otimes }}_\pi F)^*,\) via
is isometrically isomorphic to \((E{\widehat{\otimes }}_\pi F)^*,\) via  given by
given by
for  and \(\sum _{i=1}^n x_i\otimes y_i\in E\otimes F.\) Notice that the identification \(\Lambda \) in Corollary 4.2 is just \(\Phi \circ \Phi _0,\) where \(\Phi _0:f\mapsto T_f\) is the isometric isomorphism from
and \(\sum _{i=1}^n x_i\otimes y_i\in E\otimes F.\) Notice that the identification \(\Lambda \) in Corollary 4.2 is just \(\Phi \circ \Phi _0,\) where \(\Phi _0:f\mapsto T_f\) is the isometric isomorphism from  onto
onto  given in Theorem 1.2.
given in Theorem 1.2.
6 Pietsch domination for Cohen strongly p-summing holomorphic mappings
In [22], Pietsch established a domination theorem for p-summing linear operators between Banach spaces. To present a version of this theorem for Cohen strongly p-summing holomorphic mappings on Banach spaces, we first characterize the elements of the dual space of \(\Delta (U)\otimes _{g_p} F.\)
Theorem 5.1
Let \(\varphi \in (\Delta (U)\otimes F)^{\prime },\) \(C>0\) and \(1<p\le \infty .\) The following conditions are equivalent :
-
(i)
\(\left| \varphi (u)\right| \le Cg_p(u)\) for all \(u\in \Delta (U)\otimes F.\)
-
(ii)
For any representation \(\sum _{i=1}^n\lambda _i\delta (x_i)\otimes y_i\) of \(u\in \Delta (U)\otimes F,\) we have
$$\begin{aligned} \sum _{i=1}^n\left| \varphi (\lambda _i\delta (x_i)\otimes y_i)\right| \le Cg_p(u). \end{aligned}$$ -
(iii)
There exists a Borel regular probability measure \(\mu \) on \(B_{F^{*}}\) such that
$$\begin{aligned} \left| \varphi (\lambda \delta (x)\otimes y)\right| \le C\left| \lambda \right| \left\| y\right\| _{L_{p^*}(\mu )} \end{aligned}$$for all \(\lambda \in {\mathbb {C}},\) \(x\in U\) and \(y\in F,\) where
$$\begin{aligned} \left\| y\right\| _{L_{p^*}(\mu )}=\left( \int _{B_{F^{*}}}\left| y^*(y)\right| ^{p^*}\ {\textrm{d}}\mu (y^*)\right) ^{\frac{1}{p^*}}. \end{aligned}$$
Proof
\((\text {i})\ \Rightarrow \ (\text {ii})\): Let \(u\in \Delta (U)\otimes F\) and let \(\sum _{i=1}^n\lambda _i\delta (x_i)\otimes y_i\) be a representation of u. It is elementary that the function \(T:{\mathbb {C}}^n\rightarrow {\mathbb {C}}\) defined by
is linear and continuous on \(({\mathbb {C}}^n,\left\| \cdot \right\| _{\ell _{\infty }^n})\) with \(\left\| T\right\| =\sum _{i=1}^n\left| \varphi (\lambda _i\delta (x_i)\otimes y_i)\right| .\)
For any \((t_1,\ldots ,t_n)\in {\mathbb {C}}^n\) with \(\left\| (t_1,\ldots ,t_n)\right\| _{\ell _{\infty }^n}\le 1,\) by (i) we have
and, therefore,
Taking infimum over all the representations of u, we deduce that
\((\text {ii})\ \Rightarrow \ (\text {iii})\): Let  be the set of all Borel regular probability measures \(\mu \) on \(B_{F^*}.\) Clearly, it is a convex compact subset of \((C(B_{F^*})^*,w^*).\) Assume first \(1<p<\infty .\) Let M be set of all functions from
be the set of all Borel regular probability measures \(\mu \) on \(B_{F^*}.\) Clearly, it is a convex compact subset of \((C(B_{F^*})^*,w^*).\) Assume first \(1<p<\infty .\) Let M be set of all functions from  to \({\mathbb {R}}\) of the form
to \({\mathbb {R}}\) of the form
where \(n\in {\mathbb {N}},\) \(\lambda _{i}\in {\mathbb {C}},\) \(x_{i}\in U\) and \(y_{i}\in F\) for \(i=1,\ldots ,n.\)
It is easy check that M satisfies the three conditions of Ky Fan’s Lemma (see [6, 9.10]):
-
(a)
Each \(f_{((\lambda _{i})_{i=1}^{n},(x_{i})_{i=1}^{n},(y_{i})_{i=1}^{n})}\in M\) is convex and lower semicontinuous.
-
(b)
If \(g\in {\textrm{co}}(M),\) there is \(f_{((\lambda _{i})_{i=1}^{n},(x_{i})_{i=1}^{n},(y_{i})_{i=1}^{n})}{\in }M\) with \(g(\mu ){\le } f_{((\lambda _{i})_{i=1}^{n},(x_{i})_{i=1}^{n},(y_{i})_{i=1}^{n})} (\mu )\) for all
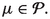
-
(c)
Each \(f_{((\lambda _{i})_{i=1}^{n},(x_{i})_{i=1}^{n},(y_{i})_{i=1}^{n})}\in M\) has a value less or equal than 0.
By Ky Fan’s Lemma, there is a  such that \(f(\mu )\le 0\) for all \(f\in M.\) In particular, we have
such that \(f(\mu )\le 0\) for all \(f\in M.\) In particular, we have
for all \(t\in {\mathbb {R}}^{+},\) \(\lambda \in {\mathbb {C}},\) \(x\in U\) and \(y\in F.\) It follows that
and, applying again the aforementioned identity, we conclude that
The case \(p=\infty \) is similarly proved but without applying the cited identity and taking \(C/p=0\) and \(p^*=1.\)
\((\text {iii})\ \Rightarrow \ (\text {i})\): Let \(u\in \Delta (U)\otimes F\) and let \( \sum _{i=1}^n\lambda _i\delta (x_i)\otimes y_i\) be a representation of u. Using (iii) and the Hölder inequality, we obtain
and taking infimum over all the representations of u, we conclude that \(\left| \varphi (u)\right| \le Cg_p(u).\) \(\square \)
We are now ready to present the announced result. Compare to [5, Theorem 2.3.1].
Theorem 5.2
(Pietsch Domination) Let \(1<p\le \infty \) and  The following conditions are equivalent :
The following conditions are equivalent :
-
(i)
f is Cohen strongly p-summing holomorphic.
-
(ii)
For any \(\sum _{i=1}^n\lambda _i\delta (x_i)\otimes y^*_i\in \Delta (U)\otimes F^*,\) we have
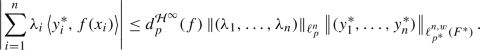
-
(iii)
There is a constant \(C>0\) and a Borel regular probability measure \(\mu \) on \(B_{F^{**}}\) such that
$$\begin{aligned} \left| \left\langle y^*,f(x)\right\rangle \right| \le C\left\| y^*\right\| _{L_{p^*}(\mu )} \end{aligned}$$for all \(x\in U\) and \(y^*\in F^*,\) where
$$\begin{aligned} \left\| y^*\right\| _{L_{p^*}(\mu )}=\left( \int _{B_{F^{**}}}\left| y^{**}(y^*)\right| ^{p^*}d\mu (y^{**})\right) ^{\frac{1}{p^*}}. \end{aligned}$$
In this case,  is the minimum of all constants \(C>0\) satisfying the preceding inequality.
is the minimum of all constants \(C>0\) satisfying the preceding inequality.
Proof
\((\text {i})\ \Rightarrow \ (\text {ii})\) is immediate from Definition 2.2.
\((\text {ii})\ \Rightarrow \ (\text {iii})\): Clearly,  Appealing to Corollary 3.5, consider its associate linear functional \(\Lambda _0(\kappa _F\circ f):\Delta (U)\otimes F^*\rightarrow {\mathbb {C}}.\) Given \(u=\sum _{i=1}^n\lambda _i\delta (x_i)\otimes y^*_i\in \Delta (U)\otimes F^*,\) we have
Appealing to Corollary 3.5, consider its associate linear functional \(\Lambda _0(\kappa _F\circ f):\Delta (U)\otimes F^*\rightarrow {\mathbb {C}}.\) Given \(u=\sum _{i=1}^n\lambda _i\delta (x_i)\otimes y^*_i\in \Delta (U)\otimes F^*,\) we have

by (ii). Since it holds for each representation of u, we deduce that

By Theorem 5.1, there exists a Borel regular probability measure \(\mu \) on \(B_{F^{**}}\) such that

for all \(x\in U\) and \(y^*\in F^*.\) Moreover,  belongs to the set of all constants \(C>0\) satisfying the inequality in (iii).
belongs to the set of all constants \(C>0\) satisfying the inequality in (iii).
\((\text {iii})\ \Rightarrow \ (\text {i})\): Given \(x\in U\) and \(y^*\in F^*,\) we have
by applying (iii). Now, Theorem 5.1 tells us that for any representation \(\sum _{i=1}^n\lambda _i\delta (x_i)\otimes y^*_i\) of \(u\in \Delta (U)\otimes F^*,\) we have
Hence  with
with  This also shows the last assertion of the statement. \(\square \)
This also shows the last assertion of the statement. \(\square \)
Remark 5.3
Theorem 5.2 is mainly a particular case of Theorem 4.6 in [21] since a Cohen strongly p-summing holomorphic mapping \((1<p<\infty )\) is an \(R_1,R_2-S\)-abstract \((p,p^*)\)-summing mapping for \(R_1:[0,1]\times U\times {\mathbb {C}}\rightarrow [0,\infty )\) defined by
\(R_2:B_{F^{**}}\times U\times F^*\rightarrow [0,\infty )\) given by
and  defined by
defined by
This unified abstract version of Pietsch Domination Theorem has been used by several authors whenever trying to get a domination result in a very short way. Our proof is also short and appeals directly to Ky Fan’s Lemma as it was made to establish such an abstract version.
We now study the relationship between a Cohen strongly p-summing holomorphic mapping from U to F and its associate linearization from  to F.
to F.
Theorem 5.4
Let \(1<p\le \infty \) and  The following conditions are equivalent :
The following conditions are equivalent :
-
(i)
\(f:U\rightarrow F\) is Cohen strongly p-summing holomorphic.
-
(ii)
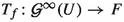 is strongly p-summing.
is strongly p-summing.
In this case,  Furthermore, the mapping \(f\mapsto T_f\) is an isometric isomorphism from
Furthermore, the mapping \(f\mapsto T_f\) is an isometric isomorphism from  onto
onto 
Proof
\((\text {i})\ \Rightarrow \ (\text {ii})\): Assume that  By Theorem 5.2, there is a constant \(C>0\) and a Borel regular probability measure \(\mu \) on \(B_{F^{**}}\) such that \(\left| \left\langle y^*,f(x)\right\rangle \right| \le C\left\| y^*\right\| _{L_{p^*}(\mu )}\) for all \(x\in U\) and \(y^*\in F^*.\)
By Theorem 5.2, there is a constant \(C>0\) and a Borel regular probability measure \(\mu \) on \(B_{F^{**}}\) such that \(\left| \left\langle y^*,f(x)\right\rangle \right| \le C\left\| y^*\right\| _{L_{p^*}(\mu )}\) for all \(x\in U\) and \(y^*\in F^*.\)
Let \(y^*\in F^*\) and  By Theorem 1.2, given \(\varepsilon >0,\) we can take a representation \(\sum _{i=1}^{\infty }\lambda _{i}\delta (x_i)\) of \(\gamma \) such that \(\sum _{i=1}^{\infty }\left| \lambda _i\right| \le \left\| \gamma \right\| +\varepsilon .\) We have
By Theorem 1.2, given \(\varepsilon >0,\) we can take a representation \(\sum _{i=1}^{\infty }\lambda _{i}\delta (x_i)\) of \(\gamma \) such that \(\sum _{i=1}^{\infty }\left| \lambda _i\right| \le \left\| \gamma \right\| +\varepsilon .\) We have
As \(\varepsilon \) was arbitrary, it follows that
Taking infimum over all such constants C, we have

by Theorem 5.2. It follows that

for all  Therefore
Therefore  with
with  by Pietsch Domination Theorem for strongly p-summing operators [5, Theorem 2.3.1].
by Pietsch Domination Theorem for strongly p-summing operators [5, Theorem 2.3.1].
\((\text {ii})\ \Rightarrow \ (\text {i})\): Assume that  Given \(x\in U\) and \(y^*\in F^*,\) we have
Given \(x\in U\) and \(y^*\in F^*,\) we have
by [5, Theorem 2.3.1] for some Borel regular probability measure \(\mu \) on \(B_{F^{**}}.\) It follows that  with
with  by Theorem 5.2.
by Theorem 5.2.
Since  for all
for all  to prove the last assertion of the statement, it suffices to show that the mapping \(f\mapsto T_{f}\) from
to prove the last assertion of the statement, it suffices to show that the mapping \(f\mapsto T_{f}\) from  to
to  is surjective. Indeed, take
is surjective. Indeed, take  and then \(T=T_{f}\) for some
and then \(T=T_{f}\) for some  by Theorem 1.2. Hence
by Theorem 1.2. Hence  and thus
and thus  by the above proof. \(\square \)
by the above proof. \(\square \)
The equivalence \((\text {i})\ \Leftrightarrow \ (\text {iii})\) of Theorem 5.2 admits the following reformulation.
Corollary 5.5
Let \(1<p\le \infty \) and  The following conditions are equivalent :
The following conditions are equivalent :
-
(i)
\(f:U\rightarrow F\) is Cohen strongly p-summing holomorphic.
-
(ii)
There exists a complex Banach space G and an operator
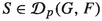 such that $$\begin{aligned} \left| \left\langle y^*,f(x)\right\rangle \right| \le \left\| S^*(y^*)\right\| \quad (x\in U,\; y^*\in F^*). \end{aligned}$$
such that $$\begin{aligned} \left| \left\langle y^*,f(x)\right\rangle \right| \le \left\| S^*(y^*)\right\| \quad (x\in U,\; y^*\in F^*). \end{aligned}$$
In this case,  is the infimum of all \(d_p(S)\) with S satisfying (ii), and this infimum is attained at \(T_f\) (Mujica’s linearization of f).
is the infimum of all \(d_p(S)\) with S satisfying (ii), and this infimum is attained at \(T_f\) (Mujica’s linearization of f).
Proof
\((\text {i})\ \Rightarrow \ (\text {ii})\): If  then
then  with
with  by Theorem 5.4. From Theorem 1.2, we infer that
by Theorem 5.4. From Theorem 1.2, we infer that
for all \(x\in U\) and \(y^*\in F^*.\)
\((\text {ii})\ \Rightarrow \ (\text {i})\): Assume that (ii) holds. Then \(S^*\in \Pi _{p^*}(F^*,G^*)\) with \(\pi _{p^*}(S^*)=d_p(S)\) by [5, Theorem 2.2.2]. By Pietsch Domination Theorem for p-summing linear operators (see [6, Theorem 2.12]), there is a Borel regular probability measure \(\mu \) on \(B_{F^{**}}\) such that
for all \(y^*\in F^*.\) For any \(x\in U\) and \(y^*\in F^*,\) it follows that
Hence,  with
with  by Theorem 5.2. \(\square \)
by Theorem 5.2. \(\square \)
As a consequence of Theorem 5.4, an application of [4, Theorem 3.2] shows that the Banach ideal  is generated by composition with the Banach operator ideal
is generated by composition with the Banach operator ideal  but we prefer to give here a proof to complete the information.
but we prefer to give here a proof to complete the information.
Corollary 5.6
Let \(1<p\le \infty \) and  The following conditions are equivalent :
The following conditions are equivalent :
-
(i)
\(f:U\rightarrow F\) is Cohen strongly p-summing holomorphic.
-
(ii)
There is a complex Banach space G,
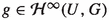 and
and 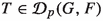 so that \(f=T\circ g.\)
so that \(f=T\circ g.\)
In this case,  where the infimum is taken over all factorizations of f as in (ii), and this infimum is attained at \(T_f\circ g_U\) (Mujica’s factorization of f).
where the infimum is taken over all factorizations of f as in (ii), and this infimum is attained at \(T_f\circ g_U\) (Mujica’s factorization of f).
Proof
\((\text {i})\ \Rightarrow \ (\text {ii})\): If  we have \(f=T_f\circ g_U,\) where
we have \(f=T_f\circ g_U,\) where  is a complex Banach space,
is a complex Banach space,  and
and  by Theorems 1.2 and 5.4. Moreover,
by Theorems 1.2 and 5.4. Moreover,

\((\text {ii})\ \Rightarrow \ (\text {i})\): Assume \(f=T\circ g\) with G, g and T being as in (ii). Since \(g=T_g\circ g_U\) by Theorem 1.2, it follows that \(f=T\circ T_g\circ g_U\) which implies that \(T_f=T\circ T_g,\) and thus  by the ideal property of
by the ideal property of  By Theorem 5.4, we obtain that
By Theorem 5.4, we obtain that  with
with

and so  by taking the infimum over all factorizations of f. \(\square \)
by taking the infimum over all factorizations of f. \(\square \)
When F is reflexive, every  factors through a Hilbert space as we see below.
factors through a Hilbert space as we see below.
Corollary 5.7
Let F be a reflexive complex Banach space. If  then there exist a Hilbert space H, an operator
then there exist a Hilbert space H, an operator  and a mapping
and a mapping  such that \(f=T\circ g.\)
such that \(f=T\circ g.\)
Proof
Assume that  By Theorem 5.4,
By Theorem 5.4,  Hence
Hence  by [5, Theorem 2.2.2]. By [6, Corollary 2.16 and Examples 2.9 (b)], there exist a Hilbert space H and operators \(T_1\in \Pi _2(F^*,H)\) and
by [5, Theorem 2.2.2]. By [6, Corollary 2.16 and Examples 2.9 (b)], there exist a Hilbert space H and operators \(T_1\in \Pi _2(F^*,H)\) and  such that \((T_f)^*=T_2\circ T_1.\)
such that \((T_f)^*=T_2\circ T_1.\)
On the one hand, we have \((T_f)^{**}=(T_1)^*\circ (T_2)^*,\) where  by [5, Theorem 2.2.2]. On the other hand, we have
by [5, Theorem 2.2.2]. On the other hand, we have  with \(\kappa _F\) being bijective (since F is reflexive). Consequently, we obtain \(f=T\circ g,\) where
with \(\kappa _F\) being bijective (since F is reflexive). Consequently, we obtain \(f=T\circ g,\) where  and
and  \(\square \)
\(\square \)
Applying Theorem 5.4 and [5, Theorem 2.4.1], we get useful inclusion relations.
Corollary 5.8
Let \(1<p_1\le p_2\le \infty .\) If  then
then  and
and  \(\square \)
\(\square \)
These inclusion relations can become coincidence relations when \(F^*\) has cotype 2 (see [6, pp. 217–221] for definitions and results on this class of spaces). Compare to [6, Corollary 11.16].
Corollary 5.9
Let \(2<p\le \infty .\) If \(F^*\) has cotype 2, then  and
and  for all
for all 
Proof
By Corollary 5.8, we have  with
with  for all
for all 
For the converse, let  Then
Then  with
with  by Theorem 5.4. Hence
by Theorem 5.4. Hence  with \(\pi _2((T_{f})^*)=d_2(T_f)\) by [5, Theorem 2.2.2]. Then, by [6, Corollary 11.16],
with \(\pi _2((T_{f})^*)=d_2(T_f)\) by [5, Theorem 2.2.2]. Then, by [6, Corollary 11.16],  with \(\pi _1((T_{f})^*)=\pi _2((T_f)^*).\) Hence,
with \(\pi _1((T_{f})^*)=\pi _2((T_f)^*).\) Hence,  with \(\pi _{p^*}((T_{f})^*)\le \pi _1((T_f)^*)\) by [6, Theorem 2.8]. Then, by [5, Theorem 2.2.2],
with \(\pi _{p^*}((T_{f})^*)\le \pi _1((T_f)^*)\) by [6, Theorem 2.8]. Then, by [5, Theorem 2.2.2],  with \(d_p(T_{f})=\pi _{p^*}((T_f)^*).\)
with \(d_p(T_{f})=\pi _{p^*}((T_f)^*).\)
Finally,  with
with  by Theorem 5.4, and therefore
by Theorem 5.4, and therefore  \(\square \)
\(\square \)
Given  the transpose of f is the mapping
the transpose of f is the mapping  defined by
defined by
It is known (see [12, Proposition 1.6]) that  with \(\Vert f^t\Vert =\left\| f\right\| _{\infty }.\) Furthermore, \(f^t=J^{-1}_U\circ (T_f)^*\) with
with \(\Vert f^t\Vert =\left\| f\right\| _{\infty }.\) Furthermore, \(f^t=J^{-1}_U\circ (T_f)^*\) with  being the identification established in Theorem 1.2.
being the identification established in Theorem 1.2.
The next result establishes the relation of a Cohen strongly p-summing holomorphic mapping \(f:U\rightarrow F\) and its transpose  Compare to [5, Theorem 2.2.2].
Compare to [5, Theorem 2.2.2].
Theorem 5.10
Let \(1<p\le \infty \) and  Then
Then  if and only if
if and only if  In this case,
In this case, 
Proof
Applying Theorem 5.4, [5, Theorem 2.2.2] and [6, 2.4 and 2.5], respectively, we have

In this case,  \(\square \)
\(\square \)
The study of holomorphic mappings with relatively (weakly) compact range was initiated by Mujica [16] and followed in [12].
Corollary 5.11
Let \(1<p\le \infty .\)
-
(i)
Every Cohen strongly p-summing holomorphic mapping \(f:U\rightarrow F\) has relatively weakly compact range.
-
(ii)
If F is reflexive, then every Cohen strongly p-summing holomorphic mapping \(f:U\rightarrow F\) has relatively compact range.
Proof
If  then
then  by Theorem 5.10. Hence the linear operator \(f^t\) is weakly compact and completely continuous by [6, 2.17]. Since \(f^t\) is weakly compact, this means that f has relatively weakly compact range by [12, Theorem 2.7]. Since \(f^t\) is completely continuous and \(F^*\) is reflexive, it is known that \(f^t\) is compact and, equivalently, f has relatively compact range by [12, Theorem 2.2]. \(\square \)
by Theorem 5.10. Hence the linear operator \(f^t\) is weakly compact and completely continuous by [6, 2.17]. Since \(f^t\) is weakly compact, this means that f has relatively weakly compact range by [12, Theorem 2.7]. Since \(f^t\) is completely continuous and \(F^*\) is reflexive, it is known that \(f^t\) is compact and, equivalently, f has relatively compact range by [12, Theorem 2.2]. \(\square \)
7 Pietsch factorization for Cohen strongly p-summing holomorphic mappings
We devote this section to the analogue of Pietsch Factorization Theorem for p-summing linear operators [6, Theorem 2.13] for the class of Cohen strongly p-summing holomorphic mappings. Recall that, for every Banach space F, we have the canonical isometric injections \(\kappa _F:F\rightarrow F^{**}\) and \(\iota _F:F\rightarrow C\left( B_{F^*}\right) \) defined, respectively, by
Moreover, if \(\mu \) is a regular Borel measure on \((B_{F^{**}},w^*),\) \(j_{p}\) denotes the canonical map from \(C\left( B_{F^*}\right) \) to \(L_{p}\left( \mu \right) .\)
Theorem 6.1
(Pietsch Factorization) Let \(1<p\le \infty \) and  The following conditions are equivalent :
The following conditions are equivalent :
-
(i)
\(f:U\rightarrow F\) is Cohen strongly p-summing holomorphic.
-
(ii)
There exist a regular Borel probability measure \(\mu \) on \((B_{F^{**}},w^*),\) a closed subspace \(S_{p^*}\) of \(L_{p^*}(\mu )\) and a bounded holomorphic mapping \(g:U\rightarrow (S_{p^*})^*\) such that the following diagram commutes :
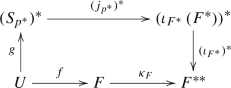
In this case, 
Proof
\((\text {i})\ \Rightarrow \ (\text {ii})\): Let  Then
Then  by Theorem 5.10. By [6, Theorem 2.13], there exist a regular Borel probability measure \(\mu \) on \((B_{F^{**}},w^*),\) a subspace \(S_{p^*}:=\overline{j_{p^*}\left( i_{F^*}\left( F^*\right) \right) }\) of \(L_{p^*}(\mu ),\) and an operator
by Theorem 5.10. By [6, Theorem 2.13], there exist a regular Borel probability measure \(\mu \) on \((B_{F^{**}},w^*),\) a subspace \(S_{p^*}:=\overline{j_{p^*}\left( i_{F^*}\left( F^*\right) \right) }\) of \(L_{p^*}(\mu ),\) and an operator  with \(\left\| T\right\| =\Vert f^t\Vert \) such that the following diagram commutes:
with \(\left\| T\right\| =\Vert f^t\Vert \) such that the following diagram commutes:

Dualizing, we obtain

Let \(g:=T^*\circ g_U.\) Clearly,  with \(\left\| g\right\| _{\infty }\le \left\| T\right\| ,\) and thus
with \(\left\| g\right\| _{\infty }\le \left\| T\right\| ,\) and thus

Moreover, since \(f^t=T\circ j_{p^*}\circ \iota _{F^*},\) we have
\((\text {ii})\ \Rightarrow \ (\text {i})\): Since \(\kappa _{F}\circ f=(\iota _{F^*})^*\circ (j_{p^*})^*\circ g,\) it follows that \(f^{t}\circ (\kappa _F)^*=((\iota _{F^*})^*\circ (j_{p^*})^*\circ g)^t.\) As \((\kappa _{F})^*\circ \kappa _{F^*}=\textrm{id}_{F^*},\) we obtain that
Since \(j_{p^*}\in \Pi _{p^*}(\iota _{F^*}(F^*),S_{p^*})\) (see [6, Examples 2.9]), then

by [5, Theorem 2.2.2]. Hence  with
with

by the ideal property of  Corollary 5.6 and [5, Theorem 2.2.2]. Applying Theorem 5.10 and the ideal property of \(\Pi _p,\) we deduce that
Corollary 5.6 and [5, Theorem 2.2.2]. Applying Theorem 5.10 and the ideal property of \(\Pi _p,\) we deduce that  Again, Theorem 5.10 gives that
Again, Theorem 5.10 gives that  with
with  Moreover,
Moreover,

\(\square \)
References
Achour, D., Mezrag, L.: On the Cohen strongly \(p\)-summing multilinear operators. J. Math. Anal. Appl. 327(1), 550–563 (2007)
Angulo-López, J.C., Fernández-Unzueta, M.: Lipschitz \(p\)-summing multilinear operators. J. Funct. Anal. 279(4), 108572 (2020)
Arendt, W., Batty, C.J.K., Hieber, M., Neubrander, F.: Vector-Valued Laplace Transforms and Cauchy Problems. Monographs in Mathematics, vol. 96. Birkhäuser, Basel (2001)
Aron, R., Botelho, G., Pellegrino, D., Rueda, P.: Holomorphic mappings associated to composition ideals of polynomials. Atti Accad. Naz. Lincei Rend. Lincei Mat. Appl. 21(3), 261–274 (2010)
Cohen, J.S.: Absolutely \(p\)-summing, \(p\)-nuclear operators and their conjugates. Math. Ann. 201, 177–200 (1973)
Diestel, J., Jarchow, H., Tonge, A.: Absolutely Summing Operators. Cambridge Studies in Advanced Mathematics, vol. 43. Cambridge University Press, Cambridge (1995)
Dimant, V.: Strongly \(p\)-summing multilinear mappings. J. Math. Anal. Appl. 278, 182–193 (2003)
Farmer, J., Johnson, W.B.: Lipschitz \(p\)-summing operators. Proc. Am. Math. Soc. 137, 2989–2995 (2009)
Floret, K.: On Ideals of n-Homogeneous Polynomials on Banach Spaces. Topological Algebras with Applications to Differential Geometry and Mathematical Physics (Athens, 1999), pp. 19–38. University of Athens, Athens (2002)
Floret, K., García, D.: On ideals of polynomials and multilinear mappings between Banach spaces. Arch. Math. (Basel) 81(3), 300–308 (2003)
Grothendieck, A.: Produits tensoriels topologiques et espaces nucléaires, vol. 16. Memoirs American Mathematical Society, Providence (1955)
Jiménez-Vargas, A., Ruiz-Casternado, D., Sepulcre, J.M.: On holomorphic mappings with compact type range. Bull. Malays. Math. Sci. Soc. 46, 20 (2023). https://doi.org/10.1007/s40840-022-01415-9
Matos, M.C.: Absolutely summing holomorphic mappings. An. Acad. Bras. Cienc. 68, 1–13 (1996)
Matos, M.C.: Nonlinear absolutely summing mappings. Math. Nachr. 258, 71–89 (2003)
Mujica, J.: Complex Analysis in Banach spaces. Dover Publications, New York (2010)
Mujica, J.: Linearization of bounded holomorphic mappings on Banach spaces. Trans. Am. Math. Soc. 324, 867–887 (1991)
Mujica, J.: Linearization of holomorphic mappings of bounded type. In: Bierstedt, K.D., Bonet, J., Horvath, J., Maestre, M. (eds.) Progress in Functional Analysis (Peñíscola, 1990). North-Holland Mathematics Studies, vol. 170, pp. 149–162. North-Holland, Amsterdam (1992)
Mujica, J.: Holomorphic functions on Banach spaces. Note Mat. 25(2), 113–138 (2005/2006)
Pellegrino, D.: Strongly almost summing holomorphic mappings. J. Math. Anal. Appl. 287(1), 244–252 (2003)
Pellegrino, D., Rueda, P., Sánchez-Pérez, E.A.: Surveying the spirit of absolute summability on multilinear operators and homogeneous polynomials. Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Mat. RACSAM 110(1), 285–302 (2016)
Pellegrino, D., Santos, J., Seoane-Sepúlveda, J.B.: Some techniques on nonlinear analysis and applications. Adv. Math. 229(2), 1235–1265 (2012)
Pietsch, A.: Absolut \(p\)-summierende Abbildungenin normierten Räumen. Stud. Math. 28, 333–353 (1967)
Pietsch, A.: Ideals of multilinear functionals (designs of a theory). In: Proceedings of the Second International Conference on Operator Algebras, Ideals, and Their Applications in Theoretical Physics, Leipzig, 1983. Teubner-Texte Math., vol. 67, pp. 185–199. Teubner, Leipzig (1984)
Popa, D.: A note on the concept of factorable strongly p-summing operators. Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Mat. RACSAM 111(2), 465–471 (2017)
Rueda, P., Sánchez Pérez, E.A.: Factorization of p-dominated polynomials through \(L_p\)-spaces. Mich. Math. J. 63(2), 345–353 (2014)
Ryan, R.A.: Introduction to Tensor Products of Banach Spaces. Springer Monographs in Mathematics, Springer, Berlin (2002)
Saadi, K.: Some properties for Lipschitz strongly \(p\)-summing operators. J. Math. Anal. Appl. 423, 1410–1426 (2015)
Yahi, R., Achour, D., Rueda, P.: Absolutely summing Lipschitz conjugates. Mediterr. J. Math. 13(4), 1949–1961 (2016)
Acknowledgements
The authors would like to thank the referees for their valuable comments that have improved considerably this paper. Research of A. Jiménez-Vargas was partially supported by project UAL-FEDER grant UAL2020-FQM-B1858, by Junta de Andalucía grants P20\(\_\)00255 and FQM194, and by grant PID2021-122126NB-C31 funded by MCIN/AEI/10.13039/501100011033 and by “ERDF A way of making Europe”. J. M. Sepulcre was also supported by PGC2018-097960-B-C22 (MCIU/AEI/ERDF, UE).
Funding
Open Access funding provided thanks to the CRUE-CSIC agreement with Springer Nature.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Jari Taskinen.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Jiménez-Vargas, A., Saadi, K. & Sepulcre, J.M. Cohen strongly p-summing holomorphic mappings on Banach spaces. Banach J. Math. Anal. 17, 44 (2023). https://doi.org/10.1007/s43037-023-00269-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s43037-023-00269-y



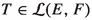 such that
such that 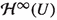 is isometrically isomorphic to
is isometrically isomorphic to 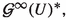 via the evaluation mapping
via the evaluation mapping 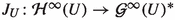 given by
given by 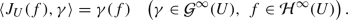
 defined by
defined by 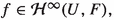 there exists a unique operator
there exists a unique operator 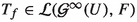 such that
such that 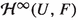 onto
onto 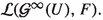
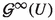 consists of all functionals
consists of all functionals 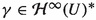 of the form
of the form 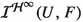 is a linear subspace of
is a linear subspace of 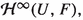
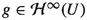 and
and 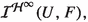
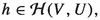
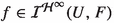 and
and 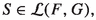 then
then 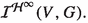
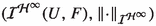 is a normed (Banach) space with
is a normed (Banach) space with 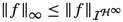 for all
for all 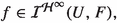
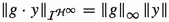 for every
for every 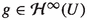 and
and 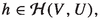
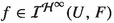 and
and 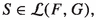 then
then 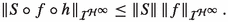
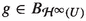 and
and 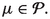
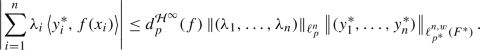
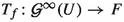 is strongly p-summing.
is strongly p-summing.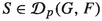 such that
such that 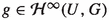 and
and 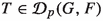 so that
so that 